Журнал вычислительной математики и математической физики, 2022, T. 62, № 12, стр. 2077-2088
Об аналитическом продолжении конформного отображения кругового треугольника
1 ФИЦ ИУ РАН
119333 Москва, ул. Вавилова, 40, Россия
* E-mail: spikulin@gmail.com
Поступила в редакцию 13.05.2022
После доработки 17.06.2022
Принята к публикации 07.07.2022
- EDN: ULZXCV
- DOI: 10.31857/S0044466922120110
Аннотация
Показано, что конформное отображение на полуплоскость кругового треугольника, имеющего один нулевой угол в бесконечно удаленной точке и два равных между собой ненулевых угла, может быть продолжено в полуполосу на основании принципа симметрии Римана–Шварца. Задача об аналитическом продолжении такого отображения возникает в качестве вспомогательной при построении конформного отображения $L$-образной области на полуплоскость. Библ. 6. Фиг. 2.
1. ВВЕДЕНИЕ
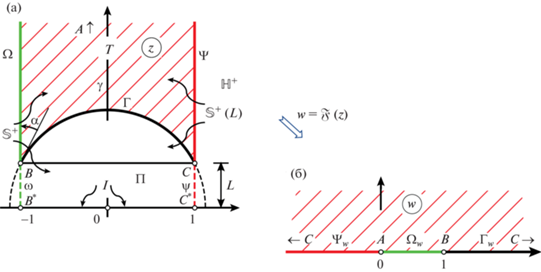
Рассмотрим конформное отображение кругового треугольника $T$, изображенного на фиг. 1а (треугольник $T$ заштрихован) на полуплоскость, осуществляемое аналитической функцией
которая переводит вершины $A,\;B,\;C$ в точки $0,1,\infty $ соответственно. Такое отображение существует и определено однозначно (см. [1], т. 2, гл. 1, § 2).Возможно ли аналитически продолжить отображение (1) через граничную дугу  треугольника $T$ в полуполосу, ограниченную прямолинейным отрезком $BC$? В этом заключается один из вопросов, возникающих при построении конформного отображения
$L$-образного многоугольника на полуплоскость (см. [2]–[5]). Положительный ответ на этот вопрос дает теорема 1 настоящей работы.
треугольника $T$ в полуполосу, ограниченную прямолинейным отрезком $BC$? В этом заключается один из вопросов, возникающих при построении конформного отображения
$L$-образного многоугольника на полуплоскость (см. [2]–[5]). Положительный ответ на этот вопрос дает теорема 1 настоящей работы.
Треугольник $T$$z \in \mathbb{C}$ обладает осевой симметрией относительно вертикальной полуоси $\gamma $, имеет нулевой угол при вершине $A$, расположенной в бесконечности, углы треугольника при вершинах $B$ и $C$ одинаковы и равны $\alpha \in (0,\pi {\text{/}}2)$. Введем для сторон этого треугольника следующие обозначения:
где $\Omega $ и $\Psi $ являются вертикальными лучами, центр дуги $\Gamma $ расположен в начале координат, которое будем обозначать через $O$. Вершины $B$ и $C$ имеют комплексные координаты $ - 1 + iL$ и $1 + iL$ соответственно, где $L = \operatorname{tg} \alpha $. Введем следующие обозначения для полуполосы и полуплоскости:Теорема 1. Функция (1) может быть аналитически продолжена в полуполосу ${{\mathbb{S}}^{ + }}(L)$.
Доказательство теоремы 1 дано разд. 2.
Обозначим через $B{\kern 1pt} *$ точку $z = - 1$ и через $C{\kern 1pt} *$ – точку $z = + 1$, а также введем обозначения для замкнутого прямоугольника $BB{\kern 1pt} *{\kern 1pt} C{\kern 1pt} *{\kern 1pt} C$ и его сторон:
(3)
$\Pi : = \{ \operatorname{Re} z \in [ - 1,1],\;\operatorname{Im} z \in [0,L]\} ,\quad I: = B{\kern 1pt} *{\kern 1pt} C{\kern 1pt} *,\quad \omega : = BB{\kern 1pt} *,\quad \psi : = CC{\kern 1pt} *.$Внутренность плоской фигуры $X \subset \mathbb{C}$ будем обозначать через ${\text{int}}\,X$, дугу $\lambda $ без концевых точек – через $\operatorname{int} \lambda $. Через ${{X}^{\lambda }}$ обозначим образ фигуры $X$ под действием круговой симметрии (инверсии) относительно окружности, содержащей дугу $\lambda $.
2. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ ПО ПРИНЦИПУ СИММЕТРИИ
2.1. Правильные круговые триангуляции
В качестве основного инструмента аналитического продолжения функции $\mathcal{F}(z)$ будем применять принцип симметрии Римана–Шварца (см. [6, ч. 3, гл. 4, § 5]), пользуясь тем, что стороны $\Omega ,\;\Gamma ,\;\Psi $ треугольника $T$ переходят в соответствующие промежутки вещественной оси ${{\Omega }_{w}}: = (0,1),$ ${{\Gamma }_{w}}: = (1, + \infty )$ и ${{\Psi }_{w}}: = ( - \infty ,0)$.
Введем следующее понятие.
Определение 1. Правильной круговой триангуляцией односвязной непустой области $\mathcal{D} \subset \mathbb{C}$ назовем тройку $(\mathcal{D},\Delta ,\Lambda )$, где $\Delta $ – конечное или счетное множество круговых треугольников, $\Lambda $ – конечное или счетное (возможно, пустое) множество круговых дуг, являющихся сторонами треугольников из $\Delta $, если выполнены следующие условия:
$1)$ различные треугольники ${{P}_{1}},{{P}_{2}} \in \Delta $ не пересекаются во внутренних точках:
$2)$ каждая дуга $\lambda \in \Lambda $ является стороной ровно двух треугольников из $\Delta $, причем эти треугольники симметричны друг другу относительно $\lambda $;
$3)$ треугольники из $\Delta $ и дуги из $\Lambda $ в совокупности исчерпывают область $\mathcal{D}$:
(5)
$\mathcal{D} = \bigcup\limits_{P \in \Delta } {\operatorname{int} P} \cup \bigcup\limits_{\lambda \in \Lambda } {\operatorname{int} \lambda } .$Подчеркнем, что множество дуг $\Lambda $, фигурирующее в определении 1, не обязательно совпадает со множеством всех граничных дуг треугольников из $\Delta $, но лишь является его подмножеством. В $\Lambda $ не входят дуги, лежащие на границе области $\mathcal{D}$.
Лемма 1. Если для некоторой правильной круговой триангуляции $\mathfrak{D} = (\mathcal{D},\Delta ,\Lambda )$ справедливо включение $T \in \Delta $, то функция (1) аналитически продолжается в область $\mathcal{D}$.
Доказательство. Введем в рассмотрение правильную круговую триангуляцию ${{\mathfrak{D}}_{1}} = ({{\mathcal{D}}_{1}},{{\Delta }_{1}},{{\Lambda }_{1}})$, отнеся к множеству ${{\Delta }_{1}}$ треугольник $T$ и все такие треугольники $P \in \Delta $, которые можно связать с $T$ цепочкой элементов из $\Delta $, имеющей конечную длину:
где каждые два соседних треугольника граничат по некоторой общей дуге ${{\lambda }_{j}} \in \Lambda $ и, следовательно, симметричны друг другу относительно ${{\lambda }_{j}}$. Все такие дуги по всевозможным цепочкам вида (6) отнесем ко множеству ${{\Lambda }_{1}}$. Покажем, что ${{\mathfrak{D}}_{1}} = \mathfrak{D}$.Рассмотрим дугу $\lambda $ из $\Lambda {{\backslash }}{{\Lambda }_{1}}$ и покажем, что она не может являться стороной какого-либо треугольника $P \in {{\Delta }_{1}}$. В самом деле, в противном случае существовала бы цепочка
вида (6), где последние два треугольника соединены через дугу $\lambda $, тогда ${{P}^{\lambda }} \in {{\Delta }_{1}}$ и $\lambda \in {{\Lambda }_{1}}$, что противоречит сделанному предположению. Следовательно, $\lambda $ является общей стороной двух треугольников из $\Delta {{\backslash }}{{\Delta }_{1}}$, и, значит, множество ${{\mathcal{D}}_{2}}: = \mathcal{D}{{\backslash }}{{\mathcal{D}}_{1}}$ является открытым, т.е. содержащим вместе с каждой своей точкой и некоторую ее окрестность. Но поскольку область $\mathcal{D}$ по определению связна, то она не может являться объединением двух непересекающихся открытых множеств, следовательно, ${{\mathcal{D}}_{2}} = \not {0}$, и $\mathcal{D} = {{\mathcal{D}}_{1}}$. Таким образом, для каждого треугольника $P \in \Delta $ существует цепочка вида (6).Далее покажем от противного, что для каждого $P \in \Delta $ существует единственная цепочка (6), состоящая из попарно различных треугольников. Предположим, что для некоторого треугольника $P \in \Delta $ найдется две такие цепочки, отличные друг от друга:
(7)
$Q,\;\;{{T}_{{m + 1}}},\;\; \ldots ,\;\;{{T}_{{{{n}_{1}} - 1}}},\;\;{{T}_{{{{n}_{1}}}}} = P = T_{{{{n}_{2}}}}^{'},\;\;T_{{{{n}_{2}} - 1}}^{'},\;\; \ldots ,\;\;T_{{m + 1}}^{'},\;\;Q,$Проведем замкнутый жорданов контур через область, объединяющую треугольники построенной циклической цепочки и их общие стороны, таким образом, чтобы путь однократно пересекал по внутренней точке каждую из граничных дуг, разделяющих пары соседних треугольников. Тогда этот контур, во-первых, лежит целиком внутри области $\mathcal{D}$, а во-вторых, заключает внутри себя по крайней мере одну вершину треугольника $Q$. Но вершины треугольников из $\Delta $ не лежат внутри области $\mathcal{D}$ согласно определению 1, – получаем противоречие с условием односвязности $\mathcal{D}$. Таким образом, цепочка попарно различных треугольников (6) для каждого $P \in \Delta $ определена однозначно.
С помощью индукции по длине цепочки устанавливаем, что функция $\mathcal{F}(z)$ допускает аналитическое продолжение по принципу симметрии в каждый из треугольников $P \in \Delta $, через какую-либо из его сторон ${{\lambda }_{P}} \in \Lambda $, при этом каждая граничная дуга такого треугольника переходит в один из трех прямолинейных участков вещественной оси – ${{\Omega }_{w}},{{\Psi }_{w}}$ либо ${{\Gamma }_{w}}$. Лемма доказана.
Определение 2. Правильные круговые триангуляции ${{\mathfrak{D}}_{1}}$ и ${{\mathfrak{D}}_{2}}$ двух не пересекающихся областей,
(8)
${{\mathfrak{D}}_{1}} = ({{\mathcal{D}}_{1}},{{\Delta }_{1}},{{\Lambda }_{1}}),\quad {{\mathfrak{D}}_{2}} = ({{\mathcal{D}}_{2}},{{\Delta }_{2}},{{\Lambda }_{2}}),\quad {{\mathcal{D}}_{1}} \cap {{\mathcal{D}}_{2}} = \not {0},$(9)
${{\mathcal{D}}_{1}}\,{{\# }_{\lambda }}\,{{\mathcal{D}}_{2}}: = ({{\mathcal{D}}_{3}},{{\Delta }_{3}},{{\Lambda }_{3}}),\quad {{\mathcal{D}}_{3}} = {{\mathcal{D}}_{1}} \cup {{\mathcal{D}}_{2}} \cup \lambda ,\quad {{\Delta }_{3}} = {{\Delta }_{1}} \cup {{\Delta }_{2}},\quad {{\Lambda }_{3}} = {{\Lambda }_{1}} \cup {{\Lambda }_{2}} \cup \{ \lambda \} ,$Предложение 1. Правильные круговые триангуляции (8) не пересекающихся областей являются смежными по дуге $\lambda $ тогда и только тогда, когда найдется пара треугольников ${{P}_{1}} \in {{\Delta }_{1}}$, ${{P}_{2}} \in {{\Delta }_{2}}$, для которых $\lambda $ является общей стороной и которые симметричны друг другу относительно $\lambda $.
Доказательство. Если найдется пара треугольников ${{P}_{1}} \in {{\Delta }_{1}}$, ${{P}_{2}} \in {{\Delta }_{2}}$, симметричных друг другу относительно их общей стороны $\lambda $, то справедливость условий определения 1 для тройки (9) проверяется непосредственно.
Обратно, предположим, что тройка (9) представляет собой правильную круговую триангуляцию. Тогда найдутся треугольники ${{P}_{1}},{{P}_{2}} \in {{\Delta }_{3}}$, для которых $\lambda $ является их общей стороной, причем они симметричны друг другу относительно $\lambda $. Если при этом оба треугольника ${{P}_{1}},\;{{P}_{2}}$ принадлежат ${{\Delta }_{1}}$, то, во-первых, множество ${{\mathcal{D}}_{1}} \cup \operatorname{int} \lambda $ является открытым, и, во-вторых, $\lambda $ не пересекается с ${{\mathcal{D}}_{2}}$. Тогда множество ${{\mathcal{D}}_{3}}$ распадается в объединение непустых непересекающихся открытых множеств ${{\mathcal{D}}_{1}} \cup \operatorname{int} \lambda $ и ${{\mathcal{D}}_{2}}$, что противоречит требованию его связности. Следовательно, ${{P}_{1}} \in {{\Delta }_{1}}$, ${{P}_{2}} \in {{\Delta }_{2}}$. Предложение доказано.
Отметим, что всякое круговое преобразование, в том числе, симметрия относительно круговой дуги, а также любое евклидово движение плоскости $\mathbb{C}$, переводит правильную круговую триангуляцию также в правильную круговую триангуляцию.
Пусть $\mathfrak{D} = (\mathcal{D},\Delta ,\Lambda )$ – некоторая правильная круговая триангуляция, содержащая треугольник $T$, область $\mathcal{D}$ которой лежит в полуполосе ${{\mathbb{S}}^{ + }}$, т.е.
Рассмотрим образы $\mathfrak{D}$ под действием преобразований ${{S}^{n}}$ параллельного переноса вдоль горизонтальной оси на расстояние, кратное ширине полуполосы:(11)
$\begin{gathered} {{S}^{n}}:z \mapsto z + 2n,\quad z \in \mathbb{C},\quad n \in \mathbb{Z}, \\ {{\mathfrak{D}}^{n}}: = ({{\mathcal{D}}^{n}},{{\Delta }^{n}},{{\Lambda }^{n}}),\quad {{\mathcal{D}}^{n}} = {{S}^{n}}\mathcal{D},\quad {{\Delta }^{n}} = {{S}^{n}}\Delta ,\quad {{\Lambda }^{n}} = {{S}^{n}}\Lambda . \\ \end{gathered} $Подчеркнем, что наличие $2$-периодической структуры в геометрическом расположении круговых треугольников триангуляции
(12) не означает, что также и функция $\mathcal{F}(z)$, аналитически продолженная в область  в соответствии с леммой 1, окажется $2$-периодичной, поскольку дуги $\Omega $ и $\Psi $ переходят в различные промежутки вещественной оси плоскости $w$. Однако поскольку точки
в соответствии с леммой 1, окажется $2$-периодичной, поскольку дуги $\Omega $ и $\Psi $ переходят в различные промежутки вещественной оси плоскости $w$. Однако поскольку точки  получаются друг из друга композицией двух отражений относительно находящихся между
ними вертикальных лучей ${{\Phi }^{j}},\;{{\Phi }^{{j + 1}}}$, образ каждого из которых под действием $\mathcal{F}(z)$ является промежутком вещественной прямой, то по принципу симметрии и в силу единственности
аналитического продолжения в односвязную область имеем $\mathcal{F}(z) = \mathcal{F}(z + 4)$, т.е. функция $\mathcal{F}(z)$ является периодической в
получаются друг из друга композицией двух отражений относительно находящихся между
ними вертикальных лучей ${{\Phi }^{j}},\;{{\Phi }^{{j + 1}}}$, образ каждого из которых под действием $\mathcal{F}(z)$ является промежутком вещественной прямой, то по принципу симметрии и в силу единственности
аналитического продолжения в односвязную область имеем $\mathcal{F}(z) = \mathcal{F}(z + 4)$, т.е. функция $\mathcal{F}(z)$ является периодической в  с периодом $4$.
с периодом $4$.
Определение 3. Правильные круговые триангуляции ${{\mathfrak{D}}_{1}} = ({{\mathcal{D}}_{1}},{{\Delta }_{1}},{{\Lambda }_{1}})$ и ${{\mathfrak{D}}_{2}} = ({{\mathcal{D}}_{2}},{{\Delta }_{2}},{{\Lambda }_{2}})$ назовем совместимыми, если их объединение, заданное равенством
(13)
${{\mathfrak{D}}_{1}} \cup {{\mathfrak{D}}_{2}}: = ({{\mathcal{D}}_{1}} \cup {{\mathcal{D}}_{2}},{{\Delta }_{1}} \cup {{\Delta }_{2}},{{\Lambda }_{1}} \cup {{\Lambda }_{2}}),$По аналогии с объединением (13) определим пересечение ${{\mathfrak{D}}_{1}} \cap {{\mathfrak{D}}_{2}}$ правильных круговых триангуляций, а также отношение включения $ \subset $. Если ${{\mathfrak{D}}_{1}} \subset {{\mathfrak{D}}_{2}}$, то справедливы равенства
Предложение 2. Если заданы правильные круговые триангуляции ${{\mathfrak{D}}_{1}} = ({{\mathcal{D}}_{1}},{{\Delta }_{1}},{{\Lambda }_{1}})$ и ${{\mathfrak{D}}_{2}} = ({{\mathcal{D}}_{2}},{{\Delta }_{2}},{{\Lambda }_{2}})$ пересекающихся областей ${{\mathcal{D}}_{1}}$ и ${{\mathcal{D}}_{2}}$,
при этом пересечение(15)
${{\mathfrak{D}}_{1}} \cap {{\mathfrak{D}}_{2}}: = ({{\mathcal{D}}_{1}} \cap {{\mathcal{D}}_{2}},\;{{\Delta }_{1}} \cap {{\Delta }_{2}},\;{{\Lambda }_{1}} \cap {{\Lambda }_{2}})$Доказательство. Поскольку пересечение областей ${{\mathcal{D}}_{1}} \cap {{\mathcal{D}}_{2}}$ обладает правильной круговой триангуляцией (15), то по определению 1 является односвязной областью. Из этого и из условия (14) следует, что объединение ${{\mathfrak{D}}_{1}} \cup {{\mathfrak{D}}_{2}}$ также является односвязной областью.
Предположим, что найдутся два различных треугольника ${{P}_{1}},{{P}_{2}} \in {{\Delta }_{1}} \cup {{\Delta }_{2}}$, пересекающихся по внутренней точке $z \in \operatorname{int} {{P}_{1}} \cap \operatorname{int} {{P}_{2}}$. Тогда ${{P}_{1}} \in {{\Delta }_{1}},$ ${{P}_{2}} \in {{\Delta }_{2}}$, так как ${{\mathfrak{D}}_{1}}$ и ${{\mathfrak{D}}_{2}}$ являются правильными триангуляциями. Поскольку (15) также является правильной триангуляцией, то точка $z$ является внутренней для некоторого элемента – треугольника или дуги, принадлежащего одновременно и к ${{\mathfrak{D}}_{1}}$, и к ${{\mathfrak{D}}_{2}}$, причем этот элемент должен совпадать одновременно и с ${{P}_{1}}$, и с ${{P}_{2}}$, так как в правильной круговой триангуляции каждая точка области принадлежит одному и только одному элементу триангуляции (дуге или треугольнику). Полученное противоречие показывает, что условие (4) выполнено для тройки (13).
Справедливость остальных требований определения 1 для тройки (13) следует из условий предложения непосредственно. Предложение 2 доказано.
2.2. Построение области аналитичности функции $\mathcal{F}(z)$
Перейдем к построению односвязной области $\mathcal{N}$, содержащей полуполосу ${{\mathbb{S}}^{ + }}(L)$ и допускающей аналитическое продолжение функции $\mathcal{F}(z)$. Для этого мы укажем правильную круговую триангуляцию $\mathfrak{N} = (\mathcal{N},\Delta ,\Lambda )$ вида (10), т.е.
(16)
$T \subset {{\mathbb{S}}^{ + }}(L) \subset \mathcal{N} \subset {{\mathbb{S}}^{ + }},\quad T \in \Delta ,$Присоединим к треугольнику $T$ в составе минимальной содержащей его триангуляции $\mathfrak{T}: = (T,\{ T\} ,\not {0})$ смежную с ней по дуге $\Gamma $ триангуляцию ${{\mathfrak{T}}^{\Gamma }} = ({{T}^{\Gamma }},\{ {{T}^{\Gamma }}\} ,\not {0})$, область которой суть симметричный $T$ относительно $\Gamma $ круговой треугольник ${{T}^{\Gamma }} = BCO$. В результате объединения получим область в виде кругового четырехугольника $W$, снабженную правильной круговой триангуляцией
(17)
$\mathfrak{W} = (W,\{ T,{{T}^{\Gamma }}\} ,\{ \Gamma \} ),\quad W: = \operatorname{int} T \cup \operatorname{int} \Gamma \cup \operatorname{int} {{T}^{\Gamma }}.$Четырехугольник $W$ имеет нулевые углы при вершинах $A$ и $O$, и углы $2\alpha \in (0,\pi )$ при верши-нах $B$ и $C$. Если значение $\alpha $ принадлежит диапазону $\alpha \in [\pi {\text{/}}4,\pi {\text{/}}2)$, то область $W$ содержит полуполосу ${{\mathbb{S}}^{ + }}(L)$, т.е. триангуляция (17) удовлетворяет условию (16), и теорема в этом случае доказана.
Рассмотрим теперь дополнительный промежуток значений угла $\alpha $, т.е. $\alpha \in (0,\pi {\text{/}}4).$ Присоединим к триангуляции (17) смежную с ней по стороне ${{\Omega }_{0}}: = {{\Omega }^{\Gamma }}$ (см. фиг. 2) четырехугольника $W$ триангуляцию
затем к результату присоединим триангуляцию ${{\mathfrak{W}}_{2}}(B)$, смежную с ${{\mathfrak{W}}_{1}}(B)$ по дуге ${{\Omega }_{1}}: = {{\Omega }^{{{{\Omega }_{0}}}}}$ и т.д. – проделаем эту операцию $N$ раз, где(18)
${{\mathfrak{W}}_{j}}(B) = ({{W}_{j}}(B),\;\{ {{T}_{j}}(B),\;T_{j}^{\Gamma }(B)\} ,\;\{ {{\Gamma }_{j}}(B)\} ),\quad {{W}_{j}}(B): = {{W}^{{{{\Omega }_{0}} \ldots {{\Omega }_{{j - 1}}}}}},$(19)
${{T}_{j}}(B): = {{T}^{{{{\Omega }_{0}}{\kern 1pt} \ldots {\kern 1pt} {{\Omega }_{{j - 1}}}}}},\quad T_{j}^{\Gamma }(B): = {{T}^{{\Gamma {\kern 1pt} {{\Omega }_{0}}{\kern 1pt} \ldots {\kern 1pt} {{\Omega }_{{j - 1}}}}}},\quad {{\Gamma }_{j}}(B): = {{\Gamma }^{{{{\Omega }_{0}}{\kern 1pt} \ldots {\kern 1pt} {{\Omega }_{{j - 1}}}}}}.$Фиг. 2.
Объединение кругового многоугольника ${{\mathcal{N}}_{0}}$, системы полукругов $K({{\Xi }_{0}})$ и замкнутого множества ${{X}_{0}}$ содержит полуполосу ${{\mathbb{S}}^{ + }}$.
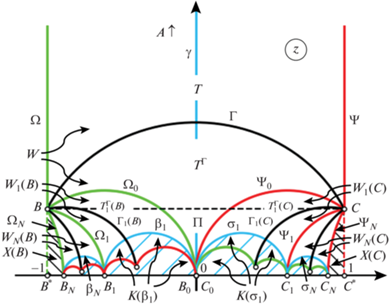
По аналогии с триангуляциями четырехугольников (18) построим серию из $N$ триангуляций ${{\mathfrak{W}}_{j}}(C)$ четырехугольных областей ${{W}_{j}}(C)$, имеющих на границе общую вершину $C$ и получаемых из $\mathfrak{W}$ последовательными отражениями относительно дуг
образующих прямые углы с вещественной осью в концевых точках ${{C}_{j}} \in I,$ $j = 0,1, \ldots ,N$. Элементы триангуляций ${{\mathfrak{W}}_{j}}(C)$ находятся по формулам, аналогичным (19), с заменой $B$ на $C$ и $\Omega $ на $\Psi $.Триангуляции ${{\mathfrak{W}}_{j}}(B)$, $\mathfrak{W}$, ${{\mathfrak{W}}_{j}}(C)$ по построению являются смежными по граничным дугам ${{\Omega }_{j}},\;{{\Psi }_{j}}$. Соединяя их, получим симметричную относительно вертикальной оси правильную круговую триангуляцию
(20)
${{\mathfrak{N}}_{0}} = ({{\mathcal{N}}_{0}},{{\Delta }_{0}},{{\Lambda }_{0}}): = {{\mathfrak{W}}_{N}}(B)\,{{\# }_{{{{\Omega }_{{N - 1}}}}}}\, \cdots \,{{\# }_{{{{\Omega }_{1}}}}}\,{{\mathfrak{W}}_{1}}(B)\,{{\# }_{{{{\Omega }_{0}}}}}\,\mathfrak{W}\,{{\# }_{{{{\Psi }_{0}}}}}\,{{\mathfrak{W}}_{1}}(C)\,{{\# }_{{{{\Psi }_{1}}}}}\, \cdots \,{{\# }_{{{{\Psi }_{{N - 1}}}}}}\,{{\mathfrak{W}}_{N}}(C),$Вертикальная полуось $\gamma = OA$ соединяет вершины двух нулевых углов четырехугольника $W$, лежит внутри него, $\operatorname{int} \gamma \subset \operatorname{int} W$, и служит осью симметрии как для самой области $W$, так и для содержащихся в ней треугольников $T,{{T}^{\Gamma }} \in {{\Delta }_{0}}$ и их общей стороны $\Gamma $.
Поскольку триангуляция ${{\mathfrak{W}}_{j}}(B)$ получена из $\mathfrak{W}$ композицией последовательных круговых симметрий относительно дуг ${{\Omega }_{0}}, \ldots ,{{\Omega }_{{j - 1}}}$, то составляющие ее элементы (19) и область ${{W}_{j}}(B)$ также обладают общей осью симметрии
Открытый полукруг, стягиваемого полуокружностью $\xi $, обозначим через $K(\xi )$, а также введем обозначение
для объединения таких полукругов по некоторому множеству $\Xi $ полуокружностей.Также отметим, что полукруг $K({{\beta }_{j}})$ имеет непустое пересечение с треугольниками ${{T}_{j}}(B)$ и $T_{j}^{\Gamma }(B)$, но с другими треугольниками из множества ${{\Delta }_{0}}$ не пересекается. Введем в связи с этим следующее понятие.
Определение 4. Полуокружность $\xi $ назовем совместимой с правильной круговой триангуляцией $\mathfrak{D} = (\mathcal{D},\Delta ,\Lambda )$ области $\mathcal{D} \subset {{\mathbb{H}}^{ + }}$, если $\xi $ опирается на некоторый интервал $D(\xi )$ вещественной оси как на диаметр, стягиваемый ею полукруг $K(\xi )$ пересекает ровно два треугольника
граничащих по некоторой дуге $\lambda (\xi ) \in \Lambda $, при этом дуга $\xi $ полностью содержится в четырехугольной области(22)
$W(\xi ): = (\operatorname{int} P(\xi ) \cup \operatorname{int} P{{(\xi )}^{{\lambda (\xi )}}} \cup \operatorname{int} \lambda (\xi )) \supset \operatorname{int} \xi $Проведенные выше построения показывают, что полуокружности ${{\beta }_{j}}$, $j = 1,2, \ldots ,N$, являются совместимыми с правильной круговой триангуляцией ${{\mathfrak{N}}_{0}}$. По аналогии с ${{\beta }_{j}}$ построим полуокружности
Отметим, что различные интервалы $({{B}_{{j - 1}}}{{B}_{j}})$, $({{C}_{{k - 1}}}{{C}_{k}})$ попарно не пересекаются между собой, как и построенные на них как на диаметрах открытые полукруги $K({{\beta }_{j}}),\;K({{\sigma }_{k}})$.
Определение 5. Множество $\Xi $ полуокружностей назовем совместимым с правильной круговой триангуляцией $\mathfrak{D} = (\mathcal{D},\Delta ,\Lambda )$, $\mathcal{D} \subset {{\mathbb{H}}^{ + }}$, если, во-первых, каждая дуга $\xi \in \Xi $ совместима с $\mathfrak{D}$ в смысле определения $4$ и, во-вторых, стягиваемые этими дугами полукруги $K(\xi )$ или, что эквивалентно, их диаметры $D(\xi )$, являющиеся интервалами вещественной оси, попарно не пересекаются между собой во внутренних точках.
Таким образом, система полуокружностей
(23)
${{\Xi }_{0}}: = \{ {{\beta }_{1}},{\kern 1pt} \ldots ,{{\beta }_{N}},{{\sigma }_{1}},{\kern 1pt} \ldots ,{{\sigma }_{N}}\} $Отметим, что любое подмножество набора полуокружностей $\Xi $, удовлетворяющего определению 5, также является совместимым с триангуляцией $\mathfrak{D}$. Кроме того, если концы всех дуг $\xi \in \Xi $ лежат на отрезке $I$ вещественной прямой, то их попарно не пересекающиеся диаметры $D(\xi )$ лежат внутри $I$, следовательно,
где $\operatorname{diam} (\xi )$ – диаметр дуги $\xi $, ${\text{|}}I{\kern 1pt} {\text{|}}$ – длина отрезка $I$. Cвойством (24) по построению обладает набор полуокружностей (23).Лемма 2. Пусть ${{\mathfrak{D}}_{1}} = ({{\mathcal{D}}_{1}},{{\Delta }_{1}},{{\Lambda }_{1}}),$ ${{\mathfrak{D}}_{2}} = ({{\mathcal{D}}_{2}},{{\Delta }_{2}},{{\Lambda }_{2}})$ – правильные круговые триангуляции областей ${{\mathcal{D}}_{1}},{{\mathcal{D}}_{2}} \subset {{\mathbb{H}}^{ + }}$, совместимые между собой, ${{\Xi }_{1}},\;{{\Xi }_{2}}$ – два набора полуокружностей, причем множество ${{\Xi }_{j}}$ является совместимым с триангуляцией ${{\mathfrak{D}}_{j}}$, $j = 1,2$, и пусть $\nu \in {{\Xi }_{1}} \cap {{\Xi }_{2}}$ – общая дуга этих наборов. Тогда
$1)$ триангуляции ${{\mathfrak{D}}_{1}}$ и ${{({{\mathfrak{D}}_{2}})}^{\nu }}$ являются совместимыми;
$2)$ множество дуг
является совместимым с объединенной триангуляцией ${{\mathfrak{D}}_{3}}: = {{\mathfrak{D}}_{1}} \cup {{({{\mathfrak{D}}_{2}})}^{\nu }}$;$3)$ справедливо неравенство
(26)
$\mathop {\sup }\limits_{\xi \in {{{({{\Xi }_{2}})}}^{\nu }}} \operatorname{diam} (\xi ) \leqslant \frac{1}{2}\operatorname{diam} (\nu ).$Доказательство. Согласно определению 4 найдется пара симметричных друг другу относительно общей стороны ${{\lambda }^{{(1)}}} \in {{\Lambda }_{1}}$ треугольников $P_{1}^{{(1)}},P_{2}^{{(1)}} \in {{\Delta }_{1}}$, для которых полуокружность $\nu $ является общей осью симметрии и содержится внутри соответствующего четырехугольника (22), который обозначим через $W$. Существуют также треугольники $P_{1}^{{(2)}},P_{2}^{{(2)}} \in {{\Delta }_{2}}$ и дуга ${{\lambda }^{{(2)}}} \in {{\Lambda }_{2}}$ с аналогичными свойствами.
Триангуляции ${{\mathfrak{D}}_{1}}$ и ${{\mathfrak{D}}_{2}}$ совместимы, следовательно, формулой (13) определена объединенная правильная круговая триангуляция ${{\mathfrak{D}}_{1}} \cup {{\mathfrak{D}}_{2}}$. В силу представления (5) и условия (4), если два элемента триангуляции пересекаются по внутренней точке, то они совпадают. В данном случае элементы $P_{k}^{{(1)}},\;\lambda _{k}^{{(1)}}$ пересекаются с элементами $P_{k}^{{(2)}},\lambda _{k}^{{(2)}}$, $k = 1,2$, по точкам дуги $\nu $. Отсюда следует совпадение (с точностью до переобозначений) треугольников и дуг:
Множество ${{\mathcal{D}}_{1}}{{\backslash }}W$ лежит целиком снаружи полукруга $K(\nu )$ согласно определению 4, а множество ${{({{\mathcal{D}}_{2}})}^{\nu }}{{\backslash }}W = ({{\mathcal{D}}_{2}}{{\backslash }}W{{)}^{\nu }}$ лежит целиком внутри $K(\nu )$, т.е. эти множества не пересекаются. Таким образом, определено непустое пересечение правильных круговых триангуляций
и согласно предложению 2 триангуляции ${{\mathfrak{D}}_{1}}$ и ${{({{\mathfrak{D}}_{2}})}^{\nu }}$ являются совместимыми. Пункт 1 леммы доказан.Семейство полуокружностей (25) состоит из двух не пересекающихся частей: во-первых, из множества ${{\Xi }_{1}}{{\backslash }}\{ \nu \} $, совместимого с ${{\mathfrak{D}}_{1}}$ и лежащего за пределами полукруга $K(\nu )$, во-вторых, из множества
Диаметр $D(\xi )$ полуокружности $\xi \in {{\Xi }_{2}}$ как интервал вещественной прямой не пересекается с интервалом $D(\nu )$ по условию леммы. При инверсии относительно $\nu $ дуга $\xi $ переходит в другую полуокружность ${{\xi }^{{{\kern 1pt} \nu }}}$, диаметр которой $D({{\xi }^{{{\kern 1pt} \nu }}})$ расположен на отрезке, соединяющем центр $\nu $ с соответствующим концом диаметра $D(\nu )$, т.е. на радиусе $\nu $. Из этого вытекает утверждение п. 3. Лемма 2 доказана.
Обозначим через $X(B)$ замкнутый круговой треугольник $BB{\kern 1pt} *{\kern 1pt} {{B}_{N}}$, ограниченный дугами $\omega ,\;{{\Omega }_{N}}$ и отрезком $B{\kern 1pt} *{\kern 1pt} {{B}_{N}}$ вещественной оси, а через $X(C)$ – аналогичный треугольник $CC{\kern 1pt} *{\kern 1pt} {{C}_{N}}$, ограниченный дугами $\psi ,\;{{\Psi }_{N}}$ и отрезком $C{\kern 1pt} *{\kern 1pt} {{C}_{N}}$. На фиг. 2 для этих треугольников дана штриховка с наклоном влево. Замкнутое множество
в совокупности с открытыми множествами ${{\mathcal{N}}_{0}}$ и $K({{\Xi }_{0}})$, не пересекаясь с ними, накрывает полуполосу ${{\mathbb{S}}^{ + }}$, т.е. справедливы следующие соотношения:Лемма 3. Существует последовательность троек
где ${{\mathfrak{N}}_{n}}$ – правильная круговая триангуляция вида (10)(30)
$K({{\Xi }_{n}}) \subset {{\mathbb{S}}^{ + }} \subset {{\mathcal{N}}_{n}} \cup K({{\Xi }_{n}}) \cup {{X}_{n}},$(32)
${{\mathfrak{N}}_{0}} \subset {{\mathfrak{N}}_{1}} \subset \cdots ,\quad {{X}_{0}} \subset {{X}_{1}} \subset \cdots \quad K({{\Xi }_{0}}) \supset K({{\Xi }_{1}}) \supset \cdots ,$(33)
$\mathop {\lim }\limits_{n \to \infty } \mathop {\max }\limits_{\xi \in {{\Xi }_{n}}} \operatorname{diam} (\xi ) = 0.$Доказательство. Будем строить последовательность (28), члены которой удовлетворяют свойствам (29)–(31), с помощью индукции. Базу индукции при $n = 0$ составляет тройка $({{\mathfrak{N}}_{0}},{{\Xi }_{0}},{{X}_{0}})$, определенная формулами (20), (23), (27).
Предположим, что тройка $({{\mathfrak{N}}_{n}},{{\Xi }_{n}},{{X}_{n}})$ построена для некоторого $n \geqslant 0$, построим тогда тройку $({{\mathfrak{N}}_{{n + 1}}},{{\Xi }_{{n + 1}}},{{X}_{{n + 1}}})$.
Поскольку триангуляция ${{\mathfrak{N}}_{n}}$ имеет вид (10), то существует ее периодическое продолжение 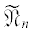 , определенное формулами (12). Определим также множество дуг ${{\widetilde \Xi }_{n}}$ и замкнутое множество ${{\widetilde X}_{n}} \subset \mathbb{C}$ формулами
, определенное формулами (12). Определим также множество дуг ${{\widetilde \Xi }_{n}}$ и замкнутое множество ${{\widetilde X}_{n}} \subset \mathbb{C}$ формулами
(34)
${{\widetilde \Xi }_{n}}: = \bigcup\limits_{j \in \mathbb{Z}} {{{S}^{j}}{\kern 1pt} {{\Xi }_{n}},} \quad {{\widetilde X}_{n}}: = \bigcup\limits_{j \in \mathbb{Z}} {{{S}^{j}}{{X}_{n}}} ,$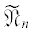 в смысле определения 5.
в смысле определения 5.
Значения диаметров дуг $\xi \in {{\Xi }_{n}}$ ограничены сверху, так как их сумма не превосходит длины отрезка $I$. Выберем полуокружность $\nu \in {{\Xi }_{n}} \subset {{\widetilde \Xi }_{n}}$, имеющую наибольший диаметр. Применяя лемму 2 к триангуляциям ${{\mathfrak{D}}_{1}} = {{\mathfrak{N}}_{n}}$ и  , а также к совместимым с ними множествам полуокружностей ${{\Xi }_{n}}$ и ${{\widetilde \Xi }_{n}}$ и их общей дуге $\nu $, получаем правильную круговую триангуляцию
, а также к совместимым с ними множествам полуокружностей ${{\Xi }_{n}}$ и ${{\widetilde \Xi }_{n}}$ и их общей дуге $\nu $, получаем правильную круговую триангуляцию
(37)
${{\Xi }_{{n + 1}}}: = {{\Xi }_{n}} \cup {{({{\widetilde \Xi }_{n}})}^{\nu }}{{\backslash }}\{ \nu \} .$При инверсии относительно окружности, имеющей центр на вещественной прямой, часть верхней полуплоскости, лежащая снаружи этой окружности, переходит в полукруг, заключенный между окружностью и вещественной осью. Ввиду этого и поскольку дуги из множества ${{\widetilde \Xi }_{n}}{{\backslash }}\{ \nu \} $ лежат за пределами полукруга $K(\nu )$, то множество
(39)
$K(({{\widetilde \Xi }_{n}}{{\backslash }}\{ \nu {{\} )}^{\nu }}) \subset K(\nu ) \subset {{\mathbb{S}}^{ + }},$Из включения (35) и из определения 4 следует, что
откуда, применяя симметрию относительно $\nu $, находим Согласно определениям (36)–(38) с учетом предположения (30) и включения (41) находим что вместе с формулой (40) доказывает свойство (30) для тройки (36)–(38).Осталось показать справедливость условий (31) для данных $(n + 1)$-го шага индукции.
Множество (38) состоит из двух частей: из множества ${{({{\widetilde X}_{n}})}^{\nu }}$, лежащего внутри полукруга $\overline {K(\nu )} $, и из множества ${{X}_{n}}$, лежащего снаружи. Область ${{\mathcal{N}}_{{n + 1}}}$, в свою очередь, состоит из трех частей: из кругового четырехугольника $W(\nu ) \supset \nu $, из множества  , лежащего внутри полукруга $\overline {K(\nu )} $, и из множества ${{\mathcal{N}}_{n}}{{\backslash }}W(\nu )$, лежащего вне этого полукруга.
, лежащего внутри полукруга $\overline {K(\nu )} $, и из множества ${{\mathcal{N}}_{n}}{{\backslash }}W(\nu )$, лежащего вне этого полукруга.
Четырехугольник $W(\nu )$ не пересекается с ${{X}_{n}}$ по предположению (31), так как $W(\nu ) \subset {{\mathcal{N}}_{n}}$, и также не пересекается с ${{\widetilde X}_{n}}$ по построению последнего. Поскольку этот четырехугольник симметричен относительно
$\nu $, то он также не пересекается и с ${{({{\widetilde X}_{n}})}^{\nu }}$. Множество  не пересекается с ${{({{\widetilde X}_{n}})}^{\nu }}$, так как
не пересекается с ${{({{\widetilde X}_{n}})}^{\nu }}$, так как 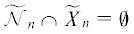 по построению периодического продолжения (11), (34) и по предположению (31). Наконец,
область ${{\mathcal{N}}_{n}}$ не пересекается с ${{X}_{n}}$ также по предположению (31). Следовательно, справедливо равенство ${{\mathcal{N}}_{{n + 1}}} \cap {{X}_{{n + 1}}} = \not {0}$.
по построению периодического продолжения (11), (34) и по предположению (31). Наконец,
область ${{\mathcal{N}}_{n}}$ не пересекается с ${{X}_{n}}$ также по предположению (31). Следовательно, справедливо равенство ${{\mathcal{N}}_{{n + 1}}} \cap {{X}_{{n + 1}}} = \not {0}$.
Объединение полукругов $K(({{\widetilde \Xi }_{n}}{{\backslash }}\{ \nu {{\} )}^{\nu }})$, лежащее внутри $K(\nu )$, не пересекается с ${{({{\widetilde X}_{n}})}^{\nu }}$, поскольку $K({{\widetilde \Xi }_{n}}) \cap {{\widetilde X}_{n}} = \not {0}$, и $K({{\widetilde \Xi }_{n}})$ не пересекается с ${{X}_{n}}$ по предположению (31). Следовательно, равенство $K({{\Xi }_{{n + 1}}}) \cap {{X}_{{n + 1}}} = \not {0}$ выполнено.
Таким образом, справедливость условий (31) для тройки (36)–(38) установлена, обоснование индуктивного перехода завершено, и последовательность (28) построена.
Выполнение свойств (32) этой последовательности следует из определений (36)–(38) и включения (39).
Проведем обоснование свойства (33). Обозначим через $({{\varepsilon }^{{(n)}}})$ упорядоченную по убыванию последовательность диаметров ${{(\operatorname{diam} (\xi ))}_{{\xi \in {{\Xi }_{n}}}}}$, тогда из неравенства (24) получаем
(42)
$\varepsilon _{1}^{{(n)}} \geqslant \varepsilon _{2}^{{(n)}} \geqslant \cdots ,\quad \sum\limits_{j = 1}^\infty \,\varepsilon _{j}^{{(n)}} < {\text{|}}I{\kern 1pt} {\text{|}} = 2.$В обозначениях леммы 3 положим
3. ЗАКЛЮЧЕНИЕ
Сформулируем некоторые следствия из теоремы 1, касающиеся области аналитичности функции (1).
Аналитически продолженная в полуполосу ${{\mathbb{S}}^{ + }}(L)$ функция $w = \mathcal{F}(z)$ отображает стороны $\Omega $ и $\Psi $ треугольника $T$ в промежутки ${{\Omega }_{w}}$ и ${{\Psi }_{w}}$ вещественной оси на плоскости $w$. Продолжая эту функцию на основании принципа симметрии в смежные полуполосы через лучи $\Psi $ и $\Omega $, затем через их образы при взаимном отражении ${{\Psi }^{\Omega }}$ и ${{\Omega }^{\Psi }}$ и т.д., получаем аналитическое продолжение отображения (1) в полуплоскость ${{\mathbb{H}}^{ + }}(L)$.
Поскольку функция $\mathcal{F}(z)$ отображает сторону $\Gamma $ треугольника $T$ в луч ${{\Gamma }_{w}}$, то эту функцию можно по принципу симметрии далее продолжить через дугу $\Gamma $ в область, получаемую инверсией из полуплоскости ${{\mathbb{H}}^{ + }}(L)$ относительно этой дуги. Такой областью является внутренность круга, описанного вокруг треугольника $BCO$ и касающегося вещественной оси в начале координат. Таким образом, в сегмент этого круга функция $\mathcal{F}(z)$ аналитически продолжается из полуполосы ${{\mathbb{S}}^{ + }}(L)$ через прямолинейный отрезок $BC$.
Рассмотрим теперь произвольно расположенный на комплексной плоскости круговой треугольник $V$, имеющий углы $0,\;\alpha ,\;\alpha $. Дробно-линейным преобразованием треугольник $V$ может быть переведен в $T$. Прообразом прямой $\{ \operatorname{Im} z = L\} $ при этом является описанная вокруг $V$ окружность, откуда получаем следующую переформулировку теоремы 1.
Теорема 1'. Конформное отображение на полуплоскость кругового треугольника $V$, имеющего один нулевой угол и два равных между собой ненулевых угла, аналитически продолжается во внутренность круга, описанного вокруг $V$.
В предельном случае $\alpha = 0$ аналитическое продолжение конформного отображения треугольника $V$ на полуплоскость, даваемое теоремой 1', является модулярной функцией (см. [6, ч. 3, гл. 7, § 4]).
Список литературы
Маркушевич A.И. Теория аналитических функций. Т. I. Начала теории. М.: Наука, 1967; Дальнейшее построение теории. Т. 2. М.: Наука, 1968.
Власов В.И., Скороходов С.Л. Конформное отображение $L$-образной области в аналитическом виде // Ж. вычисл. матем. и матем. физ. 2022. Т. 62. 12. С. 1943–1980.
Vlasov V.I., Skorokhodov S.L. A generalization and development of the Trefftz method // Zeitschr. Angew. Math. Mech. 1996. V. 76. Suppl. 1. P. 547–548.
Власов В.И., Скороходов С.Л. О развитии метода Треффца // Докл. АН. 1994. Т. 337. 6. С. 713–717.
Власов В.И., Скороходов С.Л. Аналитическое решение задачи Дирихле для уравнения Пуассона в одном классе полигональных областей // Сообщ. прикладн. матем. М.: Изд-во ВЦ АН СССР, 1988.
Гурвиц А., Курант Г. Теория функций. М.: Наука, 1968.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики