1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 62, № 12, 2022

Журнал вычислительной математики и математической физики, 2022, T. 62, № 12, стр. 2026-2042

К интегрированию уравнения Матье с затуханием в монографии Н.Н. Боголюбова и Ю.А. Митропольского “Асимптотические методы в теории нелинейных колебаний”

А. Ф. Курин 1, *

1 Воронежский гос. ун-т, физ. ф-т
394006 Воронеж, Университетская пл., 1, Россия

* E-mail: afkurin@mail.ru

Поступила в редакцию 01.03.2021
После доработки 23.06.2022
Принята к публикации 04.08.2022

Полный текст (PDF)

Аннотация

Асимптотическим методом, изложенным в монографии, указанной в заглавии статьи, получены выражения, определяющие границы трех областей параметрического резонанса однородного уравнения Матье с затуханием. Формулы для границ второй и третьей областей, справедливость которых подтверждает также численное решение уравнения, существенно отличаются от известных, полученных в монографии. Показано, что само существование областей резонанса зависит от выбора порядков малости трех малых параметров задачи. Библ. 11. Фиг. 3.

Ключевые слова: уравнение Матье, асимптотический метод, параметрический резонанс.

ВВЕДЕНИЕ

В монографии [1], посвященной приближенным асимптотическим методам решения задач теории нелинейных колебаний, рассмотрено, в частности, уравнение Матье с затуханием, для которого на плоскости параметров уравнения вычислены границы трех областей параметрического резонанса (формулы (17.62)–(17.64) в [1]). При этом авторы ограничивались тем приближением асимптотического метода, в котором появляется та или иная область резонанса: указанные три формулы получены в первом, втором и третьем приближениях соответственно. Отметим, что в [1] отсутствуют какие-либо подробности вывода формул.

В настоящей работе уравнение Матье интегрируется подробно асимптотическим методом, принятым в монографии [1], сохранены также обозначения величин. Амплитуда и фаза колебаний имеет вид разложения по степеням малого параметра $\varepsilon $. Однако теперь предусмотрена возможность в полученных выражениях устанавливать порядок малости параметров, входящих в уравнение, поскольку, как показал анализ, для существования каждой области параметрических колебаний требуется своя комбинация порядков малости трех параметров. Справедливость полученных выражений для границ второй и третьей областей резонанса (формулы (38), (48) настоящей работы) подтверждается численным решением уравнения Матье с затуханием. Эти выражения не совпадают с формулами (17.63), (17.64) в [1]. Количественные результаты различаются существенно.

Правильность формул (38), (48) статьи подтверждается еще и тем, что вычисленные из этих формул границы для уравнения Матье с затуханием в другой часто используемой записи (см. разд. 5) совпали с границами, установленными ранее для такого уравнения в статье [2] известным асимптотическим методом усреднения для систем с многими быстрыми фазами [3], [4]. Заметим, что метод усреднения использовался также для уравнения Матье без затухания [4]–[6].

Далее, формулы для границ областей резонанса (38), (48) получаются и методом И.З. Штокало [7]. Дальнейшее развитие метода изложено в статье Ю.С. Колесова и В.В. Майорова [8]. Таким образом, в случае уравнения Матье три метода дают одинаковый результат.

1. ПРЕОБРАЗОВАНИЕ УРАВНЕНИЯ МАТЬЕ

В обозначениях работы [1] запишем уравнение Матье с затуханием (см. (17.61) в [1])

(1)
$\frac{{{{d}^{2}}x}}{{d{{t}^{2}}}} + \delta \frac{{dx}}{{dt}} + {{\omega }^{2}}\left[ {1 - h\cos (\nu t)} \right]x = 0.$

Рассматриваются резонансы, когда близки частоты $\omega $ и $p\nu {\text{/}}q$. Здесь $p$ и $q$ – взаимно простые числа. Частоты связаны соотношением

(2)
${{\omega }^{2}} = {{\left( {\frac{{p\nu }}{q}} \right)}^{2}} + \varepsilon {{\Delta }_{1}} + {{\varepsilon }^{2}}{{\Delta }_{2}} + {{\varepsilon }^{3}}{{\Delta }_{3}} + \cdots ,$
где $\varepsilon $ – малый параметр. Малыми величинами являются также затухание
(3)
$\delta = \varepsilon {{\delta }_{1}} + {{\varepsilon }^{2}}{{\delta }_{2}} + {{\varepsilon }^{3}}{{\delta }_{3}} + \cdots $
и параметр
(4)
$h = \varepsilon {{h}_{1}}.$
В отличие от [1] представление частотной расстройки и коэффициента затухания рядом по степеням $\varepsilon $ позволяет выбирать порядок малости этих величин при анализе полученных формул.

Представим уравнение (1) в виде разложения по степеням малого параметра $\varepsilon $.

Для этого, следуя асимптотическому методу, изложенному в [1], с учетом (2)–(4) перепишем уравнение (1) в виде

(5)
$\begin{gathered} \frac{{{{d}^{2}}x}}{{d{{t}^{2}}}} + {{\left( {\frac{{p\nu }}{q}} \right)}^{2}}x = \varepsilon \left[ {{{{\left( {\frac{{p\nu }}{q}} \right)}}^{2}}{{h}_{1}}\cos (\nu t)x - {{\Delta }_{1}}x - {{\delta }_{1}}\frac{{dx}}{{dt}}} \right] + \\ + \;{{\varepsilon }^{2}}\left[ {{{\Delta }_{1}}{{h}_{1}}\cos (\nu t)x - {{\Delta }_{2}}x - {{\delta }_{2}}\frac{{dx}}{{dt}}} \right] + {{\varepsilon }^{3}}\left[ {{{\Delta }_{2}}{{h}_{1}}\cos (\nu t)x - {{\Delta }_{3}}x - {{\delta }_{3}}\frac{{dx}}{{dt}}} \right] + \cdots = F. \\ \end{gathered} $

Согласно [1] решение ищем в виде ряда

(6)
$x = a\cos \psi + \varepsilon {{u}_{1}}(a,t,\theta ) + {{\varepsilon }^{2}}{{u}_{2}}(a,t,\theta ) + {{\varepsilon }^{3}}{{u}_{3}}(a,t,\theta ) + \cdots ,$
в котором
(7)
$\psi = \frac{{p\nu }}{q}t + \theta $
есть быстрая фаза, а медленные амплитуда $a$ и фаза $\theta $ определяются из уравнений

(8)
$\begin{gathered} \frac{{da}}{{dt}} = \varepsilon {{A}_{1}}(a,\theta ) + {{\varepsilon }^{2}}{{A}_{2}}(a,\theta ) + {{\varepsilon }^{3}}{{A}_{3}}(a,\theta ) + \cdots , \\ \frac{{d\theta }}{{dt}} = \varepsilon {{B}_{1}}(a,\theta ) + {{\varepsilon }^{2}}{{B}_{2}}(a,\theta ) + {{\varepsilon }^{3}}{{B}_{3}}(a,\theta ) + \cdots . \\ \end{gathered} $

Функции ${{A}_{{1,2,3,...}}},\;{{B}_{{1,2,3,...}}},\;{{u}_{{1,2,3,...}}}$ подлежат вычислению.

Представим правую и левую части в виде разложения по степеням $\varepsilon $. Здесь $x$ – выражение (6). Вычислим производную

(9)
$\begin{gathered} \frac{{dx}}{{dt}} = \frac{{da}}{{dt}}\cos \psi - a\sin \psi \frac{{d\psi }}{{dt}} + \sum\limits_{n = 1} \,{{\varepsilon }^{n}}\left( {\frac{{\partial {{u}_{n}}}}{{\partial t}} + \frac{{\partial {{u}_{n}}}}{{\partial a}}\frac{{da}}{{dt}} + \frac{{\partial {{u}_{n}}}}{{\partial \theta }}\frac{{d\theta }}{{dt}}} \right) = \\ = \frac{{da}}{{dt}}\left( {\cos \psi + \sum\limits_{n = 1} \,{{\varepsilon }^{n}}\frac{{\partial {{u}_{n}}}}{{\partial a}}} \right) + \frac{{d\theta }}{{dt}}\left( { - a\sin \psi + \sum\limits_{n = 1} \,{{\varepsilon }^{n}}\frac{{\partial {{u}_{n}}}}{{\partial \theta }}} \right) - \frac{{ap\nu }}{q}\sin \psi + \sum\limits_{n = 1} \,{{\varepsilon }^{n}}\frac{{\partial {{u}_{n}}}}{{\partial t}}, \\ \end{gathered} $
где $da{\text{/}}dt$ и $d\theta {\text{/}}dt$ определяются формулами (8).

Подставляя выражения (6) и (9) в правую часть уравнения (5), получаем

$\begin{gathered} F = \varepsilon \left[ {a{{{\left( {\frac{{p\nu }}{q}} \right)}}^{2}}{{h}_{1}}\cos (\nu t)\cos \psi - a{{\Delta }_{1}}\cos \psi + a\frac{{p\nu }}{q}{{\delta }_{1}}\sin \psi } \right] + \\ + \;{{\varepsilon }^{2}}\left[ {{{{\left( {\frac{{p\nu }}{q}} \right)}}^{2}}{{h}_{1}}{{u}_{1}}\cos (\nu t) - {{\Delta }_{1}}{{u}_{1}} - {{\delta }_{1}}\left( {{{A}_{1}}\cos \psi - a{{B}_{1}}\sin \psi + \frac{{\partial {{u}_{1}}}}{{\partial t}}} \right)} \right. + \\ \end{gathered} $
(10)
$\begin{gathered} \, + \left. {a{{h}_{1}}{{\Delta }_{1}}\cos (\nu t)\cos \psi - a{{\Delta }_{2}}\cos \psi + a\frac{{p\nu }}{q}{{\delta }_{2}}\mathop {\sin \psi }\limits_{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}^{} } \right] + \\ + \;{{\varepsilon }^{3}}\left[ {{{{\left( {\frac{{p\nu }}{q}} \right)}}^{2}}{{h}_{1}}{{u}_{2}}\cos (\nu t) - {{\Delta }_{1}}{{u}_{2}} - {{\delta }_{1}}\left( {{{A}_{2}}\cos \psi - a{{B}_{2}}\sin \psi + {{A}_{1}}\frac{{\partial {{u}_{1}}}}{{\partial a}}} \right.} \right. + \\ \end{gathered} $
$\begin{gathered} \left. { + \;{{B}_{1}}\frac{{\partial {{u}_{1}}}}{{\partial \theta }} + \frac{{\partial {{u}_{2}}}}{{\partial t}}} \right) + {{h}_{1}}{{\Delta }_{1}}{{u}_{1}}\cos (\nu t) - {{\Delta }_{2}}{{u}_{1}} - {{\delta }_{2}}\left( {{{A}_{1}}\cos \psi - a{{B}_{1}}\sin \psi + \frac{{\partial {{u}_{1}}}}{{\partial t}}} \right) + \\ \, + \left. {a{{h}_{1}}{{\Delta }_{2}}\cos (\nu t)\cos \psi - a{{\Delta }_{3}}\cos \psi + a\frac{{p\nu }}{q}{{\delta }_{3}}\mathop {\sin \psi }\limits_{_{{_{{_{{_{{_{{}}}}}}}}}}}^{} } \right] + \cdots . \\ \end{gathered} $

Вторую производную ${{d}^{2}}x{\text{/}}d{{t}^{2}}$ в левой части уравнения (5) получаем дифференцированием (9). При этом используем выражения (8), а также

$\begin{gathered} {{\left( {\frac{{da}}{{dt}}} \right)}^{2}} = {{\varepsilon }^{2}}A_{1}^{2} + 2{{\varepsilon }^{3}}{{A}_{1}}{{A}_{2}} + \cdots , \\ \frac{{{{d}^{2}}a}}{{d{{t}^{2}}}} = {{\varepsilon }^{2}}\left( {{{A}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial \theta }}} \right) + {{\varepsilon }^{3}}\left( {{{A}_{1}}\frac{{\partial {{A}_{2}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{A}_{2}}}}{{\partial \theta }} + {{A}_{2}}\frac{{\partial {{A}_{1}}}}{{\partial a}} + {{B}_{2}}\frac{{\partial {{A}_{1}}}}{{\partial \theta }}} \right) + \cdots , \\ \frac{{da}}{{dt}}\frac{{d\theta }}{{dt}} = {{\varepsilon }^{2}}{{A}_{1}}{{B}_{1}} + {{\varepsilon }^{3}}({{A}_{1}}{{B}_{2}} + {{A}_{2}}{{B}_{1}}) + \cdots , \\ \end{gathered} $
$\begin{gathered} {{\left( {\frac{{d\theta }}{{dt}}} \right)}^{2}} = {{\varepsilon }^{2}}B_{1}^{2} + 2{{\varepsilon }^{3}}{{B}_{1}}{{B}_{2}} + \cdots , \\ \frac{{{{d}^{2}}\theta }}{{d{{t}^{2}}}} = {{\varepsilon }^{2}}\left( {{{A}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial \theta }}} \right) + {{\varepsilon }^{3}}\left( {{{A}_{1}}\frac{{\partial {{B}_{2}}}}{{\partial a}} + {{A}_{2}}\frac{{\partial {{B}_{1}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{B}_{2}}}}{{\partial \theta }} + {{B}_{2}}\frac{{\partial {{B}_{1}}}}{{\partial \theta }}} \right) + \cdots . \\ \end{gathered} $

После простых вычислений для левой части (5) получаем разложение

$\begin{gathered} \frac{{{{d}^{2}}x}}{{d{{t}^{2}}}} + {{\left( {\frac{{p\nu }}{q}} \right)}^{2}}x = \varepsilon \left[ { - 2\frac{{p\nu }}{q}{{A}_{1}}\sin \psi - 2a\frac{{p\nu }}{q}{{B}_{1}}\cos \psi + \frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{t}^{2}}}} + {{{\left( {\frac{{p\nu }}{q}} \right)}}^{2}}{{u}_{1}}} \right] + \\ \, + {{\varepsilon }^{2}}\left[ {\left( {{{A}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial \theta }} - aB_{1}^{2} - 2a\frac{{p\nu }}{q}{{B}_{2}}} \right)\cos \psi + } \right. \\ \end{gathered} $
(11)
$\begin{gathered} + \;\left( { - a{{A}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial a}} - a{{B}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial \theta }} - 2{{A}_{1}}{{B}_{1}} - 2\frac{{p\nu }}{q}{{A}_{2}}} \right)\sin \psi + \left. {2{{A}_{1}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial a\partial t}} + 2{{B}_{1}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial \theta \partial t}} + \frac{{{{\partial }^{2}}{{u}_{2}}}}{{\partial {{t}^{2}}}} + {{{\left( {\frac{{p\nu }}{q}} \right)}}^{2}}{{u}_{2}}} \right] + \\ \, + {{\varepsilon }^{3}}\left[ {\left( {{{A}_{1}}\frac{{\partial {{A}_{2}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{A}_{2}}}}{{\partial \theta }} + {{A}_{2}}\frac{{\partial {{A}_{1}}}}{{\partial a}} + {{B}_{2}}\frac{{\partial {{A}_{1}}}}{{\partial \theta }} - 2a{{B}_{1}}{{B}_{2}} - 2a\frac{{p\nu }}{q}{{B}_{3}}} \right)\cos \psi + } \right. \\ \, + \left( { - a{{A}_{1}}\frac{{\partial {{B}_{2}}}}{{\partial a}} - a{{A}_{2}}\frac{{\partial {{B}_{1}}}}{{\partial a}} - a{{B}_{1}}\frac{{\partial {{B}_{2}}}}{{\partial \theta }} - a{{B}_{2}}\frac{{\partial {{B}_{1}}}}{{\partial \theta }} - 2{{A}_{1}}{{B}_{2}} - 2{{A}_{2}}{{B}_{1}} - 2\frac{{p\nu }}{q}{{A}_{3}}} \right)\sin \psi + \\ \end{gathered} $
$\begin{gathered} \, + \frac{{\partial {{u}_{1}}}}{{\partial a}}\left( {{{A}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial \theta }}} \right) + A_{1}^{2}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{a}^{2}}}} + 2{{A}_{1}}{{B}_{1}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial a\partial \theta }} + 2{{A}_{2}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial a\partial t}} + 2{{A}_{1}}\frac{{{{\partial }^{2}}{{u}_{2}}}}{{\partial a\partial t}} + \\ + \;\left. {\frac{{\partial {{u}_{1}}}}{{\partial \theta }}\left( {{{A}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial \theta }}} \right) + B_{1}^{2}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{\theta }^{2}}}} + 2{{B}_{2}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial \theta \partial t}} + 2{{B}_{1}}\frac{{{{\partial }^{2}}{{u}_{2}}}}{{\partial \theta \partial t}} + \frac{{{{\partial }^{2}}{{u}_{3}}}}{{\partial {{t}^{2}}}} + {{{\left( {\frac{{p\nu }}{q}} \right)}}^{2}}{{u}_{3}}} \right]. \\ \end{gathered} $

Если отбросить члены с ${{\varepsilon }^{3}}$, приходим к выражению (4.10) в [1].

2. РЕЗОНАНС $\omega \approx \frac{\nu }{2}$

Выведем формулы для границы первой области параметрического резонанса в первом и во втором (формула (27)) приближениях асимптотического метода.

Формулы первого приближения получим из равенства выражений с $\varepsilon $ в (11) и (10) при $p = 1,$ $q = 2$;

$\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{t}^{2}}}} + \frac{{{{\nu }^{2}}}}{4}{{u}_{1}} - \nu {{A}_{1}}\sin \psi - a\nu {{B}_{1}}\cos \psi = \frac{{a{{\nu }^{2}}{{h}_{1}}}}{4}\cos (\nu t)\cos \psi - a{{\Delta }_{1}}\cos \psi + \frac{{a\nu {{\delta }_{1}}}}{2}\sin \psi .$

Решение ${{u}_{1}}$ этого дифференциального уравнения не должно содержать колебаний основной частоты $\nu {\text{/}}2$ [1]. Это требование означает отсутствие в уравнении слагаемых с $\sin \psi $ и $\cos \psi $. Поэтому с учетом формулы

(12)
$\cos (\nu t)\cos \psi = \frac{1}{2}\left[ {\cos \left( {\frac{{3\nu }}{2}t + \theta } \right) + \sin (2\theta )\sin \psi + \cos (2\theta )\cos \psi } \right]$
приравняем нулю выражения с $\sin \psi $ и $\cos \psi $. Получаем
$\nu {{A}_{1}} + \frac{{a\nu {{\delta }_{1}}}}{2} + \frac{{a{{\nu }^{2}}{{h}_{1}}}}{8}\sin (2\theta ) = 0,\quad \nu {{B}_{1}} - {{\Delta }_{1}} + \frac{{{{\nu }^{2}}{{h}_{1}}}}{8}\cos (2\theta ) = 0,$
откуда

(13)
${{A}_{1}} = - \frac{{a{{\delta }_{1}}}}{2} - \frac{{a\nu {{h}_{1}}}}{8}\sin (2\theta ),\quad {{B}_{1}} = \frac{{{{\Delta }_{1}}}}{\nu } - \frac{{\nu {{h}_{1}}}}{8}\cos (2\theta ).$

Для функции ${{u}_{1}}$ получаем дифференциальное уравнение

$\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{t}^{2}}}} + \frac{{{{\nu }^{2}}}}{4}{{u}_{1}} = \frac{{a{{\nu }^{2}}{{h}_{1}}}}{8}\cos \left( {\frac{{3\nu }}{2}t + \theta } \right),$
которое имеет общее решение
${{u}_{1}} = {{C}_{1}}\cos \left( {\frac{\nu }{2}t} \right) + {{C}_{2}}\sin \left( {\frac{\nu }{2}t} \right) - \frac{{a{{h}_{1}}}}{{16}}\cos \left( {\frac{{3\nu }}{2}t + \theta } \right).$
Полагаем ${{C}_{1}} = {{C}_{2}} = 0$, чтобы исключить в ${{u}_{1}}$ колебания с основной частотой $\nu {\text{/}}2$. Окончательно,

(14)
${{u}_{1}} = - \frac{{a{{h}_{1}}}}{{16}}\cos \left( {\frac{{3\nu }}{2}t + \theta } \right).$

Приравняем теперь выражения с ${{\varepsilon }^{2}}$ в разложениях (11) и (10)

(15)
$\begin{gathered} \frac{{{{\partial }^{2}}{{u}_{2}}}}{{\partial {{t}^{2}}}} + \frac{{{{\nu }^{2}}}}{4}{{u}_{2}} + \left( { - 2{{A}_{1}}{{B}_{1}} - a{{A}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial a}} - a{{B}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial \theta }} - \nu {{A}_{2}}} \right)\sin \psi + \left( { - aB_{1}^{2} + {{A}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial a}} + } \right. \\ \, + \left. {{{B}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial \theta }} - a\nu {{B}_{2}}} \right)\cos \psi + 2{{A}_{1}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial a\partial t}} + 2{{B}_{1}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial \theta \partial t}} = \frac{{{{\nu }^{2}}{{h}_{1}}}}{4}{{u}_{1}}\cos (\nu t) - {{\Delta }_{1}}{{u}_{1}} - \\ - \;{{\delta }_{1}}\left( {{{A}_{1}}\cos \psi - a{{B}_{1}}\sin \psi + \frac{{\partial {{u}_{1}}}}{{\partial t}}} \right) + a{{h}_{1}}{{\Delta }_{1}}\cos (\nu t)\cos \psi - a{{\Delta }_{2}}\cos \psi + \frac{{a\nu {{\delta }_{2}}}}{2}\sin \psi . \\ \end{gathered} $

Это – дифференциальное уравнение относительно ${{u}_{2}}$. Функции ${{A}_{1}},\;{{B}_{1}},\;{{u}_{1}}$ определяются формулами первого приближения (13), (14). Чтобы избежать появления в ${{u}_{2}}$ колебаний с частотой $\nu {\text{/}}2$, приравняем нулю выражения с $\sin \psi $ и $\cos \psi $, учитывая формулы (7), (12) и

(16)
${{u}_{1}}\cos (\nu t) = - \frac{{a{{h}_{1}}}}{{32}}\left[ {\cos \left( {\frac{{5\nu }}{2}t + \theta } \right) + \cos \psi } \right].$
Получаем
$\begin{gathered} \nu {{A}_{2}} = - 2{{A}_{1}}{{B}_{1}} - a{{A}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial a}} - a{{B}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial \theta }} - a{{\delta }_{1}}{{B}_{1}} - \frac{{a{{h}_{1}}{{\Delta }_{1}}}}{2}\sin (2\theta ) - \frac{{a\nu {{\delta }_{2}}}}{2}, \\ a\nu {{B}_{2}} = {{A}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial \theta }} - aB_{1}^{2} + \frac{{a{{\nu }^{2}}h_{1}^{2}}}{{128}} + {{\delta }_{1}}{{A}_{1}} - \frac{{a{{h}_{1}}{{\Delta }_{1}}}}{2}\cos (2\theta ) + a{{\Delta }_{2}}, \\ \end{gathered} $
откуда после вычислений следуют выражения

(17)
${{A}_{2}} = - \frac{{a{{\delta }_{2}}}}{2} - \frac{{a{{h}_{1}}{{\Delta }_{1}}}}{{2\nu }}\sin (2\theta ),\quad {{B}_{2}} = \frac{{{{\Delta }_{2}}}}{\nu } - \frac{{\Delta _{1}^{2}}}{{{{\nu }^{3}}}} - \frac{{\delta _{1}^{2}}}{{4\nu }} + \frac{{3\nu h_{1}^{2}}}{{128}} - \frac{{{{h}_{1}}{{\Delta }_{1}}}}{{2\nu }}\cos (2\theta ).$

Если в решении уравнения (1) ограничиться вторым приближением метода, вычисление ${{u}_{2}}$ не требуется [1].

Далее вместо системы уравнений (8) будем использовать систему для $a$ и $2\theta $, которая во втором приближении имеет вид

$\frac{{da}}{{dt}} = \varepsilon {{A}_{1}} + {{\varepsilon }^{2}}{{A}_{2}},\quad \frac{{d(2\theta )}}{{dt}} = \varepsilon 2{{B}_{1}} + {{\varepsilon }^{2}}2{{B}_{2}}.$

Подставим выражения (13), (17), получаем систему

(18)
$\frac{{da}}{{dt}} = \frac{a}{2}\left[ { - \delta + r\sin (2\theta )} \right],\quad \frac{{d(2\theta )}}{{dt}} = s + r\cos (2\theta ),$
где в коэффициентах, имеющих вид разложения по степеням $\varepsilon $
$\delta = \varepsilon {{\delta }_{1}} + {{\varepsilon }^{2}}{{\delta }_{2}},\quad r = \varepsilon {{r}_{1}} + {{\varepsilon }^{2}}{{r}_{2}},\quad s = \varepsilon {{s}_{1}} + {{\varepsilon }^{2}}{{s}_{2}},$
составляющие равны

(19)
${{r}_{1}} = - \frac{{\nu {{h}_{1}}}}{4},\quad {{r}_{2}} = - \frac{{{{h}_{1}}{{\Delta }_{1}}}}{\nu },\quad {{s}_{1}} = \frac{{2{{\Delta }_{1}}}}{\nu },\quad {{s}_{2}} = \frac{{2{{\Delta }_{2}}}}{\nu } - \frac{{2\Delta _{1}^{2}}}{{{{\nu }^{3}}}} - \frac{{\delta _{1}^{2}}}{{2\nu }} + \frac{{3\nu h_{1}^{2}}}{{64}}.$

Как в [1], систему (18) сведем к линейной однородной системе с постоянными коэффициентами с помощью замены переменных

(20)
$P = a\sin \theta ,\quad R = a\cos \theta .$
Дифференцируем
$\frac{{dP}}{{dt}} = \frac{{da}}{{dt}}\sin \theta + a\cos \theta \frac{{d\theta }}{{dt}},\quad \frac{{dR}}{{dt}} = \frac{{da}}{{dt}}\cos \theta - a\sin \theta \frac{{d\theta }}{{dt}}.$
Подставляем сюда выражения $da{\text{/}}dt,$ $d\theta {\text{/}}dt = 0,$ $5d(2\theta {\text{/}}dt)$ (18). С учетом формул (20) получаем систему

(21)
$\frac{{dP}}{{dt}} = - \frac{\delta }{2}P + \frac{{r + s}}{2}R,\quad \frac{{dR}}{{dt}} = - \frac{\delta }{2}R + \frac{{r - s}}{2}P.$

Исключая, например, $R$, приходим к уравнению осциллятора относительно $P$

$\frac{{{{d}^{2}}P}}{{d{{t}^{2}}}} + \delta \frac{{dP}}{{dt}} + \frac{{{{s}^{2}} - {{r}^{2}} + {{\delta }^{2}}}}{4}P = 0,$
характеристическое уравнение которого имеет корни

${{k}_{{1,2}}} = \frac{{ - \delta \pm \sqrt {{{r}^{2}} - {{s}^{2}}} }}{2}.$

При $D = {{r}^{2}} - {{s}^{2}} \geqslant 0$ корни вещественные. Оба они отрицательные, пока $D < {{\delta }^{2}}$. Функция $P(t)$ и, следовательно, амплитуда $a(t)$ экспоненциально затухают, не совершая колебаний. Этот режим описан в [9], [2].

Если $D > {{\delta }^{2}}$ корень ${{k}_{1}} > 0$. В этом случае функция $P(t)$ имеет экспоненциально возрастающую составляющую, что указывает на параметрический резонанс.

При ${{k}_{1}} = 0,$ $(D = {{\delta }^{2}})$ получаем уравнение, связывающее параметры уравнения (1) и определяющее границу области резонанса

(22)
${{s}^{2}} + {{\delta }^{2}} = {{r}^{2}}.$

При $D = {{r}^{2}} - {{s}^{2}} < 0$ корни ${{k}_{{1,2}}}$ комплексно-сопряженные. Функция $P(t)$ и, следовательно, амплитуда $a(t)$ экспоненциально затухают, совершая медленные колебания с частотой $\sqrt {{{s}^{2}} - {{r}^{2}}} {\text{/}}2$.

Используя формулы (19), запишем уравнение (22) в первом приближении

(23)
${{\varepsilon }^{2}}\frac{{4\Delta _{1}^{2}}}{{{{\nu }^{2}}}} + {{\varepsilon }^{2}}\delta _{1}^{2} = {{\varepsilon }^{2}}\frac{{{{\nu }^{2}}h_{1}^{2}}}{{16}}.$

В работе [1] граница построена на плоскости параметров $((2\omega {\text{/}}\nu {{)}^{2}},h)$. После подстановки выражения

(24)
$\varepsilon {{\Delta }_{1}} = {{\omega }^{2}} - \frac{{{{\nu }^{2}}}}{4},$
которое следует из (2) при $p = 1,$ $q = 2$, в формулу (23), и умножения на $4{\text{/}}{{\nu }^{2}}$ находим
${{\left( {\frac{{2\omega }}{\nu }} \right)}^{2}} = 1 \pm \sqrt {\frac{{{{h}^{2}}}}{4} - \frac{{4{{\delta }^{2}}}}{{{{\nu }^{2}}}}} ,$
т.е. выражение, определяющее границу области параметрического резонанса, которое получено в [1].

Дополним этот результат. Вычислим границу во втором приближении, считая $\Delta \sim \varepsilon ,$ $\delta \sim \varepsilon $, т.е. полагая в формулах (19) ${{\Delta }_{2}} = 0$.

Согласно (24) параметр ${{(2\omega {\text{/}}\nu )}^{2}}$ выражается через частотную расстройку ${{\Delta }_{1}}$, которая присутствует в ${{r}_{2}},\;{{s}_{{1,2}}}$. Поэтому (22) является алгебраическим уравнением относительно ${{(2\omega {\text{/}}\nu )}^{2}}$.

Запишем это уравнение. Для удобства введем

(25)
$y = {{\left( {\frac{{2\omega }}{\nu }} \right)}^{2}} - 1,$
тогда из (24) следует
$\varepsilon {{\Delta }_{1}} = \frac{{{{\nu }^{2}}}}{4}y.$
Подставим это выражение в ${{r}_{2}},{{s}_{1}},{{s}_{2}}$ (19) и запишем (22) в виде

${{y}^{4}} - 8{{y}^{3}} + \left( {16 - \frac{{19{{h}^{2}}}}{4} + \frac{{8{{\delta }^{2}}}}{{{{\nu }^{2}}}}} \right){{y}^{2}} - \left( {5{{h}^{2}} + \frac{{32{{\delta }^{2}}}}{{{{\nu }^{2}}}}} \right)y + \frac{{9{{h}^{4}}}}{{64}} - 4{{h}^{2}} - \frac{{3{{h}^{2}}{{\delta }^{2}}}}{{{{\nu }^{2}}}} + \frac{{64{{\delta }^{2}}}}{{{{\nu }^{2}}}} + \frac{{16{{\delta }^{4}}}}{{{{\nu }^{4}}}} = 0.$

Решение уравнения ищем в виде разложения по степеням $\varepsilon $

(26)
$y = \varepsilon {{y}_{1}} + {{\varepsilon }^{2}}{{y}_{2}} + \cdots $
с использованием формул

${{y}^{2}} = {{\varepsilon }^{2}}y_{1}^{2} + 2{{\varepsilon }^{3}}{{y}_{1}}{{y}_{2}} + \cdots ,\quad {{y}^{3}} = {{\varepsilon }^{3}}y_{1}^{3} + \cdots .$

Подставим в уравнение, учитывая оценки $h,\delta \sim \varepsilon $, приравняем нулю коэффициенты при степенях $\varepsilon $

$\begin{gathered} {{\varepsilon }^{2}}\,:\;\;16y_{1}^{2} - 4h_{1}^{2} + \frac{{64\delta _{1}^{2}}}{{{{\nu }^{2}}}} = 0, \\ {{\varepsilon }^{3}}\,:\;\; - {\kern 1pt} 8y_{1}^{3} + 32{{y}_{1}}{{y}_{2}} - \left( {5h_{1}^{2} + \frac{{32\delta _{1}^{2}}}{{{{\nu }^{2}}}}} \right){{y}_{1}} = 0. \\ \end{gathered} $

В полученной системе уравнений относительно ${{y}_{{1,2}}}$ первое уравнение имеет решение

${{y}_{1}} = \pm \sqrt {\frac{{h_{1}^{2}}}{4} - \frac{{4\delta _{1}^{2}}}{{{{\nu }^{2}}}}} .$
Используя (25), получаем границу области параметрического резонанса в первом приближении.

Подставим ${{y}_{1}}$ во второе уравнение и выразим ${{y}_{2}}$:

${{y}_{2}} = \frac{{7h_{1}^{2}}}{{32}}.$

Формулы для ${{y}_{{1,2}}}$ позволяют с использованием (25) записать $y$ (26) – границу области параметрического резонанса во втором приближении асимптотического метода

(27)
${{\left( {\frac{{2\omega }}{\nu }} \right)}^{2}} = 1 \pm \sqrt {\frac{{{{h}^{2}}}}{4} - \frac{{4{{\delta }^{2}}}}{{{{\nu }^{2}}}}} + \frac{{7{{h}^{2}}}}{{32}}.$
На фиг. 1 показаны границы первой области резонанса во втором приближении для трех значений $\delta {\text{/}}\nu = 0.1,0.15,0.2$ (кривые 3, 4, 5 соответственно). Линия 2 – граница (27) при отсутствии затухания ($\delta {\text{/}}\nu = 0$). Штриховые линии получены численным решением уравнения Матье: кривая 1 – из уравнения без затухания, кривая 2 – из уравнения с затуханием в случае $\delta {\text{/}}\nu = 0.1$. При численном интегрировании уравнения Матье (1) делением на ${{\nu }^{2}}$ приводилось к виду

(28)
$\frac{{{{d}^{2}}x}}{{d{{\tau }^{2}}}} + \frac{\delta }{\nu }\frac{{dx}}{{d\tau }} + \frac{1}{4}{{\left( {\frac{{2\omega }}{\nu }} \right)}^{2}}\left( {1 - h\cos \tau } \right)x = 0,\quad \tau = \nu t.$
Фиг. 1

3. РЕЗОНАНС $\omega \approx \nu $

Выведем формулы для границы второй области параметрического резонанса во втором и третьем приближениях асимптотического метода (формула (38)). Результат сравним с [1].

Теперь $p = 1,$ $q = 1$ и $\psi = \nu t + \theta $. Из равенства выражений с $\varepsilon $ в (11) и (10) следует уравнение

$\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{t}^{2}}}} + {{\nu }^{2}}{{u}_{1}} - 2\nu {{A}_{1}}\sin \psi - 2a\nu {{B}_{1}}\cos \psi = a{{h}_{1}}{{\nu }^{2}}\cos (\nu t)\cos \psi - a{{\Delta }_{1}}\cos \psi + a\nu {{\delta }_{1}}\sin \psi .$

Чтобы устранить в решении ${{u}_{1}}$ колебания с основной частотой $\nu $, приравняем нулю выражения с $\sin \psi $ и $\cos \psi $. Учитывая тригонометрическую формулу

(29)
$\cos (\nu t)\cos \psi = \frac{1}{2}[\cos (2\nu t + \theta ) + \cos \theta ],$
не содержащую колебаний с частотой $\nu $, получаем
$2\nu {{A}_{1}} + a\nu {{\delta }_{1}} = 0,\quad 2a\nu {{B}_{1}} - a{{\Delta }_{1}} = 0.$
Отсюда

(30)
${{A}_{1}} = - \frac{{a{{\delta }_{1}}}}{2},\quad {{B}_{1}} = \frac{{{{\Delta }_{1}}}}{{2\nu }}.$

Уравнение для ${{u}_{1}}$

$\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{t}^{2}}}} + {{\nu }^{2}}{{u}_{1}} = \frac{{a{{\nu }^{2}}{{h}_{1}}}}{2}[\cos (2\nu t + \theta ) + \cos \theta ]$
имеет общее решение
(31)
${{u}_{1}} = {{C}_{1}}\cos (\nu t) + {{C}_{2}}\sin (\nu t) - \frac{{a{{h}_{1}}}}{6}\cos (2\nu t + \theta ) + \frac{{a{{h}_{1}}}}{2}\cos \theta .$
Далее полагаем ${{C}_{1}} = {{C}_{2}} = 0$.

Формулы второго приближения найдем из равенства выражений с ${{\varepsilon }^{2}}$ в (11) и (10) (при $p = q = 1$)

$\begin{gathered} \frac{{{{\partial }^{2}}{{u}_{2}}}}{{\partial {{t}^{2}}}} + {{\nu }^{2}}{{u}_{2}} + \left( { - 2{{A}_{1}}{{B}_{1}} - a{{A}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial a}} - a{{B}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial \theta }} - 2\nu {{A}_{2}}} \right)\sin \psi + \left( { - aB_{1}^{2} + {{A}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial \theta }} - 2a\nu {{B}_{2}}} \right)\cos \psi + \\ \, + 2{{A}_{1}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial a\partial t}} + 2{{B}_{1}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial \theta \partial t}} = {{\nu }^{2}}{{h}_{1}}{{u}_{1}}\cos (\nu t) - {{\Delta }_{1}}{{u}_{1}} - {{\delta }_{1}}\left( {{{A}_{1}}\cos \psi - a{{B}_{1}}\sin \psi + \frac{{\partial {{u}_{1}}}}{{\partial t}}} \right) + \\ \, + a{{h}_{1}}{{\Delta }_{1}}\cos (\nu t)\cos \psi - a{{\Delta }_{2}}\cos \psi + a\nu {{\delta }_{2}}\sin \psi . \\ \end{gathered} $
Здесь присутствуют тригонометрические выражения $\cos (\nu t)\cos \psi $ (29) и
(32)
${{u}_{1}}\cos (\nu t) = - \frac{{a{{h}_{1}}}}{{12}}\cos (3\nu t + \theta ) + \frac{{a{{h}_{1}}}}{4}\sin (2\theta )\sin \psi + \left[ {\frac{{a{{h}_{1}}}}{6} + \frac{{a{{h}_{1}}}}{4}\cos (2\theta )} \right]\cos \psi ,$
которое получаем с использованием (31).

В функции ${{u}_{2}}$ будут отсутствовать колебания с основной частотой $\nu $, если приравняем нулю выражения с $\sin \psi $ и $\cos \psi $

$\begin{gathered} 2\nu {{A}_{2}} = - 2{{A}_{1}}{{B}_{1}} - a{{A}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial a}} - a{{B}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial \theta }} - a{{\delta }_{1}}{{B}_{1}} - \frac{{a{{\nu }^{2}}h_{1}^{2}}}{4}\sin (2\theta ) - a\nu {{\delta }_{2}}, \\ 2a\nu {{B}_{2}} = {{A}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial \theta }} - aB_{1}^{2} - \frac{{a{{\nu }^{2}}h_{1}^{2}}}{6} + {{\delta }_{1}}{{A}_{1}} - \frac{{a{{\nu }^{2}}h_{1}^{2}}}{4}\cos (2\theta ) + a{{\Delta }_{2}}. \\ \end{gathered} $
Отcюда после простых вычислений с использованием формул (30) получаем
(33)
${{A}_{2}} = - \frac{{a{{\delta }_{2}}}}{2} - \frac{{a\nu h_{1}^{2}}}{8}\sin (2\theta ),\quad {{B}_{2}} = \frac{{{{\Delta }_{2}}}}{{2\nu }} - \frac{{\Delta _{1}^{2}}}{{8{{\nu }^{3}}}} - \frac{{\delta _{1}^{2}}}{{8\nu }} - \frac{{\nu h_{1}^{2}}}{{12}} - \frac{{\nu h_{1}^{2}}}{8}\cos (2\theta ).$
Дифференциальное уравнение относительно ${{u}_{2}}$ приобретает вид
$\frac{{{{\partial }^{2}}{{u}_{2}}}}{{\partial {{t}^{2}}}} + {{\nu }^{2}}{{u}_{2}} = \frac{{a{{h}_{1}}{{\Delta }_{1}}}}{3}\cos (2\nu t + \theta ) - \frac{{a{{\nu }^{2}}h_{1}^{2}}}{{12}}\cos (3\nu t + \theta ).$
Оно имеет общее решение
(34)
${{u}_{2}} = {{C}_{1}}\cos (\nu t) + {{C}_{2}}\sin (\nu t) - \frac{{a{{h}_{1}}{{\Delta }_{1}}}}{{9{{\nu }^{2}}}}\cos (2\nu t + \theta ) + \frac{{ah_{1}^{2}}}{{96}}\cos (3\nu t + \theta ).$
Далее полагаем ${{C}_{1}} = {{C}_{2}} = 0$.

Приравняем выражения с ${{\varepsilon }^{3}}$ в (11) и (10), считая $p = q = 1$. Получаем дифференциальное уравнение относительно ${{u}_{3}}$:

$\begin{gathered} \frac{{{{\partial }^{2}}{{u}_{3}}}}{{\partial {{t}^{2}}}} + {{\nu }^{2}}{{u}_{3}} + \left( { - a{{A}_{1}}\frac{{\partial {{B}_{2}}}}{{\partial a}} - a{{A}_{2}}\frac{{\partial {{B}_{1}}}}{{\partial a}} - a{{B}_{1}}\frac{{\partial {{B}_{2}}}}{{\partial \theta }} - a{{B}_{2}}\frac{{\partial {{B}_{1}}}}{{\partial \theta }} - 2{{A}_{1}}{{B}_{2}} - 2{{A}_{2}}{{B}_{1}} - 2\nu {{A}_{3}}} \right)\sin \psi + \\ + \;\left( {{{A}_{1}}\frac{{\partial {{A}_{2}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{A}_{2}}}}{{\partial \theta }} + {{A}_{2}}\frac{{\partial {{A}_{1}}}}{{\partial a}} + {{B}_{2}}\frac{{\partial {{A}_{1}}}}{{\partial \theta }} - 2a{{B}_{1}}{{B}_{2}} - 2a\nu {{B}_{3}}} \right)\cos \psi + \frac{{\partial {{u}_{1}}}}{{\partial a}}\left( {{{A}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial \theta }}} \right) + A_{1}^{2}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{a}^{2}}}} + \\ \, + 2{{A}_{1}}{{B}_{1}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial a\partial \theta }} + 2{{A}_{2}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial a\partial t}} + 2{{A}_{1}}\frac{{{{\partial }^{2}}{{u}_{2}}}}{{\partial a\partial t}} + \frac{{\partial {{u}_{1}}}}{{\partial \theta }}\left( {{{A}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial \theta }}} \right) + B_{1}^{2}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{\theta }^{2}}}} + 2{{B}_{2}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial \theta \partial t}} + 2{{B}_{1}}\frac{{{{\partial }^{2}}{{u}_{2}}}}{{\partial \theta \partial t}} = \\ \end{gathered} $
$\begin{gathered} = {{\nu }^{2}}{{h}_{1}}{{u}_{2}}\cos (\nu t) - {{\Delta }_{1}}{{u}_{2}} - {{\delta }_{1}}\left( {{{A}_{2}}\cos \psi - a{{B}_{2}}\sin \psi + {{A}_{1}}\frac{{\partial {{u}_{1}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{u}_{1}}}}{{\partial \theta }} + \frac{{\partial {{u}_{2}}}}{{\partial t}}} \right) + {{h}_{1}}{{\Delta }_{1}}{{u}_{1}}\cos (\nu t) - \\ \, - {{\Delta }_{2}}{{u}_{1}} - {{\delta }_{2}}\left( {{{A}_{1}}\cos \psi - a{{B}_{1}}\sin \psi + \frac{{\partial {{u}_{1}}}}{{\partial t}}} \right) + a{{h}_{1}}{{\Delta }_{2}}\cos (\nu t)\cos \psi - a{{\Delta }_{3}}\cos \psi + a\nu {{\delta }_{3}}\sin \psi , \\ \end{gathered} $
где присутствуют тригонометрические выражения ${{u}_{1}}\cos (\nu t)$ (32), $\cos (\nu t)\cos \psi $ (29) и
${{u}_{2}}\cos (\nu t) = - \frac{{a{{h}_{1}}{{\Delta }_{1}}}}{{18{{\nu }^{2}}}}\left[ {\cos (3\nu t + \theta ) + \cos \psi } \right] + \frac{{ah_{1}^{2}}}{{192}}\left[ {\cos (4\nu t + \theta ) + \cos (2\nu t + \theta )} \right],$
которое вычислено с использованием формулы (34).

Приравняем нулю выражения с $\sin \psi $ и $\cos \psi $

$\begin{gathered} 2\nu {{A}_{3}} + a{{A}_{1}}\frac{{\partial {{B}_{2}}}}{{\partial a}} + a{{A}_{2}}\frac{{\partial {{B}_{1}}}}{{\partial a}} + a{{B}_{1}}\frac{{\partial {{B}_{2}}}}{{\partial \theta }} + a{{B}_{2}}\frac{{\partial {{B}_{1}}}}{{\partial \theta }} + 2{{A}_{1}}{{B}_{2}} + 2{{A}_{2}}{{B}_{1}} + \frac{{ah_{1}^{2}{{\Delta }_{1}}}}{4}\sin (2\theta ) + \\ \, + a{{\delta }_{1}}{{B}_{2}} + a{{\delta }_{2}}{{B}_{1}} + a\nu {{\delta }_{3}} = 0, \\ 2a\nu {{B}_{3}} - {{A}_{1}}\frac{{\partial {{A}_{2}}}}{{\partial a}} - {{B}_{1}}\frac{{\partial {{A}_{2}}}}{{\partial \theta }} - {{A}_{2}}\frac{{\partial {{A}_{1}}}}{{\partial a}} - {{B}_{2}}\frac{{\partial {{A}_{1}}}}{{\partial \theta }} + 2a{{B}_{1}}{{B}_{2}} + \frac{{ah_{1}^{2}{{\Delta }_{1}}}}{9} + \\ + \;\frac{{ah_{1}^{2}{{\Delta }_{1}}}}{4}\cos (2\theta ) - {{\delta }_{1}}{{A}_{2}} - {{\delta }_{2}}{{A}_{1}} - a{{\Delta }_{3}} = 0. \\ \end{gathered} $
Здесь ${{A}_{1}},\;{{B}_{1}}$ определяются формулами (30), ${{A}_{2}},\;{{B}_{2}}$ – (33). В результате простых вычислений получаем

(35)
${{A}_{3}} = - \frac{{a{{\delta }_{3}}}}{2} - \frac{{ah_{1}^{2}{{\Delta }_{1}}}}{{8\nu }}\sin (2\theta ),\quad {{B}_{3}} = \frac{{{{\Delta }_{3}}}}{{2\nu }} + \frac{{\Delta _{1}^{3}}}{{16{{\nu }^{5}}}} - \frac{{{{\Delta }_{1}}{{\Delta }_{2}}}}{{4{{\nu }^{3}}}} + \frac{{{{\Delta }_{1}}\delta _{1}^{2}}}{{16{{\nu }^{3}}}} - \frac{{{{\delta }_{1}}{{\delta }_{2}}}}{{4\nu }} - \frac{{h_{1}^{2}{{\Delta }_{1}}}}{{72\nu }} - \frac{{h_{1}^{2}{{\Delta }_{1}}}}{{8\nu }}\cos (2\theta ).$

Используя формулы (30), (33), (35), записываем систему (8) в виде (18), где в коэффициентах, имеющих вид разложения по степеням $\varepsilon $

$\delta = \varepsilon {{\delta }_{1}} + {{\varepsilon }^{2}}{{\delta }_{2}} + {{\varepsilon }^{3}}{{\delta }_{3}},\quad r = {{\varepsilon }^{2}}{{r}_{2}} + {{\varepsilon }^{3}}{{r}_{3}},\quad s = \varepsilon {{s}_{1}} + {{\varepsilon }^{2}}{{s}_{2}} + {{\varepsilon }^{3}}{{s}_{3}},$
составляющие равны

(36)
$\begin{gathered} {{r}_{2}} = - \frac{{\nu h_{1}^{2}}}{4},\quad {{r}_{3}} = - \frac{{h_{1}^{2}{{\Delta }_{1}}}}{{4\nu }},\quad {{s}_{1}} = \frac{{{{\Delta }_{1}}}}{\nu }, \\ {{s}_{2}} = \frac{{{{\Delta }_{2}}}}{\nu } - \frac{{\Delta _{1}^{2}}}{{4{{\nu }^{3}}}} - \frac{{\delta _{1}^{2}}}{{4\nu }} - \frac{{\nu h_{1}^{2}}}{6},\quad {{s}_{3}} = \frac{{{{\Delta }_{3}}}}{\nu } + \frac{{\Delta _{1}^{3}}}{{8{{\nu }^{5}}}} - \frac{{{{\Delta }_{1}}{{\Delta }_{2}}}}{{2{{\nu }^{3}}}} + \frac{{{{\Delta }_{1}}\delta _{1}^{2}}}{{8{{\nu }^{3}}}} - \frac{{{{\delta }_{1}}{{\delta }_{2}}}}{{2\nu }} - \frac{{h_{1}^{2}{{\Delta }_{1}}}}{{36\nu }}. \\ \end{gathered} $

Замена переменных (20) приводит к системе (21) и, как следствие, к уравнению (22), определяющему границу области параметрического резонанса. С учетом формул (36) запишем (22) подробно

$\begin{gathered} {{\varepsilon }^{2}}(s_{1}^{2} + \delta _{1}^{2}) + {{\varepsilon }^{3}}(2{{s}_{1}}{{s}_{2}} + 2{{\delta }_{1}}{{\delta }_{2}}) + {{\varepsilon }^{4}}(s_{2}^{2} + 2{{s}_{1}}{{s}_{3}} + \delta _{2}^{2} + 2{{\delta }_{1}}{{\delta }_{3}}) + {{\varepsilon }^{5}}(2{{s}_{2}}{{s}_{3}} + 2{{\delta }_{2}}{{\delta }_{3}}) + \\ \, + {{\varepsilon }^{6}}(s_{3}^{2} + \delta _{3}^{2}) = {{\varepsilon }^{4}}r_{2}^{2} + {{\varepsilon }^{5}}2{{r}_{2}}{{r}_{3}} + {{\varepsilon }^{6}}r_{3}^{2}. \\ \end{gathered} $

Приравнивая выражения с одинаковыми степенями $\varepsilon $ в левой и правой частях, получаем систему равенств

(37)
$\begin{gathered} s_{1}^{2} + \delta _{1}^{2} = 0,\quad {{s}_{1}}{{s}_{2}} + {{\delta }_{1}}{{\delta }_{2}} = 0,\quad s_{2}^{2} + 2{{s}_{1}}{{s}_{3}} + \delta _{2}^{2} + 2{{\delta }_{1}}{{\delta }_{3}} = r_{2}^{2}, \\ {{s}_{2}}{{s}_{3}} + {{\delta }_{2}}{{\delta }_{3}} = {{r}_{2}}{{r}_{3}},\quad s_{3}^{2} + \delta _{3}^{2} = r_{3}^{2}. \\ \end{gathered} $

Сначала найдем границу области параметрического резонанса во втором приближении, как в [1]. Для этого положим ${{\delta }_{3}} = {{r}_{3}} = {{s}_{3}} = 0$. Получаем

$s_{1}^{2} + \delta _{1}^{2} = 0,\quad {{s}_{1}}{{s}_{2}} + {{\delta }_{1}}{{\delta }_{2}} = 0,\quad s_{2}^{2} + \delta _{2}^{2} = r_{2}^{2}.$

Первое и второе равенства выполняются, если ${{s}_{1}} = {{\delta }_{1}} = 0$, т.е. согласно (36) при ${{\Delta }_{1}} = {{\delta }_{1}} = 0$. В этом случае частотная расстройка $\Delta \sim {{\varepsilon }^{2}}$ и коэффициент затухания $\delta \sim {{\varepsilon }^{2}}$. Далее, из (36) следуют выражения

${{s}_{2}} = \frac{{{{\Delta }_{2}}}}{\nu } - \frac{{\nu h_{1}^{2}}}{6},\quad {{r}_{2}} = - \frac{{\nu h_{1}^{2}}}{4},$
которые подставим в третье равенство
${{\left( {\frac{{{{\Delta }_{2}}}}{\nu } - \frac{{\nu h_{1}^{2}}}{6}} \right)}^{2}} = \frac{{{{\nu }^{2}}h_{1}^{4}}}{{16}} - \delta _{2}^{2}.$
Отсюда

$\frac{{{{\Delta }_{2}}}}{\nu } = \frac{{\nu h_{1}^{2}}}{6} \pm \sqrt {\frac{{{{\nu }^{2}}h_{1}^{4}}}{{16}} - \delta _{2}^{2}} .$

Умножим на ${{\varepsilon }^{2}}$

$\frac{{{{\varepsilon }^{2}}{{\Delta }_{2}}}}{\nu } = \frac{{\nu {{h}^{2}}}}{6} \pm \sqrt {\frac{{{{\nu }^{2}}{{h}^{4}}}}{{16}} - {{\delta }^{2}}} $
и подставим частотную расстройку
${{\varepsilon }^{2}}{{\Delta }_{2}} = {{\omega }^{2}} - {{\nu }^{2}},$
которая следует из формулы (2) при ${{\Delta }_{1}} = 0,$ $p = q = 1$. Приходим к выражению
$\frac{{{{\omega }^{2}} - {{\nu }^{2}}}}{\nu } = \frac{{\nu {{h}^{2}}}}{6} \pm \sqrt {\frac{{{{\nu }^{2}}{{h}^{4}}}}{{16}} - {{\delta }^{2}}} ,$
которое умножаем на $4{\text{/}}\nu $. В результате получаем границу области параметрического резонанса на плоскости параметров $((2\omega /\nu {{)}^{2}},h)$ (как в работе [1])
(38)
${{\left( {\frac{{2\omega }}{\nu }} \right)}^{2}} = 4 + \frac{{2{{h}^{2}}}}{3} \pm \sqrt {{{h}^{4}} - \frac{{16{{\delta }^{2}}}}{{{{\nu }^{2}}}}} .$
Эта формула отличается от формулы (17.63) в [1] числовым множителем при ${{\delta }^{2}}$. Там вместо 16 стоит 64.

В третьем приближении используем оценки $\Delta ,\delta \sim {{\varepsilon }^{2}}$. Тогда ${{\Delta }_{1}} = {{\delta }_{1}} = {{\Delta }_{3}} = {{\delta }_{3}} = 0$, и по формулам (36) получаем

${{s}_{2}} = \frac{{{{\Delta }_{2}}}}{\nu } - \frac{{\nu h_{1}^{2}}}{6},\quad {{r}_{2}} = - \frac{{\nu h_{1}^{2}}}{4},\quad {{s}_{3}} = {{r}_{3}} = 0,$
как во втором приближении. В результате граница области параметрического резонанса в третьем приближении совпадает с границей (38) во втором приближении.

На фиг. 2 показана граница, вычисленная по формуле (38) для трех значений $\delta {\text{/}}\nu = 0.05$; 0.1; 0.15 (линии 3, 4, 5 соответственно). Кривая 2 – граница, которая следует из (38) при отсутствии затухания ($\delta {\text{/}}\nu = 0$). Эта граница, вычисленная численным интегрированием уравнения Матье (28), изображена штриховой линией 1. Штриховая линия 6 – граница области параметрического резонанса при затухании $\delta {\text{/}}\nu = 0.05$ получена также численным интегрированием.

Фиг. 2

4. РЕЗОНАНС $\omega \approx \frac{3}{2}\nu $

Получим формулу для границы третьей области параметрического резонанса (формула (48)). Результат сравним с [1].

Из равенства выражений с $\varepsilon $ в (11) и (10) при $p = 3,q = 2$ следует дифференциальное уравнение

$\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{t}^{2}}}} + \frac{{9{{\nu }^{2}}}}{4}{{u}_{1}} - 3\nu {{A}_{1}}\sin \psi - 3a\nu {{B}_{1}}\cos \psi = \frac{{9a{{\nu }^{2}}{{h}_{1}}}}{4}\cos (\nu t)\cos \psi - a{{\Delta }_{1}}\cos \psi + \frac{{3a\nu {{\delta }_{1}}}}{2}\sin \psi .$
Здесь
$\psi = \frac{{3\nu }}{2}t + \theta $
и

(39)
$\cos (\nu t)\cos \psi = \frac{1}{2}\left[ {\cos \left( {\frac{{5\nu }}{2}t + \theta } \right) + \cos \left( {\frac{\nu }{2}t + \theta } \right)} \right].$

Приравняем нулю выражения, содержащие $\sin \psi $ и $\cos \psi $

$3\nu {{A}_{1}} + \frac{{3a\nu {{\delta }_{1}}}}{2} = 0,\quad 3a\nu {{B}_{1}} - a{{\Delta }_{1}} = 0,$
откуда

(40)
${{A}_{1}} = - \frac{{a{{\delta }_{1}}}}{2},\quad {{B}_{1}} = \frac{{{{\Delta }_{1}}}}{{3\nu }}.$

Дифференциальное уравнение приобретает вид

$\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{t}^{2}}}} + \frac{{9{{\nu }^{2}}}}{4}{{u}_{1}} = \frac{{9a{{\nu }^{2}}{{h}_{1}}}}{8}\cos \left( {\frac{\nu }{2}t + \theta } \right) + \frac{{9a{{\nu }^{2}}{{h}_{1}}}}{8}\cos \left( {\frac{{5\nu }}{2}t + \theta } \right).$
Оно имеет общее решение
(41)
${{u}_{1}} = {{C}_{1}}\cos \left( {\frac{{3\nu }}{2}t} \right) + {{C}_{2}}\sin \left( {\frac{{3\nu }}{2}t} \right) + \frac{{9a{{h}_{1}}}}{{16}}\cos \left( {\frac{\nu }{2}t + \theta } \right) - \frac{{9a{{h}_{1}}}}{{32}}\cos \left( {\frac{{5\nu }}{2}t + \theta } \right),$
в котором далее полагаем ${{C}_{1}} = {{C}_{2}} = 0$.

Приравняем теперь выражения с ${{\varepsilon }^{2}}$ в (11) и (10) c $p = 3,$ $q = 2$

(42)
$\begin{gathered} \frac{{{{\partial }^{2}}{{u}_{2}}}}{{\partial {{t}^{2}}}} + \frac{{9{{\nu }^{2}}}}{4}{{u}_{2}} + \left( { - 2{{A}_{1}}{{B}_{1}} - a{{A}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial a}} - a{{B}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial \theta }} - 3\nu {{A}_{2}}} \right)\sin \psi + \\ + \;\left( { - aB_{1}^{2} + {{A}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial \theta }} - 3a\nu {{B}_{2}}} \right)\cos \psi + 2{{A}_{1}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial a\partial t}} + 2{{B}_{1}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial \theta \partial t}} = \frac{{9{{\nu }^{2}}{{h}_{1}}}}{4}{{u}_{1}}\cos (\nu t) - {{\Delta }_{1}}{{u}_{1}} - \\ \, - {{\delta }_{1}}\left( {{{A}_{1}}\cos \psi - a{{B}_{1}}\sin \psi + \frac{{\partial {{u}_{1}}}}{{\partial t}}} \right) + a{{h}_{1}}{{\Delta }_{1}}\cos (\nu t)\cos \psi - a{{\Delta }_{2}}\cos \psi + \frac{{3a\nu {{\delta }_{2}}}}{2}\sin \psi . \\ \end{gathered} $
Здесь присутствуют тригонометрические выражения (39) и
(43)
${{u}_{1}}\cos (\nu t) = \frac{{9a{{h}_{1}}}}{{32}}\cos \left( {\frac{\nu }{2}t - \theta } \right) - \frac{{9a{{h}_{1}}}}{{64}}\cos \left( {\frac{{7\nu }}{2}t + \theta } \right) + \frac{{9a{{h}_{1}}}}{{64}}\cos \psi ,$
которое вычислено с учетом (41).

Приравняем нулю выражения с $\sin \psi $ и $\cos \psi $

$\begin{gathered} 3\nu {{A}_{2}} + 2{{A}_{1}}{{B}_{1}} + a{{A}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial a}} + a{{B}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial \theta }} + a{{\delta }_{1}}{{B}_{1}} + \frac{{3a\nu {{\delta }_{2}}}}{2} = 0, \\ 3a\nu {{B}_{2}} - {{A}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial a}} - {{B}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial \theta }} + aB_{1}^{2} + \frac{{81a{{\nu }^{2}}h_{1}^{2}}}{{256}} - {{\delta }_{1}}{{A}_{1}} - a{{\Delta }_{2}} = 0. \\ \end{gathered} $
Используя формулы (40), получаем

(44)
${{A}_{2}} = - \frac{{a{{\delta }_{2}}}}{2},\quad {{B}_{2}} = \frac{{{{\Delta }_{2}}}}{{3\nu }} - \frac{{\Delta _{1}^{2}}}{{27{{\nu }^{3}}}} - \frac{{\delta _{1}^{2}}}{{12\nu }} - \frac{{27\nu h_{1}^{2}}}{{256}}.$

Дифференциальное уравнение (42) относительно ${{u}_{2}}$ принимает вид

$\begin{gathered} \frac{{{{\partial }^{2}}{{u}_{2}}}}{{\partial {{t}^{2}}}} + \frac{{9{{\nu }^{2}}}}{4}{{u}_{2}} = \frac{{81a{{\nu }^{2}}h_{1}^{2}}}{{128}}\cos \left( {\frac{\nu }{2}t - \theta } \right) + \frac{{a{{h}_{1}}{{\Delta }_{1}}}}{8}\cos \left( {\frac{\nu }{2}t + \theta } \right) + \\ \, + \frac{{5a{{h}_{1}}{{\Delta }_{1}}}}{{16}}\cos \left( {\frac{{5\nu }}{2}t + \theta } \right) - \frac{{81a{{\nu }^{2}}h_{1}^{2}}}{{256}}\cos \left( {\frac{{7\nu }}{2}t + \theta } \right). \\ \end{gathered} $
Оно имеет общее решение
(45)
$\begin{gathered} {{u}_{2}} = {{C}_{1}}\cos \left( {\frac{{3\nu }}{2}t} \right) + {{C}_{2}}\sin \left( {\frac{{3\nu }}{2}t} \right) + \frac{{81ah_{1}^{2}}}{{256}}\cos \left( {\frac{\nu }{2}t - \theta } \right) + \frac{{a{{h}_{1}}{{\Delta }_{1}}}}{{16{{\nu }^{2}}}}\cos \left( {\frac{\nu }{2}t + \theta } \right) - \\ \, - \frac{{5a{{h}_{1}}{{\Delta }_{1}}}}{{64{{\nu }^{2}}}}\cos \left( {\frac{{5\nu }}{2}t + \theta } \right) + \frac{{81ah_{1}^{2}}}{{2560}}\cos \left( {\frac{{7\nu }}{2}t + \theta } \right). \\ \end{gathered} $
Далее полагаем ${{C}_{1}} = {{C}_{2}} = 0$.

Формулы третьего приближения получим из равенства выражений с ${{\varepsilon }^{3}}$ в (11) и (10) при $p = 3,q = 2$

$\begin{gathered} \frac{{{{\partial }^{2}}{{u}_{3}}}}{{\partial {{t}^{2}}}} + \frac{{9{{\nu }^{2}}}}{4}{{u}_{3}} + \left( { - a{{A}_{1}}\frac{{\partial {{B}_{2}}}}{{\partial a}} - a{{A}_{2}}\frac{{\partial {{B}_{1}}}}{{\partial a}} - a{{B}_{1}}\frac{{\partial {{B}_{2}}}}{{\partial \theta }} - a{{B}_{2}}\frac{{\partial {{B}_{1}}}}{{\partial \theta }} - 2{{A}_{1}}{{B}_{2}} - 2{{A}_{2}}{{B}_{1}} - 3\nu {{A}_{3}}} \right)\sin \psi + \\ + \;\left( {{{A}_{1}}\frac{{\partial {{A}_{2}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{A}_{2}}}}{{\partial \theta }} + {{A}_{2}}\frac{{\partial {{A}_{1}}}}{{\partial a}} + {{B}_{2}}\frac{{\partial {{A}_{1}}}}{{\partial \theta }} - 2a{{B}_{1}}{{B}_{2}} - 3a\nu {{B}_{3}}} \right)\cos \psi + \frac{{\partial {{u}_{1}}}}{{\partial a}}\left( {{{A}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial \theta }}} \right) + A_{1}^{2}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{a}^{2}}}} + \\ \, + 2{{A}_{1}}{{B}_{1}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial a\partial \theta }} + 2{{A}_{2}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial a\partial t}} + 2{{A}_{1}}\frac{{{{\partial }^{2}}{{u}_{2}}}}{{\partial a\partial t}} + \frac{{\partial {{u}_{1}}}}{{\partial \theta }}\left( {{{A}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{B}_{1}}}}{{\partial \theta }}} \right) + B_{1}^{2}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{\theta }^{2}}}} + 2{{B}_{2}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial \theta \partial t}} + 2{{B}_{1}}\frac{{{{\partial }^{2}}{{u}_{2}}}}{{\partial \theta \partial t}} = \\ \end{gathered} $
$\begin{gathered} = \frac{{9{{\nu }^{2}}{{h}_{1}}}}{4}{{u}_{2}}\cos (\nu t) - {{\Delta }_{1}}{{u}_{2}} - {{\delta }_{1}}\left( {{{A}_{2}}\cos \psi - a{{B}_{2}}\sin \psi + {{A}_{1}}\frac{{\partial {{u}_{1}}}}{{\partial a}} + {{B}_{1}}\frac{{\partial {{u}_{1}}}}{{\partial \theta }} + \frac{{\partial {{u}_{2}}}}{{\partial t}}} \right) + {{h}_{1}}{{\Delta }_{1}}{{u}_{1}}\cos (\nu t) - \\ \, - {{\Delta }_{2}}{{u}_{1}} - {{\delta }_{2}}\left( {{{A}_{1}}\cos \psi - a{{B}_{1}}\sin \psi + \frac{{\partial {{u}_{1}}}}{{\partial t}}} \right) + a{{h}_{1}}{{\Delta }_{2}}\cos (\nu t)\cos \psi - a{{\Delta }_{3}}\cos \psi + \frac{{3a\nu {{\delta }_{3}}}}{2}\sin \psi . \\ \end{gathered} $
Здесь присутствуют тригонометрические выражения (39), (43) и
$\begin{gathered} {{u}_{2}}\cos (\nu t) = \frac{{81ah_{1}^{2}}}{{512}}\left[ {\cos (2\theta )\cos \psi + \sin (2\theta )\sin \psi } \right] - \frac{{a{{h}_{1}}{{\Delta }_{1}}}}{{128{{\nu }^{2}}}}\cos \psi + \frac{{a{{h}_{1}}{{\Delta }_{1}}}}{{32{{\nu }^{2}}}}\cos \left( {\frac{\nu }{2}t - \theta } \right) + \\ \, + \frac{{81ah_{1}^{2}}}{{512}}\cos \left( {\frac{\nu }{2}t + \theta } \right) + \frac{{81ah_{1}^{2}}}{{5120}}\cos \left( {\frac{{5\nu }}{2}t + \theta } \right) - \frac{{5a{{h}_{1}}{{\Delta }_{1}}}}{{128{{\nu }^{2}}}}\cos \left( {\frac{{7\nu }}{2}t + \theta } \right) + \frac{{81ah_{1}^{2}}}{{5120}}\cos \left( {\frac{{9\nu }}{2}t + \theta } \right), \\ \end{gathered} $
которое получаем с использованием ${{u}_{2}}$ (45).

Приравняем нулю выражения с $\sin \psi $ и $\cos \psi $

$\begin{gathered} 3\nu {{A}_{3}} + a{{A}_{1}}\frac{{\partial {{B}_{2}}}}{{\partial a}} + a{{A}_{2}}\frac{{\partial {{B}_{1}}}}{{\partial a}} + a{{B}_{1}}\frac{{\partial {{B}_{2}}}}{{\partial \theta }} + a{{B}_{2}}\frac{{\partial {{B}_{1}}}}{{\partial \theta }} + 2{{A}_{1}}{{B}_{2}} + 2{{A}_{2}}{{B}_{1}} + \\ \, + \frac{{729a{{\nu }^{2}}h_{1}^{3}}}{{2048}}\sin (2\theta ) + a{{\delta }_{1}}{{B}_{2}} + a{{\delta }_{2}}{{B}_{1}} + \frac{{3a\nu {{\delta }_{3}}}}{2} = 0, \\ \end{gathered} $
$\begin{gathered} 3a\nu {{B}_{3}} - {{A}_{1}}\frac{{\partial {{A}_{2}}}}{{\partial a}} - {{B}_{1}}\frac{{\partial {{A}_{2}}}}{{\partial \theta }} - {{A}_{2}}\frac{{\partial {{A}_{1}}}}{{\partial a}} - {{B}_{2}}\frac{{\partial {{A}_{1}}}}{{\partial \theta }} + 2a{{B}_{1}}{{B}_{2}} + \\ \, + \frac{{63ah_{1}^{2}{{\Delta }_{1}}}}{{512}} + \frac{{729a{{\nu }^{2}}h_{1}^{3}}}{{2048}}\cos (2\theta ) - {{\delta }_{1}}{{A}_{2}} - {{\delta }_{2}}{{A}_{1}} - a{{\Delta }_{3}} = 0. \\ \end{gathered} $

Учитывая формулы (40), (44), после простых вычислений получаем

$\begin{gathered} {{A}_{3}} = - \frac{{a{{\delta }_{3}}}}{2} - \frac{{243a\nu h_{1}^{3}}}{{2048}}\sin (2\theta ), \\ {{B}_{3}} = \frac{{{{\Delta }_{3}}}}{{3\nu }} + \frac{{2\Delta _{1}^{3}}}{{243{{\nu }^{5}}}} - \frac{{2{{\Delta }_{1}}{{\Delta }_{2}}}}{{27{{\nu }^{3}}}} + \frac{{{{\Delta }_{1}}\delta _{1}^{2}}}{{54{{\nu }^{3}}}} - \frac{{{{\delta }_{1}}{{\delta }_{2}}}}{{6\nu }} - \frac{{9h_{1}^{2}{{\Delta }_{1}}}}{{512\nu }} - \frac{{243\nu h_{1}^{3}}}{{2048}}\cos (2\theta ). \\ \end{gathered} $

Эти формулы, а также (40) и (44) позволяют записать систему дифференциальных уравнений (8) в виде (18) с коэффициентами

(46)
$\delta = \varepsilon {{\delta }_{1}} + {{\varepsilon }^{2}}{{\delta }_{2}} + {{\varepsilon }^{3}}{{\delta }_{3}},\quad r = {{\varepsilon }^{3}}{{r}_{3}},\quad s = \varepsilon {{s}_{1}} + {{\varepsilon }^{2}}{{s}_{2}} + {{\varepsilon }^{3}}{{s}_{3}},$
в которых

(47)
$\begin{gathered} {{r}_{3}} = - \frac{{243\nu h_{1}^{3}}}{{1024}},\quad {{s}_{1}} = \frac{{2{{\Delta }_{1}}}}{{3\nu }},\quad {{s}_{2}} = \frac{{2{{\Delta }_{2}}}}{{3\nu }} - \frac{{2\Delta _{1}^{2}}}{{27{{\nu }^{3}}}} - \frac{{\delta _{1}^{2}}}{{6\nu }} - \frac{{27\nu h_{1}^{2}}}{{128}}, \\ {{s}_{3}} = \frac{{2{{\Delta }_{3}}}}{{3\nu }} - \frac{{4{{\Delta }_{1}}{{\Delta }_{2}}}}{{27{{\nu }^{3}}}} + \frac{{4\Delta _{1}^{3}}}{{243{{\nu }^{5}}}} + \frac{{{{\Delta }_{1}}\delta _{1}^{2}}}{{27{{\nu }^{3}}}} - \frac{{{{\delta }_{1}}{{\delta }_{2}}}}{{3\nu }} - \frac{{9{{\Delta }_{1}}h_{1}^{2}}}{{256\nu }}. \\ \end{gathered} $

Подстановка (20) приводит систему (18) к системе (21) и далее к равенству (22), определяющему границу области параметрического резонанса. При подстановке разложений (46) в (22) приходим к системе равенств

$\begin{gathered} s_{1}^{2} + \delta _{1}^{2} = 0,\quad {{s}_{1}}{{s}_{2}} + {{\delta }_{1}}{{\delta }_{2}} = 0,\quad s_{2}^{2} + 2{{s}_{1}}{{s}_{3}} + \delta _{2}^{2} + 2{{\delta }_{1}}{{\delta }_{3}} = 0, \\ {{s}_{2}}{{s}_{3}} + {{\delta }_{2}}{{\delta }_{3}} = 0,\quad s_{3}^{2} + \delta _{3}^{2} = r_{3}^{2}. \\ \end{gathered} $

Из первого следует ${{s}_{1}} = {{\delta }_{1}} = 0$. При этих значениях справедливо второе равенство. Третье принимает вид $s_{2}^{2} + \delta _{2}^{2} = 0$, откуда получаем ${{s}_{2}} = {{\delta }_{2}} = 0$, и, значит, справедливо четвертое равенство. Граница области параметрического резонанса определяется пятым равенством

$s_{3}^{2} + \delta _{3}^{2} = r_{3}^{2}.$

Уточним формулы для ${{s}_{2}}$ и ${{s}_{3}}$ (47). При ${{s}_{1}} = 0$ имеем ${{\Delta }_{1}} = 0$. Тогда с учетом значения ${{\delta }_{1}} = 0$ получаем

${{s}_{2}} = \frac{{2{{\Delta }_{2}}}}{{3\nu }} - \frac{{27\nu h_{1}^{2}}}{{128}},\quad {{s}_{3}} = \frac{{2{{\Delta }_{3}}}}{{3\nu }}.$

Из условия ${{s}_{2}} = 0$ следует

${{\Delta }_{2}} = \frac{{81{{\nu }^{2}}h_{1}^{2}}}{{256}}.$

Теперь запишем подробно пятое равенство, умножая его на ${{\varepsilon }^{6}}$:

$\frac{{4({{\varepsilon }^{3}}{{\Delta }_{3}}{{)}^{2}}}}{{9{{\nu }^{2}}}} + {{({{\varepsilon }^{3}}{{\delta }_{3}})}^{2}} = {{\left( {\frac{{243}}{{1024}}} \right)}^{2}}{{\nu }^{2}}{{(\varepsilon {{h}_{1}})}^{6}}.$
Подставим выражение
${{\varepsilon }^{3}}{{\Delta }_{3}} = {{\omega }^{2}} - \frac{{9{{\nu }^{2}}}}{4} - {{\varepsilon }^{2}}{{\Delta }_{2}},$
полученное из формулы (2):
$\frac{4}{{9{{\nu }^{2}}}}{{\left( {{{\omega }^{2}} - \frac{{9{{\nu }^{2}}}}{4} - {{\varepsilon }^{2}}{{\Delta }_{2}}} \right)}^{2}} = {{\left( {\frac{{243}}{{1024}}} \right)}^{2}}{{\nu }^{2}}{{h}^{6}} - {{\delta }^{2}}.$
Подставим сюда ${{\Delta }_{2}}$:
$\frac{4}{{9{{\nu }^{2}}}}{{\left( {{{\omega }^{2}} - \frac{{9{{\nu }^{2}}}}{4} - \frac{{81{{\nu }^{2}}{{h}^{2}}}}{{256}}} \right)}^{2}} = {{\left( {\frac{{243}}{{1024}}} \right)}^{2}}{{\nu }^{2}}{{h}^{6}} - {{\delta }^{2}}.$
Выразим ${{(2\omega {\text{/}}\nu )}^{2}}$. Для этого умножаем на $36{\text{/}}{{\nu }^{2}}$ и извлекаем квадратный корень. В результате получаем границу области параметрического резонанса на плоскости параметров $((2\omega {\text{/}}\nu {{)}^{2}},h)$
(48)
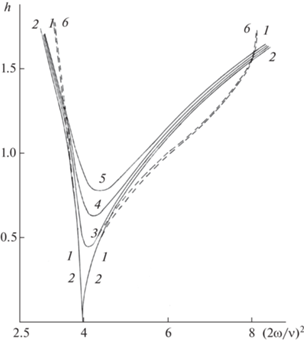
${{\left( {\frac{{2\omega }}{\nu }} \right)}^{2}} = 9 + \frac{{81{{h}^{2}}}}{{64}} \pm \sqrt {{{{\left( {\frac{{81}}{{64}}} \right)}}^{3}}{{h}^{6}} - \frac{{36{{\delta }^{2}}}}{{{{\nu }^{2}}}}} .$
В [1] под корнем при ${{\delta }^{2}}$ стоит множитель 324 (см. формулу (17.64)).

На фиг. 3 показана граница (48) третьей области параметрического резонанса при значениях затуханий $\delta {\text{/}}\nu = 0,0.01;\;0.02;\;0.04$ (кривые 2, 3, 4, 5 соответственно). При значении $\delta {\text{/}}\nu = 0.01$ изображена также граница 6 (штриховая линия), полученная численным интегрированием уравнения Матье (28). Штриховая линия 1 – граница при отсутствии затухания – также результат численного интегрирования.

Фиг. 3

5. ГРАНИЦЫ ОБЛАСТЕЙ ПАРАМЕТРИЧЕСКОГО РЕЗОНАНСА ДЛЯ УРАВНЕНИЯ $\ddot {x} + \delta \dot {x} + \left[ {a + q\cos (2t)} \right]x = 0$

Уравнение Матье в такой записи часто встречается в литературе (см., например, [4], [2]). Для него из формул (27), (38), (48), полученных из уравнения (1), выведем формулы, описывающие границы трех областей параметрического резонанса на плоскости параметров ($a,q$).

Из сравнения уравнений следуют соотношения

(49)
${{\omega }^{2}} = a,\quad h = - \frac{q}{a} \sim \varepsilon ,\quad \nu = 2.$
Формула (27), справедливая в случае резонанса $\omega \approx \nu {\text{/}}2 = 1$, приобретает вид
$a = 1 \pm \sqrt {\frac{{{{q}^{2}}}}{{4{{a}^{2}}}} - {{\delta }^{2}}} + \frac{{7{{q}^{2}}}}{{32{{a}^{2}}}}.$
Поскольку параметры $q$ и $\delta $ имеют одинаковый порядок малости ($ \sim {\kern 1pt} \varepsilon $), положим $\delta = kq$ , где $k \sim 1$, и перепишем это выражение

(50)
$a = 1 \pm q\sqrt {\frac{1}{{4{{a}^{2}}}} - {{k}^{2}}} + \frac{{7{{q}^{2}}}}{{32{{a}^{2}}}}.$

Корни $a$ уравнения будем искать в виде разложения по степеням $q$

(51)
$a = 1 + q{{a}_{1}} + {{q}^{2}}{{a}_{2}} + {{q}^{3}}{{a}_{3}} + \ldots .$
Сделаем разложение во втором слагаемом правой части (50)
$\begin{gathered} \sqrt {\frac{1}{{4{{a}^{2}}}} - {{k}^{2}}} = \sqrt {\frac{1}{4} - {{k}^{2}}} + {{\left. {\left( {\sqrt {\frac{1}{{4{{a}^{2}}}} - {{k}^{2}}} } \right)_{a}^{'}} \right|}_{{a = 1}}}(q{{a}_{1}} + {{q}^{2}}{{a}_{2}} + \cdots ) + \frac{1}{2}{{\left. {\left( {\sqrt {\frac{1}{{4{{a}^{2}}}} - {{k}^{2}}} } \right)_{{{{a}^{2}}}}^{{''}}} \right|}_{{a = 1}}}{{(q{{a}_{1}} + \cdots )}^{2}} + \cdots = \\ \, = \sqrt {\frac{1}{4} - {{k}^{2}}} - \frac{1}{{4\sqrt {\frac{1}{4} - {{k}^{2}}} }}(q{{a}_{1}} + {{q}^{2}}{{a}_{2}} + \cdots ) + \frac{{1 - 6{{k}^{2}}}}{{16{{{\left( {\frac{1}{4} - {{k}^{2}}} \right)}}^{{3/2}}}}}({{q}^{2}}a_{1}^{2} + \cdots ), \\ \end{gathered} $
в третьем слагаемом –

$\frac{1}{{{{a}^{2}}}} = 1 - 2q{{a}_{1}} + \ldots .$

Подставим эти разложения и (51) в уравнение (50), приравняем выражения с одинаковыми степенями $q$ в левой и правой частях:

$q\,:\;\;{{a}_{1}} = \pm \sqrt {\frac{1}{4} - {{k}^{2}}} ;\quad {{q}^{2}}\,:\;\;{{a}_{2}} = \mp \frac{1}{{4\sqrt {\frac{1}{4} - {{k}^{2}}} }}{{a}_{1}} + \frac{7}{{32}}.$
Отсюда

${{a}_{2}} = - \frac{1}{{32}}.$

Подставляя ${{a}_{{1,2}}}$ в (51) и учитывая формулу $k = \delta {\text{/}}q$, получаем выражение, описывающее границу области параметрического резонанса $a \approx 1$ на плоскости параметров ($a,q$)

(52)
$a = 1 \pm \frac{{\sqrt {{{q}^{2}} - 4{{\delta }^{2}}} }}{2} - \frac{{{{q}^{2}}}}{{32}}.$

При резонансе $\omega \approx \nu = 2$ с использованием формул (49) запишем выражение (38) для границы области параметрического резонанса

$a = 4 + \frac{{2{{q}^{2}}}}{{3{{a}^{2}}}} \pm \sqrt {\frac{{{{q}^{4}}}}{{{{a}^{4}}}} - 4{{\delta }^{2}}} .$
Ищем решение этого уравнения, зависящего от $a$, в виде
$a = 4 + q{{a}_{1}} + {{q}^{2}}{{a}_{2}} + {{q}^{3}}{{a}_{3}} + \ldots .$
Учитывая оценку $\delta \sim {{q}^{2}}$ и полагая $\delta = k{{q}^{2}}$, разлагая функции по степеням $q$ и приравнивая выражения с одинаковыми степенями $q$ в левой и правой частях уравнения, находим
${{a}_{1}} = 0,\quad {{a}_{2}} = \frac{1}{{24}} \pm \sqrt {\frac{1}{{256}} - 4{{k}^{2}}} ,\quad {{a}_{3}} = 0.$
Таким образом, сохраняя точность третьего приближения, получаем границу области параметрического резонанса на плоскости параметров ($a,q$)

(53)
$a = 4 + \frac{{{{q}^{2}}}}{{24}} \pm \sqrt {\frac{{{{q}^{4}}}}{{256}} - 4{{\delta }^{2}}} .$

В случае $\omega \approx 3\nu {\text{/}}2 = 3$ с использованием формул (49) и $\delta = k{{q}^{3}}$ запишем выражение (48) для границы области параметрического резонанса

$a = 9 + \frac{{81{{q}^{2}}}}{{64{{a}^{2}}}} \pm {{q}^{3}}\sqrt {\frac{{{{{81}}^{3}}}}{{{{{64}}^{3}}{{a}^{6}}}} - 9{{k}^{2}}} .$
Ищем решение $a$ в виде разложения
$a = 9 + q{{a}_{1}} + {{q}^{2}}{{a}_{2}} + {{q}^{3}}{{a}_{3}} + \ldots .$
Тогда во втором слагаемом в правой части
$\frac{1}{{{{a}^{2}}}} = \frac{1}{{81}} - \frac{{2q}}{{729}}{{a}_{1}} + \ldots .$
Из сравнения коэффициентов при одинаковых степенях $q$ получаем
${{a}_{1}} = 0,\quad {{a}_{2}} = \frac{1}{{64}},\quad {{a}_{3}} = \pm \sqrt {\frac{1}{{{{{64}}^{3}}}} - 9{{k}^{2}}} .$
Окончательно имеем

(54)
$a = 9 + \frac{{{{q}^{2}}}}{{64}} \pm \sqrt {{{{\left( {\frac{{{{q}^{3}}}}{{512}}} \right)}}^{2}} - 9{{\delta }^{2}}} .$

Формулы (52)–(54) получены асимптотическим методом усреднения [3], [4] в статье [2]. При этом уравнение Матье с параметрами $a$ и $q$ приводилось к системе уравнений, содержащей несколько быстрых фаз, как это делалось для уравнений Матье в [4]–[6], а также уравнения Хилла без затухания в [10] и с затуханием в [11].

Список литературы

  1. Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. М.: Наука, 1974.

  2. Беломытцева Е.Г., Курин А.Ф., Туленко Е.Б. Задача Коши для уравнения Матье с затуханием при параметрическом резонансе // Вестн. Воронеж. гос. ун-та. Сер. Физика, математика. 2018. № 3. С. 105–125.

  3. Моисеев Н.Н. Асимптотические методы нелинейной механики. М.: Наука, 1981.

  4. Гребеников Е.А. Метод усреднения в прикладных задачах. М.: Наука, 1986.

  5. Курин А.Ф. Задача Коши для уравнения Матье при параметрическом резонансе // Ж. вычисл. матем. и матем. физ. 2008. Т. 48. № 4. С. 633–650.

  6. Курин А.Ф. Задача Коши для уравнения Матье вдали от параметрического резонанса // Ж. вычисл. матем. и матем. физ. 2011. Т. 51. № 8. С. 1419–1433.

  7. Штокало И.З. Линейные дифференциальные уравнения с переменными коэффициентами. Киев: Изд-во АН Украинской ССР, 1960.

  8. Колесов Ю.С., Майоров В.В. Новый метод исследования устойчивости решений линейных дифференциальных уравнений с близкими к постоянным почти периодическими коэффициентами // Дифференц. ур-ния. 1974. Т. 10. № 10. С. 1778–1788.

  9. Горелик Г. Резонансные явления в линейных системах с периодически меняющимися параметрами // Ж. теор. физ. 1935. Т. 5. № 3. С. 489–517.

  10. Курин А.Ф. Спектральный критерий устойчивости и задача Коши для уравнения Хилла при параметрическом резонансе // Ж. вычисл. матем. и матем. физ. 2009. Т. 49. № 3. С. 498–511.

  11. Беломытцева Е.Г., Курин А.Ф., Туленко Е.Б. Спектральный критерий устойчивости и задача Коши для уравнения Хилла с затуханием при параметрическом резонансе// Вестн. Воронеж. гос. ун-та. Сер. Физика, математика. 2019. № 1. С. 69–90.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал