Журнал вычислительной математики и математической физики, 2022, T. 62, № 12, стр. 2002-2017

1. ВВЕДЕНИЕ

Остаточный член в проблеме круга (в проблеме Гаусса) определяется равенством

где $R(x)$ – число целых точек в круге радиуса $\sqrt x $ . Функция $P(x)$ – кусочно-линейная функция с разрывами I рода в ряде целых точек, где она непрерывна справа.

Проблема круга заключается в доказательстве оценки

для любого $\varepsilon > 0$.

Доказательству оценок вида

посвящено большое количество работ (см. [1], [2]). В настоящее время оценка (3) доказана при $\theta = 517{\text{/}}1648 = 0.31371 \ldots $ (см. [3]).

Кроме асимптотических оценок вида (3) представляют интерес и другие свойства функции $P(x)$. Это связано, в частности, с тем, что задача о числе целых точек в круге имеет спектральную интерпретацию. С точки зрения спектральной теории величина $P(x)$ – это второй член в формуле Вейля для функции распределения собственных значений оператора Лапласа на плоском торе, и свойства $P(x)$ интересны в связи с теорией “квантового хаоса”. Обзор теоретических работ, посвященных исследованию свойств $P(x)$, представлен в [4].

Функция $P(x)$ исследовалась также и численно [5]–[9]. В [5] рассматривался вопрос об определении величины $\theta $, такой что

и было показано, что $\theta \leqslant 0.35$ при ${{x}_{{\max }}} \lesssim {{10}^{{10}}}$. Этот результат был усилен в [8], где было показано, что $\theta \leqslant 0.28$ также при ${{x}_{{\max }}} \lesssim {{10}^{{10}}}$. В [9] утверждалось, что где ${{\lambda }_{ - }} = 0.6 \pm 0.1$, ${{\lambda }_{ + }} = 0.3 \pm 0.1$, ${{C}_{ \pm }}$ – некоторые константы. Представленные результаты получены путем вычисления значений функции $P(x)$ в целых точках ($x \in {{\mathbb{Z}}^{ + }}$) и построения последовательности “истинных максимумов”, т.е. такой последовательности пар $\{ {{x}_{k}},P({{x}_{k}})\} $, что ${\text{|}}P(x){\kern 1pt} {\text{|}} < {\text{|}}P({{x}_{k}}){\kern 1pt} {\text{|}}$ для всех $x < {{x}_{k}}$ (в [9] “истинные максимумы” строились отдельно для положительных и отрицательных значений $P(x)$). Отметим, что в [9] также численно исследовалась функция распределения значений величины $P(x){{x}^{{ - 1/4}}}$.

Из теоретических результатов (см. разд. 2) следует, что в интервале $[T,2T]$, $T \gg 1$, существуют непересекающиеся интервалы длины $ \sim {\kern 1pt} {{T}^{{1/2}}}{{(\ln T)}^{{ - 3}}}$, в каждом из которых

Таким образом, на объединении этих интервалов $W \subset [T,2T]$ гипотеза круга (оценка (2)) доказана. Однако мера Лебега $\mu \{ W\} \geqslant CT$, $C < 1$, и вопрос об оценке величины ${\text{|}}P(x){\text{|}}$ на дополнении $\overline W \subset [T,2T]{{\backslash }}W$ остается открытым.

Выше и везде далее символы $C,{{C}_{1}},{{C}_{2}}, \ldots $ используются для обозначения абсолютных (не зависящих от параметров) положительных констант, которые могут быть разными в разных формулах. Если такие константы входят в условия применимости некоторого утверждения или в его формулировку, то это означает, что они существуют и могут быть указаны явно.

Рассмотрим максимум (точную верхнюю грань) функции ${\text{|}}P(x){\kern 1pt} {\text{|}}$ в интервале ${{X}_{\alpha }} \subset [T,2T]$, $T \gg 1$. Пусть ${{h}_{\alpha }}$ – высота (значение) максимума:

${{x}_{\alpha }}$ – точка максимума, т.е. Определим ширину максимума ${{u}_{\alpha }}$ как размер наибольшей полуокрестности ${{U}_{\alpha }} \subseteq {{X}_{\alpha }}$ точки ${{x}_{\alpha }}$ (левой или правой), такой что ${\text{|}}P(x){\kern 1pt} {\text{|}} \geqslant {{h}_{\alpha }}{\text{/}}2$, $x \in {{U}_{\alpha }}$. Связь между шириной максимума и его высотой была установлена в работе [10]. Подробное доказательство соответствующего общего результата приведено в Приложении. Из этого результата следует, что если ширина максимума удовлетворяет неравенству где $\rho > 0$, то для высоты максимума справедливо неравенство

В [4], [10] была выдвинута гипотеза о ширинах максимумов, согласно которой все большие максимумы являются достаточно широкими, именно, существует $\rho > 0$ такое, что неравенство (4) выполнено для всех максимумов, таких что ${{h}_{\alpha }} \geqslant \eta {{T}^{{1/4}}}$, $\eta > 0$. Доказательство этой гипотезы означает решение проблемы круга.

Задача численного эксперимента состояла в исследовании характера поведения функции $P(x)$ в области больших отклонений этой функции от нуля (${\text{|}}P(x){\kern 1pt} {\text{|}} \geqslant 2{{x}^{{1/4}}}$, $x \gg 1$) и, в частности, в проверке сформулированной выше гипотезы. Для этого во всех целых точках $x$ некоторого множества ${{I}^{ \cup }}{{:[10}^{7}},3.2 \times {{10}^{8}}] \subset {{I}^{ \cup }} \subset {{[10}^{7}}{{,10}^{{12}}} + {{10}^{8}}]$ были вычислены значения функции $P(x)$, найдены области больших отклонений $P(x)$ от нуля, вычислены ширины максимумов ${{u}_{\alpha }}$ и ряд других величин, характеризующих поведение $P(x)$. Полученные результаты позволяют составить достаточно полную картину поведения функции $P(x)$ в указанных областях. В части ширин максимумов результаты показывают, что для самых высоких максимумов оценка (4) имеет место с $\rho = 1.2$. Отсюда следует, что

Кроме того, для всех максимумов, таких что ${{h}_{\alpha }} \geqslant \eta {{T}^{{1/4}}}$, $\eta = 3$, оценка (4) имеет место с $\rho = 2$. Это подтверждает гипотезу о ширинах максимумов и дает гипотетическую оценку Отметим, что, насколько нам известно, ширины максимумов ранее не исследовались.

Работа имеет следующую структуру. В разд. 2 приведены теоретические результаты, определяющие постановку вопросов и характер величин, рассматриваемых в численном эксперименте. В разд. 3 дано описание численного эксперимента и приведены полученные результаты. В разд. 4 представлены соответствующие выводы относительно поведения функции $P(x)$ в области больших отклонений от нуля. Доказательство теоремы, следствием которой является связь между шириной и высотой максимума, приведено в Приложении.

2. ТЕОРЕТИЧЕСКИЕ РЕЗУЛЬТАТЫ

Число целых точек $R(x)$ в круге радиуса $\sqrt x $, $x \geqslant 0$, может быть представлено в виде

где $r(n)$ – число представлений целого числа $n$ в виде суммы квадратов двух целых чисел. Заметим, что если $r(n) \ne 0$, то $r(n) \geqslant 4 > \pi $. Асимптотика величин $r(n)$ имеет вид [11]

В [5] доказано, что

здесь и далее $[\, \cdot \,]$ – целая часть вещественного числа. Последняя формула используется в численном эксперименте для подсчета числа целых точек в круге.

Из представления (6) следует, что определенная формулой (1) функция $P$ есть кусочно-линейная функция с разрывами I рода в целых точках $x = n$ таких, что $r(n) \ne 0$. В точках разрыва функция $P$ непрерывна справа, $P(x + 0) = P(x)$, $P(x - 0) = P(x - 1) - \pi $. В точках непрерывности $P{\kern 1pt} '(x) = - \pi $. Для любого $x$ справедливо равенство $P(x) = P([x]) - \pi (x - [x])$, поэтому вычисление функции $P$ в некотором интервале сводится к вычислению этой функции в целых точках этого интервала.

$\Omega $-оценки. Напомним определение символов Харди $\Omega $, ${{\Omega }_{ + }}$:

где $g(x) > 0$. Доказано (см., например, [12], [13]), что Неизвестно, верна ли оценка

Перемены знака с выходом за барьер. Уточняя результаты работы [14], нетрудно доказать, что функция $P(x) \pm a{{x}^{{1/4}}}$ по крайней мере один раз меняет знак в любом интервале $[x,x + \Delta x]$ ($x \gg 1$) при $\Delta x \geqslant 2b\sqrt x $ для любых $a$, $b$ таких, что

где Так как $S \lesssim 13.1$, то условие (10) выполняется, например, при $a = 0.1$, $b = 2.4$.

Большие отклонения функции ${\text{|}}P{\kern 1pt} {\text{|}}$ от нуля. Используя метод работы [14], можно доказать, что в интервале $[T,2T]$, $T \gg 1$, существуют непересекающиеся интервалы $W_{\alpha }^{ \pm }$ длины

такие что где $x_{\alpha }^{ \pm }$ – точка максимума величины ${\text{|}}P(x){\kern 1pt} {\text{|}}$ в интервале $W_{\alpha }^{ \pm }$, т.е. и при этом Здесь и далее $\mu \{ \, \cdot \,\} $ – мера Лебега.

Распределение значений величины $P(x){{x}^{{ - 1/4}}}$. В работе [15] доказано, что величина Q(x) = $ = P(x){{x}^{{ - 1/4}}}$ имеет функцию распределения $F$ с плотностью $f$:

Это означает, что имеет место равенство В работе [16] показано, что вместо (13) можно написать для любого $\Delta T \geqslant C{{T}^{{1/2 + \varepsilon }}}$, $\varepsilon > 0$. В работе [9] доказано, что $\forall \varepsilon > 0$ $\exists {{\xi }_{0}} = {{\xi }_{0}}(\varepsilon )$:

Пики (большие отклонения) функции $P$. Дадим ряд необходимых определений. Рассмотрим функцию $P$ в интервале $[T,2T]$, $T \gg 1$. Множество $X$ точек $x$, в которых ${\text{|}}P(x){\kern 1pt} {\text{|}} \geqslant {{T}^{{1/4}}}$, представляет собой объединение конечного числа непересекающихся интервалов:

Если для некоторого интервала ${{X}_{\alpha }}$ выполнено условие то график сужения функции $P$ на этот интервал назовем пиком с основанием ${{X}_{\alpha }}$ и будем обозначать через ${{\mathcal{P}}_{\alpha }}$. Величину ${{h}_{\alpha }} \equiv h({{\mathcal{P}}_{\alpha }})$ назовем высотой пика.

Пусть – замыкание графика ${{\mathcal{P}}_{\alpha }}$. Множество содержит конечное число точек (как правило, одну точку). Вершиной пика назовем ту точку указанного множества, координата $x$ которой минимальна, т.е.

при этом ${{x}_{\alpha }} \equiv x({{\mathcal{P}}_{\alpha }})$ – координата вершины.

Пусть ${{U}_{\alpha }} \subset {{X}_{\alpha }}$ – наибольшая полуокрестность (левая или правая) координаты вершины пика ${{x}_{\alpha }}$, такая что ${\text{|}}P(x){\kern 1pt} {\text{|}} \geqslant {{h}_{\alpha }}{\text{/}}2$, $x \in {{U}_{\alpha }}$. Определим ширину пика ${{u}_{\alpha }} \equiv u({{\mathcal{P}}_{\alpha }})$ (одностороннюю ширину) как размер этой окрестности: ${{u}_{\alpha }} \doteq {\text{|}}{{U}_{\alpha }}{\kern 1pt} {\text{|}}$.

Пусть ${{W}_{\alpha }} \subset {{X}_{\alpha }}$ – наибольший интервал, содержащий координату вершины пика ${{x}_{\alpha }}$, такой что ${\text{|}}P(x){\kern 1pt} {\text{|}} \geqslant {{h}_{\alpha }}{\text{/}}2$, $x \in {{W}_{\alpha }}$. Определим полную ширину пика ${{w}_{\alpha }} \equiv w({{\mathcal{P}}_{\alpha }})$ (двустороннюю ширину пика) как длину этого интервала: ${{w}_{\alpha }} \doteq {\text{|}}{{W}_{\alpha }}{\kern 1pt} {\text{|}}$.

Определим знак пика ${{\mathcal{P}}_{\alpha }}$ следующим образом: ${\kern 1pt} {\text{sgn}}{\kern 1pt} ({{\mathcal{P}}_{\alpha }}) = 1$, если $P(x) \geqslant {{T}^{{1/4}}}$, $x \in {{X}_{\alpha }}$, и ${\kern 1pt} {\text{sgn}}{\kern 1pt} ({{\mathcal{P}}_{\alpha }}) = - 1$, если $P(x) \leqslant - {{T}^{{1/4}}}$, $x \in {{X}_{\alpha }}$. В зависимости от знака будем называть пики положительными и отрицательным.

Расстоянием $D({{\mathcal{P}}_{{{{\alpha }_{1}}}}},{{\mathcal{P}}_{{{{\alpha }_{2}}}}})$ между пиками ${{\mathcal{P}}_{{{{\alpha }_{1}}}}}$ и ${{\mathcal{P}}_{{{{\alpha }_{2}}}}}$ будем считать расстояние между координатами их вершин: $D({{\mathcal{P}}_{{{{\alpha }_{1}}}}},{{\mathcal{P}}_{{{{\alpha }_{2}}}}}) \doteq {\text{|}}x({{\mathcal{P}}_{{{{\alpha }_{1}}}}}) - x({{\mathcal{P}}_{{{{\alpha }_{2}}}}}){\kern 1pt} {\text{|}}$.

Используем обозначение ${{\mathfrak{P}}_{T}}$ для множества всех пиков в интервале $[T,2T]$, $T \gg 1$.

Связь высот и ширин пиков. Рассмотрим некоторый пик ${{\mathcal{P}}_{\alpha }} \in {{\mathfrak{P}}_{T}}$. С учетом данных выше определений результат работы [10], устанавливающий связь высоты и ширины максимума, можно сформулировать следующим образом: если ширина пика достаточно велика, т.е. выполнено неравенство

где $\rho = \rho (\alpha ,T) > 0$, то для высоты пика справедливо неравенство Из приведенных в Приложении результатов вытекает, что для константы $C$ в (16) имеет место следующая оценка сверху: $C \leqslant \bar {C} = 20$.

Пусть ${{\mathfrak{P}}_{{\eta ,T}}} \subseteq {{\mathfrak{P}}_{T}}$, $\eta \geqslant 2$, множество пиков, таких что ${{h}_{\alpha }} \geqslant \eta {{T}^{{1/4}}}$, ${{\mathcal{P}}_{\alpha }} \in {{\mathfrak{P}}_{{\eta ,T}}}$. В случае $\eta = 2$ имеем все множество пиков (${{\mathfrak{P}}_{{2,T}}} = {{\mathfrak{P}}_{T}}$), поскольку по определению высота любого пика удовлетворяет неравенству ${{h}_{\alpha }} \geqslant 2{{T}^{{1/4}}}$. В случае $\eta = {{\sup }_{{x \in [T,2T]}}}{\text{|}}P(x){\kern 1pt} {\text{|}}{{T}^{{ - 1/4}}}$ множество ${{\mathfrak{P}}_{{\eta ,T}}}$ состоит из одного самого высокого пика.

Рассмотрим множество ${{\mathfrak{P}}_{{\eta ,T}}}$. Если это множество не пустое и существует $\rho = \rho (\eta ,T) > 0$, такое что неравенство (15) выполняется для всех пиков ${{\mathcal{P}}_{\alpha }} \in {{\mathfrak{P}}_{{\eta ,T}}}$, то для всех пиков выполняется неравенство (16) и, следовательно, имеет место оценка

Очевидно, что $\rho ({{\eta }_{2}},T) \leqslant \rho ({{\eta }_{1}},T)$ при ${{\eta }_{2}} \geqslant {{\eta }_{1}}$, т.е. увеличение параметра $\eta $ позволяет улучшить оценку (17).

Если ${{\rho }_{h}}(T) > 0$ такое, что неравенство (15) выполняется для самого высокого пика, то для этого пика выполняется и неравенство (16) и, следовательно, имеет место оценка

Гипотеза о ширинах максимумов. Выдвинутая в [4], [10] гипотеза о ширинах максимумов может быть переформулирована в терминах пиков следующим образом: существуют константы $\eta \geqslant 2$ и $\rho > 0$, такие что для любого $T \gg 1$ ширины всех пиков ${{\mathcal{P}}_{\alpha }} \in {{\mathfrak{P}}_{{\eta ,T}}}$ удовлетворяют неравенству (15), т.е. все достаточно высокие пики являются достаточно широкими. Если гипотеза справедлива, то из (17) следует

т.е. решение проблемы круга. Отметим, что из $\Omega $-оценки (9) следует, что $\rho > 1{\text{/}}2$.

3. ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТ

Значения функции $R(x)$ (число целых точек в круге радиуса $\sqrt x $) вычислялись для всех целых значений $x = n$ в интервалах ${{I}^{i}}$, $i = 0,1, \ldots ,13$, где

Интервалы ${{I}^{1}}, \ldots ,{{I}^{5}}$ имеют вид $[T,2T]$. Интервалы ${{I}^{6}}, \ldots ,{{I}^{{13}}}$ имеют вид $[T,T{\kern 1pt} ']$, $T{\kern 1pt} ' = T + {{10}^{8}}$; для этих интервалов $T + 100\sqrt T \leqslant T{\kern 1pt} ' < 2T$. Будем использовать следующие обозначения: ${{I}^{ \cup }} = \bigcup\nolimits_{1 \leqslant i \leqslant 13} {{I}^{i}}$, $\mathcal{I} = \{ {{I}^{1}}, \ldots ,{{I}^{{13}}}\} $.

Вычисление значений функции $R(x)$ осуществлялось по формуле (8) с использованием 64‑разрядной плавающей и целой арифметики, что обеспечивает получение точных значений. Для каждого интервала результат представляет собой массив 64-разрядных целых чисел. Соответствующие значения функции $P(x)$ вычислялись по формуле (1) с использованием 64-разрядной плавающей арифметики. Результат представляет собой массив 64-разрядных плавающих чисел. Погрешность вычислений для используемых значений аргумента ($x \lesssim {{10}^{{12}}}$) заведомо не превышает ${{10}^{{ - 3}}}$, что вполне достаточно для решения всех задач численного эксперимента.

Для каждого интервала $I \in \mathcal{I}$ по значениям $R(n)$ во всех целых точках $n$ интервала, исключая начальную точку, вычислялись величины $r(n)$ (см. (6)). В табл. 1 для каждого интервала приведено значение величины $\bar {r} = {{\max }_{{n \in I}}}\{ r(n)\} $, значение $\tilde {r}$, вычисленное для конечной точки интервала с использованием главного члена асимптотической формулы (7), а также значения величины ${{T}^{{1/4}}}$, играющей роль порога в определении пиков. Сравнение величин $\bar {r}$ и $\tilde {r}$ показывает, что величина $r(n)$ не выходит на асимптотику даже при максимальных используемых значениях $n \sim {{10}^{{12}}}$.

Для каждого из интервалов $I \in \mathcal{I}$ по массиву значений $P(n)$, $n \in I$, строится множество пиков ${{\mathfrak{P}}_{T}}$ функции $P$, точнее, описание пиков этого множества. Каждый пик ${{\mathcal{P}}_{\alpha }} \in {{\mathfrak{P}}_{T}}$, описывается следующими величинами: $x_{\alpha }^{{\text{b}}}$ – начало пика, $x_{\alpha }^{{\text{e}}}$ – конец пика, ${{x}_{\alpha }}$ – координата вершины пика, ${{h}_{\alpha }}$ – высота пика, ${{u}_{\alpha }}$ – ширина пика, ${{w}_{\alpha }}$ – полная ширина пика, ${{s}_{\alpha }}$ – знак пика. Перечисленные величины определены в разд. 2.

Алгоритм построения множества пиков достаточно прямолинеен. Выполняется просмотр последовательности значений $P(n)$, $n \in I$, и выделение таких участков последовательности ${{X}_{\alpha }} = \{ x_{\alpha }^{{\text{b}}},x_{\alpha }^{{\text{b}}} + 1, \ldots ,x_{\alpha }^{{\text{e}}}\} $, что ${\text{|}}P(n){\kern 1pt} {\text{|}} \geqslant {{T}^{{1/4}}}$, $n \in {{X}_{\alpha }}$. Если ${{h}_{\alpha }} \doteq {{\max }_{{n \in {{X}_{\alpha }}}}}\{ {\kern 1pt} {\text{|}}P(n){\kern 1pt} {\text{|}}{\kern 1pt} \} \geqslant 2{{T}^{{1/4}}}$ для данного участка, то такой участок последовательности представляет пик, начало и конец участка – это начало и конец пика, ${{h}_{\alpha }}$ – высота пика. Точка ${{x}_{\alpha }}$, такая что ${\text{|}}P({{x}_{\alpha }}){\kern 1pt} {\text{|}} = {{h}_{\alpha }}$, – координата вершины пика (если таких точек несколько, то координатой вершины считается самая левая из них). Далее выполняется последовательный просмотр значений $P(n)$, $n \in {{X}_{\alpha }}$, вправо и влево, начиная от координаты вершины ${{x}_{\alpha }}$, и находятся крайние точки $x_{\alpha }^{ + }$ и $x_{\alpha }^{ - }$, в которых выполняется неравенство ${\text{|}}P(x_{\alpha }^{ \pm }){\kern 1pt} {\text{|}} \geqslant {{h}_{\alpha }}{\text{/}}2$, после чего полагается

Наконец, ${{s}_{\alpha }} = {\text{sgn}}{\kern 1pt} (P({{x}_{\alpha }}))$. Величины $x_{\alpha }^{{\text{b}}},\;x_{\alpha }^{{\text{e}}},\;{{x}_{\alpha }},\;{{h}_{\alpha }},\;{{u}_{\alpha }},\;{{w}_{\alpha }}$ изображены на фиг. 1, ${{s}_{\alpha }} = - 1$.

В результате применения описанного алгоритма мы получаем конечную последовательность наборов чисел $\{ x_{\alpha }^{{\text{b}}},x_{\alpha }^{{\text{e}}},{{x}_{\alpha }},{{h}_{\alpha }},{{u}_{\alpha }},{{w}_{\alpha }},{{s}_{\alpha }}\} $, $\alpha \in {{{\text{A}}}_{I}} = \{ 0, \ldots ,{{N}_{I}} - 1\} $, которая представляет (описывает) множество пиков ${{\mathfrak{P}}_{T}}$, при этом каждый набор представляет (описывает) отдельный пик ${{\mathcal{P}}_{\alpha }}$. Количество наборов ${{N}_{I}} \doteq {\text{|}}{{{\text{A}}}_{I}}{\kern 1pt} {\text{|}} \equiv {\text{|}}{{\mathfrak{P}}_{T}}{\kern 1pt} {\text{|}}$ в последовательности есть число пиков в интервале $I$. Наборы нумеруются слева направо, так что $x_{{{{\alpha }_{1}}}}^{{\text{e}}} < x_{{{{\alpha }_{2}}}}^{{\text{b}}}$ при ${{\alpha }_{1}} < {{\alpha }_{2}}$.

Везде далее набор чисел, представляющий пик ${{\mathcal{P}}_{\alpha }}$, и совокупность таких наборов, представляющую множество пиков ${{\mathfrak{P}}_{T}}$, мы также будем называть пиком и множеством пиков и использовать те же обозначения, что не должно вызывать недоразумений. Как и ранее (см. разд. 2), будем использовать обозначение ${{\mathfrak{P}}_{{\eta ,T}}} \subseteq {{\mathfrak{P}}_{T}}$, $\eta \geqslant 2$, для множества пиков интервала $I$, таких что ${{h}_{\alpha }} \geqslant \eta {{T}^{{1/4}}}$ (при этом ${{\mathfrak{P}}_{{2,T}}} = {{\mathfrak{P}}_{T}}$).

В табл. 2 представлено число пиков ${{N}_{I}}$, вычисленное для всех интервалов $I \in \mathcal{I}$. Кроме того, в таблице представлены величины ${{N}_{{\eta ,I}}} \doteq {\text{|}}{{\mathfrak{P}}_{{\eta ,T}}}{\kern 1pt} {\text{|}}$ – число пиков ${{\mathcal{P}}_{\alpha }} \in {{\mathfrak{P}}_{{\eta ,T}}}$ в интервале $I$ – для значений $\eta = 3,4,5,6$.

Получим экспериментальную оценку константы $C$ в формуле (16), определив для пиков ${{\mathcal{P}}_{\alpha }}$, $\alpha \in {{{\text{A}}}_{I}}$, интервала $I$ величины $C(\alpha ,T)$ из условия

в котором величина $\rho (\alpha ,T)$ определяется равенством В табл. 3 представлены вычисленные значения величины $\bar {C} = \bar {C}(T) = {{\max }_{{\alpha \in {{{\text{A}}}_{I}}}}}\{ C(\alpha ,T)\} $ для всех интервалов $I \in \mathcal{I}$. Отметим, что полученные значения величины $\bar {C}$ значительно меньше представленной в разд. 2 теоретической верхней оценки.

Имея множество пиков ${{\mathfrak{P}}_{T}}$ в интервале $I$, можно вычислить значение показателя $\rho (\eta ,T)$ для подмножества пиков, таких что ${{h}_{\alpha }} \geqslant \eta {{T}^{{1/4}}}$, из условия

где а также показателя ${{\rho }_{h}}(T)$ для самого высокого пика интервала $I$ из условия где ${{u}_{h}}$ – ширина самого высокого пика. Значения показателей $\rho $, вычисленные для всех интервалов $I \in \mathcal{I}$, $\eta = 2,3,4,5,6$ и самых высоких пиков представлены в табл. 4.

Из неравенства (18) следует, что

где Таким образом (см. последнюю строку табл. 4), мы получаем для показателя степени логарифма в (20) верхнюю оценку $\lambda \lesssim 0.6$, что соответствует утверждению работы [9].

Рассмотрим зависимость числа пиков от ширины. Пусть ${{\tilde {N}}_{{\eta ,I}}}(\rho )$ – число пиков ${{P}_{\alpha }} \in {{\mathfrak{P}}_{{\eta ,T}}}$ в интервале $I$, таких что ${{u}_{\alpha }} < {{T}^{{1/2}}}{{(\ln T)}^{{ - \rho }}}$, ${{\bar {N}}_{{\eta ,I}}}(\rho )$ – число пиков ${{P}_{\alpha }} \in {{\mathfrak{P}}_{{\eta ,T}}}$ в интервале $I$, таких что ${{u}_{\alpha }} \geqslant {{T}^{{1/2}}}{{(\ln T)}^{{ - \rho }}}$. В табл. 5 приведены значения величин ${{\tilde {N}}_{{\eta ,I}}}(\rho )$, $\eta = 3$, $\rho = 2,3{\text{/}}2,1$, и ${{\bar {N}}_{{\eta ,I}}}(\rho )$, $\eta = 3$, $\rho = 1,3{\text{/}}4,1{\text{/}}2$, вычисленные для каждого из интервалов $I \in \mathcal{I}$.

Данные первой строки табл. 5 означают, что на множестве $x \in {{I}^{ \cup }}$ гипотеза о ширинах максимумов справедлива при $\eta = 3$, $\rho = 2$. Отсюда следует, что

Последняя строка таблицы показывает, что пики шире ${{T}^{{1/2}}}{{(\ln T)}^{{ - 1/2}}}$ встречаются крайне редко, что согласуется с $\Omega $-оценкой (9).

Для каждого из интервалов $I \in \mathcal{I}$ были вычислены сумма длин оснований всех пиков ${{S}_{X}}$, суммы длин оснований положительных и отрицательных пиков $S_{X}^{ \pm }$ по отдельности, сумма полных (двусторонних) ширин всех пиков ${{S}_{W}}$ и суммы полных (двусторонних) ширин положительных и отрицательных пиков $S_{W}^{ \pm }$ по отдельности:

В табл. 6 представлены отношения указанных величин к длине интервала ${\text{|}}I{\kern 1pt} {\text{|}}$.

Значения $S_{W}^{ \pm }{\text{/|}}I{\kern 1pt} {\text{|}}$ суть экспериментальные оценки сверху для констант ${{C}^{ \pm }}$ в (12) при условии, что в (11) ${{C}_{ \pm }} = 2$. Отметим, что представленные отношения слабо зависят от интервала $I$, для которого они вычислены, хотя некоторая тенденция к уменьшению этих величин при увеличении $T$ наблюдается.

Рассмотрим вопрос перемены знаков ${{s}_{\alpha }}$ в последовательности пиков $\{ {{\mathcal{P}}_{\alpha }}\} $, $\alpha \in {{{\text{A}}}_{I}}$, интервала $I$. Выберем из исходной последовательности $\{ {{\mathcal{P}}_{\alpha }}\} $ подпоследовательность пиков с чередующимися знаками $\{ \mathcal{P}_{{{{\alpha }_{k}}}}^{{{\text{alt}}}}\} $, ${{\alpha }_{k}} \in {\text{A}}_{I}^{{{\text{alt}}}} = \{ {{\alpha }_{0}}, \ldots ,{{\alpha }_{{K - 1}}}\} \subseteq {{{\text{A}}}_{I}}$, используя следующую рекуррентную формулу:

и вычислим расстояния ${{D}_{k}}$ между соседними пиками подпоследовательности $\{ \mathcal{P}_{{{{\alpha }_{k}}}}^{{{\text{alt}}}}\} $: Перемены знака функции $P(x)$ в интервале $I$ с выходом за барьер $ \pm 2{{T}^{{1/4}}}$ могут быть охарактеризованы следующими величинами: $\nu \doteq (K - 1){\text{/}}{{N}_{I}}$ (относительная частота перемены знака), $\bar {d} \doteq \bar {D}{{T}^{{ - 1/2}}}$, где $\bar {D} = (K - {{1)}^{{ - 1}}}\sum\nolimits_k \,{{D}_{k}}$ – среднее расстояние, и ${{d}_{{\max }}} \doteq {{D}_{{\max }}}{{T}^{{ - 1/2}}}$, где ${{D}_{{\max }}} = {{\max }_{k}}\{ {{D}_{k}}\} $ – максимальное расстояние.

Массив расстояний $D$ был построен для каждого из интервалов $I \in \mathcal{I}$. Результаты вычисления величин $\nu $, $\bar {d}$ и ${{d}_{{\max }}}$ приведены в табл. 7.

Относительная частота перемены знака $\nu $ изменяется в пределах от $0.21$ до $0.25$. Это означает, что в последовательностях пиков должны встречаться длинные ($ \geqslant {\kern 1pt} 4$) серии подряд идущих пиков одного знака. Пример такой серии положительных пиков представлен на фиг. 2, где изображен график функции $P(x)$ на части интервала ${{I}^{{13}}}$ ($T = {{10}^{{12}}}$) длиной $5 \times {{10}^{4}}$. Штриховыми горизонтальными линиями на рисунке проведены пороговые значения, используемые в процессе построения положительных пиков функции $P(x)$.

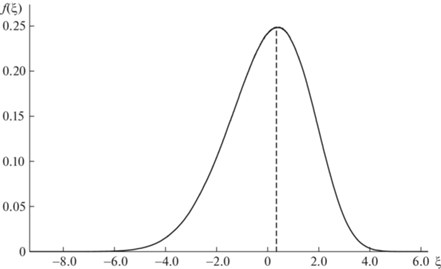
На фиг. 3 представлена построенная гистограмма распределения значений функции $Q(x) = P(x){{x}^{{ - 1/4}}}$ в целых точках интервала $\bigcup\nolimits_{0 \leqslant i \leqslant 6} \,{{I}^{i}} = [1,3.2 \times {{10}^{8}}]$, которая представляет собой приближение определенной в (13) плотности распределения $f(\xi )$ значений функции $Q(x)$.

Минимальное и максимальное значения $Q$ в интервале равны $ - 9.324$ и $6.283$ соответственно. Гистограмма построена с использованием $2000$ ячеек, размер ячейки равен $0.008$. Максимальное значение гистограммы равно $0.249$ и достигается в ячейке, центр которой имеет координату ${{\xi }_{{\max }}} = 0.341$.

4. ЗАКЛЮЧЕНИЕ

Сформулируем основные выводы относительно поведения функции $P(x)$ , $x \in {{I}^{ \cup }}$, в области больших отклонений от нуля, вытекающие из результатов численного эксперимента.

Все достаточно высокие максимумы являются широкими и гипотеза о ширинах максимумов справедлива при $\eta = 3$ (${{h}_{\alpha }} \geqslant 3{{T}^{{1/4}}}$), $\rho = 2$. Очень широкие максимумы (такие, что ${{u}_{\alpha }} \geqslant {{T}^{{1/2}}}{{(\ln T)}^{{ - 1/2}}}$) встречаются редко, что согласуется с $\Omega $-оценкой.

Имеет место оценка

Суммарная длина интервалов ${{X}_{\alpha }} \subset [T,T + \Delta T]$, $T \gg 1$, $1 \ll \Delta T \leqslant T$, в которых имеют место большие отклонения функции $P(x)$ от нуля, именно ${\text{|}}P(x){\kern 1pt} {\text{|}} \geqslant {{T}^{{1/4}}}$, $x \in {{X}_{\alpha }}$, и ${{\sup }_{{x \in {{X}_{\alpha }}}}}{\text{|}}P(x){\kern 1pt} {\text{|}} \geqslant 2{{T}^{{1/4}}}$, составляет 40–45% длины общего интервала $[T,T + \Delta T]$. Соседние большие отклонения в одну сторону (положительные и отрицательные) формируют группы; среднее число отклонений в группе составляет 4–5. Знаки соседних групп чередуются, и среднее расстояние между соседними группами составляет $ \sim {\kern 1pt} 0.6{{T}^{{1/2}}}$.

Анализ приведенных в табл. 4 величин $\rho (\eta ,T)$ при любом фиксированном значении $\eta $ показывает, что эти величины слабо зависят от интервала $I$, для которого они вычислены, и тенденция к увеличению $\rho (\eta ,T)$ при увеличении $T$ не наблюдается. Это можно считать экспериментальным подтверждением гипотезы о ширинах максимумов в целом. Кроме того, данные табл. 4 дают основание полагать, что неравенство (19) выполняется в случае $\rho = 2$ (по крайней мере, при $\eta \geqslant 3$). Таким образом, гипотетически

Авторы благодарят М.А. Королёва за помощь и полезные замечания.