Журнал вычислительной математики и математической физики, 2022, T. 62, № 4, стр. 625-641
Влияние монотонизации на спектральное разрешение бикомпактных схем в задаче о невязком вихре Тейлора–Грина
М. Д. Брагин *
ИПМ РАН
125047 Москва, Миусская пл., 4, Россия
* E-mail: michael@bragin.cc
Поступила в редакцию 28.06.2021
После доработки 29.08.2021
Принята к публикации 16.12.2021
- EDN: FCRMSY
- DOI: 10.31857/S0044466922040032
Аннотация
Рассматривается одна локально-одномерная бикомпактная схема для трехмерных уравнений Эйлера, имеющая четвертый порядок аппроксимации по пространству и второй по времени. На ее примере в задаче о вихре Тейлора–Грина в невязком совершенном газе исследуется, в какой мере метод консервативной монотонизации, применяемый в бикомпактных схемах, практически влияет на их теоретически высокое спектральное разрешение. Предлагаются два алгоритма параллельного счета по локально-одномерным бикомпактным схемам, один из которых используется для проведения вычислений. Показывается, что выбранная бикомпактная схема при наличии монотонизации разрешает 70–85% спектра кинетической энергии жидкости. Эта схема сравнивается с высокоточными схемами серии WENO5 по поведению кинетической энергии и энстрофии. Демонстрируется, что бикомпактная схема имеет заметно меньшую диссипацию и слабее подавляет вихри среднего масштаба. Библ. 32. Фиг. 9.
ВВЕДЕНИЕ
Решение задач аэрогидродинамики аппаратов, двигателей, конструкций, задач о движениях атмосферы, природных вод (океанов, морей, рек и т.д.) нередко приводит к необходимости моделирования турбулентных течений вязкой жидкости. Важнейшей особенностью таких течений является широкий диапазон характеризующих их пространственнo-временных масштабов (см. [1]). Прямое численное моделирование (DNS) состоит в непосредственном численном решении уравнений Навье–Стокса с полным разрешением на сетке всех масштабов и структур течения. Этот подход лучше всего соответствует исходной физико-математической модели ньютоновской жидкости. Однако с ростом числа Рейнольдса он быстро становится нереализуемым из-за ограниченности имеющихся на данный момент вычислительных ресурсов. Численное решение уравнений Навье–Стокса, осредненных по Рейнольдсу (RANS) (см. [1]), является одним из способов справиться с данной проблемой. Уравнения и замыкающие модели RANS совместно с классом конечнo-объемных (либо конечно-разностных) схем второго порядка точности образуют современный промышленный стандарт решения аэрогидродинамических задач. Позволяя достичь успехов в предсказании средних характеристик установившихся безотрывных течений, он оказывается плохо пригодным для изучения, например, отрывных течений, акустических шумов, генерируемых свободными струями либо обтекаемыми телами, смешивающихся потоков жидкости и т.д. (см. [2], [3]). Актуальной альтернативной стандарту RANS является моделирование крупных вихрей (LES) (см. [4]). Суть LES в общих чертах сводится к тому, что динамика структур течения размером крупнее ячеек сетки рассчитывается, исходя из пространственно фильтрованных уравнений Навье–Стокса, а динамика оставшихся мелкомасштабных структур, так называемая подсеточная турбулентность, параметризуется с помощью тех или иных априорных или полуэмпирических моделей. Можно выделить три вида LES (см. [5], [6]): собственно, вышеописанное LES с явным выделением и разделением масштабов через фильтр и подсеточную модель; неявное LES (ILES), при котором уравнения Навьe–Стокса решаются в исходном виде, а функции фильтра и подсеточной модели выполняют члены из погрешности аппроксимации используемой численной схемы (см. [7]); “LES без модели”, справедливо называемое также “DNS с недостаточным разрешением” (uDNS), которое представляет собой ILES вообще без анализа погрешности аппроксимации на предмет ее связи с какой-либо физической моделью подсеточных процессов.
Чтобы быть применимой в LES или DNS, численная схема должна обладать малыми диссипативными и дисперсионными погрешностями или, другими словами, высоким спектральным разрешением (см. [3], [8], [9]). Это требование вытекает из того, что схема должна как можно точнее воспроизводить динамику вихрей всех разрешаемых масштабов, притом нередко на больших интервалах интегрирования (и по пространству, и по времени) (см. [9]). Наиболее очевидным способом понижения численной диссипации/дисперсии является повышение порядка аппроксимации схемы. Более того, в [10], [11] на примере разрывных схем Галеркина (DG) показывается, что при равном числе степеней свободы схемы более высокого порядка превосходят по точности свои аналоги более низкого порядка. Однако сам по себе высокий порядок аппроксимации еще ничего не говорит о пригодности схемы для LES или DNS. Например, классическая схема WENO5 (см. [12]) (с аппроксимацией пятого порядка по пространству и третьего порядка по времени) из-за довольно высокого уровня численной диссипации мало пригодна для этих приложений (см. [13]), что служит одной из причин для разработки модификаций этой схемы (см. [13], [14]). Напротив, схема “КАБАРЕ” (см. [15]), имеющая формально второй порядок аппроксимации по всем переменным, обладает хорошим спектральным разрешением и потому применима для моделирования турбулентных течений. Если рассматривать схемы высокого порядка (выше второго), то среди них для LES и DNS лучше всего подходят DG-cхемы (см. [5], [6], [9]–[11], [16]) и компактные схемы (см. [8], [17], [18]), в том числе мультиоператорные (см. [19]).
В [20]–[28] развивается класс высокоточных бикомпактных схем. В их основе лежит симметричная компактная аппроксимация пространственных производных на шаблоне, который целиком помещается в одну ячейку сетки (при любом порядке схемы). Минимизация шаблона осуществляется через введение дополнительных искомых функций, для отыскания которых привлекаются дифференциальные следствия (производные) решаемых уравнений. Преимущество бикомпактных схем заключается в сочетании нескольких положительных свойств: высокой устойчивости, экономичной реализации, равном числе граничных условий в разностной и дифференциальной постановках задачи, высоком спектральном разрешении, лучшем по сравнению с классическими компактными схемами равного порядка аппроксимации (см. [22], [24], [25]). Последнее свойство, по-видимому, делает бикомпактные схемы перспективными для применения в LES. Здесь как раз возникает следующая проблема: высокое спектральное разрешение бикомпактных схем доказано лишь теоретически в случае модельного линейного уравнения переноса. На практике же, при решении настоящих гидродинамических уравнений, бикомпактные схемы (как и схемы других классов) подвергаются монотонизации, которая никак не учитывалась в анализе (см. [22], [24], [25]).
Итак, основная цель настоящей работы – выяснить, как метод консервативной монотонизации из [26], применяемый в бикомпактных схемах, влияет на их спектральное разрешение. Это исследование мы проведем для одной локально-одномерной бикомпактной схемы четвертого порядка аппроксимации по пространству и второго порядка аппроксимации по времени. В качестве конкретного гидродинамического примера возьмем задачу о вихре Тейлора–Грина (см. [29]), которая является стандартным тестом для схем, разрабатываемых для моделирования турбулентных течений. Данную задачу мы решим в предположении, что жидкость идеальная (т.е. невязкая): отсутствие физической диссипации позволит яснее проанализировать действие численной диссипации от метода из [26]. Кроме того, мы обсудим параллельную реализацию локально-одномерных бикомпактных схем и сделаем сравнение по численной диссипации с некоторыми высокоточными схемами серии WENO5.
Работа построена следующим образом. В разд. 1 формулируется постановка задачи о вихре Тейлора–Грина. В разд. 2 кратко описывается локально-одномерная бикомпактная схема с консервативной монотонизацией. В разд. 3 предлагаются два алгоритма параллельного счета по локально-одномерным бикомпактным схемам. В разд. 4 обсуждаются результаты расчетов.
1. ПОСТАНОВКА ЗАДАЧИ
Сделаем еще одно отступление от оригинальной постановки задачи о вихре Тейлора–Грина из [29]: предположим, что жидкость не только идеальная, но и сжимаемая, причем ее движение происходит при достаточно большом фоновом давлении. Данный прием избавит нас от необходимости решать эллиптическую задачу для давления и сделает систему динамических уравнений гиперболической, но при этом оставит плотность примерно постоянной.
Трехмерные течения идеальной сжимаемой жидкости описываются уравнениями Эйлера
(1)
${{\partial }_{t}}{\mathbf{Q}} + \sum\limits_{d = x,y,z} {{\partial }_{d}}{{{\mathbf{F}}}^{d}}({\mathbf{Q}}) = {\mathbf{0}},$Система уравнений (1) решается в кубе $x,y,z \in (0,2\pi L)$ при периодических граничных условиях. Начальным условием является одночастотный вихрь:
В несжимаемой постановке в силу известных свойств соответствующих уравнений движения фоновое давление ${{p}_{0}}$ не играет никакой роли, а потому может быть задано любым. Иначе обстоит дело в сжимаемом случае: ${{p}_{0}}$ как минимум должно быть задано так, чтобы ${{\left. p \right|}_{{t = 0}}} > 0$; кроме того, если ${{p}_{0}}$ недостаточно велико, то начальное возмущение скорости приведет к значительным отклонениям $\rho $ от ${{\rho }_{0}}$ при $t > 0$, что нежелательно. Чтобы плотность жидкости оставалась примерно постоянной, ${{p}_{0}}$ должно быть много большим, чем ${{\rho }_{0}}{v}_{0}^{2}$:
2. ЛОКАЛЬНО-ОДНОМЕРНАЯ БИКОМПАКТНАЯ СХЕМА
Для численного решения задачи о вихре Тейлора–Грина мы применим одну локально-одномерную бикомпактную схему четвертого порядка аппроксимации по пространству и второго порядка аппроксимации по времени. Выбор схемы с расщеплением продиктован двумя факторами: во-первых, высокое спектральное разрешение бикомпактных схем определяется преимущественно их пространственной, а не временной дискретизацией (если последняя, разумеется, имеет хотя бы второй порядок); во-вторых, расщепленные бикомпактные схемы экономичнее своих нерасщепленных аналогов. Отметим, что локально-одномерные бикомпактные схемы не являются новыми (см., например, [21], [27], [28]), поэтому мы дадим минимальное описание выбранной схемы, которое понадобится далее в разд. 3 при рассмотрении алгоритмов параллельного счета по ней.
Итак, согласно методу локально-одномерного расщепления по пространству и методу расщепления Лакса–Фридрихса по потоку, система многомерных уравнений (1) разбивается на шесть систем одномерных уравнений
(3)
${{\partial }_{t}}{\mathbf{Q}} + {{\partial }_{d}}{{{\mathbf{F}}}^{{d, \pm }}}({\mathbf{Q}}) = {\mathbf{0}},\quad d = x,y,z,$Затем в замкнутом кубе $(x,y,z) \in {{[0,2\pi ]}^{3}}$ вводится декартова сетка $\Omega = {{\Omega }_{x}} \times {{\Omega }_{y}} \times {{\Omega }_{z}}$, где
(4)
$\begin{gathered} \frac{d}{{dt}}\left( {A_{0}^{x}{{{\mathbf{Q}}}_{{j + 1/2,k,l}}}} \right) + \Lambda _{1}^{x}{\mathbf{F}}_{{j + 1/2,k,l}}^{{x, + }} = {\mathbf{0}}, \\ \frac{d}{{dt}}\left( {\Lambda _{1}^{x}{{{\mathbf{Q}}}_{{j + 1/2,k,l}}}} \right) + \Lambda _{2}^{x}{\mathbf{F}}_{{j + 1/2,k,l}}^{{x, + }} = {\mathbf{0}}. \\ \end{gathered} $(5)
$\begin{array}{*{20}{c}} a&\vline & a&{} \\ 1&\vline & {1 - a}&a \\ \hline {}&\vline & {1 - a}&a \end{array},\quad a = 1 - \frac{{\sqrt 2 }}{2}.$Как промежуточный результат для одномерных систем (3) получаются одномерные полностью дискретные бикомпактные схемы. Обозначим их операторы послойного перехода через $S_{B}^{{d, \pm }}(\tau )$, где $\tau $ – шаг по времени, при котором применяется метод (5). Удобно также ввести обозначение $S_{B}^{d}(\tau ) = S_{B}^{{d, - }}(\tau )S_{B}^{{d, + }}(\tau )$.
Локально-одномерная бикомпактная схема (немонотонная) для уравнений Эйлера (1) определяется своим оператором послойного перехода ${{S}_{B}}(\tau )$:
(6)
${{S}_{B}}(\tau ) = S_{B}^{x}(\tau {\text{/}}2)S_{B}^{y}(\tau {\text{/}}2)S_{B}^{z}(\tau )S_{B}^{y}(\tau {\text{/}}2)S_{B}^{x}(\tau {\text{/}}2).$При решении задач газовой динамики схема с оператором послойного перехода (6) обычно подвергается консервативной монотонизации по методу из [26]. Цель настоящей работы, как уже было сформулировано во Введении, состоит в том, чтобы изучить влияние численной диссипации от данного метода на спектральное разрешение выбранной бикомпактной схемы. Отметим, что задача о вихре Тейлора–Грина может быть посчитана по ней от начала до конца и без привлечения метода из [26], как показывается в разд. 4.
Остановимся кратко на методе консервативной монотонизации, чтобы обсуждение его параллельной реализации в разд. 3 было более понятным.
Рассмотрим две численные схемы для системы (1): монотонную схему $A$ первого порядка и немонотонную бикомпактную схему $B$ высокого порядка. В качестве второй выберем схему с оператором послойного перехода (6), а в качестве первой – аналогично расщепленный “явный уголок” c оператором послойного перехода
Оператор $S_{A}^{d}(\tau ) = S_{A}^{{d, - }}(\tau )S_{A}^{{d, + }}(\tau )$, а операторы $S_{A}^{{d, \pm }}(\tau )$ соответствуют одномерным “явным уголкам” для одномерных систем (3), например,Вернемся к методу консервативной монотонизации. Пусть нам дано решение ${{{\mathbf{Q}}}^{n}}$ на временном слое ${{t}^{n}}$, $n = 0,1, \ldots $ . Используя схемы $A$ и $B$, посчитаем два новых решения на следующем слое ${{t}^{{n + 1}}}$: ${{{\mathbf{Q}}}^{A}} = {{S}_{A}}(\tau ){{{\mathbf{Q}}}^{n}}$ и ${{{\mathbf{Q}}}^{B}} = {{S}_{B}}(\tau ){{{\mathbf{Q}}}^{n}}$. Вычислим по ним в каждой ячейке ${{K}_{C}} = [{{x}_{j}},{{x}_{{j + 1}}}] \times [{{y}_{k}},{{y}_{{k + 1}}}] \times [{{z}_{l}},{{z}_{{l + 1}}}]$ сетки $\Omega $ ($C = (j + 1{\text{/}}2,k + 1{\text{/}}2,l + 1{\text{/}}2)$ – мультииндекс) монотонизированное решение
(7)
${{\widetilde Q}_{s}}({\mathbf{r}};{{K}_{C}}) = \bar {Q}_{s}^{B}({{K}_{C}}) + {{\beta }_{s}}({{K}_{C}})[Q_{s}^{B}({\mathbf{r}}) - \bar {Q}_{s}^{B}({{K}_{C}})],\quad {\mathbf{r}} = (x,y,z) \in \Omega \cap {{K}_{C}},\quad s = \overline {1,5} ,$(8)
${{\beta }_{s}}({{K}_{C}}) = \frac{1}{{1 + w_{s}^{2}({{K}_{C}})}},\quad {{w}_{s}}({{K}_{C}}) = \frac{{{{C}_{1}}\mathop {\max }\limits_{{\mathbf{r}} \in \Omega \cap {{K}_{C}}} \left| {Q_{s}^{A}({\mathbf{r}}) - Q_{s}^{B}({\mathbf{r}})} \right|}}{{\mathop {\max }\limits_{{\mathbf{r}} \in \Omega \cap {{K}_{C}}} \left| {Q_{s}^{A}({\mathbf{r}})} \right|}}.$(9)
${{{\mathbf{Q}}}^{{n + 1}}}({\mathbf{r}}) = \frac{{\sum\nolimits_{{{K}_{C}}:{\mathbf{r}} \in {{K}_{C}}} {\omega ({\mathbf{r}};{{K}_{C}})\widetilde {\mathbf{Q}}({\mathbf{r}};{{K}_{C}})V({{K}_{C}})} }}{{\sum\nolimits_{{{K}_{C}}:{\mathbf{r}} \in {{K}_{C}}} {\omega ({\mathbf{r}};{{K}_{C}})V({{K}_{C}})} }},\quad {\mathbf{r}} \in \Omega ,$Поясним смысл параметра ${{C}_{1}}$ и формул (7), (8). При ${{C}_{1}} = 0$ множители ${{\beta }_{s}}({{K}_{C}}) \equiv 1$, и монотонизация не происходит; в пределе при ${{C}_{1}} \to \infty $ множители ${{\beta }_{s}}({{K}_{C}}) \equiv 0$, и монотонизация максимальна, так как решение (7) сводится к набору интегральных средних и становится кусочно-постоянным. Сами же множители ${{\beta }_{s}}({{K}_{C}})$ при $\tau \to 0$, ${{C}_{1}} = O(1) > 0$ ведут себя так: в областях гладкости точного решения $1 - {{\beta }_{s}}({{K}_{C}}) = O({{\tau }^{2}})$ (в этих точках $Q_{s}^{A} - Q_{s}^{B} = O(\tau )$), а в окрестностях сильных разрывов $1 - {{\beta }_{s}}({{K}_{C}}) = O(1)$ (в этих точках $Q_{s}^{A} - Q_{s}^{B} = O(1)$).
Методу консервативной монотонизации (7)–(9) поставим в соответствие оператор $L({{C}_{1}})$. Это оператор того же типа, что и операторы послойного перехода ${{S}_{A}}(\tau )$ и ${{S}_{B}}(\tau )$ у схем $A$ и $B$. Очевидно, $L(0) = E$ – единичному оператору. Оператор послойного перехода искомой монотонизированной локальнo-oдномерной бикомпактной схемы примет вид
Далее мы называем эту схему аббревиатурой SDIRK2B4.В завершение раздела приведем формулу для параметров потокового расщепления $C_{2}^{d}$:
(10)
$C_{2}^{d} = \frac{{1 + 2\delta }}{2}V_{{\max }}^{d},\quad V_{{\max }}^{d} = \mathop {\max }\limits_{{\mathbf{r}} \in \Omega } \left( {\left| {v_{d}^{n}({\mathbf{r}})} \right| + {{c}^{n}}({\mathbf{r}})} \right),\quad d = x,y,z,$(11)
$\tau = \kappa \mathop {\min }\limits_{d = x,y,z} \frac{{{{{\min }}_{{i = \overline {0,{{N}_{d}} - 1} }}}{{h}_{{d,i + 1/2}}}}}{{\frac{1}{2}V_{{\max }}^{d} + C_{2}^{d}}},$3. АЛГОРИТМЫ ПАРАЛЛЕЛЬНОГО СЧЕТА
Мотивация. Замена течения несжимаемой жидкости на течение сжимаемой жидкости при малых числах Маха обладает тем недостатком, что при равном числе Куранта расчет течения сжимаемой жидкости потребует равномерно меньших шагов по времени. Это объясняется тем, что число Куранта в несжимаемом случае прямо пропорционально скорости $v$, а в сжимаемом случае – сумме скоростей $v + c$, где c существенно превосходит $v$ (локальные числа Маха ${\text{M}} = v{\text{/}}c$ малы). Как следствие, расчет задачи о вихре Тейлора–Грина в сжимаемой постановке по бикомпактной схеме SDIRK2B4 на одном ядре CPU на сетках от ${{100}^{3}}$ ячеек оказывается неприемлемо долгим из-за довольно большого числа шагов по времени. Попытка воспользоваться неявностью бикомпактных схем через задание большего числа Куранта (равного 2–10) приводит к неудовлетворительным результатам из-за существенного повышения численной диссипации. Таким образом, возникает необходимость в параллельной реализации бикомпактных схем.
Мы предлагаем два алгоритма параллельного счета по локально-одномерным бикомпактным схемам. Оба алгоритма соответствуют парадигме “параллелизма задач” и предназначены для многопроцессорных вычислительных систем с распределенной памятью. Рассуждения достаточно провести на примере схемы SDIRK2B4, так как локально-одномерные бикомпактные схемы не имеют принципиальных различий в своей реализации. Отметим, что параллельная реализация нерасщепленных бикомпактных схем рассмотрена в [23].
Параллелизм локально-одномерных бикомпактных схем. Прежде чем перейти непосредственно к алгоритмам, сделаем несколько общих замечаний о составных частях схемы SDIRK2B4.
Оператор послойного перехода ${{S}_{B}}(\tau )$, согласно своему определению (6), является композицией операторов $S_{B}^{{d, \pm }}(\tau )$, $d = x,y,z$. Каждый из них реализуется посредством итерационного метода Ньютона (необходимого для решения нелинейных разностных уравнений) и совокупности независимых одномерных двухточечных матричных прогонок (циклических, с матрицами размера $5 \times 5$); последние устойчивы в силу знакоопределенности матриц ${{{\mathbf{A}}}^{{d, \pm }}}({\mathbf{Q}})$. Ясно, что прогонки на разных линиях сетки (т.е. прямых, проходящих через узлы сетки параллельно осям координат) могут выполняться параллельно. Тем не менее каждая прогонка в отдельности должна выполняться строго последовательно, так как, например, при реализации оператора $S_{B}^{{x, + }}(\tau )$ значение ${{{\mathbf{Q}}}_{{j + 1,k,l}}}$ может быть вычислено только после нахождения ${{{\mathbf{Q}}}_{{j,k,l}}},{{{\mathbf{Q}}}_{{j - 1/2,k,l}}}, \ldots ,{{{\mathbf{Q}}}_{{0,k,l}}}$.
На оператор послойного перехода ${{S}_{A}}(\tau )$ мы смотрим так же, как на оператор ${{S}_{B}}(\tau )$, хотя реализация $S_{A}^{{d, \pm }}(\tau )$ для любого $d = x,y,z$ обладает параллелизмом, в том числе и по оси $Od$ (схема $A$ – явная).
Метод консервативной монотонизации (7)–(9) и соответствующий ему ограничивающий оператор $L({{C}_{1}})$ реализуются явно и локально, так как найдены решения ${{{\mathbf{Q}}}^{A}} = {{S}_{A}}(\tau ){{{\mathbf{Q}}}^{n}}$ и ${{{\mathbf{Q}}}^{B}} = {{S}_{B}}(\tau ){{{\mathbf{Q}}}^{n}}$. Это следует из того, что (а) для применения формул (7), (8) в каждой ячейке достаточно только данных из этой ячейки, (б) для применения формулы (9) в каждом узле достаточно данных из тех ячеек, которым принадлежит этот узел. Значит, метод (7)–(9) обладает параллелизмом по ячейкам.
Алгоритм 1. Введем ${{n}_{p}}$ процессов. Совокупность всех ячеек сетки $\Omega $ разделим поровну на ${{n}_{p}}$ горизонтальных (относительно оси $Oz$) слоев и ${{n}_{p}}$ вертикальных слоев. Горизонтальный слой ячеек номер $r = 0,1, \ldots ,{{n}_{p}} - 1$ включает в себя узлы
В начале расчета каждый процесс инициализирует свою сеточную функцию ${{{\mathbf{Q}}}^{0}}$ на ${{W}_{r}}$ с помощью известного начального условия. Переход со слоя ${{t}^{n}}$ на слой ${{t}^{{n + 1}}}$ ($n = 0,1, \ldots $) на процессе номер $r$ состоит из следующих действий:
1. На ${{W}_{r}}$ вычисляются местные максимумы $V_{{\max }}^{d}$. При $r \ne 0$ числа $V_{{\max }}^{d}$ посылаются на процесс номер 0, после чего рассматриваемый процесс (номер $r$) ожидает от него в ответ параметры $C_{2}^{d}$ и шаг $\tau $. При $r = 0$ числа $V_{{\max }}^{d}$ сравниваются с аналогичными величинами, принимаемыми от остальных процессов, в результате чего становятся известными глобальные максимумы $V_{{\max }}^{d}$ на $\Omega $. Они позволяют посчитать параметры $C_{2}^{d}$ и шаг $\tau $ по формулам (10), (11). Эти четыре числа рассылаются всем остальным процессам.
2. На ${{W}_{r}}$ вычисляются два решения: ${{{\mathbf{Y}}}^{A}} = S_{A}^{y}(\tau )S_{A}^{x}(\tau ){{{\mathbf{Q}}}^{n}}$ и ${{{\mathbf{Y}}}^{B}} = S_{B}^{y}(\tau {\text{/}}2)S_{B}^{x}(\tau {\text{/}}2){{{\mathbf{Q}}}^{n}}$. Значения ${{{\mathbf{Y}}}^{A}}$ и ${{{\mathbf{Y}}}^{B}}$ в плоскости $z = {{z}_{{r{{N}_{z}}/{{n}_{p}}}}}$ не рассчитываются по схемам $A$ и $B$, а принимаются в готовом виде от процесса номер $r - 1$ (если $r = 0$, то в силу периодических граничных условий принимаются данные с плоскости $z = {{z}_{{{{N}_{z}}}}} = 2\pi $ от процесса номер ${{n}_{p}} - 1$). Это делается для того, чтобы избежать удвоения вычислений на границах между горизонтальными слоями ячеек.
3. Выполняется барьерная синхронизация процессов. Массив, отвечающий решению ${{{\mathbf{Y}}}^{A}}$ на ${{W}_{r}}$, разбивается вдоль оси $Ox$ на ${{n}_{p}}$ частей сообразно разделению области на вертикальные слои (фиг. 2). Часть номер $r{\kern 1pt} ' \ne r$ этого массива посылается на процесс с номером $r{\kern 1pt} '$; часть номер $r{\kern 1pt} ' = r$ записывается (на соответствующие ей места) в “сопряженный” массив, отвечающий решению ${{{\mathbf{Y}}}^{A}}$ на $W_{r}^{*}$. Данные, принимаемые от остальных процессов, заполняют этот “сопряженный” массив до конца. Над массивом, в котором хранится решение ${{{\mathbf{Y}}}^{B}}$ на ${{W}_{r}}$, совершаются те же операции.
4. На $W_{r}^{*}$ вычисляется два решения: ${{{\mathbf{Q}}}^{A}} = S_{A}^{z}(\tau ){{{\mathbf{Y}}}^{A}} = {{S}_{A}}(\tau ){{{\mathbf{Q}}}^{n}}$ и ${{\widetilde {\mathbf{Y}}}^{B}} = S_{B}^{z}(\tau ){{{\mathbf{Y}}}^{B}}$. Дублирование вычислений на границах между вертикальными слоями устраняется аналогично п. 2.
5. Выполняется барьерная синхронизация процессов. Над массивами, в которых хранятся решения ${{{\mathbf{Q}}}^{A}}$ и ${{\widetilde {\mathbf{Y}}}^{B}}$ на $W_{r}^{*}$, выполняются операции разбиения и рассылки, симметричные (обратные) тому, что описано в п. 3 (фиг. 2). В итоге процессу номер $r$ становятся известны решения ${{{\mathbf{Q}}}^{A}}$ и ${{\widetilde {\mathbf{Y}}}^{B}}$ на ${{W}_{r}}$.
6. На ${{W}_{r}}$, аналогично п. 2, вычисляется решение ${{{\mathbf{Q}}}^{B}} = S_{B}^{x}(\tau {\text{/}}2)S_{B}^{y}(\tau {\text{/}}2){{\widetilde {\mathbf{Y}}}^{B}} = {{S}_{B}}(\tau ){{{\mathbf{Q}}}^{n}}$.
7. На ${{W}_{r}}$ по решениям ${{{\mathbf{Q}}}^{A}}$ и ${{{\mathbf{Q}}}^{B}}$, согласно формулам (7)–(9), строится искомое финальное решение ${{{\mathbf{Q}}}^{{n + 1}}} = L({{C}_{1}}){{{\mathbf{Q}}}^{B}} = S(\tau ,{{C}_{1}}){{{\mathbf{Q}}}^{n}}$. Благодаря тому, что множество ${{W}_{r}}$ включает узлы с границ между горизонтальными слоями, формулы (7), (8) реализуются без обращения к соседним слоям и процессам, связанным с ними. Формулу (9) проще всего реализовывать не через обход по узлам, а через обход по ячейкам: сначала в каждом узле ${{W}_{r}}$ суммы, участвующие в правой части (9), полагаются нулевыми; затем в процессе обхода по ячейкам к ним добавляются составляющие их слагаемые. Однако для применения (9) на плоскостях $z = {{z}_{{r{{N}_{z}}/{{n}_{p}}}}}$ и $z = {{z}_{{(r + 1){{N}_{z}}/{{n}_{p}}}}}$ придется обратиться к процессам с номерами $r - 1$ и $r + 1$, чтобы получить нужные данные от ячеек, примыкающих к этим плоскостям снаружи рассматриваемого $r$-го слоя. В силу периодических граничных условий слоем с номером $( - 1)$ является слой ${{n}_{p}} - 1$, а слоем с номером ${{n}_{p}}$ – слой 0.
Отметим, что все обращения за границы расчетной области вызваны исключительно периодическими граничными условиями, а не особенностями схем $A$ и $B$ (пространственные шаблоны составляющих их одномерных схем и метода (7)–(9) минимальны); любые другие граничные условия не порождают таких обращений.
Дублирование вычислений на границах между слоями ячеек исключается (см. шаги 2, 4, 6 алгоритма) по двум причинам. Во-первых, расчет решения на одной плоскости при ${{N}_{d}} \gtrsim 10$ занимает на порядок больше машинного времени, чем пересылка этих данных с другого процесса. Во-вторых, например, при ${{n}_{p}} = {{N}_{z}}{\text{/}}4$ объем лишних (дублированных) вычислений на шаге 2 составляет ${{N}_{z}}{\text{/}}(4(2{{N}_{z}} + 1)) \approx 13\% $ от общего объема необходимых вычислений, что представляется достаточно неэффективным.
Все расчеты, результаты которых представлены в разд. 4, выполнены по алгоритму 1. Из-за этого далее алгоритм 2 описывается менее подробно; он нужен для того, чтобы показать альтернативный способ параллельной реализации локально-одномерных бикомпактных схем.
Алгоритм 2. Применим стратегию “управляющий–рабочие” (см. [32]). Назначим процесс с номером 0 управляющим процессом; предположим, что он имеет доступ ко всему массиву векторов ${{{\mathbf{Q}}}^{n}}$, т.е. решению на всей сетке $\Omega $. Процессы с номерами $1,2, \ldots ,{{n}_{p}} - 1$ принимают тогда роль рабочих процессов.
Рассмотрим реализацию схемы $B$ на одном временном шаге. Процесс номер 0 берет решение ${{{\mathbf{Q}}}^{n}}$ с прямых
При реализации метода консервативной монотонизации (7)–(9) управляющий процесс рассылает по рабочим процессам решения ${{{\mathbf{Q}}}^{A}}$ и ${{{\mathbf{Q}}}^{B}}$ с подмножеств ячеек, порожденных любым удобным разбиением всего множества ячеек. Например, это могут быть горизонтальные слои ячеек из алгоритма 1. Рабочие процессы получают по формулам (7), (8) данные, необходимые для применения формулы (9), и отправляют их на управляющий процесс, на котором “собирается” результирующее решение ${{{\mathbf{Q}}}^{{n + 1}}}$.
Вычисление максимумов $V_{{\max }}^{d}$, необходимых для пересчета параметров $C_{2}^{d}$ и шага $\tau $ перед каждым переходом на новый слой, выполняется по аналогии с методом (7)–(9) (с той разницей, что каждый из рабочих процессов возвращает управляющему лишь 3 числа, а не решение с некоторого подмножества ячеек).
Сравнение алгоритмов. Напомним, что реализация любого из операторов послойного перехода $S_{B}^{{d, \pm }}(\tau )$ на любой линии сетки включает в себя итерационный метод Ньютона (для решения нелинейных разностных уравнений), а значит, не является детерминированной по времени счета. Например, если решение тождественно постоянно на какой-то линии сетки, то метод Ньютона сойдется на ней всего за одну итерацию, в несколько раз быстрее предполагаемой длительности итерационного процесса. Это обстоятельство вкупе с фиксированным разбиением расчетной области на слои в алгоритме 1 создает потенциальную проблему неравномерной загрузки процессов. Заметим все же, что в задаче о вихре Тейлора–Грина решение существенно отличается от константы во всей расчетной области во все моменты времени, а потому в этой и подобной ей задачах данный недостаток алгоритма 1 не должен проявляться в заметной степени. Кроме того, эту потенциальную проблему можно решить динамической регулировкой разбиения совокупности ячеек на слои, что, однако, выходит за рамки настоящей работы. Другим недостатком алгоритма 1 является ограничение на число процессов: ${{n}_{p}} \leqslant \min ({{N}_{z}},{{N}_{x}})$ (очевидно, число слоев, на которые разбивается вся совокупность ячеек, не может превосходить числа ячеек по соответствующему направлению). В то же время алгоритм 2 лишен этих недостатков: линии сетки динамически распределяются по процессам, а число процессов ограничено довольно большим числом этих линий, порядка $4{{N}^{2}}$ при ${{N}_{x}} = {{N}_{y}} = {{N}_{z}} = N$. Тем не менее алгоритм 2 проигрывает алгоритму 1 в объеме пересылаемых данных. Пусть размер массива векторов ${\mathbf{Q}}$ на всей сетке $\Omega $ равен $M$. Тогда за один временной шаг в алгоритме 1 суммарно пересылается объем данных $4M$ (решения ${{{\mathbf{Y}}}^{A}}$, ${{{\mathbf{Y}}}^{B}}$ до реализации операторов $S_{A}^{z}(\tau )$, $S_{B}^{z}(\tau )$, решения ${{{\mathbf{Q}}}^{A}}$, ${{\widetilde {\mathbf{Y}}}^{B}}$ после; обменами на границах между слоями можно пренебречь), а в алгоритме 2 – $19M$ (по $2M$ на каждый из операторов вида $S_{A}^{d}(\tau )$, $S_{B}^{d}(\tau )$, $2M$ на оператор $L({{C}_{1}})$, $M$ на вычисление $C_{2}^{d}$ и $\tau $), что почти в пять раз больше. Из сказанного следует вывод, что в задаче о вихре Тейлора–Грина алгоритм 1 является более подходящим для параллельной реализации бикомпактной схемы SDIRK2B4.
4. АНАЛИЗ РЕЗУЛЬТАТОВ
Рассмотрим результаты расчетов задачи о вихре Тейлора–Грина по бикомпактной схеме SDIRK2B4 на сетках ${{32}^{3}}$, ${{64}^{3}}$, ${{128}^{3}}$ ячеек. Укажем значения параметров схемы: число Куранта $\kappa = 0.8$; параметр метода консервативной монотонизации ${{C}_{1}} = 0,0.2,0.5$ (по три варианта для каждой сетки); параметр потокового расщепления $\delta = 0.2$. Обратим внимание на то, что при расчетах других задач газовой динамики параметр ${{C}_{1}}$ брался примерно на порядок большим (см. [26]). Его уменьшение обусловлено тем, что характерное число Маха в задаче о вихре Тейлора–Грина примерно на порядок меньше по сравнению с задачами, которые решались ранее.
Расчетный код реализован на языке C++ с применением библиотеки MPI. Вычисления проводились на гибридном суперкомпьютере K-60, установленном в Центре коллективного пользования ИПМ им. М.В. Келдыша РАН.
Сначала проверим эффективность распараллеливания по алгоритму 1. На фиг. 3 представлена зависимость ускорения счета от числа процессов ${{n}_{p}}$; она построена по временам счета первого временного шага на сетке ${{128}^{3}}$ ячеек при ${{C}_{1}} = 0.2$. Видно, что при ${{n}_{p}} \leqslant 32$ эффективность распараллеливания достаточно высокая, не меньше 76%. Чем больше ${{n}_{p}}$ (и чем оно ближе к ${{N}_{z}}$ или ${{N}_{x}}$), тем тоньше слои ячеек, с которыми работает каждый процесс, тем больше актов обмена между процессами и тем ниже эффективность параллельного счета. Полные расчеты задачи до момента времени $t = 10$ на сетках ${{32}^{3}}$, ${{64}^{3}}$, ${{128}^{3}}$ ячеек делались соответственно на ${{n}_{p}} = 8,\;16,$ 32 процессах.
Фиг. 3.
Ускорение счета по бикомпактной схеме SDIRK2B4 в зависимости от числа процессов ${{n}_{p}}$. Сплошная прямая соответствует идеальному распараллеливанию, маркеры – фактически наблюдаемому. Подписи под маркерами означают эффективность распараллеливания. График построен по временам счета первого временного шага на сетке ${{128}^{3}}$ ячеек при ${{C}_{1}} = 0.2$.

Сравним бикомпактную схему SDIRK2B4 с другими схемами высокого порядка по уровню численной диссипации. Для сопоставления выберем две схемы серии WENO5: классическую схему WENO5-JS (см. [12]) и одну из ее последних улучшенных версий – схему WENO5-MR (см. [13]) (“nested multi-resolution WENO5”), несколько превосходящую популярную схему WENO5-Z из [14]). Обе схемы имеют аппроксимацию пятого порядка по пространству и третьего порядка по времени. Результаты для схемы WENO5-JS заимствованы из [13]. О численной диссипации мы будем судить по эволюции двух величин – кинетической энергии $K(t)$ и энстрофии $\mathcal{E}(t)$ жидкости во всем кубе ${\mathbf{r}} \in {{[0,2\pi ]}^{3}}$:
На фиг. 4 изображены кривые нормированной кинетической энергии $K(t){\text{/}}K(0)$ для всех схем и всех сеток. Для схемы SDIRK2B4 показаны лишь кривые, полученные при ${{C}_{1}} = 0$ (без монотонизации) и при ${{C}_{1}} = 0.5$, как соответственно наилучший и наихудший (в смысле диссипации) варианты. Из данной фигуры очевидно, что схема WENO5-JS имеет самую большую диссипацию; чтобы быть сопоставимой со схемами WENO5-MR и SDIRK2B4, ей требуется сетка с двукратно большим числом ячеек по всем направлениям. Схема SDIRK2B4 при ${{C}_{1}} = 0.5$ немного превосходит схему WENO5-MR. В отсутствие монотонизации схема SDIRK2B4 демонстрирует значительное преимущество перед схемами WENO5-JS и WENO5-MR. Интересно, что $L$-устойчивость временной дискретизации в бикомпактной схеме проявляет себя как своего рода “встроенный” фильтр нежелательных осцилляций, делающий возможным полный расчет задачи без монотонизации. Свойство $L$-устойчивости здесь действительно по существу, так как, например, при дискретизации по времени методом трапеций (как известно, не обладающим этим свойством) бикомпактная схема неустойчива при ${{C}_{1}} = 0$.
Фиг. 4.
Сравнение бикомпактной схемы SDIRK2B4 со схемами WENO5-JS, WENO5-MR по эволюции кинетической энергии жидкости. На графике представлены данные для всех трех сеток ${{32}^{3}}$, ${{64}^{3}}$, ${{128}^{3}}$ ячеек: чем ближе та или иная зависимость к единице, тем больше размер соответствующей сетки.

Продолжим наше сравнение схем анализом кривых нормированной энстрофии $\mathcal{E}(t){\text{/}}\mathcal{E}(0)$, изображенных на фиг. 5, 6. Из этих фигур следует, что по энстрофии схема WENO5-MR соотносится с монотонизированной схемой SDIRK2B4 так же, как по кинетической энергии схема WENO5-JS соотносится со схемой WENO5-MR: чтобы достичь примерно того же максимума энстрофии, схеме WENO5-MR нужна сетка с удвоенным числом ячеек по каждому направлению. Схема SDIRK2B4 без монотонизации дает самые высокие максимумы $\mathcal{E}(t)$: уже на сетке ${{32}^{3}}$ ячеек получается примерно такое же значение, как у схемы WENO5-MR на сетке ${{128}^{3}}$ ячеек и у монотонизированной схемы SDIRK2B4 на сетке ${{64}^{3}}$ ячеек; на сетке ${{128}^{3}}$ ячеек максимум энстрофии составляет около 56, что намного превосходит все остальные результаты, участвующие в сравнении. Добавим, что кривые энстрофии, полученные по бикомпактной схеме на сетке ${{128}^{3}}$ ячеек при всех трех значениях ${{C}_{1}}$, находятся в очень хорошем согласии с полуаналитической зависимостью для времен $t \leqslant 4$ из [29] (фиг. 6).
Фиг. 5.
Сравнение бикомпактной схемы SDIRK2B4 со схемами WENO5-JS, WENO5-MR по эволюции энстрофии. На графике представлены данные для всех трех сеток ${{32}^{3}}$, ${{64}^{3}}$, ${{128}^{3}}$ ячеек: чем выше максимум той или иной зависимости, тем больше размер соответствующей сетки. Ради лучшей читаемости фигуры значения $\mathcal{E}(t){\text{/}}\mathcal{E}(0)$ ограничены девятью; недостающие участки кривых изображены на фиг. 6.

Для полноты изложения поясним, что относительное отклонение плотности жидкости от начального значения составляет не более 2% для всех сеток, для всех выбранных значений ${{C}_{1}}$, на всех слоях по времени, во всех узлах. Следовательно, в процессе движения жидкость действительно остается примерно несжимаемой.
Перейдем к основному вопросу настоящей работы – вопросу о влиянии метода консервативной монотонизации из [26] на разрешение бикомпактной схемой SDIRK2B4 спектра ${{\sigma }_{K}}(k,t)$ кинетической энергии жидкости. Уточним, что ${{\sigma }_{K}}(k,t)$ вычисляется по формуле
На фиг. 7–9 приведены искомые графики спектров, полученных по бикомпактной схеме SDIRK2B4 на сетках ${{32}^{3}}$, ${{64}^{3}}$, ${{128}^{3}}$ ячеек соответственно (при ${{C}_{1}} = 0,0.2,0.5$). Каждый спектр построен в момент времени, отвечающий точке максимума энстрофии $\mathcal{E}(t)$. Из-за малого числа точек фиг. 7 не позволяет со всей ясностью оценить численную диссипацию при ${{C}_{1}} \ne 0$, однако эта фигура все же показывает, что даже на весьма грубой сетке ${{32}^{3}}$ ячеек схема SDIRK2B4 без монотонизации более-менее верно (не считая трех точек на правом конце спектра) воспроизводит колмогоровский наклон $( - 5{\text{/}}3)$. Фиг. 8, 9 дают более понятную картину: видно, что при ${{C}_{1}} = 0$ спектры идут вдоль прямой с наклоном $( - 5{\text{/}}3)$ без существенных отклонений вплоть до самых больших волновых чисел, а при ${{C}_{1}} = 0.2$ и ${{C}_{1}} = 0.5$ бикомпактная схема разрешает соответственно 85 и 70% спектра (по логарифмической шкале), если принимать за эталон спектр при ${{C}_{1}} = 0$ и полагать допустимым искажение амплитуды гармоники не более, чем в два раза. Нельзя не заметить, что монотонизированная схема SDIRK2B4 не подавляет полностью вихри наименьших масштабов, поэтому получаемые по ней спектры не имеют резких “уклонов вниз” на правом конце.
Фиг. 7.
Спектры кинетической энергии жидкости, полученные по бикомпактной схеме SDIRK2B4 при разных значениях параметра монотонизации ${{C}_{1}}$, сетка ${{32}^{3}}$ ячеек. Пунктирной прямой показан наклон $( - 5{\text{/}}3)$.
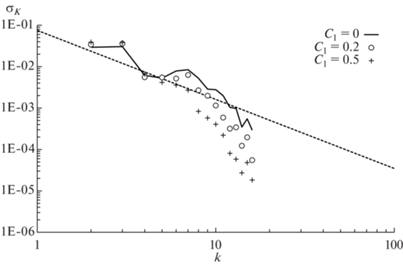
Фиг. 8.
Спектры кинетической энергии жидкости, полученные по бикомпактной схеме SDIRK2B4 при разных значениях параметра монотонизации ${{C}_{1}}$, сетка ${{64}^{3}}$ ячеек. Пунктирной прямой показан наклон $( - 5{\text{/}}3)$.

Фиг. 9.
Спектры кинетической энергии жидкости, полученные по бикомпактной схеме SDIRK2B4 при разных значениях параметра монотонизации ${{C}_{1}}$, сетка ${{128}^{3}}$ ячеек. Пунктирной прямой показан наклон $( - 5{\text{/}}3)$.

Отметим напоследок одну любопытную деталь спектра, полученного по схеме SDIRK2B4 на сетке ${{128}^{3}}$ ячеек при ${{C}_{1}} = 0$ (фиг. 9): несмотря на то, что монотонизация отсутствует (“выключена”), он все же в очень незначительной степени “загибается вниз” после $k \approx 40$. Такое поведение является следствием $L$-устойчивости временной дискретизации; выше мы уже говорили о том, что данное свойство выступает в роли некоего встроенного минимального фильтра самых высокочастотных составляющих решения.
ЗАКЛЮЧЕНИЕ
В работе предложены два алгоритма параллельной реализации локально-одномерных бикомпактных схем для систем трехмерных уравнений гиперболического типа. Оба алгоритма предназначены для многопроцессорных вычислительных систем с распределенной памятью. В основе алгоритма 1 лежит статическое разбиение совокупности ячеек пространственной сетки на горизонтальные и вертикальные слои, в основе алгоритма 2 – динамическое распределение вычислений с линий сетки между процессами. Алгоритм 1 проигрывает алгоритму 2 в равномерности загрузки процессов (в случае, если рассчитываемое решение имеет вид локализованного возмущения на постоянном фоне), но существенно выигрывает в объеме пересылаемых данных.
По локально-одномерной бикомпактной схеме SDIRK2B4 четвертого порядка аппроксимации по пространству и второго порядка аппроксимации по времени выполнены расчеты задачи о вихре Тейлора–Грина в невязком совершенном газе. На примере данной задачи и выбранной схемы выяснялось то, в какой мере теоретически высокое спектральное разрешение бикомпактных схем ухудшается практически из-за применяемого в них метода консервативной монотонизации из [26] – это важно для понимания перспективы приложения схем данного класса к LES. Вычисления проводились на сетках ${{32}^{3}}$, ${{64}^{3}}$, ${{128}^{3}}$ ячеек, при этом применялась параллельная реализация по алгоритму 1 (постановка задачи делает его более предпочтительным); эффективность распараллеливания составила примерно 75%.
Анализ результатов позволяет сделать несколько выводов. Во-первых, благодаря $L$-устойчивости временной дискретизации, бикомпактная схема SDIRK2B4 имеет встроенный механизм стабилизации счета, который позволяет решать некоторые задачи газовой динамики вообще в отсутствие какой-либо специальной монотонизации, разрешение спектра кинетической энергии при этом оказывается высоким. Во-вторых, при использовании метода консервативной монотонизации из [26] данное разрешение ухудшается в умеренной, допустимой степени – разрешаются 70–85% спектра. В-третьих, если судить по поведению энстрофии, то по сравнению с современными схемами серии WENO5 схема SDIRK2B4 лучше воспроизводит вихревой каскад и не так сильно подавляет вихри среднего масштаба. Таким образом, направлением дальнейших исследований являются обобщение бикомпактных схем на уравнения Навье–Стокса для сжимаемой жидкости и затем применение этих новых схем в LES.
Список литературы
Андерсон Д., Таннехилл Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен: В 2-х т. Т. 1: Пер. с англ. М.: Мир, 1990. 384 с.
Kawai S., Lele S.K. Large-eddy simulation of jet mixing in supersonic crossflows // AIAA J. 2010. V. 48. № 9. P. 2063–2083.
Bull J.R., Jameson A. Simulation of the Taylor–Green vortex using high-order flux reconstruction schemes // AIAA J. 2015. V. 53. № 9. P. 2750–2761.
Sagaut P. Large Eddy simulation for incompressible flows. 3rd ed. Berlin: Springer, 2006.
Moura R.C., Mengaldo G., Peiró J., Sherwin S.J. On the eddy-resolving capability of high-order discontinuous Galerkin approaches to implicit LES under-resolved DNS of Euler turbulence // J. Comput. Phys. 2017. V. 330. P. 615–623.
Flad D., Beck A., Guthke P. A large Eddy simulation method for DGSEM using non-linearly optimized relaxation filters // J. Comput. Phys. 2020. V. 408. 109303.
Drikakis D., Fureby C., Grinstein F., Youngs D. Simulation of transition and turbulence decay in the Taylor–Green vortex // J. Turbul. 2007. V. 8. № 20. P. 1–12.
Liu X., Zhang S., Zhang H., Shu C.-W. A new class of central compact schemes with spectral-like resolution I: Linear schemes // J. Comput. Phys. 2013. V. 248. P. 235–256.
De La Llave Plata M., Couaillier V., Pape M.-C. On the use of a high-order discontinuous Galerkin method for DNS and LES of wall-bounded turbulence // Comput. Fluids. 2018. V. 176. P. 320–337.
Gassner G., Beck A. On the accuracy of high-order discretizations for underresolved turbulence simulations // Theor. Comp. Fluid. Dyn. 2013. V. 27. P. 221–237.
Diosady L.T., Murman S.M. DNS of flows over periodic hills using a discontinuous-Galerkin spectral-element method // 44th AIAA Fluid Dynam. Conf. 2014.
Jiang G.-S., Shu C.-W. Efficient implementation of weighted ENO schemes // J. Comput. Phys. 1996. V. 126. № 1. P. 202–228.
Wang Z., Zhu J., Tian L., Zhao N. A low dissipation finite difference nested multi-resolution WENO scheme for Euler/Navier–Stokes equations // J. Comput. Phys. 2021. V. 429. 110006.
Borges R., Carmona M., Costa B., Don W. S. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws // J. Comput. Phys. 2008. V. 227. № 6. P. 3191–3211.
Головизнин В.М., Зайцев М.А., Карабасов С.А., Короткин И.А. Новые алгоритмы вычислительной гидродинамики для многопроцессорных вычислительных комплексов. М. : Изд-во МГУ, 2013. 472 с.
Тишкин В.Ф., Гасилов В.А., Змитренко Н.В. и др. Современные методы математического моделирования развития гидродинамических неустойчивостей и турбулентного перемешивания // Матем. моделирование. 2020. Т. 32. № 8. С. 57–90.
Grimich K., Cinnella P., Lerat A. Spectral properties of high-order residual-based compact schemes for unsteady compressible flows // J. Comput. Phys. 2013. V. 252. P. 142–162.
Толстых А.И. Компактные разностные схемы и их применение в задачах аэрогидродинамики. М.: Наука, 1990. 230 с.
Толстых А.И. Компактные и мультиоператорные аппроксимации высокой точности для уравнений в частных производных. М.: Наука, 2015. 350 с.
Брагин М.Д., Рогов Б.В. Гибридные бикомпактные схемы с минимальной диссипацией для уравнений гиперболического типа // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 6. С. 958–972.
Брагин М.Д., Рогов Б.В. О точном пространственном расщеплении многомерного скалярного квазилинейного гиперболического закона сохранения // Докл. АН. 2016. Т. 469. № 2. С. 143–147.
Рогов Б.В., Брагин М.Д. О свойствах спектрального разрешения симметричных бикомпактных схем четвертого порядка аппроксимации // Докл. АН. 2017. Т. 475. № 2. С. 140–144.
Чикиткин А.В., Рогов Б.В. Два варианта параллельной реализации высокоточных бикомпактных схем для многомерного неоднородного уравнения переноса // Препринты ИПМ им. М.В. Келдыша. 2018. № 177. 24 с.
Chikitkin A.V., Rogov B.V. Family of central bicompact schemes with spectral resolution property for hyperbolic equations // Appl. Numer. Math. 2019. V. 142. P. 151–170.
Rogov B.V. Dispersive and dissipative properties of the fully discrete bicompact schemes of the fourth order of spatial approximation for hyperbolic equations // Appl. Numer. Math. 2019. V. 139. P. 136–155.
Bragin M.D., Rogov B.V. Conservative limiting method for high-order bicompact schemes as applied to systems of hyperbolic equations // Appl. Numer. Math. 2020. V. 151. P. 229–245.
Брагин М.Д., Рогов Б.В. Бикомпактные схемы для задач газовой динамики: обобщение на сложные расчетные области методом свободной границы // Компьют. исслед. и моделирование. 2020. Т. 12. № 3. С. 487–504.
Брагин М.Д., Рогов Б.В. Высокоточные бикомпактные схемы для численного моделирования течений многокомпонентных газов с несколькими химическими реакциями // Матем. моделирование. 2020. Т. 32. № 6. С. 21–36.
Brachet M.E., Meiron D.I., Orszag S.A., et al. Small-scale structure of the Taylor–Green vortex // J. Fluid Mech. 1983. V. 130. P. 411–452.
Alexander R. Diagonally implicit Runge-Kutta methods for stiff O.D.E.’s // SIAM J. Numer. Anal. 1977. V. 14. № 6. P. 1006–1021.
Марчук Г.И. Методы расщепления. М.: Наука, 1988. 263 с.
Лупин С.А., Посыпкин М.А. Технологии параллельного программирования. М.: ИД “ФОРУМ”: ИНФРА-М, 2011. 208 с.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики





