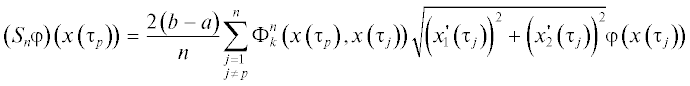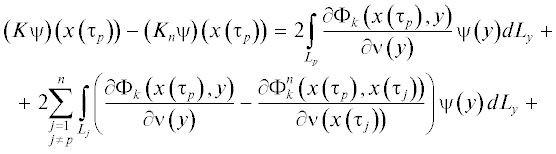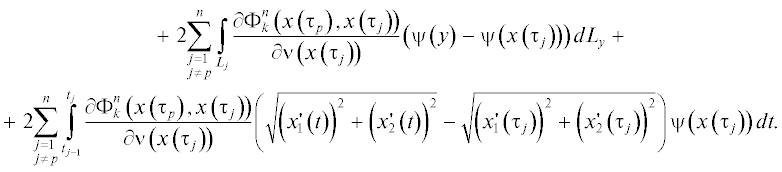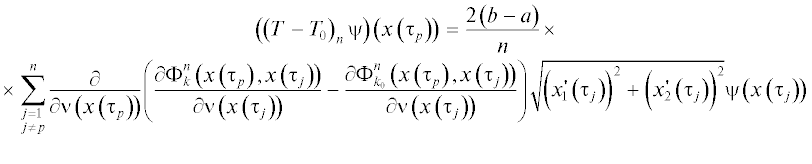1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 62, № 5, 2022

Журнал вычислительной математики и математической физики, 2022, T. 62, № 5, стр. 838-853

Исследование приближенного решения одного класса систем интегральных уравнений

Э. Г. Халилов *

Азербайджанский Государственный Университет Нефти и Промышленности
AZ 1010 Баку, пр-т Азадлыг, 20, Азербайджан

* E-mail: elnurkhalil@mail.ru

Поступила в редакцию 20.08.2021
После доработки 20.08.2021
Принята к публикации 17.11.2021

Полный текст (PDF)

Аннотация

Дано обоснование метода коллокации для системы интегральных уравнений граничной задачи сопряжения для уравнения Гельмгольца в двухмерном пространстве. Построены квадратурные формулы для потенциалов простого и двойного слоев и нормальной производной потенциала простого слоя. В определенно выбранных точках система интегральных уравнений заменяется системой алгебраических уравнений, при этом устанавливаются существование и единственность решения системы алгебраических уравнений. Доказывается сходимость решения системы алгебраических уравнений к точному решению системы интегральных уравнений и указывается скорость сходимости метода. Кроме того, построена последовательность, сходящаяся к точному решению граничной задачи сопряжения. Библ. 16.

Ключевые слова: граничная задача сопряжения, уравнение Гельмгольца, система интегральных уравнений, потенциалы простого и двойного слоев, функция Ханкеля, квадратурные формулы, метод коллокации.

1. ВВЕДЕНИЕ И ПОСТАНОВКА ЗАДАЧИ

Пусть $D \subset {{R}^{2}}$ – ограниченная область с дважды непрерывно дифференцируемой границей L. Следует указать, что (см. [1, с. 112]) математическая формулировка задачи дифракции акустических  волн на теле D с различными акустическими характеристиками в ${{R}^{2}}{{\backslash }}\bar {D}$ и D приводит к задаче сопряжения, которая заключается в следующем: найти две функции $u \in {{C}^{{\left( 2 \right)}}}\left( {{{R}^{2}}{{\backslash }}\bar {D}} \right) \cap C\left( {{{R}^{2}}{{\backslash }}D} \right)$ и ${{u}_{0}} \in {{C}^{{\left( 2 \right)}}}\left( D \right) \cap C\left( {\bar {D}} \right)$, обладающие нормальной производной в смысле равномерной сходимости и удовлетворяющие уравнениям Гельмгольца $\Delta u + {{k}^{2}}u = 0$ в ${{R}^{2}}{{\backslash }}\bar {D}$ и $\Delta {{u}_{0}} + {{k}^{2}}{{u}_{0}} = 0$ в D, условию излучения Зоммерфельда

$\left( {\frac{x}{{\left| x \right|}},{\text{grad}}\;{\kern 1pt} u\left( x \right)} \right) - iku\left( x \right) = o\left( {\frac{1}{{{{{\left| x \right|}}^{{1/2}}}}}} \right),\quad x \to \infty ,$
равномерно по всем направлениям $x{\text{/}}\left| x \right|$ и условиям сопряжения
$\mu u - {{\mu }_{0}}{{u}_{0}} = f\;{\text{на}}\;L,$
$\frac{{\partial u}}{{\partial \nu }} - \frac{{\partial {{u}_{0}}}}{{\partial \nu }} = g\;{\text{на}}\;L,$
где Δ – оператор Лапласа, k и ${{k}_{0}}$ – волновые числа, причем $\operatorname{Im} \,k \geqslant 0$ и $\operatorname{Im} \,{{k}_{0}} \geqslant 0$, $\nu (y)$ – внешняя единичная нормаль в точке $y \in L$, f и g – заданные непрерывные функции на L, а μ и ${{\mu }_{0}}$ – заданные комплексные числа, причем $\mu + {{\mu }_{0}} \ne 0$. Отметим, что с физической точки зрения надлежащий выбор постоянных μ и ${{\mu }_{0}}$ гарантирует непрерывность давления и нормальной скорости акустических волн при переходе через границу L.

Пусть ${{\Phi }_{k}}(x,y)$ – фундаментальное решение уравнения Гельмгольца, т.е.

${{\Phi }_{k}}(x,y) = \left\{ \begin{gathered} \frac{1}{{2\pi }}\ln \frac{1}{{\left| {x - y} \right|}}\quad {\text{при}}\quad k = 0, \hfill \\ \frac{i}{4}H_{0}^{{\left( 1 \right)}}\left( {k\left| {x - y} \right|} \right)\quad {\text{при}}\quad k \ne 0, \hfill \\ \end{gathered} \right.$
где $H_{0}^{{\left( 1 \right)}}$ – функция Ханкеля I рода нулевого порядка, определяемая формулой $H_{0}^{{\left( 1 \right)}}\left( z \right) = {{J}_{0}}\left( z \right) + i\,{{N}_{0}}\left( z \right)$,

${{J}_{0}}\left( z \right) = \sum\limits_{m = 0}^\infty {\frac{{{{{\left( { - 1} \right)}}^{m}}}}{{{{{\left( {m!} \right)}}^{2}}}}{{{\left( {\frac{z}{2}} \right)}}^{{2m}}}} $

есть функция Бесселя нулевого порядка,

${{N}_{0}}\left( z \right) = \frac{2}{\pi }\left( {\ln \frac{z}{2} + C} \right){{J}_{0}}\left( z \right) + \sum\limits_{m = 1}^\infty {\left( {\sum\limits_{l = 1}^m {\frac{1}{l}} } \right)\frac{{{{{\left( { - 1} \right)}}^{{m + 1}}}}}{{{{{\left( {m!} \right)}}^{2}}}}{{{\left( {\frac{z}{2}} \right)}}^{{2m}}}} $

есть функция Неймана нулевого порядка, а $C = 0.57721\; \ldots $ – постоянная Эйлера. Кресс и Роч (см. [2]) доказали, что комбинация потенциалов простого и двойного слоев

$u\left( x \right) = \int\limits_L {\left\{ {\frac{{\partial {{\Phi }_{k}}\left( {x,y} \right)}}{{\partial \nu \left( y \right)}}\psi \left( y \right) + \mu {{\Phi }_{k}}\left( {x,y} \right)\varphi \left( y \right)} \right\}d{{L}_{y}}} ,\quad x \in {{R}^{2}}{{\backslash }}\bar {D},$
${{u}_{0}}\left( x \right) = \int\limits_L {\left\{ {\frac{{\partial {{\Phi }_{{{{k}_{0}}}}}\left( {x,y} \right)}}{{\partial \nu \left( y \right)}}\psi \left( y \right) + {{\mu }_{0}}{{\Phi }_{{{{k}_{0}}}}}\left( {x,y} \right)\varphi \left( y \right)} \right\}d{{L}_{y}}} ,\quad x \in D,$
с непрерывными плотностями ψ и φ, является решением задачи сопряжения, если ψ и φ являются решениями системы интегральных уравнений
(1.1)
$\begin{gathered} \psi + \left( {\frac{\mu }{{\mu + {{\mu }_{0}}}}K - \frac{{{{\mu }_{0}}}}{{\mu + {{\mu }_{0}}}}{{K}_{0}}} \right)\psi + \left( {\frac{{{{\mu }^{2}}}}{{\mu + {{\mu }_{0}}}}S - \frac{{\mu _{0}^{2}}}{{\mu + {{\mu }_{0}}}}{{S}_{0}}} \right)\varphi = \frac{{2f}}{{\mu + {{\mu }_{0}}}}, \hfill \\ \varphi - \frac{1}{{\mu + {{\mu }_{0}}}}\left( {T - {{T}_{0}}} \right)\psi - \left( {\frac{\mu }{{\mu + {{\mu }_{0}}}}\tilde {K} - \frac{{{{\mu }_{0}}}}{{\mu + {{\mu }_{0}}}}{{{\tilde {K}}}_{0}}} \right)\varphi = - \frac{{2g}}{{\mu + {{\mu }_{0}}}}, \hfill \\ \end{gathered} $
где
(1.2)
$\left( {S\varphi } \right)\left( x \right) = 2\int\limits_L {{{\Phi }_{k}}\left( {x,y} \right)\varphi \left( y \right)d{{L}_{y}}} ,\quad x \in L,$
(1.3)
$\left( {K\psi } \right)\left( x \right) = 2\int\limits_L {\frac{{\partial {{\Phi }_{k}}\left( {x,y} \right)}}{{\partial \nu \left( y \right)}}\psi \left( y \right)d{{L}_{y}}} ,\quad x \in L,$
(1.4)
$\left( {\tilde {K}\varphi } \right)\left( x \right) = 2\int\limits_L {\frac{{\partial {{\Phi }_{k}}\left( {x,y} \right)}}{{\partial \nu \left( x \right)}}\varphi \left( y \right)d{{L}_{y}}} ,\quad x \in L,$
(1.5)
$\left( {\left( {T - {{T}_{0}}} \right)\psi } \right)\left( x \right) = 2\int\limits_L {\frac{\partial }{{\partial \nu \left( x \right)}}\left( {\frac{{\partial \left( {{{\Phi }_{k}}\left( {x,y} \right) - {{\Phi }_{{{{k}_{0}}}}}\left( {x,y} \right)} \right)}}{{\partial \nu \left( y \right)}}} \right)\psi \left( y \right)d{{L}_{y}}} ,\quad x \in L,$
и

${{\Phi }_{{{{k}_{0}}}}}\left( {x,y} \right) = {{\left. {{{\Phi }_{k}}\left( {x,y} \right)} \right|}_{{k = {{k}_{0}}}}},\quad {{\left. {{{S}_{0}} = S} \right|}_{{k = {{k}_{0}}}}},\quad {{\left. {{{K}_{0}} = K} \right|}_{{k = {{k}_{0}}}}},\quad {{\tilde {K}}_{0}} = {{\left. {\tilde {K}} \right|}_{{k = {{k}_{0}}}}}.$

Отметим, что ряд работ посвящены исследованию приближенных решений интегральных уравнений различных краевых задач для уравнения Гельмгольца (см. [3]–[7]), а в работе же [8] дано обоснование метода коллокации для системы интегральных уравнений задачи сопряжения для уравнения Гельмгольца в трехмерном пространстве. Однако до сих пор не исследованы приближенные решения задачи сопряжения для уравнения Гельмгольца в двухмерном пространстве методом интегральных уравнений. Как известно, в трехмерном пространстве фундаментальное решение уравнения Гельмгольца имеет вид

${{\Phi }_{k}}(x,y) = \frac{{\exp \left( {ik\left| {x - y} \right|} \right)}}{{4\pi \left| {x - y} \right|}},\quad x,y \in {{R}^{3}},\quad x \ne y,$
и поэтому интегральные операторы, участвующие в системе (1.1) строго отличаются от интегральных операторов, участвующих в системе интегральных уравнений для задачи сопряжения для уравнения Гельмгольца в трехмерном пространстве. Кроме того, в [9] построена квадратурная формула для логарифмических потенциалов простого и двойного слоев, а в [10] построена квадратурная формула для потенциалов простого и двойного слоев. Однако в [10] для построения квадратурных формул использована асимптотическая формула для функций Ханкеля I рода нулевого порядка, которая не дает возможность определить скорость сходимости этих квадратурных формул. Поэтому более практичным способом построения квадратурных формул для потенциалов простого и двойного слоев, а также исследование приближенного решения задачи сопряжения для уравнения Гельмгольца в двухмерном пространстве методом системы интегральных уравнений (1.1) имеет важные значения, чему и посвящена настоящая заметка.

2. ПОСТРОЕНИЕ КВАДРАТУРНЫХ ФОРМУЛЫ ДЛЯ ИНТЕГРАЛОВ (1.2)–(1.5)

Предположим, что замкнутая и дважды непрерывно дифференцируемая кривая $L \subset {{R}^{2}}$ задана параметрическим уравнением $x\left( t \right) = \left( {{{x}_{1}}\left( t \right),{{x}_{2}}\left( t \right)} \right)$, $t \in \left[ {a,b} \right]$. Разобьем промежуток $\left[ {a,b} \right]$ на $n > 2{{M}_{0}}\left( {b - a} \right){\text{/}}d$ равных частей: ${{t}_{p}} = a + \frac{{\left( {b - a} \right)p}}{n}$, $p = \overline {0,\;n} $, где ${{M}_{0}} = \mathop {\max }\limits_{t \in \left[ {a,b} \right]} \sqrt {{{{\left( {x_{1}^{'}\left( t \right)} \right)}}^{2}} + {{{\left( {x_{2}^{'}\left( t \right)} \right)}}^{2}}} < + \infty $ (см. [11, с. 560]) и d – стандартный радиус (см. [12, с. 400]). В качестве опорных точек возьмем $x\left( {{{\tau }_{p}}} \right)$, $p = \overline {1,\;n} $, где ${{\tau }_{p}} = a + \frac{{\left( {b - a} \right)\left( {2p - 1} \right)}}{{2n}}$. Тогда кривая L разбивается на элементарные части: $L = \bigcup\nolimits_{p = 1}^n {{{L}_{p}}} $, где ${{L}_{p}} = \left\{ {x\left( t \right):\;{{t}_{{p - 1}}} \leqslant t \leqslant {{t}_{p}}} \right\}$.

Известно, что (см. [9])

(1) $\forall p \in \left\{ {1,\;2,\; \ldots ,\;n} \right\}$: ${{r}_{p}}(n)\sim {{R}_{p}}(n)$, где ${{r}_{p}}\left( n \right) = \min \left\{ {\left| {x\left( {{{\tau }_{p}}} \right) - x\left( {{{t}_{{p - 1}}}} \right)} \right|} \right.,$$\left. {\left| {x\left( {{{t}_{p}}} \right) - x\left( {{{\tau }_{p}}} \right)} \right|} \right\}$, ${{R}_{p}}\left( n \right)$ = = $\max \left\{ {\left| {x\left( {{{\tau }_{p}}} \right) - x\left( {{{t}_{{p - 1}}}} \right)} \right|,\left| {x\left( {{{t}_{p}}} \right) - x\left( {{{\tau }_{p}}} \right)} \right|} \right\}$, а запись $a\left( n \right)\sim b\left( n \right)$ означает, что

${{C}_{1}} \leqslant \frac{{a\left( n \right)}}{{b\left( n \right)}} \leqslant {{C}_{2}},$
где ${{C}_{1}}$ и ${{C}_{2}}$ – положительные постоянные, не зависящие от $n$;

(2) $\forall p \in \left\{ {1,\;2,\; \ldots ,\;n} \right\}$: ${{R}_{p}}\left( n \right) \leqslant d{\text{/}}2$;

(3) $\forall p,j \in \left\{ {1,\;2,\; \ldots ,\;n} \right\}$: ${{r}_{j}}\left( n \right)\sim {{r}_{p}}\left( n \right)$;

(4) $r\left( n \right)\sim R\left( n \right)\sim \frac{1}{n}$, где $R\left( n \right) = \mathop {\max }\limits_{p = \overline {1,n} } {{R}_{p}}\left( n \right)$, $r\left( n \right) = \mathop {\min }\limits_{p = \overline {1,n} } {{r}_{p}}\left( n \right)$.

В дальнейшем такое разбиение будем называть разбиением кривой L на “регулярные” элементарные части.

Поступая точно также, как и в доказательстве леммы 2.1 работы [13], можно показать справедливость следующей леммы.

Лемма 1. Существуют такие постоянные $C_{0}^{'} > 0$ и $C_{1}^{'} > 0$, не зависящие от n, для которых при $\forall p,j \in \left\{ {1,\;2,\; \ldots ,\;n} \right\}$, $j \ne p$, и $\forall y \in {{L}_{j}}$ справедливы следующие неравенства:

$C_{0}^{'}\left| {y - x\left( {{{\tau }_{p}}} \right)} \right| \leqslant \left| {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{p}}} \right)} \right| \leqslant C_{1}^{'}\left| {y - x\left( {{{\tau }_{p}}} \right)} \right|.$

Через $C\left( L \right)$ обозначим пространство всех непрерывных функций на L с нормой ${{\left\| \varphi \right\|}_{\infty }} = \mathop {\max }\limits_{x \in L} \left| {\varphi \left( x \right)} \right|$, и для функции $\varphi \in C\left( L \right)$ вводим модуль непрерывности вида

Сначала построим квадратурную формулу для интеграла (1.2). Пусть

$\Phi _{k}^{n}(x,y) = \frac{i}{4}H_{{0,n}}^{{\left( 1 \right)}}\left( {k\left| {x - y} \right|} \right),\quad x,y \in L,\quad x \ne y,$
где
$H_{{0,n}}^{{\left( 1 \right)}}\left( z \right) = {{J}_{{0,n}}}\left( z \right) + i{{N}_{{0,n}}}\left( z \right),$
${{J}_{{0,n}}}\left( z \right) = \sum\limits_{m = 0}^n {\frac{{{{{\left( { - 1} \right)}}^{m}}}}{{{{{\left( {m!} \right)}}^{2}}}}{{{\left( {\frac{z}{2}} \right)}}^{{2m}}}} ,$
и

${{N}_{{0,n}}}\left( z \right) = \frac{2}{\pi }\left( {\ln \frac{z}{2} + C} \right){{J}_{{0,n}}}\left( z \right) + \sum\limits_{m = 1}^n {\left( {\sum\limits_{l = 1}^m {\frac{1}{l}} } \right)\frac{{{{{\left( { - 1} \right)}}^{{m + 1}}}}}{{{{{\left( {m!} \right)}}^{2}}}}{{{\left( {\frac{z}{2}} \right)}}^{{2m}}}} .$

Теорема 1. Пусть L – замкнутая и дважды непрерывно дифференцируемая кривая в ${{R}^{2}}$ и $\varphi \in C\left( L \right)$. Тогда выражение

в опорных точках $x\left( {{{\tau }_{p}}} \right)$, $p = \overline {1,\;n} $, является квадратурной формулой для интеграла (1.2), причем справедлива следующая оценка:

$\mathop {\max }\limits_{p = \overline {1,n} } \left| {\left( {S\varphi } \right)\left( {x\left( {{{\tau }_{p}}} \right)} \right) - \left( {{{S}_{n}}\varphi } \right)\left( {x\left( {{{\tau }_{p}}} \right)} \right)} \right| \leqslant M\left( {\omega \left( {\varphi ,1{\text{/}}n} \right) + {{{\left\| \varphi \right\|}}_{\infty }}\frac{{\ln n}}{n}} \right).$

(Здесь и далее через М будем обозначать положительные постоянные, разные в различных неравенствах.)

Доказательство. Несложно заметить, что

Слагаемые в последнем равенстве обозначим через $h_{1}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)$, $h_{2}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)$, $h_{3}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)$ и $h_{4}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)$ соответственно.

Очевидно, что

(2.1)
$\left| {{{J}_{0}}\left( {k\left| {x - y} \right|} \right)} \right| \leqslant \sum\limits_{m = 0}^\infty {\frac{{{{{\left( {\left| k \right|{\text{diam}}L} \right)}}^{{2m}}}}}{{{{4}^{m}}{{{\left( {m!} \right)}}^{2}}}}} \leqslant M\quad \forall x,y \in L,$
и
(2.2)
$\left| {\sum\limits_{m = 1}^\infty {\left( {\sum\limits_{l = 1}^m {\frac{1}{l}} } \right)\frac{{{{{\left( { - 1} \right)}}^{{m + 1}}}}}{{{{{\left( {m!} \right)}}^{2}}}}{{{\left( {\frac{{k\left| {x - y} \right|}}{2}} \right)}}^{{2m}}}} } \right| \leqslant \sum\limits_{m = 1}^\infty {\left( {\sum\limits_{l = 1}^m {\frac{1}{l}} } \right)\frac{{{{{\left( {\left| k \right|{\text{diam}}L} \right)}}^{{2m}}}}}{{{{4}^{m}}{{{\left( {m!} \right)}}^{2}}}}} \leqslant M\quad \forall x,y \in L,$
следовательно,

(2.3)
$\left| {{{\Phi }_{k}}(x,y)} \right| \leqslant M\left| {\ln \left| {x - y} \right|} \right|\quad \forall x,y \in L,\quad x \ne y.$

Тогда, применяя формулу вычисления криволинейного интеграла, находим

$\left| {h_{1}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)} \right| \leqslant 2{{\left\| \varphi \right\|}_{\infty }}\int\limits_{{{L}_{p}}} {\left| {{{\Phi }_{k}}\left( {x\left( {{{\tau }_{p}}} \right),y} \right)} \right|} d{{L}_{y}} \leqslant M{{\left\| \varphi \right\|}_{\infty }}\int\limits_0^{R\left( n \right)} {\left| {\ln \tau } \right|d\tau } \leqslant M{{\left\| \varphi \right\|}_{\infty }}R\left( n \right)\left| {\ln R\left( n \right)} \right|.$

Пусть $y \in {{L}_{j}}$ и $j \ne p$. Учитывая лемму 1, имеем

(2.4)
$\left| {{{{\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}^{q}} - {{{\left| {x\left( {{{\tau }_{p}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}^{q}}} \right| \leqslant Mq\left| {x\left( {{{\tau }_{j}}} \right) - y} \right|{{\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}^{{q - 1}}} \leqslant MqR\left( n \right){{\left( {{\text{diam}}L} \right)}^{{q - 1}}}$
и
(2.5)
$\begin{gathered} \left| {\ln \left( {k\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|} \right) - \ln \left( {k\left| {x\left( {{{\tau }_{p}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|} \right)} \right| = \left| {\ln \left( {1 + \frac{{\left| {x\left( {{{\tau }_{p}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right| - \left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}{{\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}} \right)} \right| \leqslant \\ \leqslant \;\left| {\ln \left( {1 + \frac{{\left| {x\left( {{{\tau }_{j}}} \right) - y} \right|}}{{\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}} \right)} \right| \leqslant M\frac{{R\left( n \right)}}{{\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}, \\ \end{gathered} $
где $q \in {\rm N}$. Тогда, принимая во внимание неравенства (2.1), (2.2), (2.4) и (2.5), получаем, что

$\begin{gathered} \left| {{{\Phi }_{k}}\left( {x\left( {{{\tau }_{p}}} \right),y} \right) - {{\Phi }_{k}}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)} \right| \leqslant \\ \leqslant \;\frac{1}{4}\left| {\sum\limits_{m = 0}^\infty {\frac{{{{{\left( { - 1} \right)}}^{m}}}}{{{{{\left( {m!} \right)}}^{2}}}}\left( {{{{\left( {\frac{{k\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}{2}} \right)}}^{{2m}}} - {{{\left( {\frac{{k\left| {x\left( {{{\tau }_{p}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}{2}} \right)}}^{{2m}}}} \right)} } \right| + \\ \end{gathered} $
$ + \;\frac{1}{{2\pi }}\left| {\left( {\ln \frac{{k\left| {x\left( {{{\tau }_{p}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}{2} + C} \right)\sum\limits_{m = 0}^\infty {\frac{{{{{\left( { - 1} \right)}}^{m}}}}{{{{{\left( {m!} \right)}}^{2}}}}\left( {{{{\left( {\frac{{k\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}{2}} \right)}}^{{2m}}} - {{{\left( {\frac{{k\left| {x\left( {{{\tau }_{p}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}{2}} \right)}}^{{2m}}}} \right)} } \right| + $
$\begin{gathered} + \;\frac{1}{{2\pi }}\left| {\left( {\ln \left( {k\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|} \right) - \ln \left( {k\left| {x\left( {{{\tau }_{p}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|} \right)} \right)\sum\limits_{m = 0}^\infty {\frac{{{{{\left( { - 1} \right)}}^{m}}}}{{{{{\left( {m!} \right)}}^{2}}}}{{{\left( {\frac{{k\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}{2}} \right)}}^{{2m}}}} } \right| + \\ + \;\frac{1}{4}\left| {\sum\limits_{m = 1}^\infty {\left( {\sum\limits_{l = 1}^m {\frac{1}{l}} } \right)\frac{{{{{\left( { - 1} \right)}}^{{m + 1}}}}}{{{{{\left( {m!} \right)}}^{2}}}}\left( {{{{\left( {\frac{{k\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}{2}} \right)}}^{{2m}}} - {{{\left( {\frac{{k\left| {x\left( {{{\tau }_{p}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}{2}} \right)}}^{{2m}}}} \right)} } \right| \leqslant \frac{{MR\left( n \right)}}{{\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}. \\ \end{gathered} $

Кроме того, учитывая неравенства

(2.6)
$\left| {{{J}_{0}}\left( {k\left| {x - y} \right|} \right) - {{J}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)} \right| \leqslant \sum\limits_{m = n + 1}^\infty {\frac{{{{{\left| k \right|}}^{{2m}}}{{{\left| {x - y} \right|}}^{{2m}}}}}{{{{4}^{m}}{{{\left( {m!} \right)}}^{2}}}}} \leqslant \frac{M}{{\left( {n + 1} \right)!}}\quad \forall x,y \in L,$
и
(2.7)
$\left| {{{N}_{0}}\left( {k\left| {x - y} \right|} \right) - {{N}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)} \right| \leqslant \frac{{M\left| {\ln \left| {x - y} \right|} \right|}}{{\left( {n + 1} \right)!}}\quad \forall x,y \in L,$
имеем

$\left| {{{\Phi }_{k}}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right) - \Phi _{k}^{n}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)} \right| \leqslant \frac{{M\left| {\ln \left| {x\left( {{{\tau }_{p}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|} \right|}}{{\left( {n + 1} \right)!}} \leqslant \frac{M}{{\left( {n + 1} \right)!\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}.$

В результате находим, что

$\begin{gathered} \left| {{{\Phi }_{k}}\left( {x\left( {{{\tau }_{p}}} \right),y} \right) - \Phi _{k}^{n}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)} \right| \leqslant \left| {{{\Phi }_{k}}\left( {x\left( {{{\tau }_{p}}} \right),y} \right) - {{\Phi }_{k}}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)} \right| + \\ + \;\left| {{{\Phi }_{k}}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right) - \Phi _{k}^{n}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)} \right| \leqslant \frac{M}{{\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}\left( {R\left( n \right) + \frac{1}{{\left( {n + 1} \right)!}}} \right). \\ \end{gathered} $

Следовательно,

$\left| {h_{2}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)} \right| \leqslant M{{\left\| \varphi \right\|}_{\infty }}\left( {R\left( n \right) + \frac{1}{{\left( {n + 1} \right)!}}} \right)\int\limits_{r\left( n \right)}^{{\text{diam}}L} {\frac{{d\tau }}{\tau }} \leqslant M{{\left\| \varphi \right\|}_{\infty }}\left( {R\left( n \right) + \frac{1}{{\left( {n + 1} \right)!}}} \right)\left| {\ln R\left( n \right)} \right|.$

Из неравенства (2.3), получаем, что

$\int\limits_L {\left| {{{\Phi }_{k}}\left( {x,y} \right)} \right|} d{{L}_{y}}$
сходится как несобственный и

$\int\limits_L {\left| {{{\Phi }_{k}}\left( {x,y} \right)} \right|} d{{L}_{y}} \leqslant M\quad \forall x \in L.$

Тогда из неравенства (2.6) и (2.7) получим

$\int\limits_L {\left| {\Phi _{k}^{n}\left( {x,y} \right)} \right|} {\kern 1pt} d{{L}_{y}} \leqslant \int\limits_L {\left| {{{\Phi }_{k}}\left( {x,y} \right)} \right|} d{{L}_{y}} + \int\limits_L {\left| {{{\Phi }_{k}}\left( {x,y} \right) - \Phi _{k}^{n}\left( {x,y} \right)} \right|} d{{L}_{y}} \leqslant M\quad \forall x \in L,\quad \forall n \in {\rm N}.$

В итоге, принимая во внимание лемму 1, получаем, что

$\left| {h_{3}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)} \right| \leqslant M\omega \left( {\varphi ,R\left( n \right)} \right)\int\limits_L {\left| {\Phi _{k}^{n}\left( {x\left( {{{\tau }_{p}}} \right),y} \right)} \right|} d{{L}_{y}} \leqslant M\omega \left( {\varphi ,R\left( n \right)} \right).$

Очевидно, что

(2.8)
$\left| {\sqrt {{{{\left( {x_{1}^{'}\left( t \right)} \right)}}^{2}} + {{{\left( {x_{2}^{'}\left( t \right)} \right)}}^{2}}} - \sqrt {{{{\left( {x_{1}^{'}\left( {{{\tau }_{j}}} \right)} \right)}}^{2}} + {{{\left( {x_{2}^{'}\left( {{{\tau }_{j}}} \right)} \right)}}^{2}}} } \right| \leqslant MR\left( n \right)\quad \forall t \in \left[ {{{t}_{{j - 1}}},{{t}_{j}}} \right].$

Пусть $y \in {{L}_{j}}$ и $j \ne p$. Учитывая леммы 1 и неравенства (2.1) и (2.2), имеем

$\left| {{{J}_{{0,n}}}\left( {k\left| {x\left( {{{\tau }_{p}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|} \right)} \right| \leqslant \sum\limits_{m = 0}^n {\frac{{{{{\left( {\left| k \right|{\text{diam}}L} \right)}}^{{2m}}}}}{{{{4}^{m}}{{{\left( {m!} \right)}}^{2}}}}} \leqslant M\quad \forall n \in {\rm N},$
и
$\left| {{{N}_{{0,n}}}\left( {k\left| {x\left( {{{\tau }_{p}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|} \right)} \right| \leqslant M\left| {\ln \left| {x\left( {{{\tau }_{p}}} \right) - y} \right|} \right|\quad \forall n \in {\rm N},$
следовательно,

$\left| {\Phi _{k}^{n}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)} \right| \leqslant M\left| {\ln \left| {x\left( {{{\tau }_{p}}} \right) - y} \right|} \right|\quad \forall n \in {\rm N}.$

Отсюда получаем, что

В результате, суммируя полученные оценки для выражений $h_{1}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)$, $h_{2}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)$, $h_{3}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)$ и $h_{4}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)$, и, принимая во внимание соотношение $R\left( n \right)\sim \frac{1}{n}$, доказываем справедливость теоремы 1.

Теперь построим квадратурную формулу для интеграла (1.3). Нетрудно показать, что

$\frac{{\partial \Phi _{k}^{n}\left( {x,y} \right)}}{{\partial \nu \left( y \right)}} = \frac{i}{4}\left( {\frac{{\partial {{J}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}} + i\frac{{\partial {{N}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}}} \right),$
где
$\frac{{\partial {{J}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}} = \left( {y - x,\nu \left( y \right)} \right)\sum\limits_{m = 1}^n {\frac{{{{{\left( { - 1} \right)}}^{m}}{{k}^{{2m}}}{{{\left| {x - y} \right|}}^{{2m - 2}}}}}{{{{2}^{{2m - 1}}}\left( {m - 1} \right)!m!}}} $
и

$\begin{gathered} \frac{{\partial {{N}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}} = \frac{2}{\pi }\left( {\ln \frac{{k\left| {x - y} \right|}}{2} + C} \right)\frac{{\partial {{J}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}} + \frac{{2\,\left( {y - x,{\kern 1pt} \nu \left( y \right)} \right)}}{{\pi \,{{{\left| {x - y} \right|}}^{2}}}}{{J}_{{0,n}}}\left( {k\left| {x - y} \right|} \right) + \\ + \;\left( {y - x,\nu \left( y \right)} \right)\sum\limits_{m = 1}^n {\left( {\sum\limits_{l = 1}^m {\frac{1}{l}} } \right)\frac{{{{{\left( { - 1} \right)}}^{{m + 1}}}{{k}^{{2m}}}{{{\left| {x - y} \right|}}^{{2m - 2}}}}}{{{{2}^{{2m - 1}}}\left( {m - 1} \right)!m!}}} . \\ \end{gathered} $

Справедлива следующая

Теорема 2. Пусть L – замкнутая и дважды непрерывно дифференцируемая кривая в ${{R}^{2}}$ и $\psi \in C\left( L \right)$. Тогда выражение

в опорных точках $x\left( {{{\tau }_{p}}} \right)$, $p = \overline {1,\;n} $, является квадратурной формулой для интеграла (1.3), причем справедлива следующая оценка:

$\mathop {\max }\limits_{p = \overline {1,\,n} } \left| {\left( {K\psi } \right)\left( {x\left( {{{\tau }_{p}}} \right)} \right) - \left( {{{K}_{n}}\psi } \right)\left( {x\left( {{{\tau }_{p}}} \right)} \right)} \right| \leqslant M\left( {\omega \left( {\psi ,1{\text{/}}n} \right) + {{{\left\| \psi \right\|}}_{\infty }}\frac{{\ln n}}{n}} \right).$

Доказательство. Нетрудно увидеть, что

Слагаемые в последнем равенстве обозначим через $\delta _{1}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)$, $\delta _{2}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)$, $\delta _{3}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)$ и $\delta _{4}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)$ соответственно.

Легко вычислить, что

$\frac{{\partial {{\Phi }_{k}}\left( {x,y} \right)}}{{\partial \nu \left( y \right)}} = \frac{i}{4}\left( {\frac{{\partial {{J}_{0}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}} + i\frac{{\partial {{N}_{0}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}}} \right),$
здесь
$\frac{{\partial {{J}_{0}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}} = \left( {y - x,\nu \left( y \right)} \right)\sum\limits_{m = 1}^\infty {\frac{{{{{\left( { - 1} \right)}}^{m}}{{k}^{{2m}}}{{{\left| {x - y} \right|}}^{{2m - 2}}}}}{{{{2}^{{2m - 1}}}\left( {m - 1} \right)!m!}}} $
и

$\begin{gathered} \frac{{\partial {{N}_{0}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}} = \frac{2}{\pi }\left( {\ln \frac{{k\left| {x - y} \right|}}{2} + C} \right)\frac{{\partial {{J}_{0}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}} + \frac{{2\left( {y - x,\nu \left( y \right)} \right)}}{{\pi {{{\left| {x - y} \right|}}^{2}}}}{{J}_{0}}\left( {k\left| {x - y} \right|} \right) + \\ + \;\left( {y - x,\nu \left( y \right)} \right)\sum\limits_{m = 1}^\infty {\left( {\sum\limits_{l = 1}^m {\frac{1}{l}} } \right)\frac{{{{{\left( { - 1} \right)}}^{{m + 1}}}{{k}^{{2m}}}{{{\left| {x - y} \right|}}^{{2m - 2}}}}}{{{{2}^{{2m - 1}}}\left( {m - 1} \right)!m!}}} . \\ \end{gathered} $

Так как (см. [12, с. 403])

(2.9)
$\left| {\left( {y - x,\nu \left( y \right)} \right)} \right| \leqslant M{{\left| {x - y} \right|}^{2}},$
то
(2.10)
$\left| {\frac{{\partial {{J}_{0}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}}} \right| \leqslant M{{\left| {x - y} \right|}^{2}}$
и
(2.11)
$\left| {\frac{{\partial {{N}_{0}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}}} \right| \leqslant M\left( {{{{\left| {x - y} \right|}}^{2}}\left| {\ln \left| {x - y} \right|} \right| + {{{\left| {x - y} \right|}}^{2}} + 1} \right),$
а значит,

(2.12)
$\left| {\frac{{\partial {{\Phi }_{k}}\left( {x,y} \right)}}{{\partial \nu \left( y \right)}}} \right| \leqslant M\quad \forall \,x,y \in L,\quad x \ne y.$

Тогда, учитывая формулу вычисления криволинейного интеграла, получаем

$\left| {\delta _{1}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)} \right| \leqslant M{{\left\| \psi \right\|}_{\infty }}\int\limits_0^{R\left( n \right)} {d\tau \leqslant M{{{\left\| \psi \right\|}}_{\infty }}} R\left( n \right).$

Пусть $y \in {{L}_{j}}$ и $j \ne p$. Из леммы 1 и неравенствa (2.9) очевидно, что

(2.13)
$\begin{gathered} \left| {\left( {y - x\left( {{{\tau }_{p}}} \right),\nu \left( y \right)} \right) - \left( {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{p}}} \right),\nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)} \right)} \right| = \left| {\left( {y - x\left( {{{\tau }_{j}}} \right),\nu \left( y \right)} \right)} \right| + \\ + \;\left| {\left( {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{p}}} \right),\nu \left( y \right) - \nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)} \right)} \right| \leqslant M\left| {y - x\left( {{{\tau }_{p}}} \right)} \right|R\left( n \right). \\ \end{gathered} $

Тогда, учитывая неравенства (2.4), получаем, что

$\left| {\frac{{\partial {{J}_{0}}\left( {k\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|} \right)}}{{\partial \nu \left( y \right)}} - \frac{{\partial {{J}_{0}}\left( {k\left| {x\left( {{{\tau }_{p}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|} \right)}}{{\partial \nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)}}} \right| \leqslant $
(2.14)
$\begin{gathered} \leqslant \;\left| {\left( {y - x\left( {{{\tau }_{p}}} \right),\nu \left( y \right)} \right) - \left( {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{p}}} \right),\nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)} \right)} \right| \times \\ \times \;\sum\limits_{m = 1}^\infty {\frac{{{{{\left| k \right|}}^{{2m}}}{{{\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}^{{2m - 2}}}}}{{{{2}^{{2m - 1}}}\left( {m - 1} \right)!m!}}} + \left| {\left( {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{p}}} \right),\nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)} \right)} \right| \times \\ \end{gathered} $
$ \times \;\sum\limits_{m = 1}^\infty {\frac{{{{{\left| k \right|}}^{{2m}}}\left| {{{{\left| {x\left( {{{\tau }_{p}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}^{{2m - 2}}} - {{{\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}^{{2m - 2}}}} \right|}}{{{{2}^{{2m - 1}}}\left( {m - 1} \right)!m!}}} \leqslant M\left| {y - x\left( {{{\tau }_{p}}} \right)} \right|R\left( n \right).$

Кроме того, из леммы 1 и неравенств (2.9) и (2.13) имеем

$\left| {\frac{{\left( {y - x\left( {{{\tau }_{p}}} \right),\nu \left( y \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}^{2}}}} - \frac{{\left( {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{p}}} \right),\nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{p}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}^{2}}}}} \right| \leqslant \frac{{MR\left( n \right)}}{{\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}.$

Тогда, принимая во внимание неравенства (2.1), (2.5), (2.10), (2.11), (2.13) и (2.14), нетрудно показать, что

$\left| {\frac{{\partial {{N}_{0}}\left( {k\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|} \right)}}{{\partial \nu \left( y \right)}} - \frac{{\partial {{N}_{0}}\left( {k\left| {x\left( {{{\tau }_{p}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|} \right)}}{{\partial \nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)}}} \right| \leqslant \frac{{MR\left( n \right)}}{{\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}.$

В результате находим

$\left| {\frac{{\partial {{\Phi }_{k}}\left( {x\left( {{{\tau }_{p}}} \right),y} \right)}}{{\partial \nu \left( y \right)}} - \frac{{\partial {{\Phi }_{k}}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)}}{{\partial \nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)}}} \right| \leqslant \frac{{MR\left( n \right)}}{{\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}}.$

Также, учитывая неравенство

(2.15)
$\left| {\frac{{\partial {{\Phi }_{k}}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)}}{{\partial \nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)}} - \frac{{\partial \Phi _{k}^{n}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)}}{{\partial \nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)}}} \right| \leqslant \frac{{M\left| {\ln \left| {x\left( {{{\tau }_{p}}} \right) - y} \right|} \right|}}{{n!}},$
получаем, что

$\left| {\frac{{\partial {{\Phi }_{k}}\left( {x\left( {{{\tau }_{p}}} \right),y} \right)}}{{\partial \nu \left( y \right)}} - \frac{{\partial \Phi _{k}^{n}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)}}{{\partial \nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)}}} \right| \leqslant M\left( {\frac{{R\left( n \right)}}{{\left| {x\left( {{{\tau }_{p}}} \right) - y} \right|}} + \frac{{\left| {\ln \left| {x\left( {{{\tau }_{p}}} \right) - y} \right|} \right|}}{{n!}}} \right).$

В итоге

$\left| {\delta _{2}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)} \right| \leqslant M{{\left\| \psi \right\|}_{\infty }}\left( {R\left( n \right)\int\limits_{r\left( n \right)}^{{\text{diam}}L} {\frac{{d\tau }}{\tau }} + \frac{1}{{n!}}\int\limits_{r\left( n \right)}^{{\text{diam}}L} {\left| {\ln \tau } \right|d\tau } } \right) \leqslant M{{\left\| \psi \right\|}_{\infty }}\left( {R\left( n \right)\left| {\ln R\left( n \right)} \right| + \frac{1}{{n!}}} \right).$

Пусть $y \in {{L}_{j}}$ и $j \ne p$. Так как из леммы 1 и неравенства (2.12) и (2.15) очевидно, что

(2.16)
$\begin{gathered} \left| {\frac{{\partial \Phi _{k}^{n}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)}}{{\partial \nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)}}} \right| \leqslant \left| {\frac{{\partial {{\Phi }_{k}}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)}}{{\partial \nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)}}} \right| + \left| {\frac{{\partial {{\Phi }_{k}}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)}}{{\partial \nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)}} - \frac{{\partial \Phi _{k}^{n}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)}}{{\partial \nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)}}} \right| \leqslant \\ \leqslant \;\frac{{M\left| {\ln \left| {x\left( {{{\tau }_{p}}} \right) - y} \right|} \right|}}{{n!}}\quad \forall n \in {\rm N}, \\ \end{gathered} $
тогда

$\left| {\delta _{3}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)} \right| \leqslant 2\omega \left( {\psi ,R\left( n \right)} \right)\int\limits_L {\left| {\frac{{\partial \Phi _{k}^{n}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)}}{{\partial \nu \left( y \right)}}} \right|} d{{L}_{y}} \leqslant M\omega \left( {\psi ,R\left( n \right)} \right).$

Кроме того, учитывая леммы 1 и неравенства (2.8) и (2.16), получаем

В результате, суммируя полученные оценки для выражений $\delta _{1}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)$, $\delta _{2}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)$, $\delta _{3}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)$ и $\delta _{4}^{n}\left( {x\left( {{{\tau }_{p}}} \right)} \right)$, и учитывая соотношение $R\left( n \right)\sim \frac{1}{n}$, получаем доказательство теоремы 2.

Очевидно, что

$\frac{{\partial \Phi _{k}^{n}\left( {x,y} \right)}}{{\partial \nu \left( x \right)}} = \frac{i}{4}\left( {\frac{{\partial {{J}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( x \right)}} + i\frac{{\partial {{N}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( x \right)}}} \right),$
где
$\frac{{\partial {{J}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( x \right)}} = \left( {x - y,\nu \left( x \right)} \right)\sum\limits_{m = 1}^n {\frac{{{{{\left( { - 1} \right)}}^{m}}{{k}^{{2m}}}{{{\left| {x - y} \right|}}^{{2m - 2}}}}}{{{{2}^{{2m - 1}}}\left( {m - 1} \right)!m!}}} $
и

$\begin{gathered} \frac{{\partial {{N}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( x \right)}} = \frac{2}{\pi }\left( {\ln \frac{{k\left| {x - y} \right|}}{2} + C} \right)\frac{{\partial {{J}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( x \right)}} + \frac{{2\left( {x - y,\nu \left( x \right)} \right)}}{{\pi {{{\left| {x - y} \right|}}^{2}}}}{{J}_{{0,n}}}\left( {k\left| {x - y} \right|} \right) + \\ + \;\left( {x - y,\nu \left( x \right)} \right)\sum\limits_{m = 1}^n {\left( {\sum\limits_{l = 1}^m {\frac{1}{l}} } \right)\frac{{{{{\left( { - 1} \right)}}^{{m + 1}}}{{k}^{{2m}}}{{{\left| {x - y} \right|}}^{{2m - 2}}}}}{{{{2}^{{2m - 1}}}\left( {m - 1} \right)!m!}}} . \\ \end{gathered} $

Тогда, поступая точно также, как и в доказательстве теоремы 2, можно доказать следующую теорему.

Теорема 3. Пусть L – замкнутая и дважды непрерывно дифференцируемая кривая в ${{R}^{2}}$ и $\varphi \in C\left( L \right)$. Тогда выражение

в опорных точках $x\left( {{{\tau }_{p}}} \right)$, $p = \overline {1,n} $, является квадратурной формулой для интеграла (1.4), причем справедлива следующая оценка:

$\mathop {\max }\limits_{p = \overline {1,n} } \left| {\left( {\tilde {K}\varphi } \right)\left( {x\left( {{{\tau }_{p}}} \right)} \right) - \left( {{{{\tilde {K}}}_{n}}\varphi } \right)\left( {x\left( {{{\tau }_{p}}} \right)} \right)} \right| \leqslant M\left( {\omega \left( {\varphi ,1{\text{/}}n} \right) + {{{\left\| \varphi \right\|}}_{\infty }}\frac{{\ln n}}{n}} \right).$

Кроме того, можно убедиться, что

$\begin{gathered} \frac{\partial }{{\partial \nu \left( x \right)}}\left( {\frac{{\partial \Phi _{k}^{n}\left( {x,y} \right)}}{{\partial \nu \left( y \right)}} - \frac{{\partial \Phi _{{{{k}_{0}}}}^{n}\left( {x,y} \right)}}{{\partial \nu \left( y \right)}}} \right) = \frac{i}{4}\frac{\partial }{{\partial \nu \left( x \right)}}\left( {\frac{{\partial {{J}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}} - \frac{{\partial {{J}_{{0,n}}}\left( {{{k}_{0}}\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}}} \right) - \\ - \;\frac{1}{4}\frac{\partial }{{\partial \nu \left( x \right)}}\left( {\frac{{\partial {{N}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}} - \frac{{\partial {{N}_{{0,n}}}\left( {{{k}_{0}}\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}}} \right), \\ \end{gathered} $
где
$\begin{gathered} \frac{\partial }{{\partial \nu \left( x \right)}}\left( {\frac{{\partial {{J}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}} - \frac{{\partial {{J}_{{0,n}}}\left( {{{k}_{0}}\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}}} \right) = \left( {\nu \left( x \right),\nu \left( y \right)} \right)\sum\limits_{m = 1}^n {\frac{{{{{\left( { - 1} \right)}}^{{m + 1}}}\left( {{{k}^{{2m}}} - {{k}_{0}}^{{2m}}} \right){{{\left| {x - y} \right|}}^{{2m - 2}}}}}{{{{2}^{{2m - 1}}}\left( {m - 1} \right)!m!}}} + \\ + \;\left( {y - x,\nu \left( y \right)} \right)\left( {x - y,\nu \left( x \right)} \right)\sum\limits_{m = 2}^n {\frac{{{{{\left( { - 1} \right)}}^{m}}\left( {{{k}^{{2m}}} - {{k}_{0}}^{{2m}}} \right){{{\left| {x - y} \right|}}^{{2m - 4}}}}}{{{{2}^{{2m - 2}}}\left( {m - 2} \right)!m!}}} \\ \end{gathered} $
и

$\frac{\partial }{{\partial \nu \left( x \right)}}\left( {\frac{{\partial {{N}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}} - \frac{{\partial {{N}_{{0,n}}}\left( {{{k}_{0}}\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}}} \right) = $
$ = \;\frac{2}{\pi }\left( {\ln k - \ln {{k}_{0}}} \right)\left( {y - x,\nu \left( y \right)} \right)\left( {x - y,\nu \left( x \right)} \right)\sum\limits_{m = 2}^n {\frac{{{{{\left( { - 1} \right)}}^{m}}{{k}^{{2m}}}{{{\left| {x - y} \right|}}^{{2m - 4}}}}}{{{{2}^{{2m - 2}}}\left( {m - 2} \right)!m!}}} + $
$ + \;\frac{{2\left( {x - y,\nu \left( x \right)} \right)}}{{\pi {{{\left| {x - y} \right|}}^{2}}}}\left( {\frac{{\partial {{J}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}} - \frac{{\partial {{J}_{{0,n}}}\left( {{{k}_{0}}\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}}} \right) + $
$ + \;\frac{2}{\pi }\left( {\ln \frac{{{{k}_{0}}\left| {x - y} \right|}}{2} + C} \right)\frac{\partial }{{\partial \nu \left( x \right)}}\left( {\frac{{\partial {{J}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}} - \frac{{\partial {{J}_{{0,n}}}\left( {{{k}_{0}}\left| {x - y} \right|} \right)}}{{\partial \nu \left( y \right)}}} \right) - $
$ - \;\frac{{2\left( {\nu \left( x \right),\nu \left( y \right)} \right){{{\left| {x - y} \right|}}^{2}} + 4\left( {y - x,\nu \left( y \right)} \right)\left( {x - y,\nu \left( x \right)} \right)}}{{\pi {{{\left| {x - y} \right|}}^{4}}}}\sum\limits_{m = 1}^n {\frac{{{{{\left( { - 1} \right)}}^{m}}\left( {{{k}^{{2m}}} - {{k}_{0}}^{{2m}}} \right){{{\left| {x - y} \right|}}^{{2m}}}}}{{{{2}^{{2m}}}{{{\left( {m!} \right)}}^{2}}}}} + $
$ + \;\frac{{2\left( {y - x,\nu \left( y \right)} \right)}}{{\pi {{{\left| {x - y} \right|}}^{2}}}}\left( {\frac{{\partial {{J}_{{0,n}}}\left( {k\left| {x - y} \right|} \right)}}{{\partial \nu \left( x \right)}} - \frac{{\partial {{J}_{{0,n}}}\left( {{{k}_{0}}\left| {x - y} \right|} \right)}}{{\partial \nu \left( x \right)}}} \right) - $
$ - \;\left( {\nu \left( x \right),\nu \left( y \right)} \right)\sum\limits_{m = 1}^n {\left( {\sum\limits_{l = 1}^m {\frac{1}{l}} } \right)\frac{{{{{\left( { - 1} \right)}}^{{m + 1}}}\left( {{{k}^{{2m}}} - {{k}_{0}}^{{2m}}} \right){{{\left| {x - y} \right|}}^{{2m - 2}}}}}{{{{2}^{{2m - 1}}}\left( {m - 1} \right)!m!}}} + $
$ + \;\left( {y - x,\nu \left( y \right)} \right)\left( {x - y,\nu \left( x \right)} \right)\sum\limits_{m = 2}^n {\left( {\sum\limits_{l = 1}^m {\frac{1}{l}} } \right)\frac{{{{{\left( { - 1} \right)}}^{{m + 1}}}\left( {{{k}^{{2m}}} - {{k}_{0}}^{{2m}}} \right){{{\left| {x - y} \right|}}^{{2m - 4}}}}}{{{{2}^{{2m - 2}}}\left( {m - 2} \right)!m!}}} .$

Тогда также справедлива следующая

Теорема 4. Пусть L – замкнутая и дважды непрерывно дифференцируемая кривая в ${{R}^{2}}$ и $\psi \in C\left( L \right)$. Тогда выражение

в опорных точках $x\left( {{{\tau }_{p}}} \right)$, $p = \overline {1,n} $, является квадратурной формулой для интеграла (1.5), причем справедлива следующая оценка:

$\mathop {\max }\limits_{p = \overline {1,n} } \left| {\left( {\left( {T - {{T}_{0}}} \right)\psi } \right)\left( {x\left( {{{\tau }_{p}}} \right)} \right) - \left( {{{{\left( {T - {{T}_{0}}} \right)}}_{n}}\psi } \right)\left( {x\left( {{{\tau }_{p}}} \right)} \right)} \right| \leqslant M\left( {\omega \left( {\psi ,1{\text{/}}n} \right) + {{{\left\| \psi \right\|}}_{\infty }}\frac{{\ln n}}{n}} \right).$

3. ОБОСНОВАНИЕ МЕТОДА КОЛЛОКАЦИИ ДЛЯ СИСТЕМЫ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ (1.1)

Пусть ${{C}^{{2n}}}$ – пространство $2n$-мерных векторов ${{z}^{{2n}}} = {{\left( {z_{1}^{{2n}},z_{2}^{{2n}},\; \ldots ,\;z_{{2n}}^{{2n}}} \right)}^{{\text{т}}}}$, $z_{l}^{{2n}} \in C$, $l = \overline {1,\;2n} $, с нормой $\left\| {{{z}^{{2n}}}} \right\| = \mathop {\max }\limits_{l = \overline {1,2n} } \left| {z_{l}^{{2n}}} \right|$, где запись “${{a}^{{\text{т}}}}$” означает транспонировку вектора a. Рассмотрим $2n$-мерную матрицу ${{A}^{{2{\kern 1pt} n}}} = \left( {{{a}_{{pj}}}} \right)_{{p,j = 1}}^{{2{\kern 1pt} n}}$ с элементами

${{a}_{{pj}}} = 0\quad {\text{при}}\quad p = \overline {1,n} ,\quad j = \overline {1,n} \quad {\text{и}}\quad p = j;$
${{a}_{{p{\kern 1pt} j}}} = \frac{{2\left( {b - a} \right)\sqrt {{{{\left( {x_{1}^{'}\left( {{{\tau }_{j}}} \right)} \right)}}^{2}} + {{{\left( {x_{2}^{'}\left( {{{\tau }_{j}}} \right)} \right)}}^{2}}} }}{{\left( {\mu + {{\mu }_{0}}} \right)n}}\left( {\mu \frac{{\partial \Phi _{k}^{n}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)}}{{\partial \nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)}} - {{\mu }_{0}}\frac{{\partial \Phi _{{{{k}_{0}}}}^{n}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)}}{{\partial \nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)}}} \right)$
${\text{при}}\quad p = \overline {1,n} ,\quad j = \overline {1,n} \quad {\text{и}}\quad p \ne j;$
${{a}_{{p{\kern 1pt} j}}} = 0\quad {\text{при}}\quad p = \overline {1,n} ,\quad j = \overline {n + 1,\;2n} \quad {\text{и}}\quad p = j - n;$
${{a}_{{pj}}} = \frac{{2\left( {b - a} \right)\sqrt {{{{\left( {x_{1}^{'}\left( {{{\tau }_{{j - n}}}} \right)} \right)}}^{2}} + {{{\left( {x_{2}^{'}\left( {{{\tau }_{{j - n}}}} \right)} \right)}}^{2}}} }}{{\left( {\mu + {{\mu }_{0}}} \right)n}}\left( {{{\mu }^{2}}\Phi _{k}^{n}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{{j - n}}}} \right)} \right) - \mu _{0}^{2}\Phi _{{{{k}_{0}}}}^{n}\left( {x\left( {{{\tau }_{p}}} \right),x\left( {{{\tau }_{{j - n}}}} \right)} \right)} \right)$
${\text{при}}\quad p = \overline {1,n} ,\quad j = \overline {n + 1,2n} \quad {\text{и}}\quad p \ne j - n;$
${{a}_{{p{\kern 1pt} j}}} = 0\quad {\text{при}}\quad p = \overline {n + 1,\;2n} ,\quad j = \overline {1,n} \quad {\text{и}}\quad p = j + n;$
$\begin{gathered} {{a}_{{p{\kern 1pt} j}}} = \frac{{2\left( {b - a} \right)\sqrt {{{{\left( {x_{1}^{'}\left( {{{\tau }_{j}}} \right)} \right)}}^{2}} + {{{\left( {x_{2}^{'}\left( {{{\tau }_{j}}} \right)} \right)}}^{2}}} }}{{\left( {\mu + {{\mu }_{0}}} \right)n}} \times \\ \times \;\frac{\partial }{{\partial \nu \left( {x\left( {{{\tau }_{{p - n}}}} \right)} \right)}}\left( {\frac{{\partial \left( {\Phi _{{{{k}_{0}}}}^{n}\left( {x\left( {{{\tau }_{{p - n}}}} \right),x\left( {{{\tau }_{j}}} \right)} \right) - \Phi _{k}^{n}\left( {x\left( {{{\tau }_{{p - n}}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)} \right)}}{{\partial \nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)}}} \right) \\ \end{gathered} $
${\text{при}}\quad p = \overline {n + 1,2n,} \quad j = \overline {1,n} \quad {\text{и}}\quad p \ne j + n;$
${{a}_{{p{\kern 1pt} j}}} = 0\quad {\text{при}}\quad p = \overline {n + 1,\;2n} ,\quad j = \overline {n + 1,\;2n} \quad {\text{и}}\quad p = j;$
${{a}_{{pj}}} = \frac{{2\left( {b - a} \right)\sqrt {{{{\left( {x_{1}^{'}\left( {{{\tau }_{{j - n}}}} \right)} \right)}}^{2}} + {{{\left( {x_{2}^{'}\left( {{{\tau }_{{j - n}}}} \right)} \right)}}^{2}}} }}{{\left( {\mu + {{\mu }_{0}}} \right)n}}\left( {{{\mu }_{0}}\frac{{\partial \Phi _{{{{k}_{0}}}}^{n}\left( {x\left( {{{\tau }_{{p - n}}}} \right),x\left( {{{\tau }_{{j - n}}}} \right)} \right)}}{{\partial \nu \left( {x\left( {{{\tau }_{{p - n}}}} \right)} \right)}} - \mu \frac{{\partial \Phi _{k}^{n}\left( {x\left( {{{\tau }_{{p - n}}}} \right),x\left( {{{\tau }_{{j - n}}}} \right)} \right)}}{{\partial \nu \left( {x\left( {{{\tau }_{{p - n}}}} \right)} \right)}}} \right)$
${\text{при}}\quad p = \overline {n + 1,\;2n} ,\quad j = \overline {n + 1,\;2n} \quad {\text{и}}\quad p \ne j.$

Если через $z_{p}^{{2n}}$, $p = \overline {1,n} $, обозначим приближенные значения $\psi \left( {x\left( {{{\tau }_{p}}} \right)} \right)$, а через $z_{{p + n}}^{{2n}}$, $p = \overline {1,n} $, приближенные значения $\varphi \left( {x\left( {{{\tau }_{p}}} \right)} \right)$, то, используя построенные квадратурные формулы для интегралов (1.2)–(1.5), система интегральных уравнений (1.1) заменяется системой алгебраических уравнений относительно ${{z}^{{2n}}} \in {{C}^{{2n}}}$, которую запишем в виде

(3.1)
$\begin{gathered} z_{p}^{{2n}} + \sum\limits_{j = 1}^{2n} {{{a}_{{p{\kern 1pt} j}}}z_{j}^{{2n}}} = \frac{{2f\left( {x\left( {{{\tau }_{p}}} \right)} \right)}}{{\mu + {{\mu }_{0}}}},\quad p = \overline {1,\;n} , \hfill \\ z_{p}^{{2n}} + \sum\limits_{j = 1}^{2n} {{{a}_{{pj}}}z_{j}^{{2n}}} = - \frac{{2g\left( {x\left( {{{\tau }_{{p - n}}}} \right)} \right)}}{{\mu + {{\mu }_{0}}}},\quad p = \overline {n + 1,\;2n} \hfill \\ \end{gathered} $

Теперь сформулируем основной результат данной работы.

Теорема 5. Пусть функции  f и g непрерывны на кривой L. Тогда уравнения (1.1) и (3.1) имеют единственные решения $\left( {{{\psi }_{*}},{{\varphi }_{*}}} \right) \in C\left( L \right) \times C\left( L \right)$ и ${{w}^{{2n}}} \in {{C}^{{2n}}}$ $\left( {n \geqslant {{n}_{0}}} \right)$ соответственно, причем справедливы следующие оценки:

$\mathop {\max }\limits_{p = \overline {1,n} } \left| {w_{p}^{{2n}} - {{\psi }_{*}}\left( {x\left( {{{\tau }_{p}}} \right)} \right)} \right| \leqslant M\left( {\omega \left( {f,1{\text{/}}n} \right) + \omega \left( {g,1{\text{/}}n} \right) + \frac{{\ln n}}{n}} \right),$
$\mathop {\max }\limits_{p = \overline {1,n} } \left| {w_{{p + n}}^{{2n}} - {{\varphi }_{*}}\left( {x\left( {{{\tau }_{p}}} \right)} \right)} \right| \leqslant M\left( {\omega \left( {f,1{\text{/}}n} \right) + \omega \left( {g,1{\text{/}}n} \right) + \frac{{\ln n}}{n}} \right).$

Доказательство. Для обоснования метода коллокации будем пользоваться теоремой Г.М. Вайникко о сходимости для линейных операторных уравнений (см. [14]). Для этого сначала запишем уравнения (1.1) и (3.1) в операторном виде.

Отметим, что $C\left( L \right) \times C\left( L \right)$ является банаховым пространством с нормой ${{\left\| \rho \right\|}_{1}} = \max \left\{ {{{{\left\| \psi \right\|}}_{\infty }},{{{\left\| \varphi \right\|}}_{\infty }}} \right\}$. Рассмотрим матричный оператор 2-го порядка

$A = \left( {\begin{array}{*{20}{c}} {\frac{\mu }{{\mu + {{\mu }_{0}}}}K - \frac{{{{\mu }_{0}}}}{{\mu + {{\mu }_{0}}}}{{K}_{0}}}&{\frac{{{{\mu }^{2}}}}{{\mu + {{\mu }_{0}}}}S - \frac{{\mu _{0}^{2}}}{{\mu + {{\mu }_{0}}}}{{S}_{0}}} \\ {\frac{1}{{\mu + {{\mu }_{0}}}}\left( {{{T}_{0}} - T} \right)}&{\frac{{{{\mu }_{0}}}}{{\mu + {{\mu }_{0}}}}{{{\tilde {K}}}_{0}} - \frac{\mu }{{\mu + {{\mu }_{0}}}}\tilde {K}} \end{array}} \right),$
определенный в пространстве $C\left( L \right) \times C\left( L \right)$. Тогда систему интегральных уравнений (1.1) можно переписать в виде
(3.2)
$\left( {I + A} \right)\rho = \chi ,$
а систему алгебраических уравнений (3.1) в виде
(3.3)
$\left( {{{I}^{{2n}}} + {{A}^{{2n}}}} \right){{z}^{{2n}}} = {{\chi }^{{2n}}},$
где I – единичный оператор на $C\left( L \right) \times C\left( L \right)$,
$\rho = \left( \begin{gathered} \psi \hfill \\ \varphi \hfill \\ \end{gathered} \right),\quad \chi = \frac{2}{{\mu + {{\mu }_{0}}}}\left( \begin{gathered} f \hfill \\ - g \hfill \\ \end{gathered} \right),$
${{I}^{{2n}}}$ – единичная матрица 2n-го порядка, ${{\chi }^{{2n}}} = {{p}^{{2n}}}\chi $, а ${{p}^{{2{\kern 1pt} n}}}{\text{:}}\;C\left( L \right) \times C\left( L \right) \to {{C}^{{2n}}}$ – линейный ограниченный оператор, определяемый формулой

${{p}^{{2n}}}\rho = {{p}^{{2n}}}\left( \begin{gathered} \psi \hfill \\ \varphi \hfill \\ \end{gathered} \right) = {{\left( {\psi \left( {x\left( {{{\tau }_{1}}} \right)} \right),\psi \left( {x\left( {{{\tau }_{2}}} \right)} \right),\; \ldots ,\;\psi \left( {x\left( {{{\tau }_{n}}} \right)} \right),\varphi \left( {x\left( {{{\tau }_{1}}} \right)} \right),\varphi \left( {x\left( {{{\tau }_{2}}} \right)} \right),\; \ldots ,\;\phi \left( {x\left( {{{\tau }_{n}}} \right)} \right)} \right)}^{{\text{т}}}}.$

Теперь проверим выполнение условий теоремы 4.2 из работы [14], при этом обозначения и необходимые  определения и предложения возьмем из [14]. В работе [2] доказано, что система интегральных уравнений (1.1) однозначно разрешима в пространстве $C\left( L \right) \times C\left( L \right)$, т.е. ${\text{Ker}}\left( {I + A} \right) = \left\{ 0 \right\}$. Кроме того, операторы ${{I}^{{2{\kern 1pt} n}}} + {{A}^{{2{\kern 1pt} n}}}$ фредгольмовы с нулевым индексом. Принимая во внимание способ разбиения кривой L на “регулярные” элементарные части, получаем, что для любого $\rho \in C\left( L \right) \times C\left( L \right)$ справедливо следующее равенство:

$\mathop {\lim }\limits_{n \to \infty } \left\| {{{p}^{{2n}}}\rho } \right\| = \mathop {\lim }\limits_{n \to \infty } \max \left\{ {\mathop {\max }\limits_{l = \overline {1,n} } \left| {\psi \left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right|,\mathop {\max }\limits_{l = \overline {1,n} } \left| {\varphi \left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right|} \right\} = \max \left\{ {\mathop {\max }\limits_{x \in L} \left| {\psi \left( x \right)} \right|,\mathop {\max }\limits_{x \in L} \left| {\varphi \left( x \right)} \right|} \right\} = {{\left\| \rho \right\|}_{1}}.$

Следовательно, система операторов $P = \left\{ {{{p}^{{2n}}}} \right\}$ является связывающей для пространств $C\left( L \right) \times C\left( L \right)$ и ${{C}^{{2n}}}$. Тогда ${{\chi }^{{2n}}}\mathop \to \limits^P \chi $ и принимая во внимание теоремы 1– 4, получаем, что по определению 2.1 из работы [14] ${{I}^{{2{\kern 1pt} n}}} + {{A}^{{2{\kern 1pt} n}}}\mathop \to \limits^{PP} I + A$. Так как по определению 3.2 из [14] ${{I}^{{2n}}} \to I$ устойчиво, то по предложению 3.5 и по определению 3.3 из [14] осталось проверить условие компактности, которое ввиду предложения 1.1 из [14] равносильно условию: $\forall \left\{ {{{z}^{{2{\kern 1pt} n}}}} \right\}$, ${{z}^{{2n}}} \in {{C}^{{2n}}}$, $\left\| {{{z}^{{2n}}}} \right\| \leqslant M$, существует относительно компактная последовательность $\left\{ {{{A}_{{2n}}}{{z}^{{2n}}}} \right\} \subset C\left( L \right) \times C\left( L \right)$ такая, что

$\left\| {{{A}^{{2n}}}{{z}^{{2{\kern 1pt} n}}} - {{p}^{{2n}}}\left( {{{A}_{{2n}}}{{z}^{{2n}}}} \right)} \right\| \to 0\quad {\text{при}}\quad n \to \infty .$

В качестве $\left\{ {{{A}_{{2n}}}{{z}^{{2{\kern 1pt} n}}}} \right\}$ выберем последовательность

$\left( {{{A}_{{2n}}}{{z}^{{2n}}}} \right)\left( x \right) = \left( \begin{gathered} \sum\limits_{j = 1}^{2{\kern 1pt} n} {a_{j}^{{\left( 1 \right)}}\left( x \right)z_{j}^{{2{\kern 1pt} n}}} \hfill \\ \sum\limits_{j = 1}^{2{\kern 1pt} n} {a_{j}^{{\left( 2 \right)}}\left( x \right)z_{j}^{{2{\kern 1pt} n}}} \hfill \\ \end{gathered} \right),$
где

$a_{j}^{{\left( 1 \right)}}\left( x \right) = \frac{2}{{\mu + {{\mu }_{0}}}}\left( {\mu \int\limits_{{{L}_{j}}} {\frac{{\partial \Phi _{k}^{n}\left( {x,y} \right)}}{{\partial \nu \left( y \right)}}d{{L}_{y}}} - {{\mu }_{0}}\int\limits_{{{L}_{j}}} {\frac{{\partial \Phi _{{{{k}_{0}}}}^{n}\left( {x,y} \right)}}{{\partial \nu \left( y \right)}}d{{L}_{y}}} } \right)\quad {\text{при}}\quad j = \overline {1,n} ,$
$a_{j}^{{\left( 1 \right)}}\left( x \right) = \frac{2}{{\mu + {{\mu }_{0}}}}\left( {{{\mu }^{2}}\int\limits_{{{L}_{{j - n}}}} {\Phi _{k}^{n}\left( {x,y} \right)d{{L}_{y}}} - \mu _{0}^{2}\int\limits_{{{L}_{{j - n}}}} {\Phi _{{{{k}_{0}}}}^{n}\left( {x,y} \right)d{{L}_{y}}} } \right)\quad {\text{при}}\quad j = \overline {n + 1,2n} ,$
$a_{j}^{{\left( 2 \right)}}\left( x \right) = \frac{2}{{\mu + {{\mu }_{0}}}}\int\limits_{{{L}_{j}}} {\frac{\partial }{{\partial \nu \left( x \right)}}\left( {\frac{{\partial \left( {\Phi _{{{{k}_{0}}}}^{n}\left( {x,y} \right) - \Phi _{k}^{n}\left( {x,y} \right)} \right)}}{{\partial \nu \left( y \right)}}} \right)d{{L}_{y}}} \quad {\text{при}}\quad j = \overline {1,n} ,$
$a_{j}^{{\left( 2 \right)}}\left( x \right) = \frac{2}{{\mu + {{\mu }_{0}}}}\left( {{{\mu }_{0}}\int\limits_{{{L}_{{j - n}}}} {\frac{{\partial \Phi _{{{{k}_{0}}}}^{n}\left( {x,y} \right)}}{{\partial \nu \left( x \right)}}d{{L}_{y}}} - \mu \int\limits_{{{L}_{{j - n}}}} {\frac{{\partial \Phi _{k}^{n}\left( {x,y} \right)}}{{\partial \nu \left( x \right)}}d{{L}_{y}}} } \right)\quad {\text{при}}\quad j = \overline {n + 1,\;2n} .$

Из неравенства (2.1), (2.2) и (2.9) очевидно, что для любых точек $x,y \in L$, $x \ne y$, и для любого натурального числа n, справедливы следующие оценки:

$\left| {\Phi _{k}^{n}\left( {x,y} \right)} \right| \leqslant M\left| {\ln \left| {x - y} \right|} \right|,\quad \left| {\frac{{\partial \Phi _{k}^{n}\left( {x,y} \right)}}{{\partial \nu \left( y \right)}}} \right| \leqslant M,\quad \left| {\frac{{\partial \Phi _{k}^{n}\left( {x,y} \right)}}{{\partial \nu \left( x \right)}}} \right| \leqslant M$
и

$\left| {\frac{\partial }{{\partial \nu \left( x \right)}}\left( {\frac{{\partial \left( {\Phi _{{{{k}_{0}}}}^{n}\left( {x,y} \right) - \Phi _{k}^{n}\left( {x,y} \right)} \right)}}{{\partial \nu \left( y \right)}}} \right)} \right| \leqslant M.$

Отсюда получаем, что

$\begin{gathered} \left| {\sum\limits_{j = 1}^{2{\kern 1pt} n} {a_{j}^{{\left( 1 \right)}}\left( x \right)z_{j}^{{2n}}} } \right| \leqslant \frac{{2\left\| {{{z}^{{2n}}}} \right\|}}{{\left| {\mu + {{\mu }_{0}}} \right|}}\int\limits_L {\left( {\left| \mu \right|\left| {\frac{{\partial \Phi _{k}^{n}\left( {x,y} \right)}}{{\partial \nu \left( y \right)}}} \right|} \right. + } \\ + \;\left| {{{\mu }_{0}}} \right|\left. {\left| {\frac{{\partial \Phi _{{{{k}_{0}}}}^{n}\left( {x,y} \right)}}{{\partial \nu \left( y \right)}}} \right| + {{{\left| \mu \right|}}^{2}}\left| {\Phi _{k}^{n}\left( {x,y} \right)} \right| + {{{\left| {{{\mu }_{0}}} \right|}}^{2}}\left| {\Phi _{{{{k}_{0}}}}^{n}\left( {x,y} \right)} \right|} \right)d{{L}_{y}} \leqslant M\left\| {{{z}^{{2n}}}} \right\|\quad \forall \;x \in L, \\ \end{gathered} $
и

$\begin{gathered} \left| {\sum\limits_{j = 1}^{2n} {a_{j}^{{\left( 2 \right)}}\left( x \right)z_{j}^{{2n}}} } \right| \leqslant \frac{{2\left\| {{{z}^{{2n}}}} \right\|}}{{\left| {\mu + {{\mu }_{0}}} \right|}}\int\limits_L {\left( {\left| \mu \right|\left| {\frac{{\partial \Phi _{k}^{n}\left( {x,y} \right)}}{{\partial \nu \left( x \right)}}} \right| + } \right.} \,\left| {{{\mu }_{0}}} \right|\left| {\frac{{\partial \Phi _{{{{k}_{0}}}}^{n}\left( {x,y} \right)}}{{\partial \nu \left( x \right)}}} \right| + \\ + \;\left. {\left| {\frac{\partial }{{\partial \nu \left( x \right)}}\left( {\frac{{\partial \left( {\Phi _{{{{k}_{0}}}}^{n}\left( {x,y} \right) - \Phi _{k}^{n}\left( {x,y} \right)} \right)}}{{\partial \nu \left( y \right)}}} \right)} \right|} \right)d{{L}_{y}} \leqslant M\left\| {{{z}^{{2n}}}} \right\|\quad \forall \;x \in L. \\ \end{gathered} $

Следовательно,

$\left| {\left( {{{A}_{{2n}}}{{z}^{{2{\kern 1pt} n}}}} \right)\left( x \right)} \right| \leqslant M\left\| {{{z}^{{2n}}}} \right\|\quad \forall \;x \in L.$

Тогда, принимая во внимание условиe $\left\| {{{z}^{N}}} \right\| \leqslant M$, получаем равномерную ограниченность последовательности $\left\{ {{{A}_{{2n}}}{{z}^{{2n}}}} \right\}$.

Теперь возьмем любые точки $x{\text{'}},x{\text{''}} \in L$ такие, что $\left| {x{\text{'}} - x{\text{''}}} \right| = \delta < d{\text{/}}2$. Тогда, поступая точно также, как и в работе [15], можно показать, что

$\left| {\sum\limits_{j = 1}^{2{\kern 1pt} n} {a_{j}^{{\left( 1 \right)}}\left( {x{\text{'}}} \right)z_{j}^{{2n}}} - \sum\limits_{j = 1}^{2n} {a_{j}^{{\left( 1 \right)}}\left( {x{\text{''}}} \right)z_{j}^{{2n}}} } \right| \leqslant M\left\| {{{z}^{{2n}}}} \right\|\delta \left| {\ln \delta } \right|\quad \forall \;x{\text{'}},x{\text{''}} \in L,$
и

$\left| {\sum\limits_{j = 1}^{2n} {a_{j}^{{\left( 2 \right)}}\left( {x{\text{'}}} \right)z_{j}^{{2n}}} - \sum\limits_{j = 1}^{2n} {a_{j}^{{\left( 2 \right)}}\left( {x{\text{''}}} \right)z_{j}^{{2n}}} } \right| \leqslant M\left\| {{{z}^{{2n}}}} \right\|\delta \left| {\ln \delta } \right|\quad \forall \;x{\text{'}},x{\text{''}} \in L.$

Следовательно,

$\left| {\left( {{{A}_{{2n}}}{{z}^{{2n}}}} \right)\left( {x{\text{'}}} \right) - \left( {{{A}_{{2n}}}{{z}^{{2n}}}} \right)\left( {x{\text{''}}} \right)} \right| \leqslant M\left\| {{{z}^{{2n}}}} \right\|\left| {x{\text{'}} - x{\text{''}}} \right|\left| {\ln \left| {{\text{'}}x - x{\text{''}}} \right|} \right|\quad \forall \;x{\text{'}},x{\text{''}} \in L,$
а значит, $\left\{ {{{A}_{{2n}}}{{z}^{{2n}}}} \right\} \subset C\left( L \right) \times C\left( L \right)$. Отсюда непосредственно вытекает равностепенная непрерывность последовательности $\left\{ {{{A}_{{2n}}}{{z}^{{2n}}}} \right\}$. Тогда из теоремы Арцеля следует относительная компактность последовательности $\left\{ {{{A}_{{2n}}}{{z}^{{2n}}}} \right\}$. Кроме того, поступая точно также, как и в доказательствах теоремы 1 и 2, получим

$\left\| {{{A}^{{2n}}}{{z}^{{2n}}} - {{p}^{{2n}}}\left( {{{A}_{{2n}}}{{z}^{{2n}}}} \right)} \right\| \to 0\quad {\text{при}}\quad n \to \infty .$

Тогда, применяя теорему 4.2 из работы [14], находим, что уравнения (3.2) и (3.3) имеют единственные решения ${{\rho }_{*}} = \left( \begin{gathered} {{\psi }_{*}} \hfill \\ {{\varphi }_{*}} \hfill \\ \end{gathered} \right) \in C\left( L \right) \times C\left( L \right)$ и ${{w}^{{2n}}} \in {{C}^{{2N}}}$ ($n \geqslant {{n}_{0}}$) соответственно, причем

${{c}_{1}}{{\delta }_{n}} \leqslant \left\| {{{w}^{{2n}}} - {{p}^{{2n}}}{{\rho }_{*}}} \right\| \leqslant {{c}_{2}}{{\delta }_{n}},$
где

${{c}_{1}} = {1 \mathord{\left/ {\vphantom {1 {\mathop {\sup }\limits_{n \geqslant {{n}_{0}}} \left\| {{{I}^{{2n}}} + {{A}^{{2n}}}} \right\|}}} \right. \kern-0em} {\mathop {\sup }\limits_{n \geqslant {{n}_{0}}} \left\| {{{I}^{{2n}}} + {{A}^{{2n}}}} \right\|}} > 0,\quad {{c}_{2}} = \mathop {\sup }\limits_{n \geqslant {{n}_{0}}} \left\| {{{{\left( {{{I}^{{2n}}} + {{A}^{{2n}}}} \right)}}^{{ - 1}}}} \right\| < + \infty ,$
${{\delta }_{n}} = \left\| {\left( {{{I}^{{2n}}} + {{A}^{{2n}}}} \right)\left( {{{p}^{{2n}}}{{\rho }_{*}}} \right) - {{\chi }^{{2n}}}} \right\|.$

Принимая во внимание равенство

${{\chi }^{{2n}}} = {{p}^{{2n}}}\chi = {{p}^{{2n}}}{{\rho }_{*}} + {{p}^{{2n}}}\left( {A{{\rho }_{*}}} \right)$
и оценки погрешности построенных квадратурных формул для интегралов (1.2)–(1.5), имеем
${{\delta }_{n}} = \left\| {{{A}^{{2n}}}\left( {{{p}^{{2n}}}{{\rho }_{*}}} \right) - {{p}^{{2n}}}\left( {A{{\rho }_{*}}} \right)} \right\| \leqslant M\left( {{{{\left\| {{{\rho }_{*}}} \right\|}}_{1}}\frac{{\ln n}}{n} + \omega \left( {{{\rho }_{*}},1{\text{/}}n} \right)} \right),$
где

Так как из неравенства (2.1), (2.2) и (2.9) ясно, что для любых точек $x,y \in L$,$x \ne y$,

$\left| {{{\Phi }_{k}}\left( {x,y} \right)} \right| \leqslant M\left| {\ln \left| {x - y} \right|} \right|,\quad \left| {\frac{{\partial {{\Phi }_{k}}\left( {x,y} \right)}}{{\partial \nu \left( y \right)}}} \right| \leqslant M,\quad \left| {\frac{{\partial {{\Phi }_{k}}\left( {x,y} \right)}}{{\partial \nu \left( x \right)}}} \right| \leqslant M$
и
$\left| {\frac{\partial }{{\partial \nu \left( x \right)}}\left( {\frac{{\partial \left( {{{\Phi }_{{{{k}_{0}}}}}\left( {x,y} \right) - {{\Phi }_{k}}\left( {x,y} \right)} \right)}}{{\partial \nu \left( y \right)}}} \right)} \right| \leqslant M,$
то, поступая точно также, как и в работе [16], можно показать, что
$\left| {\left( {S{{\rho }_{*}}} \right)\left( {x{\text{'}}} \right) - \left( {S{{\rho }_{*}}} \right)\left( {x{\text{''}}} \right)} \right| \leqslant M\left\| {{{\rho }_{*}}} \right\|\left| {x{\text{'}} - x{\text{''}}} \right|\left| {\ln \left| {x{\text{'}} - x{\text{''}}} \right|} \right|\quad \forall \;x{\text{'}},x{\text{''}} \in L,$
$\left| {\left( {K{{\rho }_{*}}} \right)\left( {x{\text{'}}} \right) - \left( {K{{\rho }_{*}}} \right)\left( {x{\text{''}}} \right)} \right| \leqslant M\left\| {{{\rho }_{*}}} \right\|\left| {x{\text{'}} - x{\text{''}}} \right|\left| {\ln \left| {x{\text{'}} - x{\text{''}}} \right|} \right|\quad \forall \;x{\text{'}},x{\text{''}} \in L,$
$\left| {\left( {\tilde {K}{{\rho }_{*}}} \right)\left( {x{\text{'}}} \right) - \left( {\tilde {K}{{\rho }_{*}}} \right)\left( {x{\text{''}}} \right)} \right| \leqslant M\left\| {{{\rho }_{*}}} \right\|\left| {x{\text{'}} - x{\text{''}}} \right|\left| {\ln \left| {x{\text{'}} - x{\text{''}}} \right|} \right|\quad \forall \;x{\text{'}},x{\text{''}} \in L,$
и

$\left| {\left( {\left( {T - {{T}_{0}}} \right){{\rho }_{*}}} \right)\left( {x{\text{'}}} \right) - \left( {\left( {T - {{T}_{0}}} \right){{\rho }_{*}}} \right)\left( {x{\text{''}}} \right)} \right| \leqslant M\left\| {{{\rho }_{*}}} \right\|\left| {x{\text{'}} - x{\text{''}}} \right|\left| {\ln \left| {x{\text{'}} - x{\text{''}}} \right|} \right|\quad \forall \;x{\text{'}},x{\text{''}} \in L.$

Следовательно,

$\left| {\left( {A{{\rho }_{*}}} \right)\left( {x{\text{'}}} \right) - \left( {A{{\rho }_{*}}} \right)\left( {x{\text{''}}} \right)} \right| \leqslant M\left\| {{{\rho }_{*}}} \right\|\left| {x{\text{'}} - x{\text{''}}} \right|\left| {\ln \left| {x{\text{'}} - x{\text{''}}} \right|} \right|\quad \forall \;x{\text{'}},x{\text{''}} \in L,$
т.е.

$\omega \left( {A{{\rho }_{*}},1{\text{/}}n} \right) \leqslant M{{\left\| {{{\rho }_{*}}} \right\|}_{1}}\frac{{\ln n}}{n}.$

Тогда, принимая во внимание неравенство

$\omega \left( {{{\rho }_{*}},1{\text{/}}n} \right) = \omega \left( {\chi - A{{\rho }_{*}},1{\text{/}}n} \right) \leqslant \omega \left( {\chi ,1{\text{/}}n} \right) + \omega \left( {A{{\rho }_{*}},1{\text{/}}n} \right) \leqslant \omega \left( {f,1{\text{/}}n} \right) + \omega \left( {g,1{\text{/}}n} \right) + M{{\left\| {{{\rho }_{*}}} \right\|}_{1}}\frac{{\ln n}}{n}$
и
${{\left\| {{{\rho }_{*}}} \right\|}_{1}} \leqslant \left\| {{{{\left( {I + A} \right)}}^{{ - 1}}}} \right\|{{\left\| \chi \right\|}_{1}},$
получаем, что

${{\delta }_{n}} \leqslant M\left( {\omega \left( {f,1{\text{/}}n} \right) + \omega \left( {g,1{\text{/}}n} \right) + \frac{{\ln n}}{n}} \right).$

Теорема доказана.

Следствие 1. Пусть ${{x}_{*}} \in D$, $x* \in {{R}^{2}}{\text{/}}\bar {D}$ и ${{w}^{{2n}}} = {{\left( {w_{1}^{{2n}},w_{2}^{{2n}},\; \ldots ,\;w_{{2n}}^{{2n}}} \right)}^{{\text{т}}}}$ является решением системы алгебраических уравнений (3.1). Тогда последовательность

${{u}^{n}}\left( {x{\text{*}}} \right) = \frac{{b - a}}{n}\sum\limits_{j = 1}^n {\left( {\frac{{\partial \Phi _{k}^{n}\left( {x*,x\left( {{{\tau }_{j}}} \right)} \right)}}{{\partial \nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)}}w_{j}^{{2n}} + \mu \Phi _{k}^{n}\left( {x*,x\left( {{{\tau }_{j}}} \right)} \right)w_{{n + j}}^{{2n}}} \right)\sqrt {{{{\left( {x_{1}^{'}\left( {{{\tau }_{j}}} \right)} \right)}}^{2}} + {{{\left( {x_{2}^{'}\left( {{{\tau }_{j}}} \right)} \right)}}^{2}}} } $
сходится к $u\left( {x{\text{*}}} \right)$, а последовательность
$u_{0}^{n}\left( {{{x}_{*}}} \right) = \frac{{b - a}}{n}\sum\limits_{j = 1}^n {\left( {\frac{{\partial \Phi _{{{{k}_{0}}}}^{n}\left( {{{x}_{*}},x\left( {{{\tau }_{j}}} \right)} \right)}}{{\partial \nu \left( {x\left( {{{\tau }_{j}}} \right)} \right)}}w_{j}^{{2n}} + {{\mu }_{0}}\Phi _{{{{k}_{0}}}}^{n}\left( {{{x}_{*}},x\left( {{{\tau }_{j}}} \right)} \right)w_{{n + j}}^{{2n}}} \right)\sqrt {{{{\left( {x_{1}^{'}\left( {{{\tau }_{j}}} \right)} \right)}}^{2}} + {{{\left( {x_{2}^{'}\left( {{{\tau }_{j}}} \right)} \right)}}^{2}}} } $
сходится к ${{u}_{0}}\left( {{{x}_{*}}} \right)$, причем

$\left| {{{u}^{n}}\left( {x{\text{*}}} \right) - u\left( {x{\text{*}}} \right)} \right| \leqslant M\left( {\frac{{\ln n}}{n} + \omega \left( {f,1{\text{/}}n} \right) + \omega \left( {g,1{\text{/}}n} \right)} \right),$
$\left| {u_{0}^{n}\left( {{{x}_{*}}} \right) - {{u}_{0}}\left( {{{x}_{*}}} \right)} \right| \leqslant M\left( {\frac{{\ln n}}{n} + \omega \left( {f,1{\text{/}}n} \right) + \omega \left( {g,1{\text{/}}n} \right)} \right).$

Список литературы

  1. Колтон Д., Кресс Р. Методы интегральных уравнений в теории рассеяния. М.: Мир, 1987. 311 с.

  2. Kress R., Roach G.F. Transmission problems Helmholtz equation // J. Math. Phys. 1978. V. 19. P. 1433–1437.

  3. Каширин А.А., Смагин С.И., Талтыкина М.Ю. Применение мозаично-скелетонного метода при численном решении трехмерных задач Дирихле для уравнения Гельмгольца в интегральной форме // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 4. С. 625–638.

  4. Халилов Э.Г. Обоснование метода коллокации для интегрального уравнения смешанной краевой задачи для уравнения Гельмгольца // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 7. С. 1340–1348.

  5. Harris P.J., Chen K. On efficient preconditioners for iterative solution of a Galerkin boundary element equation for the three–dimensional exterior Helmholtz problem // J. Comp. Appl. Math. 2003. V. 156. P. 303–318.

  6. Khalilov E.H., Aliev A.R. Justification of a quadrature method for an integral equation to the external Neumann problem for the Helmholtz equation // Math. Meth. Appl. Sci. 2018. V. 41. № 16. P. 6921–6933.

  7. Turc C., Boubendir Y., Riahi M.K. Well–conditioned boundary integral equation formulations and Nyström discretizations for the solution of Helmholtz problems with impedance boundary conditions in two-dimensional Lipschitz domains // J. Integral Eq. Appl. 2017. V. 29. № 3. P. 441–472.

  8. Халилов Э.Г. Обоснование метода коллокации для одного класса систем интегральных уравнений // Украинский матем. ж. 2017. Т. 69. № 6. С. 823–835.

  9. Khalilov E.H., Bakhshaliyeva M.N. Quadrature formulas for simple and double layer logarithmic potentials // Proceed. of IMM of NAS of Azerbaijan. 2019. V. 45. № 1. P. 155–162.

  10. Kress R. Boundary integral equations in time-harmonic acoustic scattering // Math. Comp. Modeling. 1991. V. 15. № 3–5. P. 229–243.

  11. Мусхелешвили Н.И. Сингулярные интегральные уравнения. М.: Физматлит, 1962. 599 с.

  12. Владимиров В.С. Уравнения математической физики. М.: Наука, 1976. 527 с.

  13. Халилов Э.Г. Обоснование метода коллокации для одного класса поверхностных интегральных уравнений // Матем. заметки. 2020. Т. 107. № 4. С. 604–622.

  14. Вайникко Г.М. Регулярная сходимость операторов и приближенное решение уравнений // Итоги науки и техники. Матем. анализ. 1979. Т. 16. С. 5–53.

  15. Бахшалыева М.Н., Халилов Э.Г. Обоснование метода коллокации для интегрального уравнения внешней краевой задачи Дирихле для уравнения Лапласа // Ж. вычисл. матем. и матем. физ. 2021. Т. 61. № 6. С. 936–950.

  16. Халилов Э.Г., Бахшалыева М.Н. Исследование приближенного решения интегрального уравнения, соответствующего смешанной краевой задаче для уравнения Лапласа // Уфимский матем. журн. 2021. Т. 13. № 1. С. 86–98.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал