1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 62, № 5, 2022

Журнал вычислительной математики и математической физики, 2022, T. 62, № 5, стр. 823-837

О РЕШЕНИИ ОДНОЙ ЗАДАЧИ О КОНФОРМНОМ ОТОБРАЖЕНИИ ПРИ ПОМОЩИ ФУНКЦИЙ ВЕЙЕРШТРАССА

М. Смирнов 1, 2, *

1 Ин-т вычисл. математики РАН
119333 Москва, ул. Губкина, 8, Россия

2 МГУ
119991 Ленинские горы, Москва, Россия

* E-mail: matsmir98@gmail.com

Поступила в редакцию 15.09.2021
После доработки 25.11.2021
Принята к публикации 14.01.2022

Полный текст (PDF)

Аннотация

Рассматривается задача о конформном отображении сечения канала, заполненного пористым материалом, под плотиной прямоугольного сечения на верхнюю полуплоскость. Подобные задачи возникают при расчете течения жидкости в гидротехнических сооружениях. В качестве метода решения используется представление эллиптического интеграла Кристоффеля–Шварца через функции Вейерштрасса. Для расчета используется ряд Тейлора для сигма-функции, коэффициенты которого определяются рекуррентно. Получена простая формула для конформного отображения, зависящая от четырех параметров и использующая сигма-функцию. Для конкретной области проведен численный эксперимент. Рассмотрено вырождение области, состоящее в стремлении к нулю толщины плотины, и показано, что полученная формула имеет предел, осуществляющий решение предельной задачи. Приведено уточненное доказательство рекуррентной формулы Вейерштрасса для коэффициентов ряда Тейлора сигма-функции. Библ. 17. Фиг. 5.

Ключевые слова: конформные отображения, интеграл Кристоффеля–Шварца, эллиптические функции, сигма-функция Вейерштрасса, вырождение функций Вейерштрасса.

1. ВВЕДЕНИЕ

В данной статье рассматривается одна область $\Omega \subset \mathbb{C}$, граница которой является ломаной с углами, кратными π/2. Данная область моделирует сечение канала под плотиной. Расчет течения жидкости по такому каналу сводится к задаче о конформном отображении Ω на верхнюю полуплоскость. Решение подобных задач дается интегралом Кристоффеля–Шварца (см., например, [1] или [2]), который в рассматриваемом случае живет на эллиптической римановой поверхности. В работе найдена простая формула, выражающая интеграл через сигма-функцию Вейерштрасса (см., например, [3] или [4]). Благодаря такому подходу отпадает необходимость использовать численное интегрирование, а параметры отображения находятся из достаточно простой системы нелинейных уравнений, что существенно упрощает численное решение.

Аналогичные задачи уже рассматривались в [5]–[9], где для эффективного представления интеграла Кристоффеля–Шварца использовались тэта-функции (см., например, [10]). В статье [9] также исследовалось применение функций Лауричеллы к этим задачам, а кроме того, было проведено практическое сравнение различных подходов к решению.

Основным преимуществом использования функций Вейерштрасса перед тэта-функциями является наличие у них предельных значений при вырождениях поверхности. В работе анализируется поведение построенного конформного отображения при условии, что толщина тела плотины стремится к нулю. Оказывается, что конформные отображения имеют предел, причем являющийся решением возникающей в пределе задачи. Таким образом, показано, что построенное решение устойчиво при рассмотренном вырождении.

Описанное свойство сигма-функции Вейерштрасса теряет свой смысл, если использовать для вычислений стандартный метод, выражающий сигма-функцию через тэта-функцию (поскольку она не выдерживает вырождения). Таким образом, возникает необходимость использовать независимый метод вычисления сигма-функций. В данной работе используется выражение для коэффициентов ее разложения в ряд Тейлора, полученное Вейерштрассом (см. [11]). Поскольку изложенное там доказательство, по всей видимости, не полно (в один момент используется голоморфность сигма-функции по трем переменным в окрестности нуля, что не очевидно), мы приводим более подробное доказательство в приложении. Вышеописанной формулы, однако, недостаточно для окончательного численного решения, так как ряды Тейлора не подходят для вычислений при больших аргументах (а именно такая необходимость возникает при вырождении). Таким образом, остается нерешенной еще задача о построении эффективного вычислительного метода для сигма-функции, не зависимого от тэта-функций. При наличии такого метода появится возможность строить устойчивые при различных вырождениях формулы и использовать их в вычислениях. Результаты настоящей работы иллюстрируют необходимость построения подобных методов.

Задачи, в которых возникают гиперэллиптические римановы поверхности высокого рода, рассмотренные, например, в [7], [8], можно также решать при помощи теории сигма-функций, развитой Клейном и Бейкером в [12] и [13] соответственно (более подробное изложение см. в [14]). Есть надежда, что удастся доказать устойчивость формул, выражающих решение вышеупомянутых задач через сигма-функции высокого рода. Таким образом, построение рекуррентных формул типа Вейерштрасса (которые известны для рода 1 и 2; см. [14]) и методов вычисления для сигма-функций могут оказаться крайне полезными для прикладных задач.

2. ФОРМУЛИРОВКА ЗАДАЧИ И ЕЕ ПРОИСХОЖДЕНИЕ

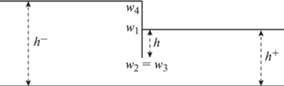
Рассмотрим область $\Omega $ в комплексной плоскости, изображенную на фиг. 1. Снизу она ограничена прямой, а сверху – ломаной с четырьмя вершинами: ${{w}_{1}},{{w}_{2}},{{w}_{3}},{{w}_{4}}$ (удобно считать, что у этой области также еще две вершины находятся в $ \pm \infty $). Будем считать, что прямая, ограничивающая снизу эту область, параллельна вещественной оси, а вершина w4 расположена в нуле. Тогда данная область определяется четырьмя вещественными параметрами ${{h}^{ - }},{{h}^{ + }},h,\delta $, где h – длина отрезка $[{{w}_{1}},{{w}_{2}}]$, $\delta $ – длина отрезка $[{{w}_{2}},{{w}_{3}}]$, а ${{h}^{ - }}$ и ${{h}^{ + }}$ – расстояние от прямой, ограничивающей область снизу до ${{w}_{4}}$ и ${{w}_{1}}$ соответственно. Параметры положительны и удовлетворяют неравенствам ${{h}^{ - }} - {{h}^{ + }} + h > 0$, что соответствует положительности длины отрезка $[{{w}_{3}},{{w}_{4}}]$, и $h < {{h}^{ + }}$. Область определяется этими параметрами однозначно.

Фиг. 1.

Область $\Omega $.

Области, подобные $\Omega $, возникают в задачах, связанных с расчетом течения жидкости через пористый материал под плотиной. Поскольку течение неразрывно и подчиняется закону Дарси, давление p является в $\Omega $ гармонической функцией. Считая, что отрезки $[{{w}_{1}},{{w}_{2}}]$, $[{{w}_{2}},{{w}_{3}}]$, $[{{w}_{3}},{{w}_{4}}]$, а также дно канала непроницаемы для жидкости, получаем естественные граничные условия: нормальная производная $\partial p{\text{/}}\partial n$ обращается в нуль на непроницаемых кусках границы, в то время как на оставшихся сегментах (т.е. на полупрямых, выходящих из ${{w}_{1}}$ и ${{w}_{4}}$) функция p локально постоянна.

Рассмотрим в области $\Omega $ такую функцию q, что $f = p + iq$ голоморфна (такая функция существует, так как $\Omega $ односвязно). Условие обращения в нуль нормальной производной функции p, как нетрудно видеть, равносильно постоянству функции q на соответствующем сегменте границы. Отсюда следует, что, если в качестве f взять функцию, конформно отображающую $\Omega $ на прямоугольник так, чтобы в его вершины перешли точки ${{w}_{1}}$, ${{w}_{4}}$ и пара бесконечно удаленных вершин области $\Omega $, то $p = {\text{Re}}f$ будет решением исходной краевой задачи. Функция $q = {\text{Im}}f$ называется функцией тока. Ее линии уровня являются линиями тока жидкости под плотиной. Ясно, что для решения обозначенной задачи достаточно решить задачу о конформном отображении $\Omega $ на верхнюю полуплоскость ${{\mathbb{C}}_{ + }}$.

В дальнейшем задача о конформном отображении будет решена явно при помощи аппарата эллиптических функций Вейерштрасса. Ниже показан расчет линий тока в области $\Omega $, полученный с помощью построенного в настоящей работе метода.

3. РЕШЕНИЕ ЗАДАЧИ О КОНФОРМНОМ ОТОБРАЖЕНИИ

3.1. Общий вид решения и определение параметров

Поскольку $\Omega $ односвязна, существует конформное отображение $W:{{\mathbb{C}}_{ + }} \to \Omega $, где ${{\mathbb{C}}_{ + }} = \{ z \in \mathbb{C}:{\text{Im}}z > 0\} $ – верхняя полуплоскость (см., например, [15] или [1]). Используя, если нужно, подходящий автоморфизм области ${{\mathbb{C}}_{ + }}$, можно добиться того, чтобы в точку ${{w}_{4}}$ при отображении W (точнее при его продолжении на границу) переходила точка $\infty $. Тогда, по теореме Кристоффеля–Шварца (см. [2]), найдутся такие ${{x}^{ - }} < {{x}^{ + }} < {{x}_{1}} < {{x}_{2}} < {{x}_{3}} \in \mathbb{R}$ и $C \in \mathbb{C}$, что

(3.1)
$dW = \phi = C\frac{{\sqrt {(x - {{x}_{2}})(x - {{x}_{3}})} }}{{(x - {{x}^{ - }})(x - {{x}^{ + }})\sqrt {x - {{x}_{1}}} }}dx.$

Замечание 1. Здесь xi – прообраз вершины ${{w}_{i}}$ при отображении W, а ${{x}^{ - }}$ и ${{x}^{ + }}$ – точки на границе верхней полуплоскости, в которых W уходит на бесконечность (прообразы бесконечно удаленных вершин).

Дифференциальную форму ϕ можно рассматривать на гиперэллиптической римановой поверхности V рода 1, заданной уравнением ${{y}^{2}} = F(x) = 4(x - {{x}_{1}})(x - {{x}_{2}})(x - {{x}_{3}})$. Используя, если нужно, сдвиг верхней полуплоскости мы можем, не ограничивая общности, считать, что ${{x}_{1}} + {{x}_{2}} + {{x}_{3}}$ = 0. Отсюда $F(x) = 4{{x}^{3}} - {{g}_{2}}x - {{g}_{3}}$ для некоторых вещественных ${{g}_{2}},{{g}_{3}}$ (определяемых числами ${{x}_{1}},{{x}_{2}},{{x}_{3}}$). На этой поверхности ϕ можно переписать в виде

(3.2)
$\phi = 2C\frac{{(x - {{x}_{2}})(x - {{x}_{3}})}}{{y(x - {{x}^{ - }})(x - {{x}^{ + }})}}dx.$

Зафиксируем ветвь функции $\sqrt {F(x)} $ в области, полученной из $\mathbb{C}$ выбрасыванием отрезка $[{{x}_{1}},{{x}_{2}}]$ и полупрямой $[{{x}_{3}},\infty ]$. Будем считать, что эта ветвь положительна при стремлении к полупрямой $({{x}_{3}},\infty )$ из верхней полуплоскости. Вспоминая, что $dx{\text{/}}y$ – голоморфная (всюду отличная от нуля) форма на $V$, получаем, что $\phi $ имеет два нуля кратности 2 в точках $({{x}_{2}},0)$ и $({{x}_{3}},0)$, а также четыре простых полюса в точках $({{x}^{ - }}, \pm \sqrt {F({{x}^{ - }})} )$ и $({{x}^{ + }}, \pm \sqrt {F({{x}^{ + }})} )$. Заметим теперь, что вычеты этой формы в данных полюсах равны $ \pm {{h}^{ - }}{\text{/}}\pi $ и $ \mp {{h}^{ + }}{\text{/}}\pi $ соответственно.

Теперь воспользуемся отображением Абеля (см., например, [16]), которое отождествляет $V$ с ${\text{Jac}}(V)$ (как обычно, начальной точкой положим бесконечно удаленную точку, а в качестве базиса голоморфных форм – $dx{\text{/}}y$). Введем полупериоды

$\omega = \int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\frac{{dx}}{y},\quad \omega ' = - \int\limits_{{{x}_{2}}}^{{{x}_{3}}} {\frac{{dx}}{y},} } $
а также величины $\eta = \zeta (\omega )$ и $\eta {\kern 1pt} ' = \zeta (\omega {\kern 1pt} ')$, где $\zeta $ – дзета-функция Вейерштрасса (см. [3]). Нетрудно видеть, что $\omega ,\eta \in \mathbb{R}$ и $\omega {\kern 1pt} ',\eta {\kern 1pt} ' \in i\mathbb{R}$. Совокупность точек $(x,\sqrt {F(x)} )$, где $x \in {{\mathbb{C}}_{ + }}$ при этом отображении перейдет в прямоугольник с вершинами $0,\omega {\kern 1pt} ',\omega {\kern 1pt} ' - \omega , - \omega $. Обозначим образы точек $({{x}^{ - }},\sqrt {F({{x}^{ - }})} )$ и $({{x}^{ + }},\sqrt {F({{x}^{ + }})} )$ через ${{z}^{ - }}$ и ${{z}^{ + }}$ соответственно (см. фиг. 3, где в скобках указаны прообразы соответствующих точек). Образы точек $({{x}^{ - }}, - \sqrt {F({{x}^{ - }})} )$ и $({{x}^{ + }}, - \sqrt {F({{x}^{ + }})} )$ равны в этом случае $ - {{z}^{ - }}$ и $ - {{z}^{ + }}$. Рассмотрим дифференциальную форму $\psi $ на торе, в которую $\phi $ переходит при отождествлении $V$ с ${\text{Jac(}}V)$. Эта форма имеет 4 простых полюса в точках $ \pm {{z}^{ - }}$ и $ \pm {{z}^{ + }}$, причем имеет в этих точках вычеты $ \pm {{h}^{ - }}{\text{/}}\pi $ и $ \mp {{h}^{ + }}{\text{/}}\pi $ соответственно.

Фиг. 2.

Линии тока в области $\Omega $.

Фиг. 3.

Образ верхней полуплоскости при отображении Абеля.

Воспользуемся теперь описанным в [3] методом представления эллиптических функций через функции Вейерштрасса. Для этого рассмотрим мероморфную функцию

(3.3)
$g(z) = \frac{{{{h}^{ - }}}}{\pi }(\zeta (z - {{z}^{ - }}) - \zeta (z + {{z}^{ - }})) - \frac{{{{h}^{ + }}}}{\pi }(\zeta (z - {{z}^{ + }}) - \zeta (z + {{z}^{ + }})).$

Из соотношений квазипериодичности функции $\zeta $ (см. [3]), легко вывести, что g – эллиптическая функция. Форма $g(z)dz$ имеет точно такие же (простые) полюса, что и $\psi $, причем в этих полюсах имеет те же вычеты. Значит, $\psi - g(z)dz$ – голоморфная форма на торе. Поскольку на торе пространство голоморфных 1-форм одномерно, получаем, что $\psi - g(z)dz = Ddz$, где D – некоторая константа (причем $D \in i\mathbb{R}$).

Теперь обратимся к отображению W. Ясно, что

$W(x) = - \int\limits_x^\infty {\phi .} $

Таким образом, положим

(3.4)
$Q(z) = \int\limits_0^z {\psi .} $

Очевидно, что $W(x)$ совпадает с $Q(z)$, где $z$ – образ точки $(x,\sqrt {F(x)} )$ при отображении Абеля. Значит, Q осуществляет конформное отображение прямоугольника с вершинами $0,\omega {\kern 1pt} ',\omega {\kern 1pt} '\, - \omega , - \omega $ на $\Omega $, причем $\omega {\kern 1pt} '$ переходит в ${{w}_{1}}$, $\omega '\, - \omega $ переходит в ${{w}_{2}}$, а $ - \omega $ – в ${{w}_{3}}$ (а 0 – в ${{w}_{4}}$). Теперь мы можем записать систему уравнений, следующих из полученных ранее соотношений:

(3.5)
$g( - \omega ) + D = 0,\quad g(\omega {\kern 1pt} '\, - \omega ) + D = 0,$
(3.6)
$Q(\omega {\kern 1pt} '\, - \omega ) - Q(\omega {\kern 1pt} ') = - ih,\quad Q( - \omega ) - Q(\omega '\, - \omega ) = - \delta .$

Замечание 2. Первая пара уравнений получается из того, что $\phi $ имеет нули в точках $({{x}_{2}},0)$ и $({{x}_{3}},0)$, а вторая пара получается из равенств ${{w}_{3}} - {{w}_{2}} = - \delta $, ${{w}_{2}} - {{w}_{1}} = - ih$.

Остается найти разумную формулу для Q. Вспомним, что $\zeta $ – логарифмическая производная функции $\sigma $. Отсюда легко получаем, что Q имеет вид

(3.7)
$Q(z) = Dz + \frac{{{{h}^{ - }}}}{\pi }\ln \left( {\frac{{\sigma (z - {{z}^{ - }})}}{{\sigma (z + {{z}^{ - }})}}} \right) - \frac{{{{h}^{ + }}}}{\pi }\ln \left( {\frac{{\sigma (z - {{z}^{ + }})}}{{\sigma (z + {{z}^{ + }})}}} \right) - i({{h}^{ - }} - {{h}^{ + }}),$
где взята ветвь функции ln, определенная на плоскости с разрезом по мнимой отрицательной полуоси, принимающая в 1 значение 0. Подставляя в (3.5) выражение для g из (3.3), а также формулу (3.7) в (3.6), применяя при этом свойства квазипериодичности $\sigma $-функции (см., например, [3]), получаем следующую систему уравнений:

(3.8)
$\begin{array}{*{20}{c}} { - D\omega - \frac{{2{{h}^{ + }}}}{\pi }\eta {{z}^{ + }} + \frac{{2{{h}^{ - }}}}{\pi }\eta {{z}^{ - }} = - ih,} \\ { - D\omega '\, - \frac{{2{{h}^{ + }}}}{\pi }\eta '{{z}^{ + }} + \frac{{2{{h}^{ - }}}}{\pi }\eta '{{z}^{ - }} = - \delta ,} \\ {D + \frac{{{{h}^{ - }}}}{\pi }(\zeta (\omega - {{z}^{ - }}) - \zeta (\omega + {{z}^{ - }})) - \frac{{{{h}^{ + }}}}{\pi }(\zeta (\omega - {{z}^{ + }}) - \zeta (\omega + {{z}^{ + }})) = 0,} \\ {D + \frac{{{{h}^{ - }}}}{\pi }(\zeta (\omega '\, + \omega - {{z}^{ - }}) - \zeta (\omega '\, + \omega + {{z}^{ - }})) - \frac{{{{h}^{ + }}}}{\pi }(\zeta (\omega '\, + \omega - {{z}^{ + }}) - \zeta (\omega '\, + \omega + {{z}^{ + }})) = 0.} \end{array}$

В записанной системе уравнений на текущий момент имеется пять независимых переменных (величины $\omega ,\omega ',\eta ,\eta '$ определяются через ${{g}_{2}}$ и ${{g}_{3}}$): ${{g}_{2}},{{g}_{3}},D,{{z}^{ + }},{{z}^{ - }}$ (первые два вещественны, а остальные – чисто мнимые) и 4 уравнения (3.8) (среди этих уравнений первое, третье и четвертое – чисто мнимые, а второе – вещественное). Поэтому для определения параметров естественно рассмотреть какое-нибудь однопараметрическое семейство кривых, среди которых заведомо найдется подходящая, т.е. рассмотреть функции ${{g}_{2}} = {{g}_{2}}(\gamma )$ и ${{g}_{3}} = {{g}_{3}}(\gamma )$ и использовать систему (3.8) для определения параметров $\gamma ,D,{{z}^{ + }},{{z}^{ - }}$.

В дальнейшем мы будем использовать семейство кривых, заданных корнями полинома F: ${{x}_{1}} = \gamma - 1{\text{/}}2$, ${{x}_{2}} = - 2\gamma $, ${{x}_{3}} = \gamma + 1{\text{/}}2$, $\gamma \in ( - 1{\text{/}}6,1{\text{/}}6)$ (более подробно изучать это семейство мы будем при анализе поведения решения при вырождении $\delta \to 0$). Это семейство соответствует нормировке ${{x}_{3}} - {{x}_{1}} = 1$ с учетом уже имеющегося тождества ${{x}_{1}} + {{x}_{2}} + {{x}_{3}} = 0$.

3.2. О численной реализации

Для численной реализации было принято решение использовать явное вычисление сигма-функции Вейерштрасса через ее параметры ${{g}_{2}},{{g}_{3}}$ при помощи ее ряда Тейлора (см. [11] или ниже теорему П.1). Ясно, что для эффективного решения системы (3.8) требуется вычислять все входящие в нее величины и их производные по параметрам. В конечном счете все сводится к вычислению величин $\omega ,\omega '$ и их производных по ${{g}_{2}},{{g}_{3}}$, а также функции $\zeta $ и ее производных по $z,{{g}_{2}},{{g}_{3}}$. Поскольку

$\zeta = \frac{1}{\sigma }\frac{{\partial \sigma }}{{\partial z}},$
задача о вычислении $\zeta $-функции и ее производных решается тривиально. Чтобы вычислить $\omega $, надо заметить, что $\sigma $-функция обращается в ноль только в точках решетки $\{ 2m\omega + 2n\omega '\,:n,m \in \mathbb{Z}\} $, причем все эти нули просты. Эффективный способ локализовать простой нуль ${{z}_{0}}$ голоморфной функции  f – найти интеграл от функции $zf'(z){\text{/}}2\pi if(z)$ по контуру, охватывающему точку ${{z}_{0}}$. Чтобы найти подходящий контур, можно применить аналог бинарного поиска, пользуясь тем, что $\omega \geqslant \pi {\text{/}}2$. Используя сформулированный метод либо напрямую, либо для приближенного вычисления нуля и последующего применения методов решения уравнений, легко построить эффективный и точный алгоритм вычисления $\omega $ (и $\omega '$). Для вычисления их производных можно продифференцировать интеграл от $z\sigma '(z){\text{/}}\sigma (z)$ по ${{g}_{2}}$ или ${{g}_{3}}$, а затем вычислить его явно, найдя вычет полученной функции в нуле функции $\sigma $. Таким образом, решение системы уравнений (3.8) можно полностью свести к вычислению сигма-функции Вейерштрасса и ее производных по z, ${{g}_{2}}$ и ${{g}_{3}}$.

Фиг. 4.

Конформное отображение Q.

Продемонстрируем решение конкретной задачи при помощи данного метода. Положим, ${{h}^{ + }} = \pi $, ${{h}^{ - }} = \pi + 0.5$, $h = 0.5$, $\delta = 0.2$. В качестве однопараметрического семейства кривых, среди которых мы будем искать решение, положим: ${{x}_{1}} = \gamma - 1{\text{/}}2$, ${{x}_{2}} = - 2\gamma $, ${{x}_{3}} = \gamma + 1{\text{/}}2$, $\gamma \in ( - 1{\text{/}}6,1{\text{/}}6)$. Решение системы (3.8) дает вектор

$(\gamma ,D,{{z}^{ + }},{{z}^{ - }}) = (0.1051616134,0.0203152915i,1.3043479103i,0.7195735824i).$

При данном $\gamma $ имеем $\omega = 1.6518996331$, $\omega '\, = 2.2939120295i$. На фиг. 4 далее демонстрируется образ прямоугольника P с вершинами $0,\omega ',\omega '\, - \omega , - \omega $ при отображении Q.

4. УСТОЙЧИВОСТЬ РЕШЕНИЯ ПРИ ВЫРОЖДЕНИИ ОБЛАСТИ

Здесь мы рассмотрим задачу о конформном отображении верхней полуплоскости на область $\widetilde \Omega $, которая из Ω получается вырождением $\delta \to 0$ (см. фиг. 5) и проанализируем поведение решения при этом вырождении, считая, что никаких других вырождений не происходит (т.е. считая, что величины ${{h}^{ - }},{{h}^{ + }},h,{{h}^{ - }} + h - {{h}^{ + }},{{h}^{ + }} - h$ имеют конечные положительные пределы). Область $\widetilde \Omega $ задается теперь тремя параметрами $h,{{h}^{ + }}$ и ${{h}^{ - }}$. Конформное отображение верхней полуплоскости на область $\widetilde \Omega $ можно искать способом, аналогичным уже разобранному (через теорему Кристоффеля–Шварца). В этом случае, поскольку соответствующая поверхность будет иметь род $0$, решение выразится в элементарных функциях. Другой же способ (рассматриваемый здесь) состоит в том, чтобы формулу (3.7) приспособить для данного случая, пользуясь тем, что $\sigma $-функция определена в том числе при тех значениях ${{g}_{2}}$ и ${{g}_{3}}$, при которых полином $F(x) = 4{{x}^{3}} - {{g}_{2}}x - {{g}_{3}}$ имеет кратные корни. Естественно предположить, что искомое отображение получается предельным переходом, при котором пара корней полинома, переходящих в ${{w}_{2}}$ и ${{w}_{3}}$, склеивается в одну точку. Вместе с этим также будет установлена устойчивость построенного решения при $\delta \to 0$.

Фиг. 5.

Область $\widetilde \Omega $.

4.1. Склеивание пары корней полинома

Снова рассмотрим семейство кривых, зависящих от параметра $\gamma \in ( - 1{\text{/}}6,1{\text{/6}})$ следующим образом: ${{F}_{\gamma }}(x) = 4(x - {{x}_{1}}(\gamma ))(x - {{x}_{2}}(\gamma ))(x - {{x}_{3}}(\gamma ))$, где ${{x}_{1}}(\gamma ) = \gamma - 1{\text{/}}2$, ${{x}_{2}}(\gamma ) = - 2\gamma $, ${{x}_{3}}(\gamma ) = \gamma + 1{\text{/}}2$. При $\gamma \to - 1{\text{/}}6$ будем иметь склейку корней ${{x}_{2}}$ и ${{x}_{3}}$. Предельные значения ${{g}_{2}}$ и ${{g}_{3}}$ равны соответственно 4/3 и –8/27. Для каждого $\gamma $ можно определить $\omega (\gamma )$, $\omega {\kern 1pt} '(\gamma )$, $\eta (\gamma )$, $\eta {\kern 1pt} '(\gamma )$. В дальнейшем мы будем опускать зависимость величин от параметра $\gamma $.

Лемма 4.1. При $\gamma \to - 1{\text{/}}6$ имеем

(4.1)
$\omega ,\eta \to \infty ,\quad \omega {\kern 1pt} ' \to \frac{{i\pi }}{2},\quad \eta {\kern 1pt} ' \to - \frac{{i\pi }}{6},\quad \frac{\eta }{\omega } \to - \frac{1}{3}.$

Кроме того,

(4.2)
$\sigma \left( {z,\frac{4}{3}, - \frac{8}{{27}}} \right) = {{e}^{{ - \frac{{{{z}^{2}}}}{6}}}}\sinh (z),\quad \zeta \left( {z,\frac{4}{3}, - \frac{8}{{27}}} \right) = \coth (z) - \frac{z}{3},\quad \wp \left( {z,\frac{4}{3}, - \frac{8}{{27}}} \right) = \frac{1}{{{{{\sinh }}^{2}}(z)}} + \frac{1}{3}.$

Наконец, существует такой $\varepsilon > 0$, что при $\gamma + 1{\text{/}}6 < \varepsilon $ имеет место оценка

(4.3)
$ - {{c}_{1}}\ln (\gamma + 1{\text{/}}6) \leqslant \omega (\gamma ) \leqslant - {{c}_{2}}\ln (\gamma + 1{\text{/}}6),$
где $0 < {{c}_{1}} < {{c}_{2}}$.

Доказательство. Предельные переходы (4.1) легко получаются из интегральных формул:

$\omega (\gamma ) = \frac{1}{2}\int\limits_{\gamma - \frac{1}{2}}^{ - 2\gamma } {\frac{{dx}}{{\sqrt {(x - \gamma - 1{\text{/}}2)(x - \gamma + 1{\text{/}}2)(x + 2\gamma )} }},} $
$\omega '(\gamma ) = \frac{1}{2}\int\limits_{ - 2\gamma }^{\gamma + \frac{1}{2}} {\frac{{dx}}{{\sqrt { - (x - \gamma - 1{\text{/}}2)(x - \gamma + 1{\text{/}}2)(x + 2\gamma )} }},} $
$\eta (\gamma ) = - \frac{1}{2}\int\limits_{\gamma - \frac{1}{2}}^{ - 2\gamma } {\frac{{xdx}}{{\sqrt {(x - \gamma - 1{\text{/}}2)(x - \gamma + 1{\text{/}}2)(x + 2\gamma )} }},} $
$\eta '(\gamma ) = - \frac{1}{2}\int\limits_{ - 2\gamma }^{\gamma + \frac{1}{2}} {\frac{{xdx}}{{\sqrt { - (x - \gamma - 1{\text{/}}2)(x - \gamma + 1{\text{/}}2)(x + 2\gamma )} }}.} $

Для вывода формул (4.2) можно рассмотреть предельный переход при $\gamma \to - 1{\text{/}}6$, воспользовавшись формулой, представляющей $\sigma $ в виде бесконечного произведения (см. [3]). Имеем

$\sigma \left( {z,\frac{4}{3}, - \frac{8}{{27}}} \right) = z\prod\limits_{n \ne 0} \left( {1 - \frac{z}{{in\pi }}} \right){{e}^{{\frac{z}{{in\pi }} - \frac{{{{z}^{2}}}}{{2{{n}^{2}}{{\pi }^{2}}}}}}}.$

Пользуясь классическими тождествами

$\sum\limits_{n = 1}^\infty \frac{1}{{{{n}^{2}}}} = \frac{{{{\pi }^{2}}}}{6},\quad \prod\limits_{n = 1}^\infty \left( {1 - \frac{{{{x}^{2}}}}{{{{n}^{2}}{{\pi }^{2}}}}} \right) = \frac{{\sin (x)}}{x},$
получаем первое тождество из (4.2). Остальные элементарно получаются из равенств $\zeta (z) = \sigma {\kern 1pt} '(z){\text{/}}\sigma (z)$, $\wp (z) = - \zeta '(z)$.

Теперь оценим рост $\omega (\gamma )$. Для этого запишем равенство

$\omega (\gamma ) = \frac{1}{2}\int\limits_0^{1/2 - 3\gamma } {\frac{{dt}}{{\sqrt {t(1 - t)(1{\text{/}}2 - 3\gamma - t)} }}.} $

Заметим, что при малых $\gamma $, интеграл по отрезку $[0,1{\text{/}}2]$ имеет ограниченное поведение, а потому

$\omega (\gamma ) \sim \frac{1}{2}\int\limits_{1/2}^{1/2 - 3\gamma } {\frac{{dt}}{{\sqrt {t(1 - t)(1{\text{/}}2 - 3\gamma - t)} }}.} $

Оценка интеграла в правой части далее не составляет труда, поскольку множитель $1{\text{/}}\sqrt t $ ограничен снизу и сверху положительными константами, а после его исключения остается вычисляемый интеграл. Лемма доказана.

Из того, что $\omega ' \to i\pi {\text{/}}2$, а $\omega \to \infty $, естественно предположить, что формула (3.7) может давать конформное отображение полуполосы

$S = \{ z \in \mathbb{C}:{\text{Re}}z < 0,{\text{Im}}z \in (0,\pi {\text{/}}2)\} $
на область $\widetilde \Omega $. Положим
(4.4)
$\widetilde Q(z) = Dz + \frac{{{{h}^{ - }}}}{\pi }\ln \left( {\frac{{\sigma (z - {{z}^{ - }})}}{{\sigma (z + {{z}^{ - }})}}} \right) - \frac{{{{h}^{ + }}}}{\pi }\ln \left( {\frac{{\sigma (z - {{z}^{ + }})}}{{\sigma (z + {{z}^{ + }})}}} \right) - i({{h}^{ - }} - {{h}^{ + }}),$
где σ взята при ${{g}_{2}} = 4{\text{/}}3$, ${{g}_{3}} = - 8{\text{/}}27$, а $D \in \mathbb{C}$, ${{z}^{ - }},{{z}^{ + }} \in (0,i\pi {\text{/}}2)$ – параметры. Подставляя выражение (4.2) для $\sigma $ в (4.4), получаем, что

(4.5)
$\widetilde Q(z) = z\left( {D + \frac{{2{{h}^{ - }}{{z}^{ - }}}}{{3\pi }} - \frac{{2{{h}^{ + }}{{z}^{ + }}}}{{3\pi }}} \right) + \frac{{{{h}^{ - }}}}{\pi }\ln \frac{{\sinh (z - {{z}^{ - }})}}{{\sinh (z + {{z}^{ - }})}} - \frac{{{{h}^{ + }}}}{\pi }\ln \frac{{\sinh (z - {{z}^{ + }})}}{{\sinh (z + {{z}^{ + }})}} - i({{h}^{ - }} - {{h}^{ + }}).$

Легко проверяется, что при наличии у $\widetilde Q$ ненулевого линейного слагаемого, эта функция не имеет предела при ${\text{Re}}z \to - \infty $. Если же

$D + \frac{{2{{h}^{ - }}{{z}^{ - }}}}{{3\pi }} - \frac{{2{{h}^{ + }}{{z}^{ + }}}}{{3\pi }} = 0,$
то она имеет предел, равный $2({{h}^{ - }}{{z}^{ - }} - {{h}^{ + }}{{z}^{ + }}){\text{/}}\pi - i({{h}^{ - }} - {{h}^{ + }})$. Таким образом, для того, чтобы $\widetilde Q$ конформно отображала S на $\widetilde \Omega $, необходимо выполнение условий

(4.6)
$\begin{array}{*{20}{c}} {D + \frac{{2{{h}^{ - }}{{z}^{ - }}}}{{3\pi }} - \frac{{2{{h}^{ + }}{{z}^{ + }}}}{{3\pi }} = 0,} \\ {{{h}^{ - }}{{z}^{ - }} - {{h}^{ + }}{{z}^{ + }} = - \frac{{ih\pi }}{2}.} \end{array}$

Очевидно, что условий (4.6) достаточно для этого при дополнительном предположении о том, что производная функции $\widetilde Q$ не обращается в ноль на множестве S и на его границе. Достаточно громоздкими (но элементарными) выкладками проверяется, что при выполнении (4.6) для этого необходимо и достаточно выполнение равенства

(4.7)
${{h}^{ - }}\sinh (2{{z}^{ - }}) = {{h}^{ + }}\sinh (2{{z}^{ + }}).$

Уравнения (4.6) и (4.7), таким образом, определяют параметры $D,{{z}^{ - }},{{z}^{ + }}$, при которых $\widetilde Q$ осуществляет искомое конформное отображение.

Покажем, что построенная формула редуцируется к интегралу Кристоффеля–Шварца в верхней полуплоскости после замены переменной $x = \wp (z) = 1{\text{/}}{{\sinh }^{2}}(z) + 1{\text{/}}3$. Переходя в формуле (4.4) к новой переменной и учитывая, что линейное слагаемое равно нулю, получаем для конформного отображения ${{\mathbb{C}}_{ + }}$ на $\widetilde \Omega $ выражение

(4.8)
$\widetilde W(x) = \frac{{{{h}^{ - }}}}{\pi }\ln \left( {\frac{{\sqrt {{{x}^{ - }} + 2/3} - \sqrt {x + 2/3} }}{{\sqrt {{{x}^{ - }} + 2/3} + \sqrt {x + 2/3} }}} \right) + \frac{{{{h}^{ + }}}}{\pi }\ln \left( {\frac{{\sqrt {{{x}^{ + }} + 2/3} - \sqrt {x + 2/3} }}{{\sqrt {{{x}^{ + }} + 2/3} + \sqrt {x + 2/3} }}} \right).$

Полученные ранее уравнения на параметры ${{z}^{ - }}$ и z+ переписываются в виде

(4.9)
$\begin{array}{*{20}{c}} {\frac{{{{h}^{ - }}\sqrt {{{x}^{ - }} + 1} }}{{{{x}^{ - }}}} = \frac{{{{h}^{ + }}\sqrt {{{x}^{ + }} + 1} }}{{{{x}^{ + }}}},} \\ {{{h}^{ - }}\ln \left( {\frac{{1 + \sqrt {{{x}^{ - }} + 4{\text{/}}3} }}{{\sqrt {{{x}^{ - }} + 1{\text{/}}3} }}} \right) + {{h}^{ + }}\ln \left( {\frac{{1 + \sqrt {{{x}^{ + }} + 4{\text{/}}3} }}{{\sqrt {{{x}^{ + }} + 1{\text{/}}3} }}} \right) = - \frac{{ih\pi }}{2}.} \end{array}$

Дифференцируя $\widetilde W$ и используя первое из уравнений (4.9), приходим к равенству

$d\widetilde W = \frac{{{{h}^{ - }}\sqrt {{{x}^{ - }} + 1} - {{h}^{ + }}\sqrt {{{x}^{ + }} + 1} }}{\pi }\frac{{(x - 1{\text{/}}3)}}{{\sqrt {x + 2{\text{/}}3} (x - {{x}^{ - }})(x - {{x}^{ + }})}}.$

Таким образом, получен явный вид константы в интеграле Кристоффеля–Шварца. Неизвестными остаются параметры ${{x}^{ - }}$ и ${{x}^{ + }}$, которые можно определить из системы (4.9).

4.2. Предельный переход

Рассмотрим последовательность областей, заданных параметрами $(h_{n}^{ - },h_{n}^{ + },{{h}_{n}},{{\delta }_{n}})$. Предположим, что эти параметры имеют предел $(h_{{\lim }}^{ - },h_{{\lim }}^{ + },{{h}_{{\lim }}},0)$. При этом также будем считать, что $h_{{\lim }}^{ + } - {{h}_{{\lim }}} > 0$ и $h_{{\lim }}^{ - } - h_{{\lim }}^{ + } + {{h}_{{\lim }}} > 0$. Мы докажем, что параметры $({{D}_{n}},{{\gamma }_{n}},z_{n}^{ - },z_{n}^{ + })$, полученные решением системы (8) для соответствующих параметров области, имеют предел $({{D}_{{\lim }}}, - 1{\text{/}}6,z_{{\lim }}^{ - },z_{{\lim }}^{ + })$, причем параметры $({{D}_{{\lim }}},z_{{\lim }}^{ - },z_{{\lim }}^{ + })$ удовлетворяют уравнениям (4.6) и (4.7). Таким образом, с учетом того, что сигма-функция Вейерштрасса является целой, получаем, что построенное решение задачи о конформном отображении устойчиво.

Последующее доказательство достаточно длинное и техническое, а потому мы позволим себе опускать большую часть выкладок.

Нам для оценок также потребуются параметры $x_{n}^{ - },x_{n}^{ + },x_{1}^{{(n)}},x_{2}^{{(n)}},x_{3}^{{(n)}},{{C}_{n}}$ отображения Wn.

Лемма 4.2. Предположим, что ${{\gamma }_{n}} \to - 1{\text{/}}6$, причем ${{\delta }_{n}}\omega ({{\gamma }_{n}}) \to 0$. Тогда описанный выше предельный переход имеет место.

Доказательство. Заметим, что из того, что ${{\gamma }_{n}} \to - 1{\text{/}}6$ следует, что последовательности $z_{n}^{ - }$ и $z_{n}^{ + }$ ограничены. Из первого уравнения системы (3.8) следует, что последовательность Dn тоже ограничена. Переходя к подпоследовательностям, можно считать, что данные последовательности сходятся (если удастся доказать, что пределы удовлетворяют уравнениям (4.6) и (4.7), то в силу единственности получим, что все подпоследовательности сходятся к одному и тому же пределу, что влечет сходимость исходной последовательности). Первое уравнение из системы (4.6) получается предельным переходом из второго уравнения системы (3.8) с учетом результатов леммы 4.1. Умножая первое уравнение из системы (3.8) на $\omega {\kern 1pt} '$, а второе на $\omega $, вычитая и переходя к пределу, получаем второе уравнение из (4.6) (слагаемое $\delta \omega $ по условию стремится к нулю).

Теперь выведем уравнение (4.7) для предела подпоследовательности. Напомним некоторые обозначения теории эллиптических функций (см. [3]):

${{\zeta }_{2}}(z) = \zeta (z + \omega ) - \eta ,$
${{\zeta }_{3}}(z) = \zeta (z + \omega + \omega {\kern 1pt} ') + \eta + \eta {\kern 1pt} '.$

Эти функции связаны с функциями ${{\sigma }_{2}},{{\sigma }_{3}}$:

${{\zeta }_{k}} = \frac{1}{{{{\sigma }_{k}}}}\frac{{d{{\sigma }_{k}}}}{{dz}} = \frac{{d\ln {{\sigma }_{k}}}}{{dz}}.$

Наконец, ${{\sigma }_{k}} = \sigma \sqrt {\wp - {{x}_{k}}} $. Последние два уравнения системы (3.8) можно записать в виде

(4.10)
$D + \frac{{{{h}^{ - }}}}{\pi }({{\zeta }_{k}}( - {{z}^{ - }}) - \zeta ({{z}^{ - }})) - \frac{{{{h}^{ + }}}}{\pi }({{\zeta }_{k}}( - {{z}^{ + }}) - \zeta ({{z}^{ + }})) = 0,\;\;k = 2,3.$

Запишем

${{\zeta }_{2}}(z) - {{\zeta }_{3}}(z) = \frac{{\sigma {\kern 1pt} '(z)\sqrt {\wp - {{x}_{2}}} + \wp {\kern 1pt} '(z)\sigma (z)(\wp - {{x}_{2}}{{)}^{{ - 1/2}}}}}{{\sigma (z)\sqrt {\wp - {{x}_{2}}} }} - \frac{{\sigma {\kern 1pt} '(z)\sqrt {\wp - {{x}_{3}}} + \wp {\kern 1pt} '(z)\sigma (z)(\wp - {{x}_{3}}{{)}^{{ - 1/2}}}}}{{\sigma (z)\sqrt {\wp - {{x}_{3}}} }},$
откуда следует

(4.11)
${{\zeta }_{2}}(z) - {{\zeta }_{3}}(z) = \frac{{\wp {\kern 1pt} '(z)({{x}_{2}} - {{x}_{3}})}}{{(\wp - {{x}_{2}})(\wp - {{x}_{3}})}}.$

Уравнение (4.7) выводится предельным переходом (при помощи леммы 4.1) из уравнений (4.10) (из которых надо исключить константу D) и подстановкой вместо ${{\zeta }_{2}} - {{\zeta }_{3}}$ формулы (4.11) Лемма доказана.

Лемма 4.3. Имеют место неравенства ${\text{|}}{{C}_{n}}{\text{|}} \geqslant {{a}_{1}}$, ${\text{|}}{{C}_{n}}{\text{|}} \leqslant {{a}_{2}}\sqrt {x_{3}^{{(n)}} - x_{n}^{ - }} $ для некоторых положительных констант a1, a2. Кроме того, последовательность $x_{n}^{ + }$ ограничена снизу.

Доказательство. Оценки на C(n) достаточно элементарно получаются из равенства

${\text{|}}{{C}_{n}}{\text{|}}\int\limits_{x_{3}^{{(n)}}}^{ + \infty } {\frac{{\sqrt {(x - x_{2}^{{(n)}})(x - x_{3}^{{(n)}})} dx}}{{\sqrt {x - x_{1}^{{(n)}}} (x - x_{n}^{ - })(x - x_{n}^{ + })}} = h_{n}^{ - } - h_{n}^{ + } + {{h}_{n}}} .$

Чтобы доказать ограниченность последовательности $x_{n}^{ + }$ снизу, надо рассмотреть равенство

${\text{|}}{{C}_{n}}{\text{|}}\int\limits_{x_{1}^{{(n)}}}^{x_{2}^{{(n)}}} {\frac{{\sqrt {(x_{2}^{{(n)}} - x)(x_{3}^{{(n)}} - x)} dx}}{{\sqrt {x - x_{1}^{{(n)}}} (x - x_{n}^{ - })(x - x_{n}^{ + })}}} = {{h}_{n}}.$

Лемма 4.4. Предположим, что последовательность $x_{n}^{ - }$ ограничена снизу. Тогда найдутся такие постоянные $0 < {{b}_{1}} < {{b}_{2}}$, что ${{b}_{1}}\sqrt {{{\delta }_{n}}} \leqslant {\text{|}}x_{2}^{{(n)}} - x_{3}^{{(n)}}{\text{|}} \leqslant {{b}_{2}}\sqrt {{{\delta }_{n}}} $.

Доказательство. Это следует из элементарных оценок на интеграл в равенстве

${\text{|}}{{C}_{n}}{\text{|}}\int\limits_{x_{2}^{{(n)}}}^{x_{3}^{{(n)}}} {\frac{{\sqrt {(x - x_{2}^{{(n)}})(x_{3}^{{(n)}} - x)} dx}}{{\sqrt {x - x_{1}^{{(n)}}} (x - x_{n}^{ - })(x - x_{n}^{ + })}} = {{\delta }_{n}}.} $

Из доказанных лемм следует, что достаточно доказать ограниченность последовательности $x_{n}^{ - }$ снизу (необходимо также принять во внимание асимптотику (4.3)). Предположим, что это не так. Переходя к подпоследовательности, можем считать, что $x_{n}^{ - } \to - \infty $ и что последовательности $x_{1}^{{(n)}},x_{2}^{{(n)}},x_{3}^{{(n)}}$, $x_{n}^{ + }$ сходятся.

Лемма 4.5. В сделанных выше предположениях имеем $x_{3}^{{(n)}} - x_{2}^{{(n)}} \to 0$, $x_{1}^{{(n)}} - x_{n}^{ + } \to 0$.

Доказательство. Из равенства

${\text{|}}{{C}_{n}}{\text{|}}\frac{{\sqrt {(x_{2}^{{(n)}} - x_{n}^{ + })(x_{3}^{{(n)}} - x_{n}^{ + })} }}{{\sqrt {x_{1}^{{(n)}} - x_{n}^{ + }} (x_{n}^{ + } - x_{n}^{ - })}} = \frac{{h_{n}^{ + }}}{\pi }$
легко выводится сходимость $x_{1}^{{(n)}} - x_{n}^{ + } \to 0$.

Для доказательства сходимости $x_{3}^{{(n)}} - x_{2}^{{(n)}} \to 0$ перейдем к параметрам $({{D}_{n}},{{\gamma }_{n}},z_{n}^{ - },z_{n}^{ + })$. Предположим, что $x_{2}^{{(n)}} - x_{1}^{{(n)}} \to 0$. Тогда $\omega {\kern 1pt} '({{\gamma }_{n}}),\eta {\kern 1pt} '({{\gamma }_{n}}) \to \infty $, а $\omega $ и $\eta $ имеют конечные пределы. Кроме того, из тождества Лежандра (см. [3] или [4]) следует, что

$\mathop {\lim }\limits_{n \to \infty } \frac{{\omega {\kern 1pt} '({{\gamma }_{n}})}}{{\eta {\kern 1pt} '({{\gamma }_{n}})}} = \mathop {\lim }\limits_{n \to \infty } \frac{{\omega ({{\gamma }_{n}})}}{{\eta ({{\gamma }_{n}})}}.$

Записывая первую пару уравнений из (3.8), получаем

$\mathop {\lim }\limits_{n \to \infty } \left( {\frac{{2h_{n}^{ + }}}{\pi }z_{n}^{ + }\left( {\frac{{\omega {\kern 1pt} '}}{{\eta {\kern 1pt} '}} - \frac{\omega }{\eta }} \right) - i\frac{{{{h}_{n}}}}{\omega }} \right) = 0.$

Отсюда получаем, что

$\mathop {\lim }\limits_{n \to \infty } \left( {\frac{{h_{n}^{ + }z_{n}^{ + }}}{{\omega {\kern 1pt} '}} - {{h}_{n}}} \right) = 0,$
а значит, в пределе ${{h}_{{\lim }}} \geqslant h_{{\lim }}^{ + }$. Это противоречит исходным предположениям.

Теперь предположим, что $x_{2}^{{(n)}} - x_{1}^{{(n)}} \nrightarrow 0$ и $x_{3}^{{(n)}} - x_{2}^{{(n)}} \nrightarrow 0$. Тогда оба периода $\omega $ и $\omega {\kern 1pt} '$ имеют конечные пределы. При этом $z_{n}^{ - } \to 0$, $z_{n}^{ + } \to \omega {\kern 1pt} '({{\gamma }_{{\lim }}})$. Очевидно, что последовательность Dn также имеет предел и, записывая в пределе второе уравнение из (3.8), имеем

$ - {{D}_{{\lim }}}\omega {\kern 1pt} '\, - \frac{{2h_{{\lim }}^{ + }\omega {\kern 1pt} '\eta {\kern 1pt} '}}{\pi } = 0.$

Подставляя в первое уравнение, получаем

$\frac{{2h_{{\lim }}^{ + }}}{\pi }\omega \eta {\kern 1pt} '\, - \frac{{2h_{{\lim }}^{ + }}}{\pi }\omega {\kern 1pt} '\eta = - i{{h}_{{\lim }}},$
что дает равенство $h_{{\lim }}^{ + } = {{h}_{{\lim }}}$. Лемма доказана.

Теперь у нас достаточно информации, чтобы вывести противоречие из того, что $x_{n}^{ - } \to - \infty $. Для этого мы будем отслеживать асимптотики некоторых последовательностей (далее эквивалентность последовательностей используется для обозначения того, что их отношение стремится к 1).

Из равенства

${\text{|}}{{C}_{n}}{\text{|}}\frac{{\sqrt {(x_{2}^{{(n)}} - x_{n}^{ - })(x_{3}^{{(n)}} - x_{n}^{ - })} }}{{\sqrt {x_{1}^{{(n)}} - x_{n}^{ - }} (x_{n}^{ + } - x_{n}^{ - })}} = \frac{{h_{n}^{ - }}}{\pi }$
следует, что

(4.12)
${\text{|}}{{C}_{n}}{\text{|}}\,{{\sim }}\frac{{h_{n}^{ - }}}{\pi }\sqrt {{\text{|}}x_{n}^{ - }{\text{|}}} .$

С другой стороны, имеем

${\text{|}}{{C}_{n}}{\text{|}}\frac{{\sqrt {(x_{2}^{{(n)}} - x_{n}^{ + })(x_{3}^{{(n)}} - x_{n}^{ + })} }}{{\sqrt {x_{1}^{{(n)}} - x_{n}^{ + }} (x_{n}^{ + } - x_{n}^{ - })}} = \frac{{h_{n}^{ + }}}{\pi },$
откуда следует, что

(4.13)
$\sqrt {x_{1}^{{(n)}} - x_{n}^{ + }} \sim \frac{{h_{n}^{ - }}}{{h_{n}^{ + }}}\frac{1}{{\sqrt {{\text{|}}x_{n}^{ - }{\text{|}}} }}.$

Теперь обратимся к равенству

${\text{|}}{{C}_{n}}{\text{|}}\int\limits_{x_{1}^{{(n)}}}^{x_{2}^{{(n)}}} {\frac{{\sqrt {(x_{2}^{{(n)}} - x)(x_{3}^{{(n)}} - x)} dx}}{{\sqrt {x - x_{1}^{{(n)}}} (x - x_{n}^{ - })(x - x_{n}^{ + })}}} = {{h}_{n}}.$

Пользуясь (4.12), легко показать, что последовательность в левой части ведет себя эквивалентно последовательности

$\frac{{h_{n}^{ - }}}{{\pi \sqrt {{\text{|}}x_{n}^{ - }{\text{|}}} }}\int\limits_{x_{1}^{{(n)}}}^{x_{2}^{{(n)}}} {\frac{{\sqrt {(x_{2}^{{(n)}} - x)(x_{3}^{{(n)}} - x)} dx}}{{\sqrt {x - x_{1}^{{(n)}}} (x - x_{n}^{ + })}}.} $

Далее, при помощи замены переменной получаем

$\int\limits_{x_{1}^{{(n)}}}^{x_{2}^{{(n)}}} {\frac{{\sqrt {(x_{2}^{{(n)}} - x)(x_{3}^{{(n)}} - x)} dx}}{{\sqrt {x - x_{1}^{{(n)}}} (x - x_{n}^{ + })}}} = \int\limits_0^{x_{2}^{{(n)}} - x_{1}^{{(n)}}} {\frac{{\sqrt {(x_{2}^{{(n)}} - x_{1}^{{(n)}} - x)(1 - x)} dx}}{{\sqrt x (x + x_{1}^{{(n)}} - x_{n}^{ + })}}} .$

Оказывается, что асимптотика последнего интеграла не зависит от характера сходимости ${\text{|}}x_{2}^{{(n)}} - x_{1}^{{(n)}}{\text{|}} \to 1$. Именно, для любых последовательностей ${{\alpha }_{n}} \to 1$ и ${{a}_{n}} \to 0$ имеет место эквивалентность

$\int\limits_0^{{{\alpha }_{n}}} {\frac{{\sqrt {({{\alpha }_{n}} - x)(1 - x)} dx}}{{\sqrt x (x + {{a}_{n}})}}} \sim \int\limits_0^1 {\frac{{(1 - x)dx}}{{\sqrt x (x + {{a}_{n}})}}} \sim \frac{\pi }{{\sqrt {{{a}_{n}}} }}.$

Наконец, с учетом (4.13), получаем

${{h}_{n}} = {\text{|}}{{C}_{n}}{\text{|}}\int\limits_{x_{1}^{{(n)}}}^{x_{2}^{{(n)}}} {\frac{{\sqrt {(x_{2}^{{(n)}} - x)(x_{3}^{{(n)}} - x)} dx}}{{\sqrt {x - x_{1}^{{(n)}}} (x - x_{n}^{ - })(x - x_{n}^{ + })}}} \sim \frac{{h_{n}^{ - }}}{{\pi \sqrt {{\text{|}}x_{n}^{ - }{\text{|}}} }}\frac{\pi }{{\sqrt {x_{1}^{{(n)}} - x_{n}^{ + }} }} \sim h_{n}^{ + }.$

Получилось противоречие с тем, что ${{h}_{{\lim }}} < h_{{\lim }}^{ + }$.

5. ЗАКЛЮЧЕНИЕ

Для конформного отображения многоугольной области Ω получено простое выражение через сигма-функцию Вейерштрасса. Для конкретного примера вычислены параметры отображения и проведены численные расчеты. Исследовано поведение при вырождении области и показано, что построенная формула устойчива и имеет предел, осуществляющий решение предельной задачи.

Дальнейшее направление исследований может быть связано как с построением и анализом решений для аналогичных задач, например, связанных с поверхностями рода 2, так и с развитием теории сигма-функций: построением рекуррентных формул для произвольного рода и развитием методов вычисления, не основанных на теории тэта-функций.

Автор выражает благодарность А. Богатыреву и О. Григорьеву за постановку задачи и полезные обсуждения, а также К. Малкову за помощь в компьютерной реализации вычислений. Также автор благодарит центр дополнительного профессионального образования “Университет Сириус” за приглашение на образовательный модуль “Вычислительные технологии, многомерный анализ данных и моделирование” в 2021 г., в ходе которого были получены некоторые из результатов данной статьи.

Список литературы

  1. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. М.: Наука, 1987.

  2. Driscoll T.A., Trefethen L.N. Schwartz-Cristoffel mapping. Cambridge: Cambridge University Press, 2002.

  3. Ахиехзер Н.И. Элементы теории эллиптических функций. М.: Наука, 1970.

  4. Chandrasekharan K. Elliptic functions. Berlin: Springer-Verlag, 1985.

  5. Bogatyrev A.B., Hassner M., Yarmolich D. An exact analytical-expression for the read sensor signal in magnetic data storage channels // Contemp. Math. 2010. V. 523. P. 155–160.

  6. Bogatyrev A.B. The conformal mapping of rectangular heptagons // Mat. Sb. 2012. V. 203. N. 12. P. 35–56.

  7. Bogatyrev A.B., Grigor’ev O.A. Conformal mapping of rectangular heptagons // Comput. Methods Funct. Theory. 2018. V. 18. N. 2. P. 221–238.

  8. Богатырев А.Б., Григорьев О.А. Фильтрация под ступенчатой плотиной и римановы тета-функции // Труды матем. института им. В.А. Стеклова. 2020. V. 311. P. 14–26.

  9. Bezrodnykh S.I., Bogatyrev A.B., Goreinov S.A., Grigor’ev O.A., Hakula H., Vuorinen M. On capacity computation for symmetric polygonal condensers // J. Comput. Appl. Math. 2019. V. 361. P. 271–282.

  10. Farkas H.M., Kra I. Riemann surfaces. New-York: Springer-Verlag, 1992.

  11. Weierstrass K. Zur Theorie der elliptischen Funktionen // Sitzungsberichte der Akademie der Wissenshaften zu Berlin. 1882. V. 1. P. 443–451.

  12. Klein F. Uber hyperelliptische Sigmafunktionen // Math. Ann. 1886. V. 27. P. 431–464.

  13. Baker H.F. On the hyperelliptic sigma-functions // Amer. J. Math. 1898. V. 20. P. 301–384.

  14. Buchstaber V.M., Leykin D.V., Enolskii V.Z. Kleinian functions, hyperelliptic Jacobians and applications // Reviews in Mathematics and Math. Physics. 1997. V. 10. N. 2. P. 3–120.

  15. Картан А. Элементарная теория функций одного и нескольких комплексных переменных. М.: Изд-во иностр. лит., 1963.

  16. Форстер О. Римановы поверхности. М.: Мир, 1980.

  17. Halphen G.H. Traite des fonctions elliptiques et de leurs applications. T. 1. Paris: Gauthier-Villars, 1886.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал