Журнал вычислительной математики и математической физики, 2022, T. 62, № 6, стр. 1030-1041

1. ВВЕДЕНИЕ

В настоящей работе изучаются композиции независимых случайных аффинных преобразований аргумента функций на конечномерном линейном пространстве, представляющие собой некоммутативный аналог случайных блужданий. Такие модели естественно возникают в задачах квантовой механики для систем, находящихся в случайных нестационарных полях. Усредненная динамика квантовых систем имеет как теоретический, так и практический интерес с точки зрения анализа средних значений наблюдаемых. В частности, важно представлять, в какой мере усреднение решений некоторого эволюционного уравнения с нестационарными параметрами связано с решением уравнения, усредненного по этим параметрам. Использование для этой цели процедуры усреднения с помощью построения эквивалентных по Чернову полугрупп является весьма эффективным методом, который был развит в [1]–[3].

В [4] были рассмотрены случайные сдвиги в пространстве бозонных когерентных состояний и показано, что их усреднение с помощью теоремы Чернова также является когерентным состоянием, которое генерируется усредненным оператором сдвига. Физическая интерпретация этого результата состояла в том, что эволюция квантового осциллятора или цепочки осцилляторов с переменной частотой может рассматриваться как результат последовательно применяемых операторов сдвига, среднее значение которых и генерирует наблюдаемое в данный момент состояние. Тем самым метод построения средней полугруппы на основе теоремы Чернова (см. [5]) может служить основой для разработки приближенной итерационной вычислительной процедуры, сходящейся к решению рассматриваемой эволюционной задачи. Когерентные, а также сжатые состояния в последнее время активно применяются не только в моделях квантовой оптики, но и в моделях высокотемпературной сверхпроводимости (см. [6]) и в задаче о поляроне в биологических структурах (см. [7], [8]). Отметим, что основной моделью в указанных работах (см. [6]–[8]) является гамильтониан Фрёлиха (см. [9]) в сверхпроводимости, описывающий взаимодействие операторов рождения-уничтожения электронов с фотонами, спектр которого точно исследовать пока не удается. Решение этой задачи представляется в виде действия произведения операторов Гейзенберга и операторов сдвига на вакуумное состояние гамильтониана. Поэтому анализ таких операторных конструкций с точки зрения применения теоремы Чернова является теоретически важным, а получаемые на его основе приближенные методы, сходящиеся к точному решению, такие как усреднение по Фейнману–Чернову, могут быть практически востребованными.

В [10] авторы рассмотрели обобщенные когерентные состояния, которые генерируются неклассическими коммутационными соотношениями. Такие соотношения возникают при анализе моделей комбинационного рассеяния в квантовой оптике при диагонализации полиномиальных гамильтонианов с полным набором законов сохранения (см. [11]). Тем самым анализ композиций преобразований, моделирующих эволюцию состояний квантовых систем, является актуальной задачей. В настоящей работе мы представим некоторые новые результаты об усреднении случайных аффинных преобразований и приведем примеры вычислительных экспериментов в качестве иллюстрации приложения развиваемого метода.

Влияние нестационарных случайных воздействий на эволюцию квантовых и классических систем изучалось в ряде работ (см., например, [1], [2], [12]–[14]). Представляет интерес описание характеристик предельного поведения случайных композиций, указанных выше, при стремлении к бесконечности числа итераций. Предельные теоремы, описывающие асимптотику распределения произведения большого числа независимых случайных матриц, изучались в [15]–[19].

В [2], [3], [12], [20] получены предельные теоремы типа закона больших чисел и центральной предельной теоремы, описывающие сходимость случайных композиций по вероятности и по распределению. В [12] получены теоремы типа закона больших чисел, утверждающие сходимость по распределению последовательности произведений случайных матриц к детерминированной предельной матрице. В статье [12] установлены предельные теоремы, описывающие предельные распределения композиций большого числа независимых случайных линейных преобразований конечномерного евклидова пространства.

Подчеркнем, что, в отличие от [12], в [2] была доказана сходимость по вероятности последовательности случайных композиций к предельной полугруппе, что позволяет дать оценку вероятности отклонения в форме неравенства Чебышёва. Отметим, что результаты работ [2], [3], [20] представляют предельные теоремы, описывающие предельные распределения композиций большого числа независимых случайных преобразований бесконечномерных банаховых пространств.

В настоящей работе мы распространяем полученные в [12] результаты на случай аффинных преобразований, а также исследуем уравнение Фоккера–Планка, порождаемое случайными аффинными преобразованиями евклидова пространства. Полученные здесь результаты развивают идеи работ [13], [21], в которых изучались случайные ортогональные преобразования пространства $E$ на случайные аффинные преобразования. Установлены условия на итерации независимых случайных групп аффинных преобразований, достаточные для сходимости к группе, разрешающей задачу Коши для эволюционного уравнения сдвига вдоль усредненного векторного поля. Установлены условия, достаточные для сходимости последовательности композиций случайных аффинных преобразований аргумента к полугруппе, разрешающей задачу Коши для уравнения Фоккера–Планка. Приведены численные оценки отклонения случайных итераций от решений предельной задачи.

2. УСРЕДНЕНИЕ СЛУЧАЙНЫХ АФИННЫХ ПРЕОБРАЗОВАНИЙ

Пусть $E = {{\mathbb{R}}^{d}}$ – конечномерное евклидово пространство, $B(E)$ – банахово пространство линейных преобразований пространства $E$. Пусть $G(E)$ – группа аффинных преобразований пространства $E$; ${\mathbf{F}} \in G(E)$ – аффинное преобразование пространства $E$. Тогда оператор ${{\hat {U}}_{{\mathbf{F}}}}$, определеный на пространстве $\mathcal{H} = {{L}_{2}}({{\mathbb{R}}^{d}})$ равенством ${{\hat {U}}_{{\mathbf{F}}}}u(x) = u({\mathbf{F}}x),$ $x \in E,$ при любом $u \in \mathcal{H}$ является ограниченным линейным оператором в пространстве $\mathcal{H}$. Поскольку якобиан преобразования ${\mathbf{F}}$ отличен от нуля и от бесконечности, то для любого $u \in {{L}_{2}}({{\mathbb{R}}^{d}})$ выполняются условие $u \circ {\mathbf{F}} \in {{L}_{2}}({{\mathbb{R}}^{d}})$ и равенство ${{\left\| {u \circ {\mathbf{F}}} \right\|}_{\mathcal{H}}} = {{\left| {\det ({{{\mathbf{F}}}^{{ - 1}}})} \right|}^{{1/2}}}{{\left\| u \right\|}_{\mathcal{H}}}$.

Каждое аффинное преобразование ${\mathbf{F}} \in G(E)$ допускает единственное представление в виде ${\mathbf{F}} = {{{\mathbf{S}}}_{h}} \circ {\mathbf{L}}$, где ${\mathbf{L}} \in B(E)$ – невырожденный линейный оператор в пространстве $E$, ${{{\mathbf{S}}}_{h}}$ – оператор сдвига аргумента на вектор $h \in E$.

Случайным аффинным преобразованием ${\mathbf{F}}$ будем называть упорядоченную пару $({\mathbf{L}},h)$ независимых случайных величин, где ${\mathbf{L}}$ – случайная величина со значениями в пространстве $B(E)$, $h$ – случайная величина со значениями в пространстве $E$. При этом ${\mathbf{F}}(\omega ) = {{{\mathbf{S}}}_{{h(\omega )}}} \circ {\mathbf{L}}(\omega ),\;\omega \in \Omega $, где $(\Omega ,\mathcal{A},\mu )$ – вероятностное пространство элементарных событий.

Случайной величиной со значениями в пространстве $B(E)$ называется слабо измеримое отображение $\xi \,:\Omega \to B(E)$, т.е. измеримое в том смысле, что для любых $x,y \in E$ комплекснозначная функция $\Omega \ni \omega \to {{(x,\xi y)}_{E}} \in \mathbb{C}$ является измеримой. Если пространство $E$ сепарабельно, то из слабой измеримости отображения $\xi \,:\Omega \to B(E)$ следует его сильная измеримость. Последнее означает, что для любого $x \in E$ вектор-функция $\xi x\,:\Omega \to E$ является измеримым отображением. Кроме того, из слабой измеримости отображения $\xi \,:\Omega \to B(E)$ следует измеримость функции $\Omega \ni \omega \to {{\left\| \xi \right\|}_{E}} \in \mathbb{R}$ (см. [13]).

Если случайный оператор ${\mathbf{L}}\,:\Omega \to B(E)$ удовлетворяет условию ${{\int_\Omega {\left\| {{\mathbf{L}}(\omega )} \right\|} }_{{B(E)}}}d\mu (\omega ) < \infty $, то для любых $x,y \in E$ числовая функция $\Omega \ni \omega \to (x,{\mathbf{L}}y) \in \mathbb{C}$ интегрируема. Следовательно, определена ограниченная полуторалинейная форма $\beta (x,y) = \int_\Omega {{{{({\mathbf{L}}x,y)}}_{E}}d\mu (\omega )} ,$ $x,y \in E,$ и ассоциированный с формой ограниченный линейный оператор ${\mathbf{\bar {L}}}$.

Случайным вектором пространства $E$ называется слабо измеримое отображение $h\,:\Omega \to E$. Для сепарабельного пространства $E$ слабая измеримость равносильна измеримости.

Лемма 1. Пусть ${\mathbf{F}}$ – аффинное преобразование пространства $E$, представимое в виде композиции ${\mathbf{F}} = {{{\mathbf{S}}}_{h}} \circ {\mathbf{L}}$ оператора сдвига ${{{\mathbf{S}}}_{h}}$ на вектор $h \in E$ и невырожденного линейного преобразования $L$. Тогда на пространстве $\mathcal{H} = {{L}_{2}}(E)$ определено ограниченное линейное преобразование ${{{\mathbf{U}}}_{{\mathbf{F}}}}$, действующее по правилу ${{{\mathbf{U}}}_{{\mathbf{F}}}}u(x) = u({\mathbf{F}}x),$ $x \in E$, норма которого допускает оценку ${{\left\| {{{{\mathbf{U}}}_{{\mathbf{F}}}}} \right\|}_{\mathcal{H}}} = {{\left| {\det ({{{\mathbf{F}}}^{{ - 1}}})} \right|}^{{1/2}}}$.

Доказательство. Поскольку преобразование сдвига аргумента на фиксированный вектор $h$ является унитарным в пространстве $\mathcal{H}$, то для любого $u \in \mathcal{H}$ выполняется равенство ${{\left\| {{{{\mathbf{U}}}_{{\mathbf{F}}}}u} \right\|}_{\mathcal{H}}} = {{\left\| {u \circ {\mathbf{L}}} \right\|}_{\mathcal{H}}} = {{\left| {{\text{det}}({{{\mathbf{L}}}^{{ - 1}}})} \right|}^{{1/2}}}{{\left\| u \right\|}_{\mathcal{H}}} = {{\left| {{\text{det}}({{{\mathbf{F}}}^{{ - 1}}})} \right|}^{{1/2}}}{{\left\| u \right\|}_{\mathcal{H}}}$.

Теорема 1. Пусть ${\mathbf{F}}\,:\Omega \to G(E)$ – случайная величина со значениями в группе аффинных преобразований пространства $E$. Тогда, если $\int_\Omega {{{{\left| {{\text{det}}({{{\mathbf{F}}}^{{ - 1}}})} \right|}}^{{1/2}}}} d\mu (\omega ) < + \infty ,$ то отображение ${{{\mathbf{U}}}_{{\mathbf{F}}}}\,:\Omega \to B(\mathcal{H})$ является случайным оператором, математическое ожидание которого ${{{\mathbf{U}}}_{{\mathbf{F}}}}$ существует и определяется равенством

Пусть $\mathcal{E} = \{ {{e}_{1}},...,{{e}_{d}}\} $ – стандартный ортонормированный базис евклидова пространства $E = {{\mathbb{R}}^{d}}$, ${{x}_{j}} = ({{e}_{j}},x),$ $x \in E,$ $j \in \overline {1,d} $. Если $u,{v} \in C_{0}^{\infty }(E)$, то $(u,{{{\mathbf{U}}}_{{\mathbf{F}}}}v)$ – непрерывная функция от $d$ случайных величин $({\mathbf{F}}x,{{e}_{1}}),...,({\mathbf{F}}x,{{e}_{d}})$, и потому функция $(u,{{{\mathbf{U}}}_{{\mathbf{F}}}}v)\,:\Omega \to \mathbb{C}$ измерима. Поскольку пространство $C_{0}^{\infty }(E)$ плотно в ${{L}_{2}}(E)$, то функция $(u,{{{\mathbf{U}}}_{{\mathbf{F}}}}v)\,:\Omega \to \mathbb{C}$ является измеримой для любых $u,v \in {{L}_{2}}(E)$.

Интегрируемость случайной величины $(u,{{{\mathbf{U}}}_{{\mathbf{F}}}}v)$ при произвольном выборе $u,v \in {{L}_{2}}(E)$ следует из оценки $\left| {(u{{{\mathbf{U}}}_{{\mathbf{F}}}}v)} \right| \leqslant \left\| v \right\|\left\| {u \circ {\mathbf{F}}} \right\| \leqslant \left\| u \right\|\left\| v \right\|{{\left| {{\text{det}}{{{\mathbf{F}}}^{{ - 1}}}} \right|}^{{1/2}}}$ и теоремы о мажорированной сходимости. Поэтому полуторалинейная форма $\mathcal{H} \times \mathcal{H} \ni (u,v) \to {{\beta }_{{\mathbf{F}}}}(u,v) = \int_\Omega {(u \circ {\mathbf{F}}(\omega ),v)d\mu (\omega )} $ определена и ограничена. Следовательно, математическое ожидание ${\text{M}}{{{\mathbf{U}}}_{{\mathbf{F}}}}$, определяемое интегралом Петтиса по мере $\mu $ от случайной операторнозначной функции ${{{\mathbf{U}}}_{{\mathbf{F}}}}$, является с ней ограниченным линейным оператором ${\text{M}}{{{\mathbf{U}}}_{{\mathbf{F}}}} \in B(\mathcal{H})$, ассоциированным с формой ${{\beta }_{{\mathbf{F}}}}$.

3. ИТЕРАЦИИ ФЕЙНМАНА–ЧЕРНОВА

Пусть ${\mathbf{F}}$ – случайное аффинное преобразование пространства $E$, представимое в виде ${\mathbf{F}} = {{{\mathbf{S}}}_{h}} \circ {\mathbf{L}}$, где ${{{\mathbf{S}}}_{h}}$ – оператор сдвига на случайный вектор $h \in E$, ${\mathbf{L}}$ – случайный невырожденный линейный оператор. Далее будут рассматриваться такие и только такие случайные линейные операторы ${\mathbf{L}}\,:\Omega \to B(E)$, значения которых допускают полярное разложение в композицию самосопряженного преобразования $\Lambda $ и ортогонального преобразования $V$. Кроме того, случайные величины $\Lambda ,\;{\mathbf{V}}$ и ${{{\mathbf{S}}}_{h}}$ в представлении ${\mathbf{F}} = {{{\mathbf{S}}}_{h}}{\mathbf{V}}\Lambda $ являются независимыми случайными операторами, причем случайный оператор $\Lambda $ принимает значения в конусе положительных самосопряженных операторов в пространстве $E$, случайный оператор ${\mathbf{V}}$ – в группе ортогональных преобразований пространства $E$, а случайный оператор ${{{\mathbf{S}}}_{h}}$ – в группе сдвигов вдоль векторов пространства $E$.

Со случайным преобразованием ${\mathbf{F}} = {{{\mathbf{S}}}_{h}} \circ {\mathbf{L}}$ свяжем однопараметрическое семейство преобразований

В формуле (3.1) дробная степень положительного оператора $\Lambda $ определяется его спектральным разложением.

Ортогональный оператор ${\mathbf{V}}$ допускает спектральное разложение вида ${\mathbf{V}} = \int_{ - \pi }^\pi {{{e}^{{i\lambda }}}d{\mathbf{E}}(\lambda )} $. Дробная степень такого оператора ${\mathbf{V}}$ определяется равенством ${{{\mathbf{V}}}^{t}} = \int_{ - \pi }^\pi {{{e}^{{i\lambda t}}}d{\mathbf{E}}(\lambda )} $. Тогда при $t \in \mathbb{R}$ операция возведения в степень $t$ однозначно определена.

Дробные степени положительного сомосопряженного и унитарного операторов в равенстве (3.1) удобно представить в форме экспоненциальных функций от оператора

Здесь логарифмом положительного оператора $\Lambda $ называется самосопряженный оператор с вещественным спектром, определяемый в силу спектральной теоремы однозначно. Логарифмом ортогонального оператора ${\mathbf{V}}$ называется кососимметрический оператор $\ln {\mathbf{V}} \in B(E)$, мнимая часть собственных значений которого лежит в промежутке $( - \pi ,\pi ]$, такой, что ${\mathbf{V}} = \exp (\ln {\mathbf{V}})$. Существование и единственность оператора $\ln {\mathbf{V}}$ следуют из того факта, что оператор ${\mathbf{V}}$ допускает разложение пространства $E$ в прямую сумму не более чем двумерных инвариантных подпространств, при том, что в одномерном подпространстве оператор ${\mathbf{V}}$ действует как тождественный, а в двумерном – как оператор поворота на некоторый угол из промежутка $( - \pi ,\pi ]$.

Пусть $\{ {{{\mathbf{F}}}_{k}}\} $ – последовательность независимых одинаково распределенных случайных аффинных преобразований, каждое из которых представимо в виде

где при каждом $k \in \mathbb{N}$ случайные величины ${{h}_{k}},\;{{{\mathbf{V}}}_{k}},\;{{\Lambda }_{k}}$ являются независимыми.

Тогда для каждого $k \in \mathbb{N}$ определено однопараметрическое семейство аффинных преобразований ${{{\mathbf{F}}}_{k}}(t) = {{{\mathbf{S}}}_{{{\text{t}}{{{\text{h}}}_{k}}}}}{\mathbf{V}}_{k}^{t}\Lambda _{k}^{t},{\kern 1pt} $ $t \geqslant 0,$ $t \in [0,1)$.

Следовательно, определена последовательность итераций Фейнмана–Чернова независимых случайных аффинных преобразований

Композиции независимых случайных аффинных преобразований ${{{\mathbf{F}}}_{n}}(t{\text{/}}n) \circ ... \circ {{{\mathbf{F}}}_{1}}(t{\text{/}}n)$ пространства $E$ сопоставим случайное линейное преобразование ${{{\mathbf{U}}}_{{{{{\mathbf{F}}}_{n}}}}}_{{(t/n) \circ ... \circ {{{\mathbf{F}}}_{1}}(t/n)}}$ пространства $\mathcal{H} = {{L}_{2}}(E)$, действующее по правилу

Далее с помощью теоремы Чернова будет дано описание предельного (при $n \to \infty $) поведения таких композиций.

4. УСРЕДНЕННОЕ ПО ЧЕРНОВУ АФФИННОЕ ПРЕОБРАЗОВАНИЕ

В этом разделе будет установлена сходимость последовательности итераций семейств независимых случайных аффинных преобразований к группе сдвигов вдоль векторного поля, определяемого усредненным аффинным преобразованием.

В [2] были доказаны утверждения о математическом ожидании композиции независимых случайных линейных операторов. Применительно к рассматриваемым нами композициям эти утверждения формулируются следующим образом.

Лемма 2 (см. [2]). Пусть $\{ {{{\mathbf{F}}}_{k}}\} $ – последовательность независимых одинаково распределенных случайных аффинных преобразований пространства $E$. Тогда для всех $t \geqslant 0,$ $n \in \mathbb{N}$ справедливо равенство ${{{\mathbf{U}}}_{{{{{\mathbf{F}}}_{n}}(t/n) \circ ... \circ {{{\mathbf{F}}}_{1}}(t/n)}}} = {{{\mathbf{U}}}_{{{{{\mathbf{F}}}_{n}}(t/n)}}} \circ ... \circ {{{\mathbf{U}}}_{{{{{\mathbf{F}}}_{1}}(t/n)}}}$.

Следовательно, для математического ожидания композиции справедливо равенство

Положим

Лемма 3 (см. [2]). Если ${\mathbf{A}}(\omega ) = {\mathbf{V}}(\omega ) \circ \Lambda (\omega ),$ $\omega \in \Omega $, где ${\mathbf{V}},\;\Lambda $ – независимые случайные операторы со значениями в простанстве $B(E)$, то $M({\mathbf{A}}) = {\text{M}}({\mathbf{V}}) \circ {\text{M}}(\Lambda ).$

Следовательно, функция ${\mathbf{G}}$ задается равенством

На основании лемм 2 и 3 докажем сходимость итераций (3.4) к полугруппе. Проверим выполнение условий теоремы Чернова для функции (4.1).

По построению ${\mathbf{G}}(0) = {\mathbf{I}}$. Оператор-функция (4.1) сильно непрерывна как композиция трех сильно непрерывных оператор-функций; сильная непрерывность каждой из трех компонент композиции (4.1) имеет место, поскольку является интегралом по вероятностной мере от функции, значениями которой являются сильно непрерывные оператор-функции. Норма среднего значения случайной оператор-функции допускает оценку

Тогда в силу неравенства Гёльдера и с учетом нормированности вероятностной меры $\mu $ получим оценку

Таким образом, условие теоремы Чернова на нормы значений операторнозначной функции ${\mathbf{G}}$ выполнено.

Для производной композиции операторнозначных функций (4.1) в силу правила Лейбница имеем

Лемма 4 (см. [2]). Пусть $h$ – случайный вектор пространства $E$, обладающий математическим ожиданием ${\text{M}}h = \bar {h} \in E$. Тогда $({\text{M}}[{{{\mathbf{U}}}_{{{{{\mathbf{S}}}_{{{\text{th}}}}}}}}]){\kern 1pt} '{{{\text{|}}}_{{t = 0}}}u = (\bar {h},\nabla u)$ $\forall u \in {{H}^{1}} = W_{2}^{1}(E)$.

Лемма 5. Пусть отображение ${\mathbf{U}}\,:{{\mathbb{R}}_{ + }} \times \Omega \to B(E)$ имеет вид $\exp (t{\mathbf{A}}(\omega )),{\kern 1pt} $ $t \geqslant 0$, где ${\mathbf{A}}\,:\Omega \to B(E)$ – случайный линейный оператор, принимающий значения в шаре радиуса $\rho \in (0, + \infty )$ пространства $B(E)$, который имеет среднее значение

Тогда для любого $u \in C_{0}^{\infty }({{\mathbb{R}}^{d}})$ выполняется равенство

где остаток $r(t)$ допускает оценку ${{\left\| {r(t)} \right\|}_{\mathcal{H}}} \leqslant C{{t}^{2}}{{\rho }^{2}}\exp (2t\rho )$.

Доказательство. Действительно, поскольку $\exp (t{\mathbf{A}}) = {\mathbf{I}} + t{\mathbf{A}} + \alpha (t)$, где ${{\left\| {\alpha (t)} \right\|}_{{B(E)}}} = o(t) \leqslant {{t}^{2}}{{\rho }^{2}}{{e}^{{\rho t}}}$ при $t \to 0$, то согласно формуле Тейлора для функции $u(\exp (t{\mathbf{A}})x)$ имеем

Поэтому в силу предположений леммы 1)–3) о случайном операторе $A$ справедливо равенство Оценим ${{L}_{2}}$-норму остаточного члена в формуле Тейлора. Поскольку $u \in C_{0}^{\infty }({{R}^{d}}),$ то существует постоянная $c > 0$, ограничивающая сверху абсолютное значение функции $u$ и всех ее частных производных не выше второго порядка. Кроме того, носитель функции $u$ заключен в шаре некоторого радиуса ${{r}_{0}}$ пространства $E$, поэтому носитель функции $u \circ \exp (t{\mathbf{A}})$ заключен в шаре радиуса ${{r}_{t}} = {{r}_{0}}\exp (t\rho )$. Из представления остаточного члена формулы Тейлора в форме Лагранжа следует, что квадрат его ${{L}_{2}}$-нормы не превосходит произведения меры Лебега носилеля на квадрат супремума по носителю дифференциала второго порядка, откуда следует оценка остаточного члена из утверждения леммы.

Теорема 2. Пусть ${\mathbf{F}}$ – случайное аффинное преобразование пространства $E$, представимое в виде ${\mathbf{F}} = {{{\mathbf{S}}}_{h}} \circ {\mathbf{L}} = {{{\mathbf{S}}}_{h}}{\mathbf{V}}\Lambda $, где операторнозначные случайные величины $\Lambda ,\;{\mathbf{V}}$ и ${{{\mathbf{S}}}_{h}}$ являются независимыми случайными операторами и принимают значения в конусе положительных самосопряженных операторов в пространстве $E$, в группе ортогональных преобразований пространства $E$ и в группе сдвигов вдоль постоянного вектора в пространстве $E$ соответственно. Пусть ${\text{M}}h = \bar {h} \in E$. Пусть случайный оператор ${\mathbf{A}} = \ln (\Lambda ) + \ln ({\mathbf{V}})$ $($см. $(3.2))$ принимает значения в некотором шаре пространства $B(E)$ и ${\text{M}}{\mathbf{A}} = {\mathbf{\bar {A}}} \in B(E)$. Тогда для любого $T > 0$ и любого $u \in \mathcal{H}$ выполняется равенство

где ${\mathbf{W}}$ – полугруппа, порождаемая решениями задачи Коши

Для доказательства теоремы 2 остается проверить условие теоремы Чернова о том, что оператор ${\mathbf{H}}\,:u \to (\bar {h} + {\mathbf{\bar {A}}}x,\nabla u)$ является генератором сильно непрерывной полугруппы в пространстве $\mathcal{H}$.

Поскольку векторное поле ${\mathbf{a}}(x) = h + {\mathbf{\bar {A}}}x$ непрерывно дифференцируемо и равномерно липшицево на пространстве $E$, то оно задает поток ${{g}_{t}},{\kern 1pt} t \in R$, непрерывно дифференцируемых преобразований пространства $E$. Следовательно, для любого ${{u}_{0}} \in C_{0}^{\infty }(E)$ задача Коши (4.4) имеет единственное классическое решение $u(t,x) = {{u}_{0}}({{g}_{{ - t}}}(x)),$ $t \in \mathbb{R}$. При этом для каждого $t \in \mathbb{R}$ справедлива оценка ${{\left\| {u(t, \cdot )} \right\|}_{\mathcal{H}}} = \exp ( - {\text{Tr}}({\mathbf{\bar {A}}})t){{\left\| {{{u}_{0}}} \right\|}_{\mathcal{H}}}$. Поэтому отображение $C_{0}^{\infty } \mathrel\backepsilon {{u}_{0}} \to u(t, \cdot ) \in C_{0}^{\infty }$ допускает единственное продолжение по непрерывности на пространство $\mathcal{H}$. Следовательно, оператор ${\mathbf{H}}$ является генератором сильно непрерывной группы $\exp ({\mathbf{H}}t)u(x) = u({{g}_{{ - t}}}(x)),$ $t \in \mathbb{R},$ $u \in \mathcal{H}$.

5. ФЕЙНМАНОВСКИЕ АППРОКСИМАЦИИ ДИФФУЗИОННЫХ ПОЛУГРУПП

В этом разделе устанавливается сходимость последовательности итераций семейств случайных блужданий под действием независимых случайных аффинных преобразований к полугруппе, разрешающей уравнение Фоккера–Планка.

Лемма 6. Пусть отображение ${\mathbf{U}}\,:{{\mathbb{R}}_{ + }} \times \Omega \to B(E)$ имеет вид $\exp (\sqrt t {\mathbf{A}}(\omega )),$ $t \geqslant 0$, где ${\mathbf{A}}\,:\Omega \to B(E)$ – случайный линейный оператор, принимающий значения в шаре радиуса $\rho \in (0, + \infty )$ пространства $B(E)$, для которого выполняются следующие условия:

$1)$ ${\text{M}}({\mathbf{A}}) = \int_\Omega {{\mathbf{A}}(\omega )d\mu (\omega )} = 0$,

$2)$ ${\text{M}}({\mathbf{A}}{\kern 1pt} *{\kern 1pt} {\mathbf{A}}) = \int_\Omega {({\mathbf{A}}(\omega )){\kern 1pt} *{\kern 1pt} {\mathbf{A}}(\omega )d\mu (\omega )} $.

Тогда для любого $u \in C_{0}^{\infty }({{\mathbb{R}}^{d}})$ выполняется равенство

где остаток $r(t)$ допускает оценку ${{\left\| {r(t)} \right\|}_{\mathcal{H}}} \leqslant C{{t}^{{3/2}}}\exp \left( {\frac{3}{2}\sqrt t \rho } \right)$.

Доказательство. Действительно, поскольку $\exp (\sqrt t {\mathbf{A}}) = {\mathbf{I}} + \sqrt t {\mathbf{A}} + \frac{1}{2}t{{{\mathbf{A}}}^{2}} + \alpha (t)$, где ${{\left\| {\alpha (t)} \right\|}_{{B(E)}}} = o(t)$ при $t \to 0$, то согласно формуле Тейлора для функции $u(\exp (\sqrt t {\mathbf{A}})x)$ имеем

Поэтому в силу предположений 1), 2) о случайном операторе ${\mathbf{A}}$ справедливо равенство Оценим ${{L}_{2}}$-норму остаточного члена в формуле Тейлора. Поскольку $u \in C_{0}^{\infty }({{\mathbb{R}}^{d}}),$ то существует постоянная $c > 0$, ограничивающая сверху абсолютное значение функции $u$ и всех ее частных производных не выше третьего порядка. Кроме того, носитель функции $u$ заключен в шаре некоторого радиуса ${{r}_{0}}$ пространства $E$, поэтому носитель функции $u \circ \exp (\sqrt t {\mathbf{A}})$ заключен в шаре радиуса ${{r}_{t}} = {{r}_{0}}\exp (\sqrt t \rho )$. Из представления остаточного члена формулы Тейлора в форме Лагранжа следует, что квадрат его ${{L}_{2}}$-нормы не превосходит произведения меры Лебега носителя на квадрат супремума по носителю дифференциала третьего порядка, откуда следует оценка остаточного члена из утверждения леммы.

По произвольному случайному линейному оператору ${\mathbf{A}}$ в пространстве $E$, удовлетворяющему условиям леммы 6, определим на пространстве $C_{0}^{\infty }({{\mathbb{R}}^{d}})$ билинейную форму

где коэффициенты $\beta $ определяются равенствами ${\text{M}}({{{\mathbf{A}}}_{{ij}}}{{{\mathbf{A}}}_{{kl}}}) = \int_\Omega {{{{\mathbf{A}}}_{{ij}}}(\omega ){{{\mathbf{A}}}_{{kl}}}(\omega )d\mu (\omega )} = {{\beta }_{{ijkl}}} \in \mathbb{R}$ при всех $i,j,k,l \in \overline {1,d} $.

Лемма 7. Пусть случайный оператор ${\mathbf{A}}$ в пространстве $E$ удовлетворяет условиям леммы $6$ и условиям

$1)$ ${\text{M}}({\mathbf{A}}{\kern 1pt} *{\kern 1pt} {\mathbf{A}}) \in B(E),$

$2)$ для любого единичного вектора $e \in E$ выполняется условие $\mathop {\inf }\limits_{\parallel f\parallel = 1} \int_\Omega {{{{\left| {({\mathbf{A}}(\omega )e,f)} \right|}}^{2}}} \geqslant \gamma $ при некотором $\gamma > 0.$

Пусть случайный вектор $h$ обладает нулевым математическим ожиданием и невырожденным ковариационным оператором ${\mathbf{D}} \in B(E).$

Тогда полуторалинейная форма $\beta (u,v) = \int_E {\int_\Omega {{{h}_{k}}{{h}_{l}}{{\partial }_{{{{x}_{k}}}}}u{{\partial }_{{{{x}_{l}}}}}v} } + \int_E {\int_\Omega {{{{\mathbf{A}}}_{{ki}}}{{{\mathbf{A}}}_{{lj}}}d\mu (\omega ){{x}_{i}}{{x}_{j}}{{\partial }_{{{{x}_{k}}}}}u{{\partial }_{{{{x}_{l}}}}}vdx} } $ является положительно-определенной и мажорирует квадратичную форму $u \to \left\| u \right\|_{{W_{2}^{1}(E)}}^{2}$.

Доказательство. Для любого $u \in C_{0}^{\infty }(E)$ выполняется

Заметим, что

$\int_E {\int_\Omega {{{{(x,{\mathbf{A}}\nabla u)}}^{2}}d\mu (\omega )dx} } \geqslant \int_E {{{{\left\| x \right\|}}^{2}}} \int_\Omega {{{{({\mathbf{A}}{\kern 1pt} *{\kern 1pt} {{e}_{x}},\nabla u)}}^{2}}d\mu (\omega )dx} $,     ${{e}_{x}} = \frac{1}{{\left\| x \right\|}}x$.

Поэтому в силу условия 2) выполнена оценка

$\int_E {\int_\Omega {{{{(x,{\mathbf{A}}\nabla u)}}^{2}}d\mu (\omega )dx} } \geqslant \gamma \int_E {{{{\left\| x \right\|}}^{2}}{{{\left\| {\nabla u(x)} \right\|}}^{2}}dx} $.

Следовательно,

где ${{d}_{1}}$ – наименьшее собственное значение оператора ${\mathbf{D}}$. Таким образом, полуторалинейная форма $\beta $ мажорирует квадратичную форму $u \to \left\| {\left| {\nabla u} \right|} \right\|_{{{{L}_{2}}(E)}}^{2},$ $u \in W_{2}^{1}(E)$. Лемма 7 доказана.

Определим линейный оператор ${\mathbf{\hat {L}}}$ в пространстве ${{L}_{2}}(E)$, ассоциированный с замыканием положительно определенной полуторалинейной формы $\beta (u,v) = \int_E {({{\beta }_{{ijkl}}}{{x}_{i}}{{x}_{j}} + {{{\mathbf{D}}}_{{k,l}}}){{\partial }_{{{{x}_{k}}}}}u{{\partial }_{{{{x}_{l}}}}}v{\kern 1pt} dx} $ на плотном в $\mathcal{H} = {{L}_{2}}(E)$ подпространстве $C_{0}^{\infty }(E).$ Поскольку полуторалинейная форма $\beta $ является положительной, то соответствующий ей оператор ${\mathbf{\hat {L}}}$ является положительным самосопряженным, а оператор $ - {\mathbf{\hat {L}}}$ является генератором сжимающей полугруппы самосопряженных сжатий в пространстве ${{L}_{2}}(E)$.

Лемма 8. Пусть выполнены условия леммы $7$. Тогда квадратичная форма оператора ${\mathbf{\hat {L}}}$ мажорирует квадратичную форму оператора ${\mathbf{\hat {K}}}$, задаваемого на пространстве $C_{0}^{\infty }(E)$ равенством ${\mathbf{\hat {K}}}u = (x,{\mathbf{B}}\nabla u{{)}_{{{{R}^{d}}}}}$, где ${\mathbf{B}} = {\text{M}}({{{\mathbf{A}}}^{2}})$.

Действительно, для любого $v \in W_{{2,0}}^{1}(E)$ и для любого p > 1 справедлива цепочка неравенств

Лемма 9. Пусть выполнены условия лемм $6$ и $7$. Тогда задача Коши

где оператор ${\mathbf{\hat {H}}}$ задан на области определения оператора ${\mathbf{\hat {L}}}$ дифференциальным выражениемимеет единственное решение $u \in C({{\mathbb{R}}_{ + }},\mathcal{H})$ при произвольном ${{u}_{0}} \in \mathcal{H}$.

Доказательство. Самосопряженный неположительный оператор $ - {\mathbf{\hat {L}}}$ является генератором сильно непрерывной сжимающей полугруппы в пространстве $\mathcal{H}$. Поскольку ${\mathbf{\hat {H}}} = {\mathbf{\hat {L}}} + {\mathbf{\hat {K}}}$ и квадратичная форма оператора ${\mathbf{\hat {L}}} + {\mathbf{I}}$ мажорирует квадратичную форму оператора ${\mathbf{\hat {K}}}$, то применима теорема о возмущении генератора полугруппы (см. [22]). Следoвательно, оператор ${\mathbf{\hat {H}}}$ является генератором сильно непрерывной полугруппы в пространстве $\mathcal{H}$, откуда и следует утверждение леммы.

Теорема 3. Пусть отображение ${\mathbf{U}}\,:{{R}_{ + }} \times \Omega \to B(E)$ имеет вид $\exp (\sqrt t {\mathbf{A}}(\omega )),$ $t \geqslant 0$, где ${\mathbf{A}}\,:\Omega \to B(E)$ – случайный линейный оператор, для которого выполняются условия лемм $6$ и $7$. Пусть $\mu (\{ \omega \,:\left| {{\text{det}}({\mathbf{A}})} \right| = 1\} ) = 1$; $h$ – случайный вектор пространства $E$ с нулевым математическим ожиданием и невырожденным ковариационным оператором ${\mathbf{D}}$; величины $h$ и ${\mathbf{A}}$ являются независимыми. Пусть $\Phi (t) \equiv {\mathbf{F}}(\sqrt t ) = {{{\mathbf{S}}}_{{\sqrt t h}}}{{e}^{{\sqrt t A}}},$ $t \geqslant 0$ – однопараметрическое семейство случайных аффинных преобразований.

Пусть $\{ {{\Phi }_{n}}\} $ – последовательность однопараметрических семейств независимых одинаково распределенных случайных аффинных преобразований, распределение каждого из которых совпадает с распределением $\Phi $.

Тогда, если $u \in {{L}_{2}}(E)$, то последовательность функций $\{ {{v}_{n}}\} :\;\mathbb{N} \to C({{\mathbb{R}}_{ + }},\mathcal{H})$, определяемых равенствами ${{v}_{n}}(t,x) = {\text{M}}u({{\Phi }_{n}}(t{\text{/}}n)...{{\Phi }_{1}}(t{\text{/}}n)x),$ $(t,x) \in {{\mathbb{R}}_{ + }} \times E,$ $n \in \mathbb{N}$, удовлетворяет условию

при любых $T > 0$. Здесь функция $v$ является решением начально-краевой задачи (5.2), (5.3).

Доказательство. Из лемм 3 и 6 следует, что оператор-функция $\bar {\Phi }(t),{\kern 1pt} \;t \geqslant 0,$ действующая в пространстве ${{L}_{2}}(E)$ по правилу

при каждом $t \geqslant 0$, удовлетворяет всем условиям теоремы Чернова. В частности, согласно (4.2), потому ${{\left\| {\bar {\Phi }(t)} \right\|}_{{B(\mathcal{H})}}} \leqslant 1$ $\forall t \geqslant 0$ в силу условий теоремы 3.

Следовательно,

при любых $T > 0$ и $u \in {{L}_{2}}(E)$. Остается заметить, что в силу независимости случайных преобразований при всех $t \geqslant 0$ и всех $n \in \mathbb{N}$ справедливо равенство что в соответствии с (5.4) и доказывает утверждение теоремы 3.

6. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

В качестве элемента пространства $\mathcal{H}$ возьмем функцию

Сгенерируем набор $m$ равномерно распределенных матриц ${{A}_{{d \times d}}}$, так что $\bar {A} = M{\mathbf{A}} = \frac{1}{m}\sum\nolimits_{k = 1}^m {{A}_{k}}$. В примерах, представленных в статье, $d = 2$, $m = 6$.

Случайное линейное преобразование ${\mathbf{A}}$ моделируется с помощью дискретного равномерного распределения на конечном множестве элементарных событий $\Omega $, которое представляет собой набор линейных преобразований ${{A}_{k}}$.

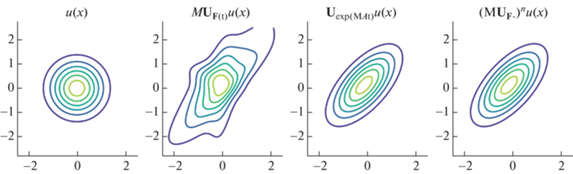
Строим операторы ${{F}_{k}}(t) = {{e}^{{t{{A}_{k}}}}}$, так что $M{\mathbf{F}} = \frac{1}{m}\sum\nolimits_{k = 1}^m {{F}_{k}}(t)$. Зададим далее последовательность $n$ итераций в соответствии с (3.3), $n{{ = 1,...,2}^{{16}}}$. Для фиксированного момента $t$ вычисляем ${{e}^{{M({\mathbf{A}})t}}}$ и ${{\left( {M{\mathbf{F}}(t{\text{/}}n)} \right)}^{n}}$ и строим зависимость нормы разности. Результаты расчетов приведены на фиг. 1 и 2.

Аналогично строится алгоритм численного моделирования для леммы 7. Отличие от леммы 5 состоит в том, что теперь рассматривается оператор ${{F}_{k}}(t) = {{e}^{{\sqrt t {{A}_{k}}}}}$, а последовательность ${{A}_{k}}$ центрирована: $M{\mathbf{A}} = 0$. Дополнительным элементом численного моделирования является вычисление оператора ${{e}^{{M(1/2{{{\mathbf{A}}}^{2}})t}}}$. Результаты представлены на фиг. 3 и 4.

При этом также была проверена оценка остаточного члена в формулах (4.3) и (5.1) и для более высоких размерностей, вплоть до шести. Полученные численные оценки порядков малости остаточных членов $r(t)$ для уравнений (4.3) и (5.1) согласуются с утверждениями лемм 5 и 6.

На фиг. 1 и 3 по осям везде отложены компоненты двумерного вектора $x$ и изображены линии уровня соответствующих функций.

Из фиг. 1 следует, что в то время, как $M{{{\mathbf{U}}}_{{{\mathbf{F}}(t)}}}u(x)$ имеет достаточно сложную структуру, в результате действия операторов ${{{\mathbf{U}}}_{{{\text{exp}}(M{\mathbf{A}}t)}}}$ и ${{(M{\mathbf{U}}_{{\mathbf{F}}}^{{1/n}})}^{n}}$ на функцию $u(x)$ линии уровня ${{x}^{2}} = $ const, представляющие собой окружности, переходят в близкие эллипсы, что иллюстрирует возможность генерации групп усредненных случайных аффинных преобразований с помощью итераций Чернова. Аналогично фиг. 3 иллюстрирует возможность генерации операторов группы ${{{\mathbf{U}}}_{{\exp \frac{1}{2}(M{{{\mathbf{A}}}^{2}}t)}}}u(x)$ для случайного линейного оператора ${\mathbf{A}}$ с нулевым математическим ожиданием и конечной дисперсией с помощью итераций Чернова ${{(M{{{\mathbf{U}}}_{{\mathbf{F}}}}(t{\text{/}}n))}^{n}}$, где ${\mathbf{F}}(t) = {\text{exp}}(\sqrt t {\mathbf{A}})$.

Все необходимые производные рассчитываются по аналитическим формулам, получаемым с помощью автоматического символьного дифференцирования.

7. ЗАКЛЮЧЕНИЕ

Таким образом, в работе установлена сходимость последовательности итераций семейств независимых случайных аффинных преобразований к группе сдвигов вдоль векторного поля, определяемого усредненным аффинным преобразованием. Используя этот результат, мы показали, что последовательность итераций семейств случайных блужданий под действием независимых аффинных преобразований сходится к полугруппе, которая разрешает соответствующее уравнение Фоккера–Планка. Доказанные в работе теоремы 2 и 3 обосновывают применение численного алгоритма, вычисляющего итерации Фейнмана–Чернова композиций независимых случайных аффинных преобразований для решения соответствующих эволюционных задач. Приведенные численные примеры носят методологический характер. Они показывают, что разрабатываемый подход может быть полезным при решении как классических, так и квантовых кинетических уравнений.