Журнал вычислительной математики и математической физики, 2022, T. 62, № 7, стр. 1180-1186

ВВЕДЕНИЕ

В рамках модели гидродинамики, описывающей течение несжимаемой жидкости, рассматривается задача о моделировании потенциального течения жидкости в области, изменяющейся во времени. Получены точные решения двух тестовых задач. Решение данного класса задач связано с задачами управления параметрами несжимаемой жидкости за счет изменения области течения. Постановка этого класса задач представлена в [1].

Исследованию задач динамики жидкости в областях, изменяющихся во времени, посвящено большое количество научных работ, например [2]–[6], однако все эти работы посвящены исключительно численному моделированию, а результаты расчетов проверяются сравнением с натурными экспериментальными данными или расчетами других авторов. Исключением является работа [7], в которой рассматривается задача о набегании волны, движущейся с постоянной скоростью, на вертикальный цилиндр. В этой статье представлено аналитическое решение внешней трехмерной задачи о потенциальном течении несжимаемой невязкой жидкости в неограниченной области со смешанными граничными условиями в области, изменяющейся во времени, при этом рассматриваются только постоянные значения потенциала скорости на границе области течения.

Верификация точными решениями результатов вычислительных экспериментов моделирования течения жидкости в изменяющихся во времени областях, как правило, отсутствует, что связано с ограниченностью количества известных классов точных решений рассматриваемых задач. В данной работе обобщаются на трехмерный случай точные решения и результаты численного моделирования потенциального течения жидкости в области, изменяющейся во времени, ранее представленные в двумерном варианте в [8]. Моделированию течения жидкости в области, изменяющейся во времени в рамках модели слоистого течения жидкости, и исследованию точного решения этой задачи посвящена работа [9].

1. ПОСТАНОВКА ЗАДАЧИ

Следуя [1], рассматривается система уравнений гидродинамики в эйлеровых координатах, описывающая течение несжимаемой жидкости в ограниченной области D(t), t > 0, изменяющейся во времени:

В качестве управляющего воздействия на течение жидкости задается нормальная проекция векторного поля u(x, t) на единичную внешнюю нормаль n к гладкой границе D(t):

В случае потенциального течения жидкости ${\mathbf{u}} = \nabla \Psi $ [10] решение задачи (1.1)–(1.3) сводится к решению задачи Неймана для уравнения Лапласа на нахождение потенциала скорости Ψ(x, t), где x ∈ D(t):

Следствием условия несжимаемости жидкости является постоянство объема области D(t) в любой момент времени $t \geqslant 0$

В [1] в качестве деформаций области течения, удовлетворяющих (1.7), рассматриваются деформации, задаваемые однопараметрической группой преобразований ${{T}_{t}}:{{R}_{n}} \to {{R}_{n}}$. Эта группа преобразований задается динамической системой, описываемой автономной системой уравнений ${\mathbf{\dot {x}}} = {\mathbf{W}}\left( {\mathbf{x}} \right)$с гладким векторным полем ${\mathbf{W}}:{{R}_{n}} \to {{R}_{n}}$, ${\text{div}}\;{\mathbf{W}} = 0$ так, что $D\left( t \right) = {{T}_{t}}D\left( 0 \right)$. В данной работе деформации области течения D(t) задаются динамической системой, описываемой неавтономной системой уравнений

2. РЕЗУЛЬТАТЫ РАСЧЕТОВ

Ниже описывается решение двух тестовых задач, при этом результаты численного моделирования верифицируются найденными точными решениями задач. В первой задаче область D(t) – прямоугольный параллелепипед. Во второй задаче D(t) – сферический слой.

Численное решение получено на основе метода контрольных объемов [11]. Решение уравнения Лапласа (1.4) найдено численно методом установления [12]. Решение системы линейных алгебраических уравнений, получаемой в результате дискретизации уравнений (1.4), (1.5) разностным оператором, найдено методом переменных направлений [11].

Аппроксимация расчетной области течения, состоящей из узлов сетки, производилась только в начальный момент времени. С течением времени эволюция узлов сетки подчиняется уравнению (1.8). В этих узлах наблюдались характеристики течения жидкости: скорость течения и давление в жидкости в каждый момент времени. То есть для идентификации параметров среды в произвольный момент времени используется лагранжева система координат [13], [14]. Подобная ситуация имеет место при применении метода “частиц” [15], часто используемого при решении задач механики сплошной среды, в которых наблюдается результат эволюции среды. Отметим, что проведение расчетов (1.4)–(1.6) в эйлеровых координатах является неудобным, поскольку для вычисления поля давления (1.6) требуется вычислить частную производную по времени от потенциала скорости Ψ(x, t), при этом необходимо учитывать, что эта функция в разные моменты времени имеет, вообще говоря, разную область определения D(t), поэтому при расчетах используется переход к лагранжевой системе координат и, так как

Расчеты выполнены на серии испытаний при увеличении числа узлов сетки, при этом их результаты демонстрировали уменьшение погрешности в узлах сетки пропорционально квадрату шага сетки по пространственной переменной в сравнении с точным решением задачи, описываемым ниже.

Фиг. 1.

Течение жидкости в плоскости yOz при t = 0.2 для теста 1.

2.1. Решение задачи в прямоугольном параллелепипеде с подвижными стенками

Первая тестовая задача рассматривается в прямоугольном параллелепипеде, одна из вершин которого остается неподвижной (ее удобно поместить в начало координат), положение остальных изменяется с течением времени. В начальный момент времени t = 0 жидкость заполняет D(0) – куб со стороной 1. В качестве управляющего воздействия на границе области течения – условие (1.5), задается следующее векторное поле:

${\mathbf{V}}({\mathbf{x}},t){\text{ }} = \alpha (t)\{ x;y; - 2z\} ,$

где α(t) – произвольная непрерывно-дифференцируемая функция времени, при расчетах в тесте 1 полагается α(t) = cosπt, {x, y, z} – декартовы координаты в области D(t).

Аналитическое решение задачи (1.4)–(1.6) имеет вид

(2.1)

$\Psi = \frac{{\alpha \left( t \right)}}{2}\left( {{{x}^{2}} + {{y}^{2}} - 2{{z}^{2}}} \right),$

(2.2)

$p = - \frac{1}{2}{{\alpha }^{2}}\left( t \right)\left( {{{x}^{2}} + {{y}^{2}} + 4{{z}^{2}}} \right) - \frac{{\alpha {\text{'}}\left( t \right)}}{2}\left( {{{x}^{2}} + {{y}^{2}} - 2{{z}^{2}}} \right).$

Преобразование области D(t) имеет вид

$\begin{gathered} x = {{x}_{0}}\exp \left\{ {\int\limits_0^t {\alpha \left( \tau \right)d\tau } } \right\}, \\ y = {{y}_{0}}\exp \left\{ {\int\limits_0^t {\alpha \left( \tau \right)d\tau } } \right\}, \\ z = {{z}_{0}}\exp \left\{ { - 2\int\limits_0^t {\alpha \left( \tau \right)d\tau } } \right\}, \\ \end{gathered} $

где (x₀, y₀, z₀) ∈ D(0). При таком преобразовании области ее объем сохраняется в любой момент времени, т.е. выполняется (1.7), что соответствует течению несжимаемой жидкости. В качестве D(0) рассматривается куб со стороной 1. При указанном преобразовании области D(t) с течением времени куб (D(0)) превращается в прямоугольный параллелепипед, вытянутый вдоль Ox и Oy, суженный вдоль Oz, а затем возвращается в исходное состояние. Далее область течения становится снова кубом, затем вытягивается вдоль Oz и сужается вдоль Ox и Oy, возвращается в исходное состояние. И описанное движение области течения повторяется сначала.

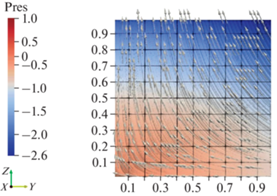
Результаты расчетов проиллюстрированы в условные моменты времени t = 0.2 и t = 1 на фиг. 1, 2 соответственно. На них изображено сечение области течения плоскостью yOz, сетка числовых значений по оси Oy, расположенной горизонтально, и по оси Oz, расположенной вертикально, цветом отображены значения поля давления p, стрелками и линиями тока показано направление поля скорости ${\mathbf{u}} = \nabla \Psi $, соответствующее потенциальному течению жидкости.

Фиг. 2.

Течение жидкости в плоскости yOz при t = 1 для теста 1.

Найденное точное решение (2.1), (2.2) использовано для верификации результатов численного моделирования потенциального течения жидкости в прямоугольном параллелепипеде с подвижными стенками. Результаты представлены в табл. 1, при этом количество узлов сетки по пространственным переменным одинаково и составляет – 42, шаг по времени – 0.001. Расчеты проведены до условного момента времени t = 1.

Таблица 1.

Результаты верификации тестовой задачи 1

Параметр, f	$\mathop {\max }\limits_{{\mathbf{x}},t} \left| {{{f}_{{an}}} - {{f}_{{calc}}}} \right|$	$\mathop {\max }\limits_{{\mathbf{x}},t} \frac{{\left| {{{f}_{{an}}} - {{f}_{{calc}}}} \right|}}{{\left| {{{f}_{{an}}}} \right|}} \times 100\% $
Ψ	3 × 10–6	0.3%
p	4 × 10–5	3%

2.2. Решение задачи в сферическом слое с переменными радиусами

Вторая тестовая задача рассматривается в сферическом слое с переменными радиусами, центр области течения удобно поместить в начало координат, его положение не меняется с течением времени. В начальный момент времени t = 0 жидкость заполняет D(0) – шар радиуса 1, предполагается, что центр шара не принадлежит области течения D(t), т.е. область течения есть сферический слой, а радиус меньшей сферы исчезающе мал. В качестве управляющего воздействия на границе области течения: условие (1.5), задается следующее векторное поле:

${\mathbf{V}}\left( {\rho ,\theta ,\varphi ,t} \right) = \left\{ {\frac{{{{\alpha }^{2}}\left( t \right)\alpha {\text{'}}\left( t \right)}}{{{{\rho }^{2}}}};\;0;\;0} \right\},$

где α(t) – произвольная дважды непрерывно-дифференцируемая функция времени, при расчетах полагалось α(t) = sinπt. Векторное поле V записано в сферической системе координат $\left\{ {\rho ,\;\theta ,\;\varphi } \right\}$, ρ – радиус-вектор некоторой точки области D(t), θ – угол между положительным направлением оси Oz и радиус-вектором, φ – угол между проекцией радиус-вектора на плоскость xOy и осью Ox.

Аналитическое решение задачи (1.4)–(1.6) имеет вид

(2.3)

$\Psi = - \frac{{{{\alpha }^{2}}\left( t \right)\alpha {\kern 1pt} '\left( t \right)}}{\rho },$

(2.4)

$p = - \frac{1}{2}\frac{{{{\alpha }^{4}}\left( t \right){{\alpha }^{{'2}}}\left( t \right)}}{{{{\rho }^{4}}}} + \frac{{2\alpha \left( t \right){{\alpha }^{{'2}}}\left( t \right) + {{\alpha }^{2}}\left( t \right)\alpha {\text{''}}\left( t \right)}}{\rho }.$

Преобразование области D(t) имеет вид

$\begin{gathered} \rho \left( t \right) = \sqrt[3]{{\rho _{0}^{3} + {{\alpha }^{3}}\left( t \right)}}, \\ \varphi = {{\varphi }_{0}}, \\ \theta = {{\theta }_{0}}, \\ \end{gathered} $

где (ρ₀, θ₀, φ₀) ∈ D(0). При таком преобразовании области течения ее объем сохраняется, т.е. выполняется 1.7, что соответствует течению несжимаемой жидкости. В качестве D(0) рассматривается шар радиуса 1. При указанном преобразовании области D(t) с течением времени шар превращается в сферический слой. Внешний радиус описывается выражением

$\rho \left( t \right) = \sqrt[3]{{1 + {{\alpha }^{3}}\left( t \right)}},$

внутренний – ρ(t) = α(t). Затем возвращается в исходное состояние.

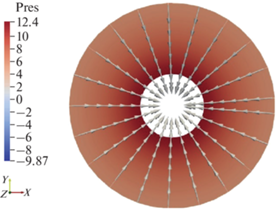
Результаты расчетов проиллюстрированы в моменты времени t = 0.3 и t = 0.9 на фиг. 3, 4 соответственно. На них изображено сечение области течения плоскостью xOy, обозначения те же, что и предыдущих фигурах. В начальный момент времени и при t = 1 жидкость покоится, давление отсутствует. В силу симметрии характеристика течения жидкости в проекции на любую плоскость, проходящую через центр области, будет иметь такой же вид, как и на представленных фигурах.

Фиг. 3.

Течение жидкости в плоскости xOy при t = 0.3 для теста 2.

Фиг. 4.

Течение жидкости в плоскости xOy при t = 0.9 для теста 2.

Найденное точное решение (2.3), (2.4) использовано для верификации результатов численного моделирования потенциального течения жидкости в сферическом слое. Результаты представлены в табл. 2, при этом количество узлов сетки по пространственным переменным соответствует значениям, представленным в тесте 1, шаг по времени тот же. Расчеты так же проведены до условного момента времени t = 1.

Таблица 2.

Результаты верификации тестовой задачи 2

Параметр,  f	$\mathop {\max }\limits_{{\mathbf{x}},t} \left| {{{f}_{{an}}} - {{f}_{{calc}}}} \right|$	$\mathop {\max }\limits_{{\mathbf{x}},t} \frac{{\left| {{{f}_{{an}}} - {{f}_{{calc}}}} \right|}}{{\left| {{{f}_{{an}}}} \right|}} \times 100\% $
Ψ	2 × 10–4	0.07%
p	0.02	0.13%

ЗАКЛЮЧЕНИЕ

В работе получены два класса точных решений уравнений Навье–Стокса в случае потенциального течения несжимаемой жидкости в переменной во времени области течения. При этом на границе области течения задается нормальная составляющая скорости течения. Результаты расчетов верифицированы найденными точными решениями.