Журнал вычислительной математики и математической физики, 2022, T. 62, № 7, стр. 1158-1179

1. ВВЕДЕНИЕ

Ниже рассматриваются математические задачи, связанные с ионизацией плазмы, применительно к процессам, происходящим в стационарных плазменных двигателях (СПД). СПД были предложены А.И. Морозовым и с 1971 г. успешно и безальтернативно используются для коррекции орбит космических летательных аппаратов. История вопроса изложена в [1]–[4].

Экспериментально фиксируется принципиально важный эффект низкочастотных (10–30 кГц) колебаний разрядного тока в камере СПД. С практической точки зрения этот эффект носит паразитический характер, а механизм указанных осцилляций неясен, но вероятной причиной, предположительно, являются возможные колебания концентраций атомов (${{n}_{a}}$) и ионов ксенона (${{n}_{i}}$) в СПД при ионизации. С другой стороны, особый интерес представляют стационарные течения плазмы в СПД. Целью работы являются, во-первых, нахождение стационарных решений нелинейных уравнений одномерной ионизации и, во-вторых, анализ причин появления периодических колебаний концентраций ${{n}_{i}}$, ${{n}_{a}}$, подчиняющихся системе

при определенных начальных и граничных условиях для ${{n}_{a}}$, ${{n}_{i}}$ (см. ниже). Здесь ${{v}_{a}}(z)$, ${{v}_{i}}(z)$ – известные продольные скорости атомов и ионов Xe, $\beta = {\text{const}} > 0$ – заданная величина (коэффициент ионизации), $L$ – длина установки СПД. Удивительным и требующим математического объяснения является факт существования периодических по времени колебаний концентраций ${{n}_{i}}$ и ${{n}_{a}}$, получаемых при решении системы (1) для непериодических входных данных – функций ${{v}_{a}}(z)$, ${{v}_{i}}(z)$ и начальных и граничных условий для ${{n}_{i}}$ и ${{n}_{a}}$. Доминирующее на сегодняшний день в научной литературе объяснение этого феномена основано на модели “хищник–жертва” Лотки–Вольтерра [5], [6], которая описывает динамику численности популяций жертв (${{N}_{1}}$) и хищников (${{N}_{2}}$), питающихся жертвами, посредством пары обыкновенных дифференциальных уравнений (ОДУ): В случае ионизации плазмы “жертвами” считаются атомы ксенона, а “хищниками” – электроны, которые в силу условия квазинейтральности плазмы отождествляются с ионами, причем ${{\gamma }_{1}} = {{\gamma }_{2}} = \beta > 0$ – коэффициент ионизации, а регенеративные члены ${{\mu }_{1}}{{N}_{1}}$, ${{\mu }_{2}}{{N}_{2}}$ обусловлены переносом атомов и ионов. При этом под ${{N}_{1}}$ и ${{N}_{2}}$ понимаются средние по отрезку $[0,L]$ концентрации атомов и ионов ксенона соответственно: ${{N}_{1}} = \left\langle {{{n}_{a}}} \right\rangle $, ${{N}_{2}} = \left\langle {{{n}_{i}}} \right\rangle $, где $\left\langle f \right\rangle = {{L}^{{ - 1}}}\int_0^L {f(z)dz} $ для любой интегрируемой на $[0,L]$ функции $f$. Впервые на феноменологическом уровне модель (2) использовалась для объяснения временных колебаний концентраций ${{n}_{a}}$ и ${{n}_{i}}$ в [7], [8]. В частности, в работе [8] считалось ${{\mu }_{1}} = {{V}_{a}}{\text{/}}L$, ${{\mu }_{2}} = {{V}_{i}}{\text{/}}L$, где ${{V}_{a}}$, ${{V}_{i}}$ – известные, не зависящие от времени скорости атомов на входе в СПД и ионов на выходе. Решениями уравнений Лотки–Вольтерра (2) являются [6] периодические кривые (циклы) на плоскости (${{N}_{1}}$,${{N}_{2}}$), расположенные в первом квадранте ${{N}_{1}} > 0$, ${{N}_{2}} > 0$ и стягивающиеся к единственной особой точке этой системы $N_{1}^{0} = {{\mu }_{2}}{\text{/}}{{\gamma }_{2}}$, $N_{2}^{0} = {{\mu }_{1}}{\text{/}}{{\gamma }_{1}}$. Предельное значение ${{\omega }_{\infty }}$ частот циклов при их стягивании к особой точке этой системы (2) проще всего получить решением линеаризованных в окрестности особой точки ($N_{1}^{0}$,$N_{2}^{0}$) уравнений системы (2). Оказывается, предельная частота ${{\omega }_{\infty }} = {{({{\mu }_{1}}{{\mu }_{2}})}^{{1/2}}}$ не зависит от ${{\gamma }_{1}}$, ${{\gamma }_{2}}$ и для предположений работы [8] дает значение ${{\omega }_{\infty }} = {{({{V}_{1}}{{V}_{2}})}^{{1/2}}}{\text{/}}L$, что примерно совпадает с экспериментально получаемой частотой колебаний разрядного тока в СПД. Этот факт совпадения экспериментальной частоты с частотой, вычисляемой по феноменологической модели (2), имеющий, не исключено, случайный характер, лежит в методологической основе и является оправданием применения модели Лотки–Вольтерра к анализу ионизационных колебаний плазмы в СПД. Дальнейшее развитие модели “хищник–жертва” применительно к процессам в СПД содержится в [9], [10]. Так, в [10] для анализа процесса ионизации предложена двухзонная модель “хищник–жертва”, в которой количество уравнений системы (2) увеличивается вдвое. В работе [11] ионизационные колебания концентраций ${{n}_{i}}$, ${{n}_{a}}$ впервые были названы “бривинг”-модами (breathing mode). Основная проблема при использовании модели Лотки–Вольтерра для анализа ионизационных колебаний плазмы в СПД сводится к нахождению математически корректного вывода феноменологических уравнений (2) из законов сохранения (1), что до сих пор никем не было сделано. В работе [12] редукция (1) $ \Rightarrow $ (2) получалась осреднением уравнений (1) по отрезку $[0,L]$ в каждый момент времени, однако при этом использовались неочевидные допущения: $\left\langle {{{n}_{i}}{{n}_{a}}} \right\rangle = \left\langle {{{n}_{i}}} \right\rangle \left\langle {{{n}_{a}}} \right\rangle $, $\left\langle {{{n}_{a}}} \right\rangle = {{n}_{a}}(t,0)$, $\left\langle {{{n}_{i}}} \right\rangle = {{n}_{i}}(t,L)$, ${{n}_{a}}(t,L) \equiv 0$, ${{n}_{i}}(t,0) \equiv 0$.

Проведенное ниже исследование показывает, что существование ионизационных колебаний (бривинг-мод) в СПД обусловлено фундаментальными математическими свойствами системы (1) и скорее всего никак не связано с феноменологической моделью Лотки–Вольтерра.

Как показывают численные расчеты, в случае знакоопределенных скоростей ${{v}_{a}}(z)$, ${{v}_{i}}(z)$ решение начально-краевой задачи для системы (1) со стационарными граничными условиями при $t \to + \infty $ выходит на установление, стремясь, как и следовало ожидать, к стационарному состоянию, определяемому системой (1). Как следствие, в этом случае бривинг-моды отсутствуют. Стационарные решения системы (1) играют особую роль, поскольку они определяют установившиеся режимы работы СПД. В разд. 2 проведено интегрирование в квадратурах стационарных уравнений (1). Показано, что краевая задача для стационарной системы (1) в случае знакоопределенных скоростей ${{v}_{a}}(z)$, ${{v}_{i}}(z)$ всегда имеет, и притом единственное, решение. В случае знакопеременных скоростей ситуация кардинально меняется. Ограничиваясь физически важным случаем ${{v}_{a}}(z) > 0$, $z \in [0,L]$ (чаще всего считается ${{v}_{a}}(z) \equiv {{v}_{a}} > 0$), установлено, что краевая задача для стационарной системы (1) имеет счетное число решений, если ${{v}_{i}}(z)$ принадлежит классу знакопеременных функций, имеющих единственный нуль ${{z}_{0}} \in (0,L)$, для которого $v_{i}^{'}({{z}_{0}}) > 0$. Скорость ${{v}_{i}}(z)$ из указанного класса функций особенно актуальна для анализа процессов в СПД. Экспериментально [13] показано, что в камере СПД всегда возникает двумерная прианодная зона, в которой продольная ионная скорость отрицательна, а вне этой зоны – положительна. Применительно к одномерной модели приходим к скорости ${{v}_{i}}(z)$ указанного выше типа. В частности, для таких скоростей ${{v}_{i}}(z)$, как показывают расчеты, могут существовать бривинг-моды. Более того, стационарные решения для скоростей ${{v}_{i}}(z)$, не входящих в указанный выше класс, отсутствуют.

В разд. 3 в случае ${{v}_{a}} = {\text{const}}$, ${{v}_{i}} = {\text{const}}$ нелинейная система (1) решается аналитически. Полученные интегральные аналитические выражения для неизвестных ${{n}_{a}}$, ${{n}_{i}}$ позволяют решить аналитически задачу Коши в полуплоскости $t \geqslant 0$ и простейшие краевые (в полуплоскости $z \geqslant 0$) и смешанные (в первом квадранте $t \geqslant 0$, $z \geqslant 0$) задачи для этой системы. Методы, развитые в этом разделе, позволяют решать и другие начально-краевые задачи для системы (1) в случае постоянных скоростей ${{v}_{a}}$, ${{v}_{i}}$. Из выведенных в разд. 3 формул для решения системы (1), в частности, следует отсутствие бривинг-мод в случае ${{v}_{a}} = {\text{const}}$, ${{v}_{i}} = {\text{const}}$.

В разд. 4 для случая ${{v}_{a}} = {\text{const}} > {\text{0}}$ и знакопеременных скоростей ${{v}_{i}}(z)$, имеющих единственный нуль ${{z}_{0}} \in (0,L)$, для которого $v_{i}^{'}({{z}_{0}}) > 0$, обсуждается причина возникновения ионизационных колебаний (бривинг-мод) при решении системы (1). В этом случае прямая $z = {{z}_{0}}$ является характеристикой системы (1), а необходимое и достаточное условие существования бривинг-мод состоит в периодичности значений функций ${{n}_{i}}$, ${{n}_{a}}$ на указанной характеристике, ${{n}_{i}}(t) = {{n}_{i}}(t,{{z}_{0}})$, ${{n}_{a}}(t) = {{n}_{a}}(t,{{z}_{0}})$ при $t \to + \infty $. В разд. 4 выведено ОДУ, которому удовлетворяет функция ${{n}_{i}}(t)$, совпадающее с условием разрешимости [14] для квазилинейных систем уравнений в частных производных, и указана процедура нахождения функции ${{n}_{a}}(t)$. Оказывается, значения ${{n}_{i}}$, ${{n}_{a}}$ на характеристике $z = {{z}_{0}}$ подчиняются системе ОДУ более сложной, чем уравнение Лотки–Вольтерра. Сами функции ${{n}_{i}}(t)$, ${{n}_{a}}(t)$ находятся численным решением уравнений ионизации (1) посредством предложенной в работе разностной схемы. Аналитическое исследование существования и свойств функций ${{n}_{i}}(t)$, ${{n}_{a}}(t)$ выходит за рамки настоящей работы.

Недостаток модели ионизации (1) в том, что скорость ионов ${{{v}}_{i}}$ стационарная и задается, а не ищется из уравнения движения ионов. Поэтому справедливость выводов, которые делаются на основе анализа решений системы (1) (в том числе о наличии ионизационных колебаний), в значительной степени зависит от того, насколько правильно выбрана скорость ${{v}_{i}}$. Скорость ионов, определяемая из уравнения движения ионов, вообще говоря, зависит от времени, ${{v}_{i}} = {{v}_{i}}(t,z)$, что не учитывается в системе (1). Поэтому в разд. 5 существование ионизационных колебаний устанавливается на базе численного исследования посредством метода макрочастиц значительно более точной модели ионизации, состоящей из кинетического уравнения для ионов, двигающихся в заданном постоянном и однородном электромагнитном поле в СПД, и уравнения переноса атомов ксенона с учетом ионизации. При этом индукционные электромагнитные поля, порождаемые плазменными токами в СПД, и рассеяние электронов и ионов на боковых стенках камеры считаются пренебрежимо малыми.

2. СТАЦИОНАРНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ИОНИЗАЦИИ

Ниже ограничимся исключительно важным случаем ${{v}_{a}}(z) > 0$ и даже еще более жестким ограничением ${{v}_{a}} = {\text{const}} > 0$.

В случае $\partial {\text{/}}\partial t = 0$ система уравнений ионизации принимает вид:

Складывая почленно уравнения (3), приходим к первому интегралу системы (3): Из (4) следует ${{n}_{a}}{{v}_{a}} = C - u$, $u\mathop = \limits_{{\text{def}}} {{u}_{i}}{{v}_{i}}$. Подставляя эти выражения во второе уравнение (3), получаем для нахождения $u(z)$ ОДУ первого порядка с разделяющимися переменными Откуда имеем Если $C = 0$, то верно Уравнение (5) имеет также два особых решения $u \equiv C$, $u \equiv 0$. Первое не имеет физического смысла, второе дает ${{n}_{i}} \equiv 0$, ${{n}_{a}} = C{\text{/}}{{v}_{a}}(z)$ и соответствует случаю, когда ионизация отсутствует. Анализ формул (6) и (7) зависит от количества и расположения нулей ${{v}_{i}}(z)$, которые входят в знаменатель подынтегрального выражения в (6) и (7).

Допустим на $[0,L]$ скорости ${{v}_{a}}(z)$, ${{v}_{i}}(z)$ знакопостоянные. Тогда из (6) следует

где $C \ne 0$, $D$ – произвольные константы. Из ${{n}_{a}}(z) \geqslant 0$ и ${{v}_{a}}(z) > 0$ следует $C(1 + D\exp F(z)) > 0$, и, значит, знак $D$ совпадает со знаком ${{v}_{i}}(z)$. Константы $C$ и $D$ в формуле (8) ищутся из граничных условий для ${{n}_{a}}$, ${{n}_{i}}$. Если ${{v}_{i}}(z) > 0$, то на левой границе $z = 0$ задаются ${{n}_{a}}(0) = {{n}_{{a0}}} > 0$, ${{n}_{i}}(z) = {{n}_{{i0}}} > 0$. Если ${{v}_{i}}(z) < 0$, то на левой границе задается ${{n}_{a}}(0) = {{n}_{{a0}}} > 0$, а на правой границе $z = L$ задается ${{n}_{i}}(L) = {{n}_{{iL}}} > 0$.

Если ${{v}_{i}}(z) > 0$ на $[0,L]$, то из (4) следует $C > 0$ и для неособого решения $D > 0$. Из (4) следует $C = {{n}_{{a0}}}{{v}_{a}}(0) + {{n}_{{i0}}}{{v}_{i}}(0)$, тогда из (8) выводим

Итак, константы $C$ и $D$ в (8) однозначно определяются по граничным условиям, а краевая задача для системы (3) имеет, и притом единственное, решение.

Если ${{v}_{i}}(z) < 0$ на $[0,L]$, то исследование разрешимости краевой задачи для системы (3) более громоздкое. Краевые условия, согласно (8), дают следующее:

Обозначая ${{k}_{i}} = {{n}_{{iL}}}\left| {{{v}_{i}}(L)} \right| > 0$, ${{k}_{a}} = {{n}_{{a0}}}{{v}_{a}}(0) > 0$ и исключая $D = C{\text{/}}{{k}_{a}} - 1$, получаем для нахождения константы $C$ трансцендентное уравнение: Уравнение (9) всегда имеет решение $C = 0$. Другие решения, отличные от $C = 0$, могут существовать только при $ - {{k}_{i}} < C < {{k}_{a}}$. На этом интервале функция $g(C)$, легко проверить, имеет единственный absmin в точке ${{C}_{0}} = ({{k}_{a}} - {{k}_{i}}){\text{/}}2$ и $g( - {{k}_{i}} + 0) = g({{k}_{a}} - 0) = + \infty $. Поэтому из геометрических соображений легко следует, что при $g{\kern 1pt} '(0) \ne f{\kern 1pt} '(0)$ $ \Leftrightarrow $ $k_{i}^{{ - 1}} - k_{a}^{{ - 1}} \ne \beta {{F}_{0}}(L)$ уравнение (9) имеет на $( - {{k}_{i}},{{k}_{a}})$ еще одно решение $C$, отличное от нуля. Для этого решения и константы $D = C{\text{/}}{{k}_{a}} - 1$ краевая задача для системы (3) имеет, и притом единственное, решение, задаваемое формулами (8). Если $g{\kern 1pt} '(0) = f{\kern 1pt} '(0)$, то прямое вычисление показывает, что $g{\kern 1pt} '{\kern 1pt} '(0) > f{\kern 1pt} '{\kern 1pt} '(0)$, и из геометрических соображений следует, что уравнение (9) имеет на $( - {{k}_{i}},{{k}_{a}})$ только нулевое решение. В этом случае стационарное решение системы (3) ищется по формуле (7), которая дает Граничные условия при $z = 0$ для ${{n}_{a}}$ и $z = L$ для ${{n}_{i}}$ дают два уравнения для нахождения одной константы $D$: которые в силу условия $g{\kern 1pt} '(0) = f{\kern 1pt} '(0)$ $ \Leftrightarrow $ $k_{i}^{{ - 1}} - k_{a}^{{ - 1}} = \beta {{F}_{0}}(L)$ совместны и имеют единственное решение $D = - k_{a}^{{ - 1}}$. В частности, $D$ отрицательно, и в формулах для ${{n}_{i}}$, ${{n}_{a}}$ не приходится делить на нуль. Итак, при ${{{v}}_{i}}(z) < 0$ краевая задача для системы (3) тоже имеет, и притом единственное, решение.

Численное решение начально-краевой задачи для системы (1) по разностной схеме, предлагаемой ниже, со стационарными краевыми условиями в случае знакопостоянных ${{{v}}_{a}}(z)$, ${{{v}}_{i}}(z)$ показывает, что ее решение при $t \to + \infty $ сходится к стационарному решению системы (1), в частности, осцилляции концентраций ${{n}_{i}}$, ${{n}_{a}}$ (бривинг-моды) отсутствуют.

Рассмотрим теперь случай знакопеременных ионных скоростей ${{{v}}_{i}}(z)$ на типичном примере ${{{v}}_{i}}(z) = \alpha (z - {{z}_{0}})$, ${{z}_{0}} \in (0,L)$, $\alpha > 0$. Тогда ${{v}_{i}}({{z}_{0}}) = 0$, $\alpha = v_{i}^{'}({{z}_{0}}) > 0$. Будем искать только такие стационарные решения, для которых ${{n}_{i}}(z)$ не обращается тождественно в нуль ни на каком интервале, лежащем в $[0,L]$ (если это не так, то ${{n}_{i}}(z) \equiv 0$ на некотором интервале $[0,L]$ и, значит, на этом интервале процесс ионизации прекратился, что противоречит экспериментальным данным по СПД). Из первого интеграла (4), вычисленного в точке ${{z}_{0}}$, следует, что $C \geqslant 0$. Случай $C = 0$ приводит к физически абсурдным решениям (см. ниже). Поэтому считаем $C > 0$. Тогда стационарное решение вычисляется по формулам (6), примененным отдельно к полуинтервалам $[0,{{z}_{0}})$ и $({{z}_{0}},L]$, и имеет вид

где константа ${{D}_{ + }}$ действует в полуинтервале $({{z}_{0}},L]$, а константа ${{D}_{ - }}$ – в полуинтервале $[0,{{z}_{0}})$. Граничное условие ставится только для ${{n}_{a}}$ на левой границе $z = 0$: ${{n}_{a}} = {{n}_{{a0}}} > 0$. Поскольку ${{v}_{i}}(0) < 0 < {{v}_{i}}(L)$, то для ${{n}_{i}}$ граничные условия на концах $z = 0$ и $z = L$ не нужны. Таким образом, для нахождения стационарного решения (10), удовлетворяющего заданному граничному условию, необходимо по одной константе ${{n}_{{a0}}}$ найти три константы $C$, ${{D}_{ + }}$, ${{D}_{ - }}$.

Проведем следующее рассуждение. Пусть ${{n}_{i}}(z)$ бесконечно дифференцируема в окрестности ${{z}_{0}}$ и не все производные ${{n}_{i}}$ в точке ${{z}_{0}}$ обращаются в нуль. Пусть $k \geqslant 0$ – наименьшее целое, для которого $n_{i}^{{(k)}}({{z}_{0}}) \ne 0$. Поскольку ${{n}_{i}} \geqslant 0$ всюду в $[0,L]$, то с помощью формулы Тейлора (см. ниже) нетрудно показать, что $k$ – четное. Пусть $k = 2\ell $, $\ell \geqslant 0$. По формуле Тейлора с остаточным членом в форме Пеано имеем

Проинтегрируем стационарное уравнение неразрывности для ${{n}_{i}}$ по отрезку $[{{z}_{0}} - \varepsilon ,{{z}_{0}} + \varepsilon ]$ для достаточно малого $\varepsilon > 0$: Выражение слева равно где из (11) следует $\Delta (\varepsilon ) = o({{\varepsilon }^{{2\ell + 1}}})$, $\varepsilon \to 0$.

Выражение справа равно

где из явного вида для $B(\varepsilon )$ и (11) легко следует $B(\varepsilon ) = o({{\varepsilon }^{{2\ell + 1}}})$, $\varepsilon \to 0$. Приравнивая выведенные выражения для правой и левой частей интегрального тождества, деля полученное равенство на ${{\varepsilon }^{{2\ell + 1}}}$ и устремляя $\varepsilon $ к нулю, имеем Подставляя найденное решение ${{n}_{a}}({{z}_{0}})$ во второе уравнение (10) в точке ${{z}_{0}}$, получаем $(\alpha {\text{/}}\beta )(2\ell + 1) = C{\text{/}}{{v}_{a}}$, откуда получаем значение константы $C = \alpha {{v}_{a}}(2\ell + 1){\text{/}}\beta $ и равенство $\zeta = (2\ell + 1)$. Поэтому первое уравнение (10) дает Из формулы Тейлора следует, что существует конечный предел Поэтому из (12) следует, что $ - {{D}_{ - }} = {{D}_{ + }}\mathop = \limits_{{\text{def}}} D$, т.к. $C \ne 0$, и тогда обе формулы (12) и обе формулы (10) для ${{n}_{a}}$ объединяются в одну уже без знака модуля Теперь ищется константа $D$ из второго равенства (13), $D = (1 - C{\text{/}}({{n}_{{a0}}}{{v}_{a}})){\text{/}}z_{0}^{{2\ell + 1}}$. Из интеграла (4) следует $C \leqslant {{n}_{{a0}}}{{v}_{a}}$, поэтому $D \geqslant 0$. Но при $D = 0$ из (13) следует ${{n}_{i}}(z) \equiv 0$, $z \in [0,L]$, что невозможно. Значит, $D > 0$.

Итак, установлено, что краевая задача для стационарной системы (1) в случае ${{v}_{a}} = {\text{const}} > {\text{0}}$, ${{v}_{i}}(z) = \alpha (z - {{z}_{0}})$, $\alpha > 0$, ${{z}_{0}} \in (0,L)$, имеет на отрезке $[0,L]$ счетное число решений, задаваемых формулой (13). Если ${{n}_{i}}(z)$ аналитична в окрестности ${{z}_{0}}$, то, очевидно, других решений указанная краевая задача не имеет, и в этом случае формула (13) дает общий вид решений краевой задачи для стационарной системы (1). Наконец, в случае $C = 0$ стационарное решение системы (1) задается формулой (7) применительно к каждому полуинтервалу $[0,{{z}_{0}})$, $({{z}_{0}},L]$:

где ${{D}_{ \pm }}$ – положительные константы, причем константа ${{D}_{ - }}$ действует для $z < {{z}_{0}}$, а ${{D}_{ + }}$ – для $z > {{z}_{0}}$. Полученное решение физически абсурдно, поскольку $\mathop {\lim }\limits_{z \to {{z}_{0}} + 0} {{n}_{i}}(z) = - \infty $, $\mathop {\lim }\limits_{z \to {{z}_{0}} - 0} {{n}_{i}}(z) = + \infty $, в частности, нарушается неотрицательность концентрации ${{n}_{i}}(z)$ и интегрируемость функции ${{n}_{i}}(z)$ на $[0,L]$ (в точке $z = {{z}_{0}}$ интеграл от ${{n}_{i}}(z)$ расходится).

Предложенный способ построения решений краевых задач пригоден для любой функции ${{v}_{i}}(z)$, имеющей единственный нуль ${{z}_{0}}$ на $[0,L]$, причем $0 < {{z}_{0}} < L$ и $v_{i}^{'}({{z}_{0}}) > 0$. Приведем два примера.

Пример 1. Пусть ${{v}_{i}}(z) = a(z + {{z}_{1}})(z - {{z}_{0}})$, ${{z}_{1}} > 0$, $0 < {{z}_{0}} < L$, $a > 0$. Тогда $\alpha = v_{i}^{'}({{z}_{0}}) = a({{z}_{0}} + {{z}_{1}}) > 0$. Действуя по схеме, предложенной выше, получаем счетное число решений краевой задачи для (3) с граничным условием ${{n}_{a}}(0) = {{n}_{{a0}}} > 0$:

При этом $D > 0$. Если ${{n}_{i}}(z)$ аналитична в окрестности ${{z}_{0}}$, то указанные функции дают общее решение краевой задачи.

Пример 2. Пусть ${{v}_{i}}(z) = - \cos (\pi z{\text{/}}L)$, ${{z}_{0}} = L{\text{/}}2$ – единственный нуль на $[0,L]$, $v_{i}^{'}({{z}_{0}}) = $ $ = \pi {\text{/}}L\mathop = \limits_{{\text{def}}} \alpha > 0$. Действуя по схеме, предложенной выше, получаем счетное число решений краевой задачи для (3) с граничным условием ${{n}_{a}}(0) = {{n}_{{a0}}} > 0$:

При этом $D > 0$. Если ${{n}_{i}}(z)$ аналитична в окрестности ${{z}_{0}}$, то указанные функции дают общее решение краевой задачи.

Интегральное тождество, из которого выводились выше значения констант $C$, ${{D}_{ \pm }}$, имеет простой смысл – это баланс количества ионов, возникающих на отрезке $[{{z}_{0}} - \varepsilon ,{{z}_{0}} + \varepsilon ]$ вследствие ионизации и за счет переноса ионов со скоростью ${{v}_{i}}$ через границы отрезка. Основная идея подсчета констант заключалась в том, чтобы найти асимптотики обоих количеств при $\varepsilon \to 0$ ($ \equiv $ главные члены разложений по $\varepsilon $ обеих частей интегрального тождества) и приравнять их. Этот прием позволяет получать и другие неочевидные результаты. Например, если ${{v}_{i}}(z)$ обращается в нуль в некоторой точке ${{z}_{0}} \in (0,L)$, в окрестности которой ${{n}_{i}}$ аналитична и для которой $\alpha = v_{i}^{'}(z) < 0$, то стационарная система (3) не имеет решений. Действительно, для такого решения, повторяя рассуждения выше, получаем равенство ${{n}_{a}}({{z}_{0}}) = \alpha (2\ell + 1){\text{/}}\beta $ для некоторого целого $\ell \geqslant 0$, из которого вытекает неравенство ${{n}_{a}}({{z}_{0}}) < 0$, что физически абсурдно. Другой пример дает функция ${{v}_{i}}(z)$, которая на отрезке $[0,L]$ имеет единственный нуль ${{z}_{0}} \in (0,L)$ и выполнено условие $v_{i}^{'}({{z}_{0}}) = 0$. Тогда система (3) решений не имеет. Действительно, повторяя рассуждения выше применительно к интегральному тождеству, получаем ${{n}_{a}}({{z}_{0}}) = 0$, и, значит, константа $C$ в первом интеграле (4) равна нулю. С другой стороны, функция ${{n}_{a}}(z)$ монотонно невозрастающая на $[0,L]$ и неотрицательная, поэтому ${{n}_{a}}(z) \equiv 0$, $z \in [{{z}_{0}},L]$, но тогда из интеграла (4) с учетом $C = 0$ и знакоопределенности ${{v}_{i}}(z)$ на $({{z}_{0}},L]$ следует, что и ${{n}_{i}}(z) \equiv 0$, $z \in [{{z}_{0}},L]$, что физически абсурдно. Добавим, если вычислить ${{n}_{i}}$ на $[0,{{z}_{0}})$ посредством формулы (7), то нетрудно убедиться в разрывности функции ${{n}_{i}}$ в точке ${{z}_{0}}$ и логарифмической расходимости интеграла от ${{n}_{i}}(z)$ по отрезку $[0,L]$, что противоречит физическому смыслу концентрации ионов. Обобщая предыдущие примеры, приходим к физически важному выводу, что граничная задача для системы (3) имеет решение только если скорость ${{v}_{i}}(z)$ обладает единственным нулем ${{z}_{0}} \in (0,L)$, для которого $\alpha = v_{i}^{'}({{z}_{0}}) > 0$. В этом случае при определенном соотношении $\beta $ и $\alpha $ возникают ионизационные колебания (бривинг-моды).

Для численного решения перепишем систему (1) в безразмерном виде, взяв за характерные масштабы длины ${{L}_{0}} = 1$ см, скорости ${{v}_{0}} = 1.5 \times {{10}^{5}}$ см/с, времени ${{t}_{0}} = {{L}_{0}}{\text{/}}{{v}_{0}} = 0.66 \times {{10}^{{ - 5}}}$ с, концентрации ${{n}_{0}} = {{10}^{{12}}}$ см^–3, $\beta = {{10}^{{ - 8}}}$ см³/с. Тогда система (1) относительно безразмерных значений всех величин перепишется в виде:

где ${{k}_{I}}$ – безразмерное значение коэффициента ионизации.

Рассмотрим типичный пример расчета бривинг-мод по дивергентной разностной схеме “разности против потока” [15] на равномерной сетке на отрезке [0, L]:

где ${{v}_{{i,k + 1/2}}} = {{v}_{i}}((k + 1{\text{/}}2)h)$, $ - 1 \leqslant k \leqslant N$. Заметим, что при $k = 0$ значение $n_{{i, - 1}}^{0}$, а при $k = N$ значение $n_{{i,N + 1}}^{0}$ умножается на нуль и в силу этого не используется. Условия устойчивости для схемы имеют вид: При соблюдении условий устойчивости нетрудно получить оценки где $\max $ берется по  $0 \leqslant k \leqslant N$. Эти оценки гарантируют вычислительную устойчивость схемы (15) на конечном временном отрезке $[0,T]$.

Рассмотрим результаты расчета по схеме (15) , представленные на фиг. 1, для ${{v}_{i}}(z) = \alpha (z - {{z}_{0}})$. Фиг. 1 демонстрирует возникновение периодических колебаний концентраций ${{n}_{a}}$, ${{n}_{i}}$ (бривинг-мод) с размерной частотой ~20 кГц. Эти колебания возникают не при всех ${{k}_{I}} > 0$, $\alpha > 0$. Очевидно, на плоскости ${{k}_{I}} > 0$, $\alpha > 0$ существует некоторая неизвестная нам область, для $({{k}_{I}},\alpha )$ из которой возникают бривинг-моды. Для $({{k}_{I}},\alpha )$, не попавших в указанную область, счет по схеме (15) приводит к установлению решения. Вероятно, появление бривинг-мод связано с неединственностью решения краевой задачи для системы (3), установленной выше. Решение начально-краевой задачи для системы (1) может при $t \to + \infty $ сходиться к одному из счетного числа стационарных состояний, задаваемых формулами (13), но может, как показывают расчеты, при $t \to + \infty $ выходить на периодический режим (фиг. 1), не притягиваясь ни к одному из стационарных состояний. Логически возможен также хаотический характер решения начально-кравевой задачи для системы (1) при $t \to + \infty $, но в расчетах он зафиксирован не был. Математическая причина возникновения бривинг-мод будет разъяснена в разд. 3.

3. РЕШЕНИЕ УРАВНЕНИЙ ИОНИЗАЦИИ В СЛУЧАЕ ПОСТОЯННЫХ СКОРОСТЕЙ

Решим систему (1) в случае ${{v}_{a}} = {\text{const}}$, ${{v}_{i}} = {\text{const}}$. В безразмерном виде она является частным случаем системы (14):

Рассмотрим основной случай ${{v}_{a}} \ne {{v}_{i}}$. Проведем замену независимых переменных: или в координатном виде: Отсюда для дифференциальных операторов получим соотношения Подставляя эти выражения в систему (16), сведем ее к эквивалентному виду: Итак, задача нахождения непрерывно дифференцируемых решений системы (16) в области $D$ переменных $(t,z)$ равносильна задаче нахождения непрерывно дифференцируемых решений системы (18) в области $\varphi (D)$ переменных $(\alpha ,\beta )$. Отображение $\varphi $ линейное, невырожденное, с определителем $\det \varphi = 1{\text{/}}({{v}_{i}} - {{v}_{a}}) \ne 0$. В частности, $\varphi $ прямые переводит в прямые, многоугольники – в многоугольники, выпуклые множества – в выпуклые множества и т.д. Элементарная теория решений системы (18) в прямоугольнике $\Pi = [{{\alpha }_{0}},{{\alpha }_{1}}] \times [{{\beta }_{0}},{{\beta }_{1}}]$, ${{\alpha }_{0}} < {{\alpha }_{1}}$, ${{\beta }_{0}} < {{\beta }_{1}}$, основана на двух результатах [16].

Теорема 1. 1) Пусть $A(\alpha )$, $B(\beta )$ – дважды непрерывно дифференцируемые функции на отрезках $[{{\alpha }_{0}},{{\alpha }_{1}}]$, $[{{\beta }_{0}},{{\beta }_{1}}]$, соответственно, причем $A(\alpha ) \ne B(\beta )$ для любых $\alpha \in [{{\alpha }_{0}},{{\alpha }_{1}}]$, $\beta \in [{{\beta }_{0}},{{\beta }_{1}}]$. Тогда функции

составляют непрерывно дифференцируемое решение системы (18) в прямоугольнике $\Pi $.

2) Если непрерывно дифференцируемые решения ${{n}_{a}}$, ${{n}_{i}}$ системы (18) таковы, что множество нулей каждой из этих функций в $\Pi $ имеет пустую внутренность и $\bar {A}(\alpha )$, $\bar {B}(\beta )$ еще один комплект функций на $[{{\alpha }_{0}},{{\alpha }_{1}}]$, $[{{\beta }_{0}},{{\beta }_{1}}]$, соответственно, удовлетворяющий условиям части 1) теоремы и восстанавливающий по формулам (19) те же самые функции ${{n}_{a}}$, ${{n}_{i}}$ в $\Pi $, то найдутся константы $R \ne 0$, $C$, для которых:

Обратно, если $\bar {A}(\alpha )$, $\bar {B}(\beta )$ вычисляются по $A(\alpha )$, $B(\beta )$ посредством формул (20) для некоторых констант $R \ne 0$, $C$, то они удовлетворяют условиям части 1) и по формулам (19) восстанавливают те же функции ${{n}_{a}}$, ${{n}_{i}}$, что и для $A(\alpha )$, $B(\beta )$.

3) В условиях части 1) теоремы функции ${{n}_{a}}$, ${{n}_{i}}$, вычисляемые по формулам (19), удовлетворяют всюду в $\Pi $ неравенствам ${{n}_{a}} \geqslant 0$, ${{n}_{i}} \geqslant 0$ тогда и только тогда, когда либо $A(\alpha )$, $B(\beta )$ монотонно не убывают на $[{{\alpha }_{0}},{{\alpha }_{1}}]$, $[{{\beta }_{0}},{{\beta }_{1}}]$, соответственно, и $\mathop {\inf }\limits_{\alpha \in [{{\alpha }_{0}},{{\alpha }_{1}}]} A(\alpha ) > \mathop {\sup }\limits_{\beta \in [{{\beta }_{0}},{{\beta }_{1}}]} B(\beta )$ ($ \equiv {\kern 1pt} A({{\alpha }_{0}}) > B({{\beta }_{1}})$), либо $A(\alpha )$, $B(\beta )$ монотонно не возрастают соответственно на $[{{\alpha }_{0}},{{\alpha }_{1}}]$, $[{{\beta }_{0}},{{\beta }_{1}}]$ и $\mathop {\sup }\limits_{\alpha \in [{{\alpha }_{0}},{{\alpha }_{1}}]} A(\alpha ) < \mathop {\inf }\limits_{\beta \in [{{\beta }_{0}},{{\beta }_{1}}]} B(\beta )$ ($ \equiv {\kern 1pt} A({{\alpha }_{0}}) < B({{\beta }_{1}})$).

Если $A(\alpha )$, $B(\beta )$ удовлетворяют условиям части 1) теоремы 1, то ${{n}_{a}}$, ${{n}_{i}}$, вычисляемые по формулам (19), непрерывно дифференцируемы в $\Pi $ и существуют непрерывные в $\Pi $ смешанные производные ${{\partial }^{2}}{{n}_{a}}{\text{/}}(\partial \alpha \partial \beta )$, ${{\partial }^{2}}{{n}_{a}}{\text{/}}(\partial \beta \partial \alpha )$ и ${{\partial }^{2}}{{n}_{i}}{\text{/}}(\partial \alpha \partial \beta )$, ${{\partial }^{2}}{{n}_{i}}{\text{/}}(\partial \beta \partial \alpha )$. Это обстоятельство позволяет сформулировать обратное утверждение.

Теорема 2. Пусть ${{n}_{a}} > 0$, ${{n}_{i}} > 0$ – непрерывно дифференцируемое решение (18) в прямоугольнике $\Pi $, для которого существуют обе непрерывные в $\Pi $ смешанные частные производные ${{\partial }^{2}}{{n}_{a}}{\text{/}}(\partial \alpha \partial \beta )$, ${{\partial }^{2}}{{n}_{a}}{\text{/}}(\partial \beta \partial \alpha )$ и ${{\partial }^{2}}{{n}_{i}}{\text{/}}(\partial \alpha \partial \beta )$, ${{\partial }^{2}}{{n}_{i}}{\text{/}}(\partial \beta \partial \alpha )$. Тогда найдутся дважды непрерывно дифференцируемые функции $A(\alpha )$, $B(\beta )$, определенные на сторонах прямоугольника, соответственно, $[{{\alpha }_{0}},{{\alpha }_{1}}]$ и $[\beta ,{{\beta }_{1}}]$, для которых $A(\alpha ) \ne B(\beta )$ при всех $\alpha \in [{{\alpha }_{0}},{{\alpha }_{1}}]$, $\beta \in [{{\beta }_{0}},{{\beta }_{1}}]$ и всюду в $\Pi $ выполнены равенства (19).

Замечание. Таким образом, для класса положительных непрерывно дифференцируемых решений системы (18), для которых в $\Pi $ существуют обе непрерывные смешанные частные производные, формулы (19) задают общий вид решений этого класса.

Из теоремы 1 п. 2) следует, что в формулах (19) всегда можно считать $A(\alpha )$, $B(\beta )$ монотонно неубывающими функциями на $[{{\alpha }_{0}},{{\alpha }_{1}}]$, $[{{\beta }_{0}},{{\beta }_{1}}]$ соответственно. Кроме того, стороны прямоугольника $\Pi $ могут быть интервалами или полуинтервалами, в том числе полубесконечными или бесконечными. Соответствующие изменения формулировки теоремы 1 п. 3) очевидны.

Из теорем 1, 2 следует, что в ${{\varphi }^{{ - 1}}}(\Pi )$ решение системы (16) задается формулами:

где $A(\alpha )$, $B(\beta )$ – произвольные функции, удовлетворяющие условию теоремы 1 п. 1.

Формулы (21) справедливы для ${{v}_{i}} \ne {{v}_{a}}$. При ${{v}_{i}} = {{v}_{a}}$ они теряют смысл. Для ${{v}_{i}} = {{v}_{a}} = v$ общее решение системы (16) получается напрямую, без введения новых координат $\alpha $, $\beta $, интегрированием уравнений этой системы вдоль характеристик. Характеристики системы (16) имеют вид $z(t) = vt + {\text{const}}$ и различаются значениями ${\text{const}}$. Пусть ${{n}_{a}}(t) = {{n}_{a}}(t,z(t))$, ${{n}_{i}}(t) = {{n}_{i}}(t,z(t))$ значения неизвестных функций ${{n}_{a}}$, ${{n}_{i}}$ вдоль фиксированной характеристики. Тогда из (16) следует, что функции ${{n}_{a}}(t)$, ${{n}_{i}}(t)$ удовлетворяют системе ОДУ

Складывая почленно эти уравнения, получаем первый интеграл системы (22): Поскольку ${{n}_{a}} \geqslant 0$, ${{n}_{i}} \geqslant 0$, то $C \geqslant 0$. При $C = 0$ имеем ${{n}_{a}}(t) \equiv 0$, ${{n}_{i}}(t) \equiv 0$ – тривиальное решение системы (22), не имеющее смысла. Поэтому ниже считаем $C > 0$. Тогда ${{n}_{a}} = C - {{n}_{i}}$, и для нахождения ${{n}_{i}}$ имеем ОДУ Интегрируя, получаем Поскольку ${{n}_{i}} \geqslant 0$, ${{n}_{a}} = C - {{n}_{i}} \geqslant 0$, то $0 \leqslant {{n}_{i}} \leqslant C$, и в последнем равенстве знак модуля можно убрать. В результате получим В случае $D = 0$ получим одно из двух особых решений (23): ${{n}_{i}} \equiv 0$. Другое особое решение ${{n}_{i}} \equiv C$. Формулы (24) задают общее решение системы (22) на произвольной характеристике. Константы $C$ и $D$ определяются значениями ${{n}_{a}}$, ${{n}_{i}}$ в произвольной точке на рассматриваемой характеристике. В частности, при решении начально-краевых задач для системы (16) значения $C$ и $D$ определяются начальными и граничными условиями (см. ниже).

Применим формулы (21), (24) для решения начально-краевых задач для системы (16), которые представляют основной практический интерес. Ограничимся следующими простейшими задачами.

Задача 1. Начальная задача (задача Коши): в полуплоскости $z \in \mathbb{R}$, $t \geqslant 0$ найти непрерывно дифференцируемое решение системы (16), для которого выполнены начальные условия ${{n}_{a}}(0,z) = n_{a}^{0}(z)$, ${{n}_{i}}(0,z) = n_{i}^{0}(z)$, $z \in \mathbb{R}$, где $n_{a}^{0}(z)$, $n_{i}^{0}(z)$ – заданные неотрицательные непрерывно дифференцируемые функции на прямой.

Задача 2. Краевая задача: для ${{v}_{a}},{{v}_{i}} \geqslant 0$ в полуплоскости $z \geqslant 0$, $t \in \mathbb{R}$ найти непрерывно дифференцируемое решение системы (16), для которого выполнены краевые условия ${{n}_{a}}(t,0) = {{n}_{{a0}}}(t)$, ${{n}_{i}}(t,0) = {{n}_{{i0}}}(t)$, $t \in \mathbb{R}$, где ${{n}_{{a0}}}(t)$, ${{n}_{{i0}}}(t)$ – заданные неотрицательные непрерывно дифференцируемые функции на прямой.

Задача 3. Начально-краевая (смешанная) задача: для ${{v}_{a}},{{v}_{i}} \geqslant 0$ в первом квадранте $z \geqslant 0$, $t \geqslant 0$ найти непрерывно дифференцируемое решение системы (16), для которого выполнены начальные условия ${{n}_{a}}(0,z) = n_{a}^{0}(z)$, ${{n}_{i}}(0,z) = n_{i}^{0}(z)$, $z \geqslant 0$ и краевые условия ${{n}_{a}}(t,0) = {{n}_{{a0}}}(t)$, ${{n}_{i}}(t,0) = {{n}_{{i0}}}(t)$, $t \geqslant 0$, где $n_{a}^{0}(z)$, $n_{i}^{0}(z)$, $z \geqslant 0$, ${{n}_{{a0}}}(t)$, ${{n}_{{i0}}}(t)$, $t \geqslant 0$ – заданные непрерывно дифференцируемые функции на полупрямых $z \geqslant 0$ и $t \geqslant 0$, подчиняющиеся условиям согласованности:

Более сложные начально-краевые задачи в этой работе не рассматриваются.

В случае ${{v}_{i}} = {{v}_{a}}$ начально-краевые задачи легко решаются по формуле (32) методом характеристик.

Рассмотрим задачу 1 в случае ${{v}_{a}} \ne {{v}_{i}}$. В переменных $(\alpha ,\beta )$ задача состоит в поиске непрерывно дифференцируемого решения системы (18) в полуплоскости $P\,\mathop = \limits_{{\text{def}}} \,\{ \alpha + \beta \geqslant 0\} $, которое на границе этой полуплоскости $\alpha + \beta = 0$ имеет заданные значения

Выше был изложен способ решения системы (18) в произвольном прямоугольнике $\Pi $. Построим решение системы (18) в бесконечном прямоугольнике ${{\Pi }_{\infty }} = \mathbb{R} \times \mathbb{R} \supseteq P$, которое на прямой $\alpha + \beta = 0$ совпадает с заданными функциями, ${{\left. {{{n}_{a}}} \right|}_{{\alpha + \beta = 0}}} = n_{a}^{0}(\beta ({{v}_{i}} - {{v}_{a}}))$, ${{\left. {{{n}_{i}}} \right|}_{{\alpha + \beta = 0}}} = n_{i}^{0}(\beta ({{v}_{i}} - {{v}_{a}}))$. Если такое решение существует, то его сужение на $P$ дает, очевидно, искомое решение задачи Коши в переменных $(\alpha ,\beta )$. Согласно теореме 1, решение системы (18) в прямоугольнике ${{\Pi }_{\infty }}$ определяется двумя дважды непрерывно дифференцируемыми функциями $A(\alpha )$, $B(\beta )$, $\alpha ,\beta \in \mathbb{R}$ и вычисляется по этим функциям посредством формул (19). При этом, согласно теореме 1, $A(\alpha )$, $B(\beta )$ должны удовлетворять двум условиям: 1) области значений функций $A(\alpha )$, $B(\beta )$ не пересекаются, $A(\mathbb{R}) \cap B(\mathbb{R}) = \emptyset $, и тогда, учитывая связность прямой $\mathbb{R}$, либо $A(\mathbb{R}) < B(\mathbb{R})$, либо $B(\mathbb{R}) < A(\mathbb{R})$, 2) если $A(\mathbb{R}) < B(\mathbb{R})$, то $A(\alpha )$, $B(\beta )$ – монотонно невозрастающие на $\mathbb{R}$ функции, если $B(\mathbb{R}) < A(\mathbb{R})$, то $A(\alpha )$, $B(\beta )$ – монотонно неубывающие на $\mathbb{R}$ функции.

Функции $A(\alpha )$, $B(\beta )$ ищутся по известным значениям ${{n}_{a}}$ и ${{n}_{i}}$ на прямой $\alpha + \beta = 0$ (т.е. из начальных условий). Из тождеств (19) получим:

Пусть ${{n}_{a}}(\beta ) = {{k}_{I}}n_{a}^{0}(\beta ({{v}_{i}} - {{v}_{a}}))$, ${{n}_{i}}(\beta ) = {{k}_{I}}n_{i}^{0}(\beta ({{v}_{i}} - {{v}_{a}}))$, ${{A}_{0}}(\beta ) = A( - \beta )$. Тогда ${{n}_{a}}$, ${{n}_{i}}$ неотрицательные функции, а условия (25) дают линейную систему обыкновенных дифференциальных уравнений с переменными коэффициентами для нахождения функций ${{A}_{0}}(\beta )$, $B(\beta )$ на прямой $\mathbb{R}$: Поскольку ${{n}_{a}}(\beta )$, ${{n}_{i}}(\beta )$ непрерывно дифференцируемы по $\beta $, то любое решение системы (26) дважды непрерывно дифференцируемо всюду на прямой. Кроме того, для любых $C,D \in \mathbb{R}$ существует, и притом единственное, решение системы (26), для которого ${{A}_{0}}(0) = C$, $B(0) = D$. Ниже считается $C \ne D$. Легко показать, что решение (26) с начальным условием ${{A}_{0}}(0) = C$, $B(0) = D$ имеет вид:

Из равенств (27) несложно вывести справедливость условий 1) и 2).

Согласно теореме 1, формулы (19) с учетом (27) дают решение задачи Коши в переменных $(\alpha ,\beta ) \in P$:

В переменных $(z,t)$ получаем следующие формулы: где $n_{i}^{0}(p) \geqslant 0$, $n_{a}^{0}(p) \geqslant 0$ – заданные произвольно непрерывно дифференцируемые функции и знаменатель в формулах (28) заведомо положителен. Итак, формулы (28) дают аналитическое решение системы (16) при $t \geqslant 0$, удовлетворяющее начальному условию ${{n}_{a}}(z,0) = n_{a}^{0}(z)$, ${{n}_{i}}(z,0) = n_{i}^{0}(z)$, $z \in \mathbb{R}$.

Рассмотрим краевую задачу 2 в случае ${{v}_{i}} \ne {{v}_{a}}$. Анализ этого случая проходит по той же схеме, что и решение задачи Коши выше. Выделим основные моменты. В переменных $(\alpha ,\beta )$ ищем непрерывно дифференцируемое решение системы (18) в полуплоскости ${{P}_{0}} = \{ \alpha {{v}_{a}} + \beta {{v}_{i}} \geqslant 0\} $, для которого функции ${{n}_{a}}$, ${{n}_{i}}$ на границе полуплоскости ${{P}_{0}}$, $\partial {{P}_{0}} = \{ \alpha {{v}_{a}} + \beta {{v}_{i}} = 0\} $ принимают заданные значения ${{n}_{a}}(\alpha ,\beta ) = {{n}_{{a0}}}(\alpha + \beta )$, ${{n}_{i}}(\alpha ,\beta ) = {{n}_{{i0}}}(\alpha + \beta )$, $\alpha {{v}_{a}} + \beta {{v}_{i}} = 0$. Построим такое непрерывно дифференцируемое решение системы (18) в бесконечном прямоугольнике ${{\Pi }_{\infty }} = \mathbb{R} \times \mathbb{R} \supseteq {{P}_{0}}$, которое на границе полуплоскости ${{P}_{0}}$, т.е. на прямой $\alpha {{v}_{a}} + \beta {{v}_{i}} = 0$, совпадает с заданными функциями ${{n}_{{a0}}}(\alpha + \beta )$, ${{n}_{{i0}}}(\alpha + \beta )$. Тогда, очевидно, сужение этого решения на ${{P}_{0}}$ будет искомым решением краевой задачи в координатах $(\alpha ,\beta )$. Согласно теореме 1, искомое решение определяется двумя непрерывно дифференцируемыми функциями $A(\alpha )$, $B(\beta )$ и вычисляется по этим функциям посредством формул (19). При этом функции $A(\alpha )$, $B(\beta )$ должны удовлетворять условиям 1) и 2), сформулированным выше. Функции $A(\alpha )$, $B(\beta )$ ищутся по известным значениям ${{n}_{a}}$, ${{n}_{i}}$ на границе ${{P}_{0}}$. На этой границе $\beta = - \alpha {{v}_{a}}{\text{/}}{{v}_{i}}$ и, значит, согласно (19), имеем

Пусть ${{n}_{a}}(\alpha ) = {{k}_{I}}({{v}_{a}}{\text{/}}{{v}_{i}}){{n}_{{a0}}}(\alpha ({{v}_{i}} - {{v}_{a}}){\text{/}}{{v}_{i}})$, ${{n}_{i}}(\alpha ) = {{k}_{I}}{{n}_{{i0}}}(\alpha ({{v}_{i}} - {{v}_{a}}){\text{/}}{{v}_{i}})$, ${{B}_{0}}(\alpha ) = B( - \alpha {{v}_{a}}{\text{/}}{{v}_{i}})$. Тогда краевое условие (29) дает линейную систему обыкновенных дифференциальных уравнений на прямой с переменными коэффициентами для нахождения функций $A(\alpha )$, ${{B}_{0}}(\alpha )$: Поскольку ${{n}_{a}}(\alpha )$, ${{n}_{i}}(\alpha )$ непрерывно дифференцируемы, то любое решение системы (30) дважды непрерывно дифференцируемо и определено на всей прямой. Рассмотрим решение задачи Коши для системы (30) с начальными условиями $A(0) = C \ne {{B}_{0}}(0) = D$. Несложно проверить, что это решение вычисляется по формулам (см. выше): Из формул (31) выводится (см. выше) справедливость условий 1) и 2) для функций $A(\alpha )$, $B(\beta ) = {{B}_{0}}( - \beta {{v}_{i}}{\text{/}}{{v}_{a}})$.

По формулам (19) с учетом выражений (31) получим решение краевой задачи в координатах $(\alpha ,\beta ) \in {{P}_{0}}$:

Подставляя в эти формулы $\alpha = (t{{v}_{i}} - z){\text{/}}({{v}_{i}} - {{v}_{a}})$, $\beta = (z - t{{v}_{a}}){\text{/}}({{v}_{i}} - {{v}_{a}})$, получаем после несложных преобразований решение краевой задачи в переменных $(z,t)$: где ${{n}_{{a0}}}(p) \geqslant 0$, ${{n}_{{i0}}}(p) \geqslant 0$ – произвольные непрерывно дифференцируемые функции. Итак, формулы (32) дают аналитическое решение системы (16) в полуплоскости $z \geqslant 0$, удовлетворяющее краевому условию ${{n}_{a}}(0,t) = {{n}_{{a0}}}(t)$, ${{n}_{i}}(0,t) = {{n}_{{i0}}}(t)$ для всех $t \in \mathbb{R}$.

Рассмотрим смешанную задачу 3 в случае ${{v}_{a}} > 0$, ${{v}_{i}} > 0$, ${{v}_{a}} \ne {{v}_{i}}$. В координатах $(\alpha ,\beta )$ ее решение сводится к поиску в тупом угле $\Lambda \mathop = \limits_{{\text{def}}} \,\{ (\alpha ,\beta ):\alpha + \beta \geqslant 0,\;\alpha {{v}_{a}} + \beta {{v}_{i}} \geqslant 0\} $ непрерывно дифференцируемых функций ${{n}_{a}}(\alpha ,\beta )$, ${{n}_{i}}(\alpha ,\beta )$, удовлетворяющих системе (18) и имеющих заданные значения на границе угла $\partial \Lambda $. Последнее множество состоит из двух лучей, которые обозначим через ${{\Lambda }_{t}}$ и ${{\Lambda }_{z}}$: $\partial \Lambda = {{\Lambda }_{t}} \cup {{\Lambda }_{z}}$, ${{\Lambda }_{t}} \cap {{\Lambda }_{z}} = \{ (0,0)\} $, ${{\Lambda }_{t}} = \varphi \{ (t,0):t \geqslant 0\} $, ${{\Lambda }_{z}} = \varphi \{ (0,z):z \geqslant 0\} $. В зависимости от ${{v}_{i}}$, ${{v}_{a}}$ угол $\Lambda $ и лучи ${{\Lambda }_{t}}$, ${{\Lambda }_{z}}$ изображены на фиг. 2.

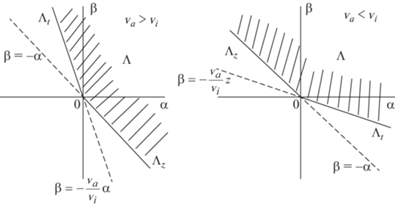
Значения искомого решения на лучах ${{\Lambda }_{t}}$, ${{\Lambda }_{z}}$ определяются равенствами ${{n}_{a}}(\alpha ,\beta ) = {{n}_{{a0}}}(\alpha + \beta )$, ${{n}_{i}}(\alpha ,\beta ) = {{n}_{{i0}}}(\alpha + \beta )$, $(\alpha ,\beta ) \in {{\Lambda }_{t}}$, $\alpha {{v}_{a}} + \beta {{v}_{i}} = 0$, $\alpha + \beta \geqslant 0$; ${{n}_{a}}(\alpha ,\beta ) = n_{a}^{0}(\alpha {{v}_{a}} + \beta {{v}_{i}})$, ${{n}_{i}}(\alpha ,\beta ) = $ $ = n_{i}^{0}(\alpha {{v}_{a}} + \beta {{v}_{i}})$, $(\alpha ,\beta ) \in {{\Lambda }_{z}}$, $\alpha + \beta = 0$, $\alpha {{v}_{a}} + \beta {{v}_{i}} \geqslant 0$. Проведем построение искомого решения для случая ${{v}_{i}} > {{v}_{a}}$. Для нахождения искомого решения в угле $\Lambda $ построим непрерывно дифференцируемое решение системы (18) в бесконечном прямоугольнике ${{\Pi }_{\infty }} = \mathbb{R} \times \mathbb{R} \supseteq \Lambda $, которое на лучах ${{\Lambda }_{t}}$ и ${{\Lambda }_{z}}$ совпадает с указанными выше значениями. Тогда сужение построенного решения в прямоугольнике ${{\Pi }_{\infty }}$ на угле $\Lambda $ даст решение смешанной задачи. Решение системы (18) в ${{\Pi }_{\infty }}$, согласно теореме 1, определяется двумя дважды непрерывно дифференцируемыми в $\mathbb{R}$ функциями $A(\alpha )$, $B(\beta )$ и вычисляется по этим функциям посредством формул (19). Покажем, что функции $A(\alpha )$, $B(\beta )$ однозначно определяются значениями искомого решения на лучах ${{\Lambda }_{t}}$ и ${{\Lambda }_{z}}$. Имеем следующее:

Введем в рассмотрение функции ${{B}_{0}}(\alpha )\mathop = \limits_{{\text{def}}} B( - \alpha {{v}_{a}}{\text{/}}{{v}_{i}})$, ${{A}_{0}}(\beta )\mathop = \limits_{{\text{def}}} A( - \beta )$, $\alpha \geqslant 0$, $\beta \geqslant 0$. Тогда на полупрямой $\alpha \geqslant 0$ функции ${{B}_{0}}(\alpha )$, $A(\alpha )$, согласно (33), удовлетворяют линейной системе ОДУ с переменными коэффициентами: а на полупрямой $\beta \geqslant 0$ функции $B(\beta )$, ${{A}_{0}}(\beta )$, согласно (33), удовлетворяют линейной системе ОДУ с переменными коэффициентами: Решая системы (34), (35), находим функции ${{B}_{0}}(\alpha )$, $A(\alpha )$, $\alpha \geqslant 0$ и $B(\beta )$, ${{A}_{0}}(\beta )$, $\beta \geqslant 0$, после чего доопределяем $A$ и $B$ в областях отрицательных значений аргументов равенствами: Полученные функции $A$ и $B$ на прямой являются искомыми, если выбрать решения систем (34) и (35) с одинаковыми начальными условиями $A(0) = C$, ${{B}_{0}}(0) = D$ и ${{A}_{0}}(0) = C$, $B(0) = D$, где $C \ne D$. Тогда функции $A(\alpha )$, $B(\beta )$ будут непрерывны на $\mathbb{R}$, а из (36) и условий согласованности в нуле следует их двукратная непрерывная дифференцируемость в нуле и, значит, на всей прямой $\mathbb{R}$.

Чтобы проверить условия 1) и 2) и преобразовать к удобному для анализа виду формулы (19), воспользуемся явными выражениями решений задач Коши для систем (35), (34), которые дают для $A(\alpha )$, $B(\beta )$ выражения:

Наконец, преобразуем формулы (19), задающие решение системы (18) в прямоугольнике ${{\Pi }_{*}} \supseteq \Lambda $, в каждом из 4 квадрантов плоскости $(\alpha ,\beta )$. При этом ограничимся только квадрантами I, II, IV, квадрант III, где $\alpha \leqslant 0$, $\beta \leqslant 0$, исключим из рассмотрения, поскольку тупой угол $\Lambda $, согласно фиг. 3, лежит в объединении квадрантов I, II, IV, а с квадрантом III пересекается только по нулевой точке. Для удобства введем в рассмотрение функции

Тогда $N(\beta ) = {{N}_{*}}(\beta ({{v}_{i}} - {{v}_{a}}))$, $M(\alpha ) = {{M}_{*}}(\alpha ({{v}_{i}} - {{v}_{a}}){\text{/}}{{v}_{i}})$ для любых $\alpha ,\beta \in \mathbb{R}$.

Для $\alpha \geqslant 0$, $\beta \geqslant 0$ имеем

Аналогично Для двух других квадрантов аналогичные подсчеты с использованием формул (19), (37) дают: Осталось перейти в полученных формулах от координат $(\alpha ,\beta )$ к координатам $(z,t)$, учитывая преобразование (17). При этом $\beta ({{v}_{i}} - {{v}_{a}}) = z - {{v}_{a}}t$, $ - \alpha ({{v}_{i}} - {{v}_{a}}) = z - {{v}_{i}}t$, $\alpha ({{v}_{i}} - {{v}_{a}}){\text{/}}{{v}_{i}} = t - z{\text{/}}{{v}_{i}}$, $ - \beta ({{v}_{i}} - {{v}_{a}}){\text{/}}{{v}_{a}} = t - z{\text{/}}{{v}_{a}}$. В итоге первый квадрант плоскости $(z,t)$, где ищется решение смешанной задачи для системы (16), прямыми $z = {{v}_{a}}t$, $z = {{v}_{i}}t$ делится на три области, изображенные на фиг. 3, в каждой из которых решение задается одной из формул Формулы (39) и (40) на луче $z = {{v}_{a}}t$, $t \geqslant 0$ и формулы (39) и (41) на луче $z = {{v}_{i}}t$, $t \geqslant 0$, очевидно, совпадают. При $z = 0$ формула (40) дает краевые условия ${{n}_{{a0}}}(t)$, ${{n}_{{i0}}}(t)$, $t \geqslant 0$, а при $t = 0$ формула (41) дает начальные условия $n_{a}^{0}(z)$, $n_{i}^{0}(z)$, $z \geqslant 0$. Итак, формулы (39)–(41) с учетом выражений (38) полностью определяют решение смешанной задачи для системы (16) по известным граничным ${{n}_{{a0}}}(t)$, ${{n}_{{i0}}}(t)$, $t \geqslant 0$, и начальным $n_{a}^{0}(z)$, $n_{i}^{0}(z)$, $z \geqslant 0$ условиям.

4. ИОНИЗАЦИОННЫЕ КОЛЕБАНИЯ (БРИВИНГ-МОДЫ)

В разд. 2 было установлено, что для знакоопределенных на отрезке $[0,L]$ скоростей ${{v}_{a}}(z)$, ${{v}_{i}}(z)$ система уравнений ионизации (1) имеет единственное стационарное решение, удовлетворяющее заданным (стационарным) граничным условиям. При этом граничные условия для ${{n}_{a}}$, ${{n}_{i}}$ в зависимости от знака соответствующей скорости ставятся либо на левом конце $z = 0$, либо на правом $z = L$. Например, если ${{v}_{i}}(z) > 0$ на $[0,L]$, то на левом конце $z = 0$ считается заданной величина ${{n}_{i}}(0,t)$ в каждый момент времени $t \geqslant 0$, а если ${{v}_{i}}(z) < 0$, то считается заданной величина ${{n}_{i}}(L,t)$, $t \geqslant 0$, и аналогично для ${{n}_{a}}$. Численно было установлено также, что в случае знакоопределенных скоростей ${{v}_{a}}$, ${{v}_{i}}$ при $t \to + \infty $ решение начально-краевой задачи для системы (1) со стационарными краевыми условиями устанавливается, т.е. при $t \to + \infty $ сходится в равномерной метрике на $[0,L]$ к единственному стационарному решению системы (1). В частности, в этом случае ионизационные колебания (бривинг-моды) отсутствуют.

При исследовании процесса ионизации в СПД обычно считается ${{v}_{a}}(z) \equiv {{v}_{a}} = {\text{const}} > {\text{0}}$. Таким образом, ограничиваясь этим практически важным случаем, можно утверждать, что необходимым (но, вероятно, не достаточным) условием существования ионизационных колебаний является знакопеременность скорости ${{v}_{i}}(z)$ на отрезке $[0,L]$. Этот вывод согласуется с экспериментальными данными по СПД, согласно которым [13] ионная скорость ${{v}_{i}}$ всегда отрицательна по направлению $z$ в прианодной области и, следовательно, применительно к одномерному случаю ${{v}_{i}}(z)$ имеет единственный нуль ${{z}_{0}}$ на $[0,L]$, причем $0 < {{z}_{0}} < L$, $v_{i}^{'}({{z}_{0}}) > 0$ и, значит, ${{v}_{i}}(z)$ меняет знак с минуса на плюс, когда $z$, возрастая, проходит через точку ${{z}_{0}}$. Типичными модельными примерами в одномерной задаче являются функции ${{v}_{i}}(z) = \alpha (z - {{z}_{0}})$, $\alpha > 0$, $0 < {{z}_{0}} < L$, ${{v}_{i}}(z) = a(z + {{z}_{1}})(z - {{z}_{0}})$, $a > 0$, ${{z}_{1}} > 0$, $0 < {{z}_{0}} < L$, ${{v}_{i}}(z) = - \cos (\pi z{\text{/}}L)$ (и тогда ${{z}_{0}} = L{\text{/}}2$).

Рассмотрим причину возникновения бривинг-мод в случае, когда ионная скорость ${{v}_{i}}(z)$ имеет указанный выше специальный вид. В этом случае граничные условия ставятся только для ${{n}_{a}}$ на левой границе $z = 0$, для ${{n}_{i}}$ они формально не нужны, поскольку ${{v}_{i}}(0) < 0 < {{v}_{i}}(L)$ и, значит, ионы через границы $z = 0$ и $z = L$ покидают область $[0,L]$. Однако при этом возникает “внутреннее” граничное условие для ${{n}_{i}}$ на характеристике $z = {{z}_{0}}$ для уравнения переноса ионов (1), которое объясняет возникновение бривинг-мод. Остановимся на этом подробнее. Начально-краевая задача на отрезке $[0,L]$ для системы (1) распадается на две начально-краевые задачи на отрезках $[0,{{z}_{0}}]$ и $[{{z}_{0}},L]$ соответственно, которые решаются последовательно. При этом краевое условие ${{n}_{i}}(t)\mathop = \limits_{{\text{def}}} {{n}_{i}}({{z}_{0}},t)$ для функции ${{n}_{i}}$ на характеристике $z = {{z}_{0}}$, являющейся границей для обеих смешанных задач, ищется из решения задачи Коши для ОДУ

где $n_{i}^{0}(z)$, $0 \leqslant z \leqslant L$, – заданное начальное условие для ${{n}_{i}}$ на отрезке $[0,L]$. Уравнение (42) является тривиальным следствием второго уравнения системы (1) в точке ${{z}_{0}}$ с учетом равенства ${{{v}}_{i}}({{z}_{0}}) = 0$. Неизвестная функция ${{n}_{a}}(t)\mathop = \limits_{{\text{def}}} {{n}_{a}}({{z}_{0}},t)$, входящая в (42), находится следующим образом. Если фиксировано граничное условие ${{n}_{{a0}}}(t)$, $t \geqslant 0$, для ${{n}_{a}}$ на левой границе $z = 0$, то функция ${{n}_{a}}(t)$ ищется в банаховом пространстве $B$ непрерывно дифференцируемых и ограниченных вместе с производной функций на полупрямой $t \geqslant 0$, как неподвижная точка отображения $F:{{B}_{0}} \to {{B}_{0}}$, где ${{B}_{0}} \subseteq B$ – замкнутая гиперплоскость в $B$ коразмерности 1, определяемая условием ${{B}_{0}} = \{ n(t) \in B:n(0) = n_{a}^{0}({{z}_{0}})\} $, а $n_{a}^{0}(z)$, $0 \leqslant z \leqslant L$ – заданное начальное условие для ${{n}_{a}}$. Отображение $F$ определяется следующим образом. Если $n(t) \in {{B}_{0}}$, то, положив ${{n}_{a}}(t) = n(t)$ в (42) и решая задачу Коши (42) на полупрямой $t \geqslant 0$ относительно ${{n}_{i}}$, находим функцию ${{n}_{i}}(t)$, $t \geqslant 0$, которую принимаем за краевое условие для ${{n}_{i}}$ на правом конце $z = {{z}_{0}}$ (вместе с краевым условием ${{n}_{{a0}}}(t)$ для ${{n}_{a}}$ на левом конце $z = 0$) в смешанной задаче на отрезке $[0,{{z}_{0}}]$ для системы (1). Решив эту смешанную задачу, получим, в частности, на правом конце $z = {{z}_{0}}$ функцию ${{n}_{a}}({{z}_{0}},t)$, $t \geqslant 0$, которая, по определению, и является образом $n(t)$ при отображении $F$. Итак, функция ${{n}_{a}}(t)$ в уравнении (42) – это неподвижная точка определенного выше отображения $F$. Решение ${{n}_{i}}(t)$ задачи Коши (42) для неподвижной точки ${{n}_{a}}(t)$ является правым краевым условием для ${{n}_{i}}$ в смешанной задаче для системы (1) на отрезке $[0,{{z}_{0}}]$, а вместе с ${{n}_{a}}(t)$ дает левые краевые условия для ${{n}_{i}}$, ${{n}_{a}}$ в смешанной задаче для системы (1) на отрезке $[{{z}_{0}},L]$. Отметим, что смешанные задачи на отрезках $[0,{{z}_{0}}]$, $[{{z}_{0}},L]$ относятся к задачам Гурса [14], а уравнение (42) совпадает с условием разрешимости [14] на характеристике для квазилинейной системы уравнений в частных производных, к которой относится и система (1). Аналитическое исследование существования и единственности неподвижной точки отображения $F$ выходит за рамки настоящей работы. Численно существование неподвижной точки $F$ одновременно с решением задачи Коши (42) устанавливается расчетом по разностной схеме (15) . В частности, если ${{k}_{0}}$ – номер узла, где ${{z}_{{{{k}_{0}}}}} = {{z}_{0}}$, то разностная схема (15) для ${{n}_{i}}$ в узле ${{k}_{0}}$ совпадает со схемой Эйлера решения задачи Коши (42) и дает сеточную функцию ${{n}_{{i,{{k}_{0}}}}}$, удовлетворяющую указанному выше начальному условию, а сеточная функция ${{n}_{{a,{{k}_{0}}}}}$ дает сеточную аппроксимацию неподвижной точки $F$.

Как показали расчеты, ионизационные колебания (бривинг-моды) имеют место только тогда, когда решение задачи Коши (42) при $t \to + \infty $ выходит на периодический режим. При этом ${{n}_{a}}(t) = {{n}_{a}}({{z}_{0}},t)$ на характеристике $z = {{z}_{0}}$ удовлетворяет уравнению

где $\gamma (t) = - {{\left. {\left[ {(\partial {{n}_{a}}{\text{/}}\partial z)({{v}_{a}}{\text{/}}{{n}_{a}})} \right]} \right|}_{{z = {{z}_{0}}}}}$ – периодическая для больших $t$ и определяется видом скорости ионов ${{v}_{i}}(z)$. Из этой констатации вытекают важные и неочевидные выводы. Например, если ионная скорость ${{v}_{i}}(z)$ имеет хотя бы один нуль ${{z}_{0}}$ на интервале $(0,L)$, для которого $v_{i}^{'}({{z}_{0}}) \leqslant 0$, то ионизационные колебания (бривинг-моды) отсутствуют. Действительно, тогда ${{n}_{i}}({{z}_{0}},t) = {{n}_{i}}(t)$, вычисляемая по решению задачи Коши (42), будет монотонно возрастающей на полупрямой $t \geqslant 0$ функцией и, следовательно, при $t \to + \infty $ не может выйти на периодический режим. Скажем, для ${{v}_{i}}(z) = - \cos [(2N + 1)\pi z{\text{/}}L]$, $N > 0$ – целое бривинг-моды отсутствуeт. Хотя приведенный пример, согласно [13], имеет, скорее, теоретическое значение, он указывает на нетривиальность полученного результата.

Функция $\gamma (t)$ находится численно, решением разностных уравнений (15): на нулевом слое ${{\gamma }^{0}} = - (n_{{a,{{k}_{0}}}}^{0} - n_{{a,{{k}_{0}} - 1}}^{0}){\text{/}}h \cdot {{v}_{a}}{\text{/}}n_{{a,{{k}_{0}}}}^{0}$, где ${{z}_{0}} = {{z}_{{{{k}_{0}}}}}$.

Расчеты значений ${{n}_{i}}$, ${{n}_{a}}$ на характеристике $z = {{z}_{0}}$ и функции $\gamma (t)$ для трех типов скоростей ионов ${{v}_{i}}(z) = \alpha (z - {{z}_{0}})$, $\alpha > 0$, ${{v}_{i}} = a(z + {{z}_{1}})(z - {{z}_{0}})$, $a > 0$, ${{v}_{i}}(z) = - \cos (\pi z{\text{/}}L)$ приведены на фиг. 4.

Если бы функция $\gamma (t)$ была положительной константой, то из (42), (43) вытекало бы, что на характеристике $z = {{z}_{0}}$ функции ${{n}_{i}}(t)$, ${{n}_{a}}(t)$ удовлетворяют уравнениям Лотки–Вольтерра, что, как показывают примеры, не имеет места. Поэтому существование бривинг-мод не удается связать с моделью Лотки–Вольтерра.

5. ИОНИЗАЦИОННЫЕ КОЛЕБАНИЯ В ОБЩЕМ СЛУЧАЕ

Недостаток ионизационной модели (1) в том, что скорости ${{v}_{a}}(z)$, ${{v}_{i}}(z)$ считаются известными и не зависящими от времени $t$. Применительно к СПД обычно считается ${{v}_{a}}(z) \equiv {{v}_{a}} = {\text{const}} > {\text{0}}$, а ${{v}_{i}}$ находится из уравнения движения ионов. Движение ионов определяется электромагнитным полем в камере СПД и их столкновениями с боковыми керамическими стенками камеры и поверхностью анода. Наличие в установке сильного почти радиального магнитного поля и продольного электрического поля и, как следствие, справедливость соотношения ${{r}_{{\Lambda i}}} \gg L$ (${{r}_{{\Lambda i}}}$ – ларморовский радиус ионов) предопределяют движение ионов преимущественно в продольном направлении, параллельно поверхностям боковых стенок. Поэтому столкновениями ионов и атомов Xe со стенками в первом приближении можно пренебречь. Электромагнитное поле в СПД складывается из индукционного и внешнего электромагнитного поля, порождаемого постоянными токами обмоток СПД и заданной разностью потенциалов между анодом и катодом. Пренебрегая индукционными полями, порождаемыми плазменными токами, в частности, столкновениями ионов с электронами, приходим к следующей упрощенной кинетической модели движения ионов и атомов:

где ${\mathbf{E}} = {\mathbf{E}}({\mathbf{x}})$, ${\mathbf{H}} = {\mathbf{H}}({\mathbf{x}})$ – известные стационарные электрическое и магнитное поля в СПД, $e$ – заряд электрона, ${{m}_{i}}$ – масса иона Xe, ${{f}_{i}} = {{f}_{i}}(t,{\mathbf{x}},{\mathbf{v}})$, ${{f}_{a}} = {{f}_{a}}(t,{\mathbf{x}},{\mathbf{v}})$ – функции распределения ионов и атомов Xe по скоростям. Равенства (44) образуют систему интегродифференциальных уравнений относительно двух функций ${{f}_{i}}$, ${{f}_{a}}$ и описывают процессы ионизации и ускорения ионов в СПД. После ее решения ионная скорость вычисляется по формуле: Система (44) в случае плоской симметрии ${{f}_{i}} = \delta ({{v}_{x}}){{f}_{i}}(t,z,{{v}_{y}},{{v}_{z}})$, ${{f}_{a}} = \delta ({{v}_{x}})\delta ({{v}_{z}})\delta ({{v}_{z}} - {{v}_{a}}){{n}_{a}}(t,z) \times $ $ \times \;{{f}_{i}}(t,z,{{v}_{y}},{{v}_{z}})$, где ${{f}_{i}}(t,z,{{v}_{y}},{{v}_{z}})$, ${{n}_{a}}(t,z)$ – неизвестные функции, подлежащие нахождению, сводится к виду: где ${{v}_{a}}$ – заданная скорость, с которой атомы Xe поступают в камеру СПД через левую границу со стороны анода. Интегрируя первое уравнение (46) по скоростному пространству ${{\mathbb{R}}^{2}} = \{ ({{v}_{y}},{{v}_{z}})\} $, получаем уравнение непрерывности для ионов с ${{{\mathbf{v}}}_{i}}$, вычисляемой по формуле (45): В результате приходим к модели ионизации (1), в которой ${{v}_{i}}(t,z)$ зависит от $t$ и определяется движением ионов. Если выпрямить коаксиальную камеру СПД посредством экспоненциального отображения, то ось $r$ перейдет в ось $x$, ось $\varphi $ – в ось $y$ и значит в (46) ${{E}_{y}}$ – азимутальное электрическое поле, ${{H}_{x}}$ – радиальное магнитное поле. Из уравнений Максвелла в случае плоской симметрии, $\partial {\text{/}}\partial y = \partial {\text{/}}\partial x = 0$, следует ${{E}_{y}} = {\text{const}}$, ${{E}_{z}} = {\text{const}}$, ${{H}_{x}} = {\text{const}}$. В физически важном случае ${{E}_{y}} = 0$ в безразмерном виде система (46) сводится к следующей: где $\varepsilon = {{t}_{0}}{{\omega }_{{ci}}}$, ${{\omega }_{{ci}}} = e{{H}_{0}}{\text{/}}(c{{m}_{i}})$, ${{f}_{0}} = {{n}_{0}}{\text{/}}v_{0}^{2}$, ${{H}_{0}} = 200$ Гс – характерный масштаб напряженности магнитного поля, ${{f}_{0}}$ – характерный масштаб значений $f$. Наконец, считается ${{E}_{0}} = {{v}_{0}}{{H}_{0}}{\text{/}}c$ (см. формулы (14)). Система (47) решается методом макрочастиц [17] на отрезке $[0,L]$ с граничным условием зеркального отражения для ионов на левой границе $z = 0$. На правой границе $z = L$ ускоренные ионы свободно покидают отрезок $[0,L]$. Начальное условие обеспечивает спокойный старт движения макрочастиц и задается в размерном виде максвеллианом где $n(z)$, $T(z)$ – заданные функции (характерный масштаб температуры ${{T}_{0}} = 12.1$ эВ – температура ионизации Xe). Подробно численный метод изложен в [18].

На фиг. 5 представлены результаты решения системы (47), демонстрирующие возникновение ионизационных колебаний при $t \to + \infty $, причем продольная скорость ионов ${{v}_{z}}$ зависит от времени, периодична для больших $t$ и меняет знак в определенные моменты времени. Заметим, что для других входных данных концентрации ${{n}_{i}}$, ${{n}_{a}}$, вычисляемые по (47), выходят на установление [18] и, таким образом, бривинг-моды отсутствуют, но при этом разрядный ток испытывает низкочастотные осцилляции вокруг некоторых средних значений. Это означает, что колебания разрядного тока необязательно обусловлены ионизационными колебаниями.

6. ЗАКЛЮЧЕНИЕ

Для изучения ионизационных колебаний (бривинг-мод) в стационарных плазменных двигателях (СПД) выше предложены две математические модели ионизации – гидродинамическая и кинетическая. Уравнения гидродинамической модели проще и поддаются аналитическому исследованию. В частности, выше были классифицированы стационарные решения уравнений гидродинамической модели и дано их полное аналитическое решение в случаях постоянных скоростей атомов и ионов, что, в свою очередь, позволяет аналитически решать различные начально-краевые задачи. Ионизационные колебания на базе гидродинамической модели исследовались численно, и выше был сформулирован критерий (необходимое и достаточное условие) существования бривинг-мод. Недостаток гидродинамической модели в том, что скорость ионов считается заданной и стационарной, а процесс ионизации никак не связан с ускорением ионов. В более сложной кинетической модели скорость ионов определяется из их движения, а процессы ионизации и ускорения ионов исследуются совместно. В кинетической модели, также как и в гидродинамической, существуют бривинг-моды, но картина ионизационных колебаний отличается от гидродинамического случая. Возможности кинетической модели намного шире, чем гидродинамической. В частности, кинетическая модель позволяет найти распределение ионного тока и силу тяги СПД и проанализировать причины паразитических колебаний тока и силы тяги.