Журнал вычислительной математики и математической физики, 2022, T. 62, № 7, стр. 1138-1157

1. ВВЕДЕНИЕ

Нелинейное уравнение Шрёдингера (НУШ) обладает чрезвычайно высокой универсальностью и применяется для описания волновых процессов во многих областях физики: в теории поверхностных волн, в моделях эволюции распределений плазменных колебаний, нелинейной оптике, биофизике и т.д.

Один известный класс решений этого уравнения описывает движение уединенных волн (солитонов), их образование и распад (см. [1]–[3]). Другой не менее важный класс решений описывает образование за конечное время особенностей – коллапсирующих каверн (см. [4] и обзор [5]).

Данное уравнение является основным уравнением нелинейной волновой оптики и активно используется, например, при математическом моделировании волоконно-оптических линий связи, волоконных лазеров и различных оптических устройств, а также в гидродинамике и физике плазмы. Для уравнений “параболического” типа, к которым относится нестационарное уравнение Шрёдингера

Несмотря на чрезвычайную важность основных точно интегрируемых систем, таких, как КдФ, НУШ, уравнение синус-Гордона и т.п., все они являются исключительными моделями в том смысле, что любое дополнительное слагаемое, учитывающее диктуемые физикой эффекты, которые не учитывались в базовой модели, разрушает точную интегрируемость.

Среди огромного потока задач, использующих обобщенные НУШ, выделяется группа, в которой расчеты нужно вести на очень большом временном интервале (см. [10], [11]) или, в силу специфики задачи [12], с очень малым шагом по времени. Для задач на больших пространственных областях актуальным является вопрос о неотражающих граничных условиях. Обзор их конструирования для нестационарного уравнения Шрёдингера приведен в [13].

Для адекватного численного расчета задач в области волоконно-оптических линий связи или волоконных лазеров с детальным пространственно-временным разрешением число точек по “пространственной” переменной может составлять ${{10}^{6}}$–${{10}^{7}}$, что приводит к огромным затратам машинного времени и быстрому накоплению ошибки. Практически единственным путем расчета таких задач является параллельная реализация численных алгоритмов. Для их эффективного применениия требуются новые математические модели, алгоритмы и математическое обеспечение.

Для НУШ и его обобщений популярна методика “slip-step” (см. [14]–[18]). Сравнение различных способов реализации метода проделано в [17], [19].

В области гидро и газодинамики в последнее время интенсивно развивается метод гиперболизации (см. [20]–[23]), хорошо зарекомендовавший себя при адаптации на архитектуру параллельных высокопроизводительных вычислительных систем. Гиперболизацией уравнений называют добавку дополнительного члена с малым параметром в качестве коэффициента перед второй производной по времени.

Впервые идея гиперболизации для задач электродинамики была предложена А. Милани (A. Milani) (см. [24]). Для задач гидрогазодинамики основополагающей работой в этом направлении является работа Б.Н. Четверушкина (см. [25]).

Обзор методов решения гиперболического уравнения теплопроводности приведен в [26]. В [27] с помощью операторного подхода построено частное решение гиперболического уравнения теплопроводности. Исследована эволюция гармонического решения, моделирующего распространение электрических сигналов в длинных проводных линиях, рассмотрено влияние фотонного способа теплопередачи в среде. Изучается влияние числа Кнудсена на теплопроводность в модели тонких пленок (oбобщение см. в [28]).

Добавка дополнительного члена с малым параметром в качестве коэффициента перед второй производной по времени позволяет строить трехслойные явные схемы, обладающие лучшим условием устойчивости, чем традиционные явные схемы для параболических уравнений и нестационарных уравнений Шрёдингера. Дополнительные члены, как правило, выступают в роли физически обоснованных регуляризаторов, сглаживая нефизические эффекты, получающиеся при численном решении. Несомненный интерес представляет вопрос, насколько решение гиперболизованных уравнений Шрёдингера с малым параметром при второй производной по времени отличается от решения исходных уравнений. Представляет интерес анализ выполнения законов сохранения для гиперболизованных уравнений и их связь с соответствующими законами для исходных уравнений.

В данной работе приведены два способа численной реализации идеи гиперболизации. Методика, основанная на операторных спектральных заменах неизвестной функции продемонстрирована на динамике скачка поля для НУШ с неограниченным по пространственной переменной оператором в разд. 2. Идея введения консервативных переменных и потоков реализована для лазерного усилителя в разд. 3.

Увеличение скорости счета достигается путем гиперболизации, т.е. добавлением второй производной по времени с малым параметром.

Как для исходных уравнений, так и для гиперболизированных вариантов на заданном малом отрезке $({{t}_{0}},{{t}_{0}} + \Delta t)$ удается построить такое приближенное решение задачи, которое кроме высокого порядка аппроксимации обладает еще и тем свойством, что в начальной и конечной точках рассматриваемого малого интервала производные по времени приближенного решения совпадают с производными точного решения. Естественно, что в конечной точке ${{t}_{0}} + \Delta t$ мы попадем на другую, близкую траекторию, но с производной, соответствующей именно этой траектории. При этом, если у решения уравнения $E(\tau ),{{t}_{0}} \leqslant \tau \leqslant {{t}_{0}} + \Delta t$ есть инварианты ${{I}_{i}}(E(t))$ = const, то автоматически выполняются равенства нулю производных по времени для всех инвариантов от приближенного решения в начальной и конечной точках этого интервала. Другими словами, предложенный алгоритм обеспечивает непрерывность как приближенного решения, так и его производной по времени.

Приближенное решение строится путем последовательных операторных замен неизвестной функции на малом интервале. При проведении замен на первом этапе мы стремимся осуществить переход от уравнения или системы уравнений с неограниченными по пространственным координатам операторами к уравнениям с ограниченными операторами. Такой переход существенно расширяет возможности последующего численного моделирования.

Последующие операторные замены сводят исходную эволюционную задачу, описывающую сложный физический процесс, к решению последовательности задач, описывающих процессы более простой физической структуры. Приближенно это удается сделать на основе аддитивности рассматриваемых процессов в малом.

Численная реализация сводится к последовательному решению задач Коши для достаточно простых и, что немаловажно, знакомых уравнений. За начальные данные для последующего уравнения при этом берутся результирующие значения предыдущего. Каждая из этих подзадач может быть решена и распараллелена отдельно. Необходимо следить лишь за тем, чтобы решение каждого из уравнений в схеме расщепления удовлетворяло граничным условиям исходного уравнения. Получившийся алгоритм фактически является реализацией метода расщепления по физическим процессам.

Одним из уравнений схемы расщепления является линейное нестационарное уравнение Шрёдингера в однородном пространстве, решение которого тривиально выражается через операторную экспоненту, наиболее просто реализуемую с помощью преобразования Фурье. Обзор достижений вычислений операторной экспоненты приведен в [29], [30]. Главный вывод работы [29] состоит в том, что для матриц большой размерности безальтернативным является метод “Scaling and squaring” – использование представления ${{e}^{A}} = ({{e}^{{A/m}}}{{)}^{m}}$.

Известно, что алгоритмы вычисления быстрого преобразования Фурье (БПФ) обладают низкой эффективностью распараллеливания, однако их применение при вычислении операторных экспонент позволяет существенно увеличить точность расчетов и использовать предельно крупные шаги по времени, по сравнению с шагами явных разностных схем. Наиболее эффективные алгоритмы реализации многомерного БПФ, в которых минимизированы передачи данных между процессорами, приведены в [31], [32].

Однако находить решение линейного нестационарного уравнения Шрёдингера не обязательно только с помощью преобразования Фурье. Например, в случае цилиндрической симметрии можно воспользоваться разностным методом типа метода интегральных тождеств Г.И. Марчука, но, естественно, для цилиндрического лапласиана. Менее затратной, чем “Scaling and squaring”, но и достаточно эффективной явилась схема удвоения шагов в трехслойной разностной схеме, использованной в [33]–[35]:

Отметим, что в своих расчетах мы всегда стремимся получить просто реализуемый и легко распараллеливаемый алгоритм, хотя способ его получения может оказаться достаточно сложным. Однако весьма важным является то, что понимание этих алгоритмов не вызывает затруднений. Они легко программируются и просты в применении. Простота реализации существенно ускоряет процесс написания программ, сокращает число ошибок программирования и в конечном итоге быстрее приводит к успеху. Путем последовательных операторных замен для гиперболизованных вариантов задач также удается построить аналог схемы расщепления по физическим процессам. Эффективное применение таких замен для гиперболизованного НУШ, реализованное через БПФ, докладывалось на 18-й международной конференции “Дифференциальные и функциональные дифференциальные уравнения – 2017” (см. [36]) и КРОМШ-2017 (см. [37]). Гиперболизация НУШ позволила не только существенно повысить точность расчетов, но и построить оценки ошибки приближенного решения. Реализация методики введения консервативных переменных и потоков докладывалась на КРОМШ-2020 (см. [38]) и КРОМШ-2021 (см. [39]).

2. НЕСТАНДАРТНАЯ ПОСТАНОВКА ЗАДАЧ

Методы, основанные на последовательных операторных заменах неизвестной функции и приводящие к схеме расщепления с использованием дискретного преобразования Фурье, успешно применялись (см. [40], [41]) при нахождении решения нелинейного уравнения Шрёдингера гиперболически-параболического типа

Эти уравнения описывают самовоздействие широкого класса волн, поверхности волновых векторов у которых имеют седловую точку (например, гравитационные волны на глубокой воде [42], плазменные колебания в замагниченной плазме [43]). Проведенные численные исследования эволюции начальных локализованных распределений поля гауссовой формы

На фиг. 1 представлены отдельные моменты развития процесса самовоздействия поля с исходным соотношением пространственных масштабов $a{\text{/}}b = 1{\text{/}}10$ и амплитудой $A = 2.5$. Прежде всего отчетливо виден монотонный характер расширения распределений вдоль оси $y$, сопровождающийся сложным пульсирующим изменением его ширины в $x$-направлении. Наблюдается эффект дробления начальной квазиоднородной структуры, приводящий к образованию дополнительного горба в распределении поля в результате каждой пульсации приосевой области пучка. На больших расстояниях процесс всегда переходит в режим самодефокусировки, сопровождающийся монотонным снижением уровня поля (обоснование корректности постановки задачи для уравнения (2) см. в [44]).

Фиг. 1.

Линии уровня функции ${{\left| E \right|}^{2}}$ из уравнения (2) при начальном соотношении между полуосями 1/10. Знак плюс соответствует максимуму распределения поля ${{\left| E \right|}^{2}}$, цифры – величина поля в максимуме.

В [10], [11] проведено исследование распространения световых импульсов в многожильных световодах, приведенных на фиг. 2.

Фиг. 2.

Различные типы световодов: (а) 19-ядерный с кольцевой решеткой, (б) 21-ядерный квадратной формы и (в) 19-ядерный шестиугольный.

Рассматривалась задача с периодическими граничными условиями для системы линейно связанных нелинейных уравнений Шрёдингера (NLSE):

Были использованы обобщения двух численных алгоритмов для решения системы линейно связанных НУШ, описывающей распространение световых импульсов в многожильных оптических световодах. В первом итеративном численном методе использовалась компактная диссипативная схема второго порядка точности по пространству и четвертого порядка по времени. Эта компактная схема обладает высокой устойчивостью за счет включения дополнительного диссипативного члена. Второй алгоритм является обобщением пошагового метода Фурье, основанного на аппроксимации Паде матричной экспоненты.

Методы тестированы на классическом солитонном решении и для солитона Кузнецова–Ма

Фиг. 3.

Фундаментальный солитон (а) и солитон Кузнецова–Ма (б) как аналитические точные решения скалярного NLSE .

Обратите внимание на разные шкалы мощности солитонов. В случае многожильных световодов система связанных NLSE включает линейную связь между соседними оболочками.

В случае с самофокусировкой, т.е. когда игра идет на все более высокочастотных гармониках (см. фиг. 4), требуется тщательное сравнение с численными результатами для уравнения Шрёдингера.

Фиг. 4.

Динамика распределения интенсивности в каждой оболочке 19-жильного кольцевого кабеля. Заданный входной импульс Гаусса достигает наилучшей энергии для этого типа кабелей, равной 80% общей энергии Et на расстоянии $z$ = 65 : 9.

2.1. Динамика падения волны на неоднородный слой плазмы

Задача о падении плоской волны на неоднородный слой плазмы рассматривалась в [12], [45], [46]. Простейшее уравнение для изучения динамики волны в неоднородном поле представляет собой аналог НУШ:

(3)

$ - 2i\frac{{\partial E}}{{\partial t}} + \frac{{{{\partial }^{2}}E}}{{\partial {{x}^{2}}}} + ( - x + {{\left| E \right|}^{2}})E = D,\; - {\kern 1pt} \infty < x < + \infty ,$

но с неограниченным оператором ${{\partial }^{2}}E{\text{/}}\partial {{x}^{2}} - xE$. Напомним, что спектр этого оператора непрерывный и заполняет всю ось.

Вместо граничных условий $E \to 0$ при $x \to \pm \infty $ можно использовать условие принадлежности решения пространству ${{L}_{2}}$. Соответственно, и начальные данные

(4)

$E(x,0) = {{E}_{0}}(x) \in {{L}_{2}}.$

Легко проверить, что решение $E(x,t)$ сохраняет первый интеграл

$I = \int\limits_{ - \infty }^{ + \infty } {{\left| E \right|}^{2}}dx = {\text{const}}{\text{.}}$

Решение нестационарной задачи без нелинейного слагаемого выражается через функции Эйри, образ Фурье которых ${{e}^{{i{{k}^{3}}t}}}$ дает ясное представление о соотношении между шагами по пространственной и временной переменным при численном счете.

Будем обозначать через

$FE(k,t) = \int\limits_{ - \infty }^{ + \infty } E(x,t){{e}^{{ - ikx}}}dx$

преобразование Фурье функции $E(x,t)$.

Применим преобразование Фурье к уравнению (3), считая, что все входящие в это уравнение слагаемые принадлежат пространству ${{L}_{2}}$:

(5)

$\begin{gathered} - 2i\frac{{\partial FE}}{{\partial t}} - {{k}^{2}}FE - i\frac{{\partial FE}}{{\partial k}} = Ff(k,t) = F( - {{\left| E \right|}^{2}}E + D), \\ - i\left( {2\frac{{\partial FE}}{{\partial t}} + \frac{{\partial FE}}{{\partial k}}} \right) = {{k}^{2}}FE + Ff(k,t). \\ \end{gathered} $

Будем опускать аргумент $k$ у функций, а аргумент $t$ будем писать только в случае необходимости. Введем новые переменные

(6)

$\xi = t - 2k,\quad \eta = k.$

Тогда уравнение примет вид

(7)

$ - i\frac{{\partial FE}}{{\partial \eta }} = {{\eta }^{2}}FE + = Ff(\eta ,\xi + 2\eta ).$

Решение, удовлетворяющее соответствующим начальным условиям, имеет вид

(8)

$FE(\eta ) = F{{E}_{0}}( - \xi {\text{/}}2){{e}^{{ - i({{\eta }^{3}} - {{\xi }^{3}}/8)/3}}} + i\int\limits_{ - \xi /2}^\eta \,{{e}^{{ - i({{\eta }^{3}} - {{\xi }^{3}}/8)/3}}}Ff(\tau ,\xi + 2\tau )d\tau .$

Вернувшись к координатам $(k,t)$, получим

(9)

$FE(k,t) = F{{E}_{0}}\left( {k - \frac{t}{2}} \right){{e}^{{ - i({{k}^{2}} - kt/2 + {{t}^{2}}/12)t/2}}} + i\int\limits_0^t \,{{e}^{{ - i({{k}^{2}} - k(t - \tau /)2 + {{{(t - \tau )}}^{2}}/12)(t - \tau )/2}}}Ff\left( {k - \frac{{t - \tau }}{2},\tau } \right)d\tau .$

Показатель экспоненты, пропорциональный ${{k}^{3}}$, характерный для образа Фурье функции Эйри, “спрятался” в сдвиг аргумента функции начальных данных. При вычислениях это приводит к накоплению ошибок за счет аппроксимаций. Сделав обратное преобразование Фурье, окончательно получаем

(10)

$\begin{gathered} E(x,t) = \frac{{1 + i}}{{2\sqrt {\pi t} }}\int\limits_{ - \infty }^\infty \,{{E}_{0}}(x - y){{e}^{{ - i({{y}^{2}} + y{{t}^{2}}/2 - x{{t}^{2}} - {{t}^{4}}/48)/2t}}}dy - \\ - \;\frac{{1 - i}}{{4\sqrt \pi }}\int\limits_0^t \frac{1}{{\sqrt {t - \tau } }}\int\limits_{ - \infty }^\infty \,f(y,\tau ){{e}^{{i((x - y{{)}^{2}} + (x - y)(t - \tau {{)}^{2}}/2 - x{{{(t - \tau )}}^{2}} - {{{(t - \tau )}}^{4}}/48)/2(t - \tau )}}}dyd\tau . \\ \end{gathered} $

Вычисление двойного сингулярного интеграла с быстроосцилирующей подынтегральной функцией на каждом шаге по времени также приводит к быстрому накоплению ошибок счета. Заметим, что в [12] устойчивые расчеты удалось провести только с помощью введения большого нефизичного затухания.

Воспользовавшись фундаментальным решением для однородного уравнения

(11)

$ - 2i\frac{{\partial E}}{{\partial t}} + \frac{{{{\partial }^{2}}E}}{{\partial {{x}^{2}}}} - xE = 0,\quad - {\kern 1pt} \infty < x < + \infty ,$

мы перешли к интегральной формулировке задачи. Для корректной постановки этой задачи вместо граничных условий на $ \pm \infty $ ставится условие принадлежности решения определенному функциональному пространству, $E \in {{L}_{p}}$. Когда спектр оператора по пространственной переменной заполняет всю действительную ось, встает вопрос о появлении комплексных собственных значений с положительной действительной частью (естественно, в окрестности $\lambda = 0$) при возмущении задачи (см., например, [47], [48]).

В [49] приведена замена переменных, сводящая оператор из (11) к стандартному нестационарному оператору Шрёдингера $ - 2i\partial E{\text{/}}\partial t + {{\partial }^{2}}E{\text{/}}\partial {{x}^{2}}$. Однако отображение пространства ${{L}_{2}}$ при этом является отображением “в” и не для всякой функции существует обратное отображение. В [50] рассмотрено дискретное уравнение Эйри, которое сводится к стандартному рекуррентному соотношению.

В [51] предложены различные стратегии для получения приближения к дискретным неотражающим (прозрачным) граничным условиям для уравнения Шрёдингера с линейным потенциальным членом во внешней области. Вывод был основан на знании точного решения (включая асимптотику) дискретного уравнения Эйри. Подход имеет два преимущества перед стандартным подходом к дискретизации непрерывного неотражающего граничного условия (НГУ): точность и эффективность; в то время как дискретные НГУ обычно имеют квадратичный порядок роста ошибки, сумма экспоненциальных приближений к дискретным блокам преобразования частоты имеет только линейный порядок. Более того, предоставлены простые критерии проверки стабильности метода.

Решение задачи (3) с начальными данными в виде функции Эйри напоминает задачу о распаде разрыва, но если в задаче о распаде разрыва начальные данные на полуоси принадлежат ${{L}_{2}}$, то в случае с функцией Эйри, принадлежащей ${{L}_{4}}$, это не так. Математическая задача состоит в исследовании механизма появления и асимптотической устойчивости у возмущенной задачи решений типа функций Эйри.

Поэтому для проведения достоверных расчетов требуется провести регуляризацию задачи, чтобы избавиться от неограниченного оператора и воспользоваться идеей гиперболизации для улучшения соотношения шагов по времени и пространству. При выводе НУШ (Леонтович 1944 г., см. [52]) было использовано предположение, что поле $E$ представляет собой огибающую быстро осциллирующей величины $\mathcal{E}$. Эта функция представляет собой произведение двух функций: быстро осциллирующей экспоненциальной функции ${{e}^{{i\phi (r,z)}}}$ и медленно изменяющейся функции $E(r,z)$. Характерное поведение $\mathcal{E}$ в фиксированной точке $r$ представлено на фиг. 5.

Фиг. 5.

Графическое представление характера поведения гиперболизованного решения.

Добавив вторую производную с малым параметром в исходное уравнение (3), мы как бы возвращаемся к уравнению для исходной величины $\mathcal{E}$, но с функцией $\phi = ct{\text{/}}\varepsilon $, т.е. спираль у нас теперь лежит на строго цилиндрической поверхности.

Сначала реализуем метод последовательных операторных замен неизвестной функции на одном шаге $t$ по времени. Затем введем новую неизвестную функцию, учитывающую малый параметр:

(12)

$E = U{{e}^{{it(x + (1/{{\mu }^{2}} - \mu ))/2}}},$

так чтобы у получившегося в результате гиперболического оператора

(13)

$4{{\mu }^{2}}\frac{{{{\partial }^{2}}U}}{{\partial {{t}^{2}}}} + 2i\frac{{\partial U}}{{\partial t}} + \frac{{{{\partial }^{2}}U}}{{\partial {{x}^{2}}}} - it\frac{{\partial U}}{{\partial x}} + \left( {\frac{i}{{{{\mu }^{2}}}} - i\mu - \frac{{{{t}^{2}}}}{4}} \right)U = - {\text{|}}U{{{\text{|}}}^{2}}U + B{{e}^{{it(x + (1/{{\mu }^{2}} - \mu )/2)}}}$

существовала явно вычисляемая функция Грина. Это позволяет, преобразовав исходное уравнение к гиперболической системе с производными по времени в левой части, использовать фундаментальное решение для проведения нескольких последовательных операторных замен неизвестных функции системы (см. [6]). Получившийся в результате оператор правой части обращается в нуль в начальной и конечной точках выбранного временного интервала. Следствием является то, что построенное на этом интервале приближенное решение в начальной и конечной точках этого интервала удовлетворяет исходному уравнению. Отметим, что операторные замены обладают автоматическим параллелизмом и просто и практически безошибочно программируются.

Так как гиперболизация для нас – это метод нахождения приближенного решения исходного уравнения Шрёдингера для функции $E$, то после каждого шага нахождения функции $U(t)$ мы возвращaемся к функции $E(t)$. Считаем, что ${{E}_{{{\text{new}}}}}(0) = E(t)$. Нам осталось перейти к ${{U}_{{{\text{new}}}}}$, и задать начальные данные для вспомогательных функций, исходя из условия, что $\partial {{U}_{{{\text{new}}}}}{\text{/}}\partial t$ в точке $t = 0$ определяется из исходного уравнения. Достаточно задать

${{U}_{{{\text{new}}}}}(0) = U(t){{e}^{{itx/2 + i({{t}^{3}} + 3t{{T}^{2}} + 3{{t}^{2}}Y)/24}}}.$

Добавим в гиперболизованное уравнение дополнительно затухание с параметром $b$:

(14)

${{a}^{2}}{{\mu }^{2}}\left( {\frac{{{{\partial }^{2}}U}}{{\partial {{t}^{2}}}} + b\frac{{\partial U}}{{\partial t}}} \right) + 2i\frac{{\partial U}}{{\partial t}} - \frac{{{{\partial }^{2}}U}}{{\partial {{x}^{2}}}} - it\frac{{\partial U}}{{\partial x}} + \left( {\frac{{{{t}^{2}}}}{4} - N - 2d} \right)U + D{{e}^{{ - it(x/2 + d)}}} = 0,$

где $\mu $ – малый параметр, а $N = {\text{|}}U{{{\text{|}}}^{2}}$. Введем новое время

(15)

$t = \frac{{{{t}_{{{\text{old}}}}}}}{{(a\mu )}}.$

Сделаем замену

(16)

$U = V{{e}^{{ - (ba\mu + 2i/a\mu )t/2}}};$

(17)

$\frac{{{{\partial }^{2}}V}}{{\partial {{t}^{2}}}} - \frac{{{{\partial }^{2}}V}}{{\partial {{x}^{2}}}} - ia\mu t\frac{{\partial V}}{{\partial x}} + \frac{{{{{(a\mu t)}}^{2}}}}{4}V + \left( {\frac{1}{{{{a}^{2}}{{\mu }^{2}}}} - \frac{{{{b}^{2}}{{a}^{2}}{{\mu }^{2}}}}{4} - 2d - N} \right)V - ibV + D{{e}^{{it(a\mu x/2 + \eta )}}} = 0.$

Здесь введено обозначение

(18)

$\eta = a\mu d + i(ba\mu + 2i{\text{/}}a\mu )t{\text{/}}2.$

Для упрощения дальнейших выкладок фиксируем параметры

(19)

$b = \frac{{a\mu }}{2},\quad d = \frac{1}{{2{{a}^{2}}{{\mu }^{2}}}} - \frac{{{{a}^{4}}{{\mu }^{4}}}}{{32}}.$

Сделаем преобразование Фурье по пространственной(ым) переменной(ым)

(20)

$\frac{{{{\partial }^{2}}FV}}{{\partial {{t}^{2}}}} + {{\left( {\frac{{a\mu }}{2}} \right)}^{2}}{{\left( {t + \frac{{2k}}{{a\mu }}} \right)}^{2}}FV - i\frac{{a\mu }}{2}FV - F(NV) + D{{e}^{{ - it\eta }}}\delta (k - a\mu t{\text{/}}2).$

Введем новый параметр и обозначение

(21)

$\alpha = \frac{{a\mu }}{2},\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} = D{{e}^{{ - it\eta }}}\delta (k - a\mu t{\text{/}}2),\quad \eta = - \frac{1}{{2a\mu }} - \frac{{{{a}^{5}}{{\mu }^{5}}}}{{32}} + i\frac{{{{a}^{2}}{{\mu }^{2}}}}{4}.$

Полученное уравнение может быть расписано в виде системы

(22)

$\frac{{\partial Fv}}{{\partial t}} = Fw,$

(23)

$\frac{{\partial Fw}}{{\partial t}} = - {{\alpha }^{2}}{{(t + 2k{\text{/}}\alpha \mu )}^{2}}Fv + i\alpha Fv + F(Nv) - \hat {\gamma }FV + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} .$

В матричной форме получаем

(24)

$\frac{\partial }{{\partial t}}\left( {\begin{array}{*{20}{c}} {Fv} \\ {Fw} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0&1 \\ { - {{\alpha }^{2}}{{{(t + k{\text{/}}\alpha )}}^{2}}}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {Fv} \\ {Fw} \end{array}} \right) + i\alpha \left( {\begin{array}{*{20}{c}} 0&0 \\ 1&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {Fv} \\ {Fw} \end{array}} \right) + F\left( {\begin{array}{*{20}{c}} 0&0 \\ N&0 \end{array}} \right){{F}^{{ - 1}}}\left( {\begin{array}{*{20}{c}} {Fv} \\ {Fw} \end{array}} \right) + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right)$

с неограниченным оператором (умножения на ${{\alpha }^{2}}{{(t + k{\text{/}}\alpha )}^{2}}$) в правой части. Такой вид упрощает применение метода операторной экспоненты.

Фундаментальное $G$, ${{G}_{1}}$ решение линейной части уравнения (24) имеет вид

(25)

$G(t) = {{e}^{{i\alpha ({{t}^{2}} + 2kt/\alpha )/2}}}\int\limits_0^t \,{{e}^{{ - i\alpha ({{s}^{2}} + 2ks/\alpha )}}}ds,\quad {{G}_{1}}(t) = {{e}^{{i\alpha ({{t}^{2}} + 2kt/\alpha )/2}}}.$

С его помощью сделаем первую операторную замену неизвестных функций

(26)

$\left( {\begin{array}{*{20}{c}} {Fv} \\ {Fw} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{G}_{1}}}&G \\ {i(\alpha t + 2k){{G}_{1}}}&{i(\alpha t + 2k)G + {{{\bar {G}}}_{1}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} A \\ B \end{array}} \right) = Q(t)\left( {\begin{array}{*{20}{c}} A \\ B \end{array}} \right).$

Тогда новые неизвестные функции

(27)

$\left( {\begin{array}{*{20}{c}} A \\ B \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {i(\alpha t + 2k)G + {{{\bar {G}}}_{1}}}&{ - G} \\ { - i(\alpha t + 2k){{G}_{1}}}&{{{G}_{1}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {Fv} \\ {Fw} \end{array}} \right) = {{Q}^{{ - 1}}}(t)\left( {\begin{array}{*{20}{c}} {Fv} \\ {Fw} \end{array}} \right)$

удовлетворяют системе уравнений в матричной форме

(28)

$\frac{\partial }{{\partial t}}\left( {\begin{array}{*{20}{c}} A \\ B \end{array}} \right) = {{Q}^{{ - 1}}}(t)F\left( {\begin{array}{*{20}{c}} 0&0 \\ N&0 \end{array}} \right){{F}^{{ - 1}}}Q(t)\left( {\begin{array}{*{20}{c}} A \\ B \end{array}} \right) + {{Q}^{{ - 1}}}(t)\left( {\begin{array}{*{20}{c}} 0 \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} } \end{array}} \right).$

Обозначим

(29)

$V = \left( {\begin{array}{*{20}{c}} A \\ B \end{array}} \right),\quad \tilde {D}(t) = {{Q}^{{ - 1}}}(t)\left( {\begin{array}{*{20}{c}} 0 \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} } \end{array}} \right)$

и введем необходимые в дальнейшем операторы

(30)

$T_{ \pm }^{1}(\tau ) = \left( {\begin{array}{*{20}{c}} 1&0 \\ { \pm \frac{1}{t}\int_0^\tau \,{{\tau }_{1}}N({{\tau }_{1}})d{{\tau }_{1}}}&1 \end{array}} \right),\quad T_{ \pm }^{2}(\tau ) = \left( {\begin{array}{*{20}{c}} 1&0 \\ { \pm \frac{1}{t}\int_0^\tau \,(t - {{\tau }_{1}})N({{\tau }_{1}})d{{\tau }_{1}}}&1 \end{array}} \right),$

(31)

${{T}_{N}}(\tau ) = \left( {\begin{array}{*{20}{c}} 0&0 \\ {N(\tau )}&0 \end{array}} \right),\quad {{T}_{b}}(\tau ) = \left( {\begin{array}{*{20}{c}} 0&0 \\ {\frac{\tau }{t}N(\tau )}&0 \end{array}} \right),\quad {{T}_{e}}(\tau ) = \left( {\begin{array}{*{20}{c}} 0&0 \\ {\frac{{t - \tau }}{t}N(\tau )}&0 \end{array}} \right).$

Для вектор-функции $V$ получим уравнение

(32)

$\frac{{dV}}{{dt}} = C(t)V + \tilde {D}(t)$

с ограниченным оператором

(33)

$C(t) = {{Q}^{{ - 1}}}(t)F\left( {\left( {\begin{array}{*{20}{c}} 0&0 \\ {N(y)}&0 \end{array}} \right){{F}^{{ - 1}}}Q(t) \ldots } \right).$

Введем на отрезке $0 \leqslant \tau \leqslant t$ оператор

(34)

${{C}_{1}}(\tau ,t) = {{Q}^{{ - 1}}}(t)F{{T}_{b}}(\tau )\left( {{{F}^{{ - 1}}}Q(t) \ldots } \right),$

действующий на вектор-функции $V(\tau )$. С помощью разложения Дайсона (см. [53]) определим операторы

(35)

${{D}_{ \pm }}(\tau ) = {{Q}^{{ - 1}}}(t)FT_{ \pm }^{1}(\tau )\left( {{{F}^{{ - 1}}}Q(t) \ldots } \right),$

представляющие собой операторные экспоненты от (34) с соответствующими знаками $ \pm $ перед $N(\tau )$. Очевидно, что ${{D}_{ + }}(\tau ) \cdot {{D}_{ - }}(\tau ) = I$, и они оба являются ограниченными операторами в пространстве ${{L}_{2}}{\kern 1pt} $. Отметим, что у образующего оператора (34) точка $\lambda = 0$ является точкой спектра. Функция

(36)

$W(\tau ) = {{D}_{ + }}(\tau )V(\tau )$

удовлетворяет при $0 \leqslant \tau \leqslant t$ уравнению

$\frac{{dW}}{{d\tau }} = \frac{d}{{d\tau }}{{D}_{ + }}(\tau )V(\tau ) + {{D}_{ + }}(\tau )\frac{{dV}}{{d\tau }} = \frac{d}{{d\tau }}{{D}_{ + }}(\tau ){{D}_{ - }}(\tau )W(\tau ) + {{D}_{ + }}(\tau )C(\tau ){{D}_{ - }}(\tau )W(\tau ) + {{D}_{ + }}(\tau )\tilde {D}(\tau ).$

Из (34) и (35) следует, что

$\frac{d}{{d\tau }}{{D}_{ + }}(\tau ){{D}_{ - }}(\tau ) = {{C}_{1}}(\tau ,t).$

Таким образом, для $W(\tau )$ получено уравнение

(37)

$\begin{gathered} \frac{{dW}}{{d\tau }} = {{C}_{2}}(\tau ,t)W(\tau ) + {{D}_{ + }}(\tau )\tilde {D}(\tau ) = \left[ {{{D}_{ + }}(\tau )C(\tau ){{D}_{ - }}(\tau ) - {{C}_{1}}(\tau ,t)} \right]W(\tau ) + {{D}_{ + }}(\tau )\tilde {D}(\tau ) = \\ = {{Q}^{{ - 1}}}(t)F\left[ {T_{ + }^{1}(\tau ){{F}^{{ - 1}}}Q(t){{Q}^{{ - 1}}}(\tau )F{{T}_{N}}(\tau ){{F}^{{ - 1}}}Q(\tau ){{Q}^{{ - 1}}}(t)FT_{ - }^{1}(\tau ) - T_{b}^{1}(\tau )} \right]{{F}^{{ - 1}}}Q(t) + {{D}_{ + }}(\tau )\tilde {D}(\tau ). \\ \end{gathered} $

Видно, что ${{C}_{2}}(t,t) = 0$, а ${{C}_{2}}(0,t) = C(0)$.

С помощью того же разложения Дайсона определим операторы

(38)

${{\widehat D}_{ \pm }}(\tau ) = {{Q}^{{ - 1}}}(0)F\left( {T_{ \pm }^{2}(\tau ){{F}^{{ - 1}}}Q(0) \ldots } \right).$

Так как матрицы $Q(0)$ и ${{Q}^{{ - 1}}}(0)$ постоянные, то они перестановочны с преобразованием Фурье и в результате

(39)

${{\widehat D}_{ \pm }}(\tau ) = F\left( {\left( {\begin{array}{*{20}{c}} 1&{ \pm \frac{1}{t}\int_0^\tau \,(t - {{\tau }_{1}})N({{\tau }_{1}})d{{\tau }_{1}}} \\ 0&1 \end{array}} \right){{F}^{{ - 1}}} \ldots } \right).$

Теперь введем новую функцию

(40)

$Z(\tau ) = {{\widehat D}_{ + }}(\tau )W(\tau ),$

удовлетворяющую уравнению

(41)

$\begin{gathered} \frac{{dZ}}{{d\tau }} = {{C}_{3}}(\tau ,y)Z + {{\widehat D}_{ + }}(\tau ){{D}_{ + }}(\tau )\tilde {D}(\tau ) = {{\widehat D}_{ + }}(\tau ){{C}_{2}}(\tau ,y){{\widehat D}_{ - }}(\tau )Z(\tau ) - \\ - \;{{Q}^{{ - 1}}}(0)F{{T}_{e}}(\tau ){{F}^{{ - 1}}}Q(0)Z(\tau ) + {{\widehat D}_{ + }}(\tau ){{D}_{ + }}(\tau )\tilde {D}(\tau ). \\ \end{gathered} $

Отметим важный для нас факт, что ${{C}_{3}}(0,t) = {{C}_{3}}(t,t) = 0$. Так как операторы ${{C}_{1}}$, ${{C}_{2}}$ и ${{C}_{3}}$ – по аналогии с $C(t)$ – ограниченные, а ${{C}_{3}} = 0$ в начальной и конечной точках интервала интегрирования, то можно ожидать, что функция $Z(\tau )$ находится приближенным интегрированием соотношения

$\frac{{dZ}}{{d\tau }} = {{\widehat D}_{ + }}(\tau ){{D}_{ + }}(\tau )\tilde {D}(\tau ).$

Отсюда

(42)

${{V}_{{{\text{ap}}}}}(\tau ) = Q(\tau ){{D}_{ - }}(\tau ){{\widehat D}_{ - }}(\tau ){{V}_{0}} + Q(\tau ){{D}_{ - }}(\tau ){{\widehat D}_{ - }}(\tau )\int\limits_0^\tau \,{{\widehat D}_{ + }}(s){{D}_{ + }}(s)\tilde {D}(s)ds.$

Заменив подынтегральное выражение линейной интерполяцией по крайним точкам интервала $(0,\;t)$, получаем

(43)

$\int\limits_0^\tau \,{{\widehat D}_{ + }}(s){{D}_{ + }}(s)\tilde {D}(s)ds \approx H(\tau ) = \frac{{{{\tau }^{2}}}}{{2t}}{{\widehat D}_{ + }}(t){{D}_{ + }}(t)\tilde {D}(t) + \left( {\tau - \frac{{{{\tau }^{2}}}}{{2t}}} \right)\tilde {D}(0).$

Следствие. Приближенное решение

${{V}_{{{\text{ap}}}}}(\tau ) = Q(\tau ){{D}_{ - }}(\tau ){{\widehat D}_{ - }}(\tau )({{V}_{0}} + H(\tau ))$

удовлетворяет уравнению (20) в начальной и конечной точках интервала интегрирования $0 \leqslant \tau \leqslant t$.

Это означает, что в конечной точке $\tau = t$ траектория ${{V}_{{{\text{ap}}}}}(\tau )$ касается траектории решения уравнения (20), близкой к траектории точного решения задачи Коши (20), (4).

Распишем подробно приближенное решение в конечной точке интервала $\;0 \leqslant \tau \leqslant t$:

(44)

$\left( {\begin{array}{*{20}{c}} v \\ w \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1&0 \\ { - tN(t){\text{/}}2}&1 \end{array}} \right){{F}^{{ - 1}}}Q(t)F\left( {\left( {\begin{array}{*{20}{c}} 1&{ - tN(0){\text{/}}2} \\ 0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{w}_{0}} + D\tau {\text{/}}2} \\ {{{v}_{0}}} \end{array}} \right)} \right) + \left( {\begin{array}{*{20}{c}} 0 \\ {t{{e}^{{i(\eta + \alpha \mu x/2)t}}}{\text{/}}2} \end{array}} \right).$

Матрица $Q(t)$ совместно с прямым и обратным преобразованием Фурье задают операторы сдвига и дифференцирования, и приближенно можно записать результат для функции ${v}$:

(45)

$v(t) \approx {{v}_{0}}(x + 2t{\text{/}}\mu ) + \frac{t}{\mu }{{N}_{0}}(x + 2t{\text{/}}\mu ){{{v}}_{0}}(x + 2t{\text{/}}\mu ) + {{w}_{0}}(x + 2t{\text{/}}\mu ) + \frac{t}{{{{\mu }^{2}}}}\frac{\partial }{{\partial x}}{{w}_{0}}(x - 2t{\text{/}}\mu ) + D\tau {\text{/}}2.$

Функцию

$w(t) \approx i{{F}^{{ - 1}}}(\alpha t + 2k{\text{/}}\mu ){{G}_{1}}F{{{v}}_{0}} + (i(\alpha t + 2k{\text{/}}\mu )G + {{\bar {G}}_{1}})\left( {F\left( { - \frac{t}{2}N(t){{v}_{0}}} \right) + F{{w}_{0}}} \right)$

можно не находить, поскольку начальные данные для $Fw(t) = \partial v(t){\text{/}}\partial t$ находятся из условия, что в точке $t = 0$ выполняется исходное уравнение Шрёдингера

(46)

$F{{w}_{0}} = i\sqrt \mu \left( { - {{k}^{2}}F{v}(0) + F(N(0)v(0))} \right).$

Для проведения следующего шага вычислений согласно использованной замене (16), получим новые начальные данные

${{V}_{{{\text{new}}}}} = E(t) = v(t){{e}^{{ - it/2\mu }}},$

$\frac{{\partial {{E}_{{{\text{new}}}}}}}{{\partial t}} = - i\left( {\frac{{{{\partial }^{2}}E(t)}}{{\partial {{x}^{2}}}} + N(t)E(t)} \right) = - i{{e}^{{ - it/2\mu }}}\left( {\frac{{{{\partial }^{2}}V(t)}}{{\partial {{x}^{2}}}} + N(t)V(t)} \right).$

Соответственно

$F{{v}_{{{\text{new}}}}} = {{e}^{{ - it/2\mu }}}Fv(t),$

$F{{w}_{{{\text{new}}}}} = i{{e}^{{ - it/2\mu }}}\left( {{{k}^{2}}Fv(t) - F(N(t)v(t))} \right).$

Для проведения устойчивых расчетов, исключающих образования случайных фаз из-за многократного умножения на ${{G}_{1}} = {{e}^{{ - i\alpha ({{t}^{2}} + 2kt/\alpha )}}}$, необходимо выполнение условия

(47)

$\alpha ({{t}^{2}} + 2kt{\text{/}}\alpha ) < \pi {\text{/}}2.$

Вычисления проводились в ограниченной спектральной области ${\text{|}}K{\text{|}} \leqslant {{K}_{{{\text{max}}}}}$, поэтому, возвращаясь к исходному времени, получаем

$\frac{{t_{{{\text{old}}}}^{2}}}{\mu } + \frac{{4{{K}_{{{\text{max}}}}}{{t}_{{{\text{old}}}}}}}{\mu } \leqslant \frac{\pi }{2}.$

Из этого неравенства находим

(48)

${{t}_{{{\text{old}}}}} \approx \pi \mu {\text{/}}8{{K}_{{{\text{max}}}}} \approx \pi \mu \Delta x{\text{/}}8.$

Подстановка в (45) начальных данных из (46) дает возможность оценить в образах Фурье вклад от $F{{w}_{0}}$ в окончательный результат $F{{W}_{{{\text{new}}}}}$: cтоящий перед $F{{w}_{0}}$ множитель имеет вид

$\frac{{2{{\mu }^{{3/2}}}{{k}^{2}}}}{{\sqrt {4\mu {{k}^{2}} + 1} }}$

и при выбранном $\mu $ имеет оценку

$\frac{{{{{\left( {\frac{k}{{{{K}_{{{\text{max}}}}}}}} \right)}}^{2}}}}{{\sqrt 2 {{K}_{{{\text{max}}}}}\sqrt {2{{{\left( {\frac{k}{{{{K}_{{{\text{max}}}}}}}} \right)}}^{2}} + 1} }} \leqslant \frac{2}{{3{{K}_{{{\text{max}}}}}}} < 1,$

т.е. не нарастает.

На фиг. 6 приведены результаты численного решения гиперболизованного НУШ (14) с нулевыми начальными данными при относительно малом внешнем воздействии $B = 0.1$. Основной результат заключается в демонстрации отличия процессов релаксации волнового потока в НУШ от релаксации тепловых потоков. Релаксация в НУШ достигается подстройкой фазы колебаний. Изначально растущее за счет внешнего воздействия поле быстро разваливается на разбегающиеся волны, типа функций Эйри, но с растущей частотой. Характерно, что гладкие передние фронты волн направлены в разные стороны. Это объясняется тем, что образующиеся при $x > 0$ и $x < 0$ волны – решения уравнения ${{\partial }^{2}}\varphi {\text{/}}\partial {{x}^{2}} \pm \varphi $ есть функции Эйри $Ai( \pm x)$, т.е. в области отрицательных $x$ получаем волну $Ai( - x)$.

Фиг. 6.

Графики релаксации амплитуды поля ${\text{|}}E{\text{|}}$ в различные моменты времени. Видно образование и эволюция бегущих волн типа функции Эйри.

На фиг. 6 продемонстрировано, что находится именно решение уравнения Шрёдингера: нет характерного признака решения гиперболического уравнения – двух одинаковых волн $\varphi (x - at)$ и $\varphi (x + at)$, бегущих в противоположных направлениях.

Для уравнения (3) разработан также алгоритм с выделением консервативных переменных и потоков, применяемый в работах [20]–[23]. Расширенный вариант из [46], чтобы не повторять аналогичных выкладок, приведен в следующем резделе.

Возможность получения решений в различных функциональных пространствах анонсирована в [54]. На выходе получаются слабо нелинейные и сильно нелинейные стационарные турбулентные состояния. Последнее состояние характеризуется спектром Фурье “с тяжелым хвостом”.

3. ЛАЗЕРНЫЙ УСИЛИТЕЛЬ

В этом разделе мы реализуем идею из [20], [21] введения консервативных переменных и потоков для системы лазерного усилителя (см. [55]–[57]), включающую как уравнения типа НУШ, так и уравнение распространения тепла. Основным отличием рассмотренной в настоящей работе конструкции от методики из [22], [23] является перенесение идеи гиперболизации на уравнения в недивергентной форме.

Рассмотрена гиперболизированная математическая модель усилителя и усовершенствован вычислительный алгоритм за счет привлечения идеи предиктора-корректора, позволившей провести так называемое расщепление по физическим процессам. Это позволило полностью векторизовать все математические операции с компонентами уравнений и использовать многопроцессорность компьютеров с наибольшей эффективностью.

Математическая модель импульсно-периодического лазерного усилителя с накачкой лазерным пучком описывается системой уравнений типа нелинейного уравнения Шрёдингера для поля накачки $U$, совмещенного с входным сигналом ${{U}_{j}}$, описанным аналогичным уравнением, уравнением для температуры $T$ и уравнением релаксации для населенности $N$, в котором поглощение ионами кристалла пропорционально интенсивности накачки.

Система уравнений усилителя приводится к виду

Граничные условия

На вход усилителя подается последовательность коротких импульсов накачки и сигнала. Накачка формирует населенность, которая, в свою очередь, создает условия для роста импульсов сигнала. Количество импульсов может быть порядка 100, так что для суммарного интервала времени необходим высокоточный эффективный алгоритм счета.

Будем конструировать метод нахождения приближенного решения этой системы. Увеличение скорости счета достигается путем гиперболизации, т.е. добавлением второй производной по времени с малым параметром. При гиперболизации мы добавили еще и затухание. Будем рассматривать отдельно гиперболизованную систему уравнений для функции $U(r,z)$:

Заменим в силу первого уравнения системы $\frac{{\sqrt \varkappa }}{r}\frac{\partial }{{\partial r}}rH$:

Гиперболизованное уравнение для функции ${{U}_{j}}$ расписывается аналогично.

При гиперболизации мы добавили еще и затухание, и будем рассматривать гиперболизованное уравнение для температуры:

Уравнение для населенности (56) осталось без изменений.

4. ЧИСЛЕННАЯ СХЕМА

В работе [46] использована численная схема, успешно применявшаяся в [6, с. 35], и сводящаяся к решению нелинейного уравнения относительно ${\text{|}}E(x,t){\kern 1pt} {{{\text{|}}}^{2}}$ отдельно для каждой точки $x$ вместо решения системы нелинейных уравнений сразу для всех $x$.

Наиболее эффективным из нескольких опробованных алгоритмов счета оказался алгоритм типа предиктор-корректор, приведенный ниже.

Введем в пространстве $(r,z,t)$ равномерные по каждому направлению расчетные сетки с целочисленными индексами

Для простоты обозначений для функций $U,\;{{U}_{j}},\;H,\;{{H}_{j}},\;G,\;{{G}_{j}}$, чтобы не таскать многоиндексные формулы, опишем переход со слоя $z = 0$ на слой $z = {{h}_{z}}$.

Чтобы сократить время счета, будем производить вычисления с максимально возможными шагами ${{h}_{r}}$. Для этого при счете производных по $r$ используем пятиточечные формулы, имеющие порядок аппроксимации $O(h_{r}^{4})$ и позволяющие векторизовать процес вычисления производных.

Проинтегрируем линейные уравнения (61), (63) по $z$ в соответствующих пределах, а получившиеся интегралы от быстро осциллирующих функций вычислим по формуле Филона. Сначала считаются $H(z{\text{/}}2),{\kern 1pt} \;G(z{\text{/}}2)$, а затем $U(z)$. Включенные в исходные уравнения затухания позволяют считать “медленные” сомножители подынтегральных функций постоянными, равными значениям этих функций в некоторых выбранных фиксированных точках $z$:

Соответственно для функции $T$ переход сделан со слоя $t = 0$ на слой $t = {{h}_{t}}$:

После нахождения $U(z),\;{{U}_{j}}(z),\;T(t),\;N(t)$ на верхних слоях соответственно по их значениям считаются $H(z),\;G(z)$ и т.д.

Таким образом, полностью заканчиваются переходы на верхние слои и готовы все данные для следующего шага.

Отметим, что во всех формулах, по которым велись вычисления, явно присутствует затухание, иными словами, алгоритм обладает внутренней устойчивостью.

Чтобы исключить возможность образования неустойчивости счета из-за нарастания случайных фаз (см. [6]) в (69) и (70) отношение $z{\text{/}}2\mu $ должно быть кратным $\pi N.$

Так как у нас для $U$ и $H \approx \partial U{\text{/}}\partial r$ считаются отдельные уравнения, то при необходимости легко моделируются условия прохождения световой волны через границу среды (см. [58], [59]). Обзор решений параболических уравнений в различных функциональных пространствах приведен в [60].

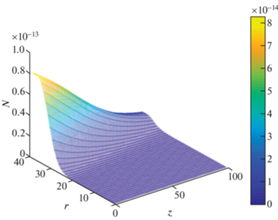
Выбор параметра $\mu $ осуществлялся опытным путем: наращиванием от минимального значения ${{10}^{{ - 10}}}$ до появления изменений значений функций при $r = 0$. На фиг. 7 приведены графики распределения амплитуды сигнала первого и последнего импульса для разного количества импульсов усиливаемого сигнала. На фиг. 8 приведен график населенности зарядов вдоль кристалла в конечный момент времени прохождения пачки импульсов.

Фиг. 7.

Слева – выходящий сигнал от первого и последнего из последовательности 100 импульсов, справа – из 10.

Фиг. 8.

Населенность при последнем импульсе.

5. ЗАКЛЮЧЕНИЕ

Грубую оценку малого параметра гиперболизации $\mu $ можно получить, рассматривая главную часть уравнения (59). Условие устойчивости ее разностной аппроксимации дает оценку соотношения шагов

Отметим также, что изложенные в работе методы легко обобщаются на многомерный случай.