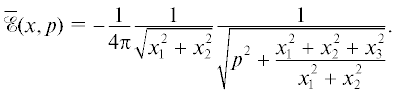Журнал вычислительной математики и математической физики, 2023, T. 63, № 1, стр. 123-144
О задачах коши для нелинейных соболевских уравнений теории сегнетоэлектричества
М. О. Корпусов 1, *, Р. С. Шафир 1, **
1 МГУ им. М.В. Ломоносова
119991 Москва, Ленинские горы, 1, Россия
* E-mail: korpusov@gmail.com
** E-mail: romanshafir@mail.ru
Поступила в редакцию 01.08.2021
После доработки 05.05.2022
Принята к публикации 04.08.2022
- EDN: LMBXET
- DOI: 10.31857/S0044466922120092
Аннотация
Исследуются две задачи Коши для нелинейных соболевских уравнений: $\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\frac{{{{\partial }^{2}}u}}{{\partial x_{3}^{2}}} + \Delta u = {{\left| u \right|}^{q}}$ и $\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{\Delta }_{ \bot }}u + \Delta u = {{\left| u \right|}^{q}}.$ Найдены условия, при которых существуют слабые обобщенные локальные во времени решения задач Коши, а также происходит разрушение слабых решений этих же задач Коши. Библ. 15.
1. ВВЕДЕНИЕ
В настоящей работе изучаются две задачи Коши. Первая задача Коши имеет вид
(1.1)
$\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\frac{{{{\partial }^{2}}u}}{{\partial x_{3}^{2}}} + \Delta u = {\text{|}}u{\kern 1pt} {{{\text{|}}}^{q}},\quad (x,t) \in {{\mathbb{R}}^{3}} \otimes (0,T],$(1.2)
$u(x,0) = {{u}_{0}}(x),\quad u{\kern 1pt} '(x,0) = {{u}_{1}}(x),\quad x \in {{\mathbb{R}}^{3}}.$Вторая задача Коши имеет вид
(1.3)
$\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{\Delta }_{ \bot }}u + \Delta u = {\text{|}}u{\kern 1pt} {{{\text{|}}}^{q}},\quad (x,t) \in {{\mathbb{R}}^{3}} \otimes (0,T],$(1.4)
$u(x,0) = {{u}_{0}}(x),\quad u{\kern 1pt} '(x,0) = {{u}_{1}}(x),\quad x \in {{\mathbb{R}}^{3}}.$В работе исследуются слабые и слабые обобщенные локальные во времени решения данных задач Коши. Доказывается существование слабых обобщенных решений при $q > 4$. При $1 < q\;\leqslant \;3$ доказано разрушение слабых решений.
Отметим работу [1], в которой исследовалась задача Коши с той же нелинейностью, но другим дифференциальным оператором, имеющим вид
Уравнения (1.1), (1.3) относятся к уравнениям соболевского типа (см. [2]), исследованию которых посвящено большое количество работ. Например, в работах Г.А. Свиридюка, С.А. Загребиной, А.А. Замышляевой [3]–[5] были рассмотрены в общем виде и в виде примеров начально-краевые задачи для различных типов линейных и нелинейных уравнений соболевского типа.
Теория потенциала для неклассических уравнений типа Соболева впервые была рассмотрена в работе Б.В. Капитонова [6], а в дальнейшем изучалась в работах С.А. Габова и А.Г. Свешникова [7], [8], а также в работах их учеников (см. работу Ю.Д. Плетнера [9]).
В классической работе [10] С.И. Похожаева и Э. Митидиери методом нелинейной емкости были получены глубокие результаты о роли критических показателей. Также можно отметить работы Е.И. Галахова и О.А. Салиевой [11] и [12].
Настоящая работа продолжает исследования, начатые в [13]–[15] и посвященные получению критических показателей для решений задач Коши для нелинейных уравнений соболевского типа.
2. ВЫВОД УРАВНЕНИЙ
Пусть $\{ O,{{{\mathbf{e}}}_{x}},{{{\mathbf{e}}}_{y}},{{{\mathbf{e}}}_{z}}\} $ – некоторая декартова прямоугольная система координат в пространстве. При рассмотрении анизотропного сегнетоэлектрика вблизи температуры Кюри с анизотропией вдоль оси $Oz$ и с учетом модельной временной дисперсии справедливы следующие уравнения:
(2.1)
${{D}_{x}} = {{\varepsilon }_{x}}{{E}_{x}} + {{\varepsilon }_{0}}\int\limits_0^t {\kern 1pt} (t - \tau ){{E}_{x}}(\tau ){\kern 1pt} d\tau ,$(2.2)
${{D}_{y}} = {{\varepsilon }_{y}}{{E}_{y}} + {{\varepsilon }_{0}}\int\limits_0^t {\kern 1pt} (t - \tau ){{E}_{y}}(\tau ){\kern 1pt} d\tau ,$(2.3)
${{D}_{z}} = {{\varepsilon }_{z}}{{E}_{z}} + {{\varepsilon }_{0}}\int\limits_0^t {\kern 1pt} (t - \tau ){{E}_{z}}(\tau ){\kern 1pt} d\tau ,$(2.4)
$\max \{ {\kern 1pt} {\text{|}}{{\varepsilon }_{x}}{\kern 1pt} {\text{|}},{\text{|}}{{\varepsilon }_{y}}{\kern 1pt} {\text{|}}{\kern 1pt} \} \ll {\text{|}}{{\varepsilon }_{z}}{\kern 1pt} {\text{|}},$(2.5)
${\mathbf{D}} = {{D}_{x}}{{{\mathbf{e}}}_{x}} + {{D}_{y}}{{{\mathbf{e}}}_{y}} + {{D}_{z}}{{{\mathbf{e}}}_{z}}.$(2.7)
$\frac{{\partial n}}{{\partial t}} = {{q}_{0}}\int\limits_0^t \,{\text{|}}\phi {\kern 1pt} {{{\text{|}}}^{q}}(\tau ){\kern 1pt} d\tau ,\quad q > 1.$(2.8)
${{\varepsilon }_{x}}{{\phi }_{{xxtt}}} + {{\varepsilon }_{y}}{{\phi }_{{yytt}}} + {{\varepsilon }_{z}}{{\phi }_{{zztt}}} + {{\varepsilon }_{0}}\Delta \phi = 4\pi {{q}_{0}}{\text{|}}\phi {\kern 1pt} {{{\text{|}}}^{q}},\quad \Delta = \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}.$(2.9)
${{\varepsilon }_{z}}{{\phi }_{{zztt}}} + {{\varepsilon }_{0}}\Delta \phi = 4\pi {{q}_{0}}{\text{|}}\phi {\kern 1pt} {{{\text{|}}}^{q}}.$3. ОБОЗНАЧЕНИЯ
Под классом функций $u(x,t) \in {{\mathbb{C}}_{b}}((1 + x_{1}^{2} + x_{2}^{2}{{)}^{{{{\gamma }_{1}}/2}}}{{(1 + x_{3}^{2})}^{{{{\gamma }_{2}}/2}}};{{\mathbb{R}}^{3}} \otimes [0,T])$ при ${{\gamma }_{1}}\; \geqslant \;0$ и ${{\gamma }_{2}}\; \geqslant \;0$ мы понимаем такие функции $u(x,t) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \otimes [0,T]),$ что конечна следующая норма:
(3.1)
${{\left\| u \right\|}_{T}}: = \mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T]} {{(1 + x_{1}^{2} + x_{2}^{2})}^{{{{\gamma }_{1}}/2}}}{{(1 + x_{3}^{2})}^{{{{\gamma }_{2}}/2}}}{\text{|}}u(x,t){\kern 1pt} {\text{|}} < + \infty .$Под классом функций $\mathbb{C}_{b}^{{(0,1)}}({{\mathbb{R}}^{3}} \otimes [0,T])$ мы понимаем такие функции $u(x,t),$ что
(3.2)
$u(x,t),\quad \frac{{\partial u(x,t)}}{{\partial t}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \otimes [0,T]).$(3.3)
$\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T]} \left[ {{\text{|}}u(x,t){\kern 1pt} {\text{|}} + \left| {\frac{{\partial u(x,t)}}{{\partial t}}} \right|} \right] < + \infty .$Под классом функций ${{\mathbb{C}}^{{2 + 2}}}({{\mathbb{R}}^{3}} \otimes (0,T])$ мы понимаем такие функции $u(x,t)$, что
(3.5)
$\begin{gathered} D_{t}^{k} = \partial _{t}^{k},\quad D_{x}^{\alpha } = \partial _{{{{x}_{1}}}}^{{{{\alpha }_{1}}}}\partial _{{{{x}_{2}}}}^{{{{\alpha }_{2}}}}\partial _{{{{x}_{3}}}}^{{{{\alpha }_{3}}}},\quad \alpha = ({{\alpha }_{1}},{{\alpha }_{2}},{{\alpha }_{3}}), \\ {{\alpha }_{j}} \in \{ 0,1,2\} ,\quad j = 1,2,3, \\ \end{gathered} $(3.6)
${\text{|}}\alpha {\kern 1pt} {\text{|}}: = {{\alpha }_{1}} + {{\alpha }_{2}} + {{\alpha }_{3}}\;\leqslant \;2,\quad k \in \{ 0,1,2\} ,$Под классом функций $\mathbb{C}_{0}^{{2 + 2}}({{\mathbb{R}}^{3}} \otimes [0,T])$ подразумеваем такие функции $u(x,t) \in \mathbb{C}_{b}^{{2 + 2}}({{\mathbb{R}}^{3}} \otimes [0,T]),$ что
а также $u(x,T) = u{\kern 1pt} '(x,T) = 0$ для всех $x \in {{\mathbb{R}}^{3}}$, и носитель – компакт в ${{\mathbb{R}}^{3}} \otimes [0,T]$.
– компакт в ${{\mathbb{R}}^{3}} \otimes [0,T]$.
Под классом функций ${{\mathbb{C}}^{{2 + 1}}}({{\mathbb{R}}^{3}} \otimes [0,T])$ мы понимаем такие функции $u(x,t)$, что
(3.9)
$\begin{gathered} D_{t}^{k} = \partial _{t}^{k},\quad D_{x}^{\alpha } = \partial _{{{{x}_{1}}}}^{{{{\alpha }_{1}}}}\partial _{{{{x}_{2}}}}^{{{{\alpha }_{2}}}}\partial _{{{{x}_{3}}}}^{{{{\alpha }_{3}}}},\quad \alpha = ({{\alpha }_{1}},{{\alpha }_{2}},{{\alpha }_{3}}), \\ {{\alpha }_{j}} \in \{ 0,1,2\} ,\quad j = 1,2,3, \\ \end{gathered} $(3.10)
${\text{|}}\alpha {\kern 1pt} {\text{|}}: = {{\alpha }_{1}} + {{\alpha }_{2}} + {{\alpha }_{3}}\;\leqslant \;2,\quad k \in \{ 0,1\} ,$Под классом функций $\mathbb{C}_{b}^{{(0,1)}}((1 + x_{1}^{2} + x_{2}^{2}{{)}^{{{{\gamma }_{1}}/2}}}{{(1 + x_{3}^{2})}^{{{{\gamma }_{2}}/2}}};{{\mathbb{R}}^{3}} \otimes [0,T])$ мы понимаем такие функции $u(x,t),$ что
(3.11)
$u(x,t),\quad \frac{{\partial u(x,t)}}{{\partial t}} \in {{\mathbb{C}}_{b}}((1 + x_{1}^{2} + x_{2}^{2}{{)}^{{{{\gamma }_{1}}/2}}}{{(1 + x_{3}^{2})}^{{{{\gamma }_{2}}/2}}};{{\mathbb{R}}^{3}} \otimes [0,T]).$(3.12)
$\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T]} {{(1 + x_{1}^{2} + x_{2}^{2})}^{{{{\gamma }_{1}}/2}}}{{(1 + x_{3}^{2})}^{{{{\gamma }_{2}}/2}}}\left( {{\text{|}}u(x,t){\kern 1pt} {\text{|}} + \left| {\frac{{\partial u(x,t)}}{{\partial t}}} \right|} \right) < + \infty .$Будем говорить, что пара функций $\{ {{u}_{0}}(x),{{u}_{1}}(x)\} $ принадлежит классу ${{H}_{{{{x}_{3}}}}},$ если ${{u}_{0}}(x),{{u}_{1}}(x) \in L_{{{\text{loc}}}}^{1}({{\mathbb{R}}^{3}})$ и найдется такой шар $O({{x}_{0}},R) \subset {{\mathbb{R}}^{3}}$ положительного радиуса $R > 0,$ что ${{u}_{0}}(x),{{u}_{1}}(x) \in {{H}^{2}}(O({{x}_{0}},R))$, и имеет место неравенство
(3.13)
${{\left( {\frac{{{{\partial }^{2}}{{u}_{0}}(x)}}{{\partial x_{3}^{2}}}} \right)}^{2}} + {{\left( {\frac{{{{\partial }^{2}}{{u}_{1}}(x)}}{{\partial x_{3}^{2}}}} \right)}^{2}} > 0\quad {\text{для почти всех}}\quad x \in O({{x}_{0}},R).$Будем говорить, что пара функций $\{ {{u}_{0}}(x),{{u}_{1}}(x)\} $ принадлежит классу ${{H}_{{{{x}_{1}}{{x}_{2}}}}},$ если ${{u}_{0}}(x),{{u}_{1}}(x) \in L_{{{\text{loc}}}}^{1}({{\mathbb{R}}^{3}})$ и найдется такой шар $O({{x}_{0}},R) \subset {{\mathbb{R}}^{3}}$ положительного радиуса $R > 0,$ что ${{u}_{0}}(x),{{u}_{1}}(x) \in {{H}^{2}}(O({{x}_{0}},R))$, и имеет место неравенство
4. ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ И СВЯЗАННЫЕ С НИМИ ОЦЕНКИ
Рассмотрим первый дифференциальный оператор, действие которого определяется равенством
(4.1)
${{\mathfrak{M}}_{{x,t}}}[u](x,t): = \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial x_{3}^{2}}}u(x,t) + \Delta u(x,t),$Найдем фундаментальное решение оператора ${{\mathfrak{M}}_{{x,t}}}$, т.е. найдем решение следующего уравнения в смысле пространства обобщенных функций:
Применим преобразование Лапласа к обеим частям равенства (4.2) и получим уравнение, понимаемое в смысле обобщенных функций:
Одним из решений данного уравнения является функция
Применим обратное преобразование Лапласа и получим следующий вид фундаментального решения:
(4.5)
$\mathcal{E}(x,t) = - \frac{{\theta (t)}}{{4\pi }}\frac{1}{{\sqrt {x_{1}^{2} + x_{2}^{2}} }}{{J}_{0}}(\beta (x)t),\quad \beta (x): = \sqrt {\frac{{x_{1}^{2} + x_{2}^{2} + x_{3}^{2}}}{{x_{1}^{2} + x_{2}^{2}}}} ,$Для функции Бесселя справедлива оценка
(4.6)
$\left| {{{J}_{0}}(y)} \right|\;\leqslant \;\frac{{{{c}_{0}}}}{{\sqrt {\left| y \right|} }}\quad {\text{для всех}}\quad y \ne 0,$(4.7)
$\begin{gathered} \left| {\mathcal{E}(x,t)} \right|\;\leqslant \;\frac{{{{c}_{1}}}}{{{{{(x_{1}^{2} + x_{2}^{2})}}^{{1/4}}}{{{(x_{1}^{2} + x_{2}^{2} + x_{3}^{2})}}^{{1/4}}}\sqrt t }}\;\leqslant \;\frac{{{{c}_{1}}}}{{{\text{|}}{{x}_{3}}{\kern 1pt} {{{\text{|}}}^{{1/2}}}{{{(x_{1}^{2} + x_{2}^{2})}}^{{1/4}}}\sqrt t }} \\ {\text{при}}\quad {{x}_{3}} \ne 0,\quad ({{x}_{1}},{{x}_{2}}) \ne (0,0),\quad t > 0,\quad {{c}_{1}} = \frac{{{{c}_{0}}}}{{4\pi }} > 0. \\ \end{gathered} $Кроме того, при $({{x}_{1}},{{x}_{2}}) \ne (0,0)$ и $t\; \geqslant \;0$ функция $\mathcal{E}(x,t)$ дифференцируема по переменной $t$, причем
(4.8)
$\frac{{\partial{ \mathcal{E}}(x,t)}}{{\partial t}} = \frac{1}{{4\pi }}\frac{{\sqrt {x_{1}^{2} + x_{2}^{2} + x_{3}^{2}} }}{{x_{1}^{2} + x_{2}^{2}}}{{J}_{1}}(\beta (x)t)\quad {\text{при}}\quad ({{x}_{1}},{{x}_{2}}) \ne (0,0),\quad t\; \geqslant \;0.$При получении формулы (4.8) было использовано соотношение
Для функции Бесселя ${{J}_{1}}(x)$ справедлива оценка, аналогичная оценке (4.6) для функции ${{J}_{0}}(x)$, поэтому из (4.6), (4.8) получаем оценку
(4.10)
$\left| {\frac{{\partial{ \mathcal{E}}(x,t)}}{{\partial t}}} \right|\;\leqslant \;{{c}_{2}}\frac{{{{{(x_{1}^{2} + x_{2}^{2} + x_{3}^{2})}}^{{1/4}}}}}{{{{{(x_{1}^{2} + x_{2}^{2})}}^{{3/4}}}\sqrt t }}\quad {\text{при}}\quad ({{x}_{1}},{{x}_{2}}) \ne (0,0),\quad t > 0,$Из оценок (4.7), (4.10) следует, что
(4.11)
$\mathcal{E}(x,t),\quad \frac{{\partial{ \mathcal{E}}(x,t)}}{{\partial t}} \in L_{{{\text{loc}}}}^{1}(\mathbb{R}_{ + }^{4}).$Теперь рассмотрим второй дифференциальный оператор, действие которого определяется равенством
(4.12)
${{\mathfrak{L}}_{{x,t}}}[u](x,t): = \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{\Delta }_{ \bot }}u(x,t) + \Delta u(x,t),$Найдем фундаментальное решение оператора ${{\mathfrak{L}}_{{x,t}}}$, т.е. найдем решение следующего уравнения в смысле пространства обобщенных функций:
Применим преобразование Лапласа к обеим частям равенства (4.13) и получим следующее уравнение, понимаемое в смысле обобщенных функций:
(4.14)
$({{p}^{2}} + 1)\frac{{{{\partial }^{2}}}}{{\partial x_{1}^{2}}}\overline {{{\mathcal{E}}_{1}}} (x,p) + ({{p}^{2}} + 1)\frac{{{{\partial }^{2}}}}{{\partial x_{2}^{2}}}\overline {{{\mathcal{E}}_{1}}} (x,p) + \frac{{{{\partial }^{2}}}}{{\partial x_{3}^{2}}}\overline {{{\mathcal{E}}_{1}}} (x,p) = \delta (x).$Одним из решений данного уравнения является функция
(4.15)
$\overline {{{\mathcal{E}}_{1}}} (x,p) = - \frac{1}{{4\pi \left| {{{x}_{3}}} \right|}}\frac{1}{{\sqrt {{{p}^{2}} + 1} }}\frac{1}{{\sqrt {{{p}^{2}} + \left( {1 + \frac{{x_{1}^{2} + x_{2}^{2}}}{{x_{3}^{2}}}} \right)} }}.$Применим обратное преобразование Лапласа и получим следующий вид фундаментального решения:
(4.16)
${{\mathcal{E}}_{1}}(x,t) = - \frac{{\theta (t)}}{{4\pi \left| {{{x}_{3}}} \right|}}\int\limits_0^t {\kern 1pt} {{J}_{0}}\left( {\beta (x)\tau } \right){{J}_{0}}\left( {t - \tau } \right){\kern 1pt} d\tau ,\quad \beta (x): = \sqrt {1 + \frac{{x_{1}^{2} + x_{2}^{2}}}{{x_{3}^{2}}}} ,$Снова воспользуемся оценкой (4.6) для функции Бесселя ${{J}_{0}}$ и получим оценку для фундаментального решения ${{\mathcal{E}}_{1}}(x,t)$:
(4.17)
$\begin{gathered} \left| {{{\mathcal{E}}_{1}}(x,t)} \right|\;\leqslant \;\frac{{{{c}_{1}}}}{{{{{\left| {{{x}_{3}}} \right|}}^{{1/2}}}{{{(x_{1}^{2} + x_{2}^{2} + x_{3}^{2})}}^{{1/4}}}}}\int\limits_0^t \frac{1}{{\sqrt \tau \sqrt {t - \tau } }}{\kern 1pt} d\tau \\ {\text{при}}\quad {{x}_{3}} \ne 0,\quad ({{x}_{1}},{{x}_{2}}) \ne (0,0),\quad t > 0,\quad {{c}_{1}} > 0. \\ \end{gathered} $(4.18)
$\int\limits_0^t \frac{1}{{\sqrt \tau \sqrt {t - \tau } }}{\kern 1pt} d\tau = \int\limits_0^1 \frac{1}{{\sqrt s \sqrt {1 - s} }}{\kern 1pt} ds < + \infty \quad {\text{при всех}}\quad t:0\;\leqslant \;t < + \infty ,$(4.19)
$\begin{gathered} \left| {{{\mathcal{E}}_{1}}(x,t)} \right|\;\leqslant \;\frac{{{{c}_{2}}}}{{{{{\left| {{{x}_{3}}} \right|}}^{{1/2}}}{{{(x_{1}^{2} + x_{2}^{2})}}^{{1/4}}}}} \\ {\text{при}}\quad {{x}_{3}} \ne 0,\quad ({{x}_{1}},{{x}_{2}}) \ne (0,0),\quad t > 0,\quad {{c}_{2}} > 0. \\ \end{gathered} $Также заметим, что при ${{x}_{3}} \ne 0$ и $t\; \geqslant \;0$ функция ${{\mathcal{E}}_{1}}(x,t)$ дифференцируема по переменной $t$, и справедливо равенство
(4.20)
$\frac{{\partial {{\mathcal{E}}_{1}}(x,t)}}{{\partial t}} = \frac{1}{{4\pi \left| {{{x}_{3}}} \right|}}\int\limits_0^t {\kern 1pt} {{J}_{0}}\left( {\beta (x)\tau } \right){{J}_{1}}\left( {t - \tau } \right){\kern 1pt} d\tau - \frac{1}{{4\pi \left| {{{x}_{3}}} \right|}}{{J}_{0}}\left( {\beta (x)t} \right)\quad {\text{при}}\quad {{x}_{3}} \ne 0,\quad t\; \geqslant \;0.$(4.21)
$\left| {\frac{{\partial {{\mathcal{E}}_{1}}(x,t)}}{{\partial t}}} \right|\;\leqslant \;\frac{{{{c}_{0}}}}{{{{{\left| {{{x}_{3}}} \right|}}^{{1/2}}}{{{(x_{1}^{2} + x_{2}^{2})}}^{{1/4}}}}}\left( {1 + \frac{1}{{\sqrt t }}} \right)\quad {\text{при}}\quad {{x}_{3}} \ne 0,\quad t > 0,\quad {{c}_{0}} > 0.$В дальнейшем нам понадобятся две леммы.
Лемма 1. При ${{\gamma }_{1}} > 2$ и ${{\gamma }_{2}} > 1$ найдется такая постоянная ${{M}_{1}} = {{M}_{1}}({{\gamma }_{1}},{{\gamma }_{2}}) > 0$, что будет выполнено неравенство
(4.22)
$\begin{gathered} I: = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{\text{|}}\mathcal{E}(x - y,t - \tau ){\text{|}}}}{{{{{(1 + y_{1}^{2} + y_{2}^{2})}}^{{{{\gamma }_{1}}/2}}}{{{(1 + y_{3}^{2})}}^{{{{\gamma }_{2}}/2}}}}}{\kern 1pt} dy{\kern 1pt} d\tau \;\leqslant \;\frac{{{{M}_{1}}\sqrt t }}{{{{{(1 + x_{1}^{2} + x_{2}^{2})}}^{{1/4}}}{{{(1 + x_{3}^{2})}}^{{1/4}}}}} \\ {\text{при}}\quad (x,t) = ({{x}_{1}},{{x}_{2}},{{x}_{3}},t) \in {{\mathbb{R}}^{3}} \otimes [0,T]. \\ \end{gathered} $Доказательство. Применим оценку (4.7) для оценки интеграла $I$. Тогда получим
где ${{c}_{1}} > 0$, а интегралы ${{I}_{t}},\;{{I}_{x}}$ определяются, как(4.25)
${{I}_{x}}: = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{d{{y}_{1}}d{{y}_{2}}d{{y}_{3}}}}{{{{{\left| {{{x}_{3}} - {{y}_{3}}} \right|}}^{{1/2}}}{{{[{{{({{x}_{1}} - {{y}_{1}})}}^{2}} + {{{({{x}_{2}} - {{y}_{2}})}}^{2}}]}}^{{1/4}}}{{{(1 + y_{1}^{2} + y_{2}^{2})}}^{{{{\gamma }_{1}}/2}}}{{{(1 + y_{3}^{2})}}^{{{{\gamma }_{2}}/2}}}}}.$Для оценки интеграла ${{I}_{x}}$ нужно перейти в цилиндрическую систему координат и воспользоваться [1, леммы 1, 2]. В результате получим, что
(4.26)
${{I}_{x}}\;\leqslant \;\frac{{{{K}_{1}}}}{{{{{(1 + x_{1}^{2} + x_{2}^{2})}}^{{1/4}}}}}\frac{{{{K}_{2}}}}{{{{{(1 + x_{3}^{2})}}^{{1/4}}}}},\quad {{K}_{1}},{{K}_{2}} > 0,$Из формул (4.23), (4.24), (4.26) и следует доказательство леммы.
Лемма 2. При ${{\gamma }_{1}} > 2$ и ${{\gamma }_{2}} > 1$ найдутся такие постоянные ${{M}_{1}} = {{M}_{1}}({{\gamma }_{1}},{{\gamma }_{2}}) > 0,$ ${{M}_{2}} = {{M}_{2}}({{\gamma }_{1}},{{\gamma }_{2}}) > 0$, что будут выполнены неравенства
(4.27)
$\begin{gathered} {{I}_{1}}: = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{\text{|}}{{\mathcal{E}}_{1}}(x - y,t - \tau ){\text{|}}}}{{{{{(1 + y_{1}^{2} + y_{2}^{2})}}^{{{{\gamma }_{1}}/2}}}{{{(1 + y_{3}^{2})}}^{{{{\gamma }_{2}}/2}}}}}{\kern 1pt} dy{\kern 1pt} d\tau \;\leqslant \;\frac{{{{M}_{1}}t}}{{{{{(1 + x_{1}^{2} + x_{2}^{2})}}^{{1/4}}}{{{(1 + x_{3}^{2})}}^{{1/4}}}}} \\ {\text{при}}\quad (x,t) = ({{x}_{1}},{{x}_{2}},{{x}_{3}},t) \in {{\mathbb{R}}^{3}} \otimes [0,T], \\ \end{gathered} $(4.28)
$\begin{gathered} {{I}_{2}}: = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\left| {\frac{{\partial {{\mathcal{E}}_{1}}(x - y,t - \tau )}}{{\partial t}}} \right|}}{{{{{(1 + y_{1}^{2} + y_{2}^{2})}}^{{{{\gamma }_{1}}/2}}}{{{(1 + y_{3}^{2})}}^{{{{\gamma }_{2}}/2}}}}}{\kern 1pt} dy{\kern 1pt} d\tau \;\leqslant \;\frac{{{{M}_{2}}(t + {{t}^{{1/2}}})}}{{{{{(1 + x_{1}^{2} + x_{2}^{2})}}^{{1/4}}}{{{(1 + x_{3}^{2})}}^{{1/4}}}}} \\ {\text{при}}\quad (x,t) = ({{x}_{1}},{{x}_{2}},{{x}_{3}},t) \in {{\mathbb{R}}^{3}} \otimes [0,T]. \\ \end{gathered} $Доказательство. Для доказательства этой леммы достаточно воспользоваться оценками (4.19), (4.21).
5. СВОЙСТВА ОБЪЕМНЫХ ПОТЕНЦИАЛОВ
Рассмотрим объемный потенциал
(5.1)
${{U}_{0}}[\rho ](x,t): = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {{K}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau )\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau ,$(5.2)
${{K}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t): = \frac{{{{{(1 + x_{1}^{2} + x_{2}^{2})}}^{{1/4}}}{{{(1 + x_{3}^{2})}}^{{1/4}}}}}{{{{{(1 + y_{1}^{2} + y_{2}^{2})}}^{{{{\gamma }_{1}}/2}}}{{{(1 + y_{3}^{2})}}^{{{{\gamma }_{2}}/2}}}}}\mathcal{E}(x - y,t),$Лемма 3. При ${{\gamma }_{1}} > 2$ и ${{\gamma }_{2}} > 1$ оператор
(5.3)
${{U}_{0}}\,:{{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \otimes [0,T]) \to {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \otimes [0,T]),$(5.4)
$\mathop {\lim }\limits_{t \to + 0} \mathop {\sup }\limits_{x \in {{\mathbb{R}}^{3}}} \left| {{{U}_{0}}(x,t)} \right| = 0.$Доказательство. Шаг 1. Сначала нужно доказать, что ${{U}_{0}}\,:\mathbb{C}({{\mathbb{R}}^{3}} \otimes [0,T]) \to \mathbb{C}({{\mathbb{R}}^{3}} \otimes [0,T]).$
Пусть $({{x}^{1}},{{t}^{1}}),({{x}^{2}},{{t}^{2}}) \in {{\mathbb{R}}^{3}} \otimes [0,T].$ Пусть также для удобства ${{t}^{2}} > {{t}^{1}}$. Оценим разностное отношение
(5.5)
$\begin{gathered} \left| {{{U}_{0}}({{x}^{2}},{{t}^{2}}) - {{U}_{0}}({{x}^{1}},{{t}^{1}})} \right| = \left| {\int\limits_0^{{{t}^{2}}} {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {{K}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}({{x}^{2}},y,{{t}^{2}} - \tau )\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau } \right. - \\ \, - \left. {\int\limits_0^{{{t}^{1}}} {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {{K}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}({{x}^{1}},y,{{t}^{1}} - \tau )\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau } \right|\;\leqslant \;{{I}_{1}} + {{I}_{2}}, \\ \end{gathered} $(5.6)
${{I}_{1}}: = \int\limits_{{{t}^{1}}}^{{{t}^{2}}} {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \left| {{{K}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}({{x}^{2}},y,{{t}^{2}} - \tau )} \right|\left| {\rho (y,\tau )} \right|{\kern 1pt} dy{\kern 1pt} d\tau ,$(5.7)
${{I}_{2}}: = \int\limits_0^{{{t}^{1}}} {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \left| {{{K}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}({{x}^{2}},y,{{t}^{2}} - \tau ) - {{K}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}({{x}^{1}},y,{{t}^{1}} - \tau )} \right|\left| {\rho (y,\tau )} \right|{\kern 1pt} dy{\kern 1pt} d\tau .$Введем следующие обозначения: ${{x}^{1}}: = (x_{1}^{1},x_{2}^{1},x_{3}^{1}),$ ${{x}^{2}}: = (x_{1}^{2},x_{2}^{2},x_{3}^{2}),$ $x_{0}^{1}: = (x_{1}^{1},x_{2}^{1}),$ $x_{0}^{2}: = (x_{1}^{2},x_{2}^{2}),$ $x_{0}^{{1,2}}$ – середина отрезка, соединяющего точки $x_{0}^{1},x_{0}^{2} \in {{\mathbb{R}}^{2}},$ $\Delta K: = {{K}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}({{x}^{2}},y,{{t}^{2}} - \tau ) - $ $ - \;{{K}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}({{x}^{1}},y,{{t}^{1}} - \tau )$.
Обозначим открытый шар с центром в точке $x$ в ${{\mathbb{R}}^{2}}$ следующим образом:
(5.8)
$O(x,r): = \{ ({{y}_{1}},{{y}_{2}}) \in {{\mathbb{R}}^{2}}:({{y}_{1}} - {{x}_{1}}{{)}^{2}} + {{({{y}_{2}} - {{x}_{2}})}^{2}} < {{r}^{2}},\;x = ({{x}_{1}},{{x}_{2}}) \in {{\mathbb{R}}^{2}}\} .$Далее выберем числа $R,\varepsilon > 0$: $R > d(x_{0}^{1},x_{0}^{2}){\text{/}}2 + \varepsilon ,$ $\varepsilon < d(x_{0}^{1},x_{0}^{2}){\text{/}}2$, где $d(x_{0}^{1},x_{0}^{2})$ – это расстояние между точками $x_{0}^{1},x_{0}^{2} \in {{\mathbb{R}}^{2}}$. Также нам потребуется множество $\Omega \subset {{\mathbb{R}}^{2}}$:
(5.9)
$\Omega : = O(x_{0}^{{1,2}},R){{\backslash }}\left( {O(x_{0}^{1},\varepsilon ) \cup O(x_{0}^{2},\varepsilon )} \right).$С учетом всех перечисленных выше обозначений и с учетом выбранных $R,\;\varepsilon $ для интеграла ${{I}_{2}}$ справедлива оценка
где(5.11)
${{I}_{{21}}}: = \int\limits_0^{{{t}^{1}}} {\kern 1pt} d\tau \int\limits_{{{\mathbb{R}}^{1}}} {\kern 1pt} d{{y}_{3}}\int\limits_{O(x_{0}^{1},\varepsilon ) \cup O(x_{0}^{2},\varepsilon )} \left| {\Delta K} \right|\left| {\rho (y,\tau )} \right|{\kern 1pt} d{{y}_{1}}d{{y}_{2}}{\kern 1pt} ,$(5.12)
${{I}_{{22}}}: = \int\limits_0^{{{t}^{1}}} {\kern 1pt} d\tau \int\limits_{{{\mathbb{R}}^{1}}} {\kern 1pt} d{{y}_{3}}\int\limits_\Omega \left| {\Delta K} \right|\left| {\rho (y,\tau )} \right|{\kern 1pt} d{{y}_{1}}d{{y}_{2}}{\kern 1pt} ,$(5.13)
${{I}_{{23}}}: = \int\limits_0^{{{t}^{1}}} {\kern 1pt} d\tau \int\limits_{{{\mathbb{R}}^{1}}} {\kern 1pt} d{{y}_{3}}\int\limits_{{{\mathbb{R}}^{2}}\backslash O(x_{0}^{{1,2}},R)} \left| {\Delta K} \right|\left| {\rho (y,\tau )} \right|{\kern 1pt} d{{y}_{1}}d{{y}_{2}}{\kern 1pt} .$(5.15)
${{I}_{{221}}}: = \int\limits_0^{{{t}^{1}}} {\kern 1pt} d\tau \int\limits_{ - {{R}_{3}}}^{{{R}_{3}}} {\kern 1pt} d{{y}_{3}}\int\limits_\Omega \left| {\Delta K} \right|\left| {\rho (y,\tau )} \right|{\kern 1pt} d{{y}_{1}}d{{y}_{2}}{\kern 1pt} ,$(5.16)
${{I}_{{222}}}: = \int\limits_0^{{{t}^{1}}} {\kern 1pt} d\tau \int\limits_{{{\mathbb{R}}^{1}}\backslash [ - {{R}_{3}},{{R}_{3}}]} {\kern 1pt} d{{y}_{3}}\int\limits_\Omega \left| {\Delta K} \right|\left| {\rho (y,\tau )} \right|{\kern 1pt} d{{y}_{1}}d{{y}_{2}}{\kern 1pt} ,\quad {{R}_{3}} > 0.$(5.17)
${{I}_{{21}}} < \frac{\delta }{4},\quad {{I}_{{23}}} < \frac{\delta }{4},\quad {{I}_{{222}}} < \frac{\delta }{8}{\kern 1pt} .$(5.18)
${\text{|}}{{x}^{2}} - {{x}^{1}}{\kern 1pt} {{{\text{|}}}^{2}}\; + \;{\text{|}}{{t}^{2}} - {{t}^{1}}{\kern 1pt} {{{\text{|}}}^{2}} < {{\eta }^{2}},$В результате мы получили, что для любого $\delta > 0$ найдется $\eta > 0$ такое, что при выполнении неравенства (5.18) имеет место неравенство
которое и означает, что ${{U}_{0}}(x,t) \in \mathbb{C}({{\mathbb{R}}^{3}} \otimes [0,T])$.Шаг 2. Теперь установим, что ${{U}_{0}}\,:{{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \otimes [0,T]) \to {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \otimes [0,T]).$
Пусть $\rho (x,t) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \otimes [0,T])$. Тогда для ${{U}_{0}}[\rho ](x,t)$ справедлива оценка
(5.21)
$\left| {{{U}_{0}}[\rho ](x,t)} \right|\;\leqslant \;\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T]} \left| {\rho (x,t)} \right|\int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \left| {{{K}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau )} \right|{\kern 1pt} dy{\kern 1pt} d\tau \;\leqslant \;{{M}_{1}}\sqrt t \mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T]} \left| {\rho (x,t)} \right|,\quad {{M}_{1}} > 0,$(5.22)
$\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T]} \left| {{{U}_{0}}[\rho ](x,t)} \right|\;\leqslant \;{{M}_{1}}\sqrt T \mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T]} \left| {\rho (x,t)} \right| < + \infty .$Теперь рассмотрим другой объемный потенциал:
(5.23)
${{V}_{0}}[\rho ](x,t): = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau )\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau ,$(5.24)
${{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t): = \frac{{{{{(1 + x_{1}^{2} + x_{2}^{2})}}^{{1/4}}}{{{(1 + x_{3}^{2})}}^{{1/4}}}}}{{{{{(1 + y_{1}^{2} + y_{2}^{2})}}^{{{{\gamma }_{1}}/2}}}{{{(1 + y_{3}^{2})}}^{{{{\gamma }_{2}}/2}}}}}{{\mathcal{E}}_{1}}(x - y,t),$Лемма 4. При ${{\gamma }_{1}} > 2$ и ${{\gamma }_{2}} > 1$ оператор
(5.25)
${{V}_{0}}\,:{{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \otimes [0,T]) \to \mathbb{C}_{b}^{{(0,1)}}({{\mathbb{R}}^{3}} \otimes [0,T]),$(5.26)
$\mathop {\lim }\limits_{t \to + 0} \mathop {\sup }\limits_{x \in {{\mathbb{R}}^{3}}} \left| {{{V}_{0}}(x,t)} \right| = 0,$(5.27)
$\mathop {\lim }\limits_{t \to + 0} \mathop {\sup }\limits_{x \in {{\mathbb{R}}^{3}}} \left| {\frac{{\partial {{V}_{0}}(x,t)}}{{\partial t}}} \right| = 0.$Доказательство. Шаг 1. Докажем сначала, что ${{V}_{0}}{\kern 1pt} :\;\mathbb{C}({{\mathbb{R}}^{3}} \otimes [0,T]) \to \mathbb{C}({{\mathbb{R}}^{3}} \otimes [0,T]).$
Пусть $({{x}^{1}},{{t}^{1}}),({{x}^{2}},{{t}^{2}}) \in {{\mathbb{R}}^{3}} \otimes [0,T]$. Пусть также для удобства ${{t}^{2}} > {{t}^{1}}$.
Оценим разностное отношение
(5.28)
$\begin{gathered} \left| {{{V}_{0}}({{x}^{2}},{{t}^{2}}) - {{V}_{0}}({{x}^{1}},{{t}^{1}})} \right| = \left| {\int\limits_0^{{{t}^{2}}} {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}({{x}^{2}},y,{{t}^{2}} - \tau )\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau } \right. - \\ \, - \left. {\int\limits_0^{{{t}^{1}}} {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}({{x}^{1}},y,{{t}^{1}} - \tau )\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau } \right|\;\leqslant \;{{I}_{1}} + {{I}_{2}}, \\ \end{gathered} $(5.29)
${{I}_{1}}: = \int\limits_{{{t}^{1}}}^{{{t}^{2}}} {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \left| {{{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}({{x}^{2}},y,{{t}^{2}} - \tau )} \right|\left| {\rho (y,\tau )} \right|{\kern 1pt} dy{\kern 1pt} d\tau ,$(5.30)
${{I}_{2}}: = \int\limits_0^{{{t}^{1}}} {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \left| {{{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}({{x}^{2}},y,{{t}^{2}} - \tau ) - {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}({{x}^{1}},y,{{t}^{1}} - \tau )} \right|\left| {\rho (y,\tau )} \right|{\kern 1pt} dy{\kern 1pt} d\tau .$(5.31)
${{U}_{\varepsilon }}: = [x_{3}^{1} - \varepsilon ,x_{3}^{1} + \varepsilon ] \cup [x_{3}^{2} - \varepsilon ,x_{3}^{2} + \varepsilon ],$(5.34)
${{I}_{{21}}}: = \int\limits_0^{{{t}^{1}}} {\kern 1pt} d\tau \int\limits_{{{U}_{\varepsilon }}} {\kern 1pt} d{{y}_{3}}\int\limits_{{{\mathbb{R}}^{2}}} \left| {\Delta G} \right|\left| {\rho (y,\tau )} \right|{\kern 1pt} d{{y}_{1}}d{{y}_{2}}{\kern 1pt} ,$(5.35)
${{I}_{{22}}}: = \int\limits_0^{{{t}^{1}}} {\kern 1pt} d\tau \int\limits_{{{U}_{R}}\backslash {{U}_{\varepsilon }}} {\kern 1pt} d{{y}_{3}}\int\limits_{{{\mathbb{R}}^{2}}} \left| {\Delta G} \right|\left| {\rho (y,\tau )} \right|{\kern 1pt} d{{y}_{1}}d{{y}_{2}}{\kern 1pt} ,$(5.36)
${{I}_{{23}}}: = \int\limits_0^{{{t}^{1}}} {\kern 1pt} d\tau \int\limits_{{{\mathbb{R}}^{1}}\backslash {{U}_{R}}} {\kern 1pt} d{{y}_{3}}\int\limits_{{{\mathbb{R}}^{2}}} \left| {\Delta G} \right|\left| {\rho (y,\tau )} \right|{\kern 1pt} d{{y}_{1}}d{{y}_{2}}{\kern 1pt} .$(5.38)
${{I}_{{221}}}: = \int\limits_0^{{{t}^{1}}} {\kern 1pt} d\tau \int\limits_{{{U}_{R}}\backslash {{U}_{\varepsilon }}} {\kern 1pt} d{{y}_{3}}\int\limits_{O\left( {0,{{R}_{{12}}}} \right)} \left| {\Delta G} \right|\left| {\rho (y,\tau )} \right|{\kern 1pt} d{{y}_{1}}d{{y}_{2}}{\kern 1pt} ,$(5.39)
${{I}_{{222}}}: = \int\limits_0^{{{t}^{1}}} {\kern 1pt} d\tau \int\limits_{{{U}_{R}}\backslash {{U}_{\varepsilon }}} {\kern 1pt} d{{y}_{3}}\int\limits_{{{\mathbb{R}}^{2}}\backslash O\left( {0,{{R}_{{12}}}} \right)} \left| {\Delta G} \right|\left| {\rho (y,\tau )} \right|{\kern 1pt} d{{y}_{1}}d{{y}_{2}}{\kern 1pt} ,\quad {{R}_{{12}}} > 0.$(5.40)
${{I}_{{21}}} < \frac{\delta }{4},\quad {{I}_{{23}}} < \frac{\delta }{4},\quad {{I}_{{222}}} < \frac{\delta }{8}.$(5.41)
${{\left| {{{x}^{2}} - {{x}^{1}}} \right|}^{2}} + {{\left| {{{t}^{2}} - {{t}^{1}}} \right|}^{2}} < {{\eta }^{2}},$В результате мы получаем, что для любого $\delta > 0$ найдется $\eta > 0$ такое, что при выполнении неравенства (5.41) имеет место неравенство
которое и означает, что ${{V}_{0}}(x,t) \in \mathbb{C}({{\mathbb{R}}^{3}} \otimes [0,T])$.Шаг 2. Теперь установим, что ${{V}_{0}}\,:{{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \otimes [0,T]) \to {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \otimes [0,T]).$
Пусть $\rho (x,t) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \otimes [0,T])$. Тогда для ${{V}_{0}}[\rho ](x,t)$ справедлива оценка
(5.44)
$\left| {{{V}_{0}}[\rho ](x,t)} \right|\;\leqslant \;\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T]} \left| {\rho (x,t)} \right|\int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \left| {{{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau )} \right|{\kern 1pt} dy{\kern 1pt} d\tau \;\leqslant \;{{M}_{1}}t\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T]} \left| {\rho (x,t)} \right|,\quad {{M}_{1}} > 0,$(5.45)
$\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T]} \left| {{{V}_{0}}[\rho ](x,t)} \right|\;\leqslant \;{{M}_{1}}T\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T]} \left| {\rho (x,t)} \right| < + \infty .$Шаг 3. Докажем теперь, что если $\rho (x,t) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \otimes [0,T])$, то ${{V}_{0}}(x,t) \in {{C}^{{(0,1)}}}({{\mathbb{R}}^{3}} \otimes [0,T])$. Пусть $(x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T],x = ({{x}^{1}},{{x}^{2}},{{x}^{3}}).$ Будем считать, что $\Delta t > 0$, тогда мы вычислим правую производную. Случай же $\Delta t < 0$ рассматривается аналогичным образом, отличие будет состоять лишь в том, что там не возникнет выражения типа ${{I}_{1}}$ (см. формулу (5.47)):
(5.46)
$\left| {\frac{{{{V}_{0}}(x,t + \Delta t) - {{V}_{0}}(x,t)}}{{\Delta t}} - \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau } \right|\;\leqslant \;{{I}_{1}} + {{I}_{2}},$(5.47)
${{I}_{1}}: = \left| {\frac{1}{{\Delta t}}\int\limits_t^{t + \Delta t} \int\limits_{{{\mathbb{R}}^{3}}} {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau + \Delta t)\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau } \right|,$(5.48)
${{I}_{2}}: = \left| {\int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \left( {\frac{{{{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau + \Delta t) - {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau )}}{{\Delta t}} - \frac{{\partial {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}} \right)\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau } \right|.$(5.49)
${{I}_{1}}\;\leqslant \;\frac{{{{c}_{0}}}}{{\Delta t}}\int\limits_0^{\Delta t} {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \left| {{{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,\Delta t - s)} \right|{\kern 1pt} dy{\kern 1pt} ds = {{I}_{{11}}} + {{I}_{{12}}} + {{I}_{{13}}},$(5.50)
${{I}_{{11}}}: = \frac{{{{c}_{0}}}}{{\Delta t}}\int\limits_0^{\Delta t} {\kern 1pt} ds\int\limits_{{{\mathbb{R}}^{2}}} {\kern 1pt} d{{y}_{1}}{\kern 1pt} d{{y}_{2}}\int\limits_{{{U}_{\varepsilon }}} {\kern 1pt} d{{y}_{3}}\left| {{{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,\Delta t - s)} \right|,$(5.51)
${{I}_{{12}}}: = \frac{{{{c}_{0}}}}{{\Delta t}}\int\limits_0^{\Delta t} {\kern 1pt} ds\int\limits_{{{\mathbb{R}}^{2}}} {\kern 1pt} d{{y}_{1}}{\kern 1pt} d{{y}_{2}}\int\limits_{{{U}_{R}}\backslash {{U}_{\varepsilon }}} {\kern 1pt} d{{y}_{3}}\left| {{{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,\Delta t - s)} \right|,$(5.52)
${{I}_{{13}}}: = \frac{{{{c}_{0}}}}{{\Delta t}}\int\limits_0^{\Delta t} {\kern 1pt} ds\int\limits_{{{\mathbb{R}}^{2}}} {\kern 1pt} d{{y}_{1}}{\kern 1pt} d{{y}_{2}}\int\limits_{{{\mathbb{R}}^{1}}\backslash {{U}_{R}}} {\kern 1pt} d{{y}_{3}}\left| {{{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,\Delta t - s)} \right|.$(5.54)
${{I}_{{121}}}: = \frac{{{{c}_{0}}}}{{\Delta t}}\int\limits_0^{\Delta t} {\kern 1pt} ds\int\limits_{O(0,{{R}_{{12}}})} {\kern 1pt} d{{y}_{1}}{\kern 1pt} d{{y}_{2}}\int\limits_{{{U}_{R}}\backslash {{U}_{\varepsilon }}} {\kern 1pt} d{{y}_{3}}\left| {{{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,\Delta t - s)} \right|,$(5.55)
${{I}_{{122}}}: = \frac{{{{c}_{0}}}}{{\Delta t}}\int\limits_0^{\Delta t} {\kern 1pt} ds\int\limits_{{{\mathbb{R}}^{2}}\backslash O(0,{{R}_{{12}}})} {\kern 1pt} d{{y}_{1}}{\kern 1pt} d{{y}_{2}}\int\limits_{{{U}_{R}}\backslash {{U}_{\varepsilon }}} {\kern 1pt} d{{y}_{3}}\left| {{{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,\Delta t - s)} \right|,$Зафиксируем произвольное $\delta > 0$. Из формул (5.24), (4.27) следует, что найдутся достаточно малое $\varepsilon > 0$ и достаточно большие $R > 0,$ ${{R}_{{12}}} > 0,$ что будут выполнены неравенства
(5.56)
${{I}_{{11}}} < \frac{\delta }{8},\quad {{I}_{{13}}} < \frac{\delta }{8},\quad {{I}_{{122}}} < \frac{\delta }{8}.$(5.58)
${{I}_{2}}\;\leqslant \;{{c}_{0}}\int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \left| {\frac{{\partial {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t{\kern 1pt} *)}}{{\partial t}} - \frac{{\partial {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}} \right|{\kern 1pt} dy{\kern 1pt} d\tau ,\quad {\text{где}}\quad t{\kern 1pt} * \in [t - \tau ,t - \tau + \Delta t].$(5.60)
${{I}_{{21}}}: = {{c}_{0}}\int\limits_0^t {\kern 1pt} d\tau \int\limits_{{{\mathbb{R}}^{2}}} {\kern 1pt} d{{y}_{1}}{\kern 1pt} d{{y}_{2}}\int\limits_{{{U}_{\varepsilon }}} {\kern 1pt} d{{y}_{3}}\left| {\frac{{\partial {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t{\kern 1pt} *)}}{{\partial t}} - \frac{{\partial {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}} \right|,$(5.61)
${{I}_{{22}}}: = {{c}_{0}}\int\limits_0^t {\kern 1pt} d\tau \int\limits_{{{\mathbb{R}}^{2}}} {\kern 1pt} d{{y}_{1}}{\kern 1pt} d{{y}_{2}}\int\limits_{{{U}_{R}}\backslash {{U}_{\varepsilon }}} {\kern 1pt} d{{y}_{3}}\left| {\frac{{\partial {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t{\kern 1pt} *)}}{{\partial t}} - \frac{{\partial {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}} \right|,$(5.62)
${{I}_{{23}}}: = {{c}_{0}}\int\limits_0^t {\kern 1pt} d\tau \int\limits_{{{\mathbb{R}}^{2}}} {\kern 1pt} d{{y}_{1}}{\kern 1pt} d{{y}_{2}}\int\limits_{{{\mathbb{R}}^{1}}\backslash {{U}_{R}}} {\kern 1pt} d{{y}_{3}}\left| {\frac{{\partial {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t{\kern 1pt} *)}}{{\partial t}} - \frac{{\partial {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}} \right|.$В результате получаем, что для любого $\delta > 0$ найдется $\eta > 0$ такое, что как только $\left| {\Delta t} \right| < \eta ,$ то выполнено неравенство
(5.64)
$\left| {\frac{{{{V}_{0}}(x,t + \Delta t) - {{V}_{0}}(x,t)}}{{\Delta t}} - \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau } \right| < \delta ,$Шаг 4. Докажем, наконец, ограниченность производной $\partial {{V}_{0}}(x,t){\text{/}}\partial t$. Пусть
${{c}_{0}}: = \mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T]} \left| {\rho (x,t)} \right| < + \infty $.
Воспользуемся оценкой (4.28)
(5.65)
$\begin{gathered} \left| {\frac{{\partial {{V}_{0}}(x,t)}}{{\partial t}}} \right|\;\leqslant \;\int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \left| {\frac{{\partial {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}\rho (y,\tau )} \right|{\kern 1pt} dy{\kern 1pt} d\tau \;\leqslant \;{{c}_{0}}{{M}_{2}}(t + {{t}^{{1/2}}})\;\leqslant \;{{c}_{1}}(T + {{T}^{{1/2}}}), \\ {{c}_{1}} > 0,\quad (x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T]. \\ \end{gathered} $(5.66)
$\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T]} \left| {\frac{{\partial {{V}_{0}}(x,t)}}{{\partial t}}} \right|\;\leqslant \;{{c}_{1}}(T + {{T}^{{1/2}}}) < + \infty ,$6. ОДНОЗНАЧНАЯ РАЗРЕШИМОСТЬ ДВУХ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
Рассмотрим первое нелинейное интегральное уравнение:
(6.1)
$u(x,t) = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \mathcal{E}\left( {x - y,t - \tau } \right)\left( {{\text{|}}u{\kern 1pt} {{{\text{|}}}^{q}}\left( {y,\tau } \right) + f(y,\tau )} \right){\kern 1pt} dy{\kern 1pt} d\tau ,$Сделаем в интегральном уравнении (6.1) замену:
(6.3)
${{f}_{0}}(x,t): = (1 + x_{1}^{2} + x_{2}^{2}{{)}^{{{{\gamma }_{1}}/2}}}{{(1 + x_{3}^{2})}^{{{{\gamma }_{2}}/2}}}f(x,t).$Тогда мы получим следующее интегральное уравнение:
(6.4)
$v(x,t) = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {{K}_{{q/2,q/2}}}(x,y,t - \tau ){\text{|}}{v}{\kern 1pt} {{{\text{|}}}^{q}}(y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau + \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {{K}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau ){{f}_{0}}(y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau ,$(6.5)
${{K}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau ) = \frac{{{{{(1 + x_{1}^{2} + x_{2}^{2})}}^{{1/4}}}{{{(1 + x_{3}^{2})}}^{{1/4}}}}}{{{{{(1 + y_{1}^{2} + y_{2}^{2})}}^{{{{\gamma }_{1}}/2}}}{{{(1 + y_{3}^{2})}}^{{{{\gamma }_{2}}/2}}}}}\mathcal{E}\left( {x - y,t - \tau } \right).$Перепишем интегральное уравнение (6.4) в виде
(6.6)
${v}(x,t) = {{U}_{{q/2,q/2}}}[{\kern 1pt} {\text{|}}v{\kern 1pt} {{{\text{|}}}^{q}}](x,t) + {{U}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}[{{f}_{0}}](x,t),$(6.7)
${{U}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}[\rho ](x,t): = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {{K}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau )\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau .$Теорема 1. Если $q > 4,$ ${{\gamma }_{1}} > 2,$ ${{\gamma }_{2}} > 1$, то для всех ${{f}_{0}}(x,t) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \otimes [0,T])$ найдется такое максимальное ${{T}_{0}} > 0,$ что для каждого $T \in (0,{{T}_{0}})$ существует единственное решение интегрального уравнения (6.4) в банаховом пространстве $v(x,t) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \otimes [0,T]),$ причем либо ${{T}_{0}} = + \infty $, либо ${{T}_{0}} < + \infty $, и в последнем случае имеет место предельное свойство
(6.8)
$\mathop {\lim }\limits_{T \uparrow {{T}_{0}}} {{\left\| v \right\|}_{T}} = + \infty ,\quad {{\left\| v \right\|}_{T}} = \mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T]} \left| {{v}(x,t)} \right|.$Непосредственным следствием данной теоремы является теорема 2.
Теорема 2. Если $q > 4,$ ${{\gamma }_{1}} > 2,$ ${{\gamma }_{2}} > 1$, то для всех $f(x,t) \in {{\mathbb{C}}_{b}}((1 + x_{1}^{2} + x_{2}^{2}{{)}^{{{{\gamma }_{1}}/2}}}{{(1 + x_{3}^{2})}^{{{{\gamma }_{2}}/2}}};$ ${{\mathbb{R}}^{3}} \otimes [0,T])$ найдется такое максимальное ${{T}_{0}} > 0,$ что для каждого $T \in (0,{{T}_{0}})$ существует единственное решение интегрального уравнения (6.1) в банаховом пространстве $u(x,t) \in $ $ \in {{\mathbb{C}}_{b}}((1 + x_{1}^{2} + x_{2}^{2}{{)}^{{1/4}}}{{(1 + x_{3}^{2})}^{{1/4}}};{{\mathbb{R}}^{3}} \otimes [0,T]),$ причем либо ${{T}_{0}} = + \infty $, либо ${{T}_{0}} < + \infty $, и в последнем случае имеет место предельное свойство
(6.9)
$\mathop {\lim }\limits_{T \uparrow {{T}_{0}}} {{\left\| u \right\|}_{T}} = + \infty ,\quad {{\left\| u \right\|}_{T}} = \mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T]} {{(1 + x_{1}^{2} + x_{2}^{2})}^{{1/4}}}{{(1 + x_{3}^{2})}^{{1/4}}}\left| {u(x,t)} \right|.$Рассмотрим второе нелинейное интегральное уравнение:
(6.10)
$u(x,t) = F(x,t) + \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {{\mathcal{E}}_{1}}\left( {x - y,t - \tau } \right)\left( {{\text{|}}u{\kern 1pt} {{{\text{|}}}^{q}}\left( {y,\tau } \right) - \rho (y,\tau )} \right){\kern 1pt} dy{\kern 1pt} d\tau ,$(6.12)
${{\rho }_{0}}(x,t): = (1 + x_{1}^{2} + x_{2}^{2}{{)}^{{{{\gamma }_{1}}/2}}}{{(1 + x_{3}^{2})}^{{{{\gamma }_{2}}/2}}}\rho (x,t).$(6.13)
$v(x,t) = {{F}_{0}}(x,t) + \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {{G}_{{q/2,q/2}}}(x,y,t - \tau ){\text{|}}v{\kern 1pt} {{{\text{|}}}^{q}}(y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau - \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau ){{\rho }_{0}}(y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau ,$(6.14)
${{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau ) = \frac{{{{{(1 + x_{1}^{2} + x_{2}^{2})}}^{{1/4}}}{{{(1 + x_{3}^{2})}}^{{1/4}}}}}{{{{{(1 + y_{1}^{2} + y_{2}^{2})}}^{{{{\gamma }_{1}}/2}}}{{{(1 + y_{3}^{2})}}^{{{{\gamma }_{2}}/2}}}}}{{\mathcal{E}}_{1}}\left( {x - y,t - \tau } \right).$(6.15)
${v}(x,t) = {{F}_{0}}(x,t) + {{V}_{{q/2,q/2}}}[{\kern 1pt} {\text{|}}{\kern 1pt} {v}{\kern 1pt} {{{\text{|}}}^{q}}](x,t) - {{V}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}[{{\rho }_{0}}](x,t),$(6.16)
${{V}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}[\rho ](x,t): = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {{G}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}(x,y,t - \tau )\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau .$Свойства объемного потенциала ${{V}_{{{{\gamma }_{1}},{{\gamma }_{2}}}}}$ изучались в разд. 5. Далее, воспользовавшись техникой, примененной при доказательстве теоремы 4 работы [1], можно установить следующий результат.
Теорема 3. Если $q > 4,$ ${{\gamma }_{1}} > 2,$ ${{\gamma }_{2}} > 1$, то для всяких ${{\rho }_{0}}(x,t),{{F}_{0}}(x,t) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \otimes [0,T])$ найдется такое максимальное ${{T}_{0}} > 0,$ что для каждого $T \in (0,{{T}_{0}})$ существует единственное решение интегрального уравнения (6.13) в банаховом пространстве $v(x,t) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \otimes [0,T]),$ причем либо ${{T}_{0}} = + \infty ,$ либо ${{T}_{0}} < + \infty $, и в последнем случае имеет место предельное свойство
(6.17)
$\mathop {\lim }\limits_{T \uparrow {{T}_{0}}} {{\left\| v \right\|}_{T}} = + \infty ,\quad {{\left\| v \right\|}_{T}} = \mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T]} \left| {v(x,t)} \right|.$Теорема 4. Если $q > 4,$ ${{\gamma }_{1}} > 2,$ ${{\gamma }_{2}} > 1$, то для всех $F(x,t) \in {{\mathbb{C}}_{b}}((1 + x_{1}^{2} + x_{2}^{2}{{)}^{{1/4}}}{{(1 + x_{3}^{2})}^{{1/4}}};$ ${{\mathbb{R}}^{3}} \otimes [0,T]),$ $\rho (x,t) \in {{\mathbb{C}}_{b}}((1 + x_{1}^{2} + x_{2}^{2}{{)}^{{{{\gamma }_{1}}/2}}}{{(1 + x_{3}^{2})}^{{{{\gamma }_{2}}/2}}};$ ${{\mathbb{R}}^{3}} \otimes [0,T])$ найдется такое максимальное ${{T}_{0}} > 0,$ что для каждого $T \in (0,{{T}_{0}})$ существует единственное решение интегрального уравне-ния (6.10) в банаховом пространстве $u(x,t) \in {{\mathbb{C}}_{b}}((1 + x_{1}^{2} + x_{2}^{2}{{)}^{{1/4}}}{{(1 + x_{3}^{2})}^{{1/4}}};{{\mathbb{R}}^{3}} \otimes [0,T]),$ причем либо ${{T}_{0}} = + \infty ,$ либо ${{T}_{0}} < + \infty $, и в последнем случае имеет место предельное свойство
7. СЛАБЫЕ ОБОБЩЕННЫЕ РЕШЕНИЯ ДВУХ ЗАДАЧ КОШИ
Рассмотрим первую задачу Коши:
(7.1)
${{\mathfrak{M}}_{{x,t}}}[u](x,t) = {\text{|}}u{\kern 1pt} {{{\text{|}}}^{q}} + f(x,t),\quad (x,t) \in {{\mathbb{R}}^{3}} \otimes (0,T],$(7.2)
$u(x,0) = {{u}_{0}}(x),\quad u{\kern 1pt} '(x,0) = {{u}_{1}}(x),\quad x \in {{\mathbb{R}}^{3}},$(7.3)
${{\mathfrak{M}}_{{x,t}}}[u](x,t): = \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial x_{3}^{2}}}u(x,t) + \Delta u(x,t).$Дадим определение слабого локального во времени решения задачи Коши (7.1), (7.2), для которого далее будем изучать явление разрушения, а также дадим определение слабого обобщенного локального во времени решения задачи Коши с нулевыми начальными условиями, для которого будем далее исследовать разрешимость.
Определение 1. Слабым локальным во времени решением задачи Коши (7.1), (7.2) называется функция $u(x,t) \in L_{{{\text{loc}}}}^{q}({{\mathbb{R}}^{3}} \otimes [0,T])$, которая удовлетворяет интегральному равенству
(7.4)
$\begin{gathered} \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} u(x,t)\left[ {\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial x_{3}^{2}}}\phi (x,t) + \Delta \phi (x,t)} \right]{\kern 1pt} {\kern 1pt} dx{\kern 1pt} dt + \int\limits_{{{\mathbb{R}}^{3}}} \left[ {{{u}_{0}}(x)\frac{{\partial {{\phi }_{{{{x}_{3}}{{x}_{3}}}}}}}{{\partial t}}(x,0) - {{u}_{1}}(x){{\phi }_{{{{x}_{3}}{{x}_{3}}}}}(x,0)} \right]{\kern 1pt} dx = \\ \, = \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}^{q}}\phi (x,t){\kern 1pt} dx{\kern 1pt} dt + \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} f(x,t)\phi (x,t){\kern 1pt} dx{\kern 1pt} dt \\ \end{gathered} $Определение 2. Слабым обобщенным локальным во времени решением задачи Коши (7.1), (7.2) с нулевыми начальными условиями называется функция $u(x,t) \in L_{{{\text{loc}}}}^{q}({{\mathbb{R}}^{3}} \otimes [0,T])$, которая удовлетворяет интегральному равенству
(7.5)
$\int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} u(x,t)\left[ {\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial x_{3}^{2}}}\phi (x,t) + \Delta \phi (x,t)} \right]{\kern 1pt} dx{\kern 1pt} dt = \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}^{q}}\phi (x,t){\kern 1pt} dx{\kern 1pt} dt + \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} f(x,t)\phi (x,t){\kern 1pt} dx{\kern 1pt} dt$Теорема 5. Пусть $u(x,t)$ – это решение нелинейного интегрального уравнения (6.1) в банаховом пространстве ${{\mathbb{C}}_{b}}((1 + x_{1}^{2} + x_{2}^{2}{{)}^{{1/4}}}{{(1 + x_{3}^{2})}^{{1/4}}};{{\mathbb{R}}^{3}} \otimes [0,T])$, причем $f(x,t) \in {{\mathbb{C}}_{b}}((1 + x_{1}^{2} + x_{2}^{2}{{)}^{{{{\gamma }_{1}}/2}}}(1 + $ $ + \;x_{3}^{2}{{)}^{{{{\gamma }_{2}}/2}}};$ ${{\mathbb{R}}^{3}} \otimes [0,T]),$ где $q > 4,$ ${{\gamma }_{1}} > 2,$ ${{\gamma }_{2}} > 1$. Тогда функция $u(x,t)$ является слабым обобщенным локальным во времени решением задачи Коши (7.1), (7.2) с нулевыми начальными условиями в смысле определения $2$.
Доказательство. Пусть $\langle \cdot , \cdot \rangle $ – это скобки двойственности между $\mathcal{D}({{\mathbb{R}}^{3}} \otimes (0,T))$ и $\mathcal{D}{\kern 1pt} '({{\mathbb{R}}^{3}} \otimes (0,T))$. Пусть функция $u(x,t)$ удовлетворяет интегральному уравнению (6.1). Тогда в смысле пространства обобщенных функций $\mathcal{D}{\kern 1pt} '({{\mathbb{R}}^{3}} \otimes (0,T))$ справедливо равенство
Тогда, с одной стороны,(7.7)
$\begin{gathered} \left\langle {{{\mathfrak{M}}_{{x,t}}}[u](x,t),\phi (x,t)} \right\rangle = \left\langle {{{\mathfrak{M}}_{{x,t}}}\left[ {\mathcal{E}(x,t) * \left( {{\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}^{q}} + f(x,t)} \right)} \right],\phi (x,t)} \right\rangle = \\ = \left\langle {{{\mathfrak{M}}_{{x,t}}}\left[ {\mathcal{E}(x,t)} \right] * \left( {{\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}^{q}} + f(x,t)} \right),\phi (x,t)} \right\rangle = \left\langle {\delta (x,t) * \left( {{\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}^{q}} + f(x,t)} \right),\phi (x,t)} \right\rangle = \\ \, = \left\langle {{\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}^{q}} + f(x,t),\phi (x,t)} \right\rangle = \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {\text{|}}u(x,t){{{\text{|}}}^{q}}\phi (x,t){\kern 1pt} dx{\kern 1pt} dt + \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} f(x,t)\phi (x,t){\kern 1pt} dx{\kern 1pt} dt. \\ \end{gathered} $С другой стороны,
(7.10)
$\left\langle {{{\mathfrak{M}}_{{x,t}}}[u](x,t),\phi (x,t)} \right\rangle = \left\langle {u(x,t),{{\mathfrak{M}}_{{x,t}}}[\phi ](x,t)} \right\rangle = \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} u(x,t)\left[ {\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial x_{3}^{2}}}\phi (x,t) + \Delta \phi (x,t)} \right]{\kern 1pt} {\kern 1pt} dx{\kern 1pt} dt.$Теперь получим результат, касающийся разрушения слабых локальных во времени решений задачи Коши (7.1), (7.2).
Теорема 6. Пусть $1 < q\;\leqslant \;3$ и $\{ {{u}_{0}}(x),{{u}_{1}}(x)\} \in {{H}_{{{{x}_{3}}}}}$. Пусть выполнены неравенства
(7.11)
${\text{|}}{{u}_{0}}(x){\kern 1pt} {\text{|}}\;\leqslant \;\frac{{{{A}_{0}}}}{{{{{(1 + {{{\left| x \right|}}^{2}})}}^{{\alpha /2}}}}},\quad {\text{|}}{{u}_{1}}(x){\kern 1pt} {\text{|}}\;\leqslant \;\frac{{{{A}_{1}}}}{{{{{(1 + {{{\left| x \right|}}^{2}})}}^{{\beta /2}}}}}\quad при\quad \alpha > 1,\quad \beta > 1.$Тогда не существует слабого локального во времени решения задачи Коши (7.1), (7.2) в смысле определения $1$ ни для какого $T > 0$.
Доказательство. Пусть функция $u(x,t)$ является слабым локальным во времени решением задачи Коши (7.1), (7.2) в смысле определения 1. Введем следующее обозначение: ${{L}_{{{{x}_{3}}}}}: = {{\partial }^{2}}{\text{/}}\partial x_{3}^{2}.$ Также введем обозначения для интегралов из равенства (7.4):
(7.12)
${{I}_{1}}: = \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} u(x,t)\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{L}_{{{{x}_{3}}}}}\phi (x,t){\kern 1pt} dx{\kern 1pt} dt,\quad {{I}_{2}}: = \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} u(x,t)\Delta \phi (x,t){\kern 1pt} dx{\kern 1pt} dt,$(7.13)
${{I}_{3}}: = \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {{u}_{0}}(x)\frac{\partial }{{\partial t}}{{L}_{{{{x}_{3}}}}}\phi (x,0){\kern 1pt} dx,\quad {{I}_{4}}: = \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {{u}_{1}}(x){{L}_{{{{x}_{3}}}}}\phi (x,0){\kern 1pt} dx,$(7.14)
$I: = \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}^{q}}\phi (x,t){\kern 1pt} dx{\kern 1pt} dt.$(7.17)
${{\phi }_{1}}(t): = {{\left( {1 - \frac{t}{T}} \right)}^{\lambda }},\quad {{\phi }_{2}}(x): = {{\phi }_{0}}\left( {\frac{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}}{{{{R}^{2}}}}} \right),\quad \lambda > 2q{\kern 1pt} ',\quad q{\kern 1pt} ' = \frac{q}{{q - 1}},\quad q > 1,$(7.18)
${{\phi }_{0}}(s): = \left\{ \begin{gathered} 1,\quad {\text{если}}\quad 0\;\leqslant \;s\;\leqslant \;1, \hfill \\ 0,\quad {\text{если}}\quad s\; \geqslant \;2, \hfill \\ \end{gathered} \right.\quad {{\phi }_{0}}(s) \in \mathbb{C}_{0}^{\infty }[0, + \infty ),$Оценим сначала интегралы, связанные с начальными условиями:
(7.19)
$\begin{gathered} {\text{|}}{{I}_{3}}{\kern 1pt} {\text{|}} = \left| {\int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {{u}_{0}}(x){{L}_{{{{x}_{3}}}}}\frac{{\partial \phi }}{{\partial t}}(x,0){\kern 1pt} dx} \right| = \left| {\int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {{u}_{0}}(x){{L}_{{{{x}_{3}}}}}{{{\left. {\frac{\partial }{{\partial t}}\left( {{{{\left( {1 - \frac{t}{T}} \right)}}^{\lambda }}{{\phi }_{2}}(x)} \right)} \right|}}_{{t = 0}}}{\kern 1pt} dx} \right| = \\ = \frac{\lambda }{T}\left| {\int\limits_{R\leqslant |x|\leqslant \sqrt 2 R} {\kern 1pt} {{u}_{0}}(x){{L}_{{{{x}_{3}}}}}{{\phi }_{2}}(x){\kern 1pt} dx} \right| = \frac{\lambda }{T}R\left| {\int\limits_{1\leqslant |y|\leqslant \sqrt 2 } {\kern 1pt} {{u}_{0}}(Ry){{L}_{{{{y}_{3}}}}}{{\phi }_{0}}({{{\left| y \right|}}^{2}}){\kern 1pt} dy} \right|\;\leqslant \;\frac{{{{A}_{1}}}}{{{{R}^{{\alpha - 1}}}}} \to + 0\quad {\text{при}}\quad R \to + \infty , \\ \end{gathered} $(7.20)
$\begin{gathered} {\text{|}}{{I}_{4}}{\kern 1pt} {\text{|}} = \left| {\int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {{u}_{1}}(x){{L}_{{{{x}_{3}}}}}\phi (x,0){\kern 1pt} dx} \right| = \left| {\int\limits_{R\leqslant |x|\leqslant \sqrt 2 R} {\kern 1pt} {{u}_{1}}(x){{L}_{{{{x}_{3}}}}}{{\phi }_{2}}(x){\kern 1pt} dx} \right| = R\left| {\int\limits_{1\leqslant |y|\leqslant \sqrt 2 } {\kern 1pt} {{u}_{1}}(Ry){{L}_{{{{y}_{3}}}}}{{\phi }_{0}}({{{\left| y \right|}}^{2}}){\kern 1pt} dy} \right|\;\leqslant \\ \leqslant \;\frac{{{{A}_{2}}}}{{{{R}^{{\beta - 1}}}}} \to + 0\quad {\text{при}}\quad R \to + \infty . \\ \end{gathered} $(7.21)
$\begin{gathered} {\text{|}}{{I}_{1}}{\kern 1pt} {\text{|}} = \left| {\int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} u(x,t)\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{L}_{{{{x}_{3}}}}}\phi (x,t){\kern 1pt} dx{\kern 1pt} dt} \right|\;\leqslant \\ \leqslant \;\frac{{\lambda (\lambda - 1)}}{{{{T}^{2}}}}\int\limits_0^T {\kern 1pt} \int\limits_{R\leqslant |x|\leqslant \sqrt 2 R} \left| {u(x,t){{{\left( {\phi (x,t)} \right)}}^{{1/q}}}} \right|{{\left( {1 - \frac{t}{T}} \right)}^{{\lambda - 2}}}\frac{{\left| {{{L}_{{{{x}_{3}}}}}{{\phi }_{2}}(x)} \right|}}{{{{{\left( {\phi \left( {x,t} \right)} \right)}}^{{1/q}}}}}{\kern 1pt} dx{\kern 1pt} dt\;\leqslant \;{{c}_{1}}(R)I_{R}^{{1/q}}, \\ \end{gathered} $(7.22)
${{I}_{R}}: = \int\limits_0^T {\kern 1pt} \int\limits_{R\leqslant |x|\leqslant \sqrt 2 R} {\kern 1pt} \phi (x,t){\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}^{q}}{\kern 1pt} dx{\kern 1pt} dt,$(7.23)
$\begin{gathered} {{c}_{1}}(R): = \frac{{\lambda (\lambda - 1)}}{{{{T}^{2}}}}{{\left[ {\int\limits_0^T {\kern 1pt} \int\limits_{R\leqslant |x|\leqslant \sqrt 2 R} {{{\left( {{{{\left( {1 - \frac{t}{T}} \right)}}^{{\lambda - 2}}}\frac{{\left| {{{L}_{{{{x}_{3}}}}}{{\phi }_{2}}(x)} \right|}}{{{{{\left( {\phi \left( {x,t} \right)} \right)}}^{{1/q}}}}}} \right)}}^{{q{\kern 1pt} '}}}{\kern 1pt} dx{\kern 1pt} dt} \right]}^{{1/q{\kern 1pt} '}}} = \\ = \frac{{\lambda (\lambda - 1)}}{{{{T}^{2}}}}{{\left[ {\int\limits_0^T {\kern 1pt} \int\limits_{R\leqslant |x|\leqslant \sqrt 2 R} {{{\left( {1 - \frac{t}{T}} \right)}}^{{\lambda - 2q'}}}\frac{{{{{\left| {{{L}_{{{{x}_{3}}}}}{{\phi }_{2}}(x)} \right|}}^{{q{\kern 1pt} '}}}}}{{{{{\left( {{{\phi }_{2}}(x)} \right)}}^{{q{\kern 1pt} '/q}}}}}{\kern 1pt} dx{\kern 1pt} dt} \right]}^{{1/q{\kern 1pt} '}}} = \frac{{\lambda (\lambda - 1)}}{{{{T}^{2}}}}{{\left( {\frac{T}{{\lambda - 2q{\kern 1pt} '\; + 1}}} \right)}^{{1/q{\kern 1pt} '}}}{{c}_{0}}{{R}^{{(3 - 2q{\kern 1pt} ')/q{\kern 1pt} '}}}, \\ \end{gathered} $(7.24)
${{c}_{0}}: = {{\left( {\int\limits_{1\leqslant |y|\leqslant \sqrt 2 } \frac{{{{{\left| {{{L}_{{{{y}_{3}}}}}{{\phi }_{0}}({{{\left| y \right|}}^{2}})} \right|}}^{{q{\kern 1pt} '}}}}}{{{{{\left( {{{\phi }_{0}}({{{\left| y \right|}}^{2}})} \right)}}^{{q{\kern 1pt} '/q}}}}}{\kern 1pt} dy} \right)}^{{1/q{\kern 1pt} '}}},$(7.25)
${\text{|}}{{I}_{2}}{\kern 1pt} {\text{|}} = \left| {\int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} u(x,t)\Delta \phi (x,t){\kern 1pt} dx{\kern 1pt} dt} \right|\;\leqslant \;\int\limits_0^T {\kern 1pt} \int\limits_{R\leqslant |x|\leqslant \sqrt 2 R} \left| {u(x,t){{{\left( {\phi (x,t)} \right)}}^{{1/q}}}} \right|{{\left( {1 - \frac{t}{T}} \right)}^{\lambda }}\frac{{\left| {\Delta {{\phi }_{2}}(x)} \right|}}{{{{{\left( {\phi (x,t)} \right)}}^{{1/q}}}}}{\kern 1pt} dx{\kern 1pt} dt\;\leqslant \;{{c}_{2}}(R)I_{R}^{{1/q}},$(7.26)
${{c}_{2}}(R): = {{\left[ {\int\limits_0^T {\kern 1pt} \int\limits_{R\leqslant |x|\leqslant \sqrt 2 R} {{{\left( {{{{\left( {1 - \frac{t}{T}} \right)}}^{\lambda }}\frac{{\left| {\Delta {{\phi }_{2}}(x)} \right|}}{{{{{\left( {\phi (x,t)} \right)}}^{{1/q}}}}}} \right)}}^{{q{\kern 1pt} '}}}{\kern 1pt} dx{\kern 1pt} dt} \right]}^{{1/q{\kern 1pt} '}}} = {{\left( {\frac{T}{{\lambda + 1}}} \right)}^{{1/q{\kern 1pt} '}}}{{c}_{1}}{{R}^{{(3 - 2q{\kern 1pt} ')/q{\kern 1pt} '}}},$(7.27)
${{c}_{1}}: = {{\left( {\int\limits_{1\leqslant |y|\leqslant \sqrt 2 } \frac{{{{{\left| {\Delta {{\phi }_{0}}({\text{|}}y{{{\text{|}}}^{2}})} \right|}}^{{q{\kern 1pt} '}}}}}{{{{{\left( {{{\phi }_{0}}({{{\left| y \right|}}^{2}})} \right)}}^{{q{\kern 1pt} '/q}}}}}{\kern 1pt} dy} \right)}^{{1/q{\kern 1pt} '}}}.$Сначала мы рассмотрим случай $1 < q < 3$. Тогда $3 - 2q{\kern 1pt} ' < 0.$
Заметим, что имеет место следующая оценка:
(7.28)
${{I}_{R}}\;\leqslant \;I: = \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \phi (x,t){\text{|}}u(x,t){{{\text{|}}}^{q}}{\kern 1pt} dx{\kern 1pt} dt.$(7.29)
$I\;\leqslant \;{{c}_{1}}(R)I_{R}^{{1/q}} + {{c}_{2}}(R)I_{R}^{{1/q}}\; + \;{\text{|}}{{I}_{3}}{\text{|}}\; + \;{\text{|}}{{I}_{4}}{\text{|}}.$(7.30)
$ab\;\leqslant \;\varepsilon {{a}^{q}} + \frac{{{{b}^{{q{\kern 1pt} '}}}}}{{q{\kern 1pt} '{{{(q\varepsilon )}}^{{q{\kern 1pt} '/q}}}}},\quad a,b\; \geqslant \;0,\quad \varepsilon > 0.$(7.31)
$(1 - 2\varepsilon )I\;\leqslant \;\frac{1}{{q{\kern 1pt} '{{{(q\varepsilon )}}^{{q{\kern 1pt} '/q}}}}}\left( {c_{1}^{{q{\kern 1pt} '}}(R) + c_{2}^{{q{\kern 1pt} '}}(R)} \right)\; + \;{\text{|}}{{I}_{3}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}{{I}_{4}}{\kern 1pt} {\text{|}}.$(7.32)
$I\;\leqslant \;2\left( {\frac{1}{{q{\kern 1pt} '}}{{{\left( {\frac{4}{q}} \right)}}^{{q{\kern 1pt} '/q}}}\left( {c_{1}^{{q{\kern 1pt} '}}(R) + c_{2}^{{q{\kern 1pt} '}}(R)} \right)\; + \;{\text{|}}{{I}_{3}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}{{I}_{4}}{\kern 1pt} {\text{|}}} \right)\;\leqslant \;k,$Положим $R = N \in \mathbb{N}$. Заметим, что последовательность функций
(7.33)
${{\chi }_{N}}(x,t): = \phi (x,t){\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}^{q}} = {{\left( {1 - \frac{t}{T}} \right)}^{\lambda }}{{\phi }_{0}}\left( {\frac{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}}{{{{N}^{2}}}}} \right){\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}^{q}}$(7.34)
${{\chi }_{N}}(x,t)\;\leqslant \;{{\chi }_{{N + 1}}}(x,t)\quad {\text{для всех}}\quad (x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T].$(7.35)
$I = I(N): = \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {{\chi }_{N}}(x,t){\kern 1pt} dx{\kern 1pt} dt \to \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {{\left( {1 - \frac{t}{T}} \right)}^{\lambda }}{\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}^{q}}{\kern 1pt} dx{\kern 1pt} dt\quad {\text{при}}\quad N \to + \infty .$(7.37)
$\int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {{\left( {1 - \frac{t}{T}} \right)}^{\lambda }}{\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}^{q}}{\kern 1pt} dx{\kern 1pt} dt = 0 \Leftrightarrow u(x,t) = 0\quad {\text{для почти всех}}\quad (x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T].$Критический случай $q = 3$ нужно рассмотреть отдельно. Если $q = 3,$ то $3 - 2q{\kern 1pt} ' = 0$, поэтому емкости ${{c}_{1}}(R),\;{{c}_{2}}(R)$ уже не стремятся к нулю при $R \to + \infty $ (но являются ограниченными). Воспользуемся неравенством (7.32), которое справедливо и для случая $q = 3.$ Тогда, снова применив теорему Беппо Леви (снова положив $R = N \in \mathbb{N}$), мы придем к тому, что
(7.38)
$I = I(N) \to \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {{\left( {1 - \frac{t}{T}} \right)}^{\lambda }}{\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}^{q}}{\kern 1pt} dx{\kern 1pt} dt < + \infty \quad {\text{при}}\quad N \to + \infty .$(7.39)
$0\;\leqslant \;{{I}_{R}} = \int\limits_0^T {\kern 1pt} \int\limits_{R\leqslant |x|\leqslant \sqrt 2 R} {\kern 1pt} \phi (x,t){\text{|}}u(x,t){{{\text{|}}}^{q}}{\kern 1pt} dx{\kern 1pt} dt\;\leqslant \;\int\limits_0^T {\kern 1pt} \int\limits_{R\leqslant |x|\leqslant \sqrt 2 R} {{\left( {1 - \frac{t}{T}} \right)}^{\lambda }}{\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}^{q}}{\kern 1pt} dx{\kern 1pt} dt \to + 0\quad {\text{при}}\quad R \to + \infty .$(7.41)
$\int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {{\left( {1 - \frac{t}{T}} \right)}^{\lambda }}{\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}^{q}}{\kern 1pt} dx{\kern 1pt} dt = 0 \Leftrightarrow u(x,t) = 0\quad {\text{для почти всех}}\quad (x,t) \in {{\mathbb{R}}^{3}} \otimes [0,T].$В результате мы приходим к тому, что при $1 < q\;\leqslant \;3$ единственным слабым локальным во времени решением задачи Коши (7.1), (7.2) является функция $u(x,t)$, равная нулю почти всюду, поэтому из (7.4) получаем, что
(7.42)
$\int\limits_{{{\mathbb{R}}^{3}}} \left[ {{{u}_{0}}(x){{L}_{{{{x}_{3}}}}}\frac{{\partial \phi }}{{\partial t}}(x,0) - {{u}_{1}}(x){{L}_{{{{x}_{3}}}}}\phi (x,0)} \right]{\kern 1pt} {\kern 1pt} dx = 0$Пусть
(7.43)
$\phi (x,t) = {{\psi }_{0}}(x){{\left( {1 - \frac{t}{T}} \right)}^{\lambda }},\quad \lambda > 1,\quad {{\psi }_{0}}(x) \in \mathbb{C}_{0}^{\infty }({{\mathbb{R}}^{3}}).$(7.44)
$\int\limits_{{{\mathbb{R}}^{3}}} \left[ {\frac{\lambda }{T}{{u}_{0}}(x) + {{u}_{1}}(x)} \right]{{L}_{{{{x}_{3}}}}}{{\psi }_{0}}(x){\kern 1pt} dx = 0$(7.45)
${{\left( {{{L}_{{{{x}_{3}}}}}{{u}_{0}}(x)} \right)}^{2}} + {{\left( {{{L}_{{{{x}_{3}}}}}{{u}_{1}}(x)} \right)}^{2}} > 0\quad {\text{для почти всех}}\quad x \in O({{x}_{0}},R).$(7.46)
$\int\limits_{O({{x}_{0}},R)} \left[ {\frac{\lambda }{T}{{L}_{{{{x}_{3}}}}}{{u}_{0}}(x) + {{L}_{{{{x}_{3}}}}}{{u}_{1}}(x)} \right]{{\psi }_{0}}(x){\kern 1pt} dx = 0$(7.48)
${{L}_{{{{x}_{3}}}}}{{u}_{0}}(x) = 0,\quad {\text{а значит, и}}\quad {{L}_{{{{x}_{3}}}}}{{u}_{1}}(x) = 0,$Теперь рассмотрим вторую задачу Коши:
(7.49)
${{\mathfrak{L}}_{{x,t}}}[u](x,t) = {\text{|}}u{\kern 1pt} {{{\text{|}}}^{q}},\quad (x,t) \in {{\mathbb{R}}^{3}} \otimes (0,T],$(7.50)
$u(x,0) = {{u}_{0}}(x),\quad u{\kern 1pt} '(x,0) = {{u}_{1}}(x),\quad x \in {{\mathbb{R}}^{3}},$(7.51)
${{\mathfrak{L}}_{{x,t}}}[u](x,t): = \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{\Delta }_{ \bot }}u(x,t) + \Delta u(x,t).$Определение 3. Слабым локальным во времени решением задачи Коши (7.49), (7.50) называется функция $u(x,t) \in L_{{{\text{loc}}}}^{q}({{\mathbb{R}}^{3}} \otimes [0,T])$, которая удовлетворяет равенству
(7.52)
$\begin{gathered} \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} u(x,t)\left[ {\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{\Delta }_{ \bot }}\phi (x,t) + \Delta \phi (x,t)} \right]{\kern 1pt} {\kern 1pt} dx{\kern 1pt} dt + \int\limits_{{{\mathbb{R}}^{3}}} \left[ {{{u}_{0}}(x){{\Delta }_{ \bot }}\frac{{\partial \phi }}{{\partial t}}(x,0) - {{u}_{1}}(x){{\Delta }_{ \bot }}\phi (x,0)} \right]{\kern 1pt} dx = \\ \, = \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\text{|}}u{\kern 1pt} {{{\text{|}}}^{q}}\phi (x,t){\kern 1pt} dx{\kern 1pt} dt \\ \end{gathered} $Определение 4. Слабым обобщенным локальным во времени решением задачи Коши (7.49), (7.50) называется функция $u(x,t) \in \mathbb{C}_{b}^{{(0,1)}}({{\mathbb{R}}^{3}} \otimes [0,T])$, которая удовлетворяет в смысле пространства обобщенных функций $\mathcal{D}{\kern 1pt} '({{\mathbb{R}}^{3}} \otimes (0,T))$ равенству
(7.53)
$\left\langle {{{\mathfrak{L}}_{{x,t}}}[u](x,t),\phi (x,t)} \right\rangle = \left\langle {{\text{|}}u{\kern 1pt} {{{\text{|}}}^{q}},\phi (x,t)} \right\rangle $Теорема 7. Пусть функция $u(x,t)$ – это решение нелинейного интегрального уравнения (6.10) в банаховом пространстве ${{\mathbb{C}}_{b}}((1 + x_{1}^{2} + x_{2}^{2}{{)}^{{1/4}}}{{(1 + x_{3}^{2})}^{{1/4}}};{{\mathbb{R}}^{3}} \otimes [0,T])$. Пусть показатель $q > 4.$ В уравнении (6.10) в качестве функций $F(x,t),$ $\rho (x,t)$ берутся следующие функции:
(7.55)
$\rho (x,t): = \chi (t)\Delta {{u}_{0}}(x) + \chi {\kern 1pt} '{\kern 1pt} '(t){{\Delta }_{ \bot }}{{u}_{0}}(x) + \eta (t)\Delta {{u}_{1}}(x) + \eta {\kern 1pt} '{\kern 1pt} '(t){{\Delta }_{ \bot }}{{u}_{1}}(x),$(7.56)
$\chi (t),\eta (t) \in {{\mathbb{C}}^{2}}([0,T]),{\kern 1pt} \quad \chi (0) = 1,\quad \chi {\kern 1pt} '{\kern 1pt} (0) = 0,{\kern 1pt} \quad \eta (0) = 0,\quad {\kern 1pt} \eta {\kern 1pt} '{\kern 1pt} (0) = 1,$(7.57)
${{u}_{0}}(x),{{u}_{1}}(x) \in {{\mathbb{C}}_{b}}((1 + x_{1}^{2} + x_{2}^{2}{{)}^{{1/4}}}{{(1 + x_{3}^{2})}^{{1/4}}};{{\mathbb{R}}^{3}} \otimes [0,T]),$(7.58)
${{\Delta }_{ \bot }}{{u}_{0}}(x),\Delta {{u}_{0}}(x),{{\Delta }_{ \bot }}{{u}_{1}}(x),\Delta {{u}_{1}}(x) \in {{\mathbb{C}}_{b}}((1 + x_{1}^{2} + x_{2}^{2}{{)}^{{{{\gamma }_{1}}/2}}}{{(1 + x_{3}^{2})}^{{{{\gamma }_{2}}/2}}};{{\mathbb{R}}^{3}}),\quad {{\gamma }_{1}} > 2,\quad {{\gamma }_{2}} > 1.$Доказательство. Шаг 1. Пусть $u(x,t)$ – это решение интегрального уравнения (6.10). Проверим, что эта функция удовлетворяет начальным условиям (7.50):
(7.60)
$\begin{gathered} \frac{{\partial u}}{{\partial t}}(x,0) = \frac{{\partial f}}{{\partial t}}(x,0) + \frac{\partial }{{\partial t}}\int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {{\mathcal{E}}_{1}}\left( {x - y,t - \tau } \right){{\left. {\left( {{\text{|}}u{\kern 1pt} {{{\text{|}}}^{q}}\left( {y,\tau } \right) - \rho \left( {y,\tau } \right)} \right){\kern 1pt} {\kern 1pt} dy{\kern 1pt} d\tau } \right|}_{{t = 0}}} = \\ \, = {{u}_{0}}(x)\chi {\kern 1pt} '{\kern 1pt} (0) + {{u}_{1}}(x)\eta {\kern 1pt} '{\kern 1pt} (0) = {{u}_{1}}(x). \\ \end{gathered} $Шаг 2. Проверим выполнение равенства (7.53).
Заметим, что в смысле пространства обобщенных функций $\mathcal{D}'({{\mathbb{R}}^{3}} \otimes (0,T))$ справедливо равенство
(7.61)
$u(x,t) = F(x,t) + {{\mathcal{E}}_{1}}(x,t) * \left[ {{{{\left| {u(x,t)} \right|}}^{q}} - \rho (x,t)} \right].$(7.62)
$\begin{gathered} = \left\langle {\chi (t)\Delta {{u}_{0}}(x) + \chi {\kern 1pt} '{\kern 1pt} '{\kern 1pt} (t){{\Delta }_{ \bot }}{{u}_{0}}(x) + \eta (t)\Delta {{u}_{1}}(x) + \eta {\kern 1pt} '{\kern 1pt} '{\kern 1pt} (t){{\Delta }_{ \bot }}{{u}_{1}}(x),\phi (x,t)} \right\rangle + \\ \, + \left\langle {{{\mathfrak{L}}_{{x,t}}}[{{\mathcal{E}}_{1}}(x,t)] * ({\kern 1pt} {\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}^{q}} - \rho (x,t)),\phi (x,t)} \right\rangle = \\ \end{gathered} $(7.63)
$\begin{gathered} {{\mathfrak{L}}_{{x,t}}}[F](x,t) = \left( {\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{\Delta }_{ \bot }} + \Delta } \right)\left( {{{u}_{0}}(x)\chi (t) + {{u}_{1}}(x)\eta (t)} \right) = \\ = {{\Delta }_{ \bot }}{{u}_{0}}(x)\chi {\kern 1pt} {\text{''}}{\kern 1pt} (t) + \Delta {{u}_{0}}(x)\chi (t) + {{\Delta }_{ \bot }}{{u}_{1}}(x)\eta {\kern 1pt} '{\kern 1pt} '{\kern 1pt} (t) + \Delta {{u}_{1}}(x)\eta (t), \\ \end{gathered} $Во-вторых, нами была использована формула дифференцирования свертки обобщенных функций
где $D$ – дифференциальный оператор. В-третьих, было учтено, что И, в-четвертых, – что $f(x,t)*\delta (x,t) = f(x,t)$ для всякой обобщенной функции $f(x,t).$ Теорема доказана.В следующей теореме сформулирован результат о разрушении слабых локальных во времени решений задачи Коши (7.49), (7.50).
Доказательство этой теоремы проводится аналогично доказательству теоремы 6, надо только заменить оператор ${{L}_{{{{x}_{3}}}}} = {{\partial }^{2}}{\text{/}}\partial x_{3}^{2}$ на оператор ${{L}_{{{{x}_{1}}{{x}_{2}}}}}: = {{\Delta }_{ \bot }}$.
Теорема 8. Пусть $1 < q\;\leqslant \;3$ и $\{ {{u}_{0}}(x),{{u}_{1}}(x)\} \in {{H}_{{{{x}_{1}}{{x}_{2}}}}}$. Пусть выполнены неравенства
(7.66)
${\text{|}}{{u}_{0}}(x){\kern 1pt} {\text{|}}\;\leqslant \;\frac{{{{A}_{0}}}}{{{{{(1 + {{{\left| x \right|}}^{2}})}}^{{\alpha /2}}}}},\quad {\text{|}}{{u}_{1}}(x){\text{|}}\;\leqslant \;\frac{{{{A}_{1}}}}{{{{{(1 + {{{\left| x \right|}}^{2}})}}^{{\beta /2}}}}}\quad при\quad \alpha > 1,\quad \beta > 1.$Список литературы
Корпусов М.О., Шафир Р.С. О разрушении слабых решений задачи Коши для $3 + 1$-мерного уравнения дрейфовых волн в плазме // Ж. вычисл. матем. и матем. физ. 2022. Т. 62. № 1. С. 124–158.
Al’shin A.B., Korpusov M.O., Sveshnikov A.G. Blow-up in nonlinear Sobolev type equations // De Gruyter Series in Nonlin. Anal. Appl. 2011. V. 15. P. 648.
Свиридюк Г.А. К общей теории полугрупп операторов // Успехи матем. наук. 1994. Т. 49. № 4. С. 47–74.
Загребина С.А. Начально-конечная задача для уравнений соболевского типа с сильно (L,p)–радиальным оператором // Матем. заметки ЯГУ. 2012. Т. 19. № 2. С. 39–48.
Zamyshlyaeva A.A., Sviridyuk G.A. Nonclassical equations of mathematical physics. Linear Sobolev type equations of higher order // Вестн. Южно-Ур. ун-та. Сер. Матем. Мех. Физ. 2016. V. 8. № 4. P. 5–16.
Капитонов Б.В. Теория потенциала для уравнения малых колебаний вращающейся жидкости // Матем. сб. 1979. Т. 109(151). № 4(8). С. 607–628.
Габов С.А., Свешников А.Г. Линейные задачи теории нестационарных внутренних волн. М.: Наука, 1990. С. 344.
Габов С.А. Новые задачи математической теории волн. М.: Физматлит, 1998. С. 448.
Плетнер Ю.Д. Фундаментальные решения операторов типа Соболева и некоторые начально-краевые задачи // Ж. вычисл. матем. и матем. физ. 1992. Т. 32. № 12. С. 1885–1899.
Похожаев С.И., Митидиери Э. Априорные оценки и отсутствие решений нелинейных уравнений и неравенств в частных производных // Тр. МИАН. 2001. Т. 234. С. 3–383.
Galakhov E.I. Some nonexistence results for quasilinear elliptic problems // J. Math. Anal. Appl. 2000. V. 252. № 1. P. 256–277.
Галахов Е.И., Салиева О.А. Об отсутствии неотрицательных монотонных решений для некоторых коэрцитивных неравенств в полупространстве // СФМН. 2017. Т. 63. № 4. С. 573–585.
Корпусов М.О. Критические показатели мгновенного разрушения или локальной разрешимости нелинейных уравнений соболевского типа // Изв. РАН. Сер. матем. 2015. Т. 79. № 5. С. 103–162.
Корпусов М.О. О разрушении решений нелинейных уравнений типа уравнения Хохлова–Заболотской // ТМФ. 2018. Т. 194. № 3. С. 403–417.
Korpusov M.O., Ovchinnikov A.V., Panin A.A. Instantaneous blow-up versus local solvability of solutions to the Cauchy problem for the equation of a semiconductor in a magnetic field // Math. Meth. Appl. Sci. 2018. V. 41. № 17. P. 8070–8099.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики