Журнал вычислительной математики и математической физики, 2023, T. 63, № 2, стр. 245-261

1.1. Математическое описание исходной физической модели на основе двумерных уравнений пограничного слоя

Рассматривается математическая модель течения в слое смешения, возникающего в результате взаимодействия двух неограниченных слоев вязкой несжимаемой жидкости, верхний из которых движется (со степенной зависимостью горизонтальной составляющей скорости течения от высоты), а нижний покоится. Для описания модели используются двумерные уравнения пограничного слоя для установившегося плоскопараллельного ламинарного течения с нулевым градиентом давления:

(см., например, [5, гл. IX] и [6, гл. I]). Здесь (1.5) – уравнение Прандтля, а (1.6) – уравнение неразрывности (несжимаемости); ось $x$ направлена вдоль потока и совпадает со свободной линией тока, $u$ и $v$ – компоненты скорости течения вдоль и поперек потока соответственно, $\nu > 0$ – кинематический коэффициент вязкости (в безразмерных переменных $\nu = 1$; см. [6, с. 14] и подробнее [1]).

Учитывая физическую интерпретацию модели и определение свободной линии тока (а также способ построения ниже автомодельных решений), получаем, что для функций $u(x,y)$ и $v(x,y)$ должны выполняться следующие условия $\forall x > 0$:

где $m$ и ${{U}_{0}}$ – задаваемые величины, $m > 0$ – числовой параметр, ${{U}_{0}} > 0$ – размерная величина, так что первое из условий в (1.9) задает поведение $u(x,y)$ в верхнем слое:

Как уже отмечено в [1], в задаче (1.5)–(1.9) рассматриваются значения $x > 0$ и никакие условия при $x = 0$ не задаются, так как при изучении установившихся автомодельных режимов течений, не зависящих от “предыстории” , задание произвольного профиля скоростей в некотором “начальном” сечении потока становится невозможным (подробнее об этом см. [7, с. 518]).

Для упрощения задачи (1.5)–(1.9) вводится, как обычно, функция тока $\psi (x,y)$, чтобы удовлетворить уравнению неразрывности (1.6). Тогда, учитывая, что ось $x$ совпадает со свободной линией тока, получаем соотношения

Для $\psi (x,y)$ получаем сингулярную задачу в бесконечной правой полуплоскости:

Отметим еще раз, что описанная выше постановка исходной задачи для компонент скорости течения (или, как следствие из нее, для функции тока) впервые приведена в [1] (в [2–4] отсутствуют как постановка исходной задачи, так и ссылки на таковую в литературе).

1.2. Переход к сингулярной нелинейной задаче для автомодельных функций

В классе автомодельных функций, введенных в [2], [3], решения (1.11) представляются в виде

Для определения $\Phi (\tau )$ получается нелинейное ОДУ (1.1). Далее при описании автомодельного режима течения в слое смешения, возникающем при взаимодействии двух потоков, верхний из которых движется, а нижний покоится, ОДУ (1.1) дополняется условиями (1.2)–(1.4), смысл которых в [2], [3] не поясняется (условие (1.4) там записано в виде $\Phi (\tau ) = b{{\tau }^{m}} + \cdots ,$ $b > 0,$ $m > 0$).

Более аккуратно: будем искать решения задачи (1.11)–(1.14) в классе автомодельных функций (1.15), где автомодельная переменная $\tau $ в (1.16) зависит от параметра $m$, причем справедливы соотношения (штрих означает производную по $\tau $)

Для функции $\Phi (\tau )$ получаем нелинейную сингулярную задачу с параметром $m > 0$:

1) из уравнения (1.11) и формул (1.15), (1.16) следует автономное нелинейное ОДУ (1.1) третьего порядка;

2) из требования (1.12) и соотношения (1.17) вытекает предельное условие (1.2);

3) из (1.13) и (1.16) следует выполнение условия в нуле (1.3) (ось $x$ совпадает со свободной линией тока, а $\tau = 0$ при $y = 0$);

4) наконец, из требований (1.14) и формул (1.17), (1.18) вытекают предельные соотношения

откуда получаем предельное равенство (1.4) и соотношения

Окончательно получаем (по крайней мере, формально) сингулярную нелинейную задачу (1.1)–(1.4) с параметрами $m > 0$ и $b > 0$. Из соотношений (1.19) следует, что задание величины $b$ в условии (1.4) эквивалентно заданию ${{U}_{0}}$ в формуле (1.10), которая описывает $y$-зависимость горизонтальной составляющий скорости верхнего потока при больших $y$ и влечет качественно различный характер ее поведения при $m < 1$, $m = 1$ и $m > 1$.

Как уже подтверждено в [1], оправданием предположений (1.9), (1.10) для профиля скорости потока в верхнем слое в приведенной физической модели является то обстоятельство, что для фиксированных значений $m{\kern 1pt} :\;1{\text{/}}2 < m < \infty $, и $b > 0$ задача (1.1)–(1.4) однозначно разрешима.

Для дальнейшего опишем некоторые семейства частных регулярных и сингулярных решений ОДУ (1.1), которые получаются методами понижения порядка этого ОДУ и не являются решениями задачи (1.1)–(1.4): наряду с очевидными решениями $\Phi (\tau ) \equiv {\text{const}}$ $\forall m \in \mathbb{R}$, ОДУ (1.1) имеет, в частности, следующие семейства решений:

1) для каждого $m:(m \ne 0) \wedge (m \ne - 1)$, существует однопараметрическое семейство сингулярных решений

с особенностью типа полюса в конечной точке $\tau = {{\tau }_{p}}$; при этом для $m = 1{\text{/}}2$ существует двухпараметрическое семейство сингулярных решений которые переходят в решения (1.20) при $a = 0$;

2) для $m \in \{ 1{\text{/}}2;1;2;\infty \} $ существуют двухпараметрические семейства решений ${{\Phi }_{m}}(\tau - {{\tau }_{s}},a)$ ($a,{{\tau }_{s}} \in \mathbb{R}$), определенных глобально – на всей вещественной оси:

В (1.20)–(1.24) произвольные величины ${{\tau }_{p}}$ и ${{\tau }_{s}}$ – параметры сдвига, $a$ – отличное от нуля произвольное число.

1.3. Уточнение постановки сингулярной нелинейной задачи для автомодельных функций

В [2], [3] задача (1.1)–(1.4) в исходном виде не изучается и, в частности, физический смысл условий (1.2)–(1.4) не поясняется. Для ее изучения используются методы понижения порядка ОДУ (1.1), инвариантного относительно двух групп преобразований подобия. В результате в фазовом пространстве новых “нефизических” переменных возникает двумерная нелинейная динамическая система с особенностями на так называемой сфере Пуанкаре (понятие сферы Пуанкаре, а также принципы анализа заданных на ней нелинейных динамических систем второго порядка, правые части которых – многочлены, см., например, [8, гл. VI]). Проведен довольно сложный качественный анализ поведения всех траекторий решений на этой сфере с отбором нужных, и описана непростая процедура возвращения к решениям исходной задачи в физических переменных. Никакие расчеты для этой задачи в [2–4] не осуществлялись (вообще говоря, непонятно, что и как можно посчитать в исходных физических переменных при таком сложном подходе этих работ), приведены только качественные иллюстрации поведения траекторий решений на сфере Пуанкаре для некоторых значений параметра $m$.

Математически другой подход осуществлен в [1], при котором задача (1.1)–(1.4) изучается в исходном виде с применением некоторых результатов классического труда Ляпунова [9], а также публикаций [10–12], а именно, результатов по сингулярным нелинейным ЗК, гладким УНМ решений и параметрическим экспоненциальным рядам Ляпунова для автономных систем нелинейных ОДУ.

Обратимся к подходу [1], где прежде всего замечено, что нелинейная сингулярная задача (1.1)–(1.4), определенная на всей вещественной оси, нуждается в более строгой математической постановке и вытекающей из нее более точной трактовке. В частности, условие (1.2) более точно означает стремление решения при $\tau \to - \infty $ к стационарной точке ОДУ (1.1). В фазовом пространстве ${{\mathbb{R}}^{3}}$ переменных $(\Phi ,\Phi {\kern 1pt} ',\Phi {\kern 1pt} '{\kern 1pt} ')$ ОДУ (1.1) имеет бесконечное множество стационарных точек (положений равновесия):

Учитывая понятие допустимых предельных условий на бесконечности для систем нелинейных автономных ОДУ (см. [10–12]), условие (1.2) следует заменить на более точное предельное условие с неизвестным параметром $a > 0$: Это условие отвечает экспоненциальному стремлению решений ОДУ (1.1) при $\tau \to - \infty $ к неподвижной точке (1.25) типа псевдо-гиперболического седла (подробнее см. [1]).

Условие (1.26) порождает локально сингулярную нелинейную ЗК (1.1), (1.26), которая при фиксированных значениях $a > 0$ и $m\not { = }0$ обладает однопараметрическим семейством решений. Эти решения представимы однопараметрическим экспоненциальным рядом Ляпунова, а именно, справедливо

Утверждение 1. При любых заданных $a > 0$ и $m \ne 0$ сингулярная нелинейная ЗК (1.1), (1.26) имеет однопараметрическое семейство решений ${{\Phi }_{m}}(\tau ,a,d)$. Эти решения представимы экспоненциальным рядом Ляпунова

где $d$ – параметр, ${\text{|}}d\exp (a\tilde {\tau }){\text{|}}$ мало, а коэффициенты ${{h}_{l}}$ не зависят от $d$ ($l \geqslant 1$, ${{h}_{1}} \doteq 1$): в частности, из (1.28) следует, что ${{h}_{2}} = - 1{\text{/}}(4am),{{h}_{3}} = (m + 4){\text{/}}(72{{a}^{2}}{{m}^{2}}), \ldots $.

В предельном случае $m \to \infty $ сингулярная нелинейная ЗК (1.1), (1.26) имеет двухпараметрическое семейство точных решений ${{\Phi }_{\infty }}(\tau ,a,d)$, существующих глобально на всей вещественной оси:

где $a$ и $d$ – параметры, $a > 0$, $d \in \mathbb{R}$.

Заметим здесь, что для приведенных в п. 1.2 некоторых частных решений справедливы утверждения: при любых заданных $a > 0$ функции $\Phi _{{{\text{sing}},1/2}}^{{(2)}}(\tau - {{\tau }_{p}},a)$, ${{\Phi }_{{1/2}}}(\tau - {{\tau }_{s}},a)$, ${{\Phi }_{\infty }}(\tau - {{\tau }_{s}},a)$ являются решениями сингулярной нелинейной ЗК (1.1), (1.26); они представимы рядами Ляпунова (1.27), (1.28) с соответствующими значениями параметра $d$:

Принимая во внимание результаты [10–12], получаем также следующее

Утверждение 2. При любых заданных $a > 0$ и $m \ne 0$ в окрестности стационарной точки (1.25) в фазовом пространстве ${{\mathbb{R}}^{3}}$ переменных $\left( {\Phi ,\Phi {\kern 1pt} ',\Phi {\kern 1pt} '{\kern 1pt} '} \right)$ значения решений сингулярной нелинейной ЗК (1.1), (1.26) образуют инвариантное относительно $\tau $ одномерное аналитическое УНМ $M_{ - }^{{(1)}}(a,m)$, которое задается двумя нелинейными соотношениями:

Здесь $\{ {{\rho }_{1}}(y),{\kern 1pt} {{\rho }_{2}}(y)\} $ – решение сингулярной нелинейной задачи типа Ляпунова: Решение $\{ {{\rho }_{1}}(y,a,m),{\kern 1pt} {{\rho }_{2}}(y,a,m)\} $ этой задачи (с вырождением в нуле по начальным данным) существует, единственно и голоморфно в точке $y = 0$: в частности, из (1.34)–(1.36) следует, что ${{c}_{2}} = 1{\text{/}}(2m{{a}^{4}})$, ${{b}_{2}} = 3{\text{/}}(4m{{a}^{5}})$, ...  .

В предельном случае $m \to \infty $ задача (1.31), (1.32) имеет точное решение

так что, в силу (1.30), одномерное УНМ $M_{ - }^{{(1)}}(a,\infty )$ становится линейным, существует глобально на ${{\mathbb{R}}^{3}}$ и порождается значениями решений (1.29).

Таким образом, значения решений, построенных в утверждении 1 и представимых однопараметрическим экспоненциальным рядом Ляпунова, порождают в окрестности стационарной точки $( - a,0,0)$ фазового пространства ${{\mathbb{R}}^{3}}$ переменных ($\Phi ,\Phi {\kern 1pt} ',\Phi {\kern 1pt} '{\kern 1pt} ')$ инвариантное относительно $\tau $ одномерное нелинейное УНМ; это УНМ задается двумя нелинейными соотношениями (1.30), связывающими переменные $\Phi $, $\Phi {\kern 1pt} '$ и $\Phi {\kern 1pt} '{\kern 1pt} '$. Тогда в конечной точке $\tau = - T$, $T \gg 1$, получаются два нелинейных условия для значений $\Phi ( - T)$, $\Phi {\kern 1pt} '{\kern 1pt} ( - T)$ и $\Phi {\kern 1pt} '{\kern 1pt} '{\kern 1pt} ( - T)$. Таким образом, для достаточно больших конечных значений ${\text{|}}\tau {\kern 1pt} {\text{|}}$, $\tau < 0$, предельное условие (1.26) эквивалентно двум нелинейным соотношениям, определяющим устойчивую сепаратрису седла, так что задача (1.1), (1.26), (1.3) – двухточечная краевая.

В итоге получаем, что на интервале $ - \infty < \tau \leqslant 0$ определена сингулярная нелинейная КрЗ (1.1), (1.26), (1.3) (а на отрезке $[ - T,0]$ – эквивалентная ей регулярная двухточечная КрЗ) с положительными параметрами $a$ и $m$. Исследование вспомогательной КрЗ (1.1), (1.26), (1.3), определенной на ${{\mathbb{R}}_{ - }}$, проведено в [1, разд. 3]: показано, что при фиксированных $a > 0$ и $m \geqslant 1{\text{/}}3$ решение ${{\Phi }_{m}}(\tau ,a)$ этой задачи существует и единственно, и получены его двусторонние оценки, причем при заданном $m \geqslant 1{\text{/}}2$ решение неограниченно продолжается вправо, а при $m{\kern 1pt} :\;1{\text{/}}3 \leqslant m < 1{\text{/}}2$, оно сингулярно – имеет особенность типа полюса на ${{\mathbb{R}}_{ + }}$. При $m{\kern 1pt} :\;m \in \{ 1{\text{/}}3,1{\text{/}}2,\infty \} $, КрЗ (1.1), (1.26), (1.3) имеет точные решения, представляющие самостоятельный физический интерес.

Заметим здесь, что точное решение ${{\Phi }_{{1/3}}}(\tau ,a)$ КрЗ (1.1), (1.26), (1.3) задается сложной неявной формулой, которая в данной работе не приводится (см. [1]).

1.4. Формулировки основных теорем из [1] для сингулярной нелинейной КрЗ

Теорема 1. При любых заданных $m \geqslant 1{\text{/}}2$ и $a > 0$ сингулярная нелинейная КрЗ (1.1), (1.26), (1.3), определенная на ${{\mathbb{R}}_{ - }}$, имеет единственное решение ${{\Phi }_{m}}(\tau ,a)$; оно есть строго возрастающая выпуклая функция, принадлежащая семейству (1.27), (1.28) при некотором $d = {{d}_{m}}(a) > 0$, причем справедливы двусторонние оценки

Теорема 2. Для решений сингулярной нелинейной КрЗ (1.1), (1.26), (1.3) при $m{\kern 1pt} :\;0 < m \leqslant 1{\text{/}}2$, следующие утверждения справедливы:

1) для любой фиксированной пары значений $\{ m,a\} $: $1{\text{/}}3 \leqslant m \leqslant 1{\text{/}}2$, $a > 0$, КрЗ (1.1), (1.26), (1.3) имеет единственное решение ${{\Phi }_{m}}(\tau ,a)$; оно есть строго возрастающая функция, принадлежащая семейству (1.27), (1.28) при некотором $d = {{d}_{m}}(a) > 0$, и справедливы двусторонние оценки

2) при $m{\kern 1pt} :\;{\kern 1pt} 1{\text{/}}3 \leqslant m < 1{\text{/}}2$, решение ${{\Phi }_{m}}(\tau ,a)$ имеет точку перегиба $\tau = {{\tau }_{{{\text{i}}n}}} \in {{\mathbb{R}}_{ - }}$, определяемую соотношением

и не существует глобально на $\mathbb{R}$ – имеет полюс первого порядка в точке $\tau = {{\tau }_{p}}(a,m) > 0$, где ${{\tau }_{p}}(a,1{\text{/}}3) = 2\pi \sqrt 3 {\text{/}}(3a)$ и ${{\tau }_{p}}(a,m) > {{\tau }_{p}}(a,1{\text{/}}3)$ $\forall m{\kern 1pt} :\;1{\text{/}}3 < m < 1{\text{/}}2$;

3) при любых $m{\kern 1pt} :\;0 < m < 1{\text{/}}3$, и $a > 0$ КрЗ (1.1), (1.26), (1.3) решений не имеет.

Здесь значения ${{d}_{{1/3}}}(a) = 2a\sqrt 3 \exp (\pi \sqrt 3 {\text{/}}6)$ и ${{\tau }_{p}}(a,1{\text{/}}3) = 2\pi \sqrt 3 {\text{/}}(3a)$, наряду с неявной формулой для функции ${{\Phi }_{{1/3}}}(\tau ,a)$, получены в [1].

1.5. Основной результат для сингулярной нелинейной НКЗ

Для всей исходной задачи (1.1)–(1.4) значение параметра $a$ не является произвольным: $a = a(b)$ находится из требования (1.4), если такое поведение решений КрЗ (1.1), (1.26), (1.3), продолженных вправо, справедливо (из [1] следует, что это имеет место при $m$: $1{\text{/}}2 < m < \infty $). В результате, при фиксированном значении параметра $m > 0$, задача (1.1)–(1.4) разбивается на две – сингулярную двухточечную КрЗ с параметром, заданную на неположительной вещественной полуоси, и ЗК на положительной полуоси, дающую продолжение решения КрЗ. В [1, разд. 4] формулируются окончательные ограничения на параметр автомодельности $m{\kern 1pt} :\;1{\text{/}}2 < m < \infty $, гарантирующие существование и единственность решения исходной задачи (1.1)–(1.4), которую по понятным причинам называем НКЗ. (Напомним еще раз, что в [2], [3] задача (1.1)–(1.4) ошибочно трактуется как трехточечная краевая.) Даются двусторонние оценки решения и исследуются его свойства для различных значений параметра автомодельности. При этом аналитическая функция ${{\Phi }_{{1/2}}}(\tau ,a)$ является для НКЗ (1.1)–(1.4) верхним решением на ${{\mathbb{R}}_{ - }}$ и нижним решением на ${{\mathbb{R}}_{ + }}$, а функция ${{\Phi }_{\infty }}(\tau ,a)$ – наоборот. Предложены численные методы и приведены результаты расчетов. Кроме того, наряду с численным моделированием функции тока (как функции автомодельной переменной), впервые приводятся некоторые результаты расчетов траекторий частиц в плоскости потока.

При этом важным является следующее замечание о применении масштабных преобразований при решении сингулярной нелинейной НКЗ. Пусть сингулярная нелинейная НКЗ (1.1), (1.26), (1.3), (1.4) однозначно разрешима при заданных $m > 0$ и $b > 0$, и пусть ${{\Phi }_{m}}(\tau ,a)$ – ее решение, где $a = a(b)$. Чтобы найти это решение, достаточно решить указанную НКЗ при $a = 1$. Действительно:

1) решаем сопутствующую сингулярную нелинейную КрЗ (1.1), (1.26), (1.3) при $a = 1$ (см. методы вычислений в [1]) и находим $d = {{d}_{m}}(1) > 0$ и соответствующее решение ${{\Phi }_{m}}(\tau ,1)$ (здесь и далее $d = {{d}_{m}}(a)$ – параметр ряда Ляпунова (1.27), (1.28));

2) продолжая решение ${{\Phi }_{m}}(\tau ,1)$ для $\tau > 0$ как решение ЗК с найденными начальными данными в точке $\tau = 0$, получаем значение $b = {{b}_{m}}(1) > 0$;

3) значение $a = a(b) > 0$ для заданного $b > 0$ в (1.4) находим с помощью масштабных преобразований

4) искомое решение ${{\Phi }_{m}}(\tau ,a)$ и значение параметра $d = {{d}_{m}}(a) > 0$, где $a = a(b)$ определено в (1.40), окончательно получаем с помощью преобразований

Значения ${{b}_{m}}(1)$ и ${{d}_{m}}(1)$, вообще говоря, не могут быть определены методами локального анализа и находятся численно (см. для этих величин [1, табл. 2, 3 ]). (В справедливости соотношений (1.40), (1.41) нетрудно убедиться непосредственно.)

Теорема 3. При любых заданных $b > 0$ и $m{\kern 1pt} :\;1{\text{/}}2 < m < \infty $, сингулярная нелинейная НКЗ (1.1)–(1.4), определенная на всей вещественной оси, имеет единственное решение ${{\Phi }_{m}}(\tau ,a,b)$, где $a = a(b) > 0$, и следующие утверждения справедливы:

(i) ${{\Phi }_{m}}(\tau ,a,b)$ – выпуклая на ${{\mathbb{R}}_{ - }}$ монотонно возрастающая на $\mathbb{R}$ функция, принадлежащая семейству (1.27), (1.28) для некоторого $d = {{d}_{m}}(a,b) > 0$ и удовлетворяющая ограничениям

(ii) решение ${{\Phi }_{m}}(\tau ,a,b)$ может быть получено следующим образом: фиксируем $a = 1$ и определяем решение ${{\Phi }_{m}}(\tau ,1)$ КрЗ (1.1), (1.26), (1.3), которое в силу теоремы $1$ существует, единственно и принадлежит семейству (1.27), (1.28) при некотором $d = {{d}_{m}}(1)$; продолженное вправо, это решение удовлетворяет предельному соотношению ${{\lim }_{{\tau \to \infty }}}[{{\Phi }_{m}}(\tau ,1){\text{/}}{{\tau }^{m}}] = {{b}_{m}}(1) > 0$; для окончательного нахождения искомого решения ${{\Phi }_{m}}(\tau ,a,b)$ при $\tau \in \mathbb{R}$ используем соотношения (1.40), (1.41).

На фиг. 1 для наглядности представлены графики из [1] решений НКЗ (1.1)–(1.4) при $a = 1$ и разных значениях параметра $m$.

Асимптотическое поведение решения ${{\Phi }_{m}}(\tau ,a,b)$ при больших $\tau > 0$ подробно исследовано в [1], на чем останавливаться не будем.

2.1. Постановка сингулярной начальной задачи для нелинейного ОДУ, вырождающегося по фазовой переменной

Рассмотрим ОДУ (2.2) с точки зрения данной работы. Заметим, что соотношение (2.1) и равенство

выполняются вдоль траектории ОДУ (1.1).

Пусть $\Phi (\tau )$ – решение сингулярной нелинейной ЗК на бесконечности (1.1), (1.26). Принимая во внимание формулы (2.1)–(2.6), условие (1.26) при $\tau \to - \infty $, утверждение 1 и разложение (1.27), получаем предельные условия для решений ОДУ (2.2) при $\Phi \to - a + 0$: ${{\lim }_{{\Phi \to - a + 0}}}f(\Phi ) = 0$, ${{\lim }_{{\Phi \to - a + 0}}}\dot {f}(\Phi ) = a$.

В результате получаем сингулярную нелинейную ЗК:

где ОДУ (2.7) совпадает с (2.2), но представлено в более удобном виде.

Пусть теперь $\Phi (\tau )$ – решение сингулярной нелинейной НКЗ (1.1)–(1.4) для заданных $b > 0$, $a = a(b) > 0$ и $m{\kern 1pt} :\;1{\text{/}}2 < m < \infty $ (в соответствии с теоремой 3). Тогда решение $f(\Phi )$ сингулярной нелинейной ЗК (2.7), (2.8) должно удовлетворять предельному условию

Прежде всего рассмотрим сингулярную нелинейную ЗК (2.7), (2.8) при $m\not { = }0$. Для ее решений, в частности, выполнено соотношение

Отсюда нетрудно проверить, что справедливо

Следствие 1. При $m = \infty $ и $m = 1{\text{/}}2$ существуют точные решения ${{f}_{m}}(\Phi ,a)$ сингулярной нелинейной ЗК (2.7), (2.8):

(Эти решения, естественно, не удовлетворяют условию (2.9).) Для исходной сингулярной ЗК (1.1), (1.26) функция (2.11) соответствует точному решению ${{\Phi }_{\infty }}(\tau - {{\tau }_{s}},a)$, определенному формулой (1.24); при ${{a}^{2}} > {{\Phi }^{2}}$ функция (2.12) соответствует точному решению ${{\Phi }_{{1/2}}}(\tau - {{\tau }_{s}},a)$, определенному в (1.22), а при ${{a}^{2}} < {{\Phi }^{2}}$ – точному решению $\Phi _{{{\text{sing}},1/2}}^{{(2)}}(\tau - {{\tau }_{p}},a)$, определенному в (1.21).

Замечание 1. ОДУ (2.7) инвариантно относительно замены переменных

Тогда в задаче (2.7), (2.8) достаточно положить $a = 1$, так как справедливо соотношение

В дальнейшем, оставляя $a$ в формулах, в численных примерах полагаем $a = 1$.

2.2. Вспомогательная сингулярная ЗК для нелинейного ОДУ с регулярной особенностью в нуле и разрешимость исходной вырожденной задачи

Из сингулярной нелинейной задачи (2.7), (2.8) следует, что ОДУ (2.7) вырождается по фазовой переменной при $\Phi \to - a + 0$. Чтобы исследовать это вырождение, положим

где $\alpha > 0$.

Подстановка (2.14), (2.15) в (2.7) дает (в главном при $\Phi \to - a$)

Чтобы удовлетворить этому соотношению при $\Phi \to - a$, приравняем нулю сумму слагаемых с наименьшими степенями. Тогда получим соотношения

откуда

Далее, учитывая формулы (2.13)–(2.16), осуществим замену переменных:

где ${{\lim }_{{t \to + 0}}}\chi (t) = 0$. Из (2.17), в частности, следуют формулы (здесь и далее штрих означает дифференцирование по $t$): Используя (2.7), (2.8) и (2.17), (2.18), получаем сингулярную нелинейную ЗК для ОДУ относительно новой искомой функции $\chi (t)$; это ОДУ имеет регулярную особенность в точке $t = 0$ (классификацию особых точек для систем линейных и нелинейных ОДУ см. в [13], [14]):

Заметим, что функция $G(t,\chi ,t\chi {\kern 1pt} ')$ голоморфна в точке $(t,\chi ,t\chi {\kern 1pt} ') = (0,0,0)$, и что из (2.21), (2.22) следуют равенства

Для собственных значений $\lambda $ линейного ОДУ

имеем $\lambda (\lambda - 1) + 3\lambda + 1 = 0$, откуда ${{\lambda }_{{1,2}}} = - 1$. Тогда сингулярная линейная ЗК (2.23), (2.20) имеет только тривиальное решение, а из результатов по сингулярным ЗК для нелинейных ОДУ (см., в частности, [15, теорема 5] и библиографию там) вытекает следующее

Утверждение 3. Для любого $m\not { = }0$ сингулярная нелинейная ЗК (2.19)–(2.22) имеет единственное решение ${{\chi }^{{(m)}}}(t)$; оно является голоморфной функцией в точке $t = 0$:

где подстановка (2.24) в (2.19) даетдля $m = \infty $ и $m = 1{\text{/}}2$ справедливо

Кроме того, при $m > 0$ справедливы соотношения

откуда

Следствие 2. Для любого $m > 1{\text{/}}2$ решение ${{\chi }^{{(m)}}}(t)$ сингулярной нелинейной ЗК (2.19)–(2.22) существует глобально на ${{\mathbb{R}}_{ + }}$ и удовлетворяет неравенству ${{\chi }^{{(m)}}}(t) > - 1$ $\forall t \in {{\mathbb{R}}_{ + }}$.

Графики к следствию 2 приведены на фиг. 2.

Более того, как несложно проверить, для любого $m\not { = }0$ нелинейное ОДУ (2.19) не имеет сингулярных решений с особенностями типа полюса в конечных точках $t > 0$.

Учитывая утверждение 3, следствие 2, соотношения (2.17) и тот факт, что для любого конечного $\Phi > - a$ решения нелинейного ОДУ (2.7) не имеют особенностей типа полюса, окончательно получаем, что справедлива

Теорема 4. Для любых $a > 0$ и $m\not { = }0$ сингулярная нелинейная ЗК (2.7), (2.8) имеет единственное решение ${{f}_{m}}(\Phi ,a)$; оно является голоморфной функцией в точке $\Phi = - a$:

где коэффициенты $\chi _{k}^{{(m)}}$ $(k \geqslant 1)$ определены рекуррентными соотношениями (2.25); при $m = \infty $ и $m = 1{\text{/}}2$ сингулярная нелинейная ЗК (2.7), (2.8) имеет точные решенияБолее того, при $m{\kern 1pt} :\;1{\text{/}}2 < m < \infty $, решение ${{f}_{m}}(\Phi ,a)$ сингулярной нелинейной ЗК (2.7), (2.8) существует глобально и является положительной функцией на интервале $( - a,\infty )$.

Из (2.27), (2.25) при $\Phi + a \to 0$, в частности, получаем

Замечание 2. В [2], [3] приводятся два первых слагаемых в разложении вида (2.28) (см. здесь формулу (2.4)), но характер представления не обсуждается. Точное утверждение следует из приведенных выше рассуждений, а члены сходящегося ряда (2.27) находятся формальной подстановкой этого ряда в (2.7).

2.3. Асимптотическое поведение на бесконечности решений исходной сингулярной задачи для различных значений $m > 0$

Изучение глобального поведения решений сингулярной нелинейной ЗК (2.7), (2.8) для различных значений параметра $m > 0$ представляет довольно сложную задачу.

Чтобы прояснить качественное поведение решений ОДУ (2.7) при больших $\Phi $, положим

Подставляя (2.29) в (2.7) и удерживая главные члены, получаем Приравнивая нулю сумму слагаемых в (2.30), быстрее всего растущих при больших $\Phi $, получаем два случая:

Случай I. Наибольшая степень в (2.30) равна $\beta $. Тогда

и параметр $B$ ( $B\not { = }0$) является свободным; действительно, в этом случае имеем

Случай II. Две наибольших степени в (2.30) совпадают: $2\beta - 2 = \beta $; тогда

Дадим более строгое доказательство существования семейств решений с помощью замены зависимой переменной в (2.7):

здесь функция $Z(\Phi )$ должна удовлетворять условиям ${{\lim }_{{\Phi \to \infty }}}Z(\Phi ) = {{\lim }_{{\Phi \to \infty }}}\dot {Z}(\Phi ) = 0$.

Получаем для $Z(\Phi )$ сингулярную ЗК на бесконечности:

Замечание 3. В случае II сингулярная нелинейная ЗК на бесконечности (2.34), (2.35) всегда имеет тривиальное решение $Z \equiv 0$; то же верно в случае I при $m = 1$, когда $\beta = 0$, и при $m = 2$, когда $\beta = 1{\text{/}}2$ ($B\not { = }0$ произвольно). Тогда представление (2.33) дает точные решения ${{f}_{{{\text{I}}I,m}}}$ и ${{f}_{{{\text{I}},m}}}$ ОДУ (2.7), которые не являются решениями сингулярной ЗК (2.7), (2.8):

Для исходного ОДУ (1.1) функция (2.36) соответствует точному сингулярному решению $\Phi _{{{\text{sing}},m}}^{{(1)}}(\tau - {{\tau }_{p}},a)$, определенному формулой (1.20), а функции (2.37) дают точные решения ${{\Phi }_{1}}(\tau - {{\tau }_{s}},a)$ и ${{\Phi }_{2}}(\tau - {{\tau }_{s}},a)$, определенные формулами (1.23).

Замечания для случая I. При $m > 0$ и $\beta = (m - 1){\text{/}}m$ имеем

Осуществим в (2.34), (2.35) замену независимой переменной:

Тогда, обозначая $\widetilde Z(x) = Z(\Phi (x))$ и учитывая равенства (2.38), из (2.34), (2.35) получаем для $\widetilde Z(x)$ сингулярную нелинейную ЗК на бесконечности, зависящую от $B\not { = }0$ и $m > 0$ как от параметров (штрих означает дифференцирование по $x$):

Согласно [14], нелинейное ОДУ (2.40) имеет иррегулярную особенность ранга $1$ при $x \to \infty $, и верно следующее

Утверждение 4. Для любых $B \ne 0$ и $m > 0$ сингулярная нелинейная ЗК (2.40), (2.41) имеет частное решение $\theta (x) = \theta (x,m,B)$, которое при больших $x$ представимо формальным рядом

где коэффициенты разложения находятся формальной подстановкой ряда (2.42) в ОДУ (2.40): здесь ${{F}_{{k - 1}}}$ получаются из величин ${{\theta }_{1}}, \ldots ,{{\theta }_{{k - 2}}}$ с помощью только операций типа сложения и умножения; при этом для частного решения $\theta (x) = \theta (x,m,B)$ ЗК на бесконечности (2.40), (2.41) ряд (2.42)–(2.44) является асимптотическим разложением при больших $x$.

После подстановки разности $w(x) = \widetilde Z(x) - \theta (x)$ в (2.40), (2.41) получается сингулярная нелинейная ЗК на бесконечности для $w(x)$:

Оставляя только главные члены в ОДУ (2.45) для $w(x)$ с коэффициентами, стремящимися к нулю не быстрее, чем $1{\text{/}}x$ при $x \to \infty $, получаем линейное ОДУ: При $B > 0$ имеем представление $\tilde {w}(x) = P{\kern 1pt} {{x}^{{ - {{a}_{2}}}}}{\kern 1pt} \exp ( - {{a}_{1}}x)$ для однопараметрического семейства решений ОДУ (2.47), стремящихся к нулю при $x \to \infty $, где $P$ – произвольная постоянная,

Тогда из [9, разд. 23] следует

Утверждение 5. Для любых $m > 0$ и $B > 0$ сингулярная нелинейная ЗК (2.45), (2.46) с данными на бесконечности имеет однопараметрическое семейство решений $w(x) = w(x,B,m,P)$; эти решения представляются экспоненциальным параметрическим рядом Ляпунова

где ${{a}_{1}}$ и ${{a}_{2}}$ определены в (2.48), $P$ – параметр, а функции ${{C}_{k}}(x)$ $(k = 2,\;3,\; \ldots )$ имеют при больших $x > 0$ порядок роста не выше степенного.

Суммируя приведенные утверждения и принимая во внимания замены переменных, получаем следующее

Утверждение 6. Для любого $m > 0$ нелинейное ОДУ (2.7) имеет двухпараметрическое семейство решений ${{f}_{m}}(\Phi ,B,D)$, которое при больших положительных $\Phi $ представимо в виде

где $B$ и $D$ – параметры, $B > 0$, ${{\varkappa }_{1}} = - (3{{m}^{2}} + 4m - 5){\text{/}}[m(m + 1)]$, а $\theta (x,m,B)$ определено в утверждении $4$.

Замечания для случая II. В этом случае точное решение при $m > 0$ $f = - {{\Phi }^{2}}(m + 1){\text{/}}(6m)$ не соответствует никакому глобальному решению, а ЗК на бесконечности (2.34), (2.35) принимает вид (см. замечание 3)

2.4. Основной результат для случая $m{\kern 1pt} :\;{\kern 1pt} 1{\text{/}}2 < m < \infty $

В указанном случае решение сингулярной нелинейной ЗК (2.7), (2.8) существует глобально и положительно на $( - a,\infty )$ (см. теорему 4). Следовательно, представление (2.49) имеет место для больших $\Phi $ и некоторых значений $B > 0$ и $D$.

Далее, пусть $\Phi (\tau )$ – решение сингулярной нелинейной НКЗ (1.1)–(1.4) для некоторых $b > 0$ и $m{\kern 1pt} :\;{\kern 1pt} 1{\text{/}}2 < m < \infty $ (см. теорему 3). Тогда решение $f(\Phi )$ сингулярной начальной задачи (2.7), (2.8) должно удовлетворять условию (2.9), т.е. в (2.49) имеем $B = m{{b}^{{1/m}}}$.

Теорема 5. Пусть функция ${{f}_{m}}(\Phi ) = {{f}_{m}}(\Phi (\tau ))$ при заданном $m{\kern 1pt} :\;{\kern 1pt} 1{\text{/}}2 < m < \infty $, является решением сингулярной нелинейной ЗК (2.7), (2.8) вдоль траектории $\Phi (\tau ) = \Phi (\tau ,b)$, отвечающей решению сингулярной НКЗ (1.1)–(1.4) для фиксированного $b > 0$. Тогда

(i) ${{f}_{m}}(\Phi )$ удовлетворяет ограничениям

(ii) для конечных $\Phi $ представление решения ${{f}_{m}}(\Phi )$ дается теоремой $4$;

(iii) при больших положительных $\Phi $ для решения ${{f}_{m}}(\Phi )$ справедливо представление (2.49), где $B = m{{b}^{{1/m}}}$, а $D$ – параметр.

Учитывая соотношения

и формулы (2.42)–(2.44), из теоремы 5 приближенно получаем где ${{\varkappa }_{2}} = - (2{{m}^{2}} + 4m - 4){\text{/}}[m(m + 1)]$, $D = {\text{const}}$ (ср. с укороченной формулой (2.5), в которой опущено экспоненциально убывающее слагаемое, хотя в [2] оно присутствует, см. там формулу (1.10), и совпадает с формулой (2.50)).

На фиг. 3 представлены графики решений сингулярной нелинейной ЗК (2.7), (2.8) в предположениях теоремы 5.

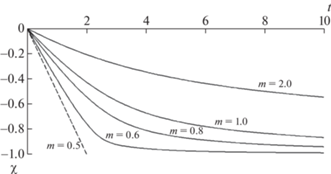
2.5. Замечания к случаю $m{\kern 1pt} :\;0 < m < 1{\text{/}}2$

В этом случае решение ${{f}_{m}}(\Phi )$ сингулярной нелинейной ЗК (2.7), (2.8) может менять знак в некоторой конечной точке $\Phi = {{\Phi }_{{{\text{z}}ero}}}$. Тогда в окрестности этой точки будет

где ${{C}_{z}}$ – константа. Следовательно, $\Phi = {{\Phi }_{{{\text{zero}}}}}$ является точкой ветвления, и решение становится многозначной функцией.

Графики решений ${{f}_{m}}(\Phi )$ сингулярной нелинейной ЗК (2.7), (2.8) для этого случая представлены на фиг. 4.