Журнал вычислительной математики и математической физики, 2023, T. 63, № 3, стр. 424-435

В работе [1] построено точное решение задачи обтекания цилиндра около плоскости с циркуляцией, определенной из минимаксного принципа Гольдштика (см. [2]). Решение выражено через тета-функции. Проведенное в указанной работе сопоставление с экспериментальными данными и численными расчетами (см. [3], [4]) показало, что даже без учета отрывной зоны распределение давления на цилиндре и плоскости, найденное из интеграла Бернулли, качественно согласуется с экспериментальными данными (см. [3]). В этой же работе дана подробная библиография различных аналитических решений, представленных в монографиях [5], [6] и журналах [7–13]. В них описаны решения для частных случаев, выраженные через аналитические функции, либо представленные рядами, и часто плохо сходящимися.

В настоящей работе рассмотрены две численные схемы метода граничных элементов для решения плоской задачи обтекания контура – около прямолинейной и криволинейной границ. Циркуляция вычисляется из минимаксного принципа Гольдштика. Точность численных схем демонстрируется на сравнении их друг с другом и с точными решениями. Из анализа экспериментальных данных и расчетов турбулентного обтекания кругового цилиндра около различных прямолинейных и криволинейных донных поверхностей делается вывод о геометрии отрывной зоны за цилиндром. Напряжение на донной поверхности предлагается определять с помощью численного решения методом граничных элементов задачи обтекания контура, включающего цилиндр и отрывную зону. Такой способ расчета на несколько порядков сокращает время расчета гидродинамической задачи в сравнении с $k$–$\omega $ моделью.

1. Общая постановка задачи потенциального обтекания цилиндра около произвольной донной поверхности. Для удобства построения численной схемы рассматривается приближение задачи об обтекании цилиндра произвольного сечения около донной поверхности потенциальным потоком жидкости. Суть приближения заключается в том, что поле скорости течения полагается периодическим по оси $x$ с периодом $L$, который много больше размера обтекаемого контура (фиг. 1). Скорость натекающего потока $U$ для простоты полагается равной единице. Это не ограничивает общность постановки задачи в силу ее линейности по параметру $U$. Формы обтекаемого контура и одного периода дна заданы (в декартовых координатах). Тогда задачу можно свести к рассмотрению области $\Omega $, заключенной между поверхностью дна ${{S}_{w}}$, контуром обтекаемого тела ${{S}_{b}}$ и парой вертикальных прямых $x = - L{\text{/}}2$ и $x = L{\text{/}}2$. Для описания течения будем использовать функцию потенциала $\Phi $. Так как класс изучаемых в работе течений имеет отличные от нуля циркуляции вдоль ${{S}_{w}}$ и ${{S}_{b}}$, для построения численного алгоритма необходимо уметь учитывать многозначность $\Phi $. Для этого будем представлять искомый потенциал течения, обтекающего ${{S}_{w}}$ и ${{S}_{b}}$, в виде суммы циркуляционной и бесциркуляционной, но однозначно заданной частей:

Функция ${{\Phi }_{{x + \Gamma }}}$ – это явно заданная функция, которая определяется как вещественная часть следующего комплексного потенциала: Здесь ${{z}_{b}}$ и ${{z}_{w}}$ относятся к двум произвольно заданным точкам внутри цилиндра и под поверхностью дна соответственно, а $\lambda : = 2\pi {\text{/}}L$. Введенный таким образом потенциал определяет течение, для которого где обход дна выполняется в направлении от $x = - L{\text{/}}2$ к $L{\text{/}}2$, а обход тела – по часовой стрелке. Циркуляция $\Gamma $ подлежит определению в соответствии с принципом Гольдштика (этот вопрос будет рассмотрен в следующих разделах). Кроме того, введенный потенциал за счет линейной части учитывает асимптотику течения на бесконечности. Указанные свойства ${{\Phi }_{{x + \Gamma }}}$ позволяют сформулировать для остаточной части $\tilde {\Phi }$, как для однозначной в $\Omega $ функции, следующую краевую задачу: Здесь направления обхода контуров определены аналогично случаю выше, а $n$ – нормаль, внешняя по отношению к жидкости.

В силу гармоничности рассматриваемых функций, поиск решения задачи сводится к нахождению значений $\tilde {\Phi }$ на границах ${{S}_{w}}$ и ${{S}_{b}}$, с помощью которых могут быть определены соответствующие граничные скорости:

Значений $V$, в свою очередь, достаточно для построения картины линий тока и эпюр давления на границах.

Наконец, для нахождения значений $\tilde {\Phi }$ на контурах ${{S}_{w}}$ и ${{S}_{b}}$ при заданной циркуляции $\Gamma $ воспользуемся следующим интегральным уравнением, вытекающим из постановки краевой задачи:

Отметим, что в [14] рассматривалось поле напряженности двух заряженных электрических проводников. При отсутствии скорости натекающего потока задача в настоящей работе была бы эквивалентом задачи для электрического потенциала из [14]. Как следствие, при отсутствии скорости потока на бесконечности можно было бы проследить связь между интегральным уравнением (1.2) и уравнениями из [14].

2. Численная схема задачи потенциального обтекания цилиндра около донной поверхности. Для аппроксимации интегрального уравнения системой линейных уравнений вводятся параметризации ${{\zeta }_{w}},{{\zeta }_{b}} \in [0,{\kern 1pt} 1]$ для границ ${{S}_{w}}$ и ${{S}_{b}}$ соответственно. На указанных отрезках вводятся равномерные сетки из ${{N}_{w}}$ и ${{N}_{b}}$ точек. Пусть отображение координат по ${{\zeta }_{w}}$ и ${{\zeta }_{b}}$ в пространственные координаты удовлетворяет следующим тождествам:

Здесь ${{L}_{q}}$ обозначают длины соответствующих границ, а ${{\sigma }_{q}}$ – заданные положительные функции, с помощью которых можно управлять распределением точек сетки вдоль границы. Пространственные координаты точек сетки обозначим как $M_{w}^{i}(x_{w}^{i},y_{w}^{i}),$ $i = \overline {1,{{N}_{w}}} $, и $M_{b}^{i}(x_{b}^{i},y_{b}^{i}),$ $i = \overline {1,{{N}_{b}}} $. В общем виде аппроксимация системой линейных уравнений записывается как Вектор неизвестных состоит из ${{N}_{w}} + {{N}_{b}}$ неизвестных Матрица $M$ выражается в виде $M = B - \pi I$, где $I$ обозначает единичную матрицу, а $B$ – аппроксимация оператора двойного слоя. Так как у подынтегральной функции имеется особенность при $M = M{\kern 1pt} '$, при построении численного алгоритма ее необходимо учесть. Пользуясь тем, что устраним особенность под интегралом, преобразовав оператор двойного слоя к виду Как следует из [15], для преобразованного оператора достаточно квадратурной формулы трапеций, чтобы учесть запас гладкости, получаемой под знаком интеграла функции. Поэтому аппроксимация оператора имеет вид Для вычисления правой части системы линейных уравнений необходимо построить аппроксимацию интегрального оператора простого слоя, имеющего логарифмическую особенность. В [15] для этого была предложена квадратурная формула с экспоненциальным порядком аппроксимации. В предположениях настоящей работы формула принимает вид где матрица ${{A}^{{ij}}}$ состоит из четырех подблоков: Здесь

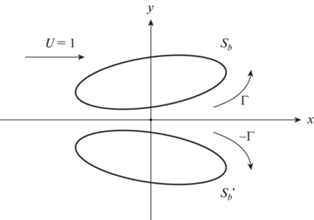
3. Случай прямолинейного дна. В частном случае ${{y}_{w}} = 0$ задача обтекания контура ${{S}_{b}}$ эквивалентна обтеканию пары контуров ${{S}_{b}}$ и $S_{b}^{'}$, расположенных симметрично относительно оси $x$ (фиг. 2). Независимое рассмотрение этого случая важно тем, что введение искусственного периода $L$ и сопутствующей ему погрешности не требуется. В этом случае краевая задача будет иметь иной вид. Зафиксируем внешнее по отношению к жидкости направление нормали и направление обхода контуров по часовой стрелке. Функцию потенциала течения будем искать в виде

где ${{\Phi }_{\Gamma }}$ – вещественная часть комплексного потенциала Здесь ${{z}_{b}}$ и $z_{b}^{'}$ – фиксированные точки внутри ${{S}_{b}}$ и $S_{b}^{'}$ соответственно. Краевую задачу для $\tilde {\Phi }$ в этом случае можно записать в виде Соответствующее интегральное уравнение приобретает вид Задача обтекания пары симметрично расположенных контуров является частным случаем задачи обтекания произвольных контуров ${{S}_{1}}$ и ${{S}_{2}}$. Вывод соответствующего интегрального уравнения приведен в Приложении. Система линейных уравнений, аппроксимирующая систему (3.1), строится аналогично системе п. 2.

4. Численное определение циркуляции из минимаксного принципа. Покажем, что для достаточно широкого класса областей процесс поиска циркуляции, удовлетворяющей минимаксному принципу Гольдштика, можно упростить.

Известно, что скорость на поверхности обтекаемого контура направлена по касательной. Направление касательной выберем по направлению обхода контура. Положение точки на контуре задается натуральным параметром $s$. Тогда проекцию скорости на вектор касательной можно выразить как функцию $V(s)$. Она будет положительна, если направление вектора скорости совпадает с направлением касательной, и отрицательна в противном случае.

Покажем, что при выполнении определенных требований к форме области искомая циркуляция ${{\Gamma }_{G}}$ может быть найдена как циркуляция, при которой сумма максимума и минимума $V(s)$ на контуре равна нулю. В частном случае кругового цилиндра над плоскостью это утверждение верно. Для этого достаточно показать, что при любом малом изменении циркуляции увеличится $\max {\text{|}}V(s){\kern 1pt} {\text{|}}$. Действительно, в силу линейности при изменении циркуляции по Гольдштику на величину $\Delta \Gamma $ скорость изменится на величину $\Delta \Gamma \;{{V}_{0}}(s)$, где ${{V}_{0}}(s)$ – скорость обтекания чисто циркуляционного течения с единичной циркуляцией. Это известная функция, значения которой во всех точках контура имеют один и тот же знак (т.е. на границе круга нет критических точек). Следовательно, при сдвиге на $\Delta \Gamma $ либо увеличится максимум $V(s)$, либо уменьшится минимум. В обоих случаях увеличится максимальное абсолютное значение скорости $\max {\text{|}}V(s){\kern 1pt} {\text{|}}$, что и требовалось доказать.

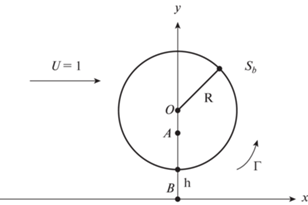
Обобщим рассмотренный случай: критических точек скорости ${{V}_{0}}(s)$ на контуре также не будет, если существует конформное отображение области течения жидкости на область, изображенную на фиг. 3, т.е. на область из задачи обтекания кругового цилиндра над плоскостью. Если указанное конформное отображение существует, поиск циркуляции можно свести к решению уравнения $\delta V: = \max V(s) + \min V(s) = 0$. Пример зависимости $\delta V$ от $\Gamma $ для задачи обтекания кругового цилиндра около плоскости при $h = 0.2$ изображен на фиг. 4.

5. Сравнение численных результатов с точным решением для обтекания кругового цилиндра около плоскости. Задача обтекания кругового цилиндра над плоскостью имеет аналитическое решение [1], что позволяет использовать ее для тестирования численных схем. Для простоты положим скорость натекащего потока и радиус цилиндра равными единице. Тогда комплексный потенциал $W(z)$ и величина циркуляции для минимаксного принципа Гольдштика из [1] в обозначениях настоящей работы принимают вид

где ${{\vartheta }_{i}}$ используются для обозначения тэта-функций.

Оценить точность расчетов по численной схеме для симметричного обтекания тел позволяют табл. 1 и 2. В первой таблице приведены точные значения циркуляции ${{\Gamma }_{G}}$, найденные из минимаксного принципа Гольдштика (5.1), которые для разных значений $h$ сравниваются с численными значениями ${{\Gamma }_{{16}}}$, ${{\Gamma }_{{24}}}$ и ${{\Gamma }_{{32}}}$, найденными с разным числом точек для сетки на контуре: $16$, $24$ и $32$ точки сетки соответственно. Для повышения эффективности точки распределялись вдоль границ неравномерно, со сгущением в области сближения контуров:

где $C$ полагалось равным $ - 0.7$ (параметру $\zeta = 0$ ставилась в соответствие крайняя нижняя точка окружности).

Значения касательных скоростей $V$ в точках сеток на ${{S}_{b}}$ и $S_{b}^{'}$, получаемые из решения системы уравнений, аппроксимирующей (3.1), позволяют численно восстановить значение функции тока во внутренних точках течения. Для этого используется следующая интегральная формула:

Соответствующая аппроксимация имеет вид Для упрощения вида формулы можно учесть симметрию между ${{S}_{b}}$ и $S_{b}^{'}$. При использовании формулы (5.2) не следует выбирать точки $M$, расстояние от которых до точек сетки меньше расстояния между самими точками сетки, так как погрешность аппроксимации в этих случаях будет выше. В целом же скорость убывания погрешности аппроксимации по формуле (5.2) имеет экспоненциальный характер (обоснование этого утверждения приведено в [15]). В табл. 2 продемонстрированы абсолютные значения невязки ${{\Delta }_{{{{x}_{0}},K}}}: = {{\max }_{{i = \overline {1,K} }}}\left| {\overline \Psi ({{x}_{0}},i{\text{/}}K) - \Psi ({{x}_{0}},i{\text{/}}K)} \right|$, наблюдавшиеся при ${{x}_{0}} = - 2$, $K = 100$ и различных $h$.

Решение (5.1) также позволяет тестировать и численную схему для расчета обтекания над дном произвольной формы на основе аппроксимации периодической решеткой профилей. В этом варианте возникает дополнительная погрешность, связанная с выбором периода $L$. В табл. 3 приведены невязки $\Delta $ при вычислении скорости в точках сетки на поверхности дна в зависимости от $L$ (метод распределения точек сетки вдоль границ аналогичен предыдущему тесту). Во всех расчетах для аппроксимации границы тела использовалось ${{N}_{b}} = 36$ точек сетки, а количество точек сетки для аппроксимации дна ${{N}_{w}}$ изменялось пропорционально $L$ для того, чтобы обеспечить постоянство шага сетки. Расчеты показали, что размер погрешности в данном случае оказывается обратно пропорционален квадрату $L$. Следует отметить, что полученный результат вполне объясним. Рассмотрим для примера комплексный потенциал обтекания единичного круга безграничным потоком жидкости:

Ему соответствует следующая сопряженная комплексная скорость: Если бы слева и справа от круга на расстоянии $L$ находились еще два единичных круга, комплексные скорости на их поверхности можно было бы грубо приблизить как ${{v}_{0}}(z \pm L)$. Отсюда их влияние, например, на скорость в верхней точке центрального цилиндра можно было бы оценить через величину ${{v}_{0}}(i + L) + {{v}_{0}}(i - L)$. Если мы вычислим главный член асимптотики этого выражения по $L$, то получим величину т.е. размер погрешности рассматриваемого приближения задачи действительно обратно пропорционален квадрату $L$.

6. Тестирование на задаче обтекания эллипса над неровным дном. Для получения примеров точных решений задач обтекания тел над неровным дном хорошо подходит метод конформных отображений. Получим с его помощью пример (бесциркуляционного) обтекания эллипса. Для этого введем вспомогательную комплексную плоскость по параметру $Z$, в которой рассмотрим круг единичного радиуса ${\text{|}}Z{\kern 1pt} {\text{|}} = 1$. Комплексный потенциал обтекания круга задается функцией

Конформно отобразим внешность круга на физическую плоскость $z$ с помощью функции При этом обтеканию круга ${\text{|}}Z{\kern 1pt} {\text{|}} = 1$ в плоскости $z$ будет соответствовать обтекание эллипса с полуосями $1 - K$ и $1 + K$. В качестве криволинейного дна зафиксируем линию тока $\operatorname{Im} W \equiv - 1$. Таким образом, мы определили расчетную область для тестирования соответствующей численной схемы. Форма этой области при $K = 0.4$ изображена на фиг. 5. Точками на фигуре отмечена сетка, на которой выполнялось тестирование схемы. При значениях параметров ${{N}_{w}} = 32$, ${{N}_{b}} = 18$ и $L = 60$ было получено, что погрешность вычислений скорости на дне по абсолютной величине не превышает $0.005$. Также было повторно проверено, что при увеличении $L$ главный член погрешности убывает обратно пропорционально ${{L}^{2}}$.

7. Сравнение численной схемы обтекания круга около плоского дна с экспериментом. Выбор циркуляции по постулату Гольдштика приводит к обтеканию кругового цилиндра, при котором распределение скорости на круговом цилиндре и плоскости качественно согласуется с экспериментом, приведенном в [3]. Однако расчетные значения максимальных скоростей на границах за счет вязкости жидкости оказываются примерно в полтора раза меньше скоростей, получаемых по модели идеальной жидкости. Этим объясняется визуальное отличие эпюр коэффициента давления ${{C}_{p}}$, приведенных на фиг. 6а и 6б. Достичь большего согласия численных расчетов с экспериментом можно, если нарастить круг с обратной стороны, добавив к нему застойную зону, возникающую при натекании реального потока жидкости на тело. Подбор формы тела с учетом застойной зоны по экспериментальным данным из [3] при значениях $h$, близких к $0.2$, продемонстрирован на фиг. 7. Точками отмечены узлы сетки, использовавшиеся для аппроксимации границы тела с учетом застойной зоны в численном алгоритме. Для аппроксимации границы всего тела оказалось достаточно сетки всего лишь из N-точек. Сплошные линии на фиг. 7 соответствуют линиям тока численного решения; они качественно согласуются с экспериментом. При таком подходе эпюра коэффициента давления ${{C}_{p}}$ приобретает вид фиг. 6в, значительно более близкий к данным эксперимента.

При этом для остальных значений $h$ минимум коэффициента давления под цилиндром меняется в небольших пределах. Это следует из малого изменения максимальной скорости, которая приведена в [1].

8. Численный расчет обтекания цилиндра над криволинейным дном. В задачах с криволинейным дном использование численной схемы обтекания двух симметричных контуров становится невозможным. Вместо нее используется схема, построенная на основе системы интегральных уравнений (1.2). Особенности ее применения в точности повторяют особенности, возникающие при использовании предыдущей схемы. Для повышения точности расчетов сетку следует сгущать в местах сближения границ, а также на участках большей кривизны. Для большего согласия с экспериментом при расчете также следует учитывать застойную зону, возникающую за телом. Пример качественного сравнения с результатами [16] изображен на фиг. 8. Преимуществом использования метода граничных элементов в данном случае является то, что для аппроксимации границ ${{S}_{b}}$ и ${{S}_{w}}$ требовалось всего 36 и 64 точки соответственно. Период $L$ полагался равным 40.

9. Выводы. Как видно из сравнения с экспериментом и численными расчетами, распределение давления на цилиндрической и донной поверхностях, определяемые предложенным методом, согласуются с достаточной точностью. Главный член погрешности (первой численной схемы) определяется искусственно введенным периодом $L$ как величина порядка c/L². Поскольку для расчетов достаточно использовать всего порядка сотни граничных элементов, метод позволяет практически мгновенно вычислять давление на поверхностях, а также строить картину линий тока на обычном компьютере. При обтекании кругового цилиндра его следует наращивать отрывной зоной. Тогда давление согласуется с экспериментом не только в области перед цилиндром, но и позади него. Форма отрывных зон зависит от расстояния цилиндра от дна и слабо зависит от формы донной поверхности. Поэтому эти закономерности можно проследить на имеющихся экспериментах и численных расчетах обтекания цилиндра над ровной поверхностью. Быстрота расчета и относительная простота численных схем являются важным преимуществом перед традиционными методами конечных элементов и использования $k{\kern 1pt} - {\kern 1pt} \omega $ моделей. К тому же в $k{\kern 1pt} - {\kern 1pt} \omega $ модель входят подгоночные параметры, значения которых часто не совсем ясны (см. [16]). Определение скорости под цилиндром важно также и для прогнозирования размыва дна под цилиндром, используя теорию русловых процессов. Потребность в таких расчетах связана со строительством трубопроводов на дне рек.

ПРИЛОЖЕНИЕ

Задача симметричного обтекания двух тел является частным случаем задачи обтекания двух произвольных тел с границами ${{S}_{1}}$ и ${{S}_{2}}$. Как уже упоминалось в основном тексте, вещественный потенциал рассматриваемого течения является многозначной функцией и выражается в виде суммы многозначной циркуляционной части ${{\Phi }_{\Gamma }}$ и однозначной бесциркуляционной части $\tilde {\Phi }$. Продемонстрируем вывод интегральных тождеств, которым удовлетворяет бесциркуляционная часть, из соответствующей краевой задачи. Для этого обозначим через $S$ объединение ${{S}_{1}}$ и ${{S}_{2}}$. Пусть $M$ – произвольная точка на $S$, для которой мы хотим сформулировать тождество. Вокруг $S$ построим окружность достаточно большого радиуса $R$ с центром в точке $M$ так, чтобы контуры ${{S}_{1}}$ и ${{S}_{2}}$ оказались внутри нее. Введем для окружности обозначение ${{C}_{R}}$. На ${{S}_{1}}$ и ${{S}_{2}}$ зафиксируем внешнее направление нормали по отношению к жидкости (т.е. нормали направлены внутрь контуров), а на ${{C}_{R}}$ зафиксируем внешнее направление по отношению к окружности. Тогда из гармоничности функции $\tilde {\Phi }$ в области, которая снаружи ограничена контуром ${{C}_{R}}$, а изнутри контурами ${{S}_{1}}$ и ${{S}_{2}}$, следует тождество

При условии, что на бесконечности скорость натекающего потока должна быть горизонтальна и равна единице, общий вид асимптотики функции $\tilde {\Phi }$ на ${{C}_{R}}$ при $R \to \infty $ будет иметь вид С ее помощью интеграл $J$ вычисляется явно. Интегрирование члена $O(1{\text{/}}R)$ в пределе при $R \to \infty $ дает нуль. Для главных членов асимптотики с помощью подстановок $x(s{\kern 1pt} '{\kern 1pt} ) = x(M) + R\cos \theta $, $ds{\kern 1pt} ' = Rd\theta $, $\partial {\text{/}}\partial n{\kern 1pt} ' = \partial {\text{/}}\partial R$ получаем С учетом этого равенства тождество (П.1) принимает вид Далее учтем условие непротекания на границе $S$: Отсюда имеем Наконец, потенциал определяется с точностью до константы, поэтому можно положить $C = 0$.