1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 63, № 3, 2023

Журнал вычислительной математики и математической физики, 2023, T. 63, № 3, стр. 436-448

Влияние интенсивности ударной волны на развитие неустойчивости на шероховатых контактных границах трехслойной газовой системы

В. В. Змушко 1, *, А. Н. Разин 1, **, А. А. Синельникова 1, ***, А. Н. Щербаков 1, ****

1 ФГУП “РФЯЦ – ВНИИЭФ”
607188 Нижегородская обл., Саров, пр-т Мира, 37, Россия

* E-mail: VVZmushko@vniief.ru
** E-mail: ANRazin@vniief.ru
*** E-mail: AnASinelnikova@vniief.ru
**** E-mail: ANScherbakov@vniief.ru

Поступила в редакцию 23.04.2022
После доработки 09.10.2022
Принята к публикации 14.11.2022

Полный текст (PDF)

Аннотация

Изучается влияние интенсивности ударной волны, прошедшей через шероховатые контактные границы, на развитие неустойчивости в трехслойной газовой системе при числах Маха М = 1.3 и М = 3. Трехслойная система сформирована с помощью постановки по сечению ударной трубы двух тонких пленок (контактных границ). Между контактными границами (в центральном слое системы) находится тяжелый газ (элегаз), а пространство слева и справа от центрального слоя заполнено воздухом. Начальная шероховатость контактных границ задается двухмодовым синусоидальным возмущением. Расчеты проведены по методике М-ИМОЗА с использованием ILES (implicit large eddy simulation) стратегии моделирования путем интегрирования уравнений Эйлера на разностной сетке с квадратными ячейками. Полученные результаты сопоставляются между собой, а при М = 1.3 и с опытными данными. Библ. 30. Фиг. 11.

Ключевые слова: газовая слойка, контактные границы, ударные волны, неустойчивость, турбулентное перемешивание, математическое моделирование.

ВВЕДЕНИЕ

Неустойчивость и турбулентное перемешивание (ТП), развивающиеся на контактных границах (КГ) слоистых систем после прохождения ударной волны (УВ), могут оказывать значительное влияние на характеристики изучаемого течения и поэтому должны быть учтены при разработке ряда устройств, например, при создании устройств, предназначенных для получения высоких концентраций энергии.

Существует ряд методологий (стратегий) и более десятка физических моделей для расчета развития неустойчивости и ТП, возникающих на шероховатых КГ слоек после прохождения УВ. Наличие большого числа методологий указывает на слабую разработанность данной темы. При этом отсутствие необходимого набора экспериментальной информации (например, по взаимодействию ударной волны с пульсациями газодинамических величин и вихрями); наличие нерешенных вопросов в используемых численных методиках (например, отсутствие сходимости решения на фронте скачка при разностном решении уравнений Эйлера, наличие диссипативных и дисперсионных погрешностей разностных схем, понижающих точность моделирования и т.п.) препятствуют получению решения с заданной точностью и не способствуют глубокому пониманию физики перемешивания.

В настоящее время в ВНИИЭФ используются, в основном, две стратегии численного моделирования развития неустойчивости. Первая стратегия – RANS (Reynolds-averaged Navier-Stokes) моделирование задачи с привлечением уравнений газовой динамики (расчет осредненного течения) и полуэмпирических моделей турбулентности (расчет пульсационных характеристик течения). В качестве полуэмпирических моделей используются три модели: Никифорова, Никифорова–Козлова и К-ε модель (см. [1]). Инициализация ТП в численных расчетах с использованием RANS стратегии требует: 1) по заданной начальной шероховатости КГ рассчитать эволюцию начального возмущения (рост амплитуды пузырей и струй), 2) на основе какого-либо критерия оценить момент перехода от этапа развития неустойчивости к ТП, 3) на момент перехода определить ширину зоны перемешивания и задать в ней начальные данные для решения уравнений ТП (например, для К-ε модели кинетическую энергию турбулентности и скорость диссипации). Такие данные должны быть рассчитаны на основе информации, полученной на этапе расчета развития неустойчивости. На сегодняшний день выбор критерия перехода к ТП и построение алгоритма формирования начальных данных для уравнений ТП остаются фундаментальными проблемами численного моделирования.

Изучению возможностей RANS стратегии моделирования посвящено довольно много работ. В частности, в [2] исследовалась зависимость скорости роста амплитуды возмущений от формы начальной шероховатости КГ. Влиянию размерности начального возмущения (2D или 3D) на переход к ТП, выбору момента времени подключения уравнений ТП к расчету и построению начальных данных для решения уравнений ТП посвящены работы [3–6]. Из других вопросов, возникающих при численном моделировании течений после прохождения УВ через КГ, отметим вопросы сходимости решения на последовательности измельчающихся сеток, наличие паразитных осцилляций газодинамических величин на скошенных сетках с вытянутыми ячейками, деформацию фронта ударной волны при ее взаимодействии с пульсациями газодинамических величин и крупными вихрями и т.п. (см. [6–8]). RANS стратегия моделирования задач с присущими ей проблемами довольно подробно описана в [6].

Во второй стратегии моделирования (ILES – implicit large eddy simulation, см. [9]) отсутствует проблема инициализации перемешивания, что делает ее применение при расчете некоторых задач вполне привлекательной. По сравнению с прямым численным моделированием (DNS – direct numerical simulation) течений и LES (large eddy simulation) моделированием методология ILES также имеет ряд преимуществ. Методология DNS дает удовлетворительные результаты для простых геометрий и лишь при умеренных числах Рейнольдса, но не способна на современных вычислительных системах с необходимой точностью описать мелкомасштабную турбулентность (вязкую диссипацию энергии). В методологии ILES нет явного фильтрования уравнений, что позволяет избежать некоторых трудностей, присущих методам LES (см. [9]). Дополнительным достоинством методологии ILES является простота ее реализации в программных комплексах. Наконец, отметим ситуацию, в которой методология ILES является чрезвычайно полезной. При падении УВ на контактную границу сложной формы (например, состоящую из нескольких участков с различными наклонами) расчет этапа развития неустойчивости и построение начальных данных для решения уравнений ТП в методологии RANS вызывает затруднения.

При постановке расчета с использованием стратегий ILES или RANS, как правило, возникает ряд вопросов, которые до сих пор не имеют законченного решения. Одним из таких вопросов является проблема задания начальной шероховатости границы для инициализации развития неустойчивости на КГ разноплотных газов. Особенно остро эта проблема проявляется при моделировании лабораторных опытов, в которых контактная граница формируется с помощью установки в трубе тонкой пленки, разделяющей газы до начала проведения опыта. После разрыва пленки на кусочки различных размеров в окрестности КГ формируется спектр начальных возмущений, зависящий от свойств пленки, описать который в расчетах не представляется возможным. К настоящему времени чувствительность результатов моделирования задачи к заданию начальной шероховатости границы хорошо известна и является темой многих экспериментальных, численных и теоретических исследований (см., например, [10–21]). В [10], [11] при моделировании лабораторных опытов, поставленных в Институте физики взрыва (ИФВ) по заданию Института теоретической и математической физики (ИТМФ) РФЯЦ-ВНИИЭФ, продемонстрировано, что без задания начальной шероховатости КГ в расчетах не удается получить согласованное с экспериментом развитие неустойчивости и ТП. В [12] при моделировании вихря Тейлора–Грина продемонстрировано влияние размера ячейки разностной сетки на время перехода от этапа развития неустойчивости к ТП для безударных течений.

Таким образом, наличие нерешенных вопросов в используемых стратегиях моделирования турбулентного перемешивания побуждает специалистов заниматься совершенствованием расчетных методик и отработкой технологии счета. Ниже приведены данные расчетного исследования формирования поля течения под действием ударной волны, проходящей по трехслойной газовой системе, в которой первая КГ имеет вид наклонной ступеньки, а вторая КГ расположена поперек ударной трубы. Выполнено две серии расчетов для чисел Маха ударной волны М = 1.3 и М = 3. Результаты расчетов, полученных при М = 1.3, сопоставляются с экспериментальной информацией, полученной в ИФВ (см. [22]). Опытные данные для М = 3 на сегодня отсутствуют, так как используемая для проведения экспериментов ударная труба не рассчитана на большие нагрузки.

1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДЛЯ ОПИСАНИЯ ТЕЧЕНИЯ

Математическое моделирование лабораторных опытов выполнялось в 2D постановке по методике МИМОЗА с использованием уравнений Эйлера без привлечения каких-либо моделей учета ТП (ILES моделирование). Расчетная методика основана на лагранжево-эйлеровой стратегии и выделении веществ концентрациями (подробности см. в [23–26]). Такой подход является эффективным при моделировании задач механики сплошной среды с большими деформациями.

Расчет счетного шага состоит из двух этапов: на первом этапе выполняется интегрирование уравнений Эйлера и уравнения переноса концентраций, записанных в лагранжевых координатах

$\frac{{dU}}{{dt}} = - \frac{1}{\rho }{\text{grad}}\left( {P + q} \right),\quad \frac{{dz}}{{dt}} = U,\quad \frac{{d\rho }}{{dt}} = - \rho \operatorname{div} U,$
$\frac{{d\varepsilon }}{{dt}} = - \frac{{P + q}}{\rho }\operatorname{div} U,\quad \frac{{d\left( {\rho {{c}_{k}}} \right)}}{{dt}} = - \operatorname{div} \left( {\rho U{{c}_{k}}} \right),\quad P = P\left( {\rho ,\varepsilon } \right),$
где $z = \left( {x,y} \right)$ – пространственные координаты, t – время, $U = \left( {u,{v}} \right)$ – компоненты скорости, ρ – плотность, ε – удельная внутренняя энергия, q – искусственная вязкость, ${{c}_{{{\kern 1pt} k}}}$ – объемная концентрация вещества k, P – давление, определяемое из уравнения состояния (в представленных ниже расчетах используется уравнение состояния идеального газа). На лагранжевом этапе расчета границы ячеек сетки перемещаются со скоростью вещества, массы ячеек не изменяются. Интегрирование системы уравнений выполняется на разнесенной разностной сетке. Термодинамические параметры задачи относятся к центрам счетных ячеек, координаты и компоненты скорости – к узлам. Используется полностью консервативная разностная схема второго порядка точности (на гладких течениях) “предиктор-корректор”, аналогичная [26].

Для подавления паразитных осцилляций численного решения в окрестности больших градиентов газодинамических величин вводится искусственная вязкость, являющаяся суммой квадратичной и линейной вязкостей. В случае необходимости для устранения коротковолновых возмущений используется процедура сглаживания оператором четвертого порядка относительно нормальных к линии сетки компонент скорости $U_{n}^{{{\text{сгл}}}} = U_{n}^{{}}\left[ {1 - {{{\left( {\alpha L} \right)}}^{2}}} \right]$. Разностная аппроксимация оператора L берется в виде

${{\left( {LU} \right)}_{m}} = \frac{2}{{{{M}_{m}}}}\left[ {{{M}_{{m + 1/2}}}\left( {{{U}_{{k + 1}}} - {{U}_{k}}} \right) - {{M}_{{m - 1/2}}}\left( {{{U}_{k}} - {{U}_{{k - 1}}}} \right)} \right],$
где ${{M}_{m}}$ – сумма плоских масс ячеек, имеющих данный узел своей вершиной, ${{M}_{{m + 1/2}}}$ – плоская масса ячейки с номером m, α – коэффициент сглаживания.

На втором этапе проводится построение новой разностной сетки и на ней выполняется пересчет полученных на лагранжевом этапе сеточных значений. Пересчет величин осуществляется с помощью алгоритма, основанного на расщеплении по координатным направлениям и использовании одномерного алгоритма повышенного порядка точности. Для повышения точности вычислений проводится реконструкция потоков на грани ячеек: кусочно-постоянное распределение величин в ячейках заменяется на кусочно-линейное. С целью предотвращения размытия контактных границ между веществами применяется алгоритм их выделения с помощью концентраций (подробности см. в [25]).

В смешанных ячейках (ячейках, содержащих несколько веществ) давление вычисляется покомпонентно, а затем усредняется с учетом объемных концентраций веществ.

Расчет многокомпонентной сплошной среды осуществляется посредством двух методов отслеживания КГ материалов: метода концентраций – Volume-of-Fluid (VoF) (см. [27]) и метода моментов концентраций – Moment-of-Fluid (MoF) (см. [28]). Особенностью метода VoF является зависимость алгоритма от объемных концентраций материала в соседних счетных ячейках. Эта информация используется для построения нормали к КГ. Поэтому реконструируемые границы в смежных многокомпонентных счетных ячейках являются зависимыми между собой, что приводит к размазыванию КГ с характерным размером удвоенного шага по сетке. Другая особенность методов VoF заключается в том, что при наличии в смешанной ячейке более двух компонентов результат реконструкции КГ зависит от порядка обработки веществ в алгоритме. Неудачный порядок обработки веществ может приводить к преждевременному переносу компонента в соседние ячейки, формируя, по сути, искусственное перемешивание веществ в расчете. Иногда оно проявляется в виде избыточного разбиения вещества на несвязанные фрагменты, размер которых меньше шага по сетке.

В методе Moment-of-Fluid, зная положение центра массы вещества и занимаемую им долю объема в ячейке, путем решения задачи минимизации определяется КГ вещества в виде прямой линии без привлечения данных из соседних счетных ячеек. Метод MoF имеет второй порядок точности, что позволяет точно реконструировать линейные КГ. Методам VoF второго порядка точности для точного восстановления линейной КГ материала требуется, чтобы КГ была линейной в кластере, состоящем из трех ячеек (см. [27], [29]). Именно поэтому теоретическое разрешение метода MoF позволяет восстанавливать детали границ раздела размером шага по сетке, что в пределах от двух до трех раз меньше, чем в методах VoF. Как уже упоминалось выше, в методах VoF также существует проблема зависимости конечного результата от порядка обработки веществ в смешанной ячейке. В алгоритме метода МoF этот вопрос решается комбинаторным способом, используя последовательный перебор всех возможных порядков обработки материалов, с выбором той последовательности, которая приводит к наименьшей ошибке при решении проблемы минимизации. Метод MoF позволяет точнее рассчитывать потоки объемов компонент на этапе адвекции и дольше удерживать целостность КГ материалов в процессе счета.

Ниже представлены результаты, полученные на сетке, состоящей из квадратных ячеек со стороной h = 0.04 см. Расчет каждой задачи выполнен с использованием алгоритмов VoF и MoF.

2. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Расчет течения при числе Маха М = 1.3 проходящей через контактные границы УВ проводился и ранее (см. [11]). При использованной в [11] начальной шероховатости контактных границ неустойчивость практически не развивалась. Полученные в расчетах данные в окрестности КГ заметно отличались от экспериментальной информации. Ниже представлены результаты расчетов с заданием шероховатости КГ в форме двухмодовых возмущений.

Схема постановки расчета приведена на фиг. 1. В начальный момент времени газы покоятся в трубе при атмосферном давлении и разделяются тонкими пленками для предотвращения взаимной диффузии перед проведением опыта. Первая пленка (КГ1) имеет два излома (в точках 2 и 3). Участки 1–2 и 3–4 расположены перпендикулярно стенкам трубы, участок 2–3 имеет наклон. Длина участков 1–2, 3–4, 4–5 составляет 6, 3 и 4.7 см соответственно.

Фиг. 1.

Схема постановки расчета, размеры в см.

Начальные параметры воздуха (Air): ρ0 = 0.0012 г/см3 – плотность, γ = 1.4 – показатель адиабаты, p0 = 0.0001 г/(см 10 мкс) – давление; параметры SF6: ρ0 = 0.0065 г/см3, γ = 1.094, p0 = = 0.0001 г/(см 10 мкс). Граничные условия: на стенках трубы ставятся условия скольжения потока, правый торец трубы – жесткая стенка. На левой границе задачи задаются газодинамические параметры, соответствующие величинам за фронтом УВ. Сформированная на левом торце трубы УВ движется направо, проходит контактные границы и на момент окончания расчета t = 750 мкс достигает правого торца трубы.

При падении УВ на контактные границы разделительные пленки разрушаются на фрагменты различных размеров, создавая спектр начальных возмущений, границы раздела газов ускоряются. Сформировавшийся спектр начальных возмущений зависит от разнотолщинности и свойств пленки, определить который не представляется возможным. Так как при проведении разных опытов для создания пленки используется лак одного состава, а масса лака, затрачиваемая на единицу площади пленки сохраняется, можно ожидать, что используемые в опытах пленки после разрыва формируют на КГ близкие начальные шероховатости (амплитуду и волновое число). В процессе проведения методических расчетов формирующиеся шероховатости были оценены путем сопоставления расчетных и экспериментальных данных по развитию неустойчивости. Отметим также, что визуальное сопоставление расчетных и опытных данных на сегодняшний день является единственно возможным путем проверки применимости методологии моделирования сложных задач с учетом ТП.

В результате взаимодействия УВ с КГ1 на участках 1–2 и 3–4 развивается неустойчивость Рихтмайера–Мешкова, на наклонном участке 2–3 развиваются неустойчивости Рихтмайера–Мешкова и Кельвина–Гельмгольца. После прохождения УВ через КГ1 фронт скачка деформируется (перестает быть плоским). Взаимодействие деформированного скачка, прошедшего КГ1, со второй контактной границей (КГ2) приводит к развитию на КГ2 неустойчивостей Рихтмайера–Мешкова и Кельвина–Гельмгольца. С течением времени на контактных границах (или отдельных частях КГ) формируются зоны перемешивания.

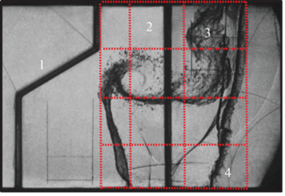
На фиг. 2 представлен фотокадр поля течения, полученный в эксперименте при М = 1.3 на момент времени t ≈ 750 мкс. За подробностями постановки экспериментов отсылаем к [11], [22]. На фиг. 2 нанесена реперная сетка, которая далее используется при сравнении расчетных данных между собой и с экспериментальной информацией.

Фиг. 2.

Фотокадр эксперимента и реперная сетка, t = 750 мкс, 1, 2 – рамки крепления контактных границ, 3, 4 – зоны перемешивания на контактных границах.

Рассматриваемая задача интересна по ряду причин. Во-первых, скорости роста возмущений уже на линейной стадии на отдельных участках первой контактной границы различны. Во-вторых, после отражения ударной волны от КГ2 на первую контактную границу приходит волна разрежения, которая усиливает развитие неустойчивости. Поскольку моделирование задачи заканчивается до момента отражения УВ от правого торца, развитие неустойчивости на КГ1 происходит при участии волны разрежения, а на КГ2 неустойчивость развивается по инерции.

Для сравнения численных результатов между собой рассчитываются зависимости от времени величины положительной и отрицательной завихренностей потока:

(1)
${{\omega }^{ + }}\left( t \right) = \int {\left( {\frac{{\partial u}}{{\partial y}} - \frac{{\partial v}}{{\partial x}}} \right)dxdy} > 0,\quad {{\omega }^{ - }}\left( t \right) = \int {{\kern 1pt} \left( {\frac{{\partial u}}{{\partial y}} - \frac{{\partial v}}{{\partial x}}} \right)dxdy} < 0.$
Интегрирование в (1) выполняется по всей области решения.

Отметим, что в выбранной стратегии моделирования задачи задание начальной шероховатости на КГ не вызывает затруднений в отличие от широко используемой исследователями RANS стратегии моделирования. Как отмечено ранее, в RANS стратегии моделирования помимо неопределенности в задании начальных возмущений на КГ возникают вопросы перехода от этапа развития неустойчивости к ТП. Для рассматриваемой задачи все отмеченные проблемы являются далеко не простыми.

Согласно импульсной модели Рихтмайера (см. [30]), амплитуда одномодовых начальных возмущений на линейной стадии растет по закону

(2)
$\frac{{da}}{{dt}} = {{k}_{0}}a_{0}^{ + }U{{A}^{ + }},\quad {{k}_{{{\kern 1pt} 0}}} = \frac{{2\pi }}{{{{\lambda }_{0}}}},$
где t – время, а – амплитуда возмущения, k – волновое число, λ – длина волны возмущения, U – скорость, которую приобретает КГ после прохождения УВ, $A = {{\left( {{{\rho }_{1}} - {{\rho }_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\rho }_{1}} - {{\rho }_{2}}} \right)} {\left( {{{\rho }_{1}} + {{\rho }_{2}}} \right)}}} \right. \kern-0em} {\left( {{{\rho }_{1}} + {{\rho }_{2}}} \right)}}$ – число Атвуда (ρ1, ρ2 – плотности слева и справа от КГ). Верхним индексом (+) обозначены величины, получающиеся после прохождения УВ через контактную границу. Так как УВ пересекает контактную границу со стороны легкого вещества, то $a_{0}^{ + } = a_{0}^{ - }\left( {1 - {U \mathord{\left/ {\vphantom {U D}} \right. \kern-0em} D}} \right)$, где $a_{0}^{ - }$ – начальная амплитуда возмущений (до прихода УВ на КГ), D – скорость падающей на КГ ударной волны. Ниже при получении оценок принимается, что линейная стадия роста амплитуды струи (пузыря) продолжается, пока выполняется условие $a \leqslant 0.1\,\lambda $ ($ak \leqslant 0.628$). Затем начинает проявляться нелинейность процесса, для моделирования которого требуется использовать нелинейные модели, которые учитывают нарушение симметрии в развитии струй и пузырей.

Из (2) следует, что в случае одномодовых стоячих волн на линейной стадии амплитуда растет по закону

(3)
$a\left( t \right) = a_{0}^{ + } + \frac{{a_{0}^{ + }}}{{{{\lambda }_{0}}}}2\pi U{{A}^{ + }}t,$
из которого заключаем, что чем больше в начальном возмущении отношение амплитуды к длине волны, тем выше скорость роста амплитуды по времени при прочих равных условиях. В выполненных расчетах начальную шероховатость УВ и контактных границ задаем двухмодовым возмущением
(4)
$D{\kern 1pt} (y) = {{a}_{1}}\sin \left( {{{k}_{1}}y} \right) + {{a}_{2}}\sin \left( {{{k}_{2}}y} \right).$
Модой с амплитудой а1 и волновым числом ${{k}_{{{\kern 1pt} 1}}}$ задаем предполагаемую шероховатость УВ, падающей на КГ, модой с амплитудой а2 и волновым числом ${{k}_{{{\kern 1pt} 2}}}$ описываем шероховатость КГ, сформировавшуюся после разрыва пленки. В (4) принято a1 = 0.01 см, λ1 = 3 см, a2 = 0.01 см, λ2 = = 0.4 см. В одном расчете возмущения на КГ не задавались.

Расчеты при М = 1.3. Во всех расчетах принята система единиц г, см, 10 мкс. Из соотношений Гюгонио находим, что за фронтом УВ, движущейся во воздуху, газодинамические параметры принимают значения ρ = 0.00182 г/см3, p = 0.00018 г/(см 10 мкс), u = 0.151 см/(10 мкс). При выходе УВ на участок 1–2 КГ1 происходит распад разрыва, в результате которого формируются две УВ и контактный разрыв. Параметры течения после распада разрыва приведены на фиг. 3.

Фиг. 3.

Схема распада разрыва на участке 1–2 КГ1, М = 1.3.

Скорость УВ, движущейся по SF6, составляет D1 ≈ 0.2 см/(10 мкс), число Атвуда после прохождения скачка А+ ≈ 0.72. Согласно (2) и данным фиг. 3, скорость роста амплитуды возмущений на участке 1–2 КГ1 равна

(5)
$\frac{{da}}{{dt}} \approx 0.036{{k}_{0}}a_{0}^{ - }.$

Скорость разбегания УВ, движущейся по центральной области (в SF6), и КГ (удаления УВ от КГ1) без учета скорости роста струй составляет ${\text{|}}{\kern 1pt} {{D}^{1}} - u{\kern 1pt} {\text{|}} \approx 0.1$ см/(10 мкс). Детальный анализа взаимодействия УВ с КГ1 показал, что растущие на КГ1 возмущения не взаимодействуют с фронтом скачка (фронт не деформируется).

На фиг. 4 показано поле функции F = 1 – exp(– 10|∇ρ|), полученное в расчете при М = 1.3, выполненном без задания начальных возмущений, и реперная сетка, перенесенная с фиг. 2.

Фиг. 4.

Поле функции F, расчет без задания возмущений на КГ; здесь и далее время на фигурах измеряется в десятках мкс.

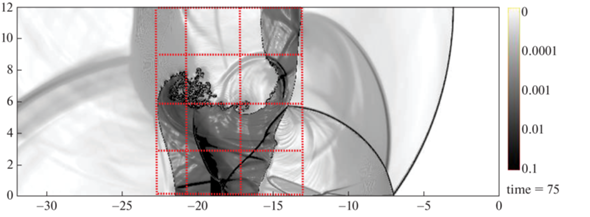
Согласно расчетным данным (фиг. 4), при выбранной технологии моделирования задачи развитие неустойчивости происходит лишь на участке 2–3 КГ1, т.е. там, где направление КГ не совпадает с направлениями линий сетки. Из фиг. 4 следует, что без навязывания шероховатости на КГ, направление которых совпадает с направлениями линий сетки, получить (как в опыте) намешивания контактирующих газов в окрестности контактных границ в рассматриваемой задаче не удается. Из сопоставления экспериментальной информации (фиг. 2) и численных результатов (фиг. 4) заключаем, что формы центральной области в эксперименте и расчете удовлетворительно согласуются между собой.

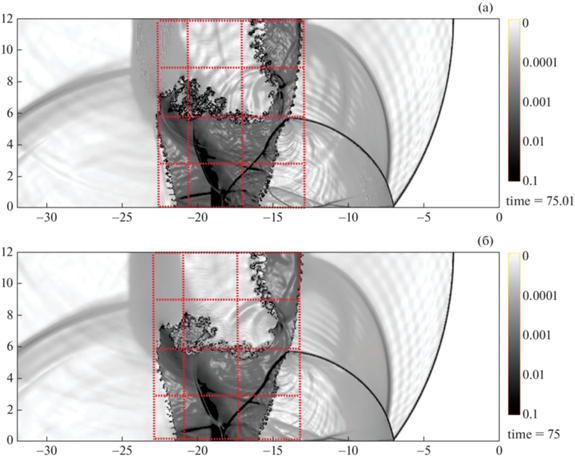
Динамика формирования течения с навязанной шероховатостью КГ в системе видна из фиг. 5, на которой представлено поле функции F на характерные времена t = 500 мкс и на момент окончания расчета t = 750 мкс.

Фиг. 5.

Поля функции F в расчете с использованием алгоритма VoF: (а) – t = 50 мкс, (б) – t = 75 мкс, М = 1.3.

Из данных фиг. 5 следует, что в момент времени t = 500 мкс волна разрежения приближается к возмущенному участку 3–4 КГ1, а при t = 750 мкс скачок выходит на правый торец трубы.

При заданной начальной шероховатости контактных границ для первой и второй мод имеем

(6)
$\frac{{{{a}_{1}}}}{{{{\lambda }_{1}}}} = 0.0033,\quad \frac{{{{a}_{2}}}}{{{{\lambda }_{2}}}} = 0.025.$
Из (3) и (6) заключаем, что амплитуда длинноволнового возмущения растет значительно медленнее (≈ в 7 раз), чем амплитуда второй моды. Согласно фиг. 5б, на КГ2 развивается 30 струй, что указывает на доминирование второй моды в процессе развития неустойчивости.

Расчеты при М = 3. Из соотношений Гюгонио находим, что за фронтом УВ, движущейся по воздуху, газодинамические параметры принимают значения ρ = 0.0046 г/см3, p = 0.00103 г/(см 10 мкс), u = 0.759 см/(10 мкс). При выходе УВ на участок 1–2 КГ1 происходит распад разрыва, при котором формируются две УВ и контактный разрыв. Параметры течения после распада разрыва приведены на фиг. 6.

Фиг. 6.

М = 3. Результат распада разрыва на участке 1–2 КГ1.

Скорость УВ, движущейся по SF6, составляет D1 ≈ 0.57 см/(10 мкс), число Атвуда после прохождения скачка через КГ А+ ≈ 0.72. Согласно (2) и фиг. 6, скорость роста амплитуды на участке 1–2 КГ1 равна

(7)
$\frac{{da}}{{dt}} \approx 0.049{{k}_{0}}a_{0}^{ - }.$

Скорость разбегания УВ, движущейся по центральной области (в SF6), и КГ (удаления УВ от КГ1) без учета скорости роста струй составляет ≈0.07 см/(10 мкс). Из (5) и (7) следует, что при М = 3 скорость роста амплитуды возмущений на линейной стадии несколько больше, чем при М = 1.3, а скорость разбегания УВ и КГ меньше. В результате детального анализа прохождения УВ через участок 1–2 КГ1 заключаем, что при М = 3 растущие на КГ1 возмущения не воздействуют на фронт скачка. Но на участках 2–3 и 3–4 из-за близости возмущений и фронта скачка наблюдается слабое воздействие возмущений на фронт скачка, что приводит к деформации фронта, заметной по данным фиг. 7а.

Фиг. 7.

Поля функции F в расчете с использованием алгоритма VoF, М = 3: (а) – t = 10 мкс, (б) – t = 20 мкс.

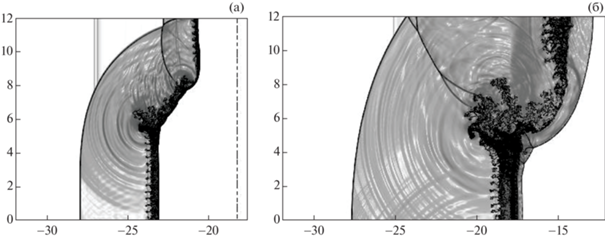
Проанализируем развитие неустойчивости на отдельных (трех) участках первой контактной границы (фиг. 7). В момент времени t = 100 мкс на участке 1–2 КГ1 явно наблюдается рост пузырей, на участке 2–3 уже происходит перемешивание тяжелого и легкого слоев, а на участке 3–4 формируется стадия перехода к ТП. Подобная ситуация наблюдается и на момент времени t = 130 мкс (мгновенное поле функции F на это время здесь не приводится). Очевидно, что при использовании RANS стратегии моделирования данной задачи могут возникнуть трудности при инициализации ТП на контактной границе и преимущество ILES методологии в данной ситуации становится очевидным.

Сравнение результатов, полученных по алгоритмам MoF и VoF, М = 1.3. Для сравнения результатов расчетов используем поле функции F (фиг. 8) с реперной сеткой на момент времени t = = 750 мкс и график эволюции завихренности (фиг. 9). Из данных фиг. 8 заключаем, что формы центральных областей удовлетворительно согласуются между собой и с экспериментальной информацией. Заметные различия наблюдаются на участке 2–3 границы, где после развития неустойчивости Кельвина–Гельмгольца формируется зона ТП. При сравнении эволюции завихренности замечаем, что в расчете по алгоритму MoF завихренность потока выше, чем в расчете по VoF.

Фиг. 8.

Поля функции F, М = 1.3: (а) – расчет по алгоритму VoF, (б) – расчет по алгоритму MoF.

Фиг. 9.

Эволюция завихренности (1), М = 1.3: (а) – ω > 0, (б) – ω < 0; штриховые линии – расчет по алгоритму VoF, сплошные линии – расчет по алгоритму MoF.

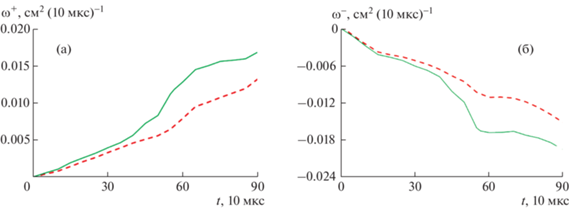
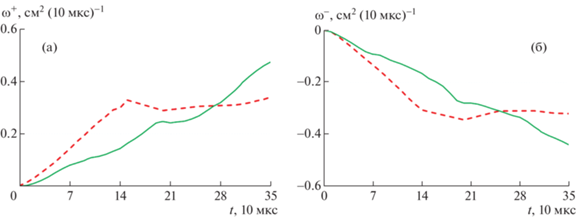
Сравнение результатов, полученных по алгоритмам MoF и VoF, М = 3. Для сравнения результатов расчетов используем поле функции F (фиг. 10) на момент времени t =340 мкс и график эволюции завихренности (фиг. 11). По информации фиг. 10 заключаем, что имеются некоторые расхождения в описании зоны перемешивания. Сравнивая фиг. 10а и 10б, замечаем, что в расчете по алгоритму VoF отслеживается больше волн слабой интенсивности, чем в расчете по алгоритму MoF. Также отмечаем, что в расчете с использованием алгоритма MoF абсолютное значение завихренности (фиг. 9) на последний момент времени выше, чем в расчете по алгоритму VoF.

Фиг. 10.

Поля функции F, М = 3: (а) – расчет по алгоритму VoF, (б) – расчет по алгоритму MoF.

Фиг. 11.

Эволюция завихренности (1), М = 3: (а) – ω > 0, (б) – ω < 0; штриховые линии – расчет по алгоритму VoF, сплошные линии – расчет по алгоритму MoF.

Замечание. На протяжении всего времени расчета в зоне перемешивания газов отсутствуют УВ и, следовательно, генерация турбулентности происходит под действием градиентов средних газодинамических величин, не содержащих разрывов (отсутствует проблема сходимости решения на фронте скачка). Однако следует принять во внимание, что расчеты проводятся на сетке с квадратными ячейками (отсутствуют скошенные и вытянутые ячейки), что обеспечивает монотонность численного решения и препятствует появлению дополнительных погрешностей. Из детального анализа полученных результатов заключаем, что сходимость решения при измельчении сетки отсутствует по энстрофии (при измельчении сетки моделируются все более мелкие вихри).

ЗАКЛЮЧЕНИЕ

Представлена новая стратегия моделирования газодинамических течений с учетом турбулентного перемешивания, возникающего на шероховатых контактных границах разноплотных веществ после прохождения ударной волны. Методика расчета основана на лагранжево-эйлеровой стратегии интегрирования уравнений Эйлера, выделении веществ концентрациями, использовании алгоритмов высокого порядка точности при реконструкции потоков на грани ячеек.

На основе разработанной стратегии моделировался лабораторный опыт, который представляет интерес для отработки технологии счета подобных задач по ряду причин. Во-первых, скорости роста начальных возмущений (и время перехода к стадии ТП) на различных участках первой контактной границы различны. Поэтому задача является прекрасным тестом для отработки алгоритма перехода от неустойчивости к турбулентному перемешиванию. Во-вторых, развитие возмущений (рост пузырей и струй) на обеих контактных границах происходит при участии неустойчивостей Рихтмайера–Мешкова и Кельвина–Гельмгольца, что довольно часто встречается в практических задачах (другие подобные опыты авторам не известны).

В результате анализа полученных в расчетах данных установлено, что без навязывания начальных возмущений на контактных границах развитие неустойчивости не наблюдается (за исключением участка наклонной контактной границы), что не согласуется с экспериментом. С навязанными двухмодовыми возмущениями форма центральной области и положение скачков в поле течения при числе Маха ударной волны М = 1.3 удовлетворительно согласуются как между собой, так и с экспериментом. В окрестности контактных границ, где происходит наиболее интенсивное развитие неустойчивости, при использованной тактике моделирования задачи наблюдается лишь гетерогенное перемешивание (отсутствует турбулентная диффузия). Интенсивность перемешивания газов увеличивается при увеличении числа Маха ударной волны.

Для лучшего понимания физики перемешивания предполагается продолжить работы по совершенствованию как экспериментальных методов диагностики течения, так и численных алгоритмов. В частности, предполагается внедрить в методику МИМОЗА алгоритм учета турбулентной диффузии в зонах завихренности потока, т.е. в зонах, где происходит перемешивание веществ. Для более детального изучения влияния интенсивности ударной волны на развитие неустойчивости предполагается провести эксперимент при числе Маха ударной волны М = 3.

Список литературы

  1. Янилкин Ю.В., Стаценко В.П., Козлов В.И. Математическое моделирование турбулентного перемешивания в сжимаемых средах. Саров: Изд-во ФГУП РФЯЦ-ВНИИЭФ. Курс лекций, 2019. Т. 1. 358 с.

  2. Groom M., Thornber B. The influence of initial perturbation power spectra on the growth of a turbulent mixing layer by Richtmyer–Meshkov instability // Physica D. 407. 2020. 132463.

  3. Grinstein F.F. Initial conditions and modeling for simulations of shock driven turbulent material mixing // Comput. Fluid. 2017. V. 151. P. 58–72.

  4. Haines B., Grinstein F., Schwarzkopf J. Reynolds-averages Navier-Stokes initialization and benchmarking in shock-driven turbulent mixing // J. Turbulence. 2013. V. 14. № 2. P. 46–70.

  5. Gregoire O., Souffland D., Gauthier S. A second-order turbulence model for gaseous mixtures induced by Richtmyer–Meshkov instability // J. Turbulence. 2005. V. 6. № 92. P. 1–20.

  6. Разин А. Н. Моделирование турбулентного перемешивания в газовых слойках. Саров: Изд-во ФГУП РФЯЦ-ВНИИЭФ, 2020. 289 с.

  7. Gauthier S., Bonnet M. A K–ε model for turbulent mixing in shock–tube flows induced by Rayleigh–Taylor instability // Phys. Fluid. 1990. V. 2. № 9. P. 1685–1684.

  8. Sinha K., Mahesh K., Candler G. Modeling shock unsteadiness in shock/turbulence interaction // Phys. Fluid. 2003. V. 15. № 8. P. 2290–2297.

  9. Grinstein F.F., Margolin L.G. and Rider W.J. editors. Implicit Large Eddy Simulation: Computing Turbulent Flow Dynamics, Cambridge Univ. Press, New York, 2007.

  10. Бодров Е.В., Змушко В.В., Невмержицкий Н.В., Разин А.Н., Сеньковский Е.Д., Сотсков Е.А. Расчетно-экспериментальное исследование развития турбулентного перемешивания в газовой слойке при прохождении ударной волны // Изв. РАН. МЖГ. 2018. № 3. С. 54–62.

  11. Большакова А.Э., Змушко В.В., Невмержицкий Н.В., Разин А.Н., Сеньковский Е.Д., Сотсков Е.А. Численное моделирование развития неустойчивости на контактных границах трехслойной газовой системы. Сравнение с экспериментальными данными // ПМТФ. 2021. Т. 62. № 1. С. 43–54.

  12. Drikakis D., Fureby C., Grinstein F., Youngs D. Simulation of transition and turbulence decay in the Taylor–Green vortex // J. Turbulence. 2007. V. 8. № 20. P. 1–12.

  13. Ukai S., Balakrishnan K., Menon S. Growth rate predictions of single- and multi-mode Richtmyer–Meshkov instability with reshock // Shock Wave. 2011. V. 21. P. 533–546.

  14. Olson B., Greenough J. Large eddy simulation requirements for Richtmyer–Meshkov instability // Phys. Fluid. 2014. V. 26. P. 044103.

  15. Cohen R., Dannevik W., Dimits A., Eliason D., Mirin A.A., Zhou Ye, Porter D.H., Woodward P.R. Three-dimensional simulation of a Richtmyer–Meshkov instability with a two-scale initial perturbation // Phys. Fluid. 2002. V. 14. P. 3692–709.

  16. Thornber B., Drikakis D., Williams R., Youngs D. The influence of initial conditions on turbulent mixing due to Richtmyer-Meshkov instability // J. Fluid. Mech. 2010. 654. P. 99–139.

  17. Grinstein F., Gowardhan A., Wachtor A. Simulations of Richtmyer–Meshkov instabilities in planar shock-tube experiments // Phys. Fluid. 2011. V. 23. P. 034106.

  18. Gowardhan A., Grinstein F. Numerical simulation of Richtmyer–Meshkov instabilities in shocked gas curtains // J. Turbulence. 2011. V. 12. № 43. P. 1–24.

  19. Змитренко Н.В., Ладонкина М.Е., Тишкин В.Ф. Численное исследование турбулентного перемешивания для одной задачи о развитии неустойчивости Рихтмайера-Мешкова // ВАНТ. Сер.: Матем. моделир. физ. процессов. 2004. Вып. 1. С. 12–26.

  20. Синькова О.Г., Стаценко В.П., Янилкин Ю.В. Численное моделирование опыта по исследованию турбулентного перемешивания после неоднократного прохождения ударной волны через границу раздела // ВАНТ. Сер.: Теор. и прикл. физ. 2004. Вып. 3. С. 17–22.

  21. Hahn M., Drikakis D., Youngs D., Williams R. Richtmyer–Meshkov turbulent mixing arising from an inclined material interface with realistic surface perturbations and reshocked flow // Phys. Fluid. 2011. V. 23. P. 046101.

  22. Невмержицкий Н.В. Гидродинамические неустойчивости и турбулентное перемешивание веществ. Лабораторное моделирование. Саров: Всерос. науч.-исслед. ин-т эксперим. физики, 2018. 245 с.

  23. Змушко В.В., Плетенёв Ф.А., Сараев В.А., Софронов И.Д. Методика решения трехмерных уравнений газовой динамики в смешанных лагранжево-эйлеровых координатах // ВАНТ. Сер. Методики и программы числ. решения задач матем. физ. 1988. Вып. 1. С. 22–27.

  24. Софронов И.Д., Афанасьева Е.А., Винокуров О.А., Воропинов А.И., Змушко В.В., Плетенев Ф.А., Рыбачен-ко П.В., Сараев В.А., Соколова Н.В., Шамраев Б.Н. Комплекс программ МИМОЗА для решения многомерных задач механики сплошной среды на ЭВМ “Эльбрус-2” // ВАНТ. Сер. Матем. моделир. физ. процессов. 1990. Вып. 2. С. 3–9.

  25. Zmushko V. V. Computation of convective flows and their realization in MIMOZA code // Proceedings International Workshop “New Models of Numerical Codes for Shock Wave Processes in Condensed Media” / Oxford / September 15–19. 1997. P. 423–429.

  26. Ладагин В.К., Пастушенко А.М. Об одной схеме расчета газодинамических течений // Численные методы механики сплошной среды. 1977. Т. 8. № 2. С. 66–72.

  27. Benson D.J. Volume of fluid interface reconstruction methods for multi-material problems. // Appl. Mech. Rev. 2002. V. 55. № 2. P. 151–165.

  28. Dyadechko V., Shashkov M. Multi-material interface reconstruction from the moment data. Technic. Rep. L-A‑UR-07-0656, LANL. 2006.

  29. Pilliod J.E., Pucket E.G. Second order accurate volume-of-fluid algorithms for tracking material interfaces // J. Comput. Phys. 2004. V. 199. P. 465–502.

  30. Richtmyer R.D. Taylor Instability in shock acceleration of compressible fluids // Commun. Pure Appl. Math. 1960. V. 13. P. 297–319.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал