Журнал вычислительной математики и математической физики, 2023, T. 63, № 3, стр. 408-423

Об одной обратной задаче для уравнения Колмогорова–Фоккера–Планка

Н. В. Трусов^1, 2, *

¹ ФИЦ ИУ РАН
119333 Москва, ул. Вавилова, 44, кор. 2, Россия

² Московский Центр фундаментальной и прикладной математики
119991 Москва, Ленинские горы, Россия

^* E-mail: trunick.10.96@gmail.com

Поступила в редакцию 15.09.2022
После доработки 15.09.2022
Принята к публикации 17.11.2022

EDN: DZOHBT
DOI: 10.31857/S0044466923030110

Полный текст (PDF)

Аннотация

В работе исследуется математическое описание экономического поведения домашних хозяйств с помощью уравнения Колмогорова–Фоккера–Планка. Данное уравнение описывает динамику плотности распределения домашних хозяйств по двум характеристикам: финансовому состоянию и доходам. Основываясь на статистических данных Росстата об экономическом положении домашних хозяйств России, исследуется вопрос о согласованности статистических данных с решением уравнения Колмогорова–Фоккера–Планка. Задача формализована в виде минимизации отклонения решения уравнения Колмогорова–Фоккера–Планка от статистических данных за счет управления расходами домашних хозяйств. Представлено численное решение экстремальной задачи, приведены результаты расчетов. Библ. 10. Фиг. 11. Табл. 1.

1. ВВЕДЕНИЕ

Моделирование экономического поведения домашних хозяйств опирается на концепцию рационального репрезентативного экономического агента и восходит к работе Ф. Рамсея [1]. Модели поведения репрезентативного домашнего хозяйства для различных социальных слоев разрабатывались в [2], [3] и использовались для анализа состояния рынка потребительского кредита. Динамика поведения репрезентативного домашнего хозяйства характеризует “среднее” поведение домашних хозяйств в рассматриваемом социальном слое. Исследование поведения большого количества домашних хозяйств в рамках социального слоя позволяет более качественно отслеживать их экономическую динамику. Большое количество домашних хозяйств можно описывать плотностью их распределения по финансовому состоянию и доходам. Финансовое состояние – величина, характеризующая разницу между доступными ликвидными средствами с депозитарными счетами домашнего хозяйства и его задолженностью перед банковским сектором. Динамику эволюции плотности распределения можно описать с помощью уравнения Колмогорова–Фоккера–Планка (см. [4]).

В данной работе исследуется вопрос о качестве моделирования экономического поведения домашних хозяйств с помощью уравнения Колмогорова–Фоккера–Планка в сравнении со статистическими данными обследования бюджетов домашних хозяйств (ОБДХ) в России за период 2015–2020 гг. [5]. В разд. 2 поставлена задача согласованности наблюдаемой статистики с динамикой распределения домашних хозяйств, описываемой уравнением Колмогорова–Фоккера–Планка. В разд. 3 представлен алгоритм численного решения данной задачи, результаты которого апробированы на данных российской статистики и представлены в разд. 4. В заключение (разд. 5) обсуждаются пути дальнейших исследований.

2. ЗАДАЧА МОДЕЛИРОВАНИЯ ДИНАМИКИ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ

Мы полагаем, что доходы домашнего хозяйства $S$ являются стохастическим процессом и описываются стохастическим дифференциальным уравнением

$dS = S\left( {\gamma dt + \sigma dW} \right),$

$S(0) = {{S}_{0}},$

где $\gamma \in \mathbb{R}$ характеризует темп роста доходов, $dW$ – стохастический дифференциал винеровского процесса $W$, $\sigma > 0$. Пусть $M(t)$ – ликвидные средства домашнего хозяйства, которые описываются дифференциальным уравнением

(1)

$\frac{{dM}}{{dt}} = S(t) - p(t)C(t) + {{H}_{L}}(t) - {{H}_{D}}(t),$

где $C(t)$ – расходы домашнего хозяйства; $p(t)$ – индекс потребительских цен, растущий с темпом инфляции $j$, т.е. $p(t) = {{p}_{0}}{{e}^{{jt}}}$, p₀ > 0; величина ${{H}_{L}}(t) \in \mathbb{R}$ описывает заимствования по потребительскому кредиту, а величина ${{H}_{D}}(t) \in \mathbb{R}$ характеризует пополнение/снятие сбережений в форме депозитов в коммерческих банках. Изменение задолженности $L(t)\; \geqslant \;0$ описывается дифференциальным уравнением

(2)

$\frac{{dL}}{{dt}} = {{H}_{L}}(t) + {{r}_{L}}L(t),$

где ${{r}_{L}} > 0$ является процентной ставкой по потребительскому кредиту. Изменение сбережений в форме депозитов $D(t)\; \geqslant \;0$ описывается дифференциальным уравнением

(3)

$\frac{{dD}}{{dt}} = {{H}_{D}}(t) + {{r}_{D}}D(t),$

где ${{r}_{D}} > 0$ является процентной ставкой по депозитам, причем предполагается выполнение условия отсутствия арбитража, т.е. ${{r}_{L}} > {{r}_{D}} > 0$. Закон Фишера связывает между собой ликвидные средства $M(t)$ с потребительскими расходами домашнего хозяйства $C(t)$ через величину $\frac{1}{\theta } > 0$, характеризующую скорость обращения денег

$M(t) = \theta p(t)C(t).$

Пусть $x(t)$ – финансовое состояние домашнего хозяйства. Оно задается выражением

(4)

$x(t) = M(t) + D(t) - L(t).$

Рациональное поведение предполагает, что домашнее хозяйство не имеет задолженности по потребительскому кредиту и сбережений в коммерческих банках одновременно, поэтому

$L(t) = \max \{ M(t) - x(t),0\} = {{\left( {M(t) - x(t)} \right)}_{ + }},$

$D(t) = {{\left( {x(t) - M(t)} \right)}_{ + }}.$

Дифференцируя уравнение (4) в силу уравнений (1)–(3), мы получаем динамику изменения финансового состояния домашнего хозяйства

(5)

$\frac{{dx}}{{dt}} = S - \frac{1}{\theta }M - {{r}_{L}}{{\left( {M - x} \right)}_{ + }} + {{r}_{D}}{{\left( {x - M} \right)}_{ + }},\quad x(0) = {{x}_{0}}.$

Таким образом, финансовое сотояние $x$ домашнего хозяйства и его доходы $S$ описываются динамической системой

$\frac{{dx}}{{dt}} = S - \frac{1}{\theta }M - {{r}_{L}}{{\left( {M - x} \right)}_{ + }} + {{r}_{D}}{{\left( {x - M} \right)}_{ + }},$

$dS = S\left( {\gamma dt + \sigma dW} \right),$

$x(0) = {{x}_{0}},$

$S(0) = {{S}_{0}}.$

В работе [2] исследуется задача рамсеевского типа о максимизации дисконтированного потребления репрезентативного домашнего хозяйства, которое управляет потреблением $C(t)$. Условие расплаты по потребительскому кредиту к конечному моменту времени влечет ограничение на финансовое состояние $x\; \geqslant \;{\kern 1pt} \frac{{ - S}}{{{{r}_{L}} - \gamma }}$. Если данное неравенство нарушается, то домашнее хозяйство не может расплатиться с потребительским кредитом при сложившейся конъюнктуре (см. [2]).

Пусть $m(x,S,t)$ описывает плотность распределения домашних хозяйств по финансовым состояниям $x$ и доходам $S$ в момент времени $t$. В [4] выведено уравнение Колмогорова–Фоккера–Планка, которое описывает эволюцию плотности распределения $m(x,S,t)$

(6)

$\frac{{\partial m(x,S,t)}}{{\partial t}} - \frac{1}{2}\frac{{{{\partial }^{2}}}}{{\partial {{S}^{2}}}}\left( {S{{\sigma }^{2}}(x,S)m(x,S,t)} \right) + \frac{\partial }{{\partial S}}\left( {Sm(x,S,t)\gamma (x,S)} \right) + \frac{\partial }{{\partial x}}\left( {mf(x,S)} \right) = 0,$

с начальными условиями

(7)

$m(x,S,0) = {{m}_{0}}(x,S),$

где $f(x,S)$ является правой частью дифференциального уравнения (5), т.е.

(8)

$f(x,S) = S - \frac{1}{\theta }M - {{r}_{L}}{{\left( {M - x} \right)}_{ + }} + {{r}_{D}}{{\left( {x - M} \right)}_{ + }}.$

Замечание 1. Отметим, что $\int_\mathbb{R} {\int_{{{\mathbb{R}}_{ + }}} {m(x,S,t)dSdx} } = C$, $\forall t \in [0,T]$ в уравнении (6), $C > 0$.

Пусть $\tilde {m}(x,S,t)$ – наблюдаемая статистика плотности распределения домашних хозяйств на временном отрезке $[0,T]$. В данной работе исследуется задача воспроизведения статистической плотности распределения $\tilde {m}(x,S,t)$ с помощью уравнения Колмогорова–Фоккера–Планка (6), (7) за счет управления ликвидными средствами $M(t)$, т.е.

(9)

(10)

$m(x,S,0) = \tilde {m}(x,S,0),$

(11)

$J = \int\limits_0^T {\kern 1pt} \int\limits_\mathbb{R} {\kern 1pt} \int\limits_{{{\mathbb{R}}_{ + }}} {{\left( {\tilde {m}(x,S,t) - m(x,S,t)} \right)}^{2}}dSdxdt \to \mathop {\min }\limits_{M(x,S,t)\, \geqslant \,\mu (x,S,t)} ,$

где $\mu (x,S,t) = \theta (x,S,t){{C}_{{\min }}}(t)$, ${{C}_{{\min }}}(t)$ – минимальное потребление в момент времени $t \in [0,T]$.

Для решения экстремальной задачи (9)–(11) необходимо выписать сопряженное уравнение. Пусть $v(x,S,t)$ – гладкая функция с компактным носителем. Построим лагранжиан экстремальной задачи (9)–(11), где в качестве множителя Лагранжа выступает функция $v(x,S,t)$:

(12)

$\begin{gathered} \mathcal{L}(m,v) = \int\limits_0^T {\kern 1pt} \int\limits_\mathbb{R} {\kern 1pt} \int\limits_{{{\mathbb{R}}_{ + }}} {{\left[ {\tilde {m}(x,S,t) - m(x,S,t)} \right]}^{2}}dSdxdt + \int\limits_\mathbb{R} {\kern 1pt} \int\limits_{{{\mathbb{R}}_{ + }}} \left[ {m(x,S,T)v(x,S,T) - } \right. \\ - \;\left. {\tilde {m}(x,S,0)v(x,S,0)} \right]dSdx - \int\limits_0^T {\kern 1pt} \int\limits_\mathbb{R} {\kern 1pt} \int\limits_{{{\mathbb{R}}_{ + }}} {\kern 1pt} m(x,S,t)\left[ {\frac{{\partial v}}{{\partial t}} + \frac{1}{2}{{\sigma }^{2}}{{S}^{2}}\frac{{{{\partial }^{2}}v}}{{\partial {{S}^{2}}}} + \gamma S\frac{{\partial v}}{{\partial S}} + f\frac{{\partial v}}{{\partial x}}} \right]dSdxdt. \\ \end{gathered} $

Замечание 2. Для получения лагранжиана (12) используется интегрирование по частям в уравнении Колмогорова–Фоккера–Планка.

Сопряженное уравнение для экстремальной задачи (9)–(11) имеет вид

(13)

$\frac{{\partial v}}{{\partial t}} + \frac{1}{2}{{\sigma }^{2}}{{S}^{2}}\frac{{{{\partial }^{2}}v}}{{\partial {{S}^{2}}}} + \gamma S\frac{{\partial v}}{{\partial S}} + f\frac{{\partial v}}{{\partial x}} = 0,$

с терминальным условием

(14)

$v(x,S,T) = 0.$

Представим алгоритм решения экстремальной задачи (9)–(11):

Шаг 1. Задаем начальное управление ${{M}^{0}}(x,S)$.

Шаг 2. Решаем уравнение Колмогорова–Фоккера–Планка (9), (10) в прямом времени.

Шаг 3. Решаем сопряженное уравнение (13), (14) в попятном времени.

Шаг 4. Находим новое управление ${{M}^{\kappa }}(x,S)$, где $\kappa \in \mathbb{N}$ – номер итерации:

${{M}^{\kappa }}(x,S): = {{M}^{{\kappa - 1}}}(x,S) + hm\frac{{\partial v}}{{\partial x}}\left( {\frac{1}{\theta } + {{r}_{L}} \cdot {{\mathbb{I}}_{{{{M}^{{\kappa - 1}}} > x}}} + {{r}_{D}} \cdot {{\mathbb{I}}_{{{{M}^{{\kappa - 1}}} < x}}}} \right),$

где $h > 0$ – шаг сходимости,

${{\mathbb{I}}_{{a > b}}} = \left\{ \begin{gathered} 1,\quad {\text{если}}\quad a > b, \hfill \\ 0\quad {\text{иначе}}{\text{.}} \hfill \\ \end{gathered} \right.$

Шаг 5. Переходим к шагу 2 до тех пор, пока не будет выполнен критерий останова

$\left| {\sqrt {{{J}^{\kappa }}} - \sqrt {{{J}^{{\kappa - 1}}}} } \right| < \varepsilon .$

3. ЧИСЛЕННОЕ РЕШЕНИЕ ЭКСТРЕМАЛЬНОЙ ЗАДАЧИ

3.1. Разностная схема для уравнения Колмогорова–Фоккера–Планка

Ограничим множество финансовых состояний $x$ и множество доходов $S$. Пусть $x \in [ - {{L}_{1}},{{L}_{2}}]$, $S \in [{{S}_{1}},{{S}_{2}}]$, где ${{L}_{1}} > 0$, ${{L}_{2}} > 0$, ${{S}_{2}} > {{S}_{1}}\; \geqslant \;0$. Разобьем диапазон финансовых состояний на $M + 1$ узлов, диапазон доходов на $H + 1$ узлов, временной отрезок на $N + 1$ узлов. Будем полагать, что все разбиения равномерны. Определим длины отрезков: $\Delta x = \frac{{{{L}_{1}} + {{L}_{2}}}}{M}$, $\Delta S = \frac{{{{S}_{2}} - {{S}_{1}}}}{H}$, $\Delta t = \frac{T}{N}$. Для адвективной части уравнения Колмогорова–Фоккера–Планка (9) мы используем противопоточную схему Годунова первого порядка. Разностные схемы такого вида были успешно применены в работах [6–8].

Будем придерживаться следующих обозначений. Пусть $m_{{j,k}}^{i}$ характеризует значение функции $m(x,S,t)$ в точке $\left( {j\Delta x,k\Delta S,i\Delta t} \right)$, $j = \overline {1,M - 1} $, $k = \overline {1,H - 1} $, $i = \overline {0,N} $. Разностная схема уравнения Колмогорова–Фоккера–Планка (9) представляется в виде

(15)

$\begin{gathered} m_{{j,k}}^{{i + 1}} = m_{{j,k}}^{i} + \frac{1}{2}\frac{{\Delta t}}{{\Delta {{S}^{2}}}}\left( {m_{{j,k + 1}}^{i}S_{{k + 1}}^{2}{{{\left( {\sigma _{{j,k + 1}}^{i}} \right)}}^{2}} - 2m_{{j,k}}^{i}S_{k}^{2}{{{\left( {\sigma _{{j,k}}^{i}} \right)}}^{2}} + m_{{j,k - 1}}^{i}S_{{k - 1}}^{2}{{{\left( {\sigma _{{j,k - 1}}^{i}} \right)}}^{2}}} \right) - \\ - \;\frac{{\Delta t}}{{\Delta S}}\left( {m_{{j,k + \frac{1}{2}}}^{i}{{S}_{{k + \frac{1}{2}}}}\gamma _{{j,k + \frac{1}{2}}}^{i} - m_{{j,k - 1 + \frac{1}{2}}}^{i}{{S}_{{k - 1 + \frac{1}{2}}}}\gamma _{{j,k - 1 + \frac{1}{2}}}^{i}} \right) - \frac{{\Delta t}}{{\Delta x}}\left( {m_{{j + \frac{1}{2},k}}^{i}f_{{j + \frac{1}{2},k}}^{i} - m_{{j - 1 + \frac{1}{2},k}}^{i}f_{{j - 1 + \frac{1}{2},k}}^{i}} \right), \\ j = \overline {2,M - 2} ,\quad k = \overline {2,H - 2} ,\quad i = \overline {0,N - 1} , \\ \end{gathered} $

где

$m_{{j,k + \frac{1}{2}}}^{i} = \left\{ \begin{gathered} m_{{j,k + 1}}^{i},\quad {\text{если}}\quad {{S}_{{k + \frac{1}{2}}}}\gamma _{{j,k + \frac{1}{2}}}^{i} < 0, \hfill \\ m_{{j,k}}^{i},\quad {\text{если}}\quad {{S}_{{k + \frac{1}{2}}}}\gamma _{{j,k + \frac{1}{2}}}^{i}\; \geqslant \;0, \hfill \\ \end{gathered} \right.\quad m_{{j + \frac{1}{2},k}}^{i} = \left\{ \begin{gathered} m_{{j + 1,k}}^{i},\quad {\text{если}}\quad {{S}_{{k + \frac{1}{2}}}}f_{{j + \frac{1}{2},k}}^{i} < 0, \hfill \\ m_{{j,k}}^{i},\quad {\text{если}}\quad {{S}_{{k + \frac{1}{2}}}}f_{{j + \frac{1}{2},k}}^{i}\; \geqslant \;0. \hfill \\ \end{gathered} \right.$

Мы накладываем гомогенные условия Неймана на границе области: $f_{{\frac{1}{2},k}}^{i} = f_{{M - 1 + \frac{1}{2},k}}^{i} = \gamma _{{j,\frac{1}{2}}}^{i} = \gamma _{{j,H - 1 + \frac{1}{2}}}^{i} = 0$, и граничные условия $m_{{j,1}}^{i} = m_{{j,H - 1}}^{i} = m_{{1,k}}^{i} = m_{{M - 1,k}}^{i} = 0$, где $j = \overline {1,M - 1} $, $k = \overline {1,H - 1} $, $i = \overline {0,N - 1} $.

Схематично, разностная схема уравнения Колмогорова–Фоккера–Планка может быть представлена в следующем виде (фиг. 1).

Фиг. 1.

Разностная схема уравнения Колмогорова–Фоккера–Планка.

Естественным требованием является неотрицательность плотности распределения. Выражение этого требования можно обеспечить за счет условий из следующей леммы.

Лемма 1. Пусть ${{m}^{i}} \in {{\mathbb{R}}^{{(M - 1) \times (H - 1)}}}$ является матрицей с неотрицательными компонентами. Пусть $\tilde {\sigma } = \mathop {\max }\limits_{i \in I,j \in J,k \in K} \sigma _{{j,k}}^{i}$, где $I{\kern 1pt} \in \left\{ {0, \ldots ,N - 1} \right\}$, $J \in \left\{ {1, \ldots ,M - 1} \right\}$, $K \in \left\{ {1, \ldots ,H - 1} \right\}$. Если выполнены ограничения (16), (17) на $f_{{j + \frac{1}{2},k}}^{i}$, $j = \overline {1,M - 2} $, $k \in K$, $i \in I$, и $\gamma _{{j,k + \frac{1}{2}}}^{i}$ $j \in J$, $k = \overline {1,H - 2} $, $i \in I$, тогда матрица ${{m}^{{i + 1}}} \in {{\mathbb{R}}^{{(M - 1) \times (H - 1)}}}$ состоит из неотрицательных элементов.

(16)

$\frac{{\Delta x}}{2}\left( {\frac{{{{{\tilde {\sigma }}}^{2}}}}{2}\frac{1}{{\Delta {{S}^{2}}}}S_{k}^{2} - \frac{1}{{2\Delta t}}} \right)\;\leqslant \;f_{{j + \frac{1}{2},k}}^{i}\;\leqslant \;\frac{{\Delta x}}{2}\left( {\frac{1}{{2\Delta t}} - \frac{{{{{\tilde {\sigma }}}^{2}}}}{2}\frac{1}{{\Delta {{S}^{2}}}}S_{k}^{2}} \right),$

(17)

$\frac{{\Delta S}}{{2{{S}_{{k + \frac{1}{2}}}}}}\left( {\frac{{{{{\tilde {\sigma }}}^{2}}}}{2}\frac{1}{{\Delta {{S}^{2}}}}\hat {S}_{{k + 1}}^{2} - \frac{1}{{2\Delta t}}} \right)\;\leqslant \;\gamma _{{j,k + \frac{1}{2}}}^{i}\;\leqslant \;\frac{{\Delta S}}{{2{{S}_{{k + \frac{1}{2}}}}}}\left( {\frac{1}{{2\Delta t}} - \frac{{{{{\tilde {\sigma }}}^{2}}}}{2}\frac{1}{{\Delta {{S}^{2}}}}\hat {S}_{{k + 1}}^{2}} \right),$

где ${{\hat {S}}_{{k + 1}}} = \min \left\{ {{{S}_{{k + 1}}},{{S}_{2}}} \right\}$.

Доказательство. Зафиксируем $i$, $j$, $k$. Нам необходимо показать, что компоненты $m_{{j - 1,k}}^{i}$, $m_{{j,k + 1}}^{i}$, $m_{{j,k}}^{i}$, $m_{{j,k - 1}}^{i}$, $m_{{j + 1,k}}^{i}$ являются неотрицательными величинами. Для этого необходимо рассмотреть всевозможные комбинации знаков величин $f_{{j + \frac{1}{2},k}}^{i}$, $f_{{j - 1 + \frac{1}{2},k}}^{i}$, $\gamma _{{j,k + \frac{1}{2}}}^{i}$, $\gamma _{{j,k - 1 + \frac{1}{2}}}^{i}$. Легко видеть, что величины $f_{{j + \frac{1}{2},k}}^{i}$, $f_{{j - 1 + \frac{1}{2},k}}^{i}$ перемещаются горизонтально вдоль компонентов $m_{{j - 1,k}}^{i}$, $m_{{j,k}}^{i}$, $m_{{j + 1,k}}^{i}$ в зависимости от своих знаков, тогда как величины $\gamma _{{j,k + \frac{1}{2}}}^{i}$, $\gamma _{{j,k - 1 + \frac{1}{2}}}^{i}$ перемещаются вертикально вдоль компонентов $m_{{j,k - 1}}^{i}$, $m_{{j,k}}^{i}$, $m_{{j,k + 1}}^{i}$.

При компонентах $m_{{j - 1,k}}^{i}$, $m_{{j,k + 1}}^{i}$, $m_{{j,k - 1}}^{i}$, $m_{{j + 1,k}}^{i}$ знаки величин $f_{{j + \frac{1}{2},k}}^{i}$, $f_{{j - 1 + \frac{1}{2},k}}^{i}$, $\gamma _{{j,k + \frac{1}{2}}}^{i}$, $\gamma _{{j,k - 1 + \frac{1}{2}}}^{i}$, входящие со своими множителями в уравнение Колмогорова–Фоккера–Планка (15) положительны (например, если $f_{{j + \frac{1}{2},k}}^{i} < 0$, тогда эта величина соответствует узлу $m_{{j + 1,k}}^{i}$ и входит со множителем $ - \frac{{\Delta t}}{{\Delta x}} < 0$, таким образом, знак в узле $m_{{j + 1,k}}^{i}$ положителен).

Прежде чем переходить к рассмотрению значения $m_{{j,k}}^{i}$ в центральном узле $(i,j,k)$, рассмотрим подробнее лапласиан в уравнении (15). Пусть

${{\varphi }_{1}} = \frac{1}{2}\frac{{\Delta t}}{{\Delta {{S}^{2}}}}S_{{k + 1}}^{2}{{(\sigma _{{j,k + 1}}^{i})}^{2}},\quad {{\varphi }_{2}} = 1 - \frac{{\Delta t}}{{\Delta {{S}^{2}}}}S_{k}^{2}{{(\sigma _{{j,k}}^{i})}^{2}},\quad {{\varphi }_{3}} = \frac{1}{2}\frac{{\Delta t}}{{\Delta {{S}^{2}}}}S_{{k - 1}}^{2}{{(\sigma _{{j,k - 1}}^{i})}^{2}}.$

Очевидно, что ${{\varphi }_{1}}\; \geqslant \;0$, ${{\varphi }_{3}}\; \geqslant \;0$. Величина ${{\varphi }_{2}}\; \geqslant \;0$ в соответствии с условиями Куранта о сходимости явной разностной схемы параболического уравнения (15) (см. [9]). Мы накладываем ограничения Куранта в виде $\frac{{{{{\tilde {\sigma }}}^{2}}}}{2}\frac{{\Delta t}}{{\Delta {{S}^{2}}}}S_{2}^{2} < \frac{1}{2}$, где ${{S}_{2}}$ является правой границей фазового пространства $S$.

Теперь рассмотрим центральный узел $(i,j,k)$. Если мы докажем, что значение $m_{{j,k}}^{i}$ является неотрицательным для случая $f_{{j + \frac{1}{2},k}}^{i} > 0$, $f_{{j - 1 + \frac{1}{2},k}}^{i} < 0$, $\gamma _{{j,k + \frac{1}{2}}}^{i} > 0$, $\gamma _{{j,k - 1 + \frac{1}{2}}}^{i} < 0$, тогда для других возможных случаев сочетания знаков величин $f_{{j + \frac{1}{2},k}}^{i}$, $f_{{j - 1 + \frac{1}{2},k}}^{i}$, $\gamma _{{j,k + \frac{1}{2}}}^{i}$, $\gamma _{{j,k - 1 + \frac{1}{2}}}^{i}$ значение $m_{{j,k}}^{i}$ также будет неотрицательным. Рассмотрим компоненты $m_{{j,k}}^{i}$ для данного случая для узла $(i,j,k)$. Согласно ограничениям (16), (17) мы получаем следующую оценку:

$\begin{gathered} 1 - \frac{{\Delta t}}{{\Delta {{S}^{2}}}}S_{k}^{2}{{\left( {\sigma _{{j,k}}^{i}} \right)}^{2}} - \frac{{\Delta t}}{{\Delta S}}{{S}_{{k + \frac{1}{2}}}}\gamma _{{j,k + \frac{1}{2}}}^{i} + \frac{{\Delta t}}{{\Delta S}}{{S}_{{k - 1 + \frac{1}{2}}}}\gamma _{{j,k - 1 + \frac{1}{2}}}^{i} - \frac{{\Delta t}}{{\Delta x}}f_{{j + \frac{1}{2},k}}^{i} + \frac{{\Delta t}}{{\Delta x}}f_{{j - 1 + \frac{1}{2},k}}^{i}\; \geqslant \\ \geqslant \;1 - \frac{{\Delta t}}{{\Delta {{S}^{2}}}}S_{k}^{2}{{\left( {\sigma _{{j,k}}^{i}} \right)}^{2}} - \frac{{\Delta t}}{2}\left( {\frac{1}{{2\Delta t}} - \frac{{{{{\tilde {\sigma }}}^{2}}}}{2}\frac{1}{{\Delta {{S}^{2}}}}\hat {S}_{{k + 1}}^{2}} \right) + \frac{{\Delta t}}{2}\left( {\frac{{{{{\tilde {\sigma }}}^{2}}}}{2}\frac{1}{{\Delta {{S}^{2}}}}\hat {S}_{k}^{2} - \frac{1}{{2\Delta t}}} \right) - \\ \end{gathered} $

$\begin{gathered} - \frac{{\Delta t}}{2}\left( {\frac{1}{{2\Delta t}} - \frac{{{{{\tilde {\sigma }}}^{2}}}}{2}\frac{1}{{\Delta {{S}^{2}}}}S_{k}^{2}} \right) + \frac{{\Delta t}}{2}\left( {\frac{{{{{\tilde {\sigma }}}^{2}}}}{2}\frac{1}{{\Delta {{S}^{2}}}}S_{k}^{2} - \frac{1}{{2\Delta t}}} \right) = \\ = 1 - \frac{{\Delta t}}{{\Delta {{S}^{2}}}}S_{k}^{2}{{\left( {\sigma _{{j,k}}^{i}} \right)}^{2}} - \frac{1}{4} + \frac{{{{{\tilde {\sigma }}}^{2}}}}{4}\frac{{\Delta t}}{{\Delta {{S}^{2}}}}\hat {S}_{{k + 1}}^{2} + \frac{{{{{\tilde {\sigma }}}^{2}}}}{4}\frac{{\Delta t}}{{\Delta {{S}^{2}}}}\hat {S}_{k}^{2} - \frac{1}{4} - \frac{1}{4} + \frac{{{{{\tilde {\sigma }}}^{2}}}}{4}\frac{{\Delta t}}{{\Delta {{S}^{2}}}}S_{k}^{2} + \frac{{{{{\tilde {\sigma }}}^{2}}}}{4}\frac{{\Delta t}}{{\Delta {{S}^{2}}}}S_{k}^{2} - \frac{1}{4}\; \geqslant \\ \end{gathered} $

$\begin{gathered} \geqslant \;1 - \frac{{\Delta t}}{{\Delta {{S}^{2}}}}S_{k}^{2}{{\left( {\sigma _{{j,k}}^{i}} \right)}^{2}} - \frac{1}{4} + \frac{{{{{\tilde {\sigma }}}^{2}}}}{4}\frac{{\Delta t}}{{\Delta {{S}^{2}}}}S_{k}^{2} + \frac{{{{{\tilde {\sigma }}}^{2}}}}{4}\frac{{\Delta t}}{{\Delta {{S}^{2}}}}S_{k}^{2} - \frac{1}{4} - \frac{1}{4} + \frac{{{{{\tilde {\sigma }}}^{2}}}}{4}\frac{{\Delta t}}{{\Delta {{S}^{2}}}}S_{k}^{2} + \frac{{{{{\tilde {\sigma }}}^{2}}}}{4}\frac{{\Delta t}}{{\Delta {{S}^{2}}}}S_{k}^{2} - \frac{1}{4}\; \geqslant \\ \geqslant \;1 - \frac{{\Delta t}}{{\Delta {{S}^{2}}}}S_{k}^{2}{{{\tilde {\sigma }}}^{2}} + {{{\tilde {\sigma }}}^{2}}\frac{{\Delta t}}{{\Delta {{S}^{2}}}}S_{k}^{2} - 1 = 0. \\ \end{gathered} $

Таким образом, мы показали, что значения коэффициентов, соответствующие компонентам $m_{{j - 1,k}}^{i}$, $m_{{j,k + 1}}^{i}$, $m_{{j,k}}^{i}$, $m_{{j,k - 1}}^{i}$, $m_{{j + 1,k}}^{i}$, при ограничениях (16)–(17) являются неотрицательными. Лемма доказана.

3.2. Разностная схема для сопряженного уравнения

Прежде чем переходить к разностой схеме для сопряженного уравнения, отметим, что дискретное уравнение Колмогорова–Фоккера–Планка (15) может быть записано через индикаторные функции:

$m_{{j,k}}^{{i + 1}} = m_{{j,k}}^{i} + \frac{1}{2}\frac{{\Delta t}}{{\Delta {{S}^{2}}}}\left( {m_{{j,k + 1}}^{i}S_{{k + 1}}^{2}{{{\left( {\sigma _{{j,k + 1}}^{i}} \right)}}^{2}} - 2m_{{j,k}}^{i}S_{k}^{2}{{{\left( {\sigma _{{j,k}}^{i}} \right)}}^{2}} + m_{{j,k - 1}}^{i}S_{{k - 1}}^{2}{{{\left( {\sigma _{{j,k - 1}}^{i}} \right)}}^{2}}} \right) - $

$\begin{gathered} - \;\frac{{\Delta t}}{{\Delta S}}\left( {m_{{j,k + 1}}^{i}{{S}_{{k + \frac{1}{2}}}}\gamma _{{j,k + \frac{1}{2}}}^{i} \cdot {{\mathbb{I}}_{{\gamma _{{j,k + \frac{1}{2}}}^{i} < 0}}} + m_{{j,k}}^{i}{{S}_{{k + \frac{1}{2}}}}\gamma _{{j,k + \frac{1}{2}}}^{i} \cdot {{\mathbb{I}}_{{\gamma _{{j,k + \frac{1}{2}}}^{i}\, \geqslant \,0}}} - } \right. \\ \left. { - \;m_{{j,k}}^{i}{{S}_{{k - 1 + \frac{1}{2}}}}\gamma _{{j,k - 1 + \frac{1}{2}}}^{i} \cdot {{\mathbb{I}}_{{\gamma _{{j,k - 1 + \frac{1}{2}}}^{i} < 0}}} - m_{{j,k - 1}}^{i}{{S}_{{k - 1 + \frac{1}{2}}}}\gamma _{{j,k - 1 + \frac{1}{2}}}^{i} \cdot {{\mathbb{I}}_{{\gamma _{{j,k - 1 + \frac{1}{2}}}^{i}\, \geqslant \,0}}}} \right) - \\ \end{gathered} $

$\begin{gathered} - \;\frac{{\Delta t}}{{\Delta x}}\left( {m_{{j + 1,k}}^{i}f_{{j + \frac{1}{2},k}}^{i} \cdot {{\mathbb{I}}_{{f_{{j + \frac{1}{2},k}}^{i} < 0}}} + m_{{j,k}}^{i}f_{{j + \frac{1}{2},k}}^{i} \cdot {{\mathbb{I}}_{{f_{{j + \frac{1}{2},k}}^{i}\, \geqslant \,0}}} - } \right. \\ \left. { - \;m_{{j,k}}^{i}f_{{j - 1 + \frac{1}{2},k}}^{i} \cdot {{\mathbb{I}}_{{f_{{j - 1 + \frac{1}{2},k}}^{i} < 0}}} - m_{{j - 1,k}}^{i}f_{{j - 1 + \frac{1}{2},k}}^{i} \cdot {{\mathbb{I}}_{{f_{{j - 1 + \frac{1}{2},k}}^{i}\, \geqslant \,0}}}} \right), \\ \end{gathered} $

где $j = \overline {2,M - 2} ,$ $k = \overline {2,H - 2} ,$ $i = \overline {0,N - 1} $. Чтобы избавиться от громоздких выражений, для простоты введем следующие обозначения: пусть

$a_{{j,k}}^{i} = S_{{k + 1}}^{2}{{\left( {\sigma _{{j,k}}^{i}} \right)}^{2}},\quad \bar {b}_{{j,k + \frac{1}{2}}}^{i} = {{S}_{{k + \frac{1}{2}}}}\gamma _{{j,k + \frac{1}{2}}}^{i} \cdot {{\mathbb{I}}_{{\gamma _{{j,k + \frac{1}{2}}}^{i} < 0}}},\quad b_{{j,k + \frac{1}{2}}}^{i} = {{S}_{{k + \frac{1}{2}}}}\gamma _{{j,k + \frac{1}{2}}}^{i} \cdot {{\mathbb{I}}_{{\gamma _{{j,k + \frac{1}{2}}}^{i}\, \geqslant \,0}}},$

$\bar {c}_{{j + \frac{1}{2},k}}^{i} = f_{{j + \frac{1}{2},k}}^{i} \cdot {{\mathbb{I}}_{{f_{{j + \frac{1}{2},k}}^{i} < 0}}},\quad c_{{j + \frac{1}{2},k}}^{i} = f_{{j + \frac{1}{2},k}}^{i} \cdot {{\mathbb{I}}_{{f_{{j + \frac{1}{2},k}}^{i}\, \geqslant \,0}}}.$

Тогда дискретная запись экстремальной задачи имеет вид

$\frac{{m_{{j,k}}^{{i + 1}} - m_{{j,k}}^{i}}}{{\Delta t}} - \frac{1}{2}\frac{1}{{\Delta {{S}^{2}}}}\left( {m_{{j,k + 1}}^{i}a_{{j,k + 1}}^{i} - 2m_{{j,k}}^{i}a_{{j,k}}^{i} + m_{{j,k - 1}}^{i}a_{{j,k - 1}}^{i}} \right) + $

(18)

$ + \;\frac{1}{{\Delta S}}\left( {m_{{j,k + 1}}^{i}\bar {b}_{{j,k + \frac{1}{2}}}^{i} + m_{{j,k}}^{i}\left( {b_{{j,k + \frac{1}{2}}}^{i} - \bar {b}_{{j,k - 1 + \frac{1}{2}}}^{i}} \right) - m_{{j,k - 1}}^{i}b_{{j,k - 1 + \frac{1}{2}}}^{i}} \right) + $

$ + \;\frac{1}{{\Delta x}}\left( {m_{{j + 1,k}}^{i}\bar {c}_{{j + \frac{1}{2},k}}^{i} + m_{{j,k}}^{i}\left( {c_{{j + \frac{1}{2},k}}^{i} - \bar {c}_{{j - 1 + \frac{1}{2},k}}^{i}} \right) - m_{{j - 1,k}}^{i}c_{{j - 1 + \frac{1}{2},k}}^{i}} \right) = 0,$

(19)

$m_{{j,k}}^{0} = \tilde {m}_{{j,k}}^{0},$

(20)

$J = \Delta t\Delta x\Delta S\sum\limits_{i = 0}^N {\kern 1pt} \sum\limits_{j = 1}^{M - 1} {\kern 1pt} \sum\limits_{k = 1}^{H - 1} {{\left( {\tilde {m}_{{j,k}}^{i} - m_{{j,k}}^{i}} \right)}^{2}} \to \mathop {\min }\limits_{M_{{j + \frac{1}{2},k}}^{i}\, \geqslant \,\theta _{{j + \frac{1}{2},k}}^{i}C_{{{\text{min}}}}^{i}} .$

С учетом нулевых граничных условий, лагранжиан к дискретной экстремальной задаче (18)–(20) имеет вид

$\mathcal{L}(m,v) = \Delta t\Delta x\Delta S\sum\limits_{i = 1}^N {\kern 1pt} \sum\limits_{j = 1}^{M - 1} {\kern 1pt} \sum\limits_{k = 1}^{H - 1} {{\left( {\tilde {m}_{{j,k}}^{i} - m_{{j,k}}^{i}} \right)}^{2}} + \Delta t\Delta x\Delta S\sum\limits_{i = 0}^{N - 1} {\kern 1pt} \sum\limits_{j = 2}^{M - 2} {\kern 1pt} \sum\limits_{k = 2}^{H - 2} \,v_{{j,k}}^{i}\left[ {\frac{{m_{{j,k}}^{{i + 1}} - m_{{j,k}}^{i}}}{{\Delta t}} - } \right.$

(21)

$\begin{gathered} \, - \frac{1}{2}\frac{1}{{\Delta {{S}^{2}}}}\left( {m_{{j,k + 1}}^{i}a_{{j,k + 1}}^{i} - 2m_{{j,k}}^{i}a_{{j,k}}^{i} + m_{{j,k - 1}}^{i}a_{{j,k - 1}}^{i}} \right) + \\ + \;\frac{1}{{\Delta S}}\left( {m_{{j,k + 1}}^{i}\bar {b}_{{j,k + \frac{1}{2}}}^{i} + m_{{j,k}}^{i}\left( {b_{{j,k + \frac{1}{2}}}^{i} - \bar {b}_{{j,k - 1 + \frac{1}{2}}}^{i}} \right) - m_{{j,k - 1}}^{i}b_{{j,k - 1 + \frac{1}{2}}}^{i}} \right) + \\ \end{gathered} $

$\left. { + \;\frac{1}{{\Delta x}}\left( {m_{{j + 1,k}}^{i}\bar {c}_{{j + \frac{1}{2},k}}^{i} + m_{{j,k}}^{i}\left( {c_{{j + \frac{1}{2},k}}^{i} - \bar {c}_{{j - 1 + \frac{1}{2},k}}^{i}} \right) - m_{{j - 1,k}}^{i}c_{{j - 1 + \frac{1}{2},k}}^{i}} \right)} \right].$

Выделим слагаемые с компонентами $m_{{j,k}}^{i}$. С учетом граничных условий на плотность распределения $m$ и терминального условия на сопряженную функцию $v_{{j,k}}^{{N - 1}} = 0$, $j = \overline {2,M - 2} $, $k = \overline {2,H - 2} $, лагранжиан (21) можно представить в виде

$\begin{gathered} \mathcal{L}(m,v) = \Delta t\Delta x\Delta S\sum\limits_{i = 1}^N {\kern 1pt} \sum\limits_{j = 1}^{M - 1} {\kern 1pt} \sum\limits_{k = 1}^{H - 1} {{\left( {\tilde {m}_{{j,k}}^{i} - m_{{j,k}}^{i}} \right)}^{2}} + \\ + \;\Delta t\Delta x\Delta S\left\{ {\sum\limits_{i = 1}^{N - 1} {\kern 1pt} \sum\limits_{j = 3}^{M - 3} {\kern 1pt} \sum\limits_{k = 3}^{H - 3} \,m_{{j,k}}^{i}} \right.\left[ {\frac{{v_{{j,k}}^{{i - 1}} - v_{{j,k}}^{i}}}{{\Delta t}} - \frac{1}{2}\frac{1}{{\Delta {{S}^{2}}}}a_{{j,k}}^{i}\left( {v_{{j,k - 1}}^{i} - 2v_{{j,k}}^{i} + v_{{j,k + 1}}^{i}} \right) + } \right. \\ \end{gathered} $

$\begin{gathered} \, + \frac{1}{{\Delta S}}\left( {\bar {b}_{{j,k - 1 + \frac{1}{2}}}^{i}v_{{j,k - 1}}^{i} + \left( {b_{{j,k + \frac{1}{2}}}^{i} - \bar {b}_{{j,k - 1 + \frac{1}{2}}}^{i}} \right)v_{{j,k}}^{i} - b_{{j,k + \frac{1}{2}}}^{i}v_{{j,k + 1}}^{i}} \right) + \\ \left. { + \;\frac{1}{{\Delta x}}\left( {\bar {c}_{{j - 1 + \frac{1}{2},k}}^{i}v_{{j - 1,k}}^{i} + \left( {c_{{j + \frac{1}{2},k}}^{i} - \bar {c}_{{j - 1 + \frac{1}{2},k}}^{i}} \right)v_{{j,k}}^{i} - c_{{j + \frac{1}{2},k}}^{i}v_{{j + 1,k}}^{i}} \right)} \right] + \sum\limits_{j = 2}^{M - 2} {\kern 1pt} \sum\limits_{k = 2}^{H - 2} \left[ {\frac{{ - m_{{j,k}}^{0}v_{{j,k}}^{0}}}{{\Delta t}}} \right] - \\ \end{gathered} $

$\begin{gathered} - \;\frac{1}{2}\frac{1}{{\Delta {{S}^{2}}}}\sum\limits_{i = 0}^{N - 2} {\kern 1pt} \sum\limits_{j = 2}^{M - 2} \left[ {m_{{j,H - 2}}^{i}a_{{j,H - 2}}^{i}v_{{j,H - 3}}^{i} - 2m_{{j,2}}^{i}a_{{j,2}}^{i}v_{{j,2}}^{i} - 2m_{{j,H - 2}}^{i}a_{{j,H - 2}}^{i}v_{{j,H - 2}}^{i} + m_{{j,2}}^{i}a_{{j,2}}^{i}v_{{j,3}}^{i}} \right] + \\ \\ \end{gathered} $

$\begin{gathered} + \;\frac{1}{{\Delta S}}\sum\limits_{i = 0}^{N - 2} {\kern 1pt} \sum\limits_{j = 2}^{M - 2} \left[ {m_{{j,H - 2}}^{i}\bar {b}_{{j,H - 3 + \frac{1}{2}}}^{i}v_{{j,H - 3}}^{i} + m_{{j,2}}^{i}\left( {b_{{j,2 + \frac{1}{2}}}^{i} - \bar {b}_{{j,1 + \frac{1}{2}}}^{i}} \right)v_{{j,2}}^{i} + } \right. \\ \left. {\, + m_{{j,H - 2}}^{i}\left( {b_{{j,H - 2 + \frac{1}{2}}}^{i} - \bar {b}_{{j,H - 3 + \frac{1}{2}}}^{i}} \right)v_{{j,H - 2}}^{i} + m_{{j,2}}^{i}b_{{j,2 + \frac{1}{2}}}^{i}v_{{j,3}}^{i}} \right] + \\ \end{gathered} $

$\begin{gathered} + \;\frac{1}{{\Delta x}}\sum\limits_{i = 0}^{N - 2} {\kern 1pt} \sum\limits_{k = 2}^{H - 2} \left[ {m_{{M - 2,k}}^{i}\bar {c}_{{M - 3 + \frac{1}{2},k}}^{i}v_{{M - 3,k}}^{i} + m_{{2,k}}^{i}\left( {c_{{2 + \frac{1}{2},k}}^{i} - \bar {c}_{{1 + \frac{1}{2},k}}^{i}} \right)v_{{2,k}}^{i} + } \right. \\ \left. {\left. {\, + m_{{M - 2,k}}^{i}\left( {c_{{M - 2 + \frac{1}{2},k}}^{i} - \bar {c}_{{M - 3 + \frac{1}{2},k}}^{i}} \right)v_{{M - 2,k}}^{i} + m_{{2,k}}^{i}c_{{2 + \frac{1}{2},k}}^{i}v_{{3,k}}^{i}} \right]} \right\}. \\ \end{gathered} $

Откуда получаем уравнение на сопряженную переменную в попятном времени

$v_{{j,k}}^{{i - 1}} = v_{{j,k}}^{i} + \frac{1}{2}\frac{{\Delta t}}{{\Delta {{S}^{2}}}}a_{{j,k}}^{i}\left( {v_{{j,k - 1}}^{i} - 2v_{{j,k}}^{i} + v_{{j,k + 1}}^{i}} \right) - $

(22)

$\begin{gathered} \, - \frac{{\Delta t}}{{\Delta S}}\left( {\bar {b}_{{j,k - 1 + \frac{1}{2}}}^{i}v_{{j,k - 1}}^{i} + \left( {{{b}_{{j,k + \frac{1}{2}}}} - \bar {b}_{{j,k - 1 + \frac{1}{2}}}^{i}} \right)v_{{j,k}}^{i} - b_{{j,k + \frac{1}{2}}}^{i}v_{{j,k + 1}}^{i}} \right) - \\ - \;\frac{{\Delta t}}{{\Delta x}}\left( {\bar {c}_{{j - 1 + \frac{1}{2},k}}^{i}v_{{j - 1,k}}^{i} + \left( {{{c}_{{j + \frac{1}{2},k}}} - \bar {c}_{{j - 1 + \frac{1}{2},k}}^{i}} \right)v_{{j,k}}^{i} - c_{{j + \frac{1}{2},k}}^{i}v_{{j + 1,k}}^{i}} \right) + 2\Delta t\left( {\tilde {m}_{{j,k}}^{i} - m_{{j,k}}^{i}} \right), \\ \end{gathered} $

$i = \overline {1,N - 1} ,\quad j = \overline {3,M - 3} ,\quad k = \overline {3,H - 3} ,$

терминальное условие

(23)

$v_{{j,k}}^{{N - 1}} = 0,\quad j = \overline {2,M - 2} ,\quad k = \overline {2,H - 2} ,$

а также граничные условия. Введем обозначения

$h_{3}^{{1,i}} = \frac{1}{{\Delta x}}\bar {c}_{{M - 3 + \frac{1}{2},3}}^{i},\quad h_{{H - 3}}^{{1,i}} = \frac{1}{{\Delta x}}\bar {c}_{{M - 3 + \frac{1}{2},H - 3}}^{i},\quad h_{3}^{{2,i}} = \frac{1}{{\Delta x}}\left( {c_{{M - 2 + \frac{1}{2},3}}^{i} - \bar {c}_{{M - 3 + \frac{1}{2},3}}^{i}} \right),$

$h_{{H - 3}}^{{2,i}} = \frac{1}{{\Delta x}}\left( {c_{{M - 2 + \frac{1}{2},H - 3}}^{i} - \bar {c}_{{M - 3 + \frac{1}{2},H - 3}}^{i}} \right),\quad \tilde {h}_{3}^{{1,i}} = \frac{1}{{\Delta x}}\left( {c_{{2 + \frac{1}{2},3}}^{i} - \bar {c}_{{1 + \frac{1}{2},3}}^{i}} \right),$

$\tilde {h}_{{H - 3}}^{{1,i}} = \frac{1}{{\Delta x}}\left( {c_{{2 + \frac{1}{2},H - 3}}^{i} - \bar {c}_{{1 + \frac{1}{2},H - 3}}^{i}} \right),\quad h_{3}^{{2,i}} = - \frac{1}{{\Delta x}}c_{{2 + \frac{1}{2},3}}^{i},\quad h_{{H - 3}}^{{2,i}} = - \frac{1}{{\Delta x}}c_{{2 + \frac{1}{2},H - 3}}^{i},$

$g_{{2,H - 3}}^{i} = - \frac{1}{2}\frac{1}{{\Delta {{S}^{2}}}}a_{{2,H - 2}}^{i} + \frac{1}{{\Delta S}}\bar {b}_{{2,H - 3 + \frac{1}{2}}}^{i},\quad g_{{2,3}}^{i} = - \frac{1}{2}\frac{1}{{\Delta {{S}^{2}}}}a_{{2,2}}^{i} - \frac{1}{{\Delta S}}b_{{2,2 + \frac{1}{2}}}^{i},$

$g_{{2,H - 2}}^{i} = \frac{1}{{\Delta {{S}^{2}}}}a_{{2,H - 2}}^{i} + \frac{1}{{\Delta S}}\left( {b_{{2,H - 2 + \frac{1}{2}}}^{i} - \bar {b}_{{2,H - 3 + \frac{1}{2}}}^{i}} \right) + \frac{1}{{\Delta x}}\left( {c_{{2 + \frac{1}{2},H - 2}}^{i} - \bar {c}_{{1 + \frac{1}{2},H - 2}}^{i}} \right),$

$g_{{2,2}}^{i} = \frac{1}{{\Delta {{S}^{2}}}}a_{{2,2}}^{i} + \frac{1}{{\Delta S}}\left( {b_{{2,2 + \frac{1}{2}}}^{i} - \bar {b}_{{2,1 + \frac{1}{2}}}^{i}} \right) + \frac{1}{{\Delta x}}\left( {c_{{2 + \frac{1}{2},2}}^{i} - \bar {c}_{{1 + \frac{1}{2},2}}^{i}} \right),$

$g_{{3,H - 2}}^{i} = - \frac{1}{{\Delta x}}c_{{2 + \frac{1}{2},H - 2}}^{i},\quad g_{{3,2}}^{i} = - \frac{1}{{\Delta x}}c_{{2 + \frac{1}{2},2}}^{i},$

$g_{{M - 2,H - 3}}^{i} = - \frac{1}{2}\frac{1}{{\Delta {{S}^{2}}}}a_{{M - 2,H - 2}}^{i} + \frac{1}{{\Delta S}}\bar {b}_{{M - 2,H - 3 + \frac{1}{2}}}^{i},$

$g_{{M - 2,3}}^{i} = - \frac{1}{2}\frac{1}{{\Delta {{S}^{2}}}}a_{{M - 2,2}}^{i} - \frac{1}{{\Delta S}}b_{{M - 2,2 + \frac{1}{2}}}^{i},$

$g_{{M - 2,H - 2}}^{i} = \frac{1}{{\Delta {{S}^{2}}}}a_{{M - 2,H - 2}}^{i} + \frac{1}{{\Delta S}}\left( {b_{{M - 2,H - 2 + \frac{1}{2}}}^{i} - \bar {b}_{{M - 2,H - 3 + \frac{1}{2}}}^{i}} \right) + \frac{1}{{\Delta x}}\left( {c_{{M - 2 + \frac{1}{2},H - 2}}^{i} - \bar {c}_{{M - 3 + \frac{1}{2},H - 2}}^{i}} \right),$

$g_{{M - 2,2}}^{i} = \frac{1}{{\Delta {{S}^{2}}}}a_{{M - 2,2}}^{i} + \frac{1}{{\Delta S}}\left( {b_{{M - 2,2 + \frac{1}{2}}}^{i} - \bar {b}_{{M - 2,1 + \frac{1}{2}}}^{i}} \right) + \frac{1}{{\Delta x}}\left( {c_{{M - 2 + \frac{1}{2},2}}^{i} - \bar {c}_{{M - 3 + \frac{1}{2},2}}^{i}} \right),$

$g_{{M - 3,H - 2}}^{i} = \frac{1}{{\Delta x}}\bar {c}_{{M - 3 + \frac{1}{2},H - 2}}^{i},\quad g_{{M - 3,2}}^{i} = \frac{1}{{\Delta x}}\bar {c}_{{M - 3 + \frac{1}{2},2}}^{i},$

$g_{{j,H - 3}}^{i} = - \frac{1}{2}\frac{1}{{\Delta {{S}^{2}}}}a_{{j,H - 2}}^{i} + \frac{1}{{\Delta S}}\bar {b}_{{j,H - 3 + \frac{1}{2}}}^{i},\quad j = \overline {3,M - 3} ,$

$g_{{j,3}}^{i} = - \frac{1}{2}\frac{1}{{\Delta {{S}^{2}}}}a_{{j,2}}^{i} - \frac{1}{{\Delta S}}b_{{j,2 + \frac{1}{2}}}^{i},\quad j = \overline {3,M - 3} ,$

$g_{{j,H - 2}}^{i} = \frac{1}{2}\frac{1}{{\Delta {{S}^{2}}}}a_{{j,H - 2}}^{i} + \frac{1}{{\Delta S}}\left( {b_{{j,H - 2 + \frac{1}{2}}}^{i} - \bar {b}_{{j,H - 3 + \frac{1}{2}}}^{i}} \right),\quad j = \overline {3,M - 3} ,$

$g_{{j,2}}^{i} = \frac{1}{2}\frac{1}{{\Delta {{S}^{2}}}}a_{{j,2}}^{i} + \frac{1}{{\Delta S}}\left( {b_{{j,2 + \frac{1}{2}}}^{i} - \bar {b}_{{j,1 + \frac{1}{2}}}^{i}} \right),\quad j = \overline {3,M - 3} ,$

$r_{{j,k}}^{i} = 2\left( {\tilde {m}_{{j,k}}^{i} - m_{{j,k}}^{i}} \right).$

Тогда граничные условия задаются следующим образом:

(24)

$v_{{M - 3,H - 2}}^{{i - 1}} = \frac{{r_{{M - 3,H - 2}}^{{i - 1}} - g_{{M - 3,H - 3}}^{{i - 1}}v_{{M - 3,H - 3}}^{i}}}{{g_{{M - 3,H - 2}}^{{i - 1}}}},\quad i = \overline {1,N - 1} ,$

(25)

$v_{{M - 3,2}}^{{i - 1}} = \frac{{r_{{M - 3,2}}^{{i - 1}} - g_{{M - 3,3}}^{{i - 1}}v_{{M - 3,3}}^{i}}}{{g_{{M - 3,2}}^{{i - 1}}}},\quad i = \overline {1,N - 1} ,$

(26)

$v_{{M - 2,H - 3}}^{{i - 1}} = \frac{{r_{{M - 2,H - 3}}^{{i - 1}} - h_{{H - 3}}^{{1,i - 1}}v_{{M - 3,H - 3}}^{i}}}{{h_{{H - 3}}^{{2,i - 1}}}},\quad i = \overline {1,N - 1} ,$

(27)

$v_{{M - 2,3}}^{{i - 1}} = \frac{{r_{{M - 2,3}}^{{i - 1}} - h_{3}^{{1,i - 1}}v_{{M - 3,3}}^{i}}}{{h_{3}^{{2,i - 1}}}},\quad i = \overline {1,N - 1} ,$

(28)

$v_{{M - 2,H - 2}}^{{i - 1}} = \frac{{r_{{M - 2,H - 2}}^{{i - 1}} - g_{{M - 2,H - 3}}^{{i - 1}}v_{{M - 2,H - 3}}^{i} - g_{{M - 3,H - 2}}^{{i - 1}}v_{{M - 3,H - 2}}^{i}}}{{g_{{M - 2,H - 2}}^{{i - 1}}}},\quad i = \overline {1,N - 1} ,$

(29)

$v_{{M - 2,2}}^{{i - 1}} = \frac{{r_{{M - 2,2}}^{{i - 1}} - g_{{M - 2,3}}^{{i - 1}}v_{{M - 2,3}}^{i} - g_{{M - 3,2}}^{{i - 1}}v_{{M - 3,2}}^{i}}}{{g_{{M - 2,2}}^{{i - 1}}}},\quad i = \overline {1,N - 1} ,$

(30)

$v_{{2,H - 3}}^{{i - 1}} = \frac{{r_{{2,H - 3}}^{{i - 1}} - \tilde {h}_{{H - 3}}^{{2,i - 1}}v_{{3,H - 3}}^{i}}}{{\tilde {h}_{{H - 3}}^{{1,i - 1}}}},\quad i = \overline {1,N - 1} ,$

(31)

$v_{{2,3}}^{{i - 1}} = \frac{{r_{{2,3}}^{{i - 1}} - \tilde {h}_{3}^{{2,i - 1}}v_{{3,3}}^{i}}}{{\tilde {h}_{3}^{{1,i - 1}}}},\quad i = \overline {1,N - 1} ,$

(32)

$v_{{3,H - 2}}^{{i - 1}} = \frac{{r_{{3,H - 2}}^{{i - 1}} - g_{{3,H - 3}}^{{i - 1}}v_{{3,H - 3}}^{i}}}{{g_{{3,H - 2}}^{{i - 1}}}},\quad i = \overline {1,N - 1} ,$

(33)

$v_{{3,2}}^{{i - 1}} = \frac{{r_{{3,2}}^{{i - 1}} - g_{{3,3}}^{{i - 1}}v_{{3,3}}^{i}}}{{g_{{3,2}}^{{i - 1}}}},\quad i = \overline {1,N - 1} ,$

(34)

$v_{{2,H - 2}}^{{i - 1}} = \frac{{r_{{2,H - 2}}^{{i - 1}} - g_{{2,H - 3}}^{{i - 1}}v_{{2,H - 3}}^{i} - g_{{3,H - 2}}^{{i - 1}}v_{{3,H - 2}}^{i}}}{{g_{{2,H - 2}}^{{i - 1}}}},\quad i = \overline {1,N - 1} ,$

(35)

$v_{{2,2}}^{{i - 1}} = \frac{{r_{{2,2}}^{{i - 1}} - g_{{2,3}}^{{i - 1}}v_{{2,3}}^{i} - g_{{3,2}}^{{i - 1}}v_{{3,2}}^{i}}}{{g_{{2,2}}^{{i - 1}}}},\quad i = \overline {1,N - 1} .$

Таким образом, сопряженное уравнение задается динамическим уравнением (22), терминальным условием (23) и краевыми условиями (24)–(35).

Замечание 3. Если знаменатель обращается в ноль в уравнениях (24)–(35), то это соответствует нулевой плотности распределения в данной точке, и значение сопряженной переменной может быть любым. Для определенности будем считать, что сопряженная переменная в этой точке равна нулю.

4. РЕЗУЛЬТАТЫ РАСЧЕТОВ

Статистические данные ОБДХ собираются Росстатом ежеквартально и охватывают около 50 000 домашних хозяйств из 82 регионов России. На основе данных по уровню потребления на душу населения эти регионы были разделены на 3 группы: богатую, среднюю и бедную. Согласно статистике ОБДХ, около половины домашних хозяйств из бедной группы регионов проживают в городском типе населенного пункта, а оставшееся половина в селе. Поскольку стиль жизни в городе отличается от села, то данная группа регионов была разделена еще на две. В каждой группе регионов выделяются слои населения с разными уровнями доходов и расходов.

Среди участников опроса ОБДХ мы выделили заемщиков в каждой группе регионов. Заемщики делятся на два типа: низкодоходные и высокодоходные. Они имеют разные поведенческие параметры, такие как скорость обращения денег $\frac{1}{\theta }$, темп роста доходов $\gamma $, параметр волатильности доходов $\sigma $. Граница разделения заемщиков на низкодоходных и высокодоходных проводится с помощью программного комплекса [10]. Чтобы обеспечить непрерывность этих параметров, вводится “серая зона”, центром которой является граница разделения заемщиков, склеивающая параметры $\theta $, $\sigma $, $\gamma $ по непрерывности.

Участники опроса ОБДХ меняются каждый год, но в течение каждого года опрашиваются одни и те же домашние хозяйства. Исходя из этого, алгоритм идентификации статистической плотности распределения проводился в каждом году независимо с 2015 по 2020 г. В качестве примера рассмотрим домашние хозяйства, проживающие в средней группе регионов в 2020 г. Статистическую плотность распределения построим на плоскости $S$, $x$, основываясь практически на 5000 домашних хозяйств, которые оказались заемщиками из средней группы регионов. Обозначим через ${{D}_{1}}$ низкодоходных заемщиков, а через ${{D}_{2}}$ – высокодоходных. Пусть ${{\sigma }_{{{{D}_{1}}}}} = 0.01$, ${{\sigma }_{{{{D}_{2}}}}} = 0.02$, ${{\theta }_{{{{D}_{1}}}}} = 1$, ${{\theta }_{{{{D}_{1}}}}} = 3$. Для удобства масштабирования денежные единицы будем понимать в тысячах рублей. Параметры сетки: ${{L}_{1}} = 500$, ${{L}_{2}} = 150$, ${{S}_{1}} = 0$, ${{S}_{2}} = 60$, $M = 400$, $H = 100$, $N = 100$. Временной горизонт $T = 1$, параметры оптимизационного алогритма $h = 4$, $\varepsilon {{ = 10}^{{ - 4}}}$. Ограничим вариацию управления на каждой итерации величиной $0.2$. Оптимизацию будем проводить в области платежеспособных заемщиков, в случае, если домашнее хозяйство находится в области банкроства, мы считаем, что его потребление находится на минимуме. Функционал экстремальной задачи также рассматривается на области платежеспособных заемщиков.

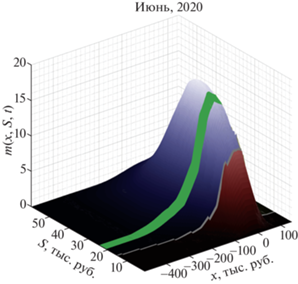
На фиг. 2–7 представлены расчетные данные, полученные с помощью решения уравнения Колмогорова–Фоккера–Планка в различные временные периоды 2020 г. На фиг. 2, 4, 6 показаны плотности распределения в трехмерном отображении, а на фиг. 3, 5, 7 – в проекции на плоскость доходов и финансового состояния. Синим цветом изображены заемщики, красным – банкроты, которые не имеют возможности расплатиться с потребительским кредитом при текущей экономической ситуции. Оранжевым изображены домашние хозяйства, которые не берут займы по потребительскому кредиту. Зеленая полоса вдоль оси $x$ – “серая зона”, склеивающая до непрерывности параметры низкодоходных и высокодоходных заемщиков.

Фиг. 2.

Расчет плотности распределения домашних хозяйств в январе 2020 г.

Фиг. 3.

Расчет плотности распределения домашних хозяйств в январе 2020 г. (вид сверху).

Фиг. 4.

Расчет плотности распределения домашних хозяйств в июне 2020 г.

Фиг. 5.

Расчет плотности распределения домашних хозяйств в июне 2020 г. (вид сверху).

Фиг. 6.

Расчет плотности распределения домашних хозяйств в декабре 2020 г.

Фиг. 7.

Расчет плотности распределения домашних хозяйств в декабре 2020 г. (вид сверху).

Для данного примера среднее отклонение плотности распределения, полученной при решении уравнения Колмогорова–Фоккера–Планка, по сравнению со статистической плотностью распределения составляет $9.4\% $, т.е.

$\frac{{\int\limits_0^T {\kern 1pt} \iint\limits_\Omega \left| {\tilde {m}(x,S,t) - m(x,S,t)} \right|dxdSdt}}{{\int\limits_0^T {\kern 1pt} \iint\limits_\Omega \,\tilde {m}(x,S,t)dxdSdt}} = 0.094,$

где $\Omega $ – область платежеспособных заемщиков на плоскости $x$ и $S$. Средние отклонения для остальных групп регионов на всех рассматриваемых периодах представлены в Приложении.

Отметим, что для данного примера были проведены $139$ итераций алгоритма поиска минимизатора, представленного в разд. 2. Поскольку мы ищем локальный экстремум задачи, нет гарантии монотонности итерационого алгоритма. В случае нарушения монотонности, воспроизводится предыдущая итерация и делится шаг сходимости $h$ пополам. Динамика итерационной сходимости представлена на фиг. 8.

Фиг. 8.

Значение функционала экстремальной задачи в зависимости от номера итерации оптимизационного алгоритма.

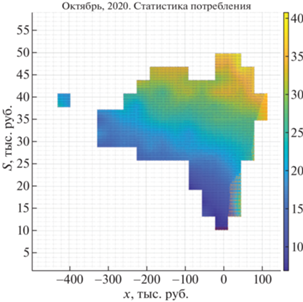
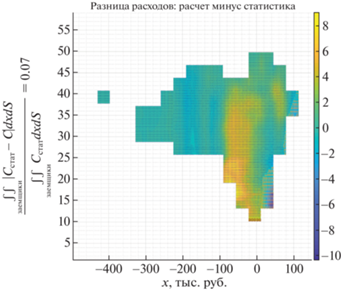
Представим зачение потребления, полученного при решении экстремальной задачи и сравним его со статистическими данными в октябре 2020 г. (см. фиг. 9–11). Как видно, найденное потребление сопоставляется со статистическими данными, погрешность составляет порядка $7\% $.

Фиг. 9.

Статистическое потребление по данным ОБДХ.

Фиг. 10.

Разница рассчитанного потребления и статистического.

Фиг. 11.

Рассчитанное потребление.

5. ЗАКЛЮЧЕНИЕ

В работе исследовался вопрос согласованности статистических данных ОБДХ с динамикой плотности распределения домашних хозяйств по доходам и финансовым состояниям с решением уравнения Колмогорова–Фоккера–Планка. Множество всевозможных решений уравнения Колмогорова–Фоккера–Планка формирует подпространство, на которое искалась проекция статистических данных. Задача формализована в виде экстремальной, представлен итерационный алгоритм поиска проекции, построены соответствующие разностные схемы. Численные результаты демонстрируют возможность описания эволюции экономического поведения домашних хозяйств с помощью уравнения Колмогорова–Фоккера–Планка на качественном уровне.

Темой для дальнейшего исследования может служить использование построенной проекции в качестве входных данных для определения поведенческих характеристик домашних хозяйств: отвращения к риску и коэффициента дисконтирования, как это было реализовано для репрезентативного домашнего хозяйства (см. [2]); настройка поведенческих характеристик домашних хозяйств для идентификации полученного потребления в разрезе социальных слоев на региональном уровне, построение прогнозных сценариев.

Автор выражает искренную признательность своему научному руководителю, Александру Алексеевичу Шананину за руководство и помощь в исследовании стохастических задач рамсеевского типа.

Список литературы

Ramsey F.P. A mathematical theory of savings // The Economic Journal. 1928. V. 152. № 38. P. 543–559.
Тарасенко М.В., Трусов Н.В., Шананин А.А. Математическое моделирование экономического положения домашних хозяйств в России // Ж. вычисл. матем. и матем. физ. 2021. Т. 61. № 6. С. 1034–1056.
Shananin A.A., Tarasenko M.V., Trusov N.V. Consumer Loan Demand Modeling // Mathematical Optimization Theory and Operations Research: Recent Trends. 2021. CCIS. V. 1476. P. 417–428.
Shananin A.A., Trusov N.V. The household behaviour modelling based on Mean Field Games approach // Lobachevskii Journal of Mathematics. 2021. V. 42. № 7. P. 1738–1752.
Обследование бюджетов домашних хозяйств [Электронный ресурс] / Федеральная служба государственной статистики. 2015–2020. https://obdx.gks.ru/ (дата обращения: 15.10.2022)
Lachapelle A., Salomon J., Turinici G. Computation of Mean Field equilibria in economics // Mathematical Models and Methods in Applied Sciences. 2010. V. 20. P. 567–588.
Trusov N. Numerical solution of Mean Field Games problems with turnpike effect // Lobachevskii J. Math. 2020. V. 41. № 4. P. 559–573.
Trusov N. Numerical study of the stock market crises based on mean field games approach. Journal of Inverse and Ill-posed Problems. 2021. V. 29. № 6. P. 849–865.
Гулин А.В., Самарский А.А. Численные методы. Москва, 1989.
Свидетельство о государственной регистрации программы для ЭВМ No. 2022619524. “Анализ спроса на потребительский кредит в РФ”. Правообладатель: Трусов Николай Всеволодович. Заявка No. 2022618580. Дата государственной регистрации в Реестре программ для ЭВМ 23 мая 2022 г.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал