Журнал вычислительной математики и математической физики, 2023, T. 63, № 3, стр. 449-464

1. ВВЕДЕНИЕ

При онкологической диагностике в последние десятилетия все чаще используются методы медицинской визуализации, составляющие новое направление – эластографию (см. [1–5] и др.). Эластографические методы основаны на различиях в механических характеристиках (например, в значениях модуля Юнга) здоровых и опухолевых биологических тканей определенных типов. Для иллюстрации приведем следующую таблицу из [6].

Эластографические методы позволяют определить распределения модулей упругости в ткани по ее деформациям в результате внешних сжатий и тем самым выделить подозрительные на онкологию области с повышенными значениями модулей упругости. Некоторые из этих методов уже внедрены в диагностическую практику, а другие, кажущиеся весьма перспективными, находятся в стадии разработки. К числу последних относится так называемая квазистатическая эластография. Она состоит в воздействии на исследуемую часть тела постоянными поверхностными силами, в измерении (или вычислении) возникающих смещений исследуемой биологической ткани, в определении модулей упругости ткани путем решения обратной задачи: “по смещениям найти модули” и в трехмерной визуализации распределений этих модулей.

Деформации (смещения) тканей определяются по данным ультразвуковых исследований или с помощью магнитно-резонансного метода. Принципиальным моментом в такой схеме является решение обратной математической задачи в рамках некоторой модели биологической ткани.

Разработано множество таких моделей различного уровня сложности. Так как зачастую указанные обратные задачи решаются с использованием различной вычислительной техники (персональные компьютеры, вычислительные кластеры, суперкомпьютеры и т.д.), то наиболее перспективными для практической диагностики являются те математические модели, в которых обратные задачи могут быть решены в реальном времени или близко к нему. Поэтому возникают ограничения на модели такого рода. С одной стороны, они должны адекватно отражать соответствующие процессы в биологических тканях, а с другой стороны – быть как можно более простыми с точки зрения математики, давая возможность постановки не очень сложной обратной задачи определения механических характеристик тканей.

Большое распространение получили двумерная и трехмерная эластографические модели, основанные на уравнениях квазистатической теории упругости (см. [5–8]). В них участок исследуемой ткани, характеризуемый распределениями механических модулей, представляется как линейно-упругое изотропное тело, подвергаемое малым поверхностным сжатиям. Решение обратной задачи для таких моделей позволяет найти по известным смещениям ткани распределение этих модулей в рассматриваемой области и, тем самым, найти характерные онкологические включения с повышенным значением модулей. Известно, что трехмерная квазистатическая модель адекватно описывает исследуемые ткани, но обратная задача поиска механических модулей для нее оказывается чрезвычайно трудоемкой. Многочисленные численные эксперименты показали, что для решения трехмерной обратной задачи на персональном компьютере (ПК) средней производительности требуются десятки часов (см. [7–11]). Поэтому решить ее в реальном времени невозможно. Именно по этой причине в настоящее время наиболее интенсивно изучаются двумерные постановки обратных задач квазистатической эластографии, в которых трехмерная биологическая ткань моделируется ее двумерными сечениями (см., например, [5], [7], [9], [12] и др.). Однако даже в двумерных постановках нахождение распределений модулей упругости на ПК требует значительного времени (от десятков минут до часов). Отметим также, что при использовании двумерных постановок обратных задач эластографии (например, в рамках модели плоского деформированного состояния “plane strain”) в сечениях исследуемой ткани могут появляться расчетные ложные включения и другие артефакты (см. [13]).

Таким образом, для эластографии весьма актуальна модификация упомянутой модели квазистатической теории упругости с целью ее возможного упрощения. Оказалось, это можно сделать, учитывая, что соответствующие дифференциальные уравнения модели содержат малый параметр. Соответствующее исследование было проведено для двумерного случая в работе [14], где обратная задача была решена с помощью теории регулярных возмущений уравнений в частных производных. Была получена простая формула, позволяющая решать двумерную обратную задачу на ПК за десятки микросекунд на достаточно подробных сетках. Возникает вопрос: можно ли сделать нечто подобное для трехмерных задач эластографии? Ответ на это положителен, и данная статья посвящена развитию метода малого параметра для решения трехмерных обратных задач эластографии с целью применения к онкологической диагностике в реальном времени.

2. ПРЯМАЯ И ОБРАТНАЯ ЗАДАЧИ ТРЕХМЕРНОЙ ЭЛАСТОГРАФИИ

Будем считать, что исследуемый участок биологической ткани моделируется областью (слоем) $\Omega = [ - \infty ,\infty ] \times [ - \infty ,\infty ] \times [0,c] \subset R_{{xyz}}^{3}$ с границами

а сама ткань характеризуется распределением модуля Юнга $E = E(x,y,z)$ и постоянным коэффициентом Пуассона $\nu = 0.495$. Этот слой подвергается на верхней поверхности ${{G}_{2}}$ воздействию направленной вертикально вниз распределенной силы, а нижняя поверхность слоя ${{G}_{1}}$ неподвижна. Такие предположения характерны для постановок задач трехмерной эластографии (см., например, [12]). В предположениях выполнения для тела $\Omega $ линейной теории упругости (см., например, [5–9]) связь смещений ткани $u(x,y,z),$ $v(x,y,z),$ $w(x,y,z)$ (по осям $Ox,{\kern 1pt} \;Oy,\;Oz$ соответственно) с распределением модуля Юнга и коэффициентом Пуассона описывается системой уравнений в частных производных: где $\theta = \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}$. Считаются также выполненными граничные условия: на ${{G}_{2}}$ и на ${{G}_{1}}$: $u = v = w = 0$. Здесь $({{n}_{x}} = 0,{{n}_{y}} = 0,{{n}_{z}} = - 1) = n$ – нормаль к ${{G}_{2}}$, а ${{f}_{z}} = {{f}_{z}}(x,y)$ есть вертикальная компонента давления на поверхность ${{G}_{2}}$. Определение смещений $u(x,y,z),$ $v(x,y,z),$ $w(x,y,z)$ по известным коэффициентам $E(x,y,z),\;\nu $ составляет прямую задачу трехмерной квазистатической эластографии. Если слой $\Omega $ конечен, т.е. представляется параллелепипедом $[ - a,a] \times [ - b,b] \times [0,c]$ с теми же граничными условиями на верхней и нижней поверхностях и с условиями свободных боковых сторон, то при условиях ${{f}_{z}}(x,y) \in {{C}^{1}}({{G}_{2}}),$ $E(x,y,z) \in {{C}^{1}}(\bar {\Omega })$ и $0 < {{E}_{1}} \leqslant E(x,y,z) \leqslant {{E}_{2}}$ прямая задача однозначно разрешима на классе функций $u(x,y,z)$, ${v}(x,y,z)$, $w(x,y,z) \in W_{2}^{1}(\Omega )$ (см., например, [15, гл. 2, 11], где получены более общие результаты). Здесь ${{E}_{{1,2}}}$ – известные константы. Случай бесконечной области будет изучен ниже. Соответствующие обратные задачи эластографии, с качественной точки зрения, заключаются в нахождении распределения модуля Юнга $E(x,y,z)$ по известным смещениям или функционалам от них (см. [5–12]). Детализация постановки обратной задачи будет рассмотрена в следующих разделах.

Равенства (1), (2) содержат величину $\varepsilon = 1{\text{/}}2 - \nu \approx 0.005$ ($2\varepsilon \approx 0.01$), которую мы будем считать малым параметром. Тогда уравнения (1) можно переписать в форме

где $(x,y,z) \in \Omega {{\backslash }}\partial \Omega $, а граничные условия (2) – в виде При этом по-прежнему выполнены условия на ${{G}_{1}}$: ${{\left. u \right|}_{{z = 0}}} = {{\left. v \right|}_{{z = 0}}} = {{\left. w \right|}_{{z = 0}}} = 0$. В дальнейшем правую часть последнего равенства в (4), связанную с давлением на ${{G}_{2}}$, будем обозначать как

$F(x,y) = - \frac{{(1 + \nu )}}{\nu }{{f}_{z}}(x,y){\kern 1pt} {\kern 1pt} .$

Как уже отмечалось, в практических приложениях прямой и обратной задачи эластографии нужно получать решение быстро и достаточно точно. Только тогда соответствующий алгоритм можно использовать в реальной диагностике. Однако даже численное решение трехмерной прямой задачи (1), (2), основанное на методе конечных элементов или на сеточных методах, весьма трудоемко для сравнительно подробных сеток и требует десятков минут, а иногда и часов, расчетов на ПК средней производительности. Для решения обратной задачи требуются уже десятки часов, и только решение обратной задачи на специальных параметрических классах несколько уменьшает это время (см., например, [13]). В настоящей работе мы предлагаем метод приближенного решения прямой задачи как системы уравнений в частных производных с малым параметром. Этот подход позволяет при определенных дополнительных предположениях получить простые аналитические формулы для решений, которые можно использовать для “быстрого” приближенного решении обратной задачи.

3. ИССЛЕДОВАНИЕ ФОРМАЛЬНОЙ ПРОЦЕДУРЫ МЕТОДА МАЛОГО ПАРАМЕТРА ДЛЯ РЕШЕНИЯ ПРЯМОЙ ЗАДАЧИ

Запишем уравнения (3), (4) в операторной форме. Для этого введем векторную функцию $U = (u(x,y,z),v(x,y,z),w(x,y,z))$, в которой $u(x,y,z),v(x,y,z),w(x,y,z) \in W_{2}^{2}(\Omega )$. Определим дифференциальные операторы, действующие из $W = W_{2}^{2}(\Omega ) \times W_{2}^{2}(\Omega ) \times W_{2}^{2}(\Omega )$ в L₂ = L₂(Ω) × L₂(Ω) × $ \times \;{{L}_{2}}(\Omega )$, предполагая, что гладкость коэффициента $E(x,y,z)$ это гарантирует:

Определим также дифференциальные операторы, определяющие граничные условия: Тогда прямую задачу можно записать в форме Решая задачу (5) формально по методу малого параметра для регулярных возмущений (см., например, [16], [17]), получим $U(x,y,z) = \sum\nolimits_{n = 0}^\infty \,{{\varepsilon }^{n}}{{U}_{n}}(x,y,z)$. Здесь векторные функции ${{U}_{n}}(x,y,z),$ $n = 0,1, \ldots ,$ суть решения задач в классе функций $W$ с нормой $\left\| U \right\|_{W}^{2} = \left\| u \right\|_{{W_{2}^{2}}}^{2} + \left\| v \right\|_{{W_{2}^{2}}}^{2} + \left\| w \right\|_{{W_{2}^{2}}}^{2}$.

Если известно, что задачи (6), (7) однозначно разрешимы, то можно ввести линейный оператор $P(U)$ решения задач (7), и тогда

Ряд Неймана (8) сходится к решению задачи (3), (4) если $\varepsilon {{\left\| {P({{U}_{0}})} \right\|}_{W}} < 1$ (см., например, [17]). В этом случае для приближенного решения прямой задачи надо решить задачу для ${{U}_{0}}$ и затем проделать несколько итераций по вычислению величин ${{U}_{n}} = P({{U}_{{n - 1}}}),{\kern 1pt} $ $n = 1,2, \ldots $.

Однако эта формальная схема уже для нулевого приближения ${{U}_{0}} = ({{u}_{0}},{{v}_{0}},{{w}_{0}})$ сталкивается с проблемой неоднозначности решения. Действительно, из задачи для ${{U}_{0}}$ получим:

и поэтому $E{{\theta }_{0}} = {{F}_{0}} = {\text{const}}$ $\forall (x,y,z) \in \Omega $. С другой стороны, из граничного условия ${{\ell }_{0}}({{U}_{0}}) = (0,0,F(x,y{{))}^{{\text{т}}}},$ $(x,y) \in R_{{xy}}^{2}$, следует: ${{\left. {E(x,y,z){{\theta }_{0}}} \right|}_{{z = c}}} = {{F}_{0}} = F(x,y)$. Поэтому задача для нулевого приближения разрешима только при условии $F(x,y) = {{F}_{0}} = {\text{const}}$. Заметим также, что задача (9) для трех компонент нулевого приближения ${{U}_{0}}$ свелась лишь к одному уравнению: $\frac{{\partial {{u}_{0}}}}{{\partial x}} + \frac{{\partial {{v}_{0}}}}{{\partial y}} + \frac{{\partial {{w}_{0}}}}{{\partial z}} = \frac{{{{F}_{0}}}}{E}$, и это делает данную задачу недоопределенной даже при условии $F(x,y) = {{F}_{0}}$. Таким образом, формальная схема метода малого параметра не реализуема здесь без специальных дополнительных предположений о компонентах решения. Аналогичные проблемы возникают и при решении задач для ${{U}_{n}},\;n > 0$.

4. ДОПОЛНИТЕЛЬНЫЕ ПРЕДПОЛОЖЕНИЯ И АНАЛИТИЧЕСКОЕ РЕШЕНИЕ ДЛЯ ПРИБЛИЖЕНИЙ МАЛОГО ПАРАМЕТРА

Сформулируем группу предположений, используемых в версии метода малого параметра, которую мы будем применять.

Модельные предположения. а) $F(x,y) = {{F}_{0}} = {\text{const}}$ для любых $(x,y) \in R_{{xy}}^{2}$; б) величины $\frac{{\partial u}}{{\partial x}},\;\frac{{\partial v}}{{\partial y}}$ “малы”: формально $\frac{{\partial u}}{{\partial x}}(x,y,z) = 0,{\kern 1pt} $ $\frac{{\partial v}}{{\partial y}}(x,y,z) = 0,{\kern 1pt} $ $(x,y,z) \in \Omega $; в) $E(x,y,z) \in {{C}^{2}}(\Omega ),{\kern 1pt} $ $E(x,y,z) > 0$ и выполнены условия

Полагая ${{U}_{0}} = ({{u}_{0}},{{v}_{0}},{{w}_{0}}{{)}^{{\text{т}}}}$, получим из (9) и (6) для нулевого приближения ${{w}_{0}}$:

Отсюда выводим Поэтому нулевое приближение вертикального смещения есть Формулы (12) и (11) можно использовать при решении прямой и обратной задачи эластографии в нулевом приближении.

Кроме того, из граничного условия ${{\ell }_{0}}({{U}_{0}}) = (0,0,{{F}_{0}}{{)}^{{\text{т}}}},$ $(x,y) \in R_{{xy}}^{2}$, получается связь смещений ${{u}_{0}}(x,y,z),{\kern 1pt} $ ${{v}_{0}}(x,y,z)$ и ${{w}_{0}}(x,y,z)$:

Из предположения б) следует также, что операторы ${{L}_{0}}(U)$ и ${{L}_{1}}(U)$ можно записать как

и, получающаяся из (7) задача для ${{U}_{1}} = ({{u}_{1}}(x,y,z),{{v}_{1}}(x,y,z),{{w}_{1}}(x,y,z))$ – следующего приближения, имеет вид и снова оказывается недоопределенной, так как не заданы ${{u}_{0}}(x,y,z),$ ${\kern 1pt} {{v}_{0}}(x,y,z)$. В дальнейшем мы доопределим эту задачу, используя следующую лемму.

Лемма 1. Если при сделанных модельных предположениях в) функции $u(x,y,z),$ $v(x,y,z)$ подчиняются равенствам

то $\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}} = 0,$ $\frac{{\partial u}}{{\partial x}} = 0,$ $\frac{{\partial v}}{{\partial y}} = 0$ в $\Omega $.

Доказательство. Из равенств (15) получим

Отсюда, с учетом вида (12) функции ${{w}_{0}}$ и свойств в) функции $E$, следует Но должны также выполняться равенства $\frac{{\partial u}}{{\partial x}}(x,y,z) = 0,{\kern 1pt} $ $\frac{{\partial v}}{{\partial y}}(x,y,z) = 0,{\kern 1pt} $ $(x,y,z) \in \Omega $. Проверим это для одной из производных, снова учитывая предположения (10) о $E$ и формулы (16): Аналогичное равенство получается и для другой производной. Лемма 1 доказана.

Подчеркнем, что в лемме доказано следующее: при условиях (15) предположения б) вытекают из в). Из условий (15) и самой леммы 1 также ясно, что для фигурирующих в ней функций $u(x,y,z),$ $v(x,y,z)$ и для элемента $U = (u,v,{{w}_{0}})$ справедливы равенства

Основываясь на этом, доопределим процесс вычисления приближений по методу малого параметра следующим образом. Вычислим ${{w}_{0}}$ по формуле (12). Затем выберем ${{u}_{0}},\;{{v}_{0}}$ так, что они удовлетворяют условиям (15):

Тогда по лемме 1 и в силу равенств (17), (18) задача (14) принимает вид и ее решение есть ${{w}_{1}} = - \frac{2}{\nu }{{w}_{0}}$. Далее, задавая ${{u}_{1}},\;{{v}_{1}}$ в форме ${{u}_{1}} = - \frac{2}{\nu }{{u}_{0}},$ ${{v}_{1}} = - \frac{2}{\nu }{{v}_{0}}$, мы получим функции, для которых снова выполнены условия (15): действительно, и аналогично $\frac{{\partial {{v}_{1}}}}{{\partial z}} = - \frac{{\partial {{w}_{1}}}}{{\partial y}}$. Поэтому по лемме 1 для функций ${{u}_{1}},\;{{{v}}_{1}}$ также получаются равенства $\frac{{\partial {{u}_{1}}}}{{\partial y}} + \frac{{\partial {{v}_{1}}}}{{\partial x}} = 0$, $\frac{{\partial {{u}_{1}}}}{{\partial x}} = 0,$ $\frac{{\partial {{v}_{1}}}}{{\partial y}} = 0$. Тогда, согласно (7) и равенствам (17), (18), получаем задачу для ${{w}_{2}}$: аналогичную по форме задаче для ${{w}_{1}}$. Поэтому ${{w}_{2}} = - \frac{2}{\nu }{{w}_{1}} = {{\left( { - \frac{2}{\nu }} \right)}^{2}}{{w}_{0}}$. Далее, можно взять ${{u}_{2}} = - \frac{2}{\nu }{{u}_{1}} = {{\left( { - \frac{2}{\nu }} \right)}^{2}}{{u}_{0}},$ ${{v}_{2}} = - \frac{2}{\nu }{{v}_{1}} = {{\left( { - \frac{2}{\nu }} \right)}^{2}}{{v}_{0}}$ и аналогичным образом вычислить ${{w}_{3}}$ и т.д. В результате этого процесса получаются функции ${{w}_{n}} = {{\left( { - \frac{2}{\nu }} \right)}^{n}}{{w}_{0}},$ ${{u}_{n}} = {{\left( { - \frac{2}{\nu }} \right)}^{n}}{{u}_{0}},$ ${{{v}}_{n}} = {{\left( { - \frac{2}{\nu }} \right)}^{n}}{{{v}}_{0}},$, $n = 0,1, \ldots $, и решение прямой задачи по методу малого параметра в форме (8) принимает вид Отсюда и из (12), (11) получим а также и эти формулы можно использовать при решении прямой и обратной задач эластографии для рассматриваемой модели. Аналогично можно найти и функции $u,\;{v}$: Важным свойством решения $w$ является то, что оно отличается от ${{w}_{0}}$ на постоянный нормирующий множитель. Это значит, что при практической визуализации нулевое приближение будет отличаться от решения лишь “яркостью”, имея те же структурные особенности изображения. Это важно, так как при эластографической диагностике часто нужно знать не абсолютные значения модуля Юнга, а отношение $E(x,y,z){\text{/}}{{E}_{0}}$, где ${{E}_{0}}$ – характерная величина модуля Юнга здоровой ткани. Существенное превышение единицы для такого отношения есть признак, на который следует обратить внимание при диагностике.

5. РЕШЕНИЕ ПРЯМОЙ ЗАДАЧИ В КОНЕЧНОЙ ОБЛАСТИ

Рассмотренная модель биологической ткани как бесконечного слоя является весьма идеализированной, хотя полученная формула для решения прямой и обратной задач весьма удобна для практического приложения. Оказывается, что эта формула верна и для конечной области – параллелепипеда ${{\Omega }_{0}} = [ - a,a] \times [ - b,b] \times [0,c]$, если сделать дополнительное предположение о давлениях на поверхностях $x = \pm a,$ $y = \pm b$, т.е. задать граничные условия на этих поверхностях в виде

со специальными ${{\bar {f}}_{x}},\;{{\bar {f}}_{y}},\;{{\bar {f}}_{z}}$. Здесь ${{n}_{x}},\;{{n}_{y}},\;{{n}_{z}}$ – соответственно взятые компоненты внутренних нормалей к граням $x = \pm a,$ $y = \pm b$ параллелепипеда. На гранях $z = 0,$ $z = c$ сохраняются условия (2).

Теорема 1. Пусть предположения в) выполнены в ${{\Omega }_{0}}$. Если функции ${{\bar {f}}_{x}},\;{{\bar {f}}_{y}},\;{{\bar {f}}_{z}}$ в граничных условиях (22) имеют вид

где ${{F}_{1}} = \frac{{\nu {{F}_{0}}}}{{(1 + \nu )\left( {1 + \frac{{2\varepsilon }}{\nu }} \right)}}$, то функции $u,\;v,\;w$, вычисляемые по формулам (19), (20), являются решением задачи (1), (2) в области ${{\Omega }_{0}}$.

Доказательство. Так как функции $u,{v},w \in {{C}^{2}}(\Omega )$ удовлетворяют уравнениям (3) и граничным условиям (4) в области ${{\Omega }_{0}}$, а значит, и в области ${{\Omega }_{0}},{{\Omega }_{0}} \subset \Omega $, то для доказательства теоремы достаточно проверить выполнение граничных условий (22) для указанных значений величин ${{\bar {f}}_{x}},\;{{\bar {f}}_{y}},\;{{\bar {f}}_{z}}$. Например, на поверхности $x = a$ с ${{n}_{x}} = - 1,$ ${{n}_{y}} = 0,{\kern 1pt} $ ${{n}_{z}} = 0$, эти условия имеют вид

Для функций $u,\;v,\;w$, представленных формулами (19), (21), верны предположения и заключение леммы 1. Используя это, получим из последних формул: Таким образом, граничные условия (22) на этой поверхности выполнены с указанными в (23) величинами ${{\bar {f}}_{x}},\;{{\bar {f}}_{y}},\;{{\bar {f}}_{z}}$. Аналогично проверяются и другие граничные условия. Поэтому функции $u,\;v,\;w$ из формул (19), (21) удовлетворяют условиям прямой задачи в области ${{\Omega }_{0}}$ и, значит, представляют единственное ее решение для коэффициентов $E(x,y,z)$, подчиненных предположениям в). Теорема 1 доказана.

В заключение этого раздела выясним, какой смысл имеют предположения (10) о модуле Юнга.

Теорема 2. Если в области $\Omega $ (или ${{\Omega }_{0}}$) выполнены условия в), то функция $E$ имеет там вид

$E = \frac{1}{{A(z)x + B(z)y + C(z)}},$

где $A(z),\;B(z),\;C(z)$ – некоторые функции класса ${{C}^{2}}[0,c]$.

Для доказательства достаточно выписать хорошо известные общие решения каждого из уравнений (10) и убедиться, что система этих уравнений имеет общее решение $1{\text{/}}E = A(z)x + B(z)y + C(z)$.

6. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ПО РЕШЕНИЮ ПРЯМОЙ И ОБРАТНОЙ ЗАДАЧ

В этом разделе мы изучим на типичных примерах, насколько точно формула (19) для смещений $w$, полученная при довольно жестких предположениях о модуле Юнга и об исследуемой области, позволяет решать обратную задачу в конечной области и для распределений модуля Юнга, которые могут и не подчиняются предположениям (10). Во всех рассматриваемых задачах величины $E$, $u,\;v,\;w$ выражены в паскалях и метрах соответственно.

Для всех примеров используем следующую схему численных экспериментов по решению обратных задач.

А) Задачи решаем в конечном параллелепипеде ${{\Omega }_{1}} = [0,a] \times [0,b] \times [0,c]$.

Б) Задаем “точное” (модельное) распределение модуля Юнга $E$ в области ${{\Omega }_{1}}$. Решаем для этого $E$ краевую задачу (1) в области ${{\Omega }_{1}}{{\backslash }}\partial {{\Omega }_{1}}$ с граничным условием (2) на поверхности $z = c$ при ${{f}_{z}} = \frac{{\nu {{F}_{0}}}}{{(1 + \nu )}},$ ${{F}_{0}} = {{10}^{3}}$, с условием $u = v = w = 0$ на границе $z = 0$ и с условием типа (22) при ${{\bar {f}}_{x}} = {{\bar {f}}_{y}} = {{\bar {f}}_{z}} = 0$ на границах $x = 0,$ $x = a,$ $y = 0,$ $y = b$ (свободные границы). Для решения такой прямой задачи применяем метод конечных элементов на достаточно подробной сетке. В результате получаются распределения смещений в области ${{\Omega }_{1}}$. Найденные таким путем смещения $w(x,y,z)$ мы будем считать “точными данными” для решения обратной задачи.

В) Решаем обратную задачу по методу малого параметра, т.е. с использованием формулы (19) для нахождения $w(x,y,z)$. Производная в формуле вычисляется в случае приближенных данных с помощью известных методов регуляризации на сетке по переменной $z$ (см., например, [18], [19]).

Модельный пример 1. Соответствующая область ${{\Omega }_{1}}$ представлена на фиг. 1а. Для расчетов при нахождении точных данных обратной задачи по МКЭ использовались сетки, показанные на фиг. 1б. Сетка содержит 90  116 узлов метода конечных элементов. Точное (модельное) распределение модуля Юнга в области задано как

Геометрически это два трехмерных сферически симметричных, “узких” гауссиана. Изобразим их сначала на фиг. 2а как набор точек соответствующей “яркости”, помещенных в ячейки сетки (решение в виде “облака”). Кроме того, изобразим поверхности уровня этих гауссианов, соответствующей половине максимума функции $E(x,y,z)$ из приведенной модельной формулы (фиг. 2б).

Отметим, что для такого распределения $E(x,y,z)$ в пунктах А) и Б) процедуры решения обратной задачи заведомо нарушается ряд предположений, при которых получена формула (19). Кроме того, нарушены и условия (23) теоремы 1, дающей эту формулу для конечной области.

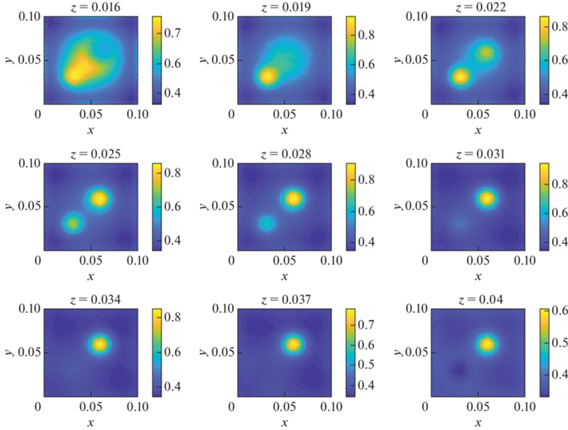
Решим для такого распределения модуля Юнга прямую задачу нахождения смещений $w(x,y,z)$ по МКЭ. Решение для некоторых избранных $z$ представлено на фиг. 3. Теперь по полученным смещениям $w(x,y,z)$ решим обратную задачу восстановления модуля Юнга по методу малого параметра (20). Можно качественно оценить близость точного решения и полученного приближения, сравнивая сечения точного распределения модуля Юнга для разных $z$ (фиг. 4) и аналогичные сечения для приближения (фиг. 5). Для удобства визуализации на этих рисунках приведены отношения $E(x,y,z){\text{/}}{{E}_{{{\text{max}}}}}$, где ${{E}_{{{\text{max}}}}} = 100 \times {{10}^{3}}$ Па. Видно, что “глубокие” слои ($z = 0.016$) решения восстанавливаются хуже, чем верхние ($z = 0.04$). Этот эффект характерен и для других решенных модельных обратных задач. Несмотря на нарушения ряда условий, при которых получены формулы (19), (20), найденное приближенное решение обратной задачи с качественной точки зрения достаточно хорошо отражает структуру неоднородности модельного модуля Юнга. С количественной точки зрения (по цветовому масштабу) оно с удовлетворительной точностью представляет величины отношения $E(x,y,z){\text{/}}{{E}_{{{\text{max}}}}}$.

Можно также представить данные и решение в трехмерной форме (см. фиг. 6).

Модельный пример 2 отличается от первого видом точного решения. Оно представлено на фиг. 7 слева как облако точек и справа – как поверхность уровня, соответствующая половине максимального значения $E$. Геометрически – это трехмерный гауссиан, распределенный около части окружности. Точные данные $w$ для решения обратной задачи и полученное трехмерное приближенное решение $E$ изображены на фиг. 8.

Приведем также пример решения этой модельной задачи для данных, поточечно возмущенных нормально распределенной случайной ошибкой с нулевым средним. Возмущенные данные ${{w}_{\delta }}$ удовлетворяют неравенству

где число $\delta > 0$ определяет уровень относительной поточечной ошибки приближенных данных. Найденное по этим данным при $\delta = 0.001$ приближенное решение обратной задачи изображено на фиг. 9. Из этих расчетов видно, что качественная структура решения сохраняется и при использовании в нашем методе приближенных данных с небольшой ошибкой.

Расчет по формуле (20) на персональном компьютере средней производительности занимает для решенных обратных задач около $20{\kern 1pt} - {\kern 1pt} 25$ миллисекунд для сеток метода конечных элементов с 90 116 узлами (см. фиг. 1). Скорость расчета и достаточная для визуального распознавания точность получаемого приближенного решения позволяют надеяться, что этот подход можно использовать в реальной онкологической диагностике. Можно также использовать такое приближенное решение в качестве начального приближения при решении обратной задачи трехмерной квазистатической эластографии для исходной системы (1), (2) по методам из работ [9–11].

7. ВЫВОДЫ

1. Применение метода малого параметра к решению краевой задачи трехмерной квазистатической эластографии в бесконечном слое, моделирующем исследуемую биологическую ткань, позволяет при определенных предположениях о распределении модуля Юнга получить простую формулу (19) для смещений ткани, вызванных поверхностным сжатием.

2. Полученную формулу можно использовать в виде (20) для приближенного решения трехмерной обратной задачи эластографии: по заданным (измеренным) вертикальным смещениям найти распределение модуля Юнга. Для этого необходимо использовать регуляризованное на сетке приближение для частной производной вертикального смещения по координате $z$.

3. Численные эксперименты для ряда модельных задач показали, что и для конечной области приближенное решение обратной задачи с помощью полученной формулы адекватно отражает основные особенности точного модельного распределения модуля Юнга даже в случае, когда оно не подчиняется ряду условий, использованных при выводе формулы (19).

4. Модельные расчеты на трехмерных сетках размера порядка $100 \times 100 \times 100$ показали, что время решения обратных задач по полученной формуле (20) составляет несколько десятков миллисекунд на персональном компьютере средней производительности. Такая скорость расчета и достаточная для качественной визуализации точность получаемого приближенного решения позволяют надеяться, что предлагаемый подход к решению обратной задачи квазистатической эластографии можно использовать в реальной трехмерной онкологической диагностике.