Акустический журнал, 2019, T. 65, № 3, стр. 311-316
Медленная динамика упругости и диэлектрической проницаемости структурно неоднородных сред, индуцированная интенсивной акустической волной
К. С. Е. Халлер a, К. М. Хедберг a, О. В. Руденко b, c, d, *
a Технологический институт Блекинге
Карлскрона, Швеция
b Московский государственный университет им. М.В. Ломоносова, физический факультет
119991 Москва, Ленинские горы, Россия
c Институт общей физики им. А.М. Прохорова РАН
119991 Москва, ул. Вавилова 38, Россия
d Институт физики Земли им. О.Ю. Шмидта РАН
123242 Москва, Б. Грузинская ул. 10, стр. 1, Россия
* E-mail: rudenko@acs366.phys.msu.ru
Поступила в редакцию 05.01.2019
После доработки 05.01.2019
Принята к публикации 05.01.2019
Аннотация
Экспериментально обнаружена взаимосвязь между изменениями упругости и диэлектрической проницаемости структурно неоднородных конденсированных сред при воздействии на них интенсивного ультразвука. Для объяснения результатов измерений разработана феноменологическая теория, обобщающая подход Дебая для полярных жидкостей. Замена акустических измерений на диэлектрические в ряде случаев не только упрощает процедуру, но и открывает новые возможности для дистанционной оценки механических свойств материалов и природных сред.
ВВЕДЕНИЕ
В последние 20 лет наблюдается повышенный интерес к проблемам медленной динамики сред с неоднородностями мезоскопического (надмолекулярного) масштаба [1]. К настоящему времени накоплено много экспериментальных данных по эволюции параметров структурно неоднородных материалов, подвергнутых акустическому облучению. Среди них – гранит, песчаник, известняк, гранулированные сыпучие среды, а также стекла, пластмассы и другие материалы со сложной надмолекулярной структурой. Такие среды часто обладают большой акустической нелинейностью, на 2–4 порядка превосходящей нелинейности обычных однородных сред. Это свойство сейчас широко используется для акустической диагностики и неразрушающего контроля материалов, промышленных изделий, строительных объектов и геологических структур [2].
Примером “медленной динамики” может служить “размягчение” материала на временах порядка десятков секунд, минут и даже часов, то есть на временах, существенно превышающих период акустических колебаний. Чаще всего измерения проводят в стержне (керне) из материала, который является акустическим резонатором. Его резонансная частота обычно со временем медленно “ползет” вниз; при этом часто наблюдается нелинейная деформация частотной характеристики, типичная для нелинейных сред. Иногда при включении звука частота незначительно увеличивается, но с течением времени вновь начинает уменьшаться [3].
Изменения механических свойств неизбежно сопровождаются изменением электрических параметров, таких как диэлектрическая проницаемость и поляризуемость среды. Этот факт открывает возможность наблюдения медленной динамики с помощью электрических измерений. Тем самым может быть реализован новый способ акустоэлектрической или акустомагнитной диагностики.
ВЛИЯНИЕ УПРУГОСТИ НА ПОЛЯРИЗАЦИЮ ДИЭЛЕКТРИКОВ
Как известно, молекулы полярных диэлектриков (например, воды) обладают дипольным моментом в отсутствие внешнего электрического поля. Механизм поляризации такого диэлектрика сводится к ориентирующему действию поля на молекулы. Ориентационная поляризация является основным механизмом для газов, жидкостей, а также кристаллов, в которых дипольные моменты могут поворачиваться. Преимущественную ориентацию способны приобретать не только молекулы, но и поляризованные зерна поликристаллов или домены магнетиков в магнитном поле. Однако при изложении теории мы будем говорить (для определенности) о вращении ансамбля полярных молекул твердой среды в электрическом поле.
Уравнение вращательного движения молекулы имеет вид [4]:
Здесь ${{I}_{{ik}}}$ – тензор инерции, ${{\Omega }_{k}}$ – угловая скорость, ${{K}_{i}}$ – момент действующих сил. Для движения в плоскости, проходящей через ось молекулы (ее дипольный момент ${\mathbf{d}}$) и вектор электрического поля ${\mathbf{E}}$, уравнение (1) примет вид
(2)
$I\frac{{d\Omega }}{{dt}} = {{\left[ {{\mathbf{d}} \times {\mathbf{E}}} \right]}_{{\vec {\Omega }}}} = - dE\sin \theta .$Здесь $\theta $ – угол между векторами дипольного момента и поля. Проекция векторного произведения берется на направление вектора угловой скорости, ортогонального рассматриваемой плоскости. Добавляя в уравнение (2) моменты сил трения, действующих на молекулу при ее вращении, и сил упругого сопротивления окружающей молекулу среды, получим
(3)
$I\frac{{{{d}^{2}}\theta }}{{d{{t}^{2}}}} + \nu \frac{{d\theta }}{{dt}} + dE\sin \theta + \beta {{R}^{2}}\sin \left( {\theta - {{\theta }_{0}}} \right) = 0.$Здесь $\nu $ – эффективная вязкость, $\beta $ – упругость, $R$ – характерная длина диполя, ${{\theta }_{0}}$ – значение угла $\theta $ в отсутствие поля.
Очевидно, что для медленных движений (на низких частотах) диполь “демпфирован” и не может совершать добротных колебаний; в этом интересующем нас случае второй производной по времени в уравнении (3) можно пренебречь. Решение получаемого при этом упрощении нелинейного уравнения первого порядка имеет вид
(4)
$\cos \left( {\theta - {{\theta }_{{{\text{st}}}}}} \right) = \frac{{\operatorname{th} \left( {{t \mathord{\left/ {\vphantom {t {t{\text{*}}}}} \right. \kern-0em} {t{\text{*}}}}} \right) + \cos \left( {{{\theta }_{0}} - {{\theta }_{{{\text{st}}}}}} \right)}}{{1 + \operatorname{th} \left( {{t \mathord{\left/ {\vphantom {t {t{\text{*}}}}} \right. \kern-0em} {t{\text{*}}}}} \right)\cos \left( {{{\theta }_{0}} - {{\theta }_{{{\text{st}}}}}} \right)}}.$Решение (4) описывает поворот молекулы из исходного положения (при $t = 0$), характеризуемого углом ${{\theta }_{0}},$ в конечное (при $t \to \infty $), для которого угол $\theta $ принимает стационарное значение ${{\theta }_{{{\text{st}}}}},$ определяемое соотношением
(5)
${\text{tg}}{{\theta }_{{{\text{st}}}}} = \frac{{\beta {{R}^{2}}\sin {{\theta }_{0}}}}{{dE + \beta {{R}^{2}}\cos {{\theta }_{0}}}}.$Во всех случаях ${{\theta }_{{{\text{st}}}}} < {{\theta }_{0}},$ то есть с течением времени угол между дипольным моментом и вектором напряженности поля уменьшается. Этот процесс идет с характерным временем
(6)
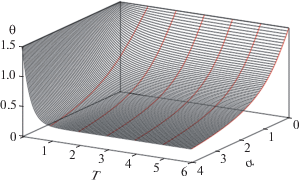
$t* = \frac{{{{t}_{0}}}}{{\sqrt {1 + 2\alpha \cos {{\theta }_{0}} + {{\alpha }^{2}}} }},\,\,\,\,{{t}_{0}} = \frac{\nu }{{\beta {{R}^{2}}}},\,\,\,\,\alpha = \frac{{dE}}{{\beta {{R}^{2}}}}.$На рис. 1 изображен процесс приближения угла между осью диполя и направлением электрического поля к своему стационарному значению, определяемому уравнением (5), при различных значениях параметра α. Исходное (в момент $T = {t \mathord{\left/ {\vphantom {t {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}} = 0)$ значение этого угла для всех кривых положено равным ${{\theta }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}.$ Время установления (6) уменьшается с ростом как напряженности поля, так и механической упругости среды. В очень сильных полях, при значениях $E \to \infty ,$ стационарный угол ${{\theta }_{{{\text{st}}}}} \to 0,$ то есть дипольный момент ориентируется вдоль поля. В слабых полях $\theta \approx {{\theta }_{0}}.$ Зависимость времени установления от электрических и упругих свойств свидетельствует о том, что в сильных электрических и механических полях частотная зависимость диэлектрической проницаемости определяется напряженностью этих полей, то есть является нелинейной.
Потенциал приложенных сил, как следует из уравнения (3), дается формулой
(7)
$U - {{U}_{0}} = - dE\cos \theta - \beta {{R}^{2}}\cos \left( {\theta - {{\theta }_{0}}} \right).$Несущественную константу ${{U}_{0}}$ положим равной нулю. Поскольку в отсутствие электрического поля оси диполей расположены хаотически и не имеют преимущественной ориентации, проведем усреднение по углам ${{\theta }_{0}}$ в сферической системе координат, полярная ось которой направлена вдоль вектора ${\mathbf{E}}$. С учетом очевидных соотношений
(8)
$\overline {\sin {{\theta }_{0}}} = \frac{{\int\limits_0^\pi {{{{\sin }}^{2}}{{\theta }_{0}}d{{\theta }_{0}}} }}{{\int\limits_0^\pi {\sin {{\theta }_{0}}d{{\theta }_{0}}} }} = \frac{\pi }{4},\,\,\,\,\overline {\cos {{\theta }_{0}}} = 0$Дипольный момент единицы объема (поляризация) среды складывается из суммы проекций на направление ${\mathbf{E}}$ дипольных моментов всех N молекул, находящихся в этом объеме. Поскольку тепловое движение молекул приводит к флуктуациям углов θ, поляризация равна
В данном случае угловые скобки означают усреднение по углам между векторами ${\mathbf{E}}$ и ${\mathbf{d}}$.
Воспользуемся статистическим законом распределения Больцмана и вычислим интеграл
(11)
$\left\langle {\cos \theta } \right\rangle = C\int\limits_0^\pi {\cos \theta \exp \left( { - \frac{{\overline {U\left( \theta \right)} }}{{kT}}} \right)\sin \theta d\theta } .$Здесь $C$ – нормировочная константа, а $\bar {U}$ дается формулой (9). Нас интересуют слабые электрические поля, в которых нелинейные поляризационные эффекты не существенны. Поэтому разложим под интегралом (11) потенциальную энергию в ряд по степеням ${\mathbf{E}}$ с удержанием только линейных членов. При этом формула (11) примет вид
(12)
$\begin{gathered} \left\langle {\cos \theta } \right\rangle = \frac{{dE}}{{kT}}F(b), \\ F(b) = \frac{{\int\limits_0^\pi {\sin \theta {{{\cos }}^{2}}\theta \exp \left( {b\sin \theta } \right)d\theta } }}{{\int\limits_0^\pi {\sin \theta \exp \left( {b\sin \theta } \right)d\theta } }},\,\,\,\,\,b = \frac{\pi }{4}\frac{{\beta {{R}^{2}}}}{{kT}}. \\ \end{gathered} $Видим, что расчет поляризации свелся к расчету функции $F(b).$ При малых значениях $b \ll 1$ нетрудно вычислить
(13)
$F \approx \frac{1}{3}\left( {1 - \frac{\pi }{{16}}b} \right),\,\,\,\,\left\langle {\cos \theta } \right\rangle = \frac{{dE}}{{3kT}}\left( {1 - \frac{{{{\pi }^{2}}}}{{64}}\frac{{\beta {{R}^{2}}}}{{kT}}} \right).$Первое слагаемое в формуле (13) описывает поляризацию среды без учета упругих сил и является основным для жидкостей и газов. Второе слагаемое описывает уменьшение поляризации с ростом упругого сопротивления повороту элементарных диполей среды. В пределе $b \to \infty $ интегралы (12) можно оценить, используя метод перевала. При этом получается асимптотическая зависимость
(14)
$F \approx \frac{1}{b},\,\,\,\,\left\langle {\cos \theta } \right\rangle = \frac{4}{\pi }\frac{{dE}}{{\beta {{R}^{2}}}}.$Видно, что поляризация (14) убывает с ростом упругости среды так же, как и при $b \ll 1$ (13), однако при сильном влиянии упругости тепловые флуктуации несущественны.
Можно предложить удобную модель, дающую хорошую аппроксимацию функции $F(b)$ при любых значениях b. Заменим экспоненту в интеграле (12) модифицированной функцией Бесселя:
При малых значениях аргументов обеих функций их степенные разложения в первых членах совпадают, а при больших значениях аргументов правая часть (15) обнаруживает приблизительно экспоненциальный рост. Модель (15) сводит интегралы (12) к табличным интегралам вида
(16)
$\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\cos \left( {2\mu x} \right){{I}_{1}}(2b\cos x)dx = \frac{\pi }{2}} {{I}_{{\frac{1}{2} - \mu }}}(b){{I}_{{\frac{1}{2} + \mu }}}(b).$Используя (16), получим общую формулу, аппроксимирующую точные зависимости:
(17)
$\left\langle {\cos \theta } \right\rangle = \frac{{dE}}{{3kT}}\frac{{1 + \frac{{3kT}}{{\beta {{R}^{2}}}}I_{1}^{2}\left( {\frac{\pi }{4}\frac{{\beta {{R}^{2}}}}{{kT}}} \right)}}{{1 + \frac{\pi }{2}{{I}_{0}}\left( {\frac{\pi }{4}\frac{{\beta {{R}^{2}}}}{{kT}}} \right){{I}_{1}}\left( {\frac{\pi }{4}\frac{{\beta {{R}^{2}}}}{{kT}}} \right)}}.$При малых значениях параметра b из этой формулы следует результат (13), а при больших b получается зависимость $\sim {1 \mathord{\left/ {\vphantom {1 {2b}}} \right. \kern-0em} {2b}},$ аналогичная (14).
Зная поляризацию, найдем диэлектрическую проницаемость среды:
(18)
$\varepsilon = 1 + \frac{{4\pi N{{d}^{2}}}}{{kT}}F\left( {\frac{\pi }{4}\frac{{\beta {{R}^{2}}}}{{kT}}} \right).$При получении результата (18) использованы формулы (10), (12), а также известное соотношение ${\mathbf{D}} = \varepsilon {\mathbf{E}} = {\mathbf{E}} + 4\pi {\mathbf{P}},$ связывающее векторы напряженности, электрической индукции и поляризации среды. Поскольку $F(b)$ – убывающая функция, рост упругости среды должен сопровождаться уменьшением ее диэлектрической проницаемости.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Экспериментальные измерения проводились в цилиндрических стержнях из гранита, основной механизм поляризации которых – дипольно-ориентационный. Следовательно, для этого материала справедлива теория, изложенная в предыдущем разделе. Акустическая волна возбуждалась пьезоэлектрическим преобразователем, помещенным на одном из торцов стержня (рис. 2). В стержне возникала стоячая волна на основной моде акустического резонатора. Частота этой волны уменьшалась [3] с увеличением амплитуды переменного напряжения, подаваемого на преобразователь (рис. 3). Этот эффект объясняется влиянием кубичной акустической нелинейности [5, 6]. К поверхности стержня приклеивались пары металлических электродов, формировавшие электрические емкости. Эти емкости измерялись резонансным методом по частоте электрических колебаний, возбуждавшихся электрическим генератором.
Рис. 2.
Схема экспериментальной установки. 1 – гранитный стержень (резонатор), 2 – пластины конденсатора, 3 – пьезоэлектрические преобразователи.
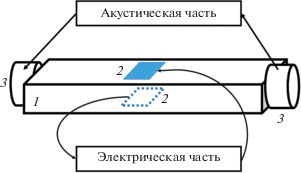
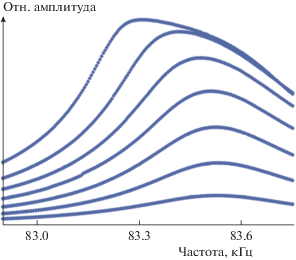
Рис. 3.
Частотная характеристика стержня. Нелинейный сдвиг максимума, вызванный медленным размягчением слабых связей между зернами, растет с увеличением амплитуды ультразвуковых колебаний.
Для сравнения с экспериментом удобно переписать формулу (18) в следующем виде:
(19)
$\frac{d}{{dI}}\ln \left( {\varepsilon - 1} \right) = \frac{d}{{dI}}\ln \left[ {\frac{1}{{kT}}F\left( {\frac{\pi }{4}\frac{{\beta {{R}^{2}}}}{{kT}}} \right)} \right].$Здесь от обеих частей уравнения взята производная по интенсивности звука I. В формуле (19) теперь отсутствуют два физических параметра (дипольный момент одной молекулы d и число дипольно-активных молекул в единице объема N), которые трудно оценить для сред со сложной мезоскопической структурой.
При температурах, меньших температуры плавления образцов, можно положить $b \gg 1$ и воспользоваться соответствующей асимптотикой функции F. При этом явная зависимость от температуры исчезает и остается только зависимость через модуль упругости $\beta = \beta (T).$ В свою очередь, температура растет с увеличением интенсивности ультразвука, то есть $T = T(I),$ поэтому
Можно было бы выписать явные формулы для указанных связей $\beta = \beta (T),$ $T = T(I),$ но в этом нет необходимости. В экспериментах измерялся сдвиг резонансной частоты, которая пропорциональна скорости звука c. В свою очередь, скорость звука пропорциональна квадрату модуля упругости. Поэтому формула (20) примет вид:
Наконец, учтем, что интенсивность пропорциональна квадрату амплитуды колебаний. Кроме того, в экспериментах и резонансная частота, и диэлектрическая проницаемость изменяются мало по сравнению со своими исходными значениями, то есть
Здесь штрихами помечены малые приращения к равновесным значениям, содержащим индекс “ноль”. С учетом сказанного получим формулу
(20)
$\frac{{d\varepsilon {\text{'}}}}{{dA}} = \frac{2}{{{{f}_{0}}}}\left( {{{\varepsilon }_{0}} - 1} \right)\frac{{df{\text{'}}}}{{dA}}.$Здесь в качестве переменной A можно принять как амплитуду электрических колебаний генератора, подаваемых на акустический преобразователь, так и пропорциональную ей амплитуду акустических колебаний.
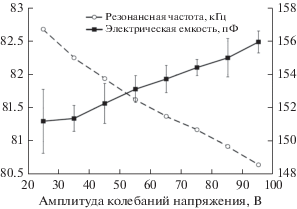
Экспериментально полученная зависимость резонансной частоты от амплитуды показана на рис. 4 штриховой линией. Измеренные зависимости емкости (которая может быть пересчитана в значения диэлектрической проницаемости) для гранита от той же амплитуды изображены сплошной линией. Видно, что наблюдается согласие с формулой (20) в пределах ошибки измерений. Использованы известные данные о диэлектрической проницаемости гранита при заданной влажности.
Рис. 4.
Частота ультразвукового резонанса и электрическая емкость как функции амплитуды возбуждающего напряжения.
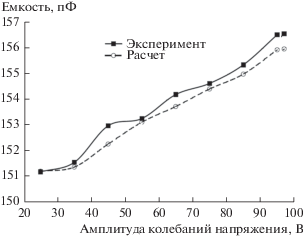
На рис. 5 проведено сравнение измеренной электрической емкости конденсатора (сплошная кривая) и теоретической зависимости емкости от амплитуды возбуждающего акустическую волну напряжения (штриховая кривая). Как видно, поведение кривых качественно не отличается.
Рис. 5.
Измеренная электрическая емкость (сплошная кривая) и теоретическая (штриховая кривая) зависимость емкости от амплитуды возбуждающего акустическую волну напряжения.
Имеющиеся в нашем распоряжении экспериментальные данные позволяют провести лишь простейшее сравнение теории с экспериментом. На самом же деле теория содержит в себе более интересные возможности. Основной вывод, следующий из теоретической модели, заключается в том, что любые изменения упругих свойств и температуры образца должны сопровождаться соответствующим изменением его диэлектрических параметров. В общем случае как электрические, так и упругие свойства зависят от приложенных полей нелинейно. Иными словами, при сильных воздействиях на среду должны наблюдаться явления трех типов: нелинейные акустические, нелинейные электрические явления и эффекты медленной (по сравнению с периодом колебаний) динамики.
Зависимость диэлектрических свойств материалов от их мезоскопической структуры дает возможность судить о наличии внутренних дефектов, включений другой фазы, а также об их прочностных характеристиках на основе точных электрических измерений. С точки зрения физических приложений интересно исследовать этими методами релаксационную и гистерезисную динамику, а также кинетику фазовых переходов.
ЗАКЛЮЧЕНИЕ
Как показано выше, упругие и электрические характеристики многих диэлектриков оказываются связанными между собой. В частности, рост упругости среды должен сопровождаться уменьшением ее диэлектрической проницаемости. Факт существования такой связи хорошо известен.
Известно также, что диэлектрические и упругие свойства сред зависят от их структуры и состава, например, пористости и относительного содержания твердой, жидкой и газовой фаз. Так, с увеличением пористости сухих грунтов диэлектрическая проницаемость уменьшается, а с увеличением влажности растет. Параллельно изменяются и акустические параметры; зернистая среда, содержащая включения в виде слоев жидкости и газовых пор, обладает повышенной акустической нелинейностью и аномально малой скоростью звука [8]. Однако эти и многие другие подобные “электроакустические” связи изучены недостаточно хорошо. Необходимость их изучения связана как с физикой явлений, так и с приложениями.
В области фазового перехода, в процессе плавления конденсированной среды, значение модуля сдвиговой упругости обращается в ноль. Это означает, что исчезает (при плавлении) или появляется (при отвердевании) новая мода – сдвиговая волна. Наличие этой моды служит информативным признаком для акустической диагностики, позволяющим судить о состоянии среды. Измерение скорости сдвиговой волны широко используется в медицинской эластографии [9].
Во многих ситуациях акустическое измерение модуля сдвига не дает приемлемой точности или вообще технически трудно реализуемо. В этих случаях измерение диэлектрической проницаемости и пересчет данных в акустические параметры (на основе адекватной теоретической модели “электроакустической” связи) приобретает особую важность. Принципиальное значение такой подход может иметь для дистанционной диагностики, которая возможна лишь с помощью электрических измерений [10, 11].
Сегодня накоплен большой объем данных по диэлектрической проницаемости влажных и мерзлых почв [12–14], в том числе измеренной в процессе их замерзания [15]. В северных странах, где обширные территории находятся в зоне вечной мерзлоты, дистанционная диагностика акустических (механических) параметров грунта имеет важное значение для предотвращения разрушений строительных объектов. Диагностика состояния ледовых дорог и ледяного покрова также необходима для задач освоения севера, в частности Арктического шельфа.
Заметим, что связь акустических и электрических характеристик в биологических тканях используется в клинической практике, например, при снятии электрокардиограмм. По-видимому, существуют либо могут быть разработаны и другие диагностические методы, использующие подобные связи физических параметров.
Работа частично поддержана грантом РФФИ 19-02-00937.
Список литературы
Guyer R.A., Johnson P.A. Nonlinear mesoscopic elasticity: evidence for a new class of materials // Physics Today. April 1999. P. 30–36.
Rudenko O.V. Giant nonlinearities in structurally inhomogeneous media and the fundamentals of nonlinear acoustic diagnostic techniques // Physics – Uspekhi. 2006. V. 49. № 1. P. 69–87.
Haller K.C.E., Hedberg C.M. Constant strain frequency sweep measurements on granite rock // Phys. Rev. Lett. 2008. V. 100. 068501.
Landau L.D., Lifshitz E.M. Theory of Elasticity. New York: Pergamon, 1986.
Rudenko O.V., Hedberg C.M., Enflo B.O. Finite-amplitude standing acoustic waves in a cubically nonlinear medium // Acoust. Phys. 2007. V. 53. № 4. P. 455–464.
Rudenko O.V. Nonlinear standing waves, resonance phenomena, and frequency characteristics of distributed systems // Acoust. Phys. 2009. V. 55. № 1. P. 27–54.
Gueguen Y., Palciauskas V. Introduction to the physics of rocks. Princeton Univ.Press, 1994.
Руденко О.В., Собисевич А.Л., Собисевич Л.Е., Хедберг К.М., Шамаев Н.В. Нелинейная модель гранулированной среды, содержащей слои вязкой жидкости и газовые полости // Акуст. журн. 2012. Т. 58. № 1. С. 112–120.
Руденко О.В., Сафонов Д.В., Рыхтик П.И., Гурбатов С.Н., Романов С.В. Физические основы эластографии. Часть 2. Эластография на сдвиговой волне (лекция) // Радиология – практика. 2014. Т. 46. № 4. С. 62–72.
Миронов В.Л., Михайлов М.И., Музалевский К.В., Сорокин А.В. Измерение влажности почвы сельскохозяйственных полей с использованием сигналов ГЛОНАСС и GPS // Совр. пробл. дистанц. зондирования Земли из космоса. 2014. Т. 11. № 4. С. 230–343.
Музалевский К.В., Михайлов М.И., Миронов В.Л. Возможности бистатической радиолокации пространственных вариаций влажности и рельефа поверхности почвенного покрова на основе сигналов ГЛОНАСС и GPS // Совр. пробл. дистанц. зондирования Земли из космоса. 2018. Т. 15. № 5. С. 75–82.
Боярский Д.А., Тихонов В.В. Влияние связанной воды на диэлектрическую проницаемость влажных и мерзлых почв. М.: Изд. ИКИ РАН, 2003.
Нерадовский Л.Г. Количественная оценка объемной льдистости мерзлых грунтов методом дипольного электромагнитного профилирования // Лед и Снег. 2018. Т. 58. № 1. С. 94–104.
Бордонский Г.С., Орлов А.О., Хапин Ю.Б. Коэффициент затухания и диэлектрическая проницаемость переохлажденной объемной воды в интервале температур 0–90°С на частотах 11–140 ГГц // Совр. пробл. дистанц. зондирования Земли из космоса. 2017. Т. 14. № 3. С. 255–270.
Бордонский Г.С., Орлов А.О., Филиппова Т.Г. Измерения диэлектрической проницаемости увлажненных дисперсных сред вблизи температуры фазового перехода вода–лед в процессе охлаждения // Конденсир. среды и межфаз. границы. 2006. Т. 8. № 2. С. 95–100.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал