Акустический журнал, 2019, T. 65, № 3, стр. 305-310
О нелинейных и линейных волновых явлениях в узких трубках
О. В. Руденко a, *, А. Б. Шварцбург b
a Московский государственный университет им. М.В. Ломоносова, физический факультет
119991 Москва, Ленинские горы, Россия
b Объединенный институт высоких температур Российской академии наук
125412 Москва, Ижорская ул. 13/19, Россия
* E-mail: rudenko@acs366.phys.msu.ru
Поступила в редакцию 11.01.2019
После доработки 11.01.2019
Принята к публикации 18.02.2019
Аннотация
Рассмотрены явления, возникающие при распространении волн в узких трубках. Для нелинейных волн, описываемых обобщенным уравнением типа Вебстера, получено упрощенное нелинейное уравнение. Оно учитывает низкочастотную геометрическую дисперсию, которая приводит к несимметричному искажению профиля периодической волны, качественно похожему на искажение нелинейной волны в дифрагирующем пучке. Исследован режим туннелирования волны через сужение трубки специального вида. Обсуждены возможные приложения явления и его связь с задачами квантовой механики, обусловленная аналогией базовых уравнений типа Клейна–Гордона и Шредингера. Указано на важность изучения туннелирования нелинейных волн и широкополосных сигналов.
Уравнение Вебстера [1–3] описывает распространение звука в трубках, рупорах, концентраторах и других волноведущих системах переменного поперечного сечения $S(x).$ Здесь $x$ – координата, отсчитываемая вдоль оси системы. Оно применимо для трубок, характерный радиус которых мал по сравнению с длиной волны: ${{r}_{0}}(x) \ll \lambda .$ Кроме того, сечение должно изменяться достаточно медленно, ${{d{{r}_{0}}} \mathord{\left/ {\vphantom {{d{{r}_{0}}} {dx}}} \right. \kern-0em} {dx}} \ll 1.$ Это значит, что касательная к функции, описывающей профиль трубки ${{r}_{0}}(x),$ должна составлять с осью $x$ малые углы [3].
Обобщенное уравнение типа Вебстера возникает в задачах распространения в трубках интенсивного звука [4–6]. Оно используется также при расчетах акустического поля в неоднородных средах в приближении геометрической акустики [4, 5], играя при этом роль уравнения переноса, записанного в лучевых координатах. Осью лучевой трубки является геометрический луч, рассчитанный из уравнения эйконала, а функция $S(x)$ является сечением лучевой трубки. Запишем это уравнение в виде:
(1)
$\frac{{{{\partial }^{2}}p}}{{\partial {{t}^{2}}}} - \frac{{{{c}^{2}}}}{{S\left( x \right)}}\frac{\partial }{{\partial x}}\left[ {S\left( x \right)\frac{{\partial p}}{{\partial x}}} \right] = \frac{\varepsilon }{{{{c}^{2}}\rho }}\frac{{{{\partial }^{2}}{{p}^{2}}}}{{\partial {{t}^{2}}}}.$Здесь $p$ – акустическое давление, $c$ – скорость звука, ${\rho }$ – плотность среды. Введем вместо давления новую функцию $F{\text{:}}$
(2)
$p\left( {x,\,t} \right) = {{F\left( {x,\,t} \right)} \mathord{\left/ {\vphantom {{F\left( {x,\,t} \right)} {\sqrt {S\left( x \right)} }}} \right. \kern-0em} {\sqrt {S\left( x \right)} }}.$Для этой функции уравнение (1) примет вид
(3)
$\begin{gathered} \frac{{{{\partial }^{2}}F}}{{\partial {{x}^{2}}\,}} - \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}F}}{{\partial {{t}^{2}}}} = \\ = \frac{1}{{\sqrt {S\left( x \right)} }}\frac{{{{d}^{2}}\sqrt {S\left( x \right)} }}{{d{{x}^{2}}}}F - \frac{1}{{\sqrt {S\left( x \right)} }}\frac{\varepsilon }{{{{c}^{4}}\rho }}\frac{{{{\partial }^{2}}{{F}^{2}}}}{{\partial {{t}^{2}}}}. \\ \end{gathered} $Без учета акустической нелинейности уравнение (3) является уравнением Клейна–Гордона с зависящим от координаты $x$ коэффициентом. Если ${{S}^{{ - 1/2}}}\left( x \right)$ дается одной из следующих функций:
(4)
$\begin{gathered} C\sin \,\gamma \left( {x + {{x}_{0}}} \right),\,\,\,\,C\cos \,\gamma \left( {x + {{x}_{0}}} \right),\,\,\,\,C\operatorname{sh} \,\gamma \left( {x + {{x}_{0}}} \right), \\ C\operatorname{ch} \,\gamma \left( {x + {{x}_{0}}} \right),\,\,\,\,C\exp \left[ { \pm \gamma \left( {x + {{x}_{0}}} \right)} \right] \\ \end{gathered} $(5)
$\frac{{{{\partial }^{2}}F}}{{\partial {{x}^{2}}\,}} - \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}F}}{{\partial {{t}^{2}}\,}} = \pm {{\gamma }^{2}}F.$При этом волна приобретает низкочастотную дисперсию, закон которой ${{k}^{2}} = {{{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\omega }^{2}}} {{{c}^{2}} \pm {{\gamma }^{2}}}}} \right. \kern-0em} {{{c}^{2}} \pm {{\gamma }^{2}}}}.$ В случаях, когда
Поскольку в модели (1), (3) сечение изменяется медленно на расстояниях порядка длины волны, а нелинейность мала, для бегущих волн уравнение может быть упрощено. Пользуясь методом медленно изменяющегося профиля (см., например, [7]), для волны, бегущей в сторону возрастающих значений координаты $x$, приведем уравнение (3) к виду
(6)
$\frac{\partial }{{\partial \tau }}\left[ {\frac{{\partial F}}{{\partial x\,}} - \frac{\varepsilon }{{{{c}^{3}}\rho \sqrt {S\left( x \right)} }}F\frac{{\partial F}}{{\partial \tau }}} \right] = - \frac{c}{{2\sqrt {S\left( x \right)} }}\frac{{{{d}^{2}}\sqrt {S\left( x \right)} }}{{d{{x}^{2}}}}F.$Здесь $\tau = t - {x \mathord{\left/ {\vphantom {x c}} \right. \kern-0em} c}$ – время в системе координат, бегущей вместе с волной со скоростью звука. Заметим, что переход к приближению медленно изменяющегося профиля в исходной форме уравнения (1) приводит к менее точному уравнению для акустического давления
(7)
$\frac{{\partial p}}{{\partial x}} + \frac{p}{{2S}}\frac{{dS}}{{dx}} - \frac{\varepsilon }{{{{c}^{3}}\rho }}p\frac{{\partial p}}{{\partial \tau }} = 0.$Уравнение (7) эквивалентно уравнению (6) с нулевой правой частью, то есть оно не учитывает дисперсию. Однако уравнение (7) имеет решение (см. [8], задача 7.11) для любой исходной (при $x = 0$) формы профиля волны $p(x = 0,\,t) = {{p}_{0}}\Phi (t){\text{:}}$
(8)
$p = {{p}_{0}}\sqrt {\frac{{S(0)}}{{S(x)}}} \Phi \left( {\tau + \frac{\varepsilon }{{{{c}^{3}}\rho }}p\sqrt {\frac{{S(x)}}{{S(0)}}} \int\limits_0^x {\sqrt {\frac{{S(0)}}{{S(x{\text{'}})}}} } dx{\text{'}}} \right).$В то же время уравнение (6) решается только для некоторых форм поперечного сечения $S(x)$ трубки [9]. Решение (8) описывает волну, нелинейные искажения в которой происходят одинаково в областях положительного и отрицательного давления, поскольку $p( - \tau ) = - p(\tau ).$ При наличии дисперсии в уравнении (6) данная симметрия исчезает. Поэтому, если исходный сигнал был гармоническим, в среде формируется пилообразная волна, в которой полупериод отрицательного давления растянут по длительности и сглажен, а полупериод положительного давления имеет меньшую длительность и большую “амплитуду” [9]. Между гармониками появляются сдвиги фаз, чего не было в решении (8). Аналогичное поведение обнаруживает волна в дифрагирующем пучке; дифракция приводит к схожей низкочастотной дисперсии.
Таким образом, слабая дисперсия, связанная с изменением сечения трубки, ведет к появлению качественно новых особенностей в поведении нелинейной волны.
Интересные явления в трубках обнаруживаются уже в линейном приближении. Одно из принципиальных явлений – эффект туннелирования – изучен недостаточно [10]. Вместе с тем, он представляет большой интерес для акустических, электромагнитных волн и волн иной физической природы. В силу аналогии с уравнением Шредингера классические результаты важны также для понимания тонких эффектов прохождения частиц через потенциальный барьер в задачах квантовой механики.
Интересуемся волнами, гармоническими во времени. Для таких волн уравнение (3) без нелинейного члена примет вид
(9)
$\frac{{{{d}^{2}}F}}{{d{{x}^{2}}}} + \left( {k_{1}^{2} - \frac{1}{{\sqrt {S\left( x \right)} }}\frac{{{{d}^{2}}\sqrt {S\left( x \right)} }}{{d{{x}^{2}}}}} \right)F = 0.$Рассмотрим один из указанных ранее в (4) важный частный случай, когда уравнение (9) превращается в уравнение с постоянными коэффициентами и допускает простое общее решение. Полагая
(10)
$S(x) = {{S}_{m}}{{\operatorname{ch} }^{2}}\left[ {\gamma \left( {x - \frac{d}{2}} \right)} \right],\,\,\,\,\gamma = \frac{2}{d}\operatorname{arch} \,\frac{1}{{\sqrt {{{S}_{m}}} }},$Этот случай соответствует задаче о прохождении волны через перетяжку трубки $0 < x < d,$ изображенную на рис. 1. Участок $0 < x < d$ заполнен средой с плотностью ${{\rho }_{1}}$ и скоростью звука ${{c}_{1}}.$ Вне этого участка трубка заполнена другой средой с плотностью ${{\rho }_{0}}$ и скоростью звука ${{c}_{0}}.$
Рис. 1.
Трубка, которая содержит область сужения II ($0 < x < d$), заполненную средой с плотностью ${{\rho }_{1}}$ и скоростью звука ${{c}_{1}}.$
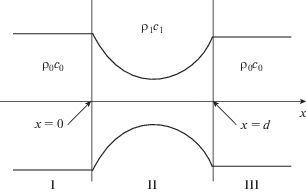
В формулах (9)–(11) ${{k}_{1}} = {\omega \mathord{\left/ {\vphantom {\omega {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}},$ константы ${{S}_{m}},$ $d$ обозначают две геометрические характеристики участка переменной толщины: минимальную безразмерную площадь сужения, достигаемую при значении координаты $x = {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2},$ и длину $d$ этого участка.
Режим туннелирования волны отвечает значению ${{\gamma }^{2}} > k_{1}^{2}.$ Этот режим может быть реализован для низких частот ${{k}_{1}} < \gamma $ или
(12)
$\omega < \frac{{2{{c}_{1}}}}{d}\operatorname{arch} \frac{1}{{\sqrt {{{S}_{m}}} }},\,\,\,\,{{k}_{1}}d < 2\operatorname{arch} \frac{1}{{\sqrt {{{S}_{m}}} }} \equiv 2\varphi .$При этом комплексные амплитуды давления и колебательной скорости в области II, $0 < x < d,$ описываются выражениями
(13)
$\begin{gathered} {{p}_{{{\text{II}}}}} = \frac{1}{{\sqrt S }}\left( {{{P}_{ + }}{{e}^{{ - \mu \,x}}} + {{P}_{ - }}{{e}^{{\mu \,x}}}} \right), \\ {{u}_{{{\text{II}}}}} = \frac{i}{{{{k}_{1}}{{\rho }_{1}}{{c}_{1}}\sqrt S }}\left[ {{{P}_{ + }}{{e}^{{ - \mu \,x}}}\left( {\mu + \frac{{S{\text{'}}}}{{2S}}} \right) - {{P}_{ - }}{{e}^{{\mu \,x}}}\left( {\mu - \frac{{S{\text{'}}}}{{2S}}} \right)} \right]. \\ \end{gathered} $Здесь использовано обозначение $\mu = \sqrt {{{\gamma }^{2}} - k_{1}^{2}} .$ В двух других областях: перед неоднородностью ($x < 0$) и после нее ($x > d$), поля даются формулами
(14)
$\begin{gathered} {{p}_{{\text{I}}}} = {{P}_{i}}{{e}^{{i{{k}_{0}}\,x}}} + {{P}_{r}}{{e}^{{ - i{{k}_{0}}\,x}}}, \\ {{u}_{{\text{I}}}} = \frac{1}{{{{\rho }_{0}}{{c}_{0}}}}\left( {{{P}_{i}}{{e}^{{i{{k}_{0}}\,x}}} - {{P}_{r}}{{e}^{{ - i{{k}_{0}}\,x}}}} \right), \\ \end{gathered} $(15)
${{p}_{{{\text{III}}}}} = {{P}_{t}}{{e}^{{i{{k}_{0}}\,(x - d)}}},\,\,\,\,{{u}_{{{\text{III}}}}} = \frac{1}{{{{\rho }_{0}}{{c}_{0}}}}{{P}_{t}}{{e}^{{i{{k}_{0}}\,(x - d)}}}.$В формулах (14), (15) величины ${{P}_{i}}\,,\,\,\,{{P}_{r}}\,,\,\,{{P}_{t}}$ – это амплитуды падающей, отраженной и прошедшей волн.
Будем считать $S(0) = S(d) = 1.$ Пользуясь выражением (10) для площади сечения, найдем производные на границах неоднородности:
(16)
$\begin{gathered} {{\left. {\frac{{dS}}{{dx}}} \right|}_{{x = 0}}} = - 2b,\,\,\,\,{{\left. {\frac{{dS}}{{dx}}} \right|}_{{x = d}}} = + 2b, \\ b \equiv \frac{2}{d}\sqrt {1 - {{S}_{m}}\,} \operatorname{arch} \frac{1}{{\sqrt {{{S}_{m}}} }}. \\ \end{gathered} $Для того чтобы рассчитать коэффициенты отражения и прохождения волны, нужно потребовать непрерывности полей давления $p$ и скорости $u$
(18)
${{P}_{i}} - {{P}_{r}} = i\frac{\alpha }{{{{k}_{1}}}}\left[ {{{P}_{ + }}\left( {\mu - b} \right) - {{P}_{ - }}\left( {\mu + b} \right)} \right],$(20)
$i\frac{\alpha }{{{{k}_{1}}}}\left[ {{{P}_{ + }}{{e}^{{ - \mu \,d}}}\left( {\mu + b} \right) - {{P}_{ - }}{{e}^{{\mu \,d}}}\left( {\mu - b} \right)} \right] = {{P}_{t}}.$Отношение акустических импедансов двух сред мы обозначили как $\alpha = \left( {{{{{\rho }_{0}}{{c}_{0}}} \mathord{\left/ {\vphantom {{{{\rho }_{0}}{{c}_{0}}} {{{\rho }_{1}}{{c}_{1}}}}} \right. \kern-0em} {{{\rho }_{1}}{{c}_{1}}}}} \right).$
Удобно решать систему (17)–(20) так. Исключим вначале из уравнений (17), (18) амплитуду отраженной волны, а из уравнений (19), (20) – амплитуду прошедшей волны. Тогда получится система двух уравнений
(21)
${{P}_{ + }}\left[ {1 + i\frac{\alpha }{{{{k}_{1}}}}\left( {\mu - b} \right)} \right] + {{P}_{ - }}\left[ {1 - i\frac{\alpha }{{{{k}_{1}}}}\left( {\mu + b} \right)} \right] = 2{{P}_{i}},$(22)
$\begin{gathered} {{P}_{ + }}{{e}^{{ - \mu \,d}}}\left[ {1 - i\frac{\alpha }{{{{k}_{1}}}}\left( {\mu + b} \right)} \right] + \\ + \,\,{{P}_{ - }}{{e}^{{\mu \,d}}}\left[ {1 + i\frac{\alpha }{{{{k}_{1}}}}\left( {\mu - b} \right)} \right] = 0. \\ \end{gathered} $Решение системы (21), (22) имеет вид:
(23)
$\begin{gathered} {{P}_{ + }} = \frac{{2{{P}_{i}}}}{\Delta }{{e}^{{\bar {\mu }\,}}}\left[ {1 + i\frac{\alpha }{{{{{\bar {k}}}_{1}}}}\left( {\bar {\mu } - \bar {b}} \right)} \right], \\ {{P}_{ - }} = - \frac{{2{{P}_{i}}}}{\Delta }{{e}^{{ - \bar {\mu }}}}\,\left[ {1 - i\frac{\alpha }{{{{{\bar {k}}}_{1}}}}\left( {\bar {\mu } + \bar {b}} \right)} \right], \\ \Delta = {{e}^{{\bar {\mu }\,}}}{{\left[ {1 + i\frac{\alpha }{{{{{\bar {k}}}_{1}}}}\left( {\bar {\mu } - \bar {b}} \right)} \right]}^{2}} - {{e}^{{ - \bar {\mu }\,}}}{{\left[ {1 - i\frac{\alpha }{{{{{\bar {k}}}_{1}}}}\left( {\bar {\mu } + \bar {b}} \right)} \right]}^{2}}. \\ \end{gathered} $Здесь чертой сверху обозначены безразмерные величины:
(24)
$\begin{gathered} {{{\bar {k}}}_{1}} = {{k}_{1}}d,\,\,\,\,\bar {\mu } = \mu \,d = \sqrt {4{{\varphi }^{2}} - \bar {k}_{1}^{2}} \,, \\ \bar {b} = bd = \,2\varphi \,\operatorname{th} \varphi . \\ \end{gathered} $Для краткости ниже в тексте статьи черту над безразмерными величинами (24) будем опускать. С помощью выражений (22) и (23) нетрудно рассчитать коэффициенты отражения $R$ и прохождения $T$ волны:
(25)
$\begin{gathered} R = \frac{{{{P}_{r}}}}{{{{P}_{i}}}} = \\ = \frac{{{{e}^{{\mu \,}}}\left[ {1 + \frac{{{{\alpha }^{2}}}}{{k_{1}^{2}}}{{{\left( {\mu - b} \right)}}^{2}}} \right] - {{e}^{{ - \mu \,}}}\left[ {1 + \frac{{{{\alpha }^{2}}}}{{k_{1}^{2}}}{{{\left( {\mu + b} \right)}}^{2}}} \right]}}{{{{e}^{{\mu \,}}}{{{\left[ {1 + i\frac{\alpha }{{{{k}_{1}}}}\left( {\mu - b} \right)} \right]}}^{2}} - {{e}^{{ - \mu \,}}}{{{\left[ {1 - i\frac{\alpha }{{{{k}_{1}}}}\left( {\mu + b} \right)} \right]}}^{2}}}}, \\ \end{gathered} $(26)
$\begin{gathered} T = \frac{{{{P}_{t}}}}{{{{P}_{i}}}} = \\ = \frac{{i\frac{{4\alpha \,\mu }}{{{{k}_{1}}}}}}{{{{e}^{{\mu \,}}}{{{\left[ {1 + i\frac{\alpha }{{{{k}_{1}}}}\left( {\mu - b} \right)} \right]}}^{2}} - {{e}^{{ - \mu \,}}}{{{\left[ {1 - i\frac{\alpha }{{{{k}_{1}}}}\left( {\mu + b} \right)} \right]}}^{2}}}}. \\ \end{gathered} $Выражения (25) и (26) удовлетворяют закону сохранения энергии:
Кроме того, поскольку числитель у выражения (25) чисто действительный, а у (26) – чисто мнимый, между фазами отраженной и прошедшей волн существует связь:
Действительно, расчет приводит к следующим выражениям:
(29)
$\begin{gathered} {{\left| R \right|}^{2}}{{\left| \Delta \right|}^{2}} = \left\{ {{{e}^{{\mu \,}}}\left[ {1 + \frac{{{{\alpha }^{2}}}}{{k_{1}^{2}}}{{{\left( {\mu - b} \right)}}^{2}}} \right]} \right. - \\ {{\left. { - \,\,{{e}^{{ - \mu \,}}}\left[ {1 + \frac{{{{\alpha }^{2}}}}{{k_{1}^{2}}}{{{\left( {\mu + b} \right)}}^{2}}} \right]} \right\}}^{2}}, \\ {{\left| T \right|}^{2}}{{\left| \Delta \right|}^{2}} = 16\frac{{{{\alpha }^{2}}}}{{k_{1}^{2}}}{{\mu }^{2}}\,, \\ {{\left| \Delta \right|}^{2}} = 16\frac{{{{\alpha }^{2}}}}{{k_{1}^{2}}}{{\mu }^{2}} + \\ + \,\,{{\left\{ {{{e}^{{\mu \,}}}\left[ {1 + \frac{{{{\alpha }^{2}}}}{{k_{1}^{2}}}{{{\left( {\mu - b} \right)}}^{2}}} \right] - {{e}^{{ - \mu \,}}}\left[ {1 + \frac{{{{\alpha }^{2}}}}{{k_{1}^{2}}}{{{\left( {\mu + b} \right)}}^{2}}} \right]} \right\}}^{2}}, \\ \end{gathered} $Интересен случай отсутствия отраженной волны (полное прохождение), который, как это следует из формулы (25), может быть реализован при условии
(30)
$\exp \left( {2\mu \,} \right) = \frac{{k_{1}^{2} + {{\alpha }^{2}}{{{\left( {\mu + b} \right)}}^{2}}}}{{k_{1}^{2} + {{\alpha }^{2}}{{{\left( {\mu - b} \right)}}^{2}}}}.$Условие (30) с помощью формул (24) перепишем так:
(31)
$\begin{gathered} \exp \left( {2\sqrt {4{{\varphi }^{2}} - k_{1}^{2}} } \right) = \\ = \frac{{k_{1}^{2} + {{\alpha }^{2}}{{{\left( {\sqrt {4{{\varphi }^{2}} - k_{1}^{2}} + 2\varphi \operatorname{th} \varphi } \right)}}^{2}}}}{{k_{1}^{2} + {{\alpha }^{2}}{{{\left( {\sqrt {4{{\varphi }^{2}} - k_{1}^{2}} - 2\varphi \operatorname{th} \varphi } \right)}}^{2}}}}. \\ \end{gathered} $Для краткости здесь использовано обозначение $\varphi ({{S}_{m}}) = \operatorname{arch} \left( {S_{m}^{{ - 1/2}}} \right).$
Интересно, что при значении $\alpha = 1,$ то есть когда акустические импедансы обеих сред одинаковы, условие (31) принимает следующий вид:
(32)
$\frac{{\operatorname{th} \left( {\sqrt {4{{\varphi }^{2}} - k_{1}^{2}} } \right)}}{{\sqrt {4{{\varphi }^{2}} - k_{1}^{2}} }} = \frac{{\operatorname{th} \left( {2\varphi } \right)}}{{2\varphi }}.$Уравнение (32) имеет единственное решение ${{k}_{1}} = 0,$ отвечающее суживающемуся участку трубки, волновая толщина которого (или частота волны) равна нулю. Нетривиальный по смыслу корень появляется лишь в том случае, когда импедансы сред различны ($\alpha \ne 1$) (см. уравнение (31)).
При фиксированных параметрах сред (число $\alpha > 1$ выбрано), выражение (31) задает неявную зависимость $k_{1}^{2}$от $\varphi .$ Корень этого уравнения определяет частоту, на которой возникает полное прохождение волны, как функцию от геометрических параметров неоднородного участка трубки ${{S}_{m}}$ и $d.$
Результаты анализа уравнения (31) представлены на рис. 2. Верхняя кривая $S_{m}^{{(1)}}$ изображает зависимость минимального сечения в перетяжке от квадратов отношения импедансов ${{\alpha }^{2}}$ двух сред. Эта зависимость монотонно убывает от единицы (при ${{\alpha }^{2}} = 1$) до значения 0.305, определяемого условием
Рис. 2.
Верхняя кривая $S_{m}^{{(1)}}$ дает зависимость минимального сечения в перетяжке неоднородности от квадратов отношения импедансов ${{\alpha }^{2}}$ двух сред, которой соответствует кривая 1 для ${{k}_{1}}d.$ Кривой $S_{m}^{{(2)}}$отвечает значение ${{k}_{1}}d = 0$ – прямая 2. Указан диапазон изменения минимальных сечений, в котором возможно полное прохождение для двух значений частоты и почти полное – в заштрихованной полосе частот между двумя максимумами коэффициента пропускания.
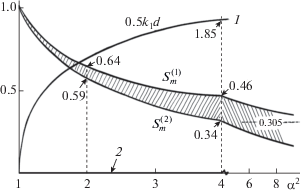
Выбрав некоторое значение ${{\alpha }^{2}}$ и отвечающее ему минимальное сечение $S_{m}^{{(1)}},$ определяем с помощью кривой 1 безразмерную частоту ${{\bar {k}}_{1}} = {{k}_{1}}d.$ Вторая кривая $S_{m}^{{(2)}}$ описывает монотонно убывающую (от единицы до нуля) функцию от ${{\alpha }^{2}};$ этим значениям минимального сечения отвечает значение нулевой частоты ${{\bar {k}}_{1}} = {{k}_{1}}d = 0$ – прямая 2.
Заштрихован диапазон изменения минимальных сечений, в котором возможно полное прохождение волны для двух значений частоты и почти полное – в полосе частот между двумя максимумами коэффициента пропускания.
Итак, для данного значения ${{\alpha }^{2}}$ (параметры сред заданы) из рис. 2 определяется диапазон значений ${{S}_{m}}$. Затем выбирается конкретное значение ${{S}_{m}}$; при этом фиксируется геометрия неоднородности. Наконец, вычисляется значение ${{\bar {k}}_{1}} = {{k}_{1}}d$ (однозначно определяющее частоту), которое лежит между кривой 1 и прямой 2.
Чтобы конкретно пояснить, как можно использовать рис. 2, зафиксируем значение ${{\alpha }^{2}},$ равное, например, ${{\alpha }^{2}} = 4.$ При движении вдоль вертикального штрихового отрезка от оси абсцисс до пересечения с кривой $S_{m}^{{(2)}}$ происходит рост минимального сечения ${{S}_{m}}$ от нуля до 0.34. В этом диапазоне значений ${{S}_{m}}$ коэффициент пропускания имеет только один максимум, равный единице, который достигается при значении безразмерной частоты ${{k}_{1}}d = 0.$ Когда сечение становится равным ${{S}_{m}} = 0.34,$ появляется второй максимум $\left| T \right| = 1,$ лежащий при ${{k}_{1}}d > 0.$ Между двумя максимумами формируется “площадка”, где $\left| T \right| \approx 1$ в конечной полосе частот. Так продолжается вплоть до пересечения с кривой $S_{m}^{{(1)}},$ когда площадь сечения ${{S}_{m}} = 0.46.$ При этом второй максимум $\left| T \right| = 1$ попадает на границу области, в которой справедливо решение (29). Этот качественный анализ с использованием рис. 2 подтверждается результатами численного расчета коэффициента пропускания, изображенными на рис. 3.
Рис. 3.
Частотные зависимости квадрата коэффициента прохождения волны для отношения параметров $\alpha = 2$ и четырех значений минимального сечения трубки ${{S}_{m}} = 0.09,\,0.34,\,0.46,\,0.6$ (кривые 1–4, соответственно).
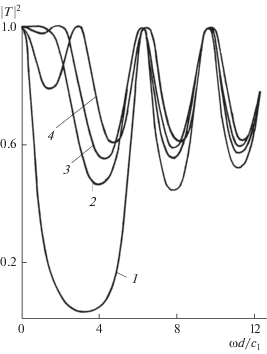
Расчет проведен на основе общих выражений для коэффициента прохождения волны через изображенную на рис. 1 комбинированную неоднородность, которые удобно записать в виде
(33)
$\begin{gathered} {{\left| {T\left( {{{k}_{1}}} \right)} \right|}^{{ - 2}}} = 1 + \frac{{k_{1}^{2}}}{{16{{\alpha }^{2}}{{\mu }^{2}}}}\left\{ {{{e}^{{\mu \,}}}\left[ {1 + \frac{{{{\alpha }^{2}}}}{{k_{1}^{2}}}{{{\left( {\mu - b} \right)}}^{2}}} \right]} \right. - \\ - \,\,{{\left. {{{e}^{{ - \mu \,}}}\left[ {1 + \frac{{{{\alpha }^{2}}}}{{k_{1}^{2}}}{{{\left( {\mu + b} \right)}}^{2}}} \right]} \right\}}^{2}},\,\,\,\,\mu = \sqrt {4{{\varphi }^{2}} - k_{1}^{2}} , \\ 0 < {{k}_{1}} < 2\varphi \,, \\ \end{gathered} $(34)
$\begin{gathered} {{\left| {T\left( {{{k}_{1}}} \right)} \right|}^{{ - 2}}} = 1 + \frac{{k_{1}^{2}}}{{4{{\alpha }^{2}}{{\nu }^{2}}}}\left\{ {\left[ {1 + \frac{{{{\alpha }^{2}}}}{{k_{1}^{2}}}\left( {{{b}^{2}} - {{\nu }^{2}}} \right)} \right]} \right.\sin \nu - \\ - \,\,{{\left. {2\frac{{{{\alpha }^{2}}}}{{k_{1}^{2}}}\nu \,b\,\cos \nu } \right\}}^{2}},\,\,\,\,\nu = \sqrt {k_{1}^{2} - 4{{\varphi }^{2}}} , \\ 2\varphi < {{k}_{1}} < \infty \,. \\ \end{gathered} $Выражения (33) и (34) непрерывно сшиваются в точке ${{k}_{1}} = 2\varphi .$ При больших значениях безразмерной частоты ${{k}_{1}} \gg 2\varphi $ формула (34) переходит в хорошо известное решение (см., например, [11]), описывающее осцилляции коэффициента пропускания $\left| {T\left( {{{k}_{1}}} \right)} \right|.$ Зависимость коэффициента прохождения от частоты, определяемая формулами (33) и (34), изображена на рис. 3. Принято значение $\alpha = 2$ для отношения акустических импедансов, а минимальные сечения суженного участка трубки полагались равными ${{S}_{m}} = 0.09,\,0.34,\,0.46,\,0.6.$
Интересно решить задачу о прохождении широкополосного импульса через неоднородность, имеющую область слабого изменения $\left| {T\left( {{{k}_{1}}} \right)} \right|.$ Такая область может реализоваться, в частности, для параметров ${{S}_{m}} = 0.46,$ $\alpha = 2$ (кривая 3 на рис. 3). Если спектр импульсного сигнала на входе ограничен и лежит в низкочастотной области, например, $0 < \omega < {{2{{c}_{1}}} \mathord{\left/ {\vphantom {{2{{c}_{1}}} d}} \right. \kern-0em} d},$ где коэффициент пропускания примерно равен единице (для кривой 3 на рис. 3), импульс может туннелировать через неоднородность, испытывая лишь фазовые искажения.
При больших значениях ${{\alpha }^{2}} \gg 1$ (это может быть слой газа, окруженный конденсированной средой) и малых сечениях ${{S}_{m}}$ для частоты полного прохождения из выражения (31) получается простая приближенная формула
(35)
$f = \frac{{\sqrt 2 }}{{2\pi }}\frac{{{{c}_{1}}}}{d}\sqrt {{{S}_{m}}} \,\ln \frac{4}{{{{S}_{m}}}}.$Например, при $d = 0.33$ см, ${{S}_{m}} = 0.1$ и для воздушного слоя, ${{c}_{1}} = 330$ м/с, получаем из (30) оценку частоты $f = 26$ кГц.
Явление туннелирования, описанное выше, может, по-видимому, быть использовано при создании частотно-избирательных фильтров с управляемыми характеристиками. По аналогии с лазерной физикой можно подумать и о создании “вентиля”, или модулятора добротности акустического резонатора. Если в начальный момент времени сужение трубки полностью закрыто, ${{S}_{m}} = 0,$ волна через неоднородность пройти не сможет и полностью отразится вовнутрь резонатора, где при высокой добротности может быть накоплена значительная энергия. Если затем достаточно быстро (например, с помощью пьезоэлектрического элемента) увеличить ${{S}_{m}}$ до значения, обеспечивающего режим туннелирования, добротность резко упадет и акустическая энергия “высветится” наружу. Описанный процесс аналогичен действию керровского затвора в лазерах с модулированной добротностью.
В заключение укажем, что данная заметка имеет целью привлечь внимание к проблеме туннелирования волн через специальные профили суживающегося участка трубки. Здесь интересно исследовать прохождение широкополосных сигналов – импульсов и нелинейных волн. Эти явления, конечно, требуют самостоятельного изучения.
Укажем, что эффект туннелирования описан также в обзорных статьях [12, 13]. Нелинейные волны в трубах переменного сечения изучались в работах [14–17].
Работа поддержана грантом РФФИ 18-02-00736.
Список литературы
Webster A.G. Acoustical impedance, and the theory of horns and of the phonograph // Proc. Nat. Acad. Sci. 1919. V. 5. P. 275–282. Reprinted in: J. Audio Eng. Society. 1977. V. 25. № 1–2. P. 24–28.
Eisner E. Resonant oscillation system design. Physical Acoustics (Ed. Mason W.P.). V. 1. Pt. B. Ch. 6. New York: Academic Press, 1964.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1986.
Руденко О.В. Нелинейные пилообразные волны // Успехи физ. наук. 1995. Т. 165. № 9. С. 1011–1036.
Руденко О.В., Сухорукова А.К., Сухоруков А.П. Уравнения высокочастотной нелинейной акустики неоднородных сред // Акуст. журн. 1994. Т. 40. № 2. С. 290–294.
Enflo B.O., Rudenko O.V. To the theory of generalized Burgers’ equation // Acta Acustica. 2002. V. 88. P. 155–162.
Руденко О.В., Солуян С.И. Теоретические основы нелинейной акустики. М.: Наука, 1975.
Руденко О.В., Гурбатов С.Н., Хедберг К.М. Нелинейная акустика в задачах и примерах. М.: Физматлит, 2007.
Ибрагимов Н.Х., Руденко О.В. Принцип априорного использования симметрии в теории нелинейных волн // Акуст. журн. 2004. Т. 50. № 4. С. 481–495.
Шварцбург А.Б. Туннелирование электромагнитных волн – парадоксы и перспективы // Успехи физ. наук. 2007. Т. 177. № 1. С. 43–58.
Акустика в задачах / Под ред. Гурбатова С.Н. и Руденко О.В. М.: Физматлит, 2009.
Шварцбург А.Б., Ерохин Н.С. Резонансное туннелирование сверхкоротких электромагнитных импульсов в градиентных метаматериалах: парадоксы и перспективы // Успехи физ. наук. 2011. Т. 181. № 11. С. 1212–1217.
Шварцбург А.Б., Ерохин Н.С. Градиентные акустические барьеры (точно решаемые модели) // Успехи физ. наук. 2011. Т. 181. № 6. С. 627–646.
Ковалев В.Ф., Руденко О.В. Нелинейные акустические волны в каналах переменного сечения // Акуст. журн. 2012. Т. 58. № 3. С. 296–303.
Лапидус Ю.Р., Руденко О.В. Нелинейная генерация высших гармоник как способ профилирования каналов // Акуст. журн. 1990. Т. 36. № 6. С. 1055–1058.
Руденко О.В., Гурбатов С.Н. Статистические задачи для обобщённого уравнения Бюргерса: интенсивный шум в волноведущих системах // Докл. Акад. наук. 2017. Т. 478. № 1. С. 25–28.
Руденко О.В., Солуян С.И. Самоотражение волны на разрывах как способ нелинейной диагностики сред // Докл. Акад. наук. 1988. Т. 298. № 2. С. 361–362.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал


