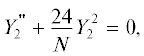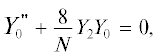Акустический журнал, 2019, T. 65, № 3, стр. 291-297
Локализованные волновые структуры, определяемые точными решениями уравнения Хохлова–Заболотской
a Московский государственный университет им. М.В. Ломоносова, физический факультет
119991 Москва, Ленинские горы, Россия
b Институт общей физики им. А.М. Прохорова РАН
119991 Москва, ул. Вавилова 38, Россия
* E-mail: yuri_makov@mail.ru
Поступила в редакцию 18.02.2019
После доработки 20.02.2019
Принята к публикации 20.02.2019
Аннотация
Дана краткая характеристика физически содержательных точных решений нелинейных уравнений в частных производных, описывающих конкретные физические объекты, процессы и т.п. Представлены новые точные и имеющие физический смысл решения уравнения Хохлова–Заболотской (в т.ч. стационарного относительно направления распространения волновой структуры варианта уравнения), соответствующие описанию локализованных волновых структур либо только с пространственной локализацией (пучки в режиме самолокализованного распространения), либо с пространственно-временной локализацией (структуры импульсного типа, иногда именуемые волновыми (акустическими) пулями). Найденные решения и описываемые ими локализованные структуры не являются для нелинейной акустики очевидными или предсказуемыми из “физических соображений” (как, например, для самолокализованного распространения пучков в нелинейной оптике), поскольку при ее бездисперсионности отсутствуют явные условия баланса “нужных” эффектов.
Заметное для акустического сообщества юбилейное событие, приходящееся на начало этого года, – 50-летие уравнения Хохлова–Заболотской (работа [1], опубликованная ровно 50 лет тому назад в Акустическом журнале, содержала вывод уравнения; подробная фактологически обоснованная научная история уравнения изложена в [2]) послужило стимулом для представления данного научного материала, имеющего прямое отношение к уравнению-юбиляру. Далее будем использовать уравнение Хохлова–Заболотской (ХЗ уравнение) в следующем безразмерном виде:
(1)
$\frac{{{{\partial }^{2}}V}}{{\partial z\partial \tau }} = \frac{N}{4}{{\Delta }_{ \bot }}V + \frac{\partial }{{\partial \tau }}\left( {V\frac{{\partial V}}{{\partial \tau }}} \right),$Не пытаясь иллюстрировать “бесчисленными” данными, ссылками и т.п. значение указанного уравнения для акустики и других областей науки, а также его использование не только как “математического инструмента” при решении задач, но и как самостоятельного математического объекта изучения, отметим лишь одно, несколько парадоксальное с нашей точки зрения, явление, связанное с этим уравнением. Речь идет о том, что, несмотря на заметное число работ по поиску и методам поиска аналитических решений ХЗ уравнения и уже накопленных результатов этого поиска, причем не только “чисто математических”, но и имеющих “физическое содержание” с их интерпретацией эффектов нелинейной пучковой акустики, нередко приходится видеть в работах по акустике утверждение о “нерешаемости” аналитически и, соответственно, об отсутствии точных аналитических решений ХЗ уравнения. Наличие подобного утверждения в той или иной работе является для ее автора как бы дополнительным обоснованием проводимой им далее процедуры либо численного, либо с помощью приближенных методов решения ХЗ уравнения.
Для конкретизации данных об имеющихся решениях обсуждаемого уравнения сошлемся, во-первых, на присутствие коллекции точных решений в известном справочном источнике [3]; собранные здесь решения условно можно отнести к “1-му поколению”, поскольку получены они сравнительно давно (в прошедшем столетии) и с помощью ставших уже стандартными приемов (методов) для применения в качестве “пробных” процедур решения нелинейных уравнений в частных производных (характеристику этих методов см. в [4]). Дальнейшие поиски и прибавления в коллекции точных решений ХЗ уравнения были связаны, в основном, с успехами развития теории групп применительно к анализу трансформационных свойств дифференциальных уравнений, а через это и к нахождению (построению) новых решений уравнений, в т.ч. ХЗ уравнения (см. для примера одну из последних работу [5] и приведенную там литературу).
Необходимо еще раз подчеркнуть, что большинство имеющихся решений ХЗ уравнения – это чисто математические результаты (см. [3]), “не привязанные” к соответствующему объекту акустики – пучкам, их параметрам, к описанию реальной динамики пучка. Это не удивительно, поскольку обычно в процедуре нахождения таких решений “не заложена” связь с физическим объектом, с его структурными особенностями и характеристиками. В противоположность этому, “физически обоснованные” решения (которых среди прочих решений ХЗ уравнения меньшинство) ищутся с явной ориентацией на описание “нужного” физического объекта (в данном случае – акустического пучка). При этом основные математические детали такого решения соответствуют физическому объекту (например, математические переменные соответствуют физическим с их характерным поведением, начальный вид решения относительно каждой переменной отвечает начально-граничным условия для пучка, решение “разумно” отражает пространственную структуру и пространственно-временную динамику пучка и так далее).
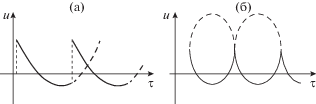
В части предыдущих работ автора данной статьи не безуспешно решались подобные задачи с учетом отмеченной их специфики. В нашей работе [6], по-видимому, впервые было найдено физически содержательное точное аналитическое решение ХЗ уравнения, причем основное достижение состояло даже не столько в получении решения, сколько в его содержании: полученное аналитическое решение показало существование (при различных соотношениях параметра Хохлова N и параметра фокусировки – фокусного расстояния) двух типов асимптотически универсальных для фокальной области волновых профилей: “привычного” на тот момент (1997 г.) кусочно-непрерывного профиля (рис. 1а) из участков гипербол, соединенных через период разрывом (ударным фронтом), и профиля второго типа (на тот момент обойденного вниманием акустиков), являющегося безразрывным и состоящим из соединенных между собой “нижних” частей вертикальных эллипсов (рис. 1б). Второй тип профиля был нами назван “дугообразным” (определение, созвучное классическому для нелинейной акустики “пилообразному профилю”). Полученное аналитическое решение показывало динамику этих двух типов профилей.
Рис. 1.
Графическое представление решения (3) с волновым профилем из части гиперболы и ударными фронтами (а) и с безразрывным дугообразным из повторяющихся частей эллипса профилем (б).
В более поздней нашей работе [7] поиск точных аналитических решений уравнений нелинейной акустики (в т.ч. ХЗ уравнения) с требуемым физическим содержанием производился на основе т.н. анзаца относительно неискажающихся волн, введенного и теоретически обоснованного классиками математической физики (см. [8, 9]) и в то же время хорошо обусловленного основными структурными особенностями волн и пучков нелинейной акустики.
Для нахождения в [7] физически мотивированного аналитического решения ХЗ уравнения для описания “щелевого” пучка (только в этом случае на всех этапах решения получались явные аналитические выражения) использовался анзац следующего конкретного вида
который содержал в себе все элементы, соответствующие основным структурным особенностям пучка с их эволюцией по мере распространения пучка, причем волновой характер распространения также был “проявлен” в (2). Действительно, соответствие состоит в следующем: W – форма волны (волновой профиль), $S\, = \,\tau \, + \,\psi (z,y)$ – фазовая функция, обобщающая простейший вид “бегущей” переменной (“запаздывающего” времени), g(.) – амплитудная функция, описывающая масштабные изменения формы волны при сохранении характерного вида этой формы, q(.) – функция, корректирующая сдвиг волнового профиля относительно нулевого уровня для обеспечения нулевого среднего по площади профиля в пределах одного периода (один из интегралов ХЗ уравнения). Таким образом, уже на этапе выбора вида решения закладывалось “нужное” физическое содержание самого решения. В этом принципиальное отличие от деятельности математиков по нахождению решений того же ХЗ уравнения, для которых важно найти любой подходящий метод нахождения решения и найти само решение, проведя соответствующие математические действия; интерпретация решения при этом остается в стороне.Процедура нахождения физически содержательного решения на основе, например, приведенного анзаца (2), подразумевает получение (после подстановки (2) в (1)) и решение в общем случае связанных уравнений для искомых функций, входящих в (2), причем вся эта процедура носит “нестандартный” характер. Для иллюстрации приведем полученный в [7] аналитический вид решения с физическим содержанием, соответствующим “щелевому” пучку:
(3)
$\begin{gathered} V(\tau ,\,z,\,y)\, = \,{{Z}^{{ - 1/2}}}\left[ { \pm \,{{{({{D}^{2}}BN)}}^{{1/{{2}^{{^{{}}}}}}}}} \right. \times \\ \times \,\,\sqrt {{{{\left( {\tau \, - \,2{{N}^{{ - 1}}}{{y}^{2}}(z + {{Z}_{1}}){{Z}^{{ - 1}}}\, + \,{{\psi }_{0}}(z)\, + \,{{S}_{0}}} \right)}}^{2}}\, + \,K} - \\ - \,\,\left. {BD{{y}^{2}}{{Z}^{{ - 1/2}}} + {{{({{\psi }_{0}})}}_{z}}{{Z}^{{1/2}}}} \right]. \\ \end{gathered} $Здесь $Z \equiv Z(z) = {{z}^{2}} + 2{{Z}_{1}}z + 2{{Z}_{0}},$ ${{\psi }_{0}}(z)$ – произвольная функция, которая может быть определена из условия на временное среднее профиля по периоду волны; $B,\,D,\,\,K,\,{{S}_{0}},\,\,{{Z}_{1}},\,\,{{Z}_{0}}$ – произвольные постоянные.
Выбор определенных значений для входящих в (3) произвольных постоянных отражает возможные вариации вида профиля волны, что, в свою очередь, определяется условиями формирования пучка (граничными условиями), характеристикой нелинейности среды и т.п.
Наиболее существенные изменения вида профиля происходят при определенном изменении значения произвольной постоянной B. При B > 0 решение (3) дает ветвь гиперболы (действительно, при положительных значениях B возведение обеих частей (3) в квадрат дает явное уравнение гиперболы в координатах (V, τ)). Далее, вырезая периодом волны “нужный” кусок гиперболы (из ее верхней ветви), так чтобы при вертикальном сдвиге за счет внекоренных слагаемых в (3) получалось бы нулевое временное среднее (интеграл ХЗ уравнения), и повторяя этот результат с данным периодом по оси τ, получаем типичный для нелинейного акустического пучка профиль с развитыми ударными фронтами (см. рис. 1а). При В < 0 получаются эллипсообразные профили (названные нами дугообразными), характерной особенностью которых является отсутствие ударных фронтов при их нелинейной трансформации (рис. 1б). Такие профили характерны для фокусированных пучков при умеренной нелинейности, что показано в нашей работе [10], где на основе сопоставления числовых значений параметров N и фокусного расстояния и с учетом изменения значений этих параметров вдоль оси сфокусированного пучка, найдены “пороговые значения” этих параметров, разделяющие условия формирования в фокальной области пучка того или иного типа волнового профиля из тех, что получены аналитически в [6, 7] и показаны на рис. 1.
Следует констатировать, что основанный на использовании “правильного” анзаца, отражающего нужную структуру искомого объекта (например, акустического пучка), подход для поиска физически содержательных решений нелинейных уравнений в частных производных является плодотворным и результативным. Этот метод использовался нами для поиска новых с точки зрения нелинейной акустики волновых структур (см. далее). Кроме того, с определенными вариациями этот метод применялся и другими авторами для получения некоторых разновидностей решений ХЗ уравнения относительно пучков более высокой размерности (см. относительно недавнюю работу [11]).
Продолжая характеризовать особенности и возможности поиска точных аналитических решений нелинейных уравнений в частных производных применительно к ХЗ уравнению, следует остановиться на том важном случае, когда ищутся точные решения с целью подтвердить (или опровергнуть) возможность существование новых для нелинейной акустики в рамках этого уравнения волновых структур, причем эти новые структуры могут быть “нетипичными” для нелинейной акустики, а поэтому, неожидаемыми в сопоставлении с практикой предшествующей работы с данным уравнением. В подобном случае поиск нового “неожиданного” решения эквивалентен доказательству существования нового класса волновых структур “в рамках” анализируемого уравнения. Говоря об этом применительно к ХЗ уравнению, имеем в виду интерес к возможности существования локализованных решений уравнения и существования реальных локализованных волновых структур, описываемых этими решениями, при том, что в данном уравнении отсутствуют слагаемые (см. уравнение (1)), ответственные за “явную” дисперсию; следовательно, нет оснований принимать в расчет явный механизм взаимной компенсации нелинейности и дисперсии, что обычно обуславливает существование решений (и, соответственно, волновых структур) типа солитонов или, при нелинейных законах дисперсии, решений в виде [12, 13] компактонов (солитонов конечной протяженности) или пиконов (солитонов с заострением в максимуме). По указанной причине явной “бездисперсионности” уравнения (1) также не очевидна ситуация со вторым классическим типом пространственной локализации – возможностью реализации самолокализованного (волноводного) распространения звуковых пучков. В 60-е годы прошлого века было дано теоретическое обоснование возможности самолокализованного (self-trapped) относительно поперечных координат распространения волновых пучков в нелинейных оптических или плазменных средах [14, 15]. Однако, только в 2000 г. в работе [16] на основе нахождения точного аналитического решения ХЗ уравнения нами была показана теоретическая возможность такого же волноводного характера распространения акустических пучков, обусловленного компенсацией дифракционной расходимости нелинейной неинерциальной рефракцией в акустических средах с квадратичной нелинейностью. В отличие от самолокализованного (волноводного) распространения пучка в оптике, где достаточно энергетической компенсации двух указанных основных эффектов, в нелинейной акустике при квадратичной нелинейности эта компенсация гораздо более “тонкая” и сложная, в которой участвуют “специального вида” поперечный профиль пучка (форма пучка) и его волновой (временной) профиль. Но указанная сложность обусловлена именно квадратичной нелинейностью; для кубичной нелинейности ситуация несколько упрощается. Для того чтобы понять эти особенности, проведем краткое “качественно-количественное” сравнение всех упомянутых выше моделей.
Напомним, что математическое обоснование существования эффекта волноводного распространения в кубично-нелинейных оптических и плазменных средах с выделенной из-за дисперсии одной гармонической составляющей дает определяющее нелинейное уравнение Шредингера для комплексной амплитуды $A,$ полученное для пучков с узким угловым спектром, вытянутым вдоль оси распространения $z{\text{:}}$
(4)
$2ik\frac{{\partial A}}{{\partial z}} = {{\Delta }_{ \bot }}А + \frac{{{{k}^{2}}{{\varepsilon }_{{nl}}}{{{(A)}}^{2}}}}{{{{\varepsilon }_{0}}}}A,$Из уравнения (4) легко увидеть, что для самофокусирующих сред с ${{\varepsilon }_{{nl}}} > 0$ знаки первого (описывающего дифракционную расходимость) и второго (определяющего результат нелинейной рефракции) слагаемых в правой части (4) различны, что дает возможность их взаимной компенсации. Таким образом, задача о волноводном (стационарном по $z$) распространении оптических (электромагнитных) пучков с аксиальной симметрией, а также “щелевых” пучков сводится, как это видно из (4), к решению дифференциального уравнения в обыкновенных производных. Резюмируя, можно сказать, что, во-первых, характер нелинейности для оптических и других электромагнитных волновых пучков позволяет наперед прогнозировать наличие или отсутствие эффекта волноводного распространения в зависимости от типа среды (от знака ${{\varepsilon }_{{nl}}}$) и, во-вторых, в случае возможной реализации этого эффекта (${{\varepsilon }_{{nl}}} > 0$) стационарный по $z$ вариант уравнения (1) для щелевого или аксиально-симметричного пучка является дифференциальным уравнением в обыкновенных производных, решение которого находится без особых математических трудностей.
При постановке и анализе аналогичной проблемы для звуковых пучков в нелинейной акустике оба вышеуказанных вывода недействительны. Это значительное усложнение анализа по сравнению с ситуацией в оптике отчасти явилось причиной долгого отсутствия положительных или отрицательных результатов по прогнозированию возможности волноводного распространения звуковых пучков. Специфика (в сопоставлении с (4)) математической модели распространения звуковых пучков в нелинейной акустике определяется двумя отличительными особенностями. Во-первых, отсутствие дисперсии и, как следствие, лавинообразное уширение спектра исходного волнового профиля за счет нелинейности заставляет в этом случае находить формирующийся волновой (временной) профиль, что усложняет по сравнению с (4) определяющее акустическое уравнение из-за введения дифференциального оператора еще по одной независимой переменной – времени. Во-вторых, характерной для акустики нелинейностью является квадратичная (в отличие от кубичной нелинейности в (4)). С учетом указанных различий, соответствующее уравнение пучковой акустики (ХЗ уравнение (1)) является более сложным, как для предварительного качественного анализа (что сделано выше в отношении (4)), так и для его решения (прежде всего, имеется в виду нахождение точных аналитических решений, физически содержательных в отношении нужного режима распространения пучка). Структура нелинейного члена уравнения (1) не позволяет (в отличие от (4)) предварительно прогнозировать возможность компенсации дифракционной расходимости, описываемой первым членом в правой части (1), нелинейной рефракцией. Поэтому возможность волноводного режима распространения звуковых пучков будет определяться наличием физически обоснованного решения уравнения (1) в стационарном по $z$ случае, который как раз и обусловлен указанной компенсацией. При этом, однако, возникает кажущийся парадокс относительно существования такого решения. Действительно, хорошо известно, что упоминавшееся ранее лавинообразное уширение спектра начального профиля волны за счет нелинейности и отсутствия дисперсии приводит к формированию пилообразных волн с ударными (разрывными) фронтами, пиковые значения которых из-за нелинейного высокочастотного затухания уменьшаются при распространении вдоль оси z, что впервые наглядно было продемонстрировано в эксперименте Владимиром Александровичем Красильниковым и Валентином Андреевичем Буровым в 1958 году [17]. Это, казалось бы, исключает стационарные по $z$ решения. Однако пилообразная волна – это единственный асимптотически универсальный тип нелинейной волны в плоском (одномерном) случае. Для неодномерной (пучковой) нелинейной акустики, как уже обсуждалось выше (см. [6, 7]), возможно наличие второго асимптотически универсального типа волновых профилей (см. рис. 1б) с сильными нелинейными искажениями относительно синусоидального профиля, но не имеющих разрывов. Такие профили можно отнести к нелинейно-безразрывному типу, что отражает их специфику. Для них отсутствует нелинейное высокочастотное затухание и поэтому профиль такого типа может являться стационарным по $z$ решением уравнения (1), что возможно при компенсационном условии $\frac{N}{4}\sim 1.$ Это условие также удобно представить в виде $\frac{N}{4} \equiv \frac{{{{F}_{{cr}}}}}{{{{F}_{a}}}}\sim 1,$ где ${{F}_{{cr}}} = \frac{{\beta {{\rho }_{0}}c_{0}^{4}}}{{2{{\omega }^{2}}}}$ значение “критической” силы, ${{F}_{a}} = \beta {{p}_{0}}{{a}^{2}}$ – усредненная сила акустического воздействия пучка на площадь поперечного сечения ${{a}^{2}},$ $\beta $ – безразмерный коэффициент, определяемый распределением давления по поперечному сечению пучка и его изменением во времени. Для взаимной компенсации дифракции и нелинейной рефракции отношение двух указанных сил должно быть порядка единицы (аналогия с соотношением между критической мощностью и мощностью пучка в оптическом случае).
В [16] нами была рассмотрена задача по поиску решения, соответствующего волноводному распространению акустического пучка. В указанной работе был дан положительный ответ на вопрос о возможности такого распространения. При этом, как обсуждалось выше, большую (и даже определяющую) роль сыграл правильный выбор исходного для поиска решения анзаца
в котором имеется первичная информация о нужной структуре и физическом содержании решения. В этом выражении ${{Y}_{2}}(y)$ и ${{Y}_{0}}(y)$ – искомые функции, для которых при подстановке (5) в (1) получается система нелинейных уравнений: с граничным значением ${{Y}_{0}}(1)$ для нормировки формы пучка.Важным замечанием является то, что предложенный анзац (5) без дополнительного решения указывает на волновой (временной) профиль в виде соприкасающихся через период парабол; в таком профиле нет разрывов (а значит отсутствует высокочастотная диссипация) и его можно отнести к введенному нами классу дугообразных профилей.
В целом, полученная теоретически (на основе аналитического решения системы уравнений (6)) волновая структура самолокализованного (self-trapped) в квадратично нелинейной среде пучка показана на рис. 2 и 3.
Рис. 2.
Волновое поле (на рис. представлены три периода волнового профиля) при самолокализованном распространении звукового пучка в среде с квадратичной нелинейностью. Для наглядности показано амплитудное распределение только вдоль полуоси y (т.е. половина симметричной формы пучка).
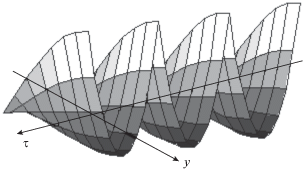
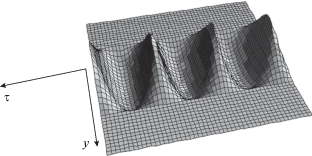
Рис. 3.
Полная структура поля самолокализованного пучка в квадратично-нелинейной среде (вид сверху).
В дополнение к результату работы [16] проанализируем возможность волноводного распространения акустического пучка в средах с кубичной нелинейностью на основе уравнения
(7)
$\frac{{{{\partial }^{2}}V}}{{\partial z\partial \tau }} = \frac{N}{4}{{\Delta }_{ \bot }}V - \frac{\partial }{{\partial \tau }}\left( {{{V}^{2}}\frac{{\partial V}}{{\partial \tau }}} \right).$Выбранный знак “–” перед последним слагаемым соответствует самофокусирующим средам, в которых и может происходить компенсация дифракционной расходимости. При этом кубичная нелинейность является более простой для анализа и поиска “подходящего” решения уравнения (7). Действительно, требование нулевой суммарной площади положительной и отрицательной полуволн волнового профиля решения (7) на периоде (интеграл ХЗ уравнения), а также независимость результата проявления нелинейности от знака $V$ указывает на симметричность искомого решения относительно оси $\tau $ при его очевидной симметричности вдоль оси $y$ относительно центра. Этому условию удовлетворяет простое по структуре и допускающее разделение переменных частное решение
которое при подстановке в (7) приводит к следующим зависимостям, удовлетворяющим вышеуказанным требованиям:(9)
$\begin{gathered} \pm \tau + 2\pi k = \sqrt {\frac{2}{{{{\lambda }^{2}}}}T_{0}^{2}} \int\limits_{\tilde {T}}^1 {\frac{{{{{\tilde {T}}}^{2}}d\tilde {T}}}{{\sqrt {1 - {{{\tilde {T}}}^{4}}} }}} \\ \left( {\tilde {T} = {T \mathord{\left/ {\vphantom {T {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}};\,\,0 \leqslant \tilde {T} \leqslant 1} \right), \\ \end{gathered} $(10)
$\begin{gathered} \pm y = \sqrt {\frac{N}{2}\frac{1}{{{{\lambda }^{2}}Y_{0}^{2}}}} \int\limits_{\tilde {Y}}^1 {\frac{{d\tilde {Y}}}{{\sqrt {1 - {{{\tilde {Y}}}^{4}}} }}} \\ \left( {\tilde {Y} = {Y \mathord{\left/ {\vphantom {Y {{{Y}_{0}}}}} \right. \kern-0em} {{{Y}_{0}}}};\,\,0 \leqslant \tilde {Y} \leqslant 1} \right), \\ \end{gathered} $Соответствующая решениям (9), (10) структура самолокализованного в кубичной среде акустического пучка представлена на рис. 4. Рис. 2 и 4 показывают сложную структуру (сочетание специфических формы пучка и волнового профиля) для реализации самолокализованного распространения акустических пучков, причем структура такого пучка резко меняется при изменении характера нелинейности среды.
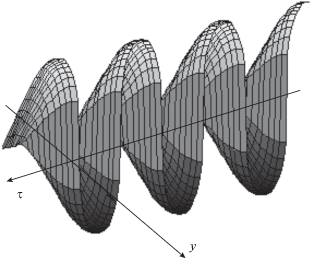
Рис. 4.
Волновое поле (на рис. представлены три периода волнового профиля) при самолокализованном распространении звукового пучка в среде с кубичной нелинейностью. Для наглядности показано амплитудное распределение только вдоль полуоси y.
В качестве развития рассматриваемой в данной работе проблемы естественно интересоваться возможностью существования полностью локализованных в пространстве и времени решений, которые были бы определенным эквивалентом солитонам или компактонам для нелинейных дисперсионных уравнений. Такие полностью пространственно-временные локализованные волновые структуры (пространственно-временные “порции” акустического поля) образно называют “акустическими пулями” [18]. Рассмотрим стационарный по продольной координате z вариант уравнения (1) в цилиндрической осесимметричной геометрии:
(11)
$\frac{N}{4}\left( {\frac{{{{\partial }^{2}}V}}{{\partial {{y}^{2}}}}\,\,\, + \,\,\frac{1}{y}\frac{{\partial V}}{{\partial y}}} \right) + \frac{\partial }{{\partial \tau }}\left( {V\frac{{\partial V}}{{\partial \tau }}} \right) = 0\,\,\,\,\left( {y \equiv r} \right)$Интересным математическим фактом является то, что, несмотря на нахождение из (13) функции f в зависимости от автомодельной переменной $f\left( {\chi \equiv \tau {{y}^{{ - 2/3}}}} \right),$ в записи энергетической характеристики ${{V}^{2}}$ (при этом ${{f}^{2}}$ выражаем из (13), используем для оказавшейся в знаменателе функции f явное решение кубического уравнения (13) по общеизвестному алгоритму и окончательно формируем выражение для ${{V}^{2}}$ с помощью (12)) исходные переменные, объединенные в автомодельной переменной $\chi ,$ “разъединяются”:
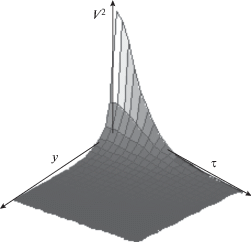
Анализ полученного решения для ${{V}^{2}}$ показывает, что при $N < 0$ (соответствует замене V на –V в (4), т.е. так называемому “темному” импульсу или импульсу разрежения) и при $D > 0$ оно локализовано по пространственно-поперечной $y \equiv r$ и временной τ координатам (см. рис. 5). Отметим, что за счет “бегущей” переменной τ эта локализованная структура движется со скоростью звука вдоль продольной оси z.
Если ранее полученный эффект волноводного (стационарного) распространения звукового пучка объяснялся “уравновешиванием” действия дифракции и нелинейной рефракции, то показанная возможность существования пространственно-временных локализованных решений обеспечивается более “тонким” балансом между нелинейностью и дисперсионным проявлением дифракции (зависимостью от частоты (т.е. номера гармоники) фазового смещения гармоник за счет дифракции).
Список литературы
Заболотская Е.Л., Хохлов Р.В. Квазиплоские волны в нелинейной акустике ограниченных пучков // Акуст. журн. 1969. Т. 15. № 1. С. 40–47.
Руденко О.В. К 40-летию уравнения Хохлова–Заболоцкой // Акуст. журн. 2010. Т. 56. № 4. С. 452–462.
Polyanin A.D. and Zaitsev V.F. Handbook of Nonlinear Partial Differential Equations, 2nd Edition. Chapman & Hall/CRC Press, Boca Raton, 2012.
Полянин А.Д., Зайцев В.Ф., Журов А.И. Методы решения нелинейных уравнений математической физики и механики. М.: Физматлит, 2005. 254 с.
Kumar M., Kumar R., Kumar A. On similarity solutions of Zabolotskaya–Khokhlov equation // Comput. Math. Appl. 2014. V. 68. P. 454–463.
Маков Ю.Н. Об универсальном автомодельном решении уравнения Хохлова–Заболотской для волн с ударными фронтами // Акуст. журн. 1997. Т. 43. № 6. С. 828–833.
Маков Ю.Н. Относительно неискажающиеся волны и профили в нелинейной акустике // Акуст. журн. 2009. Т. 55. № 2. С. 160–170.
Курант Р., Гильберт Д. Методы математической физики. Том 2. М.-Л.: ГТТИ, 1945. 620 с.
Курант Р. Уравнения с частными производными. М.: Мир, 1964. 830 с.
Маков Ю.Н. Реализация и критерии двух типов “асимптотически универсальных” волновых профилей в нелинейных фокусированных пучках // Труды 19-ой сессии РАО. Москва, 2007. Т. 1. С. 166–170.
Kamchatnov A.M., Pavlov M.V. On exact solutions of nonlinear acoustic equations // Wave Motion. 2016. V. 67. P. 81–88.
Rosenau P., Hyman J.M. Compactons: solitons with finite wavelength // Phys. Rev. Lett. 1993. V. 70. № 5. P. 564–567.
Rosenau P. On nonanalytic solitary waves formed by a nonlinear dispersion // Phys. Lett. A. 1997. V. A230. P. 305–318.
Таланов В.И. О самофокусировке электромагнитных волн в нелинейных средах // Изв. вузов. Радиофизика. 1964. Т. 7. № 5. С. 564–565.
Chiao R.Y., Garmire E., Townes C.H. Self-trapping of optical beams // Phys. Rev. Lett. 1964. V. 13. P. 479–482.
Маков Ю.Н. Волноводное распространение звуковых пучков в нелинейной среде // Акуст. журн. 2000. Т. 46. № 5. С. 680–684.
Буров В.А., Красильников В.А. Непосредственное наблюдение искажения формы интенсивных ультразвуковых волн в жидкостях // Докл. АН СССР. 1958. Т. 118. № 5 С. 920–923.
Stepanishen P.R., Sun J. Acoustic bullets: transient Bessel beams generated by planar apertures // J. Acoust. Soc. Am. 1997. V. 102. P. 3308–3318.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал