Акустический журнал, 2019, T. 65, № 3, стр. 298-304
Возбуждение колебаний и волн в квадратично-нелинейных системах с селективным подавлением второй гармоники
a Московский государственный университет им. М.В. Ломоносова, физический факультет
119991 Москва, ГСП-1, Ленинские горы, Россия
b Институт общей физики им. А.М. Прохорова РАН
119991 Москва, ул. Вавилова 38, Россия
c Институт физики Земли им. О.Ю. Шмидта РАН
123242 Москва, Б. Грузинская ул. 10, стр. 1, Россия
* E-mail: rudenko@acs366.phys.msu.ru
Поступила в редакцию 15.02.2019
После доработки 15.02.2019
Принята к публикации 20.02.2019
Аннотация
Изучены процессы возбуждения колебаний и волн в системах с квадратичной нелинейностью при наличии селективного поглощения на частоте второй гармоники. Рассмотрен ряд примеров: возбуждение волн источниками, движущимися со скоростью, близкой к скорости собственных возмущений в среде; возбуждение волн в плоском слое (одномерном резонаторе) за счет колебаний одной из стенок; вынужденные колебания двух связанных осцилляторов. Показано, что с увеличением коэффициента поглощения второй гармоники амплитуда колебаний на основной частоте возрастает. Такая же закономерность проявляется для недиспергирующих нелинейных волн, в которых происходит формирование ударных фронтов и “растекание” энергии по высшим гармоникам. Подавление второй гармоники “запирает” каскадный процесс передачи энергии вверх по спектру и “выключает” нелинейное поглощение. Ряд описанных систем уже создан и изучен в экспериментах. Селективно поглощающие среды для высокочастотных волн можно рассматривать как метаматериалы и синтезировать их на основе соответствующих технологий.
ПРИМЕРЫ СИСТЕМ И УПРОЩЕННЫЕ УРАВНЕНИЯ
Исследуемые здесь нелинейные процессы и описывающие их уравнения имеют довольно общий характер. Поэтому желательно привести примеры реальных задач, которые соответствуют принятой математической модели. В этом разделе показано, что существует множество как сосредоточенных, так и распределенных систем, адекватно описываемых парой связанных нелинейных уравнений, являющихся основой последующего анализа.
Рассмотрим вначале процесс возбуждения волн распределенными источниками, движущимися со скоростью, близкой к скорости распространения собственных возмущений в среде. Для определенности остановимся на задаче о термооптической генерации звука с учетом квадратичной нелинейности, которая описывается неоднородным волновым уравнением [1]:
(1)
$\Delta p - \frac{1}{{c_{0}^{2}}}\frac{{{{\partial }^{2}}p}}{{\partial {{t}^{2}}}} + \frac{{\varepsilon }}{{c_{0}^{4}{{{\rho }}_{0}}}}\frac{{{{\partial }^{2}}{{p}^{2}}}}{{\partial {{t}^{2}}}} = \frac{{\beta }}{{{{c}_{p}}}}\frac{\partial }{{\partial t}}\operatorname{div} \left\langle {\mathbf{S}} \right\rangle .$Пусть след светового пучка движется вдоль оси $x,$ лежащей в плоскости границы раздела двух сред (например, вдоль поверхности воздух–вода), падая по нормали $z$ из прозрачной среды (воздух) на слабо поглощающую среду (вода). При этом
(2)
${{\left\langle {\mathbf{S}} \right\rangle }_{z}} = {{I}_{0}}\exp \left( { - \frac{z}{l}} \right)\Phi (kx - ckt).$Для простоты рассматривается двумерная геометрия задачи; зависимостью всех величин от третьей координаты $y$ мы пренебрегаем. В формуле (2) ${{I}_{0}}$ – это характерное значение интенсивности на границе $z = 0,$ $l$ – глубина проникновения света в слабо поглощающую среду, $\Phi $ – функция, описывающая распределение интенсивности света на поверхности, $c$ – скорость сканирования пучка. Для принятой формы (2) правая часть уравнения (1) запишется так:
Движущиеся со скоростью $c \approx {{c}_{0}}$ источники (3) находятся “в резонансе” с волной, бегущей в положительном направлении оси $x.$ Поэтому “правая” волна будет возбуждаться гораздо эффективнее “левой” [2–4]. Это позволяет искать решение уравнения (1) в следующем виде [1]:
где ${\mu } \ll 1$ – малый параметр. Переходя в уравнении (1), (3) к переменным (4) и пренебрегая малыми членами порядка второго (${{{\mu }}^{2}}$) и выше, получим(5)
$\begin{gathered} \frac{\partial }{{\partial {\varsigma }}}\left[ {\frac{{\partial p}}{{\partial t}} + \frac{{\varepsilon }}{{{{c}_{0}}{{{\rho }}_{0}}}}p\frac{{\partial p}}{{\partial {\varsigma }}} - \frac{{{\beta }{{c}^{2}}{{I}_{0}}}}{{2{{c}_{p}}l}}\exp \left( { - \frac{z}{l}} \right)\Phi (k{\varsigma } - t\Delta )} \right] = \\ = - \frac{{{{c}_{0}}}}{2}\frac{{{{\partial }^{2}}p}}{{\partial {{z}^{2}}}}, \\ \end{gathered} $В частном случае периодического распределения движущихся источников вдоль поверхности:
(6)
$\frac{{{\beta }{{c}^{2}}{{I}_{0}}}}{{2{{c}_{p}}l}}\Phi (k{\varsigma } - t\Delta ) = \frac{1}{2}{{F}_{0}}\exp (ik{\varsigma } - it\Delta ) + c.c.$(7)
$p(t,{\varsigma }) = \frac{1}{2}{{A}_{1}}(t)\exp \left( {ik{\varsigma }} \right) + \frac{1}{2}{{A}_{2}}(t)\exp \left( {i \times 2k{\varsigma }} \right) + c.c.$Для комплексных амплитуд этих гармоник получается следующая система:
(8)
$\frac{{d{{A}_{1}}}}{{dt}} + i\gamma A_{1}^{*}{{A}_{2}} = {{F}_{0}}\exp ( - it\Delta ),\,\,\,\,\frac{{d{{A}_{2}}}}{{dt}} + i\gamma A_{1}^{2} = 0,$Во втором рассматриваемом здесь примере распределенных источников нет, а возбуждение волн происходит в плоском слое (одномерном резонаторе) за счет колебаний одной из стенок. Скорость ее колебаний изменяется во времени по некоторому периодическому закону
в то время как вторая граница $(x = L)$ неподвижна. Движение среды в резонаторе описывается однородным волновым уравнением (1). В работах [2–4] показано, что для данных граничных условий задача сводится к решению функционального уравнения(10)
$\begin{gathered} Q\left( {\omega t + kL - \frac{\varepsilon }{{{{c}_{0}}}}kLQ} \right) - \\ - \,\,Q\left( {\omega t - kL + \frac{\varepsilon }{{{{c}_{0}}}}kLQ} \right) = \Phi \left( {\omega t} \right). \\ \end{gathered} $В этом уравнении неизвестная функция $Q({\omega }\,t)$ описывает форму любой из двух нелинейных волн, бегущих навстречу друг другу. Вблизи основного резонанса $(kL = \pi + \delta ,\delta \ll 1)$ при гармоническом законе движения стенки (9) форма волнового профиля может быть вычислена с помощью эволюционного уравнения
(11)
$\frac{{\partial Q}}{{\partial t}} + \frac{\delta }{\pi }\frac{{\partial Q}}{{\partial \tau }} - \frac{\varepsilon }{{{{c}_{0}}}}Q\frac{{\partial Q}}{{\partial \tau }} = \frac{{{{\Phi }_{0}}\omega }}{{2\pi }}\cos (\omega \tau ).$(12)
$\begin{gathered} Q(t,\tau ) = \frac{1}{2}{{A}_{1}}(t)\exp \left( { - i\omega \tau + i\omega \frac{\delta }{\pi }t} \right) + \\ + \,\,\frac{1}{2}{{A}_{2}}(t)\exp \left( { - i2\omega \tau + i2\omega \frac{\delta }{\pi }t} \right) + c.c., \\ \end{gathered} $(13)
$\begin{gathered} \frac{{d{{A}_{1}}}}{{dt}} + i\frac{{\varepsilon \omega }}{{2{{c}_{0}}}}A_{1}^{*}{{A}_{2}} = \frac{{\omega {{\Phi }_{0}}}}{{2\pi }}\exp \left( { - i\omega \frac{\delta }{\pi }t} \right), \\ \frac{{d{{A}_{2}}}}{{dt}} + i\frac{{\varepsilon \omega }}{{2{{c}_{0}}}}A_{1}^{2} = 0, \\ \end{gathered} $Третий пример связан с сосредоточенной (колебательной) системой. Рассмотрим два связанных гармонических осциллятора. Каждый в отдельности представляется точечной массой ${{m}_{j}},$ совершающей колебания вдоль оси $x$ благодаря пружинке с жесткостью ${{k}_{j}}$ ($j = 1,\,2$). Массы соединены между собой третьей (нелинейной) пружинкой, упругая возвращающая сила которой зависит от разности смещений масс ${\zeta } = {{x}_{2}} - {{x}_{1}}$ как $k{\varsigma } + {\beta }{{{\varsigma }}^{2}}.$ На первую массу действует периодическая внешняя сила $f(t).$
Функция Лагранжа описанной 1системы имеет вид
(14)
$\begin{gathered} L = \frac{1}{2}\left[ {{{m}_{1}}{{{\left( {\frac{{d{{x}_{1}}}}{{dt}}} \right)}}^{2}} + {{m}_{2}}{{{\left( {\frac{{d{{x}_{2}}}}{{dt}}} \right)}}^{2}}} \right] - \\ - \,\,\frac{1}{2}\left[ {{{k}_{1}}x_{1}^{2} + {{k}_{2}}x_{2}^{2} + k{{{({{x}_{2}} - {{x}_{1}})}}^{2}}} \right] - \frac{\beta }{3}{{\left( {{{x}_{2}} - {{x}_{1}}} \right)}^{3}} + f(t){{x}_{1}}. \\ \end{gathered} $Ограничимся случаем слабой связи, когда собственные частоты системы ${{{\omega }}_{{1,2}}}$ мало отличаются от парциальных частот ${{n}_{{1,2}}}{\text{:}}$
(15)
${\omega }_{1}^{2} = n_{1}^{2} - \frac{{s_{1}^{2}s_{2}^{2}}}{{n_{2}^{2} - n_{1}^{2}}}{\text{,}}\,\,\,\,\omega _{2}^{2} = n_{2}^{2} + \frac{{s_{1}^{2}s_{2}^{2}}}{{n_{2}^{2} - n_{1}^{2}}}.$Здесь использованы обозначения:
(16)
$n_{1}^{2} = \frac{{{{k}_{1}} + k}}{{{{m}_{1}}}},\,\,\,\,n_{2}^{2} = \frac{{{{k}_{2}} + k}}{{{{m}_{2}}}},\,\,\,\,s_{1}^{2} = \frac{k}{{{{m}_{1}}}},\,\,\,\,s_{2}^{2} = \frac{k}{{{{m}_{2}}}}.$Считая связанность малым параметром,
перейдем в выражении (14) для функции Лагранжа к нормальным переменным(18)
${{x}_{1}} = \frac{1}{{\sqrt {{{m}_{1}}} }}({{z}_{1}} - \nu {{z}_{2}}),\,\,\,\,{{x}_{2}} = \frac{1}{{\sqrt {{{m}_{2}}} }}(\nu {{z}_{1}} + {{z}_{2}}),$(19)
$\begin{gathered} L = \frac{1}{2}\left[ {{{{\left( {\frac{{d{{z}_{1}}}}{{dt}}} \right)}}^{2}} + {{{\left( {\frac{{d{{z}_{2}}}}{{dt}}} \right)}}^{2}}} \right] - \frac{1}{2}\left( {{{n}_{1}}z_{1}^{2} + {{n}_{2}}z_{2}^{2}} \right) - \\ - \,\,\frac{{\beta }}{3}{{\left( {\frac{{{{z}_{2}}}}{{\sqrt {{{m}_{2}}} }} - \frac{{{{z}_{1}}}}{{\sqrt {{{m}_{1}}} }}} \right)}^{3}} + \frac{{f(t)}}{{\sqrt {{{m}_{1}}} }}{{z}_{1}}. \\ \end{gathered} $Естественно, при выводе формулы (19) нелинейный член и вынуждающую силу также следует считать малыми порядка ν (17). Уравнения движения, соответствующие функции Лагранжа (19), таковы:
(20)
$\begin{gathered} \frac{{{{d}^{2}}{{z}_{1}}}}{{d{{t}^{2}}}} + n_{1}^{2}{{z}_{1}} = \frac{\beta }{{\sqrt {{{m}_{1}}} }}{{\left( {\frac{{{{z}_{2}}}}{{\sqrt {{{m}_{2}}} }} - \frac{{{{z}_{1}}}}{{\sqrt {{{m}_{1}}} }}} \right)}^{2}} + \frac{{f(t)}}{{\sqrt {{{m}_{1}}} }}, \\ \frac{{{{d}^{2}}{{z}_{2}}}}{{d{{t}^{2}}}} + n_{2}^{2}{{z}_{2}} = - \frac{\beta }{{\sqrt {{{m}_{2}}} }}{{\left( {\frac{{{{z}_{2}}}}{{\sqrt {{{m}_{2}}} }} - \frac{{{{z}_{1}}}}{{\sqrt {{{m}_{1}}} }}} \right)}^{2}}. \\ \end{gathered} $Левые части уравнений (20) независимы; благодаря переходу к нормальным координатам подсистемы взаимодействуют друг с другом формально только из-за нелинейной связи.
Будем считать, что первая подсистема настроена на частоту ${{\omega }_{0}},$ примерно равную частоте колебаний ω внешней силы, а вторая подсистема – на частоту $2{{\omega }_{0}}.$ Иными словами, парциальные частоты в уравнениях (20) равны ${{\omega }_{0}}$ и $2{{\omega }_{0}}$ соответственно. Отыскивая решение (20) в виде
(21)
$\begin{gathered} {{z}_{1}} = \frac{1}{2}\frac{{{{A}_{1}}(t)}}{{{{\omega }_{0}}}}\exp ( - i{{\omega }_{0}}t) + c.c., \\ {{z}_{2}} = \frac{1}{2}\frac{{{{A}_{2}}(t)}}{{2{{\omega }_{0}}}}\exp ( - i2{{\omega }_{0}}t) + c.c., \\ f = {{f}_{0}}\exp ( - i\omega t), \\ \end{gathered} $(22)
$\gamma = \frac{\beta }{{4{{m}_{1}}\sqrt {{{m}_{2}}} \omega _{0}^{2}}},\,\,\,\,{{F}_{0}} = i\frac{{{{f}_{0}}}}{{2\sqrt {{{m}_{1}}} }},\,\,\,\,\Delta = \omega - {{\omega }_{0}}.$Заметим, что функции ${{A}_{{1,2}}}$ описывают колебания скорости, а не смещения. Благодаря делению этих функций в формулах (21) на соответствующие значения частот достигается равенство нелинейных коэффициентов, обозначенных как γ в системе (8), которое приводит к очевидному энергетическому соотношению
(23)
$\frac{d}{{dt}}\left[ {{{{\left| {{{A}_{1}}} \right|}}^{2}} + {{{\left| {{{A}_{2}}} \right|}}^{2}}} \right] = 2\operatorname{Re} \left[ {A_{1}^{*}{{F}_{0}}\exp ( - it\Delta )} \right].$Когда внешнего воздействия нет, из (23) следует, что суммарная энергия колебаний на частотах первой и второй гармоник сохраняется. Для амплитуд колебаний смещения такое соотношение не выполняется.
Следует добавить, что обсуждавшиеся выше задачи есть лишь некоторая иллюстрация возможностей использования модельных уравнений (8) в акустике. Разумеется, существует немалое число колебательных и волновых процессов иной физической природы (в нелинейной оптике, в электродинамике источников мощного коротковолнового излучения и во многих других разделах физики), которые также могут быть описаны парой “укороченных” уравнений для амплитуд первой и второй гармоник [5] в присутствии внешнего источника “накачки”.
АНАЛИЗ УРАВНЕНИЙ С УЧЕТОМ СЕЛЕКТИВНОГО ПОГЛОЩЕНИЯ
Рассмотрим модель (8), добавив во второе уравнение член $\alpha {{A}_{2}},$ ответственный за поглощение второй гармоники:
(24)
$\begin{gathered} \frac{{d{{A}_{1}}}}{{dt}} + i\gamma A_{1}^{*}{{A}_{2}} = {{F}_{0}}\exp ( - it\Delta ), \\ \frac{{d{{A}_{2}}}}{{dt}} + \alpha {{A}_{2}} + i\gamma A_{1}^{2} = 0. \\ \end{gathered} $Способы технической реализации такого поглощения зависят от устройства конкретной системы, поэтому обсуждать здесь этот вопрос в общем виде не имеет смысла. Некоторые примеры, относящиеся к акустике, можно найти в работах [6–8].
Математическую модель (24) удобно анализировать, записав ее для безразмерных переменных
(25)
$\begin{gathered} {{A}_{1}} = {{\left( {\frac{{\alpha {{F}_{0}}}}{{{{\gamma }^{2}}}}} \right)}^{{1/3}}}\exp ( - it\Delta ){{B}_{1}}, \\ {{A}_{2}} = {{\left( {\frac{{F_{0}^{2}}}{{\alpha \gamma }}} \right)}^{{1/3}}}\exp ( - it2\Delta ){{B}_{2}}. \\ \end{gathered} $С помощью (25) приведем (24) к виду
(26)
$\begin{gathered} {{t}_{1}}\left( {\frac{{d{{B}_{1}}}}{{dt}} - i\Delta {{B}_{1}}} \right) + iB_{1}^{*}{{B}_{2}} = 1, \\ {{t}_{2}}\left( {\frac{{d{{B}_{2}}}}{{dt}} - i2\Delta {{B}_{2}}} \right) + {{B}_{2}} + iB_{1}^{2} = 0. \\ \end{gathered} $В системе уравнений (26) выделены три константы, имеющие размерность времени:
(27)
${{t}_{1}} = {{\left( {\frac{\alpha }{{{{\gamma }^{2}}F_{0}^{2}}}} \right)}^{{1/3}}},\,\,\,\,{{t}_{2}}\, = {{\alpha }^{{ - 1}}},\,\,\,\,{{t}_{3}} = {{\Delta }^{{ - 1}}}.$Поскольку в общем виде уравнения (26) не решаются, их анализ удобно проводить для разных предельных случаев, отличающихся соотношением характерных времен (27).
Задача будет поставлена так: решить уравнения (26) с нулевыми начальными условиями:
Это означает, что в начальный момент времени включается внешний источник, который накачивает энергию в первую гармонику. Нелинейность приводит к частичной перекачке энергии в колебание удвоенной частоты. Процесс нарастания амплитуд обеих гармоник определяется не только их взаимодействием, но и селективными потерями. Основной вопрос, который здесь возникает, связан именно с влиянием потерь на динамический баланс колебательной энергии.
Уравнения (26) записаны для комплексных амплитуд. В дальнейшем понадобятся также уравнения, записанные для действительных амплитуд ${{b}_{1}},$ ${{b}_{2}}$ и фаз ${{s}_{1}},$ ${{s}_{2}}$ взаимодействующих гармоник. Совершая в (26) замену
получим(30)
${{t}_{1}}\frac{{d{{b}_{1}}}}{{dt}} - {{b}_{1}}{{b}_{2}}\sin ({{s}_{2}} - 2{{s}_{1}}) = \cos ({{s}_{1}}),$(31)
${{t}_{1}}{{b}_{1}}\left( {\frac{{d{{s}_{1}}}}{{dt}} - \Delta } \right) + {{b}_{1}}{{b}_{2}}\cos ({{s}_{2}} - 2{{s}_{1}}) = - \sin ({{s}_{1}}),$(33)
${{t}_{2}}{{b}_{2}}\left( {\frac{{d{{s}_{2}}}}{{dt}} - 2\Delta } \right) + b_{1}^{2}\cos ({{s}_{2}} - 2{{s}_{1}}) = 0.$Рассмотрим вначале установившиеся колебания, полагая производные по времени от амплитуд и фаз в уравнениях (29)–(33) равными нулю. При этом получаемая система из четырех алгебраических уравнений сводится к кубическому уравнению относительно квадрата амплитуды первой гармоники:
(34)
$\begin{gathered} b_{1}^{6} - 4{{\Delta }^{2}}{{t}_{1}}{{t}_{2}}b_{1}^{4} + {{\left( {\Delta {{t}_{1}}} \right)}^{2}}\left[ {1 + {{{\left( {2\Delta {{t}_{2}}} \right)}}^{2}}} \right]b_{1}^{2} - \\ - \,\,\left[ {1 + {{{\left( {2\Delta {{t}_{2}}} \right)}}^{2}}} \right] = 0. \\ \end{gathered} $Решив (34), можно затем рассчитать амплитуду и второй гармоники по формуле
(35)
$b_{2}^{2} = b_{1}^{4}{{\left[ {1 + {{{\left( {2\Delta {{t}_{2}}} \right)}}^{2}}} \right]}^{{ - 1}}}.$В простейшем случае, когда расстройки нет, из уравнений (34), (35) следует $b_{1}^{{2\,}} = b_{2}^{2} = 1.$ Возвращаясь к размерным переменным с помощью формул (25), для стационарных значений амплитуд получим
(36)
$\left| {{{A}_{1}}} \right| = {{\left( {\frac{{\alpha {{F}_{0}}}}{{{{\gamma }^{2}}}}} \right)}^{{1/3}}},\,\,\,\,\left| {{{A}_{2}}} \right| = {{\left( {\frac{{F_{0}^{2}}}{{\alpha \gamma }}} \right)}^{{1/3}}}.$Нетрудно показать, что решение (36) является устойчивым.
Результат (36) демонстрирует неожиданную, на первый взгляд, тенденцию: с увеличением коэффициента поглощения α второй гармоники амплитуда колебания на основной частоте возрастает. На такую закономерность указано, например, в работах [9, 10], однако там речь шла о недиспергирующих нелинейных волнах, в которых происходит формирование ударных фронтов и “растекание” энергии по многим высшим гармоникам. Подавление второй гармоники для таких волн “запирает” каскадный процесс передачи энергии вверх по спектру и как бы “выключает” нелинейное поглощение. Дискуссия по этой проблеме отражена в ранних работах [11, 12]. Теперь оказывается, что рост энергии, сохраняемой на основной частоте при усилении нелинейных потерь, происходит даже в таких простых нелинейных системах (24), где взаимодействуют только две гармоники [13, 14].
ПОДАВЛЕНИЕ НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ И УВЕЛИЧЕНИЕ ДОБРОТНОСТИ РЕЗОНАТОРА С СЕЛЕКТИВНЫМИ ПОТЕРЯМИ
Как показано выше, влияние селективного поглощения на протекание нелинейных взаимодействий имеет общее значение с точки зрения теории колебаний и волн. Вводя селективно поглощающие элементы в систему (среду), можно управлять потоками энергии. Одно из явлений, представляющих интерес, состоит в следующем. Организуя отток энергии из полости акустического резонатора путем введения селективной диссипации на частоте второй гармоники, можно заметно усилить нелинейные колебания, повысить запасенную энергию и добротность. Парадоксальный эффект повышения добротности хорошо выражен в тех случаях, когда частоты высших гармоник, генерируемых в нелинейной среде, близки к собственным частотам резонатора. Важным примером системы, обладающей нужными свойствами, является акустический резонатор с селективными потерями.
Спектр собственных частот резонатора с жесткими стенками эквидистантен, то есть ωn = $ = n{{\omega }_{0}} = n\pi c/L.$ Поэтому генерируемая гармоника с номером $n$ является $n$-й модой. Из-за этого в резонаторе реализуется каскад нелинейных процессов, приводящих к эффективной перекачке энергии вверх по спектру. В высокочастотной области энергия колебаний интенсивно поглощается вследствие диссипативных процессов, обычно связанных с вязкостью и теплопроводностью среды.
Общие идеи управления волновыми взаимодействиями за счет внесения селективных потерь изложены в работах [9, 14–16]. В данном случае необходимо внести поглотитель на частоте $2{{\omega }_{0}};$ подавление второй гармоники прервет каскадный процесс передачи энергии вверх по спектру или, иными словами, “подавит” образование ударных фронтов. Технически потери на частоте $2{{\omega }_{0}}$ можно реализовать либо введением в объем среды резонансных рассеивающих элементов (например, пузырьков газа в жидкость), либо использовать селективные границы (например, прозрачные для волны $2{{\omega }_{0}}$ и отражающие вовнутрь все иные частоты [6–8, 16]).
Представим поле, осциллирующее между стенками резонатора $x = 0$ и $x = L$, как суперпозицию двух встречных нелинейных волн [2, 4]. Функция $u,$ описывающая “правую” волну колебательной скорости, подчиняется уравнению
(37)
$\begin{gathered} \frac{1}{c}\frac{{\partial u}}{{\partial t}} - \frac{\varepsilon }{{{{c}^{2}}}}u\frac{{\partial u}}{{\partial \tau }} - \frac{b}{{2{{c}^{3}}\rho }}\frac{{{{\partial }^{2}}u}}{{\partial {{\tau }^{2}}}} = \\ = \frac{A}{{2L}}\sin \omega t - \frac{\alpha }{c}{{b}_{2}}(t)\sin 2\omega t. \\ \end{gathered} $(38)
${{b}_{2}}(t) = \frac{2}{\pi }\int\limits_0^\pi {u(t,\tau )\sin 2\omega \tau d\left( {\omega \tau } \right)} ,$Введем безразмерные переменные
(39)
$\begin{gathered} V = \frac{u}{{{{u}_{0}}}},\,\,\,\,\theta = \omega \tau ,\,\,\,\,T = \frac{t}{{{{t}_{{SH}}}}}; \\ {{t}_{{SH}}} = \frac{c}{{\varepsilon \omega {{u}_{0}}}},\,\,\,\,{{u}_{0}} = \sqrt {\frac{{Ac}}{{2\pi \varepsilon }}} . \\ \end{gathered} $(40)
$\begin{gathered} \frac{{\partial V}}{{\partial T}} - V\frac{{\partial V}}{{\partial {\theta }}} - \Gamma \frac{{{{\partial }^{2}}V}}{{\partial {{{\theta }}^{2}}}} = \\ = \sin \theta - D\sin 2\theta \frac{2}{\pi }\int\limits_0^\pi {V\left( {T,\theta {\text{'}}} \right)} \sin 2\theta {\text{'}}d\theta {\text{'}}. \\ \end{gathered} $Здесь присутствуют безразмерные числа:
(41)
$\Gamma = \frac{{b\omega }}{{2\varepsilon \rho c{{u}_{0}}}} = \frac{{{{t}_{{SH}}}}}{{{{t}_{{DIS}}}}},\,\,\,\,D = \frac{{\alpha c}}{{\varepsilon \omega {{u}_{0}}}} = \alpha {{t}_{{SH}}}.$Они определяются отношением нелинейного времени ${{t}_{{SH}}}$ ко времени обычного диссипативного (вязкостного) поглощения (это число $\Gamma $) либо к характерному времени ${{\alpha }^{{ - 1}}}$ селективного поглощения (число $D$).
Для расчета процесса возбуждения вынужденных колебаний в резонаторе нужно решить уравнение (40) с нулевым начальным условием $V\left( {T = 0,\,\,{\theta }} \right) = 0.$ При больших значениях “медленного” времени, при $T \to \infty ,$ достигается баланс между поступлением энергии от источника (колеблющейся стенки) и потерями трех типов: вязкостными, нелинейными и селективными. Анализ удается провести только для установившихся колебаний. В стационарном режиме нелинейность выражена сильнее всего, поэтому этот режим наиболее интересен.
Интегрируем, положив для простоты вязкость равной нулю:
Здесь черта сверху означает усреднение по периоду колебаний. Константа $\overline {{{V}^{2}}} $ пропорциональна средней интенсивности волны. Определим ее как $\overline {{{V}^{2}}} = 2 + D{{B}_{2}}$ из условия $V\left( {{\theta } = \pi } \right) = 0.$ Решение при этом имеет вид
(43)
$\begin{gathered} \frac{{{{V}_{{ST}}}(\theta )}}{{\sqrt 2 }} = \pm \left[ {(1 + \cos \theta ) + D(1 - {{{\cos }}^{2}}\theta )\,\, \times \frac{{{{2}^{{^{{^{{}}}}}}}}}{{{{\pi }_{{_{{}}}}}}}} \right. \\ \times \,\,\frac{{{{2}^{{^{{^{{}}}}}}}}}{{{{\pi }_{{_{{}}}}}}}{{\left. {\int\limits_0^\pi {{{V}_{{ST}}}\left( {\theta {\text{'}}} \right)} \sin 2\theta {\text{'}}d\theta {\text{'}}} \right]}^{{1/2}}}. \\ \end{gathered} $Знак “плюс” берется в (43) для полупериода $0 < \theta \leqslant \pi ,$ знак “минус” – для $ - \pi \leqslant \theta < 0.$ В окрестности точки $\theta = 0$ формируется ударный фронт. Не интересуясь его структурой, мы положили параметр $\Gamma = 0.$ Учет конечности $\Gamma $ может быть произведен методом сращиваемых асимптотических разложений и даст малые поправки (в режиме сильно выраженной нелинейности) к энергетическим характеристикам поля.
Профили одного периода колебаний (43) изображены на рис. 1 для различных значений коэффициента селективного поглощения $D = 0,\,\,1,\,\,4,\,\,10,\,\,20.$ Профиль при наличии лишь нелинейного поглощения ($D = 0$) отвечает известному решению неоднородного уравнения Бюргерса [14, 15]
Рис. 1.
Профили одного периода одной из двух бегущих волн, формирующих нелинейное поле в резонаторе с селективными потерями $D = 0,\,\,1,\,\,4,\,\,10,\,\,20$ на частоте второй гармоники.
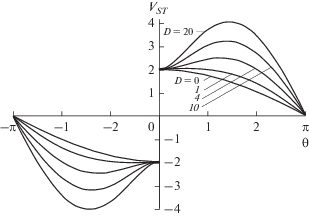
С увеличением селективного поглощения $D$ безразмерная амплитуда разрыва на рис. 1 не растет, зато наблюдается рост возмущения ${{V}_{{ST}}}$ на гладких участках профиля. При $D \gg 1$ колебание описывается выражением ${{V}_{{ST}}} \approx {{V}_{0}}\sin {\theta }{\text{.}}$ Оно происходит почти по гармоническому закону, но в точке ${\theta } = 0$ сохраняется разрыв. Однако при больших числах $D$ безразмерная величина скачка ($ = \,2$) становится малой по сравнению с амплитудой волны ${{V}_{0}},$ т.е. $2 \ll {{V}_{0}}.$
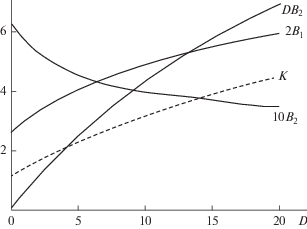
Таким образом, с увеличением числа $D$ наблюдается заметное падение амплитуды ${{B}_{2}}$ второй гармоники $2\omega .$ Начало этого процесса показано на рис. 2. Подавление волны $2{\omega }$ тормозит переброс энергии в высшие гармоники $3\omega ,4\omega ,....,$ поэтому энергия накапливается в волне основной частоты ω, которая практически не затухает. Рост амплитуды первой гармоники ${{B}_{1}}(D)$ также показан на рис. 2. Здесь же дана зависимость $D{{B}_{2}}(D).$ Максимальное значение возмущения (43) ${{V}_{{ST}}} = 2$ достигается при $\theta = 0$ для $D{{B}_{2}} \leqslant 0.5,$ а для $D{{B}_{2}} > 0.5$ максимум (см. рис. 1) сдвигается в точку ${{\theta }_{{\max }}},$ где
(45)
$\begin{gathered} {{V}_{{\max }}}({{\theta }_{{\max }}}) = \frac{{1 + 2D{{B}_{2}}}}{{\sqrt {2D{{B}_{2}}} }}, \\ {{\theta }_{{\max }}} = \arccos \frac{1}{{2D{{B}_{2}}}}. \\ \end{gathered} $Рис. 2.
Зависимости амплитуд первой и второй гармоник, а также произведения $D{{B}_{2}}$ для различных значений селективного поглощения $D$ (сплошные линии) и “коэффициентa усиления” энергии колебаний $K,$ накопленной в полости резонатора (штриховая кривая).
Средняя интенсивность волны также растет с усилением селективного поглощения:
Добротность резонатора в режиме нелинейных колебаний, имеющих сложный спектральный состав, может быть определена как отношение максимального возмущения скорости в стоячей волне $2{{u}_{{\max }}}$ к амплитуде скорости $A$ колебаний границы:
(47)
$\begin{gathered} Q = \frac{{2{{u}_{{\max }}}}}{A} = \sqrt {\frac{{2c}}{{\pi \varepsilon A}}} \,\Phi \left( {2D{{B}_{2}}} \right); \\ \Phi \left( {x \equiv 2D{{B}_{2}}} \right) = \frac{{1 + x}}{{\sqrt x }},\,\,\,\,x > 1; \\ \Phi = 2,\,\,\,\,x \leqslant 1. \\ \end{gathered} $Можно также определить квадрат добротности через отношение средних интенсивностей этих колебаний:
(48)
${{Q}^{2}} = \frac{{2\overline {{{u}^{2}}} }}{{{{{{A}^{2}}} \mathord{\left/ {\vphantom {{{{A}^{2}}} 2}} \right. \kern-0em} 2}}} = \frac{{2c}}{{\pi \varepsilon A}}\left( {2 + D{{B}_{2}}} \right).$Обе формулы (47), (48) описывают возрастание добротности с ростом селективного поглощения $D$.
Оценки по этим формулам показывают, что если правая стенка $x = L$ резонатора селективно пропускает наружу 98% мощности падающего излучения на частоте второй гармоники, то добротность резонатора увеличивается примерно в 3.5 раза, а энергия колебаний – на порядок.
Работа поддержана грантом РФФИ 19-02-00937.
Список литературы
Новиков Б.К., Руденко О.В., Тимошенко В.И. Нелинейная гидроакустика. Ленинград: Судостроение, 1981.
Руденко О.В., Хедберг К.М., Энфло Б.О. Нелинейные стоячие волны в слое, возбуждаемые периодическим движением его границы // Акуст. журн. 2001. Т. 47. № 4. С. 525–533.
Руденко О.В., Шанин А.В. Нелинейные явления при установлении колебаний слоя линейной диссипативной среды, возбуждаемых конечными смещениями его границы // Акуст. журн. 2000. Т. 46. № 3. С. 392–400.
Rudenko O.V. Nonlinear standing waves, resonant phenomena and frequency characteristics of distributed systems (Review) // Acoust. Phys. 2009. V. 55. № 1. P. 27–54.
Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн (3-е изд.). М.: Ленанд, 2015. 432 с.
Андреев В.Г., Гусев В.Э., Карабутов А.А., Руденко О.В., Сапожников О.А. Повышение добротности нелинейного акустического резонатора с помощью селективно поглощающего зеркала // Акуст. журн. 2000. Т. 31. № 2. С. 275–276.
Красильников М.В., Руденко О.В. Генерация второй гармоники в резонаторе типа многослойного интерференционного фильтра // Акуст. журн. 1979. Т. 25. № 5. С. 744–748.
Руденко О.В., Хирных К.Л. Модель резонатора Гельмгольца для поглощения интенсивного звука // Акуст. журн. 1990. Т. 36. № 3. С. 527–534.
Руденко О.В. К проблеме искусственных нелинейных сред с резонансным поглотителем // Акуст. журн. 1983. Т. 29. № 3. С. 398–402.
Андреев В.Г., Васильева О.А., Лапшин Е.А., Руденко О.В. Процессы генерации второй гармоники и вырожденного параметрического усиления в среде с селективным поглощением // Акуст. журн. 1985. Т. 31. № 1. С. 12–16.
Moffett M.B., Mellen R.H. On absorption as a means of saturation suppression // J. Sound Vibr. 1981. V. 76. № 2. P. 295–297. Woodsum H.C. Author’s reply // J. Sound Vibr. 1981. V. 76. № 2. P. 297–298.
Woodsum H.C. Enhancement of parametric efficiency by saturation suppression // J. Sound and Vibration. 1980. V. 69. № 1. P. 27–33.
Андреев В.Г., Руденко О.В., Сапожников О.А., Хохлова В.А. Подавление нелинейного затухания звуковой волны в среде, содержащей резонансный поглотитель с конечной шириной линии // Вест. Моск. Ун-та. Сер. 3: Физ., астрон. 1985. Т. 26. № 3. С. 58–62.
Руденко О.В. Нелинейные пилообразные волны // Успехи физ. наук. 1995. Т. 165. № 9. С. 1011–1036.
Гурбатов С.Н., Руденко О.В., Саичев А.И. Волны и структуры в нелинейных средах без дисперсии. М.: Физматлит, 2008. 296 с.
Руденко О.В., Собисевич Л.Е., Собисевич А.Л., Хедберг К.М. Рост энергии и добротности нелинейного резонатора с усилением его потерь // Докл. Акад. наук. 2002. Т. 383. № 3. С. 330–333.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал


