Акустический журнал, 2019, T. 65, № 4, стр. 435-439

Дифракция гауссова пучка на сильно вытянутом сфероиде

И. В. Андронов^*

Санкт-Петербургский государственный университет, НИИФ
198504 Петродворец, ул. Ульяновская, дом 1/1, Россия

Поступила в редакцию 09.01.2019
После доработки 13.02.2019
Принята к публикации 20.03.2019

DOI: 10.1134/S0320791919040014

Аннотация

Рассмотрена задача высокочастотной дифракции гауссова пучка, падающего параллельно оси сильно вытянутого сфероида. Методом параболического уравнения в сфероидальных координатах построен старший член асимптотики поля в пограничном слое у поверхности в виде интеграла, содержащего функции Уиттекера. Рассчитаны значения поля на поверхности идеально жесткого сфероида. Проведено обсуждение эффектов высокочастотной дифракции.

Ключевые слова: дифракция, сильно вытянутый сфероид, высокочастотная асимптотика, метод параболического уравнения

ВВЕДЕНИЕ

Напомним, что сильно вытянутым телом в задачах высокочастотной дифракции [1] мы называем такое выпуклое тело, радиусы кривизны поверхности которого удовлетворяют соотношению

(1)

$k\rho \sim {{\left( {k{{\rho }_{t}}} \right)}^{3}}$

или эквивалентно

(2)

$k\rho \sim {{\left( {\frac{\rho }{{{{\rho }_{t}}}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}.$

Здесь $k$ – волновое число, $\rho $ – радиус кривизны поверхности в плоскости падения, ${{\rho }_{t}}$ – радиус кривизны поверхности в поперечной плоскости.

Отметим, что в соотношения (1), (2) входит частота. Таким образом, при достаточном увеличении частоты тело, характеризуемое любым сколь угодно большим отношением ${\rho \mathord{\left/ {\vphantom {\rho {{{\rho }_{t}}}}} \right. \kern-0em} {{{\rho }_{t}}}},$ перестает быть сильно вытянутым в указанном выше смысле, и для описания процессов дифракции на нем могут быть применены классические высокочастотные асимптотики.

Обычно, в задачах дифракции выделяются две частотные области. На низких и умеренных частотах возможен прямой численный счет методом конечных или граничных элементов, на высоких частотах хорошо работают асимптотические приближения. Однако, в задачах дифракции на вытянутых телах на шкале частот может наблюдаться область, в которой прямой численный счет уже невозможен, а асимптотические подходы еще недостаточно точны. Для того чтобы повысить диапазон частот, доступных для численного счета, и сделать счет устойчивым к степени вытянутости тела, плодотворными являются подходы, связанные с диаграммными уравнениями [2] и методом дискретных источников [3]. В случае же умеренно высоких частот, для которых величины $k\rho $ и $k{{\rho }_{t}}$ асимптотически велики, но связаны соотношением (1), необходимы специальные асимптотические подходы, разработанные в [1, 2, 6] и др. работах.

Процессы высокочастотной дифракции на сильно вытянутых телах имеют определенную специфику. Трактовать эти явления с точки зрения классической теории высокочастотной дифракции не всегда возможно, поскольку принцип локальности, установленный Фоком [7] и лежащий в основе классического асимптотического подхода, в случае сильно вытянутых тел оказывается недостаточно локальным. Другими словами, дифракционное поле на сильно вытянутом теле зависит от геометрии поверхности и поля лучей не только в малой окрестности рассматриваемой точки, но определяется геометрией всей задачи. Происходит это от того, что масштабы пограничного слоя, определяемого как и в классическом случае радиусом кривизны геодезической на поверхности тела, оказываются сравнимыми с размером всего тела. В связи с этим привычная логика анализа и интерпретации процессов дифракции в случае сильно вытянутых тел не работает. Так, на сильно вытянутом теле нет области глубокой тени, все тело располагается в полутени. Соответственно, говорить о волнах соскальзывания можно лишь с определенными оговорками, поскольку отделить их одну от другой по разности фаз не удается. Нет также и некоторых других объектов, привычных для высокочастотной дифракции.

Для того чтобы хоть в какой-то мере воспользоваться идеей локальности, необходимо произвести локализацию дифракционного процесса некоторым дополнительным способом. В этой статье мы рассматриваем дифракцию гауссовых пучков на сильно вытянутом сфероиде.

ПОСТАНОВКА ЗАДАЧИ ДИФРАКЦИИ

Рассматривается стационарная задача дифракции на сильно вытянутом сфероиде. Множитель, выражающий зависимость от времени, принят в виде ${{e}^{{ - i\omega t}}}$ и всюду опущен. Будем пользоваться цилиндрической системой координат $(r,\varphi ,z),$ ось которой совпадает с осью вращения сфероида, а начало координат находится в его центре (см. рис. 1). Поверхность сфероида зададим уравнением

(3)

$\frac{{{{r}^{2}}}}{{{{a}^{2}}}} + \frac{{{{z}^{2}}}}{{{{b}^{2}}}} = 1.$

Рис. 1.

Геометрия задачи.

Во внешности сфероида поле удовлетворяет уравнению Гельмгольца

(4)

$\Delta u + {{k}^{2}}u = 0,$

где $k = {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c}$ – волновое число. На поверхности будем рассматривать два варианта краевых условий. Либо поверхность идеально жесткая

(5)

$\frac{{\partial u}}{{\partial n}} = 0,$

где $n$ – нормаль к поверхности, либо идеально мягкая

(6)

$u = 0.$

Рассмотрим дифракцию гауссова пучка ${{u}^{i}},$ который в локальной системе координат описывается формулой

(7)

$\begin{gathered} {{u}^{i}} = \frac{C}{{s - s{\text{*}} - id}} \times \\ \times \,\,exp\left\{ {iks + i\frac{k}{2}\frac{{{{{(\Delta r)}}^{2}}\left( {s - s{\text{*}}} \right)}}{{{{{\left( {s - s{\text{*}}} \right)}}^{2}} + {{d}^{2}}}} - \frac{{kd}}{2}\frac{{{{{\left( {\Delta r} \right)}}^{2}}}}{{{{{\left( {s - s{\text{*}}} \right)}}^{2}} + {{d}^{2}}}}} \right\}. \\ \end{gathered} $

Здесь $C$ – амплитуда, $s$ – координата, измеряемая вдоль оси пучка, $\Delta r$ – поперечная координата, расстояние от точки наблюдения до оси пучка, $s{\text{*}}$ и $d$ – параметры, характеризующие положение плоскости перетяжки пучка и степень его фокусировки.

Будем рассматривать гауссовы пучки, распространяющиеся параллельно оси z. Тогда $s = z$ и, если ось пучка имеет координаты $r = {{r}_{0}},$ $\varphi = 0,$ то

$\Delta r = \sqrt {{{r}^{2}} + r_{0}^{2} - 2r{{r}_{0}}cos(\varphi )} .$

Будем считать частоту достаточно высокой, так что $kb \gg 1.$ При этом сфероид настолько вытянут, что выполнены соотношения (1), (2). Степень вытянутости будем характеризовать параметром

(8)

$\chi = \frac{{k{{a}^{2}}}}{b},$

который является величиной порядка единицы, т.е.

(9)

$\chi = O(1).$

ПАРАБОЛИЧЕСКОЕ УРАВНЕНИЕ

Процедура построения старшего члена асимптотики поля повторяет приведенную в [5, 6]. Кратко напомним основные моменты. Во-первых, воспользовавшись симметрией вращения поверхности, представим поле в виде ряда Фурье по угловой переменной φ:

(10)

$u = {{u}_{0}}(r,z) + 2\sum\limits_{m = 1}^{ + \infty } {{{u}_{m}}} (r,z)cos(n\varphi ).$

Каждая гармоника ${{u}_{m}}$ удовлетворяет соответствующему уравнению

(11)

$\frac{{{{\partial }^{2}}{{u}_{m}}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial {{u}_{m}}}}{{\partial r}} + \frac{{{{\partial }^{2}}{{u}_{m}}}}{{\partial {{z}^{2}}}} - \frac{{{{m}^{2}}}}{{{{r}^{2}}}}{{u}_{m}} + {{k}^{2}}{{u}_{m}} = 0$

и краевым условиям (5) или (6).

Во-вторых, перейдем к эллиптическим координатам $(\eta ,\xi ),$ которые связаны с цилиндрическими формулами [8]

(12)

$r = p\sqrt {1 - {{\eta }^{2}}} \sqrt {{{\xi }^{2}} - 1} ,\,\,\,\,z = p\eta \xi .$

Здесь введена величина

(13)

$p = \sqrt {{{b}^{2}} - {{a}^{2}}} ,$

имеющая смысл половины расстояния между фокусами сфероида. В координатах $(\eta ,\xi )$ поверхность сфероида является координатной и задается уравнением

(14)

$\xi = {b \mathord{\left/ {\vphantom {b p}} \right. \kern-0em} p}.$

В-третьих, заметив, что, ввиду принятого предположения (9), величина ${b \mathord{\left/ {\vphantom {b p}} \right. \kern-0em} p}$ асимптотически близка к единице, произведем растяжение радиальной координаты ξ, путем перехода к координате τ, которую введем формулой

(15)

$\tau = \frac{{2kb}}{\chi }\left( {\xi - 1} \right).$

Наконец, используя η и τ как координаты пограничного слоя, выделим быстро осциллирующий множитель

(16)

${{u}_{m}} = {{e}^{{ikp\eta }}}{{U}_{m}}(\eta ,\tau ),$

а функции ослабления ${{U}_{m}}$ будем искать в виде асимптотического ряда по обратным степеням большого параметра kp. В старшем порядке, для которого сохраним обозначение ${{U}_{m}},$ получим параболическое уравнение

(17)

$\begin{gathered} \tau \frac{{{{\partial }^{2}}{{U}_{m}}}}{{\partial {{\tau }^{2}}}} + \frac{{\partial {{U}_{m}}}}{{\partial \tau }} + \frac{{i\chi }}{2}\left( {1 - {{\eta }^{2}}} \right)\frac{{\partial {{U}_{m}}}}{{\partial \eta }} + \\ + \,\,\left( {\frac{{{{\chi }^{2}}}}{4}\tau - \frac{{{{m}^{2}}}}{{4\tau }} - \frac{{i\chi }}{2}\eta } \right){{U}_{m}} = 0. \\ \end{gathered} $

В уравнении (17) переменные делятся, что позволяет получить представление

(18)

$\begin{gathered} {{U}_{m}} = \frac{1}{{\sqrt {1 - {{\eta }^{2}}} }}\int {{{{\left( {\frac{{1 - \eta }}{{1 + \eta }}} \right)}}^{{it}}}} \times \\ \times \,\,\left\{ {{{A}_{m}}(t)\frac{{{{M}_{{it,{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0em} 2}}}}( - i\chi \tau )}}{{\sqrt {\chi \tau } }} + {{B}_{m}}(t)\frac{{{{W}_{{it,{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0em} 2}}}}( - i\chi \tau )}}{{\sqrt {\chi \tau } }}} \right\}dt. \\ \end{gathered} $

Здесь M и W – функции Уиттекера [9]. В фигурных скобках записано общее решение дифференциального уравнения по переменной τ, которое возникает при разделении переменных в (17) и содержит две произвольные на данном этапе построения решения функции ${{A}_{m}}$ и ${{B}_{m}},$ зависящие от параметра разделения переменных. Так же как и в случае падения плоской волны, рассмотренного в [4–6], интегрирование в (18) будем проводить по вещественной оси (здесь и ниже пределы $ \pm \infty $ опущены).

Как показано в цитируемых выше работах, слагаемое с функцией Уиттекера M отвечает падающей волне, а слагаемое с функцией Уиттекера W удовлетворяет условию излучения. Тогда, требуя выполнения краевого условия при каждом t, получим

(19)

${{B}_{m}}(t) = {{A}_{m}}(t){{R}_{m}}(t),$

где

${{R}_{m}} = - \frac{{2i\chi {{{\dot {M}}}_{{it,{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0em} 2}}}}( - i\chi ) + {{M}_{{it,{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0em} 2}}}}( - i\chi )}}{{2i\chi {{{\dot {W}}}_{{it,{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0em} 2}}}}( - i\chi ) + {{W}_{{it,{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0em} 2}}}}( - i\chi )}}$

в случае идеально жесткой поверхности, описываемой условием (5), и

${{R}_{m}} = - \frac{{{{M}_{{it,{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0em} 2}}}}( - i\chi )}}{{{{W}_{{it,{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0em} 2}}}}( - i\chi )}}$

в случае идеально мягкой поверхности, описываемой условием (6). Точка над функцией означает ее производную по аргументу.

Амплитуда ${{A}_{m}}$ определена в следующем параграфе при помощи сшивания с падающим гауссовым пучком (7).

ПРЕДСТАВЛЕНИЕ ДЛЯ ГАУССОВА ПУЧКА

Выражение (7) можно интерпретировать как поле точечного источника, смещенного в комплексном направлении, т.е. имеющего координаты

$z = {{z}_{0}} \equiv s{\text{*}} + id,\,\,\,\,r = {{r}_{0}},\,\,\,\varphi = 0.$

Дифракция поля точечного источника на сильно вытянутом сфероиде рассмотрена в [10]. Для амплитуды ${{A}_{m}}$ в представлении (18) там получена формула

(20)

$\begin{gathered} {{A}_{m}} = \frac{{2C{{i}^{m}}}}{{\pi {{{(m!)}}^{2}}}}\frac{{exp\left( { - ik{{z}_{0}} - \tfrac{{i{{z}_{0}}}}{{2b}}\delta } \right)}}{{\sqrt {kp} {{r}_{0}}}}{{\left( {\frac{{{{z}_{0}} + b}}{{{{z}_{0}} - b}}} \right)}^{{it}}} \times \\ \times \,\,\Gamma \left( {\frac{{m + 1}}{2} + it} \right)\Gamma \left( {\frac{{m + 1}}{2} - it} \right){{M}_{{it,{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0em} 2}}}}\left( {i\delta } \right). \\ \end{gathered} $

Здесь введено обозначение

$\delta = \frac{{kbr_{0}^{2}}}{{z_{0}^{2} - {{b}^{2}}}}.$

Эта формула получена в предположении, что источник находится в узком конусе на достаточно большом расстоянии левее сфероида, поскольку только в этом случае падающее поле отвечает лучам, бегущим под малыми углами к оси сфероида, и имеет зависимость от z, близкую к выделенной в (16).

В случае комплексных координат источника условия применимости формулы (20) необходимо исследовать дополнительно. Очевидно, что множитель ${{e}^{{ikz}}}$ присутствует в (7) и, следовательно, для возможности использования приближения параболического уравнения необходимо лишь, чтобы оставшиеся два слагаемых в показателе экспоненты в (7), будучи записанными в координатах $(\eta ,\tau ),$ выражали бы медленно меняющуюся функцию. Иными словами, для применимости формулы (20) необходимо, чтобы выполнялись следующие соотношения

(21)

$\frac{{k{{{(\Delta r)}}^{2}}(z - s*)}}{{{{{(z - s*)}}^{2}} + {{d}^{2}}}} < {\text{const}},$

(22)

$\frac{{k{{{(\Delta r)}}^{2}}d}}{{{{{(z - s*)}}^{2}} + {{d}^{2}}}} < {\text{const}}.$

Будем рассматривать только такие ${{r}_{0}},$ которые не превосходят нескольких a. Тогда в условиях (21), (22) можно заменить $\Delta r$ на a. В результате для применимости формулы (20) достаточно, чтобы было выполнено

(23)

$d > b.$

Таким образом, допустимы большие значения d, то есть сколь угодно узкие пучки. Величина $s*,$ определяющая положение плоскости перетяжки, при этом может быть любой, как меньше –b, что требовалось в случае дифракции поля точечного источника, так и больше –b, и даже больше b. Таким образом, можно рассматривать дифракцию как расходящихся, так и сходящихся гауссовых пучков.

АСИМПТОТИКА ПОЛЯ

Подставим выражения (20) и (19) в (18). В случае абсолютно жесткого сфероида получим

(24)

$\begin{gathered} {{U}_{m}} = - \frac{{C{{i}^{m}}}}{{\pi m!}}\frac{{exp\left( { - ik{{z}_{0}} - \tfrac{{i{{z}_{0}}}}{{2b}}\delta } \right)}}{{ka{{r}_{0}}\sqrt {1 - {{\eta }^{2}}} }}\int {{{{\left( {\frac{{1 - \eta }}{{1 + \eta }}\frac{{{{z}_{0}} + b}}{{{{z}_{0}} - b}}} \right)}}^{{it}}}} \times \\ \times \,\,\Gamma \left( {\frac{{m + 1}}{2} + it} \right)\Gamma \left( {\frac{{m + 1}}{2} - it} \right) \times \\ \times \,\,\frac{{{{M}_{{it,{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0em} 2}}}}\left( {i\delta } \right)}}{{{{{\dot {W}}}_{{it,{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0em} 2}}}}( - i\chi ) - \tfrac{i}{{2\chi }}{{W}_{{it,{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0em} 2}}}}( - i\chi )}}dt. \\ \end{gathered} $

В задаче дифракции на абсолютно мягком сфероиде получим

(25)

$\begin{gathered} \frac{{\partial {{U}_{m}}}}{{\partial \tau }} = \frac{{C{{i}^{m}}}}{{\pi m!}}\frac{{exp\left( { - ik{{z}_{0}} - \tfrac{{i{{z}_{0}}}}{{2b}}\delta } \right)}}{{ka{{r}_{0}}\sqrt {1 - {{\eta }^{2}}} }}\int {{{{\left( {\frac{{1 - \eta }}{{1 + \eta }}\frac{{{{z}_{0}} + b}}{{{{z}_{0}} - b}}} \right)}}^{{it}}}} \times \\ \times \,\,\Gamma \left( {\frac{{m + 1}}{2} + it} \right)\Gamma \left( {\frac{{m + 1}}{2} - it} \right)\frac{{{{M}_{{it,{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0em} 2}}}}\left( {i\delta } \right)}}{{{{W}_{{it,{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0em} 2}}}}( - i\chi )}}dt. \\ \end{gathered} $

При вещественных ${{z}_{0}}$ множитель ${{({{({{z}_{0}} + b)} \mathord{\left/ {\vphantom {{({{z}_{0}} + b)} {({{z}_{0}} - b)}}} \right. \kern-0em} {({{z}_{0}} - b)}})}^{{it}}}$ является осциллирующим, при комплексных ${{z}_{0}}$ он дает экспоненциальный рост на плюс или минус бесконечности. Однако, можно проверить, что интегралы в (24) и (25) сходятся за счет убывания, обеспечиваемого гамма-функциями.

Для того чтобы получить представление об особенностях дифракции гауссовых пучков на сильно вытянутом сфероиде, проведем расчеты по формуле (24) для двух идеально жестких сфероидов. Пусть первый сфероид (сфероид № 1) не очень сильно вытянут и характеризуется параметром $\chi = 10.$ У более сильно вытянутого сфероида № 2 примем $\chi = 1.$ Для придания более универсального характера результатам расчета введем безразмерные параметры пучка ${{s{\text{*}}} \mathord{\left/ {\vphantom {{s{\text{*}}} b}} \right. \kern-0em} b},$ ${d \mathord{\left/ {\vphantom {d b}} \right. \kern-0em} b}$ и ${{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} a}} \right. \kern-0em} a}.$

На рис. 2 представлены результаты расчетов для пучков, характеризуемых параметрами ${{s{\text{*}}} \mathord{\left/ {\vphantom {{s{\text{*}}} b}} \right. \kern-0em} b} = - 2,$ ${d \mathord{\left/ {\vphantom {d b}} \right. \kern-0em} b} = 1,$ но распространяющихся по разным лучам, определяемым параметром ${{r}_{0}}.$ На рис. 3 рассматриваются пучки с разными положениями сечения перетяжки. На обоих рисунках представлены значения поля в двух сечениях при $\varphi = 0^\circ $ и при $\varphi = 180^\circ .$ Первое из этих сечений, за исключением случая ${{r}_{0}} = 0,$ является более освещенным, чем второе. Таким образом, из двух линий одного стиля, та, что проходит выше, отвечает сечению $\varphi = 0^\circ ,$ а та, что проходит ниже, сечению $\varphi = 180^\circ .$ На основании проведенных расчетов можно указать на следующие закономерности:

Рис. 2.

Распределения поля в сечениях $\varphi = 0^\circ $ (верхние кривые) и $\varphi = 180^\circ $ (нижние кривые) (а) на поверхности сфероида № 1 и (б) на поверхности сфероида № 2 при возбуждении пучками с параметрами $s* = - 2b,$ $d = b$ и разными значениями ${{r}_{0}}$.

Рис. 3.

Распределения поля в сечениях $\varphi = 0^\circ $ (верхние кривые) и $\varphi = 180^\circ $ (нижние кривые) (а) на поверхности сфероида № 1 и (б) на поверхности сфероида № 2 при возбуждении пучками с параметрами ${{r}_{0}} = a,$ $d = b$ и разными значениями $s{\text{*}}.$

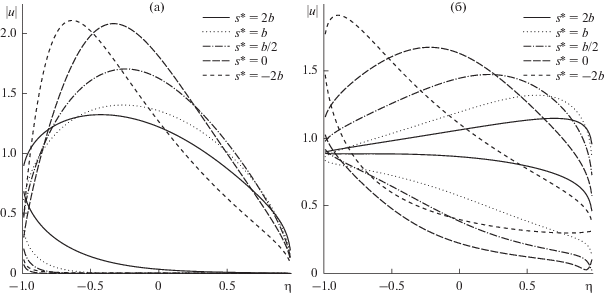
1. Так же как и в случае падения плоской волны, поле имеет большую амплитуду на менее вытянутом сфероиде, однако убывает оно по координате η быстрее.

2. Пучок, ось которого совпадает с осью сфероида, засвечивает преимущественно лишь небольшую область вблизи переднего конца сфероида (при $\eta \approx - 1$), а при увеличении η амплитуда поля монотонно уменьшается, и уменьшается быстрее, чем в случае падения плоской волны.

3. При увеличении ${{r}_{0}}$ ось пучка сдвигается от оси сфероида, в результате максимум амплитуды смещается в сторону больших значений координаты η. При этом скорость убывания поля вдоль поверхности уменьшается.

4. В отличие от случая дифракции плоской волны тень, образующаяся с противоположной стороны сфероида по отношению к оси пучка, оказывается более глубокой.

5. При дифракции сходящегося пучка на достаточно сильно вытянутом сфероиде увеличение амплитуды поля в пучке конкурирует с убыванием поля вследствие дифракции, в результате амплитуда поля увеличивается вдоль поверхности и максимум поля наблюдается в области геометрической тени.

В заключение отметим, что в этой статье мы проводили расчеты лишь для пучков, распространяющихся параллельно оси сфероида. Однако, формулы (24) и (25) позволяют также рассчитывать дифракцию пучков, падающих под углом. Для этого надо лишь соответствующим образом задать мнимые части координат ${{z}_{0}}$ и ${{r}_{0}}.$ При этом для справедливости параболического приближения угол $\theta $ должен быть мал настолько, чтобы $\sqrt {kb} {\kern 1pt} \theta = O(1).$

Список литературы

Andronov I.V., Bouche D. Asymptotic of creeping waves on a strongly prolate body // Ann. Télécommun. 1994. V. 49. № 3–4. P. 205–210.
Клеев А.И., Кюркчан А.Г. Использование метода диаграммных уравнений в сфероидальных координатах для решения задач дифракции на сильно вытянутых рассеивателях // Акуст. журн. 2015. Т. 61. № 1. С. 21–29.
Маненков С.А. Новая версия модифицированного метода дискретных источников применительно к задаче дифракции на теле вращения // Акуст. журн. 2014. Т. 60. № 2. С. 129–136.
Андронов И.В. Дифракция на сильно вытянутом теле вращения // Акуст. журн. 2011. Т. 57. № 2. С. 147–152.
Андронов И.В. Дифракция плоской волны, падающей под малым углом к оси вращения сильно вытянутого сфероида // Акуст. журн. 2012. Т. 58. № 5. С. 571–579.
Andronov I.V. High-frequency acoustic scattering from prolate spheroids with high aspect ratio // J. Acoust. Soc. Am. 2013. V. 134. № 6. P. 4307–4316.
Фок В.А. Новые методы в теории дифракции // Вестник Ленинградского университета. 1947. № 4. С. 5–11.
Комаров И.В., Пономарев Л.И., Славянов С.Ю. Сфероидальные и кулоновские сфероидальные функции. М.: Наука, 1976. 320 с.
Справочник по специальным функциям / Под ред. Абрамовица М., Стиган И. М.: Наука, 1979. 832 с.
Andronov I.V. Point source diffraction by a strongly elongated spheroid // J. Sound and Vibration. 2015. V. 355. P. 360–368.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал