1. На главную
  2. Электронные версии
  3. Акустический журнал
  4. T. 65, № 4, 2019

Акустический журнал, 2019, T. 65, № 4, стр. 520-532

Восстановление ультразвуковых изображений отражателей по неполным данным методом распознавания со сжатием

Е. Г. Базулин a, *, Д. М. Соколов a, **

a Научно-производственный центр “ЭХО+”
123458 Москва, ул. Твардовского 8, Россия

* E-mail: bazulin@echoplus.ru
** E-mail: Sokolov@echoplus.ru

Поступила в редакцию 15.01.2019
После доработки 19.02.2019
Принята к публикации 20.03.2019

Полный текст (PDF)

Аннотация

В статье исследована возможность восстановления изображения отражателей методом Compressive Sensing (CS) по неполному набору эхосигналов, измеренных антенной решеткой в режиме двойного или тройного сканирования. Для сравнения с методом CS были также рассмотрены применяемые в ультразвуковом контроле методы восстановления отражателей: метод корреляции, метод комбинированного SAFT (C-SAFT) и метод максимальной энтропии. Последний метод позволяет восстанавливать изображения со сверхразрешением по неполному набору измеренных эхосигналов. В численных и модельных экспериментах продемонстрирована возможность восстанавления изображения отражателей со сверхразрешением при значительном уменьшении объема используемых данных. Восстановленные методом CS изображения сравнивались с изображениями, восстановленными другими методами.

Ключевые слова: ультразвуковой неразрушающий контроль (УЗК), комбинированный SAFT (С-SAFT), двойное сканирование, Full Matrix Capture (FMC), метод максимальной энтропии (МЭ), метод Compressive Sensing (CS)

1. ВВЕДЕНИЕ

Получение информации о внутренней структуре промышленных объектов является актуальной проблемой и относится к классу обратных задач рассеяния, которые состоят в определении количественных характеристик неизвестных несплошностей на основе наблюдения за рассеянным облучающем полем. Для неразрушающего контроля важнейшая задача заключается в классификации обнаруженных отражателей, определении их размеров и координат залегания. Эта информация может быть использована специалистами по прочностным расчетам для оценки эксплуатационного ресурса объекта контроля.

В настоящее время широко используется технология ультразвукового контроля (УЗК) с применением пьезоэлектрических антенных решеток (АР), излучающих и принимающих акустические волны в исследуемом объекте. Широкое применение в практике УЗК нашли две технологии восстановления изображения отражателей с использованием АР: фазированные антенные решетки (ФАР) [1] и цифровая фокусировка антенной решетки (ЦФА) [2]. В работе [3] обе технологии сравниваются и делается вывод, что ЦФА-технология более перспективна в плане применения разнообразных алгоритмов восстановления изображения отражателей. Режим ЦФА – это технология получения акустических изображений со сплошной фокусировкой во всех точках области восстановления изображения (ОВИ). На первом этапе с помощью АР регистрируются эхосигналы при переборе всех комбинаций излучатель-приемник. Этот режим регистрации называется двойным сканированием (в зарубежных источниках – Full Matrix Capture (FMC)). На втором этапе по измеренным эхосигналам методом комбинационного SAFT (C-SAFT) [4] восстанавливается изображение отражателей.

Недостатком метода ЦФА является большой объем эхосигналов, измеренных АР в режиме двойного сканирования, который растет квадратично количеству ее элементов ${{N}_{e}}.$ К примеру, для линейной 32-х элементной АР количество измеренных эхосигналов равно 1024, а для 64-х элементной – уже 4096. Это приводит к уменьшению скорости контроля из-за регистрации большого объема эхосигналов и их обменом между модулями ЦФА-дефектоскопа, что может быть достаточно критичным при контроле оборудования атомных электростанций, где время нахождения оператора в условиях повышенной радиации должно быть минимизировано. Один из вариантов уменьшения объема измеренных эхосигналов – это использование прореженной коммутационной матрицы $С $ размерами ${{N}_{e}} \times {{N}_{e}}.$ Если элемент ${{C}_{{nm}}} = 1,$ то это означает, что регистрируется эхосигнал, излученный n-м элементом и принятый m-м элементом АР. Для неактивных пар ${{C}_{{nm}}} = 0.$ В режиме двойного сканирования все элементы матрицы $С $ равны единице. В ЦФА-дефектоскопе A1550 [5] коммутационная матрица $С $ имеет вид треугольной матрицы (Half Matrix Capture (HMC)), в которой от нуля отличны только ${{N}_{{tr}}} = ({{N}_{e}} + 1){{{{N}_{e}}} \mathord{\left/ {\vphantom {{{{N}_{e}}} 2}} \right. \kern-0em} 2}$ элементов. Для уменьшения объема регистрируемых эхосигналов коммутационную матрицу $С $ можно случайным образом заполнить ${{N}_{{tr}}}$ единицами. Однако для случая ${{N}_{{tr}}} < 0.3N_{e}^{2}$ восстановить изображение отражателей методом ЦФА без заметной потери качества не удается.

Уменьшить объем измеренных эхосигналов и увеличить скорость их регистрации можно с использованием технологии CDMA (Code Division Multiple Access – множественный доступ с кодовым разделением) [6]. В этом случае все элементы АР одновременно излучают импульсы, но каждому элементу приписан свой сигнал из набора псевдоортогональных сигналов. В идеальном случае скорость регистрации эхосигналов может быть сокращена до одного такта, а количество измеренных эхосигналов уменьшено с $N_{e}^{2}$ до ${{N}_{e}}.$ Однако необходимость излучать сложные сигналы усложняет электронный такт дефектоскопа.

Еще одной актуальной задачей УЗК является повышение качества и разрешающей способности изображения отражателей. Для этого разработаны относительно простые методы, например, метод когерентного фактора (CF) [7], метод Кейпона (Capon), Multiple Signal Classification (MUSIC) [8, 9], которые повышают разрешающую способность изображения и уменьшают уровень спеклового шума. Существуют нелинейные методы восстановления изображения отражателей, основанные на алгоритме Гершберга–Папулиса [10], которые позволяют получить разрешающую способность изображения, превышающую рэлеевскую. Особый класс составляют методы, которые также относятся к классу нелинейных, позволяющие получать изображения по неполным данным. К ним относятся метод максимальной энтропии (МЭ) [11] и метод распознавания со сжатием (в зарубежной литературе Compressive Sensing (CS)) [12–14]. Оба алгоритма позволяют восстановить изображение отражателей со сверхразрешением и с малым уровнем “боковых лепестков” функции рассеивания точки, используя около 10% эхосигналов от полного набора $\left( {{{N}_{{tr}}} < 0.1N_{e}^{2}} \right).$

Метод CS позволяет обеспечить дополнительное уменьшение объема данных при их передаче, хранении и восстановлении изображения. Может возникнуть ситуация, что в ОВИ находится только один точечный отражатель, то есть в восстановленной матрице с изображением будет отличен от нуля только один элемент. Если АР измерено 1024 эхосигнала, каждый длиной 1000 отсчетов, то объем измеренных эхосигналов будет равен $N = 1\,024\,000$ отсчета. Возникает парадоксальная ситуация – для того чтобы получить ЦФА-изображение, в котором от нуля отличен только один пиксель, нужно зарегистрировать, обработать, передать и запомнить в 1 024 000 раз больше чисел. Метод CS при определенных условиях позволяет устранить это противоречие. В настоящий момент метод CS пытаются активно применять для получения высококачественных изображений по неполным данным в различных областях: компьютерная томография, УЗК [15], магнитно-резонансная томография [16], фотоакустическая томография [17], радиолокация [18] и многих других.

Данная статья посвящена применению метода CS для решения актуальных задач УЗК, а именно уменьшения объема данных, используемых для восстановления высококачественного изображения отражателей.

2. МЕТОДЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЯ

В этом разделе рассмотрены несколько линейных и нелинейных методов восстановления изображения отражателей.

2.1. Корреляционный метод, C-SAFT

Решение обратной задачи рассеивания заключается в том, чтобы по известным источникам поля $q({{{\mathbf{r}}}_{t}},t),$ расположенным в области ${{S}_{t}},$ и по измеренному в области ${{S}_{r}}$ рассеянному полю $p({{{\mathbf{r}}}_{r}},t)$ найти функцию ${\varepsilon }({\mathbf{r}}),$ описывающую отражающие свойства неоднородности в области S. Формально решение прямой задачи, то есть расчет рассеянного поля $p({{{\mathbf{r}}}_{r}},t) = p({{{\mathbf{r}}}_{r}},t;{{{\mathbf{r}}}_{t}})$ по известным функциям $q({{{\mathbf{r}}}_{t}},t)$ и ${\varepsilon }({\mathbf{r}}),$ можно записать в следующем виде

(1)
$p({{{\mathbf{r}}}_{r}},t) = P\left( {{{{\mathbf{r}}}_{r}},{\varepsilon }({\mathbf{r}}),q({{{\mathbf{r}}}_{t}},t)} \right).$

Помещая точечный отражатель в произвольную точку ${{{\mathbf{r}}}_{i}},$ то есть полагая ${\varepsilon }({\mathbf{r}}) = {\delta }({\mathbf{r}} - {{{\mathbf{r}}}_{i}}),$ можно оценить вид функции ${\varepsilon }({\mathbf{r}})$ по корреляционной формуле

(2)
$\begin{gathered} {\hat {\varepsilon }}({{{\mathbf{r}}}_{i}}) = \int {\int\limits_{{{S}_{t}}} {\int\limits_{{{S}_{r}}} {\int\limits_S {p({{{\mathbf{r}}}_{r}},t)G({{{\mathbf{r}}}_{r}},{{{\mathbf{r}}}_{i}},{{{\mathbf{r}}}_{t}},t)} d{\mathbf{r}}d{{{\mathbf{r}}}_{r}}d{{{\mathbf{r}}}_{t}}dt} } } , \\ G({{{\mathbf{r}}}_{r}},{{{\mathbf{r}}}_{i}},{{{\mathbf{r}}}_{t}},t) = P\left( {{{{\mathbf{r}}}_{r}},{\delta }({\mathbf{r}} - {{{\mathbf{r}}}_{i}}),q({{{\mathbf{r}}}_{t}},t)} \right). \\ \end{gathered} $

Функция $G({{{\mathbf{r}}}_{r}},{{{\mathbf{r}}}_{i}},{{{\mathbf{r}}}_{t}},t)$ зависит от формы излученного импульса $s(t)$ и должна учитывать эффекты отражения, преломления и трансформации типов волн, анизотропии акустических свойств материалов и затухания звуковой волны. Чем точнее удастся решить прямую задачу (1) на основе выбранного варианта описания процесса излучения, распространения и рассеивания ультразвуковой волны, тем точнее можно восстановить изображение отражателей. Смысл функции ${\varepsilon }({\mathbf{r}}),$ которую иногда называют рассеивающим потенциалом, зависит от типа решаемой задачи.

Часто функцию $s(t)$ заменяют на ${\delta }(t - {{t}_{{\max }}}),$ где ${{t}_{{\max }}}$ – время нарастания импульса, и выбирают одну акустическую схему. Под акустической схемой, которую обозначим как $as$, будем подразумевать описание лучевой траектории распространения импульса от излучателя до приемника при отражении от неровных границ объекта контроля с учетом трансформации типа волны. В этом случае выражение (2) трансформируется в формулу, описывающую метод C-SAFT [19]

(3)
${\hat {\varepsilon }}({{{\mathbf{r}}}_{i}};as) = \int\limits_{{{S}_{t}}} {\int\limits_{{{S}_{r}}} {p({{{\mathbf{r}}}_{r}},t - {{t}_{{del}}}({{{\mathbf{r}}}_{r}},{{{\mathbf{r}}}_{t}},{{{\mathbf{r}}}_{i}};as) + {{t}_{{\max }}})d{{{\mathbf{r}}}_{r}}} } d{{{\mathbf{r}}}_{t}},$
где ${{t}_{{del}}}({{{\mathbf{r}}}_{r}},{{{\mathbf{r}}}_{t}},{{{\mathbf{r}}}_{i}};as)$ – время пробега импульса от излучателя до точки ${{{\mathbf{r}}}_{i}}$ и к приемнику для заданной акустической схемы as. Для расчета времени пробега импульса по лучевой траектории можно воспользоваться вариационным принципом Ферма [20] или методом трассировки [21].

Если АР перемещается ${{N}_{w}}$ раз по поверхности объекта контроля, регистрируя эхосигналы в режиме двойного сканирования в каждой точке, то такой режим назовем режимом тройного сканирования. Когерентная сумма парциальных изображений, восстановленных для каждого положения АР согласно (3), позволит получить объединенное (итоговое) изображение отражателей с более высокой фронтальной разрешающей способностью, например, за счет когерентного сложения по формуле

(4)
$I({{{\mathbf{r}}}_{i}};as) = \left| {\sum\limits_{w = 1}^{{{N}_{w}}} {{\hat {\varepsilon }}({{{\mathbf{r}}}_{i}},{{{\mathbf{r}}}_{w}};as)} } \right|,$
где ${{{\mathbf{r}}}_{w}}$ – вектор, определяющий положение АР на поверхности объекта контроля.

2.2. Метод максимальной энтропии

Если прямая задача линейна или ее удается линеаризовать, как в случае борновского приближения, то формулу (1) можно записать в матричном представлении в виде системы линейных алгебраических уравнений (СЛАУ)

(5)
${\mathbf{p}} = {\mathbf{G\varepsilon }} + {\mathbf{n}},$
где матрица $G$ описывает распространение ультразвуковых волн от их источников в области ${{S}_{t}}$ до точечного отражателя в области S и до области приема ${{S}_{r}},$ вектор $n$ – шум измерений. Так как матрица $G$ плохо обусловлена, то один из способов оценки $\hat {\varepsilon }$ из уравнения (5) сводится к задаче безусловной оптимизации, когда в качестве критерия качества восстановленного изображения выбирается квадрат невязки решения
(6)
${{\chi }^{2}}(\hat {\varepsilon }) = \left\| {G\hat {\varepsilon } - p} \right\| = {{(G\hat {\varepsilon } - p)}^{T}}(G\hat {\varepsilon } - p),$
где символ T обозначает операцию транспонирования. Оценку $\hat {\varepsilon }$ можно записать в виде
(7)
$\hat {\varepsilon } = \mathop {{\text{argmin}}}\limits_{{\mathbf{\hat {\varepsilon }}} \in {{R}^{{{{N}_{{i,x}}} \times {{N}_{{i,z}}}}}}} ({{\chi }^{2}}(\hat {\varepsilon })),$
где ${{N}_{{i,x}}}$ и ${{N}_{{i,z}}}$ – размеры матрицы изображения в отсчетах. Решение уравнения (7) существует в явном виде и совпадает с расчетом корреляции, как и формула (2),

(8)
${{\hat {\varepsilon }}_{c}} = 2{{G}^{T}}p.$

Дальнейшее развитие метода (7), так называемая регуляризация по Тихонову А.Н. [22], заключается в добавлении к невязке штрафного функционала, один из вариантов которого имеет вид максимальной энтропии или, так называемой, кросс-энтропии [23]

(9)
$H({{{\varepsilon }}_{i}}) = - \sum\limits_{i = 1}^N {{{{\varepsilon }}_{i}}\ln \left( {\frac{{{{{\varepsilon }}_{i}}}}{{\mu }}} \right)} ,$
где N – количество точек ${{{\mathbf{r}}}_{i}}$, в которых рассчитывается изображение, μ – оценка среднего значения интенсивности фона изображения. Таким образом, решение задачи сводится к минимизации невязки следующего выражения
(10)
${{{\mathbf{\hat {\varepsilon }}}}_{\alpha }} = \mathop {\arg \min }\limits_{{\mathbf{\hat {\varepsilon }}} \in {{R}^{{{{N}_{{i,x}}} \times {{N}_{{i,z}}}}}}} \left( {{{\chi }^{2}}({\mathbf{\hat {\varepsilon }}}) - {\alpha }H({\mathbf{\hat {\varepsilon }}})} \right),$
где α – параметр регуляризации. Важное свойство функционала в виде энтропии заключается в том, что, используя формулу (10), можно получить изображение отражателей со сверхразрешением, то есть с разрешением выше чем рэлеевское разрешение. Для достижения максимальной скорости решения задачи минимизации (10) нужно пользоваться методами второго порядка [24], для чего требуется формула расчета градиента и гессиана целевой функции ${{\chi }^{2}}(\hat {\varepsilon }).$ Статья [25] посвящена получению изображения отражателей со сверхразрешением методом МЭ по эхосигналам, измеренным ультразвуковой АР решеткой.

2.3. Метод распознавания со сжатием (CS)

Описание метода. Идея метода заключается в переходе от определенной СЛАУ размерностью $N \times N$ согласно (5) к решению недоопределенной СЛАУ размерностью $K \times N,$ причем при $K \ll N.$ Такой переход можно осуществить, используя матрицу $A$ размерами $N \times K$ и сводя задачу (5) к уравнению

(11)
${\mathbf{y}} = {\mathbf{Ap}} = {\mathbf{AG\varepsilon }} = {\mathbf{\Phi \varepsilon }},\,\,\,\,{\text{г д е }}\,\,\,\,{\mathbf{ \Phi }} = {\mathbf{AG}},$
в которой результаты измерений представлены как вектор ${\mathbf{y}}$ длиной всего $K$ “отсчетов”. Для однозначного решения задачи (11) нужно, чтобы сигнал ${\mathbf{\varepsilon }}$ обладал определенными свойствами, специальным образом перейти к недоопределенной системе СЛАУ и разработать методы решения задачи (11).

Необходимым условием работы CS-метода, то есть однозначного решения недоопределенного уравнения (11), является разреженность восстанавливаемого сигнала $\varepsilon $. Сигнал называется S-разреженным [11], если большинство его элементов равны нулю, то есть

(12)
${{\left\| \varepsilon \right\|}_{0}} = S \ll N,$
где ${{\left\| \varepsilon \right\|}_{0}}$ – норма $l{}_{0},$ представляющая собой количество ненулевых компонент в векторе ${\mathbf{\varepsilon }}$ и $N$ – длина вектора ${\mathbf{\varepsilon }}$.

Для разреженного сигнала ${\mathbf{\varepsilon }}$ можно подобрать специальную матрицу $A$ размерами $K \times N,$ причем $K$ связан с разреженностью $S$ через формулы (16) или (17), см. ниже. Для применимости метода CS, согласно [11], необходимыми и достаточными, являются следующие условия.

1) Сигнал ${\mathbf{\varepsilon }}$ должен быть S-разреженным, то есть в базисе $G$ иметь вид

(13)
${\mathbf{p}} = \sum\limits_{i = 1}^N {{{{\varepsilon }}_{i}}{{G}_{i}}} ,$
где среди $N$ отсчетов только $S$ отсчетов ${{{\varepsilon }}_{i}} \ne 0.$

2) Должно выполняется “свойство ограниченной изометрии” (Restricted Isometry Property) [26]

(14)
$\sqrt {1 - {\delta }} \leqslant \frac{{{{{\left\| {AG{\mathbf{\varepsilon }}} \right\|}}_{2}}}}{{{{{\left\| {\mathbf{\varepsilon }} \right\|}}_{2}}}} \leqslant \sqrt {1 + {\delta }} ,$
где ${\delta } \in (0,1)$ и ${\mathbf{\varepsilon }}$ – произвольный ненулевой вектор. Это свойство означает, что после воздействия оператора $AG$ на вектор ${\mathbf{\varepsilon }}$ ${{l}_{2}}$-норма вектора ${\mathbf{y}}$ не может стать равной нулю или превысить свое значение в ≈1.4 раза.

3) Матрицы $A$ и $G$ должны удовлетворять свойству некогерентности, то есть векторы матриц ${\mathbf{A}}$ и $G$ должны быть практически ортогональны между собой

(15)
${\mu }(A,G) = \sqrt N \mathop {\max }\limits_{i,j} \frac{{\left| {\left\langle {{{a}_{i}},{{G}_{j}}} \right\rangle } \right|}}{{{{{\left\| {{{a}_{i}}} \right\|}}_{2}}}}.$

Из работы [13] следует, что с высокой долей вероятности точное восстановление S-разреженных векторов по K измерениям будет достигнуто при выполнении следующего условия:

(16)
$K \geqslant c{\mu }{{(A,G)}^{2}}S\lg N,$
где $c$ – некоторая положительная константа. Хорошие результаты получаются и для более простого соотношения

(17)
$K = 4S\lg ({N \mathord{\left/ {\vphantom {N S}} \right. \kern-0em} S}).$

Матрица A, составленная из случайных чисел, с большой вероятностью удовлетворяет второму и третьему из перечисленных выше требований. Существуют различные принципы построения рандомизированных матриц [27]. При проведении исследований использовались следующие типы распределений: равномерное распределение, нормальное распределение и распределение Бернулли. Для разных вариантов формирования матрицы A численная проверка показала соблюдение условий согласно формулам (14) и (15), необходимым для корректной работы метода CS. Для выбора оптимального распределения матрицы A оценивалось также качество восстановленных изображений, при одинаковых параметрах и размерностях, но для разных типов распределения при формировании рандомизированной матрицы A. При этом заметного преимущества одного способа формирования матрицы A перед другим не было выявлено, однако, в статье [28] утверждается, что наилучшим является вариант построения матрицы с использованием распределения Бернулли.

В концепции CS решение уравнения (11), при условии разреженности сигнала, сводится к задаче оптимизации

(18)
${{\left\| {{{{\hat {\varepsilon }}}_{{CS}}}} \right\|}_{1}} \to \min \,\,\,\,{\text{п р и }}\,\,\,{{{\mathbf{p}}}_{{CS}}} = AG{{\hat {\varepsilon }}_{{CS}}}.$

Решение задачи (11) возможно различными способами, однако наиболее распространенным является метод линейного программирования, позволяющий производить поиск максимально разреженного вектора ${{\hat {\varepsilon }}_{{CS}}},$ удовлетворяющего заданному условию.

В постановке задачи при условии наличия шума решение уравнения (11) сводится к решению задачи оптимизации

(19)
$\begin{gathered} {{\left\| {{{{\hat {\varepsilon }}}_{{CS}}}} \right\|}_{1}} \to \min \,\,\,\, \\ {\text{п р и }}\,\,{{\left\| {{{{\mathbf{p}}}_{{CS}}} - AG{{{\hat {\varepsilon }}}_{{CS}}}} \right\|}_{2}} < {\delta ,} \\ \end{gathered} $
где δ – регуляризирующий параметр, величина которого влияет на точность работы алгоритма. Данный параметр можно определить, воспользовавшись формулой
(20)
${\delta } = {\sigma }\sqrt K \sqrt {1 + \frac{{\sqrt 2 }}{{\sqrt K }}} ,$
где σ – величина дисперсии шума [29].

Существует также альтернативная постановка задачи (11), называемая LASSO-задачей [30], подобная методу наименьших квадратов и заключающаяся в минимизации ${{\left\| {{{{\mathbf{p}}}_{{CS}}} - AG{{{\hat {\varepsilon }}}_{{CS}}}} \right\|}_{2}}$ при условии разреженности вектора ε, которую можно представить как

(21)
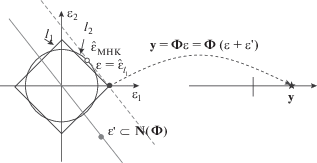
$\begin{gathered} {{\left\| {{{{\mathbf{p}}}_{{CS}}} - AG{{{\hat {\varepsilon }}}_{{CS}}}} \right\|}_{2}} \to \min \\ {\text{п р и }}\,\,\,{{\left\| {{{{\hat {\varepsilon }}}_{{CS}}}} \right\|}_{1}} < {\tau }, \\ \end{gathered} $
где τ – параметр, учитывающий разреженность вектора ε. Восстановление отражателей по формулам (18) и (21) производилось при использовании библиотеки SPGL1 [31].

Геометрическая интерпретация работы метода CS. Для геометрической интерпретации работы метода CS рассмотрим вариант, когда $N = 2.$ Разреженность сигнала $\varepsilon $ означает, что он может иметь либо вид $\left\{ {{{{\varepsilon }}_{1}},0} \right\},$ либо вид $\left\{ {0,{{{\varepsilon }}_{2}}} \right\},$ то есть $S = 1.$ На левой части рис. 1 кругом показан сигнал, который нужно восстановить по вектору y размером $K = 1$ и который получен по формуле (18) в результате измерения сигнала (показан на правой части рис. 1 звездой). Так как $N > K,$ то матрица Φ имеет нуль-плоскость ${\mathbf{{\rm N}}}({\mathbf{\Phi }}),$ схематически показанную на левой части рис. 1 серой сплошной линией. Если справедливо утверждение ${\mathbf{y}} = {\mathbf{\Phi \varepsilon }},$ то для любого ${\mathbf{\varepsilon }}{\text{'}} \subset {\mathbf{N}}({\mathbf{\Phi }}),$ который показан на рис. 1 кружком, также справедливо ${\mathbf{y}} = {\mathbf{\Phi }}({\mathbf{\varepsilon }} + {\mathbf{\varepsilon }}{\text{'}}).$

Рис. 1.

Геометрическая интерпретация работы метода CS.

При использовании $l{}_{2}$-нормы восстановить ε по ${\mathbf{y}}$ можно, найдя кратчайшее расстояние от центра координат системы $\left\{ {{{{\varepsilon }}_{1}},{{{\varepsilon }}_{2}}} \right\}$ до смещенной нуль-плоскости, которая на левой части рис. 1 показана серой пунктирной линией. Решением задачи будет точка соприкосновения “раздувающейся” окружности со смещенной нуль-плоскостью. Полученное решение ${{{\mathbf{\hat {\varepsilon }}}}_{{{\text{М Н К }}}}},$ отмеченное толстой окружностью, не является разреженным сигналом и не совпадает с точным решением ε. Если матрицу A сконструировать таким образом, что нуль-плоскость будет перпендикулярна оси ${{{\varepsilon }}_{1}},$ то в этом частном случае будет найдено точное решение ε. Однако поиск решения на оси ${{{\varepsilon }}_{2}}$ даст неверный ответ. Если воспользоваться $l{}_{1}$-нормой, то решением задачи будет нахождение точки соприкосновения “раздувающегося” квадрата со смещенной нуль-плоскостью. Как видно из рис. 1, найденное решение ${{{\mathbf{\hat {\varepsilon }}}}_{{{{l}_{1}}}}}$ будет совпадать с искомым ε.

Интерпретировать работу метода CS можно и с лингвистической точки зрения. Представим ситуацию, что человека, владеющего двумя языками – языком первобытного племени и русским языком11, – нужно попросить из множества разложенных перед ним предметов выбрать зонт ε. Обращаясь к нему на языке племени, мы опишем искомый предмет так: “Складной домик, под которым бледнолицые люди прячутся от дождя”. Этой информации в виде последовательности из 9 слов (вектор p) вполне хватает, чтобы найти зонт и решить обратную задачу. Если бы мы обратились к человеку на русском языке, сказав только одно слово “зонт” (вектор y), то задача поиска также была бы решена.

3. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ

В численных экспериментах восстанавливались изображения 12 точечных отражателей с коэффициентами отражения 1.0, 0.5 и 0.1, расположенных в вершинах квадратов с ребром 1 мм и центрами в точках (4, 9), (0, 13) и (–4, 17) мм. Предполагалось, что для излучения и приема импульсов использовалась АР с рабочей частотой 5.0 МГц, состоящая из 8-ми точечных элементов на расстоянии друг от друга 2 мм. На рис. 2а показано изображение, восстановленное методом корреляции по формуле (8) при отсутствии шума. Высокий уровень ложных бликов, связанный с грубым шагом в 2 мм между элементами АР при длине волны 1.18 мм, не позволил обнаружить отражатели с коэффициентами отражения 0.1, а обнаруженные отражатели с коэффициентами отражения 0.5 и 1.0 не разрешились между собой. На рис. 2б показано CS-изображение, восстановленное по формуле (18), на котором удалось обнаружить все 12 точечных отражателей и с высокой точностью определить их коэффициент отражения.

Рис. 2.

Изображение 12 точечных отражателей: (а) корреляция, (б) метод CS.

Если добавить к эхосигналам шум с равномерным распределением в диапазоне 5% от максимального значения эхосигналов, то изображение, восстановленное по формуле (18), оказывается настолько зашумленным, что обнаружить точечные отражатели совершенно невозможно. Это связано с тем, что алгоритм (18) эффективно работает только при отсутствии шума. Алгоритмы (19) или (21) по зашумленным эхосигналам восстанавливают CS-изображение, по которому сложно уверено обнаружить все отражатели из-за большого количества ложных бликов. Однако, если использовать ${{N}_{{\mathbf{A}}}}$ рандомизирующих матриц A для восстановления ${{N}_{{\mathbf{A}}}}$ CS-изображений, то после их объединения, например, как сумма или медиана, можно получить изображение, очень близкое к тому, что показано на рис. 2б. Понятно, что такой подход замедляет работу метода CS и снижает степень сжатия D, которую можно определить как

(22)
$D = {{D}_{{\mathbf{C}}}}\frac{N}{{K{{N}_{{\mathbf{A}}}}}},$
где ${{D}_{{\mathbf{C}}}} = {{N_{e}^{2}} \mathord{\left/ {\vphantom {{N_{e}^{2}} {{{N}_{{tr}}}}}} \right. \kern-0em} {{{N}_{{tr}}}}}$ – отношение числа полного набора эхосигналов $N_{e}^{2}$ коммутационной матрицы C к числу используемых ${{N}_{{tr}}}.$ Чем больше $D$, тем больше степень сжатия. Если для восстановления изображения отражателей используются все измеренные эхосигналы, то $D = 1.$

3.1. Требования к объему памяти

Оценим требуемый объем оперативной памяти (ОП), необходимой для работы CS-метода, и сравним его с объемом ОП, требуемым для методов C-SAFT, корреляции и МЭ. Будем исходить из того, что с помощью 32-х элементной АР в режиме двойного сканирования измеряется 1024 эхосигнала, каждый длиной 1024 двухбайтовых чисел. Объем измеренных эхосигналов будет равен 2 Мбайт. Будем полагать, что для методов корреляции, МЭ и CS за счет применения прореженной коммутационной матрацы C используется только четверть эхосигналов (${{D}_{{\mathbf{C}}}} = 4$). Комплексное изображение восстанавливается на ОВИ размерами $256 \times 256$ пикселей, для хранения которого потребуется 0.5 Мбайт ОП. Таким образом, для работы метода C-SAFT нужно выделить всего 2.5 Мбайт для хранения измеренных эхосигналов и ОВИ (см. табл. 1). Для работы метода корреляции по формуле (8) требуется матрица ${{{\mathbf{G}}}^{T}}$ размерами $N \times N$ ($N = 256 \times 256 = 65\,536$ чисел в вещественном формате), для хранения которой необходимо 16 Гбайт ОП. Методу МЭ для хранения матриц G, ${{{\mathbf{G}}}^{T}}$ и H нужно выделить уже 48 Гбайт ОП. Метод CS использует матрицу G и матрицы A и Φ размерами $N \times K.$ Если $K = 1024,$ то необходимый объем ОП для хранения матрицы A и Φ равен 0.25 Гбайт.

Таблица 1.

Оценка объема ОП, необходимого для восстановления изображения

Операция/Метод С-SAFT Корреляция МЭ CS
Эхосигналы, Гбайт 0.002 0.0005 0.0005 0.0005
Изображение, Гбайт 0.0005 0.0005 0.0005 0.0005
Матрица ${\mathbf{G}},$ Гбайт – – 16.0 16.0
Матрица ${{{\mathbf{G}}}^{T}},$ Гбайт – 16.0 16.0 –
Гессиан ${\mathbf{H}},$ Гбайт – – 16.0 –
Матрица ${\mathbf{A}},$ Гбайт – – – 0.25
Матрица ${\mathbf{Ф }},$ Гбайт – – – 0.25
Итоговый размер, Гбайт 0.0025 ≈16.0 ≈48.0 ≈16.5

Таким образом, исходя из размеров рассчитываемых матриц, необходимый объем ОП для расчетов методом МЭ должен быть не менее 64 Гбайт. Отметим, что современный персональный компьютер с ОП объемом 128 Гбайт и более не является исключительным случаем.

Определенные проблемы вызывает скорость расчета матрицы G. Достичь значительного ускорения расчетов (в ≈ 103 раза) можно, используя графические карты с технологией NVIDIA CUDA™ [32], с помощью которых можно распараллелить вычисления элементов матрицы G.

4. МОДЕЛЬНЫЕ ЭКСПЕРИМЕНТЫ

В данном разделе представлены результаты восстановления изображений несплошностей в образцах с применением описанных выше алгоритмов. Для регистрации эхосигналов 1использовался ЦФА-дефектоскоп “АВГУР АРТ”, разработанный и изготавливаемый “Научно-производственным центром неразрушающего контроля “ЭХО+” [33].

4.1. Тест перерассеяния, продольная волна

На рис. 3 приведена схема эксперимента с дюралюминиевым образцом, в котором были просверлены 12 отверстий бокового сверления диаметром 0.5 мм. Восстанавливались изображения четырех отверстий, расположенных в вершинах квадрата с ребром 2 мм и центром на глубине ≈38 мм. Для регистрации эхосигналов использовалась АР (5 МГц, 32 элемента, размер пьезоэлемента 0.9 × 10 мм, зазор между пьезоэлементами 0.1 мм), установленная на плексигласовую призму с углом наклона 20°. Квадратом отмечена ОВИ.

Рис. 3.

Изображение теста перерассеяния и АР на призме.

На рис. 4 показаны изображения отражателей, восстановленные методами C-SAFT и корреляции по акустической схеме, когда излучается и принимается продольная волна. На рис. 4б окружностями нанесены контуры отверстий, а используемая при восстановлении акустическая схема показана на изображении в правом верхнем углу. Лучи продольной волны показаны стрелками. C-SAFT-изображение было получено по формуле (3) по полному набору из эхосигналов, а корреляционное изображение было получено по формуле (8) с использованием ${{N}_{{tr}}}$ = 200 эхосигналов, что составляет 19.5% от полного набора из $N_{e}^{2} = 1024$ эхосигналов. Меньшее количество используемых эхосигналов в корреляционном методе обусловлено тем, что для расчета изображения по формуле (8) в памяти компьютера объемом 64 Гбайт можно было хранить матрицу ${{{\mathbf{G}}}^{T}}$ размерами 20 000 × 20 000 элементов. Поэтому из всех измеренных эхосигналов пришлось выделить фрагмент из 100 отсчетов. Это привело к появлению на рис. 4б характерной дуги, которой нет на рис. 4а. Недостаточно высокая разрешающая способность изображений на рис. 4 не позволила определить не только тип отражателей, но и их количество.

Рис. 4.

Изображение самой близкой к поверхности группы отверстий бокового сверления теста перерассеяния: (а) метод C-SAFT, (б) корреляция.

На рис. 5а показан результат восстановления изображения методом МЭ по формуле (10) по 200 эхосигналам (${\alpha } = 10,$ ${\mu } = {{10}^{{ - 5}}}$). Продольная и фронтальная разрешающие способности изображения возросли более чем в два раза в сравнении с изображениями, полученными методами C-SAFT и корреляции (рис. 4). На МЭ-изображении уверенно видны блики трех отверстий. Амплитуда блика четвертого отверстия из-за эффекта затенения оказалась недостаточно большой для его обнаружения. На рис. 5б показано CS-изображение (${\tau } = 0.1,$ ${{N}_{{\mathbf{A}}}} = 15$), восстановленное по формуле (19) с матрицей Φ размерами $K \times N,$ где $K = 180.$ Пятнадцать парциальных CS-изображений объединялись в итоговое изображение как медиана. CS-изображение оказалось достаточно похожим на МЭ-изображение как по величине разрешающей способности, так и по уровню шума. Однако, восстановление 15 парциальных CS-изображений привело к увеличению времени расчетов. Но даже в этом случае степень сжатия достаточно высокая, $D = 35.$ В табл. 2 сведены основные параметры изображений, полученные рассмотренными методами. Отношение сигнал/шум оценивалось по отношению максимального значения модуля изображения к его среднему.

Рис. 5.

Изображение самой близкой к поверхности группы отверстий бокового сверления теста перерассеяния: (а) метод МЭ, (б) метод CS.

Таблица 2.

Параметры восстановленных изображений методами: С-SAFT, корреляция, МЭ и CS для теста перерассеяния

Метод С-SAFT Корреляция МЭ CS
Степень сжатия $D$ 1 5 5 35
Лучевое разрешение, мм 0.9 0.9 0.4 0.4
Фронтальное разрешение, мм 2.5 2.5 1.2 1.2
Отношение сигнал/шум, дБ 47.0 44.0 70.0 77.0

4.2. Тест перерассеяния, поперечная волна, технология CDMA

Как упоминалось в разделе 1, для реализации технологии CDMA все элементы АР должны одновременно излучать каждый свой специальный зондирующий импульс ${{s}_{n}}(t),$ а эхосигналы должны одновременно приниматься всеми элементами АР. Эхосигнал ${{p}_{m}}(t),$ измеренный в режиме CDMA $m$-ым элементном АР, можно представить как

(23)
${{p}_{m}}(t) = \sum\limits_{n = 1}^{{{N}_{e}}} {{{p}_{{n,m}}}(t)} ,$
где ${{p}_{{n,m}}}(t)$ – эхосигнал, измеренный в режиме двойного сканирования, когда излучил n-ый элемент АР, а зарегистрировал эхосигнал элемент с номером m.

Первый вариант восстановления изображения отражателей при одновременном излучении заключается в декодировании эхосигналов ${{p}_{m}}(t)$ для оценки эхосигналов ${{\tilde {p}}_{{n,m}}}(t),$ которые были бы измерены в режиме двойного сканирования. По декодированным эхосигналам ${{\tilde {p}}_{{n,m}}}(t)$ можно восстановить изображение методом C-SAFT по формуле (3) или корреляционным методом по формуле (2) или (8).

Для эффективного декодирования эхосигналов корреляционная функция ${{R}_{{n,m}}}({\tau })$ набора кодирующих сигналов $\left\{ {{{s}_{n}}(t)} \right\}_{{n = 1}}^{{{{N}_{e}}}},$ состоящего из ${{N}_{e}}$ сигналов и предназначенного для возбуждения элементов АР, должна обладать свойством ортогональности

(24)
$\begin{gathered} {{R}_{{n,m}}}({\tau }) = \int\limits_{ - \infty }^\infty {{{s}_{n}}(t){{s}_{m}}(t + {\tau })dt} = {{{\delta }}_{{n,m}}}{\delta }({\tau }), \\ n,m = 1,2,...{{N}_{e}}, \\ \end{gathered} $
где ${{{\delta }}_{{n,m}}}$ – символ Кронекера. Сигналов для практического использования с таким свойством не известно, однако разработано несколько наборов из ${{N}_{e}}$ кодирующих сигналов ${{s}_{n}}(t)$, которые в той или иной степени приближаются к идеальному набору со свойством (24). Наборы таких сигналов называются псевдоортогональными. К ним относятся фазоманипулированные сигналы, кодированные последовательностью длиной ${{N}_{c}}.$ Закон изменения фазы каждого периода зондирующего сигнала может определятся кодами Касáми [34], Голда [35], де Брейна [36], у которых фаза каждого чипа может принимать значения 0 или 180 градусов. Можно использовать последовательности Задова–Чу [37], имеющие специально рассчитанную фазу каждого чипа в диапазоне от –180 до 1180 градусов. Каждый чип может определять фазу одного периода на несущей частоте ${{f}_{c}},$ но возможен вариант случайного изменения частоты ${{f}_{c}} + {\delta }f$ от чипа к чипу.

Распространенным методом декодирования сигналов ${{p}_{m}}(t)$ является согласованная фильтрация с кодовым сигналом ${{s}_{n}}(t)$ по формуле

(25)
${{\tilde {p}}_{{n,m}}}(t) = \int\limits_{ - \infty }^\infty {{{p}_{m}}({\tau }){{s}_{n}}({\tau } - t)d{\tau }} .$

Такой алгоритм сжатия сложных сигналов обладает высоким быстродействием и позволяет получать изображения с частотой более 10 Гц, но он не позволяет получить низкий уровень межканальных помех и достичь эффекта сверхразрешения. При декодировании эхосигналов по формуле (25) уровень межканальных помех, то есть среднюю величину функции корреляции ${{R}_{{n,m}}}({\tau })$ для $n \ne m,$ можно оценить как ${1 \mathord{\left/ {\vphantom {1 {\sqrt {{{N}_{c}}} }}} \right. \kern-0em} {\sqrt {{{N}_{c}}} }}.$

Второй вариант восстановления изображения не предполагает декодирования эхосигналов ${{p}_{m}}(t),$ а изображение отражателей получается методом МЭ (см. раздел 2.2) или методом CS (см. раздел 2.3), когда матрица ${\mathbf{G}}$ формируется из эхосигналов ${{p}_{m}}(t).$

Для регистрации эхосигналов использовалась АР (5 МГц, 32 элемента, размер пьезоэлемента 0.75 × 10 мм, зазор между пьезоэлементами 0.25 мм), установленная на рексолитовую призму с углом наклона 35°. Призма была размещена на образце примерно так же, как показано на рис. 3. Измерения в режиме CDMA проводились для двух положений АР, в каждом из которых использовался свой кодовый набор $\left\{ {{{s}_{n}}(t)} \right\}_{{n = 1}}^{{{{N}_{e}}}}$ из ${{N}_{e}} = 32$ сигналов, сформированных из кодов Касами длиной ${{N}_{c}} = 15.$ Несущая частота каждого периода зондирующего сигнала случайно менялась в диапазоне от 3.0 до 7.0 МГц (${\delta }f$ = 2.0 МГц).

На рис. 6а показано C-SAFT-изображение, восстановленное по формуле (3) по полному набору эхосигналов ${{p}_{{n,m}}}(t)$ на поперечной волне при излучении простого сигнала, и поэтому имеет более высокую разрешающую способность, чем изображение на рис. 4а. Ложные блики, сформированные импульсами, перерассеянными между отверстиями, не позволяют определить тип и количество отражателей. На рис. 6б показано корреляционное изображение, восстановленное по формуле (8) по эхосигналам ${{p}_{m}}(t),$ полученным по технологии CDMA для двух кодовых наборов $\left\{ {{{s}_{n}}(t)} \right\}_{{n = 1}}^{{{{N}_{e}}}}.$ Использовалось ${{N}_{{tr}}}$ = 64 суммарных эхосигналов ${{p}_{m}}(t),$ что составляет 3.1% от полного набора из 2048 эхосигналов при использовании простого зондирующего сигнала для двух положений АР. Корреляционное изображение имеет ложные блики большой амплитуды, возникшие из-за высокого межканального шума кодового набора $\left\{ {{{s}_{n}}(t)} \right\}_{{n = 1}}^{{{{N}_{e}}}},$ которые делают это изображение не пригодным для анализа. На рис. 6б окружностями нанесены контуры отверстий, а используемая при восстановлении акустическая схема показана на изображении в правом верхнем углу. Лучи поперечной волны показаны стрелками.

Рис. 6.

Изображение самой близкой к поверхности группы отверстий бокового сверления теста перерассеяния: (а) метод C-SAFT простой, сигнал, (б) корреляция, CDMA, коды Касами.

На рис. 7а показано МЭ-изображение, восстановленное по формуле (10) по 64 эхосигналам (${\alpha } = 25,$ ${\mu } = {{10}^{{ - 5}}}$) с размером матрицы G, равным $N \times N,$ где $N = 25\,600.$ Продольная и фронтальная разрешающие способности изображения возросли более чем в два раза (см. табл. 3) в сравнении с изображениями, полученными методами C-SAFT и корреляции (рис. 6). На МЭ-изображении уверенно видны блики четырех отверстий, но имеется ложный блик, близкий по амплитуде к блику границы отверстия, что затрудняет точное определение числа отражателей. На рис. 7б показано CS-изображение (${\tau } = 3,$ ${{N}_{{\mathbf{A}}}} = 10$), восстановленное по формуле (21) с матрицей Φ размерами $K \times N,$ где $K = 449.$ Десять парциальных CS-изображений объединялись в итоговое как медиана. CS-изображение оказалось достаточно похожим на МЭ-изображение как по величине разрешающей способности, так и по уровню шума. В данном примере удалось, за счет замены исходных эхосигналов ${\mathbf{p}}$ на “информационно обогащенный” вектор ${\mathbf{y}}$, достичь очень высокого коэффициента сжатия $D = 182.$

Рис. 7.

Изображение самой близкой к поверхности группы отверстий бокового сверления теста перерассеяния: (а) метод МЭ, (б) метод CS

Таблица 3.

Параметры восстановленных изображений методами: С-SAFT, корреляция, МЭ и CS для теста перерассеяния в режиме CDMA

Метод по режиму CDMA С-SAFT Корреляция МЭ CS
Степень сжатия $D$ 1 32 32 182
Лучевое разрешение, мм 0.6 0.6 0.3 0.3
Фронтальное разрешение, мм 1.8 1.8 0.7 0.5
Отношение сигнал/шум, дБ 23.6 11.2 52.4 68.3

4.3. Модель придонной трещины в образце с неровным дном

На рис. 8 показано фото стального образца толщиной $h = 18$ мм с неровным дном и с моделью придонной трещины в виде паза шириной 0.7 мм с вершиной на глубине 12 мм. Для регистрации эхосигналов использовалась АР (5 МГц, 32 элемента, размер пьезоэлемента 0.5 × 10 мм, зазор между пьезоэлементами 0.1 мм), установленная на рексолитовую призму с углом наклона 35°. Эхосигналы измерялись для двух положений АР: 0 и –13 мм от передней грани призмы до начала трещины, как показано на рис. 8.

Рис. 8.

Фотография образца с моделью трещины и схематическое изображение АР в двух положениях, где измерялись эхосигналы (0 и –13 мм).

На рис. 9 показано изображение трещины, восстановленное методом С-SAFT (формула (3)) и корреляции (формула (8)) при однократном отражении от дна эхосигналов для двух положений АР в предположении, что излучение и прием происходит на поперечной волне. Сплошной линией представлен контур дна и паза образца, а используемая акустическая схема показана на изображении в правом верхнем углу. C-SAFT-изображение (рис. 9а) было получено по полному набору из $2N_{e}^{2}$ эхосигналов, а корреляционное изображение (рис. 9б) было восстановлено с использованием ${{N}_{{tr}}}$ = 288 эхосигналов, что составляет 14.1% от полного набора из 2048 эхосигналов. Несмотря на то, что удалось восстановить изображение границы трещины, наличие ложных бликов затрудняет анализ изображения, а невысокая разрешающая способность не позволяет определить высоту паза даже с точностью ±0.5 мм.

Рис. 9.

Изображение модели трещины при однократном отражении от дна: (а) метод C-SAFT, (б) корреляция.

На рис. 10 показаны результаты восстановления изображения трещины по 288 эхосигналам методами МЭ по формуле (10) (${\alpha } = 7,$ ${\mu } = {{10}^{{ - 5}}}$) и методом CS (${\tau } = 0.1,$ ${{N}_{{\mathbf{A}}}} = 5$). CS-изображение было восстановлено по формуле (21) как медиана парциальных изображений для ${{N}_{{\mathbf{A}}}} = 5$ вариантов рандомизирующей матрицы А с матрицей ${\mathbf{\Phi }}$ размерами $K \times N,$ где $K = 400.$ Размер матрицы G равен $N \times N,$ где $N = 14\,400.$ При сравнении с изображениями, полученными методом C-SAFT и корреляции (рис. 9), оба метода позволили увеличить лучевую и фронтальную разрешающие способности более чем в два раза, при уменьшении амплитуды ложных бликов более чем на 20 дБ. Высота трещины оценивалась по координатам точки перегиба среза изображения вдоль оси z для координаты $x$ = –0.1 мм (см. табл. 4).

Рис. 10.

Изображение трещины в виде паза шириной 0.7 мм с неровным дном по акустической схеме: (а) метод МЭ, (б) метод CS.

Таблица 4.

Параметры восстановленных изображений методами: С-SAFT, корреляция, МЭ и CS для трещины с неровным дном при эхо-регистрации

Метод С-SAFT Корреляция МЭ CS
Степень сжатия $D$ 1 7.1 7.1 51.2
Отношение сигнал/шум, дБ 21.7 11.3 40.1 46.7
Высота паза, мм 4.6 4.7 4.1 4.1

5. ЗАКЛЮЧЕНИЕ

В статье было проведено сравнение изображений объемных и плоскостных отражателей, восстановленных методом C-SAFT, корреляционным методом, методом МЭ и методом CS, по эхосигналам, измеренным АР. На основе проведенных исследований можно сделать выводы, что CS-метод позволяет:

1) Повысить скорость регистрации эхосигналов в среднем в пять раз за счет уменьшения числа измеряемых эхосигналов. Такого же эффекта можно достичь и при восстановлении изображения отражателей методом МЭ.

2) Дополнительно уменьшить объем данных, по которым в модельном эксперименте удалось восстановить CS-изображение отражателей, более чем в пять раз.

3) Повысить лучевую и фронтальную разрешающие способности CS-изображения более чем в 2 раза по сравнению с изображениями полученными методами C-SAFT и корреляции. По полученной разрешающей способности CS-изображения соизмеримы с МЭ-изображениями.

4) уменьшить уровень шума более чем на 20 дБ. По достигнутому уровню шума CS-изображения соизмеримы с МЭ-изображениями.

5) Восстановить высококачественное изображение отражателей по эхосигналам, полученным по технологии CDMA.

Список литературы

  1. Advances in Phased Array Ultrasonic Technology Applications. Publisher: Waltham, MA: Olympus NDT, 2007.

  2. Воронков В.А., Воронков И.В., Козлов В.Н., Самокрутов А.А., Шевалдыкин В.Г. О применимости технологии антенных решеток в решении задач ультразвукового контроля опасных производственных объектов // В мире неразрушающего контроля. 2011. № 1. С. 64–70.

  3. Базулин Е.Г. Сравнение систем для ультразвукового неразрушающего контроля, использующих антенные решетки или фазированные антенные решетки // Дефектоскопия. 2013. № 7. С. 51–75.

  4. Парфенов В.И., Голованов Д.Ю. Обнаружение дискретных разреженных сигналов с частотой дискретизации, не превышающей частоту Найквиста // Журн. радиоэлектроники [электронный журнал]. 2017. № 6. URL: http://jre.cplire.ru/jre/jun17/1/text.pdf (дата обращения: 23.03.2019).

  5. Высокочастотный ультразвуковой томограф “А1550 IntroVisor” // URL: http://acsys.ru/production/?type_id=16&subtype_id=7&product_id=106 (дата обращения: 23.03.2019).

  6. Bazulin A., Bazulin E. Increasing ultrasonic array data acquisition rate through the use of Kasami codes and the maximum entropy method // Applied Physics Research. 2016. V. 8. № 1. P. 47–63. https://doi.org/10.5539/apr.v8n1p47

  7. Camacho J., Parrilla M., Fritsch C. Phase Coherence Imaging // IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2009. V. 56. № 5. P. 958–974.

  8. Okumura S., Taki H., Sato T. Stabilization techniques for high resolution ultrasound imaging using beamspace Capon method // 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD. 2015. P. 892–896.

  9. Малышкин Г.С., Сидельников Г.Б. Оптимальные и адаптивные методы обработки гидроакустических сигналов (обзор) // Акуст. Журн. 2014. Т. 60. № 5. С. 526–545.

  10. Базулин Е.Г. Двумерная адаптивная экстраполяция спектра многочастотных акустических голограмм // Акуст. Журн. 1991. Т. 37. № 1. С. 8–16.

  11. Базулин А.Е., Базулин Е.Г. Деконволюция сложных эхосигналов методом максимальной энтропии в ультразвуковом неразрушающем контроле // Акуст. Журн. 2009. № 6. С. 772–783.

  12. Граничин О.Н. Рандомизация измерений и ${{l}_{1}}$-оптимизация // Стохастическая оптимизация в информатике. 2009. № 5. С. 3–23.

  13. Donoho D.L. Compressed sensing // IEEE Trans. Inform. Theory. 2006. P. 1289–1306.

  14. Foucart S., Rauhut H. A mathematical introduction to compressive sensing. Basel, Birkhauser, 2013. 585 p.

  15. Guarneri G.A., Pipa D.R., Junior F.N., de Arruda L.V.R., Zibetti M.V.W. A sparse reconstruction algorithm for ultrasonic images in nondestructive testing // Sensors. 2015. V. 15. P. 9324–9343.

  16. Минаков Е.И., Серегин П.С. Сравнительный анализ методов параллельной реконструкции изображений магнитно-резонансной томографии // Цифровая обработка сигналов. 2012. № 3. С. 23–28.

  17. Provost J., Lesage F. The application of compressed sensing for photo-acoustic tomography // IEEE Trans. Med. Imag. 2009. V. 28. № 4. P. 585–594.

  18. Knee P. Sparse representations for radar with MATLAB R examples. Synthesis Lectures on Algorithms and Software in Engineering. 2012. V. 4. № 1. P. 1–85.

  19. Ковалев А.В., Козлов В.Н., Самокрутов А.А., Шевалдыкин В.Г., Яковлев Н.Н. Импульсный эхо-метод при контроле бетона. Помехи и пространственная селекция // Дефектоскопия. 1990. № 2. С. 29–41.

  20. Борн М., Вольф Э. Основы оптики. М.: Наука, 1973. 720 с.

  21. Базулин Е.Г. Учет анизотропных свойств сварного соединения при восстановлении изображения отражателей по эхосигналам, измеренным ультразвуковой антенной решеткой // Дефектоскопия. 2017. № 1. С. 11–25.

  22. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. Изд. 3-е, исправл. М.: Наука, 1986. 288 с.

  23. Kullback S. Information Theory and Statistics. New York, 1968. 416 p.

  24. Летова Т.А., Пантелеев А.В. Экстремум функций в примерах и задачах. Учебное пособие. М.: Издательство МАИ, 1998. 376 с.

  25. Базулин Е.Г. О возможности использования в ультразвуковом неразрушающем контроле метода максимальной энтропии для получения изображения рассеивателей по набору эхосигналов // Акуст. Журн. 2013. Т. 59. № 2. С. 235–254.

  26. Candes E.J. The restricted isometry property and its implications for compressed sensing // Comptes Rendus de l’Acad. des Sci. Serie I. 2008. V. 346. 589592.

  27. Candes E., Wakin M. People hearing without listening: An Introduction to Compressive Sampling // IEEE Signal Processing Magazine. 2008. V. 25. № 2. P. 21–30.

  28. Baraniuk R.G., Davenport M., DeVore R., Wakin M.B. A simple proof of the restricted isometry principle for random matrices (aka the Johnson-Lindenstrauss lemma meets compressed sensing) // Constructive Approximation. 2007.

  29. Candes E., Romberg J., Tao T. Stable signal recovery from incomplete and inaccurate measurements // Communications on Pure and Aplied Mathematics. 2006. V. 59. Is. 8. P. 1207–1223.

  30. Efron B., Hastie T., Johnstone Y., Tibshirani R. Least angle regression // The Annals of Statistics. 2004. V. 32. № 2. P. 407–499.

  31. SPGL1: A solver for large-scale sparse reconstruction. URL: https://www.cs.ubc.ca/~mpf/spgl1/index.html (дата обращения: 23.03.2019).

  32. Технология NVIDIA CUDA™, URL: https://www.nvidia.ru/object/cuda-parallel-computing-ru.html (дата обращения: 23.03.2019).

  33. Официальный сайт фирмы “ЭХО+” URL: http://www.echoplus.ru (дата обращения: 23.03.2019).

  34. Kasami T. Weight Distribution Formula for Some Class of Cyclic Codes // Tech. Report No. R-285. Univ. of Illinois, 1966.

  35. Gold R. Optimal binary sequences for spread spectrum multiplexing // IEEE Transactions on Information Theory. October 1967. V. 13(4). P. 619–621. https://doi.org/10.1109/TIT.1967.1054048

  36. de Bruijn N.G. A combinatorial problem // Koninklijke Nederlandse Akademie v. Wetenschappen. 1946. V. 49. P. 758-764.

  37. Chu D.C. Polyphase codes with good periodic correlation properties // IEEE Trans. Inform. Theory. July. 1972. P. 531–532. https://doi.org/10.1109/TIT.1972.1054840

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал