Акустический журнал, 2019, T. 65, № 6, стр. 723-735
Распределение энергии ультразвукового излучателя между бегущими волнами, возбуждаемыми в погруженном упругом волноводе
Е. В. Глушков a, *, Н. В. Глушкова a, О. А. Мякишева a, **
a Институт математики, механики и информатики, Кубанский государственный университет
350040 Краснодар, ул. Ставропольская 149, Россия
* E-mail: evg@math.kubsu.ru
** E-mail: miakisheva.olga@gmail.com
Поступила в редакцию 13.08.2018
После доработки 10.06.2019
Принята к публикации 09.07.2019
Аннотация
Изучается распределение волновой энергии бесконтактного ультразвукового пьезопреобразователя между отраженными, прошедшими и бегущими волнами, возбуждаемыми при зондировании упругой пластины, погруженной в акустическую жидкость. Анализируется зависимость осредненного за период колебаний количества энергии, переносимой каждой из возбуждаемых волн различного типа (акустические объемные волны, вытекающие волны Лэмба и волны Шолте-Стоунли), от относительных размеров источника, расстояния до пластины и частоты, а также структура энергетических потоков и пространственное распределение волновой энергии. Численное исследование проводится в рамках полуаналитической модели, базирующейся на интегральных и асимптотических представлениях для функции Грина рассматриваемой задачи. Графики зависимости волновой энергии от параметров задачи указывают на существование локальных максимумов (лучших частот) возбуждения бегущих волн, которые не совпадают с частотами локальных максимумов мощности источника.
ВВЕДЕНИЕ
В акустоэлектронике и мехатронике используются ультразвуковые поверхностные акустические волны (ПАВ). Они распространяются вдоль границ упругого тела на сравнительно большие расстояния от источника и взаимодействуют с неоднородностями (дефектами) любой природы, выявляя тем самым их местоположение. Рассеянные дефектом ПАВ несут информацию о его виде, размере, форме и ориентации, позволяя создавать на этой основе системы обнаружения и оценки потенциальной опасности дефектов, зарождающихся в элементах тонкостенных конструкций (судостроение, аэрокосмические изделия, емкости для химреактивов и радиоактивных отходов и т.п.). К настоящему времени разработка таких систем постоянного волнового контроля состояния элементов конструкций с помощью сети активных пьезодатчиков, возбуждающих и регистрирующих ультразвуковые ПАВ, сформировалась в самостоятельное направление научно-технического развития – Structural Health Monitoring (SHM) [1, 2].
Разработка SHM систем существенным образом базируется на решении задач возбуждения, распространения и дифракции бегущих упругих волн в рассматриваемых образцах, в том числе и в волноводных структурах достаточно сложного строения, например, в слоистых волоконно-армированных композитах [3]. Среди указанных проблем важную роль играют задачи моделирования взаимодействия активных пьезоэлементов (пьезоактуаторов) с упругой подложкой. Их решение позволяет определять параметры работы пьезоактуатора, обеспечивающие максимальный отток волновой энергии возбуждаемыми ПАВ, повышая тем самым разрешающую способность SHM системы.
Для пленочных пьезоактуаторов, приклеенных к поверхности упругой пластины, хорошо известен эффект чередования частот максимального и минимального излучения энергии, уносимой бегущими волнами определенного типа [4–6]. В первую очередь интерес здесь представляют амплитудно-частотные характеристики возбуждаемых фундаментальных антисимметричной и симметричной волн Лэмба – ${{A}_{0}}$ и ${{S}_{0}}.$ Для частот, на которых энергия ${{A}_{0}}$ и ${{S}_{0}}$ мод достигает локальных максимумов, в SHM используется специальный термин “sweet spots” (“лучшие частоты”) [4]. Их конкретные значения зависят от соотношения радиуса актуатора, толщины пластины и сочетания упругих свойств пьезонакладки и волновода. На плоскости частота-радиус $({\omega },a)$ графики зависимости общего количества энергии пьезоактуатора ${{E}_{0}}({\omega },a)$ и энергии, уносимой модами ${{A}_{0}}$ и ${{S}_{0}},$ выглядят как чередующиеся светлые и темные полосы минимальных и максимальных значений, структура которых резко меняется на частотах отсечки, т.е. при появлении каждой следующей высшей моды (см., например, рис. 4–5 работы [7]).
Наряду со встроенными пьезоисточниками в последние годы в SHM все шире применяются бесконтактные преобразователи (air-coupled transducers – ACT [3, 8–10]) в сочетании с сетью пассивных пьезосенсоров. Взаимодействие акустического пучка, генерируемого АСТ, с упругой структурой также приводит к появлению бегущих волн, распространяющихся вдоль волновода, погруженного в акустическую среду (газ или жидкость), поэтому такие источники, перемещаемые вдоль поверхности специальными манипуляторами, также используются для инспекции больших площадей, например, подводной части корпуса судна или обшивки авиалайнера [11, 12].
Здесь возникает такая же задача определения лучших частот возбуждения бегущих волн, в которой появляются дополнительные параметры: расстояние от источника до поверхности инспектируемой структуры и соотношение ее упругих свойств и свойств окружающей среды. Взаимодействие акустических волн с упругими телами является классической задачей структурной акустики, возникающей в таких практических приложениях, как виброизоляция и акустическая скрытность, бесконтактное определение свойств материалов, неразрушающий контроль, акустоэлектроника, акустическая микроскопия и многих других. Развитые здесь методы и подходы [13–20] позволяют исследовать закономерности прохождения и отражения акустических сигналов через твердую преграду и характеристики возбуждаемых в ней бегущих упругих волн. Для определения оптимальных параметров бесконтактного преобразователя большое значение имеют также результаты по моделированию работы источника вблизи упругого препятствия и оценке количества отдаваемой им энергии в зависимости от расстояния до твердой поверхности и частоты [13, 16]. Тем не менее, определение доли излучаемой энергии, идущей на возбуждение бегущих волн, и изучение ее распределения между нормальными модами, все еще требует более детального исследования.
В настоящей работе формулы, выведенные для анализа распределения энергии контактного источника между объемными и поверхностными волнами многослойного упругого полупространства [21, 22], модифицируются на случай бесконтактного АСТ-излучателя, работающего вблизи погруженного упругого волновода. Как и ранее, явные выражения для потока энергии, переносимой волнами различных типов, получены через элементы матрицы Грина рассматриваемой слоистой среды и характеристики источника. Возможность практического использования этих выражений определяется наличием эффективных алгоритмов построения Фурье-символа матрицы Грина рассматриваемой волноводной структуры, поиска их вещественных и комплексных полюсов, вычисления контурных интегралов и вычетов в этих полюсах. Для структур с плоскопараллельными границами, к которым относится рассматриваемая погруженная пластина, применение преобразования Фурье по горизонтальным координатам позволяет получить явное интегральное представление функции Грина в виде контурных интегралов обратного преобразования Фурье [23, 24].
Основываясь на опыте разработки методов построения матрицы Грина для многослойных упругих сред, в том числе и с такими усложненными свойствами как произвольная анизотропия, пористость и градиентность (см., например, обзор в работе [25]), создан набор математических и компьютерных моделей для иерархии погруженных упругих волноводов различной сложности, начиная от пластин Кирхгофа-Лява до многослойных композитов с произвольной анизотропией слоев. В их рамках рассматривались такие вопросы, как трансформация классических волн Лэмба в вытекающие бегущие волны и особенности проявления феномена обратных волн, зависимость коэффициентов прохождения и отражения от строения (многослойности) пластины и частоты, эффект резонансного прохождения сигнала через пластину, энергетический баланс и структура энергетических потоков, уходящих от источника на бесконечность (см. [26] и цитируемые в ней статьи). Настоящая работа посвящена исследованию зависимости количества волновой энергии, поступающей от плоского кругового источника, моделирующего работу бесконтактного преобразователя, от его размера, расстояния до пластины и частоты, а также анализу ее распределения между отраженными, прошедшими и возбуждаемыми в пластине бегущими волнами.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Рассматриваются установившиеся гармонические колебания $u(x){{e}^{{ - i{\omega }t}}},$ $u = ({{u}_{x}},{{u}_{y}},{{u}_{z}}),$ $x = (x,y,z)$ упругого слоя толщины $h,$ погруженного в акустическую среду (рис. 1a); гармонический множитель ${{e}^{{ - i{\omega }t}}}$ далее опущен. Акустическое давление $p({\mathbf{x}})$ в верхнем и нижнем полупространствах $z \geqslant 0$ и $z \leqslant - h$ удовлетворяет уравнению Гельмгольца
где ${{\kappa }_{0}} = {{\omega } \mathord{\left/ {\vphantom {{\omega } {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}$ – волновое число, ${{c}_{0}}$ – скорость звука в акустической среде, а функция ${{q}_{0}}$ описывает распределение некоторой силы ${\mathbf{F}}$ на ограниченной поверхности ${{D}_{0}}$ излучающего элемента источника, моделируя его действие.Рис. 1.
(а) Геометрия задачи; (б) боковая и горизонтальные поверхности цилиндра, через которые проходит энергия ${{E}_{R}}$ и $E_{V}^{ \pm }.$

Предполагается, что источник расположен в верхнем полупространстве, поэтому поле давлений может быть представлено в следующем виде:
(2)
$p(x) = \left\{ {\begin{array}{*{20}{c}} {{{p}_{0}}(x) + p_{{{\text{sc}}}}^{ - }(x),}&{z \geqslant 0,} \\ {p_{{{\text{sc}}}}^{ + }(x),}&{z \leqslant - h,} \end{array}} \right.$(3)
${{u}_{z}} = \frac{1}{{{{\rho }_{0}}{{{\omega }}^{2}}}}\frac{{\partial p}}{{\partial z}},\,\,\,\,{{{\sigma }}_{z}} = - p\,\,\,\,{\text{при}}\,\,\,\,z = 0\,\,\,\,{\text{и}}\,\,\,\,z = - h.$(4)
${{\tau }_{{xz}}} = {{\tau }_{{yz}}} = 0\,\,\,\,{\text{при}}\,\,\,\,z = 0\,\,\,\,{\text{и}}\,\,\,\,z = - h.$В случае контакта пластины с акустической жидкостью только с одной стороны $z = 0$ ее нижняя поверхность считается свободной от напряжений, т.е. $p_{{sc}}^{ + } = 0.$ Замыкают постановку условия излучения на бесконечности, вытекающие из принципа предельного поглощения [23, 28].
При наличии функции Грина для поля давлений $g(x,{\mathbf{\xi }})$ и вектор-функции Грина для поля смещений ${{g}_{u}}(x,{\mathbf{\xi }})$ решение рассматриваемой краевой задачи представимо в виде поверхностных интегралов [29]:
(5)
$\begin{gathered} p(x) = \int\limits_{{{D}_{0}}} {g(x,{\mathbf{\xi }}){{q}_{0}}({\mathbf{\xi }})d{\mathbf{\xi }},} \\ u(x) = \int\limits_{{{D}_{0}}} {{{{\mathbf{g}}}_{u}}(x,{\mathbf{\xi }}){{q}_{0}}({\mathbf{\xi }})d{\mathbf{\xi }}} , \\ \end{gathered} $ФУНКЦИЯ ГРИНА
Функции $g(x,{\mathbf{\xi }})$ и ${{{\mathbf{g}}}_{u}}(x,{\mathbf{\xi }})$ определяются как решение связной краевой задачи с дельта-функцией в правой части уравнения Гельмгольца вместо ${{q}_{0}}{\text{:}}$
Функции $g$ и ${{{\mathbf{g}}}_{u}}$ стоят в уравнениях и граничных условиях на месте $p$ и u соответственно. Вектор-функция ${{{\mathbf{g}}}_{u}},$ определенная как решение в слое $ - h \leqslant z \leqslant 0,$ доопределяется во внешней акустической среде соотношением
(7)
${{{\mathbf{g}}}_{u}} = {{\nabla g} \mathord{\left/ {\vphantom {{\nabla g} {({{{\rho }}_{0}}{{{\omega }}^{2}})}}} \right. \kern-0em} {({{{\rho }}_{0}}{{{\omega }}^{2}})}}\,\,\,\,{\text{при}}\,\,\,\,z \geqslant 0\,\,\,\,{\text{и}}\,\,\,\,z \leqslant - h.$Аналогично представлению (3), функция Грина давления $g$ для источника, расположенного в точке  верхнего полупространства ($\zeta = d > 0,$ $d$ – расстояние от источника до пластины), также может быть представлена как сумма падающего
поля ${{g}_{0}}(x)$ и отраженного $g_{{{\text{sc}}}}^{ - }(x):g = {{g}_{0}} + g_{{{\text{sc}}}}^{ - }.$ Сферические объемные волны, излучаемые точечным источником, описываются классическим
частным решением уравнения Гельмгольца
верхнего полупространства ($\zeta = d > 0,$ $d$ – расстояние от источника до пластины), также может быть представлена как сумма падающего
поля ${{g}_{0}}(x)$ и отраженного $g_{{{\text{sc}}}}^{ - }(x):g = {{g}_{0}} + g_{{{\text{sc}}}}^{ - }.$ Сферические объемные волны, излучаемые точечным источником, описываются классическим
частным решением уравнения Гельмгольца
(8)
${{g}_{0}} = - \frac{1}{{4{\pi }R}}{{e}^{{i{{\kappa }_{0}}R}}},\,\,\,\,R = \left| {x - {\mathbf{\xi }}} \right|.$Применение преобразования Фурье ${{\mathcal{F}}_{{xy}}}$ по горизонтальным координатам $x$ и $y$ к уравнениям и граничным условиям позволяет получить явные интегральные представления функций Грина через их Фурье-символы $G = {{\mathcal{F}}_{{xy}}}[g]$ и ${{{\mathbf{G}}}_{u}} = {{\mathcal{F}}_{{xy}}}[{{{\mathbf{g}}}_{u}}]{\text{:}}$
(9)
$\begin{gathered} g(x,{\mathbf{\xi }}) = \mathcal{F}_{{xy}}^{{ - 1}}[G] = \frac{1}{{{{{(2{\pi })}}^{2}}}} \times \\ \times \,\,\iint\limits_{{{\Gamma }_{1}}{{\Gamma }_{2}}} {G({{{\alpha }}_{1}},{{{\alpha }}_{2}},z;{\mathbf{\xi }}){{e}^{{ - i({{{\alpha }}_{2}}x + {{{\alpha }}_{2}}y)}}}d{{{\alpha }}_{1}}d{{{\alpha }}_{2}}} \\ \end{gathered} $Для получения Фурье-символов $G$ и ${{{\mathbf{G}}}_{u}}$ используются разработанные ранее алгоритмы построения символа матрицы Грина K упругого стратифицированного полупространства $z \leqslant 0,$ к поверхности которого приложена нагрузка ${\mathbf{q}}:{\tau }{\kern 1pt} {{|}_{{z = 0}}} = {\mathbf{q}}.$ Матрица K определяет связь между Фурье-символами поверхностных напряжений ${\mathbf{Q}} = {{\mathcal{F}}_{{xy}}}[{\mathbf{q}}]$ и смещений ${\mathbf{U}} = {{\mathcal{F}}_{{xy}}}[u]{\text{:}}$
где $\alpha = ({{{\alpha }}_{1}},{{{\alpha }}_{2}})$ – вектор параметров обратного преобразования Фурье. В соответствии с условиями (5) ${\mathbf{q}} = {{(0,0,q)}^{{\text{T}}}},$ т.е. в соотношении (10) работает только третий столбец ${{{\mathbf{K}}}_{3}}$ матрицы K. Учитывая условия непрерывности (4), Фурье-символ $Q = {{\mathcal{F}}_{{xy}}}[q]$ несложно выразить через Фурье-символ ${{\mathcal{F}}_{{xy}}}{{\left. {[{{g}_{0}}]} \right|}_{{z = 0}}} = ({{ - {{e}^{{ - {{\sigma }_{0}}\zeta }}}} \mathord{\left/ {\vphantom {{ - {{e}^{{ - {{\sigma }_{0}}\zeta }}}} {{\text{2}}{{\sigma }_{{\text{0}}}}}}} \right. \kern-0em} {{\text{2}}{{\sigma }_{{\text{0}}}}}}){{e}^{{i({{{\alpha }}_{{\text{1}}}}\xi + {{{\alpha }}_{{\text{2}}}}{\eta })}}}$ поля источника (8) при $z = 0{\text{:}}$(11)
$\begin{gathered} Q({\mathbf{\alpha }},\xi ) = \tilde {Q}{{e}^{{i({{\alpha }_{1}}\xi + {{\alpha }_{2}}\eta )}}},\,\,\,\,\tilde {Q}({\mathbf{\alpha }},\zeta ) = {{ - \Delta {{e}^{{ - {{\sigma }_{0}}\zeta }}}} \mathord{\left/ {\vphantom {{ - \Delta {{e}^{{ - {{\sigma }_{0}}\zeta }}}} {{{\Delta }_{0}}}}} \right. \kern-0em} {{{\Delta }_{0}}}}, \\ {{\Delta }_{0}} = {{\sigma }_{0}}\Delta - {{\rho }_{o}}{{\omega }^{2}}{{{\hat {K}}}_{{33}}}({\mathbf{\alpha }},0),\,\,\,\,{{\sigma }_{0}} = \sqrt {{{\alpha }^{2}} - \kappa _{0}^{2}} , \\ \operatorname{Re} {{\sigma }_{0}} \geqslant 0,\,\,\,\,\operatorname{Im} {{\sigma }_{0}} \leqslant 0,\,\,\,\,{{\alpha }^{2}} = \alpha _{1}^{2} + \alpha _{2}^{2}, \\ \end{gathered} $Таким образом, приходим к следующему представлению Фурье-символов функций Грина:
(12)
$G(\alpha ,z;\,\,{\xi }) = \left[ {\mathop {\tilde {G}}\nolimits_0 + \mathop {\tilde {G}}\nolimits_{{\text{sc}}}^ - } \right]{{e}^{{i({{{\alpha }}_{{\text{1}}}}{\xi } + {{{\alpha }}_{{\text{2}}}}{\eta })}}},\,\,\,\,z \geqslant 0,$(13)
$\begin{gathered} {{{\tilde {G}}}_{0}}(a,z;\,\,{\zeta }) = - \frac{{{{e}^{{ - {{{\sigma }}_{0}}|z - {\zeta }|}}}}}{{2{{\sigma }_{0}}}},\,\,\,\,\tilde {G}_{{{\text{sc}}}}^{ - }(\alpha ,z;\,\,{\zeta }) = \\ = - \frac{{{\rho }{{{\omega }}^{2}}\mathop {\hat {K}}\nolimits_{33} + {{{\sigma }}_{0}}\Delta }}{{2{{{\sigma }}_{0}}{{\Delta }_{0}}}}{{e}^{{ - {{{\sigma }}_{0}}(z + {\zeta })}}}, \\ {{{\mathbf{G}}}_{u}}(a,z;\,\,{\mathbf{\xi }}) = {{{\mathbf{K}}}_{3}}Q,\,\,\,\,z \leqslant 0. \\ \end{gathered} $Эти представления справедливы для произвольного вертикально-неоднородного упруго-акустического полупространства $z \leqslant 0,$ контактирующего с акустическим полупространством $z \geqslant 0.$ В случае контакта нижней поверхности слоя с вакуумом, K – матрица Грина упругого слоя конечной толщины h, а в случае полностью погруженного волновода – матрица Грина многослойного полупространства $z \leqslant 0,$ в котором нижнее полупространство $z \leqslant - h$ – акустическая среда. Используя разработанные алгоритмы построения матрицы K, функции Грина вида (12)–(13) можно использовать для анализа волновых процессов в погруженных волноводах с усложненными свойствами, например, в случае волоконно-армированных углепластиков [31].
В изотропном случае компоненты вектора-столбца ${{{\mathbf{K}}}_{3}} = ( - i{{{\alpha }}_{1}}S({\alpha },z),$ $ - i{{{\alpha }}_{2}}S({\alpha },z),$ $R({\alpha },z){{)}^{{\text{T}}}}$ выражаются через две функции $S({\alpha },z)$ и $R({\alpha },z)$, зависящие в плоскости $\alpha $ только от радиальной координаты ${\alpha } = \left| \alpha \right|$ = $\sqrt {{\alpha }_{1}^{2} + {\alpha }_{2}^{2}} $ [23], что позволяет свести двукратные контурные интегралы вида (10) к однократным интегралам по α. Конкретный вид функций $S({\alpha },z)$ и $R({\alpha },z)$ зависит от строения пластины (однородная, многослойная, градиентная и т.п.). В случае однородного изотропного слоя, лежащего на акустическом полупространстве, они выписываются в явном виде [26].
ПОЛЕ БЕСКОНТАКТНОГО ИЗЛУЧАТЕЛЯ
В приведенных ниже численных примерах предполагается, что круговая излучающая пластина преобразователя радиуса $a$ расположена параллельно погруженному слою на расстоянии $d$ от него (рис. 1a), а моделирующая ее действие нагрузка $F$ – равномерно распределена в области ${{D}_{0}}{\text{:}}$ $0 \leqslant r$ = $\sqrt {{{x}^{2}} + {{y}^{2}}} \leqslant a.$ В этом случае подстановка функций Грина (10), (13)–(14) в выражения для генерируемых волновых полей (6) и замена порядка интегрирования приводит к представлениям в виде двукратных контурных интегралов обратного преобразования Фурье (как (10)) от произведений Фурье-символов $G{{Q}_{0}}$ и ${{{\mathbf{G}}}_{u}}{{Q}_{0}}$ для $p$ и u соответственно; здесь ${{Q}_{0}} = {{\mathcal{F}}_{{xy}}}[{{q}_{0}}]$. Для равномерно-распределенной нагрузки (${{q}_{0}} = {F \mathord{\left/ {\vphantom {F {{\pi }{{a}^{2}}}}} \right. \kern-0em} {{\pi }{{a}^{2}}}}$ при $r \leqslant a$) ${{Q}_{0}}({\alpha })$ = ${{2F{{J}_{1}}(a{\alpha })} \mathord{\left/ {\vphantom {{2F{{J}_{1}}(a{\alpha })} {(a{\alpha })}}} \right. \kern-0em} {(a{\alpha })}}.$ В силу осевой симметрии эти интегралы сводятся к однократным интегралам по контуру $\Gamma ,$ идущему вдоль положительной полуоси комплексной плоскости ${\alpha ,}$ отклоняясь от нее при обходе вещественных полюсов ${{{\zeta }}_{n}}$ в соответствии с принципом предельного поглощения:
(14)
$\begin{array}{*{20}{c}} {p_{{{\text{sc}}}}^{ - }(r,z) = \frac{1}{{2\pi }}\int\limits_\Gamma {\tilde {G}_{{{\text{sc}}}}^{ - }} (\alpha ,z;d){{Q}_{0}}(\alpha ){{J}_{0}}(\alpha r)\alpha d\alpha ,\,\,\,\,z \geqslant 0,} \\ \begin{gathered} {{u}_{r}}(r,z) = \frac{1}{{2\pi }}\int\limits_\Gamma {S(\alpha ,z)\tilde {Q}(\alpha ,d){{Q}_{0}}(\alpha ){{J}_{1}}(\alpha r){{\alpha }^{2}}d\alpha } , \\ - h \leqslant z \leqslant 0, \\ \end{gathered} \\ \begin{gathered} {{u}_{z}}(r,z) = \frac{1}{{2\pi }}\int\limits_\Gamma {R(\alpha ,z)\tilde {Q}(\alpha ,d){{Q}_{0}}(\alpha ){{J}_{0}}(\alpha r)\alpha d\alpha } , \\ - h \leqslant z \leqslant 0, \\ \end{gathered} \\ {p_{{{\text{sc}}}}^{ + }(r,z) = \frac{1}{{2\pi }}\int\limits_\Gamma {\tilde {G}_{{{\text{sc}}}}^{ + }(\alpha ,z;d){{Q}_{0}}(\alpha ){{J}_{0}}(\alpha r)\alpha d\alpha } ,\,\,\,\,z \leqslant - h,} \end{array}$Представления (14) дают решение рассматриваемой задачи, являясь основой для численного анализа. В ближней зоне он может проводиться с помощью прямого численного интегрирования, а в дальней зоне используются асимптотические представления, которые обычно применимы, начиная от расстояния 3–5 длин волн. Для отраженных и прошедших объемных волн $p_{{{\text{sc}}}}^{ \pm }$ асимптотики получены методом стационарной фазы, а для цилиндрических бегущих и вытекающих волн, распространяющихся вдоль пластины в радиальном направлении, – как вклад вычетов в первых $N$ вещественных и близких к вещественным полюсах подынтегральных функций ${{\zeta }_{n}}{\text{:}}$
(15)
$\begin{gathered} u(r,z) \approx \sum\limits_{i = 1}^N {{{{\mathbf{a}}}_{n}}(z)H_{0}^{{(1)}}({{\zeta }_{n}}r){{\zeta }_{n}}} \\ {\text{и}}\,\,\,\,p_{{{\text{sc}}}}^{ \pm }(r,z) \approx \sum\limits_{i = 1}^N {b_{n}^{ \pm }(z)H_{0}^{{(1)}}({{\zeta }_{n}}r){{\zeta }_{n}}} , \\ {{{\mathbf{a}}}_{n}} = {{\left. {\frac{i}{2}{\text{res}}{{{\mathbf{K}}}_{3}}(\partial {\text{/}}\partial x,\partial {\text{/}}\partial y,z)} \right|}_{{{\alpha } = {{{\zeta }}_{n}}}}}Q({{\zeta }_{n}}){{Q}_{0}}({{\zeta }_{n}}), \\ b_{{{\text{sc}}}}^{ \pm } = {{\left. {\frac{i}{2}{\text{res}}P_{{{\text{sc}}}}^{ \pm }(\alpha ,z)} \right|}_{{{\alpha } = {{{\zeta }}_{n}}}}}, \\ \end{gathered} $Следует отметить, что в интегралах (14) общий знаменатель элементов матрицы K сокращается с $\Delta ,$ входящей в числитель $Q$ вида (11), и общим знаменателем всех подынтегральных функций становится ${{\Delta }_{0}}.$ Поэтому волновые числа ${{\zeta }_{n}}$ определяются из характеристического уравнения
(16)
${{\Delta }_{0}} = {{\sigma }_{0}}\Delta - {{\rho }_{0}}{{\omega }^{2}}{{\hat {K}}_{{33}}}(\alpha ,0) = 0,$ВЕРИФИКАЦИЯ МОДЕЛИ
Для проверки полученных представлений численно контролировалось выполнение энергетического баланса и проводилось сопоставление с результатами других авторов. В качестве примера таких тестовых сопоставлений на рис. 2 приводятся нормированные к значениям в начале координат частотные зависимости давления в дальнем поле, полученные в работе [34] для пластины Кирхгофа (пунктир) и упругого слоя (сплошные линии), контактирующих с акустическим полупространством только с одной стороны. Источник – точечная вертикальная нагрузка ${{F}_{0}},$ приложенная к поверхности пластины со стороны жидкости (рис. 2а) и вакуума (рис. 2б); частота $f$ отнесена к частоте ${{f}_{c}},$ на которой длина изгибной волны в пластине совпадает с длиной звуковой волны в акустической среде. Круговыми маркерами нанесены результаты, полученные с помощью асимптотик, выведенных из интегральных представлений (14).
Рис. 2.
Относительное давление в дальнем поле на расстоянии $R$ от поверхности $z = 0{\text{:}}$ тестовые сопоставления с результатами работы [34] для пластины Кирхгофа (пунктир) и упругого слоя (сплошные линии) при одностороннем нагружении жидкостью; результаты, полученные на основе представлений (14), нанесены круговыми маркерами; источник – точечная нагрузка амплитуды ${{F}_{0}},$ приложенная со стороны (а) жидкости и (б) вакуума.

Для верификации разрабатываемой 1модели особенно полезными оказались результаты работы [35], в которой численно и экспериментально исследуется взаимодействие волнового поля, излучаемого ACT преобразователем, с погруженной в воду стальной пластиной. В этой работе численное моделирование проводится с помощью метода конечных элементов (МКЭ), учитывая реальное строение источника (корпус, излучающая пластина и другие элементы конструкции). Результаты, полученные на основе представлений (14), в которых источник моделируется распределенной нагрузкой ${{q}_{0}},$ показали такое же хорошее совпадение с экспериментальными данными, как и МКЭ моделирование, что подтверждает их практическую применимость. Сопоставления проводились как для волновых полей, так и для коэффициента прохождения ${{\kappa }_{T}}$ = $20{\text{lg}}\left| {{{H}_{{pp}}}(0,0,{{z}_{2}},f)} \right|,$ где ${{H}_{{pp}}} = {{p({{x}_{2}})} \mathord{\left/ {\vphantom {{p({{x}_{2}})} {p({{x}_{1}})}}} \right. \kern-0em} {p({{x}_{1}})}}$ для точек x1 и x2, взятых на верхней границе пластины $\left( {{{z}_{1}} = 0} \right)$ и в воде на глубине 100 мм от ее нижней границы; бесконтактный преобразователь радиуса a = 15 мм расположен на расстоянии d = 270 мм от пластины толщины $h = 6.05$ мм.
Сплошной линией на рис. 3 показана экспериментальная частотная зависимость коэффициента ${{\kappa }_{T}}$ [35], пунктирной – рассчитанная по формулам (14). Пики резонансного прохождения, исследованию которого посвящена работа [35], наблюдаются на частотах появления новых вытекающих волн Лэмба (на частотах отсечки). Изменение структуры потоков волновой энергии в пластине при резонансном прохождении изучается также в работе [26].
Рис. 3.
Сопоставление численных результатов, полученных на основе полуаналитической модели (пунктирная линия), с экспериментальными результатами работы [35] (сплошная линия).

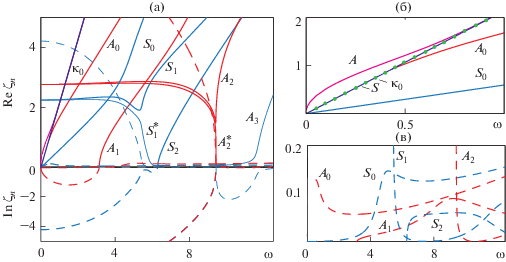
Рис. 4.
(а) Вещественные (${\text{Re}}{{\zeta }_{n}}$ – сплошные линии) и мнимые (${\text{Im}}{{\zeta }_{n}}$ – пунктирные линии) части комплексных волновых чисел ${{\zeta }_{n}}$ для стальной пластины, погруженной в воду; увеличенные фрагменты (б) для чисто вещественных дисперсионных кривых волн Шолте-Стоунли $A$ и $S$ и (в) для мнимых частей ${\text{Im}}{{\zeta }_{n}}$ вытекающих волн Лэмба.
БЕГУЩИЕ ВОЛНЫ
Взаимодействие акустических пучков, генерируемых бесконтактным преобразователем, с погруженной пластиной приводит к появлению бегущих волн, описываемых асимптотикой (15). В свободном упругом слое это классические волны Лэмба [36], распространяющиеся вдоль него без экспоненциального затухания и потому переносящие энергию на бесконечность. Для пластины, погруженной в акустическую среду, распространение бегущих волн сопровождается переизлучением волновой энергии в окружающую среду, поэтому волны Лэмба трансформируются в вытекающие бегущие волны, которые уже не переносят энергию на бесконечность из-за ее оттока в акустическую среду возбуждаемыми в процессе их распространения объемными волнами.
Математически на трансформацию волн Лэмба в вытекающие бегущие волны указывает появление у волновых чисел ${{\zeta }_{n}}$ ненулевой мнимой части, определяющей декремент их затухания ${{\delta }_{n}}$ = = ${{2\pi {\text{Im}}{{\zeta }_{n}}} \mathord{\left/ {\vphantom {{2\pi {\text{Im}}{{\zeta }_{n}}} {{\text{Re}}{{\zeta }_{n}}}}} \right. \kern-0em} {{\text{Re}}{{\zeta }_{n}}}}$ [37, 38]. При переходе к дисперсионному уравнению (16) чисто вещественные корни дисперсионного уравнения волн Лэмба сдвигаются с вещественной оси в комплексную плоскость α. Типичный вид получающихся дисперсионных кривых показан на рис. 4. Сплошными и пунктирными линиями изображены вещественная и мнимая части ${\text{Re}}{{\zeta }_{n}}$ и ${\text{Im}}{{\zeta }_{n}}$ комплексных волновых чисел ${{\zeta }_{n}}$ в зависимости от безразмерной круговой частоты $\omega = {{2\pi fh} \mathord{\left/ {\vphantom {{2\pi fh} {{{c}_{s}}}}} \right. \kern-0em} {{{c}_{s}}}},$ где ${{c}_{s}}$ – скорость поперечных волн в упругой среде.
Ниже численные результаты приводятся в безразмерном виде, получающемся при отнесении линейных размеров к толщине пластины h, скоростей – к скорости ${{c}_{s}}$ и плотностей – к плотности пластины ρ. Безразмерные параметры стальной пластины: ${{c}_{p}} = 1.85,$ ${{c}_{s}} = 1,$ $\rho = 1$ и $h = 1;$ параметры жидкости (вода): ${{c}_{0}} = 0.47$ и ${{\rho }_{0}} = 0.125.$
Вещественные части дисперсионных кривых вытекающих бегущих волн расположены ниже луча ${{\kappa }_{0}} = {\omega \mathord{\left/ {\vphantom {\omega {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}$ (их фазовая скорость больше скорости звука ${{c}_{0}}$). Они мало отличаются от дисперсионных кривых классических волн Лэмба для свободной упругой пластины, а амплитуда мнимых частей сравнительно мала (см. рис. 4в; практически такие же кривые приведены на рис. 8 [39], хорошее качественное совпадение наблюдается также с кривыми рис. 2 [37], построенными методом возмущения по малому параметру). Кроме вытекающих волн в случае погруженного слоя появляются две новые незатухающие бегущие волны Шолте-Стоунли [32, 33] (вещественные кривые для антисимметричной волны $A$ и симметричной $S$, рис. 4б). Эти волны распространяются с почти такой же фазовой скоростью, что и объемные акустические волны в жидкости, поэтому их дисперсионные кривые, идущие выше луча ${{\kappa }_{0}} = {\omega \mathord{\left/ {\vphantom {\omega {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}},$ тесно прижимаются к нему с ростом частоты, но не сливаются. В то время как энергия, полученная вытекающими волнами Лэмба от источника, рассеивается вверх и вниз, не доходя вместе с ними до бесконечности, волны Шолте-Стоунли обеспечивают перенос энергии вдоль пластины на бесконечность.
Следует отметить, что для свободного слоя дисперсионная кривая моды ${{A}_{0}}$ выходит из начала координат вертикально вверх, поэтому в случае погруженного волновода должен существовать некоторый низкочастотный диапазон $0 < \omega < {{\omega }_{0}},$ в котором ${\text{Re}}{{\zeta }_{n}} > {{\kappa }_{0}},$ т.е. ее фазовая скорость меньше ${{c}_{0}}$. С физической точки зрения такая волна должна распространяться без переизлучения энергии в окружающую среду (волновое число остается вещественным). Однако, соответствующий корень ${{\zeta }_{n}}$ оказывается на нефизическом листе римановой поверхности, который отделяется от физического листа разрезом ${\text{Re}}\alpha = {{\kappa }_{0}},$ ${\text{Im}}\alpha > 0,$ идущим в комплексной плоскости $\alpha $ из точки ветвления ${{\kappa }_{0}}.$ Соответственно, дисперсионная кривая моды ${{A}_{0}}$ начинается на рис. 4б с частоты ${{\omega }_{0}} = 0.44,$ на которой этот корень выходит на физический лист, пересекая разрез.
РАСПРЕДЕЛЕНИЕ ЭНЕРГИИ ИСТОЧНИКА
Осредненный за период колебаний поток энергии E, переносимой в поле гармонических колебаний через некоторую поверхность D, определяется интегралом [40]:
(17)
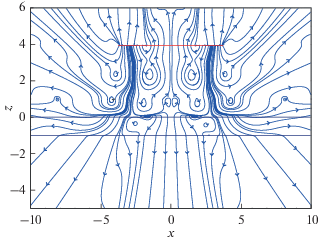
$E = \int\limits_D {{{e}_{n}}d{{S}_{n}}} ,\,\,\,\,{{e}_{n}} = ({\mathbf{e}},{\mathbf{n}}) = \frac{\omega }{2}{\text{Im}}({{{\mathbf{\tau }}}_{n}},u).$Визуализация траекторий переноса энергии от источника на бесконечность обеспечивается линиями тока энергии, задаваемыми векторным полем ${\mathbf{e}}(x).$ В качестве примера, на рис. 5 показаны линии тока энергии, излучаемой круговым преобразователем безразмерного радиуса $a = 3.75,$ расположенным на расстоянии $d = 4$ от пластины при частоте $\omega = 1$ (в размерных переменных это может быть тот же преобразователь, что и в примере рис. 3, но на расстоянии 16 мм от стальной пластины толщиной 4 мм).
Линии тока показывают осредненный за период колебаний путь переноса энергии, однако не дают информации о мощности потоков. Для количественной оценки распределения энергии источника между волнами различного типа и по направлениям излучения используются формулы, полученные из общего представления (17).
Энергия ${{E}_{0}},$ поступающая от источника в среду (т.е. осредненная мощность источника), в общем случае вычисляется интегрированием плотности потока ${{e}_{n}}$ по окружающей источник замкнутой поверхности D; причем, в силу закона сохранения энергии результат не зависит от ее размера и формы. Для рассматриваемой модели бесконтактного преобразователя удобно взять в качестве D верхнюю и нижнюю поверхности круговой излучающей пластины D0, что с учетом выражения для плотности потока энергии в акустической среде ${{e}_{z}}$ = ${\text{Im}}{{[p_{z}^{'}p{\text{*}}]} \mathord{\left/ {\vphantom {{[p_{z}^{'}p{\text{*}}]} {(2\omega {{\rho }_{0}})}}} \right. \kern-0em} {(2\omega {{\rho }_{0}})}}$ и выражений (12), (14) приводит к представлению:
(18)
$\begin{gathered} {{E}_{0}} = \frac{1}{{4{{\rho }_{0}}\omega \pi }}{\text{Im}}\int\limits_\Gamma {\left[ {2\tilde {G}_{{0,z}}^{'}(\alpha ,z)\tilde {G}_{0}^{*}(\alpha {\text{*}},z) + } \right.} \\ \left. { + \,\,\tilde {G}_{{{\text{sc}}}}^{{ - *}}(\alpha {\text{*}},z)} \right]{{Q}_{0}}(\alpha )Q_{0}^{*}(\alpha {\text{*}})\alpha d\alpha ,\,\,\,\,z = \zeta \\ \end{gathered} $Для анализа распределения энергии источника между возбуждаемыми волнами в качестве $D$ используется поверхность цилиндра большого радиуса ${{r}_{c}}$ (рис. 1б). Потоки энергии $E_{V}^{ + }$ и $E_{V}^{ - }$ через горизонтальные поверхности цилиндра $z = {{z}_{1}}$ и $z = {{z}_{2}}$ дают часть энергии источника, уносимой на бесконечность прошедшими и отраженными волнами $p_{{{\text{sc}}}}^{ + }$ и $p_{{{\text{sc}}}}^{ - },$ а поток ${{E}_{R}}$ через боковую поверхность – долю энергии бегущих волн. При ${{\kappa }_{0}}{{r}_{c}} \gg 1$ поток ${{E}_{R}}$ фактически складывается только из энергии, переносимой модами $A$ и $S$, так как количество энергии, переносимое вытекающими модами, убывает с расстоянием экспоненциально. Исходя из закона убывания амплитуды n-той моды
В силу закона сохранения суммарное количество энергии через полную поверхность цилиндра ${{E}_{c}}$ должно совпадать с энергией источника ${{E}_{0}}{\text{:}}$
При осевой симметрии вектор плотности энергии выражается через две не зависящие от полярного угла $\varphi $ компоненты – радиальную ${{e}_{r}}$ и вертикальную ${{e}_{z}}{\text{:}}$ ${\mathbf{e}} = ({{e}_{r}},{{e}_{z}}).$ Используя представления для потоков энергии через горизонтальную плоскость и боковую поверхность цилиндра [21], выражения для $E_{V}^{ \pm }$ и ${{E}_{R}}$ сводятся в этом случае к виду
(20)
$E_{V}^{ + } = - \frac{1}{{4\pi {{\rho }_{0}}\omega }}{\text{Im}}\int\limits_0^{{{\kappa }_{{\text{0}}}}} {{{\sigma }_{0}}{{{\left| {\tilde {G}_{{{\text{sc}}}}^{ + }{{Q}_{0}}} \right|}}^{2}}\alpha d\alpha } ,\,\,\,\,z \leqslant - h,$(21)
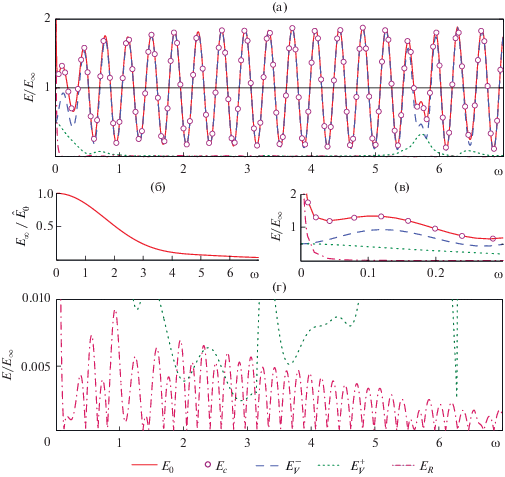
$E_{V}^{ - } = - \frac{1}{{4\pi {{\rho }_{0}}\omega }}{\text{Im}}\int\limits_0^{{{\kappa }_{{\text{0}}}}} {{{\sigma }_{0}}{{{\left| {\left( {{{{\tilde {G}}}_{0}} + \tilde {G}_{{{\text{sc}}}}^{ - }} \right){{Q}_{0}}} \right|}}^{2}}\alpha d\alpha } ,\,\,z \geqslant d,$В качестве примера распределения энергии кругового источника ${{E}_{0}}$ (a = 3.75, d = 4) между потоками $E_{V}^{ - },$ $E_{V}^{ + }$ и ${{E}_{R}}$ на рис. 6а и его укрупненных фрагментах 6в и 6г приведены частотные зависимости этих величин и суммарного потока ${{E}_{c}}$ (19), нормированные на мощность ${{E}_{\infty }}$ такого же источника, но в безграничной акустической среде без пластины. Для количественной оценки изменения энергии источника с частотой на рис. 6б приведен график ${{{{E}_{\infty }}(\omega )} \mathord{\left/ {\vphantom {{{{E}_{\infty }}(\omega )} {{{{\tilde {E}}}_{0}}}}} \right. \kern-0em} {{{{\tilde {E}}}_{0}}}},$ где ${{\hat {E}}_{0}} = {F \mathord{\left/ {\vphantom {F {(8\pi {{\rho }_{0}}{{c}_{0}})}}} \right. \kern-0em} {(8\pi {{\rho }_{0}}{{c}_{0}})}}$ – мощность эквивалентного по силе точечного источника ${{q}_{0}} = F\delta ({\mathbf{x}})$ в безграничной среде.
Рис. 6.
(а) Распределение энергии кругового преобразователя ($a = 3.75,$ $d = 4$) между возбуждаемыми волнами: частотные зависимости для энергии источника ${{E}_{0}}$ (сплошная линия), суммарного потока через полную поверхность цилиндра ${{E}_{c}}$ (круговые маркеры) и потоков энергии через его верхнюю $E_{V}^{ - }$ (штриховая линия), нижнюю $E_{V}^{ + }$ (пунктирная линия) и боковую ${{E}_{R}}$ (штрих-пунктир) поверхности по отдельности (все величины отнесены к энергии ${{E}_{\infty }}$ такого же источника, но в безграничной среде; (б) частотная зависимость ${{{{E}_{\infty }}} \mathord{\left/ {\vphantom {{{{E}_{\infty }}} {{{{\hat {E}}}_{0}}}}} \right. \kern-0em} {{{{\hat {E}}}_{0}}}},$ где ${{\hat {E}}_{0}}$ – не зависящая от частоты энергия эквивалентного точечного источника; (в) и (г) укрупненные фрагменты, показывающие распределение энергии в низкочастотном диапазоне и долю энергии проходящих и бегущих волн $E_{V}^{ + }$ и ${{E}_{R}}.$
Данный и другие численные примеры показывают, что баланс энергии (19) сохраняется для любых горизонтальных плоскостей $z = {{z}_{1}} < - h,$ $z = {{z}_{2}} > d$ и боковой поверхности цилиндра достаточно большого радиуса ${{\kappa }_{0}}{{r}_{c}} \gg 1$ (круговые маркеры для ${{E}_{c}}$ лежат на сплошной линии для ${{E}_{0}}$). Видно, что доля энергии прошедших через пластину и бегущих волн $E_{V}^{ + }$ и ${{E}_{R}}$ значительна только на низких частотах (рис. 6в), а для $E_{V}^{ + }$ – и при резонансном прохождении в окрестности частот отсечки и в диапазонах обратных волн, например, при $\omega \approx 5.7$ на рис. 6а. Для остальных частот с ростом $\omega $ основная часть энергии уходит на бесконечность через верхнюю плоскость $z = {{z}_{2}}$ вместе с полем объемных волн ${{p}_{0}} + p_{{{\text{sc}}}}^{ - }$ ($E_{V}^{ - }$ практически совпадает с ${{E}_{0}}$). Деформация пластины при этом фактически не влияет на мощность источника, на этих частотах она работает как жесткая преграда. Это согласуется с хорошо известными в структурной акустике законами рассеяния акустических волн на упругих телах – на высоких частотах последние можно рассматривать как недеформируемые [13, 16, 41].
В зависимости от частоты отраженное поле $p_{{{\text{sc}}}}^{ - }$ складывается с прямым полем источника ${{p}_{0}}$ в фазе или противофазе. Соответственно, график ${{{{E}_{0}}} \mathord{\left/ {\vphantom {{{{E}_{0}}} {{{E}_{\infty }}}}} \right. \kern-0em} {{{E}_{\infty }}}}$ (рис. 6а) быстро выходит на режим колебаний вокруг единицы с минимумами и максимумами, близкими к нулю и двум. Периодичность их чередования слегка нарушается только при переходе через диапазон появления обратной волны (мода $S_{1}^{*}$ на рис. 4а). Здесь же наблюдается и резонансное прохождение звука сквозь пластину (рост значений энергии прошедших волн $E_{V}^{ + }$). Это тот же резонансный пик, что и на частоте $f = 457$ кГц на рис. 3 (безразмерная частота $\omega = 5.5$). Следующий пик на частоте $f = 774$ кГц ($\omega = 9.4$) вызван появлением обратной волны $A_{2}^{*}.$ Анализ изменения картины линий тока и плотности потока энергии при переходе от нерезонансных частот (как на рис. 5) к резонансным проводится в работе [20].
Общие закономерности изменения суммарной мощности ${{E}_{0}}$ при варьировании положения и размера источника иллюстрируют линии уровня функций ${{{{E}_{0}}(\omega ,d)} \mathord{\left/ {\vphantom {{{{E}_{0}}(\omega ,d)} {{{E}_{\infty }}}}} \right. \kern-0em} {{{E}_{\infty }}}}$ (рис. 7а) и ${{{{E}_{0}}(\omega ,a)} \mathord{\left/ {\vphantom {{{{E}_{0}}(\omega ,a)} {{{E}_{\infty }}}}} \right. \kern-0em} {{{E}_{\infty }}}}$ (рис. 7б) (относительное по сравнению с безграничной средой изменение отдаваемой мощности источника ${{E}_{0}}$ как функция частоты и расстояния при фиксированном $a = 3.75,$ и как функция частоты и размера при фиксированном $d = 4$). Горизонтальными пунктирными линиями показаны сечения этих поверхностей, дающие график ${{{{E}_{0}}(\omega )} \mathord{\left/ {\vphantom {{{{E}_{0}}(\omega )} {{{E}_{\infty }}}}} \right. \kern-0em} {{{E}_{\infty }}}}$ на рис. 6. Чередование максимумов и минимумов на рис. 7а, как и ожидалось, определяется четным или нечетным числом акустических полуволн длины $\lambda = {{2\pi {{c}_{0}}} \mathord{\left/ {\vphantom {{2\pi {{c}_{0}}} \omega }} \right. \kern-0em} \omega },$ укладывающихся в расстояние d. Соответственно, полосы максимумов идут в плоскости $(\omega ,d)$ вдоль гипербол с небольшим сдвигом при переходе через диапазон обратных волн и частоты отсечки моды ${{S}_{2}}$ (после $\omega = 5.5$). А вот рис. 7б демонстрирует отсутствие зависимости лучших частот от радиуса источника $a$ в отличие от случая контактного пьезоактуатора, для которого характерны такие же идущие вдоль гипербол полосы максимумов, как и на рис. 7а [7].
Рис. 7.
(а) Относительная мощность преобразователя ${{{{E}_{0}}} \mathord{\left/ {\vphantom {{{{E}_{0}}} {{{E}_{\infty }}}}} \right. \kern-0em} {{{E}_{\infty }}}}$ в зависимости от частоты ω и расстояния $d$ при $a = 3.75$ и (б) частоты $\omega $ и радиуса $a$ при $d = 4;$ график ${{{{E}_{0}}} \mathord{\left/ {\vphantom {{{{E}_{0}}} {{{E}_{\infty }}}}} \right. \kern-0em} {{{E}_{\infty }}}}$ на рис. 6а – сечение данных поверхностей вдоль показанных пунктиром горизонтальных прямых.
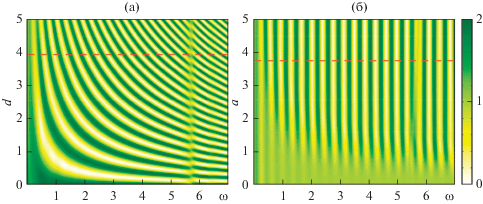
На укрупненном графике для энергии бегущих волн ${{{{E}_{R}}(\omega )} \mathord{\left/ {\vphantom {{{{E}_{R}}(\omega )} {{{E}_{\infty }}}}} \right. \kern-0em} {{{E}_{\infty }}}}$ (рис. 6г) видно такое же чередование максимумов и минимумов, как и у ${{E}_{0}},$ т.е. для бегущих волн, возбуждаемых в пластине акустическим пучком, также существуют периодически повторяющиеся лучшие частоты, однако их значения не совпадают с максимумами энергии, отдаваемой источником. Это означает, что работа источника на максимуме мощности совсем не обязательно приводит к возбуждению бегущих волн максимальной амплитуды. Рис. 8 иллюстрирует зависимость ${{{{E}_{R}}} \mathord{\left/ {\vphantom {{{{E}_{R}}} {{{E}_{\infty }}}}} \right. \kern-0em} {{{E}_{\infty }}}}$ от частоты и от параметров d и a.
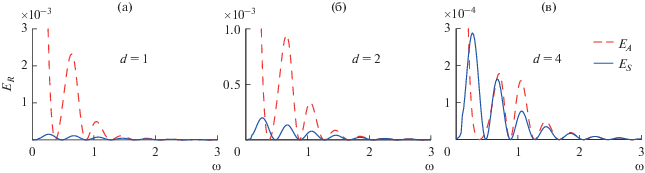
Что касается распределения энергии бегущих волн между двумя модами Шолте-Стоунли, то графики ${{E}_{A}}$ и ${{E}_{S}},$ приведенные на рис. 9, показывают, что при расположении источника возле пластины большую часть энергии переносит антисимметричная волна $A$ (рис. 8а для d = 1), а с увеличением расстояния ее вклад уменьшается и энергия волн $A$ и $S$ становится сопоставимой.
Рис. 8.
(а) Относительная энергия бегущих волн ${{{{E}_{R}}} \mathord{\left/ {\vphantom {{{{E}_{R}}} {{{E}_{\infty }}}}} \right. \kern-0em} {{{E}_{\infty }}}}$ в зависимости от частоты $\omega $ и расстояния $d$ при $a = 3.75$ и (б) частоты $\omega $ и радиуса $a$ при $d = 4;$ график ${{{{E}_{R}}} \mathord{\left/ {\vphantom {{{{E}_{R}}} {{{E}_{\infty }}}}} \right. \kern-0em} {{{E}_{\infty }}}}$ на рис. 6г – сечение данных поверхностей вдоль показанных пунктиром горизонтальных прямых.

ЗАКЛЮЧЕНИЕ
На основе интегральных и асимптотических представлений для функции Грина рассматриваемой задачи разработаны, реализованы и верифицированы математические и компьютерные модели, предназначенные для численного анализа волновых полей и энергетических потоков в системе бесконтактный ультразвуковой преобразователь –акустическая среда – погруженный упругий волновод. В рамках разработанной модели анализируется распределение волновой энергии бесконтактного ультразвукового преобразователя между отраженными, прошедшими и бегущими волнами, возбуждаемыми в погруженной однородной упругой пластине в зависимости от размера источника, расстояния до зондируемой пластины и частоты. Численные примеры показывают, что лучшие частоты возбуждения бегущих волн не обязательно совпадают с частотами локальных максимумов мощности источника, чередование которых с минимумами мощности определяется хорошо известными в акустике закономерностями сложения прямого и отраженного полей в фазе или противофазе.
Работа выполнена при финансовой поддержке Российского Научного Фонда (проект № 17-11-01191).
Список литературы
Giurgiutiu V. Structural health monitoring with piezoelectric wafer active sensors. 2nd Edition. Oxford. UK: Elsevier Academic Press, 2014. 1024 p.
Lammering R., Gabbert U., Sinapius M., Schuster Th., Wierach P. Lamb-wave based Structural Health Monitoring in polymer composites. Springer, 2018. 479 p.
Masmoudi M., Castaings M. Three-dimensional hybrid model for predicting air-coupled generation of guided waves in composite material plates // Ultrasonics. 2012. V. 52(1). P. 81–92.
Giurgiutiu V. Tuned Lamb wave excitation and detection with piezoelectric wafer active sensors for structural health monitoring // J. Intell. Mater. Syst. Struct. 2005. V. 16. P. 291–305.
Raghavan A., Cesnik C.E.S. Finite-dimensional piezoelectric transducer modeling for guided wave based structural health monitoring // Smart Mater. Struct. 2005. V. 14. P. 1448–1461.
Glushkov E.V., Glushkova N.V., Eremin A.A., Lammering R., Neumann M. Lamb wave excitation and propagation in elastic plates with surface obstacles: proper choice of central frequencies // Smart Mater. Struct. 2011. V. 20(1). 015020.
Глушков Е.В., Глушкова Н.В., Евдокимов А.А. Распределение энергии пьезоактуатора между бегущими волнами, возбуждаемыми в упругом слое // Прикладная механика и техническая физика. 2015. Т. 56. № 6. С. 84–93.
Grandia W., Fortunko C. NDE applications of air-coupled ultrasonic transducers // IEEE Ultrasonic Symposium, Proceedings. 1995. V. 1. P. 697–709.
Green R.E. Non-contact ultrasonic techniques // Ultrasonics. 2004. V. 42. P. 9–16.
Fan Z., Jiang W., Cai M., Wright W.M.D. The effects of air gap reflections during air-coupled leaky Lamb wave inspection of thin plates // Ultrasonics. 2016. V. 65. P. 282–295.
Huber A. Non-destructive testing of future rocket boosters using air-coupled ultrasound // Proceeding of the 19th World Conference on Non-Destructive Testing (WCNDT 2016). Germany, Munich, June 13th–June 17th, 2016. 9 p.
Adebahr W., Bernhardt Y., Kreutzbruck M. 3d-robotized air-coupled ultrasound measurements of large components // Proceeding of the 19th World Conference on Non-Destructive Testing (WCNDT 2016). Germany, Munich, June 13th–June 17th, 2016. 8 p.
Junger M.C., Feit D. Sound structures and their interaction. 2nd Edition. Boston, MA: MIT Press, 1986. 462 p.
Ross D. Mechanics of Underwater Noise. N.Y.: Pergamon Press. 1976. 375 p.
Lyon R.H. Theory and application of statistical energy analysis. 2-nd edition. Elsevier. 1994. 400 p.
Шендеров Е.Л. Излучение и рассеяние звука. Л.: Судостроение, 1989. 304 с.
Авербух А.А., Вейцман Р.И., Генкин М.Д. Колебания элементов конструкций в жидкости. М.: Наука. 1987. 157 с.
Гринченко В.Т., Вовк И.В. Волновые задачи рассеяния звука на упругих оболочках. Киев: Наукова Думка, 1986. 240 с.
Jensen F.B., Kuperman W.A., Porter M.B., Schmidt H. Computational Ocean Acoustics. 2-nd edition. Springer. 2011. 794 p.
Бреховских Л.M. Волны в слоистых средах. М.: Наука, 1973. 342 с.
Глушков Е.В. Распределение энергии поверхностного источника в неоднородном полупространстве // Прикл. математика и механика. 1983. Т. 47. Вып. 1. С. 94–100.
Glushkov E., Glushkova N., Fomenko S. Wave energy transfer in elastic half-spaces with soft interlayers // J. Acoust. Soc. Am. 2015. V. 137(4). P. 1802–1812.
Ворович И.И., Бабешко В.А. Динамические смешанные задачи теории упругости для неклассических областей. М.: Наука, 1978. 319 с.
Crighton D.G. The 1988 Rayleigh medal lecture: fluid loading – the interaction between sound and vibration // J. Sound Vibr. 1989. V. 133(1). P. 1–27.
Глушков Е.В., Глушкова Н.В., Фоменко С.И., Жанг Ч. Поверхностные волны в материалах с функционально-градиентными покрытиями // Акуст. журн. 2012. Т. 58. № 3. С. 370–385.
Glushkov E.V., Glushkova N.V., Miakisheva O.A. Backward waves and energy fluxes excited in acoustic medium with an immersed plate // Ultrasonics. 2019. V. 92. P. 158–168.
Исакович М.А. Общая акустика. М.: Наука, 1973. 496 с.
Свешников А.Г. Принцип предельного поглощения для волновода // Докл. АН СССР. 1951. Т. 80. № 3. С. 345–347.
Бреховских Л.М. Отражение и преломление сферических волн // Усп. физ. наук. 1949. Т. 38. Вып. 5. С. 1–42.
Титов С.А., Маев Р.Г., Богаченков А.Н. Линзовый многоэлементный акустический микроскоп в режиме измерения параметров слоистых объектов // Акуст. журн. 2017. Т. 63. № 5. С. 546–552.
Glushkov E.V., Glushkova N.V., Eremin A.A., Miakisheva O.A. Ultrasonic inspection of anisotropic laminate plates immersed in acoustic medium // Materials Physics and Mechanics. 2019 (to appear).
Osborne M.F.M., Hart S.D. Transmission, Reflection, and Guiding of an Exponential Pulse by a Steel Plate in Water. I. Theory // J. Acoust. Soc. Am. 1945. V. 17(1). P. 1–18.
Sessarego J.-P., Sagéloli J., Gazanhes C., Überall H. Two Scholte-Stoneley waves on doubly fluid-loaded plates and shells // J. Acoust. Soc. Am. 1997. V. 101(1). P. 135–142.
Shen C., Xin F.X., Lu T.J. A 3-D elasticity theory based model for acoustic radiation from multilayered anisotropic plates // J. Acoust. Soc. Am. 2014. V. 135(5). P. EL232–8.
Aanes M., Lohne K., Lunde P., Vestrheim M. Beam diffraction effects in sound transmission of a fluid-embedded viscoelastic plate at normal incidence // J. Acoust. Soc. Am. 2016. V. 140. EL67.
Lamb H. On waves in an elastic plate // Proc. Roy. Soc. London. 1917. V. A 93. P. 114–128.
Меркулов Л.Г. Затухание нормальных волн в пластинах, находящихся в жидкости // Акуст. журн. 1964. Т. 10. № 2. С. 206–212.
Rokhlin S.I., Chimenti D.E., Nayfeh A.H. On the topology of the complex wave spectrum in a fluid-coupled elastic layer // J. Acoust. Soc. Am. 1989. V. 85(3). P. 1074–1080.
Inoue D., Hayashi T. Transient analysis of leaky Lamb waves with a semi-analytical finite element method // Ultrasonics. 2015. V. 62. P. 80–88.
Умов Н.А. Избранные сочинения. М.–Л.: Гостехиздат, 1950. 492 с.
Veksler N.D. Resonance acoustic spectroscopy. Berlin: Springer-Verlag, 1993. 282 p.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал