Акустический журнал, 2019, T. 65, № 6, стр. 736-739

Разрезной стержень как вибрационная черная дыра

М. А. Миронов^*

АО “Акустический институт им. акад. Н.Н. Андреева”
117036 Москва, ул. Шверника 4, Россия

Поступила в редакцию 30.06.2019
После доработки 30.06.2019
Принята к публикации 09.07.2019

DOI: 10.1134/S0320791919060108

Аннотация

Вибрационная черная дыра (ВЧД) – замедляющая структура, обеспечивающая замедление скорости распространения волны на отрезке конечной длины до нуля. При этом время распространения волны на этом отрезке равно бесконечности. Рассмотрена новая структура, реализующая приближенно эффект ВЧД для изгибных волн. Это стержень/пластина с канавками, глубина которых постепенно увеличивается. Изгибная жесткость такой конструкции постепенно уменьшается, при этом погонная масса остается постоянной. Найдены зависимости изменения параметров, при которых структура ведет себя аналогично вибрационной черной дыре, а соответствующее уравнение имеет точное аналитическое решение.

Ключевые слова: стержень, вибрации, время распространения, черная дыра

ВВЕДЕНИЕ

В работах [1, 2] рассмотрено распространение волн по волноводу при скорости распространения $c(x),$ уменьшающейся до нуля на конечном интервале (рис. 1). При определенных законах замедления время распространения волны на этом интервале оказывается равным бесконечности. Волна не доходит до конца волновода и, следовательно, не отражается от него. В [1, 2] конкретно рассматривается распространение изгибных волн по стержню, сечение которого уменьшается вдоль его оси и стремится к нулю при конечной длине стержня. При этом скорость распространения изгибных волн также стремится к нулю. Показано, что время распространения волны от начального сечения до конечного может быть равно бесконечности. Скорость уменьшения сечения должна быть достаточно плавной, чтобы избежать отражений от промежуточных сечений. Отсутствие отражения от заостренного конца стержня вызвано не физическим поглощением в материале стержня, а именно невозможностью достичь конца стержня за конечное время. По аналогии с космологическими объектами – черными дырами, в которых скорость распространения света в сильном гравитационном поле замедляется, в [1] введен термин “вибрационная черная дыра” (ВЧД). В западной литературе подобные конструкции называются Acoustic Black Hole (ABH) [2]. В обширной литературе по ABH (см. напр. обзоры [2, 3]) исследуются различные конструкции, ориентированные на поглощение изгибных волн. Основой таких конструкций служит стержень (пластина) с толщиной, меняющейся по степенному закону $h{\kern 1pt} '(x)\sim {{x}^{n}}$ [1]. При показателе степени n ≥ 2 скорость распространения изгибных волн для достаточно высоких частот стремится к нулю при приближении к кромке заострения. На практике идеальное заострение вплоть до толщины, равной нулю, нереализуемо. Поэтому для эффективного поглощения на оконечную часть заострения необходимо добавлять небольшое количество поглощающего материала (см., например, [4]). В литературе рассматривались и другие возможности эффективной работы неидеальной ВЧД – рассеяние на неровностях заостренной кромки [5, 6], нелинейные эффекты [7, 8].

Рис. 1.

Замедление скорости распространения волны на конечном интервале [L–0] до нулевого значения.

В настоящей работе предложена конструкция ВЧД для изгибных волн в стержне. Эта конструкция не требует заострения оконечной части ВЧД до очень малых толщин при практической реализации. Далее будем называть ее модифицированной ВЧД.

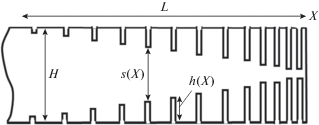
Эскиз модифицированной ВЧД приведен на рис. 2. В исходно однородном стержне толщиной $H$ на длине $L$ прорезываются канавки перпендикулярно оси стержня. Глубина канавок $h(x)$ постепенно увеличивается по мере приближения к концу стержня. Из-за разрезов внешние слои стержня, между разрезами, не деформируются (точнее, деформируются меньше) и, следовательно, не создают напряжений, препятствующих изгибанию стержня. Локальная жесткость стержня на изгиб уменьшается. При этом локальная погонная масса остается постоянной.

Рис. 2.

Эскиз модифицированной вибрационной черной дыры в виде стержня с прорезями.

В общей постановке поля смещений и характеристики распространения в МВЧД конструкции могут быть найдены только численно. В качестве разумного аналитического приближения можно предложить следующий подход. Он позволяет гомогенизировать дискретную структуру конструкции с канавками. Предлагается пользоваться обычным уравнением изгибных колебаний неоднородного вдоль оси стержня для поперечного смещения $\eta (x){\text{:}}$

(1)

$ - \rho S(x){{\omega }^{2}}\eta + (EI(x)\eta {\kern 1pt} ''){\kern 1pt} '' = 0,$

где ρ, $E$ – плотность и модуль Юнга материала стержня, $S(x)$ – площадь поперечного сечения, $I(x)$ – момент инерции поперечного сечения. Первое слагаемое в (1) описывает силу инерции, второе слагаемое – изгибающий момент, связанный с растяжением/сжатием слоев стержня. Для стержня с прямоугольным сечением шириной $a$ и толщиной $s$

(2)

$S = as,\,\,\,\,I = \frac{1}{{12}}a{{s}^{3}}.$

В используемом ниже методе расчета считается, что наличие прорезей в стержне обеспечивает отсутствие растягивающих/сжимающих напряжений в областях, заключенных между соседними прорезями. Это означает, что в величину $I(x)$ в качестве $s$ следует подставлять ширину зазора между противоположными прорезями $s(x) = H - 2h(x)$ (рис. 2). Если глубину канавок увеличивать при продвижении по $x$, то эффективная цилиндрическая жесткость такого разрезанного стержня будет уменьшаться. Вопрос о том, как часто нужно делать прорези и насколько точно выполняется равенство (2), остается пока открытым. Интуитивно ясно, что расстояние между соседними прорезями должно быть не больше глубины прорезей. Толщина прорезей теоретически может быть бесконечно малой. При этом погонная масса стержня будет постоянной вдоль стержня. Уравнение (1) запишется, с учетом (2), в виде

(3)

$ - \rho H{{\omega }^{2}}\eta + {{\left[ {E\frac{1}{{12}}s{{{(x)}}^{3}}\eta {\kern 1pt} ''} \right]}^{{''}}} = 0.$

Уравнение (3) можно исследовать, используя метод ВКБ, как это первоначально было сделано в [1] для заостренного по степенному закону стержня. Однако в [9] было показано, что для параболического заострения стержня полный набор фундаментальных решений дается степенными функциями $\eta (x) = {{x}^{\gamma }}.$ Показатели степени $\gamma $ удовлетворяют алгебраическому уравнению четвертой степени. Решения алгебраического уравнения находятся путем замены переменной и сведения исходного уравнения к биквадратному.

Следуя [7], рассматриваем далее в (3) степенную зависимость $s(x)$

(4)

$s(x) = H{{({x \mathord{\left/ {\vphantom {x L}} \right. \kern-0em} L})}^{\alpha }},$

где $H$ – толщина стержня, $L$ – длина отрезка стержня, в котором сделаны прорези. Показатель степени $\alpha $ считаем положительным.

Решения уравнения (3) $\eta (x)$ с зависимостью (4) ищем в виде степенной зависимости

(5)

$\eta (x) = {{x}^{\gamma }}.$

Подставляя (4), (5) в (3), получим:

(6)

$ - {{x}^{\gamma }}b + \frac{{{{d}^{2}}}}{{d{{x}^{2}}}}\left[ {{{x}^{{3\alpha }}}\frac{{{{d}^{2}}}}{{d{{x}^{2}}}}{{x}^{\gamma }}} \right] = 0,$

где

(7)

$b = 12\frac{{\rho {{\omega }^{2}}}}{{E{{H}^{2}}}}{{L}^{{3\alpha }}}.$

Проведя дифференцирования в (6), получим

(8)

$ - {{x}^{\gamma }}b + \gamma (\gamma - 1)(3\alpha + \gamma - 2)(3\alpha + \gamma - 3){{x}^{{3\alpha + \gamma - 4}}} = 0.$

Приравнивая в (8) показатели степени,

$\gamma = 3\alpha + \gamma - 4,$

получим выражение для α:

(9)

$\alpha = {{\text{4}} \mathord{\left/ {\vphantom {{\text{4}} {\text{3}}}} \right. \kern-0em} {\text{3}}}.$

Подставляя (9) в (8), получаем уравнение для показателя степени γ:

(10)

$\gamma (\gamma - 1)(\gamma + 2)(\gamma + 1) - b = 0.$

Подставляя (9) в (7), получим выражение для $b$

(11)

$b = 12\frac{{\rho {{\omega }^{2}}}}{E}{{\left( {\frac{{{{L}^{2}}}}{H}} \right)}^{2}}.$

Алгебраическое уравнение четвертой степени (10) решается заменой переменной

(12)

$\gamma = \mu - \frac{1}{2},$

которая, при подстановке в (11), дает биквадратное уравнение для μ:

(13)

$[{{\mu }^{2}} - {{(1{\text{/}}2)}^{2}}][{{\mu }^{2}} - {{(3{\text{/}}2)}^{2}}] - b = 0.$

Решая это уравнение и подставляя решения в (12), получим выражения для показателей степени в решениях (5):

(14)

${{\gamma }_{{1,2,3,4}}} = - \frac{1}{2} \pm \sqrt {\frac{5}{4} \pm \sqrt {1 + b} } .$

Полученные формулы (4), (9), (11), (14) аналогичны формулам работы [7], описывающим точные решения для стандартной ВЧД – параболически заостренного стержня. Нетрудно проверить, что при $b \to 0$ (низкие частоты) все корни (14) вещественны. Все точки стержня колеблются в фазе, волновое движение отсутствует. В другом предельном случае $b \to \infty $ (высокие частоты) уравнение (14) дает два вещественных корня и два комплексно сопряженных корня. Комплексные корни соответствуют распространяющимся волнам, а вещественные корни – затухающим волнам. Критическая величина b, которая соответствует появлению мнимой компоненты, равна

(15)

$b* = \frac{9}{{16}}.$

Соответствующая критическая частота равна

(16)

$\omega * = \sqrt {\frac{E}{{12\rho }}b{\text{*}}} \frac{H}{{{{L}^{2}}}} = \frac{1}{{\sqrt {12} }}{{c}_{Y}}\frac{3}{4}\frac{H}{{{{L}^{2}}}}.$

Здесь ${{c}_{Y}} = \sqrt {\frac{E}{\rho }} $ – скорость распространения продольной юнговской волны в стержне.

Следует отметить, что для стандартной ВЧД в форме параболически заостренного стержня критическая частота $\omega _{0}^{*}$ существенно выше (уравнение (17) в [9]):

(17)

$b_{0}^{*} = {{\left( {\frac{3}{2}} \right)}^{2}}{{\left( {\frac{5}{2}} \right)}^{2}},$

(18)

$\omega _{0}^{*} = \sqrt {\frac{E}{{12\rho }}b_{0}^{*}} \frac{H}{{{{L}^{2}}}} = \frac{1}{{\sqrt {12} }}{{c}_{Y}}\frac{{15}}{4}\frac{H}{{{{L}^{2}}}}.$

Частота, начиная с которой и выше модифицированная ВЧД проявляет эффект ЧД, в пять раз ниже, чем у стандартной ВЧД.

В работе [9] приведено выражение критической частоты через полную массу ${{M}_{0}}$ традиционной ВЧД:

(19)

$\omega _{0}^{*} = \frac{1}{{4\sqrt {12} }}\frac{5}{3}{{c}_{Y}}{{H}^{3}}{{({\rho \mathord{\left/ {\vphantom {\rho {{{M}_{0}}}}} \right. \kern-0em} {{{M}_{0}}}})}^{2}}.$

Здесь подразумевается, что ширина стержня равна 1.

Выразим длину модифицированной ВЧД через ее массу M: L = M/(Hρ). Подставив в (16), получим выражение критической частоты через массу модифицированной ВЧД:

(20)

$\omega * = \frac{1}{{4\sqrt {12} }}3{{c}_{Y}}{{H}^{3}}{{({\rho \mathord{\left/ {\vphantom {\rho M}} \right. \kern-0em} M})}^{2}}.$

При одинаковых критических частотах $\omega _{0}^{*} = \omega {\text{*}}$ масса модифицированной ВЧД при одинаковых толщинах $H$ оказывается больше массы стандартной ВЧД в

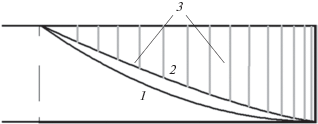
$\frac{M}{{{{M}_{0}}}} = \sqrt {\frac{3}{{5/3}}} = \frac{3}{{\sqrt 5 }} = 1.34\,\,{\text{раза}}{\text{.}}$

Из формул (4), (9) следует, что степенная зависимость профиля непрорезанной части стержня $s(x)\sim {{x}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}$ оказывается более медленной по сравнению с утоньшением стандартной ВЧД [9] $h(x)\sim {{x}^{2}}.$ На рис. 3 сравниваются профили стандартного параболического заострения (кривая 1) и огибающей прорезей (кривая 2) предлагаемой модифицированной ВЧД (кривая 3). Очевидно, профиль огибающей прорезей в оконечной части модифицированной ВЧД не требует такой точности исполнения, как параболический профиль стандартной ВЧД.

Рис. 3.

Сравнение профилей параболического заострения в стандартной ВЧД и огибающей прорезей модифицированной ВЧД. 1 – параболическая граница стандартной ВЧД, 2 – огибающая прорезей модифицированной ВЧД, 3 – прорези в модифицированной ВЧД.

В заключение отметим два преимущества предложенной конструкции. Первое – сильное снижение пороговой частоты эффекта ЧД при фиксированной длине L. При одинаковых габаритах – длине и толщине – модифицированная ВЧД имеет критическую частоту в 5 раз более низкую, чем традиционная ЧД. Масса конструкции при этом увеличивается. Второе – ослабление требований к точности ее исполнения. Учитывая приближенный характер аналитической модели, использованной в расчетах, требуются дополнительные экспериментальные и численные исследования.

Список литературы

Миронов М.А. Распространение изгибной волны в пластине, толщина которой плавно уменьшается до нуля на конечном интервале // Акуст. журн. 1988. Т. 34. № 1. С. 546–547.
Krylov V. Acoustic black holes for flexural waves: a smart approach to vibration damping // Procedia Engineering. 2017. V. 199. P. 56–61.
Zhao C., Prasad M.G. Acoustic black holes in structural design for vibration and noise control // Acoustics. 2019. V. 1. № 1. P. 220–251.
Krylov V.V. New type of vibration dampers utilizing the effect of acoustic “black holes” // Acta Acustica united with Acustica. 2004. V. 90. P. 605–619.
Bowyer E.P., O’Boy D.J., Krylov V.V., Horner J.L. Effect of geometrical and material imperfections on damping flexural vibrations in plates with attached wedges of power law profile // Applied Acoustics. 2012. V. 73. P. 514–523.
Denis V., Pelat A. and Gautier F. Scattering effects induced by imperfections on an acoustic black hole placed at a structural waveguide termination // J. Sound Vib. 2016. V. 362. P. 56–71.
Denis V., Pelat A., Touzé C., Gautier F. Improvement of the acoustic black hole effect by using energy transfer due to geometric nonlinearity // Int. J. Non-Linear Mechanics. 2017. V. 94. P. 134–145.
Gusev V.E., Ni C., Lomonosov A. and Shen Z. Propagation of flexural waves in inhomogeneous plates exhibiting hysteretic nonlinearity: Nonlinear acoustic black holes // Ultrasonics. 2015. V. 61. P. 126–135.
Миронов М.А. Точные решения уравнения поперечных колебаний стержня со специальным законом изменения поперечного сечения // Акуст. журн. 2017. Т. 63. № 5. С. 3–8.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал