Акустический журнал, 2019, T. 65, № 6, стр. 758-762

ВВЕДЕНИЕ

Как известно, в среде с дисперсией эволюция плоских нелинейных волн описывается интегро-дифференциальным уравнением следующего вида:

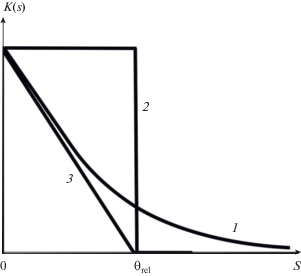
Здесь $K\left( s \right)$ – ядро интегрального члена уравнения (1), конкретная форма которого определяет линейные частотно-зависимые свойства (дисперсию и диссипацию) среды. Смысл обозначений таков: $V$ – акустическое давление, нормированное на характерную величину (исходную амплитуду волны), $\theta $ – время в сопровождающей системе координат, нормированное на исходную частоту сигнала, $z$ – пройденное волной расстояние, отнесенное к характерной нелинейной длине.

Для вырожденных ядер $K\left( s \right),$ представляющих собой линейную комбинацию дельта-функции и ее производных, из (1) получаются простые дифференциальные уравнения типа Хопфа, Бюргерса и аналогичные эволюционные уравнения с высшими производными. Дифференциальные уравнения следуют из (1) и для некоторых других ядер [2]. Наиболее известны уравнения с экспоненциальным ядром (рис. 1, кривая 1):

Ядро (2) предсказывается релаксационной моделью Мандельштама–Леонтовича [3]. В этом случае из общего уравнения (1) получается:

Это уравнение в дифференциальной форме (3) получено в работе [4]; его интегральная форма приведена в работе [5].

Разнообразные формы ядер, полезные для приложений, обсуждаются в статье [6]. В частности, степенные зависимости коэффициента затухания волны от частоты с дробными показателями степени, типичные для биологических тканей и геофизических структур, принципиально требуют интегро-дифференциального описания. Это же относится к средам со сложной внутренней динамикой релаксационного типа.

Кратко напомним схему нахождения ядра $K\left( s \right)$ в каждом конкретном случае. Частотные зависимости дисперсии и поглощения, которые даются действительной и мнимой частями $k{\kern 1pt} '\left( \omega \right),k{\kern 1pt} ''\left( \omega \right)$ волнового числа, измеряются или определяются из физической модели типа Мандельштама–Леонтовича. Затем решается обратная задача и ядро реконструируется стандартными методами, использующими принцип причинности и соотношения типа Крамерса–Кронига [7].

Известно, например, что показатель степени в частотной зависимости затухания ультразвука в биологических тканях является дробным. Он изменяется от 2.1 (кости черепа) до 1.1 (скелет) и 0.6 (кожа) [8]. Чаще всего в диапазоне нескольких МГц (медицинский ультразвук) $\,k{\kern 1pt} ''\sim {{\omega }^{{2 - \nu }}},$ $0 < \nu < 1.$ Для такой зависимости ядро имеет вид $K\left( s \right)\sim {{s}^{{\nu - 1}}}\,.$ Особенность функции $K\left( s \right)$ в точке $s = 0$ часто оказывается несущественной, поскольку уравнение содержит “свертку” сингулярного ядра с осциллирующей функцией, описывающей поле волны.

Если интересоваться волнами не в конкретной релаксирующей среде, а общими свойствами нелинейных волн, удобен прием, сводящий интегро-дифференциальное уравнение к дифференциально-разностной модели или даже к простому отображению. Этот переход [6, 7] эффективен для ядер, отличных от нуля на конечном интервале. Простейший случай соответствует среде с постоянной “памятью” [9], для которой

Ядро (4) означает, что в течение промежутка времени $0 < s < {{\theta }_{{{\text{rel}}}}}$ среда “все помнит”, а в момент $s = {{\theta }_{{{\text{rel}}}}}$ “все забывает” (рис. 1, кривая 2). При наличии такого ядра уравнение (2) принимает вид:

Распространение импульсных сигналов в релаксирующей среде с ядром (4) для трех типов нелинейности (модульной, квадратичной и квадратично-кубичной) изучено в работе [9].

Еще одна упрощенная модель получается с использованием ядра со следующей линейно убывающей “памятью” (рис. 1, кривая 3):

При этом вместо (5) получается такое дифференциально-разностное уравнение:

Чтобы найти закон дисперсии, “занулим” нелинейный член и будем искать решение в виде

Подставляя (8) в (7), получим

В показателе экспоненты (9) присутствуют два дополнительных члена, пропорциональных коэффициенту $D$ (“силе” релаксации). Мнимый член есть добавка к скорости распространения волны, зависящая от частоты. Действительная часть показателя описывает затухание – амплитуда волны экспоненциально уменьшается с ростом пройденного расстояния z.

ЭВОЛЮЦИЯ ФОРМЫ ИМПУЛЬСНЫХ СИГНАЛОВ

Пусть на границе $z = 0$ исходная форма сигнала дается функцией $V\left( {z = 0,\,\theta } \right) = \sin \theta ,$ отличной от нуля в области $0 < \theta < \pi .$ Иными словами, рассматриваемый положительный однополярный импульс представляет собой отрезок синусоиды, содержащий половину ее периода.

Процесс эволюции такого импульса показан на рис. 2 для значений параметров $D = 0.1,$ ${{\theta }_{{{\text{rel}}}}} = 5.$ Профили импульса построены для четырех значений пройденного волной расстояния, равных $z = 0,\,\,1,\,\,2,\,\,5.$ Наблюдается формирование ударных фронтов сжатия. Задний фронт затянут сильнее, чем в отсутствие релаксации (см. [10–12]).

Для того чтобы выяснить роль релаксационных явлений, эволюционный процесс, иллюстрированный на рис. 2, был рассчитан для $D = 0.1$ и различных значений времени релаксации ${{{\theta }}_{{{\text{rel}}}}} = 1,\,\,2.5,\,\,5.$ Результаты изображены на рис. 3.

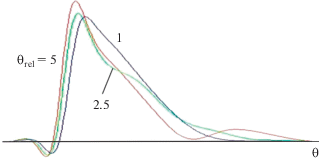
Видно, что при ${{\theta }_{{{\text{rel}}}}} = 1$ форма импульса качественно такая же, как в нелинейной диссипативной среде в отсутствие релаксации. Передний фронт – крутой, но имеет конечную ширину из-за диссипации, вносимой релаксационным процессом (см. (9)). Задний фронт затянут и заметно сдвинут относительно точки $\theta = \pi .$ При увеличении времени релаксации форма ударного фронта изменяется незначительно, в то время как задний фронт затягивается сильнее и даже становится осциллирующим.

Процесс эволюции импульса отрицательной полярности изображен на рис. 4 для значений параметров $D = 0.1,$ ${{\theta }_{{{\text{rel}}}}} = 5.$ Профили импульса построены для четырех значений пройденного волной расстояния, равных $z = 0,\,\,1,\,\,2,\,\,5.$ Сравнивая кривые рис. 4 с соответствующими кривыми на рис. 2, построенными для тех же значений параметров, но для положительного импульса, видим заметные различия. Действительно, ударные фронты сжатия смещаются в другую сторону и имеют несколько иную форму. Различия в форме как фронта, так и гладких участков профиля связаны с отсутствием инвариантности уравнения (7) относительно преобразования $V\left( {z,\, - \theta } \right)$ = $ - V\left( {z,\,\theta } \right).$ Такая симметрия, как известно, имеется в уравнении Бюргерса (см. [10–13]).

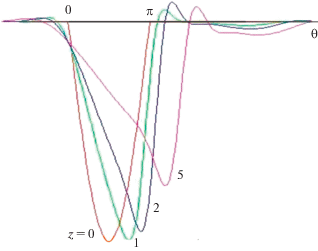
На рис. 5 изображено поведение двуполярного импульса – отрезка синусоиды $V\left( {z = 0,\,\theta } \right) = \sin \theta ,$ содержащего один период $ - \pi < \theta < \pi .$ Расчет проведен для значений параметров $D = 0.1,$ ${{\theta }_{{{\text{rel}}}}} = 5$ на расстояниях $z = 0,\,\,1,\,\,2,\,\,5.$

Импульсный сигнал, в котором за отрицательной фазой (область разрежения) движется фаза положительного давления (область сжатия), обычно называют $S$-волной. В такой волне образуется один ударный фронт, разделяющий две указанные области. Если бы релаксационные процессы отсутствовали, интенсивный сигнал при больших значениях акустического числа Рейнольдса оставался бы полностью внутри области $ - \pi < \theta < \pi .$ Как видно из рис. 5, релаксация в среде приводит к заметному “просачиванию” сигнала как в область $\theta < - \pi ,$ так и в положительную область $\theta > \pi .$

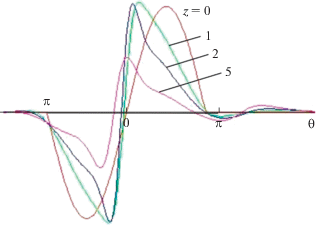
На рис. 6 изображено поведение сложного двойного двуполярного импульса $V\left( {z = 0,\,\theta } \right) = - \sin \theta ,$ заданного в области $ - 2\pi < \theta < 2\pi .$ Как и прежде, расчет проведен для значений параметров $D = 0.1,$ ${{\theta }_{{{\text{rel}}}}} = 5$ на расстояниях $z = 0,\,\,1,\,\,2,\,\,5.$ Исходный профиль этого импульса представляет собой двукратное продолжение $S$-формы на рис. 5. Здесь образуются два ударных фронта, поведение каждого из которых аналогично поведению единственного фронта на рис. 5. Однако стыковка гладких участков профиля в окрестности точки $\theta = 0$ происходит таким образом, что релаксационное “затягивание” исчезает. Образуется узел, в котором пересекаются все кривые, изображающие профиль волны на различных расстояниях z. На образование такого узла было указано еще в монографии [12] при анализе волновых профилей в среде с экспоненциальной релаксацией (2).

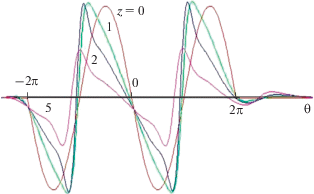
На рис. 7 изображено поведение сложного двойного двуполярного импульса $V\left( {z = 0,\,\theta } \right) = \sin \theta ,$ заданного в области $ - 2\pi < \theta < 2\pi .$ Здесь иной порядок следования областей сжатия и разрежения по сравнению с профилями на рис. 5 и рис. 6. Именно, первой идет фаза сжатия, за ней – фаза разрежения. Затем области разных знаков чередуются. Такие импульсные сигналы называют волнами N-типа. Они эволюционируют иначе по сравнению с $S$-волнами. В частности, сравнивая рис. 7 и рис. 6, видим, что формируются не два, а три ударных фронта.

Видно, что “головная” и “хвостовая” ударные волны движутся относительно сопровождающей системы координат в противоположные стороны. В целом импульс уширяется как из-за “разбегания” ударных фронтов, занимавших исходное положение в точках $\theta = \pm 2\pi ,$ так и в результате действия релаксационных процессов, приводящих к дополнительному сглаживанию профиля. Третья ударная волна, образовавшаяся в окрестности точки $\theta = 0,$ ведет себя по типу фронта S-волны (см. рис. 5) и уменьшается по амплитуде быстрее, чем два других фронта. Эти процессы приводят на больших расстояниях к превращению исходного сигнала в универсальный двуполярный импульс N-типа.

ЗАКЛЮЧЕНИЕ

Укажем, что проведенный анализ процессов эволюции импульсов различной формы в квадратично нелинейной релаксирующей среде дает основу для дальнейших исследований. Во-первых, нам удалось показать, что модельный вид релаксационного ядра, отвечающий “линейно слабеющей памяти” среды, позволяет значительно упростить используемые алгоритмы и снизить трудоемкость вычислений. Во-вторых, мы планируем использовать развитые методы для решения связанных задач по распространению импульсных сигналов в средах с модульной и квадратично-кубичной нелинейностями. Такие нелинейности представляют интерес, поскольку реализуются в ряде искусственных метаматериалов, имеющих перспективы для практического использования. Аналогичные задачи для среды с ядром иного вида (4) решены в работе [9].

При численном исследовании сформулированных в этой статье задач мы использовали разностные схемы третьего порядка точности сквозного расчета разрывов, аналогичные описанным нами в работах [12, 14].

Отметим также, что помимо метаматериалов [15–18], экзотические ядра встречаются в сложно структурированных средах, например, в полимерных материалах [19]. Обычно говорят о материалах с несколькими временами экспоненциальной релаксации или же о спектре времен такой релаксации. Нетрудно видеть, что, например, ядро (6) может быть представлено в виде

Здесь ядро (6) отлично от нуля в области $0 < s < {{\theta }_{{{\text{rel}}}}}.$ Ясно, что функция распределения времен релаксации $W\left( {{{\theta }_{{{\text{rel}}}}}} \right)$ находится через обратное преобразование Лапласа от данной “экзотической” формы ядра.

Авторы считают своим долгом почтить память Е.А. Лапшина, который совсем недавно ушел от нас. Евгений Александрович внес большой вклад в разработку специальных численных методов, которые позволяют эффективно рассчитывать поведение нелинейных волн, содержащих ударные фронты. Настоящая статья есть продолжение большого цикла работ по численному решению задач нелинейной теории волн, выполненных под руководством и при непосредственном участии Е.А. Лапшина и регулярно публиковавшихся с 1975 г. [20] вплоть до наших дней [9].

Работа поддержана грантом Российского Научного Фонда № 19-12-00098.