Акустический журнал, 2020, T. 66, № 2, стр. 198-205
Исследование влияния вклада объемных волн на результат применения метода микросейсмического зондирования
А. А. Цуканов a, *, А. В. Горбатиков b, **
a Институт физики прочности и материаловедения СО РАН
634055 Томск, просп. Академический 2/4, Россия
b Институт физики Земли им. О.Ю. Шмидта РАН
123995 Москва, Большая Грузинская ул. 10, стр. 1, Россия
* E-mail: microseismic@yandex.ru
** E-mail: avgor70@mail.ru
Поступила в редакцию 29.04.2019
После доработки 26.08.2019
Принята к публикации 05.09.2019
Аннотация
Представлено численное исследование формирования амплитудной реакции на свободной поверхности от одновременного рассеяния на заглубленном скоростном включении поверхностных волн Рэлея и вертикально падающих продольных волн. Установлено, что значительное присутствие объемных волн в микросейсмическом поле принципиально не меняет результат применения метода микросейсмического зондирования, который основан на представлении о подавляющем вкладе в формирование микросейсмического поля Земли фундаментальной моды волны Рэлея. Рассмотрены случаи, когда микросейсмический сигнал на одной и той же частоте моделируется только фундаментальной модой волны Рэлея, только продольной волной с вертикальным падением и обоими типами волн одновременно. Рассмотрены варианты с различными размерами и скоростными свойствами неоднородности. Анализ выполнен в (λ, r)-пространстве, по аналогии с процедурой восстановления структуры геологической среды в методe микросейсмического зондирования, где λ – длина волны фундаментальной моды Рэлея, а r – координата на дневной поверхности.
ВВЕДЕНИЕ
Исследованный ранее авторами метод микросейсмического зондирования (ММЗ) [1–4] опирается на представление об определяющем вкладе в энергию микросейсмического поля фундаментальной моды волны Рэлея. Такое представление позволяет без дополнительных условий применять ММЗ для диапазона глубин земной коры с низким градиентом скоростей по глубине, то есть там, где амплитуды высших мод существенно ниже амплитуды фундаментальной моды. Однако, даже в таких благоприятных условиях применимость ММЗ зачастую вызывает вопросы ввиду важного обстоятельства. В ряде экспериментальных исследований показано, что в определенных условиях микросейсмическое поле может содержать заметную долю волн объемного типа. В частности, Л.П. Винник с соавторами показал, что в тихой внутриконтинентальной области доля объемных волн может составлять до 60% энергии микросейсмического поля в области частот около 1 Гц [5, 6]. Анализ функций взаимной корреляции записей микросейсмического фона в области 1 Гц, проведенный на территории штата Юта (Uinta Basin) США [7], свидетельствует о присутствии объемных волн в микросейсмическом поле от сильно удаленных слабых источников. Сравнительно недавние исследования также свидетельствуют о наличии в составе микросейсмического поля P-волн, источником которых являются удаленные штормовые процессы и ураганы [8–11]. Преобладание в микросейсмическом сигнале волн поверхностного или объемного типа, по всей видимости, определяется региональными особенностями самого явления [6].
В этой связи необходимо выяснить, как присутствие большой доли объемных волн в микросейсмическом поле искажает результат применения ММЗ. Правомерен вопрос, возможно ли вообще применять ММЗ (даже в благоприятных условиях слабого присутствия высших мод Рэлея), если в зондирующем микросейсмическом сигнале до 60% энергии формируется объемными волнами? Достаточно очевидно, что ввиду использования в ММЗ исключительно вертикальных компонент, а также с учетом уменьшения скоростей сейсмических волн при приближении к поверхности, в данном случае достаточно проанализировать осложнение микросейсмического поля за счет только объемных продольных сейсмических волн с падением, близким к вертикальному.
Важно отметить, что помимо поверхностных волн Рэлея и объемных волн на поверхности могут регистрироваться волны Лява. Однако, в ММЗ используются только вертикальные компоненты микросейсмического поля, поэтому ввиду своей природы волны Лява не участвуют ни в формировании сигнала, ни в его зашумлении.
Известно, что модель формирования сигнала в геофизических методах является основой построения процедуры инверсии – точного или приближенного решения обратной задачи. Ввиду сложности решения обратной задачи в общем виде, как правило, прибегают к упрощению модели формирования сигнала, снижая размерность задачи или используя то или иное допущение относительно свойств среды или свойств источника, либо используют более грубые физические закономерности в самой модели [12–14]. Проверка выполнения условий модели может требоваться в каждом конкретном случае.
В рамках решения поставленной задачи авторы исследовали закономерности формирования амплитудной реакции модельного микросейсмичeского поля на заглубленную неоднородность в присутствии поверхностных и объемных продольных волн на численной модели с использованием метода конечных разностей.
ОПИСАНИЕ МЕТОДА
Математическая модель, построенная из первых принципов на основе II-го закона Ньютона в дифференциальной форме для сплошной среды (1) и обобщенного закона Гука (2), использовалась для описания моделируемой системы в приближении небольших деформаций (3) [15, 16]:
(1)
$\rho ({\mathbf{r}})\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{u}_{i}}({\mathbf{r}},t) = \sum\limits_j {{{\partial }_{j}}{{\sigma }_{{ij}}}({\mathbf{r}},t)} + {{f}_{i}}({\mathbf{r}},t),$(2)
$\hat {\sigma }({\mathbf{r}},t) = \lambda ({\mathbf{r}}){\hat {I}} \cdot {\text{trace}}[{\hat {u}}({\mathbf{r}},t)] + 2\mu ({\mathbf{r}})\hat {u}({\mathbf{r}},t),$(3)
${{u}_{{ij}}} = \frac{1}{2}\left( {{{\partial }_{j}}{{u}_{i}} + {{\partial }_{i}}{{u}_{j}}} \right),$1) на свободной поверхности y = 0 условие отсутствия нормальных напряжений ${{\sigma }_{{xy}}} = {{\sigma }_{{yy}}} = 0$ приводит к системе уравнений
(4)
$\frac{{\partial {{u}_{x}}}}{{\partial y}} + \frac{{\partial {{u}_{y}}}}{{\partial x}} = 0,\,\,\,\,\nu \frac{{\partial {{u}_{x}}}}{{\partial x}} = \left( {\nu - 1} \right)\frac{{\partial {{u}_{y}}}}{{\partial y}},$2) вертикальная граница расчетной области $x = 0$ – источник фундаментальной моды волны Рэлея заданной амплитуды A (по вертикали) на поверхности и циклической частоты ωn [17]:
(5)
$\begin{gathered} {{u}_{x}}\left( {0,y,t} \right) = \\ = A~W\left( {t,~{\theta }} \right)\frac{k}{q}\left( {{{e}^{{ - qy}}} - \frac{{2{{k}^{2}}}}{{{{k}^{2}} + {{s}^{2}}}}{{e}^{{ - sy}}}} \right)\sin \left( {{\varphi } - {\omega }t} \right), \\ {{u}_{y}}\left( {0,y,t} \right) = \\ = A~W\left( {t,~{\theta }} \right)\left( {{{e}^{{ - qy}}} - \frac{{2qs}}{{{{k}^{2}} + {{s}^{2}}}}{{e}^{{ - sy}}}} \right)\cos \left( {{\varphi } - {\omega }t} \right), \\ \end{gathered} $(6)
$W\left( {t,{\theta }} \right) = \left\{ \begin{gathered} \frac{1}{2}\left( {1 - \cos \frac{{2{\pi }}}{{\theta }}t} \right),~\,\,t \leqslant \theta , \hfill \\ 1,~~~~~~~~~~~~\,\,\,\,\,\,\,\,\,\,\,\,\,~t > \theta . \hfill \\ \end{gathered} \right.$Вспомогательные константы q и s, зависящие от волновых чисел продольных, поперечных и рэлеевских волн kP, kS, kR, во вмещающей среде
где значение волнового числа фундаментальной моды волны Рэлея kR во вмещающей среде явно определяется с использованием точной формулы Малишевского [18]3) нижняя горизонтальная граница y = Y – источник восходящей плоской P-волны единичной амплитуды с той же сеткой частот ωn:
(7)
${{u}_{x}}\left( {x,Y,t} \right) = 0,\,\,\,\,{{u}_{y}}\left( {x,Y,t} \right) = A~w\left( {t,~{\theta }} \right)\sin \left( {{\varphi } - {\omega }t} \right);$4) граничные условия (ГУ) на удаленной вертикальной границе в случае расчетов с волной Рэлея ${{{\Gamma }}_{\infty }}$ – отражающая граница:
5) периодическое граничное условие вдоль оси x в расчетах с объемной P-волной, что позволяет избежать возникновения краевых артефактов и разрыва фронта плоской волны:
Таким образом, получаем две задачи, отличающиеся набором граничных условий – первая система уравнений (1)–(3) с ГУ (4), (5), (8) для случая облучения волной Рэлея (см. рис. 1) и вторая система (1)–(3) с ГУ (4), (7), (9) для случая облучения исследуемой области восходящей продольной волной. Для численного интегрирования указанных уравнений используем в прямоугольной расчетной области xy равномерную квадратную сетку $0 \leqslant i < {{N}_{X}},$ $0 \leqslant j < {{N}_{Y}}$ с шагом, одинаковым по обеим осям. Для сеточного аналога векторного поля ${{u}_{k}}\left( {x,y,t} \right)$ смещений точек среды на введенной сетке используем обозначение $U_{k}^{{ijt}},$ где $k = x,y$ – компоненты вектора смещений.
Рис. 1.
Постановка численного эксперимента. Однородное полупространство со свободной поверхностью y = 0 и заглубленной неоднородностью прямоугольной формы. В зависимости от варианта расчета источником облучающей волны является либо вертикальная граница x = 0, излучающая волну Рэлея, либо нижняя горизонтальная, излучающая продольную волну вверх.

Правую часть уравнения (1) без внешней силы f с учетом (2) и (3) можно записать в виде
(10)
$\begin{gathered} {{F}_{{ij}}}({\mathbf{r}},t) = \left( {\frac{{\partial \lambda }}{{\partial {{x}_{j}}}}\frac{{\partial {{u}_{k}}}}{{\partial {{x}_{k}}}} + \lambda \frac{{{{\partial }^{2}}{{u}_{k}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}} \right){{\delta }_{{ij}}} + \\ + \,\,\frac{{\partial \mu }}{{\partial {{x}_{j}}}}\left( {\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{u}_{j}}}}{{\partial {{x}_{i}}}}} \right) + \mu \left( {\frac{{{{\partial }^{2}}{{u}_{i}}}}{{\partial {{x}_{j}}^{2}}} + \frac{{{{\partial }^{2}}{{u}_{j}}}}{{\partial {{x}_{i}}\partial {{x}_{j}}}}} \right), \\ \end{gathered} $Сеточная запись выражения (10) с использованием схемы второго порядка аппроксимации для всех производных по пространственным переменным (11), (12)
(11)
$\begin{gathered} \frac{{\partial w({{x}_{i}})}}{{\partial x}} = \frac{{{{w}_{{i + 1}}} - {{w}_{{i - 1}}}}}{{2h}} + o({{h}^{2}}), \\ \frac{{{{\partial }^{2}}w({{x}_{i}})}}{{\partial {{x}^{2}}}} = \frac{{{{w}_{{i + 1}}} - 2{{w}_{i}} + {{w}_{{i - 1}}}}}{{{{h}^{2}}}} + o({{h}^{2}}), \\ \end{gathered} $(12)
$\frac{{{{\partial }^{2}}w({{x}_{i}},{{y}_{j}})}}{{\partial x\partial y}} = \frac{{w_{{j + 1}}^{{i + 1}} - w_{{j - 1}}^{{i + 1}} - w_{{j + 1}}^{{i - 1}} + w_{{j - 1}}^{{i - 1}}}}{{4{{h}^{2}}}} + o({{h}^{2}}),$(13)
$\begin{gathered} F_{{11}}^{{ij}} = \frac{1}{{2h}}(\lambda _{x}^{{ij}} + 2\mu _{x}^{{ij}})\left[ {U_{x}^{{i + 1j}} - U_{x}^{{i - 1j}}} \right] + \\ + \,\,\frac{1}{{{{h}^{2}}}}({{\lambda }^{{ij}}} + 2{{\mu }^{{ij}}})\left[ {U_{x}^{{i + 1j}} - 2U_{x}^{{ij}} + U_{x}^{{i - 1j}}} \right] + \\ + \frac{1}{{2h}}\lambda _{x}^{{ij}}\left( {U_{y}^{{ij + 1}} - U_{y}^{{ij - 1}}} \right) + \\ + \,\,\frac{1}{{4{{h}^{2}}}}{{\lambda }^{{ij}}}\left( {U_{y}^{{i + 1j + 1}} - U_{y}^{{i + 1j - 1}} - U_{y}^{{i - 1j + 1}} + U_{y}^{{i - 1j - 1}}} \right), \\ \end{gathered} $(14)
$\begin{gathered} F_{{12}}^{{ij}} = \frac{1}{{2h}}\mu _{y}^{{ij}}\left( {U_{x}^{{ij + 1}} - U_{x}^{{ij - 1}} + U_{y}^{{i + 1j}} - U_{y}^{{i - 1j}}} \right) + \\ + \,\,\frac{1}{{{{h}^{2}}}}{{\mu }^{{ij}}}(4U_{x}^{{ij + 1}} - 8U_{x}^{{ij}} + 4U_{x}^{{ij - 1}} + \\ + \,\,U_{y}^{{i + 1j + 1}} - U_{y}^{{i + 1j - 1}} - U_{y}^{{i - 1j + 1}} + U_{y}^{{i - 1j - 1}}), \\ \end{gathered} $(15)
$\begin{gathered} F_{{21}}^{{ij}} = \frac{1}{{2h}}\mu _{x}^{{ij}} \times \\ \times \,\,\left( {U_{x}^{{ij + 1}} - U_{x}^{{ij - 1}} + U_{y}^{{i + 1j}} - U_{y}^{{i - 1j}} + U_{x}^{{ij + 1}} - U_{x}^{{ij - 1}}} \right) + \\ + \,\,\frac{1}{{{{h}^{2}}}}{{\mu }^{{ij}}}(U_{x}^{{i + 1j + 1}} - U_{x}^{{i + 1j - 1}} - U_{x}^{{i - 1j + 1}} + U_{x}^{{i - 1j - 1}} + \\ + \,\,4U_{y}^{{i + 1j}} - 8U_{y}^{{ij}} + 4U_{y}^{{i - 1j}}), \\ \end{gathered} $Симметричная схема для второй производной по времени также имеет второй порядок аппроксимации
(17)
$\frac{{{{\partial }^{2}}{{u}_{k}}}}{{\partial {{t}^{2}}}} = \frac{1}{{{{\tau }^{2}}}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} }}_{k}} - 2{{U}_{k}} + {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{U} }}_{k}}} \right) + o({{\tau }^{2}}),$ $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{U} _{k}^{{ij}} = U_{k}^{{ij(t - 1)}}$ и $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{k}^{{ij}} = U_{k}^{{ij(t + 1)}}$ соответственно, по аналогии с принятыми обозначениями в [19]. С учетом (13)–(16) и (17) для интегрирования основных уравнений (1)–(3) получаем
явную схему во внутренних (не граничных) точках области:
$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{U} _{k}^{{ij}} = U_{k}^{{ij(t - 1)}}$ и $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{k}^{{ij}} = U_{k}^{{ij(t + 1)}}$ соответственно, по аналогии с принятыми обозначениями в [19]. С учетом (13)–(16) и (17) для интегрирования основных уравнений (1)–(3) получаем
явную схему во внутренних (не граничных) точках области:
(18)
$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{k}^{{ij}} = \frac{{{{\tau }^{2}}}}{{{{\rho }_{{ij}}}}}\left( {\sum\limits_l {F_{{kl}}^{{ij}}} } \right) + 2U_{k}^{{ij}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{U} _{k}^{{ij}},\,\,\,\,k = x,y.$Для интегрирования граничного условия на свободной поверхности (4) с использованием несимметричной сеточной разности второго порядка аппроксимации
(19)
$\left\{ \begin{gathered} 3\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{x}^{{i0}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{y}^{{i + 1,0}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{y}^{{i - 1,0}} = 4\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{x}^{{i1}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{x}^{{i2}}, \hfill \\ 3\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{y}^{{i0}} - \vartheta (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{x}^{{i + 1,0}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{x}^{{i - 1,0}}) = 4\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{y}^{{i1}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{y}^{{i2}}, \hfill \\ \end{gathered} \right.$(20)
$\left\{ \begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{x}^{{i0}} = \frac{1}{3}(4\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{x}^{{i1}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{x}^{{i2}} - U_{y}^{{i - 1,0}} + U_{y}^{{i + 1,0}}), \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{y}^{{i0}} = \frac{1}{3}[\vartheta (U_{x}^{{i + 1,0}} - U_{x}^{{i - 1,0}}) + 4\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{y}^{{i1}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} _{y}^{{i2}}], \hfill \\ \end{gathered} \right.$Шаг интегрирования по времени τ выбирается согласно теореме Котельникова в зависимости от максимальной частоты ωn колебаний в системе $\tau \leqslant \frac{1}{\zeta }\frac{\pi }{{{{\omega }_{n}}}},$ а также из условия сходимости схемы согласно обобщенному условию Куранта [19], определяемому выражением $\tau = \frac{1}{\chi }\frac{h}{{{{V}_{{P\max }}}\sqrt 2 }},$ где ξ, $\chi \geqslant 1$ – коэффициенты запаса прочности, ${{V}_{{P\max }}}$ – максимальное значение скорости распространения P-волн в модельной среде. Реализацию описанного подхода для построения модели в трехмерном случае, а также описание численного алгоритма и его верификацию можно найти в [1] или более подробно в [20].
Физические параметры среды и неоднородности выбраны в соответствии с вариантами, рассмотренными в предыдущих исследованиях [1, 2, 21, 22] для возможности сопоставления получаемых результатов моделирования:
1) параметры вмещающей среды: vP = 3193.74 м/с, vS = 1843.91 м/с, vR = 1695.29 м/с, упругие модули Ламэ λ = μ = 6.8 ГПа;
2) низкоскоростная неоднородность: vP = = 2554.99 м/с, vS = 1475.13 м/с, λ = μ = 4.352 ГПа;
3) высокоскоростная неоднородность: vP = = 3992.17 м/с, vS = 2304.89 м/с, λ = μ = 10.625 ГПа.
Плотности материала вмещающей среды и неоднородности одинаковы и составляют ρ = 2000 кг/м3, коэффициент Пуассона также сохраняет значение по всему объему ν = 0.25. Горизонтальный размер рассмотренных неоднородностей L = 2, 10, 20 км, вертикальный d = 1 км, глубина залегания кровли h1 = 1.5 км, подошвы h2 = 2.5 км (см. схему на рис. 1). Размер расчетной области 80 × 36 км при шаге сетки h = 100 м, всего 288 000 ячеек квадратной сетки. Шаг интегрирования по времени составлял τ = 7.83 мс, обеспечивающий сходимость интегрирования. Продолжительность каждого расчета составляла 6028 временных шагов, что соответствует 47.2 с модельного времени.
Набор частот fn гармонических источников P- и R-волн выбирался в полосе 0.125–1.695 Гц таким образом, чтобы обеспечить равномерное покрытие диапазона длин волн фундаментальной моды волны Рэлея λR(fn) = 1000, …, 13600 м с шагом 200 м (всего 64 частоты). С использованием параллельных вычислений для каждого численного эксперимента в рамках одного расчета на 64 ядрах выполнялось облучение 64 волнами разной частоты. При этом на каждом расчетном ядре облучение происходило независимо, после чего данные собирались первым процессом и подготавливались к анализу.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
С использованием описанных моделей была проведена серия из 12 численных экспериментов – для двух противоположных скоростных контрастов неоднородности (0.8 – низкоскоростная по отношению к вмещающему полупространству, 1.25 – высокоскоростная), для трех различных латеральных размеров (2 км – меньше длины волны Рэлея ${\lambda }_{R}^{*}$ на частоте максимальной амплитудной реакции f *, 10 км – сравнима с длиной волны ${\lambda }_{R}^{*}$ и 20 км – больше нее) и для двух типов источника (объемные продольные волны с вертикальным направлением прихода или волны Рэлея, облучающие сбоку). Важно отметить, что вертикальный размер неоднородности во всех численных экспериментах составлял 1 км, что составляет 1/8–1/4 реагирующей длины волны Рэлея.
Синтетические изображения модельных неоднородностей, полученные в соответствии с процедурой ММЗ, примененной к синтетическому полю на поверхности, которое сформировано в результате рассеяния P-волн, R-волн и равнозначной смеси из P- и R-волн, представлены на рис. 2 и 3. Изображения строились путем вычисления квадрата амплитуды вертикальной компоненты смещения в каждой точке поверхности как функции частоты и расстояния вдоль профиля $V\left( {x,f} \right)$. Облучение производилось волнами с единичной амплитудой вертикальных колебаний. Согласно процедуре ММЗ из пространства (x, f) осуществлялся переход в пространство (x, λR(f)) или (x, h), где h – глубина, определяемая соотношением
kG – коэффициент глубинной привязки [1].Рис. 2.
Результаты численного решения прямой и оценки обратной задачи в соответствии с процедурой ММЗ для случая низкоскоростной заглубленной неоднородности с относительным скоростным контрастом 0.8 при различном составе облучающего микросейсмического поля: 100% объемные P-волны с вертикальным падением, 100% фундаментальная мода волны Рэлея и смесь из 50% P-волны и 50% волн Рэлея. Пунктирные границы соответствуют заданным границам модельной неоднородности. Значение коэффициента глубинной привязки 0.35 (согласно двумерному модельному случаю [1]).
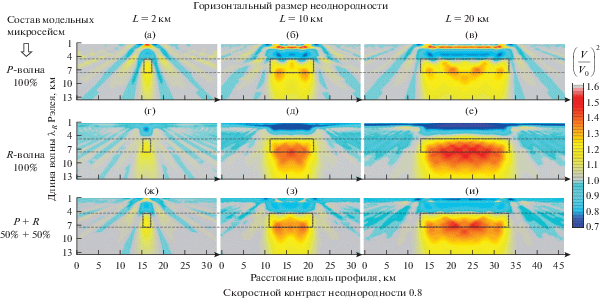
Рис. 3.
Результаты численного моделирования для случая высокоскоростной заглубленной неоднородности (с размерами 2, 10 и 20 км по горизонтали) и трех вариантов состава модельного микросейсмического поля (P-волна, R-волна и P + R волны). Содержание рисунка аналогично рис. 2.

Рассмотрим вначале случай с низкоскоростной неоднородностью, малой по сравнению с длиной падающей волны (рис.2). Видно, что над основной аномалией, формирующей изображение исходного объекта, присутствуют значительные по величине аномалии того же знака, что и в основной (рис. 2а). При облучении волной Рэлея основная аномалия проявляется в тех же частотах, что и в продольной волне, но над основным изображением формируется аномалия обратного знака по отношению к основной (рис. 2г). Когда модельное зондирующее поле представлено обоими типами волн в равных долях (рис. 2ж), основная аномалия имеет размер и форму, близкие к случаям отдельных облучений (рис. 2а и 2г), однако артефакты в зоне коротких волн над основным изображением взаимно компенсируют друг друга. В этом случае можно даже говорить о своеобразном улучшении изображения при использовании ММЗ, если около 50% энергии микросейсмического сигнала составляют P-волны.
При облучении P-волной низкоскоростной неоднородности с латеральным размером, сравнимым с длиной падающей волны (рис. 2б, 2д, 2з), основная аномалия имеет более искаженную форму границы (рис. 2б), чем при облучении R-волной (рис. 2д). Как и в случае малой неоднородности, формируется ложная положительная аномалия в коротких волнах. При облучении волнами обоих типов (рис. 2з) аномалия взаимно компенсируется. Присутствие 50% P-волн в облучающем поле (рис. 2з) искажает форму изображения по сравнению с облучением чистой волной Рэлея (рис. 2д). Незначительно увеличивается глубина изображения неоднородности. Аналогичные эффекты наблюдаются в случае протяженной по горизонтали неоднородности (рис. 2в, 2е, 2и).
Результаты моделирования с высокоскоростной неоднородностью представлены на рис. 3. Как видно, высокоскоростное включение проявляется падением интенсивности в определенной области спектра, связанной с глубиной и вертикальным размером включения. Изображение малой неоднородности по ММЗ в поле объемных волн (рис. 3а) близко к изображению в поле поверхностных волн (рис. 3г). Различие состоит в присутствии малой интенсивной аномалии в коротких волнах. При облучении P-волной основная аномалия более четкая и имеет несколько меньший горизонтальный размер, что более контрастно выделяет объект (рис. 3а). Результат при смешанном облучении (50% P-волны, 50% R-волны) малой неоднородности (рис. 3ж) в сравнении с вариантом рис. 3г имеет более интенсивный “обратный эффект” над неоднородностью, а также более четкое основное изображение неоднородности. Оба варианта с крупным высокоскоростным включением (рис. 3б, 3д, 3з и рис. 3в, 3е, 3и) имеют сходные черты. В присутствии P-волн усиливается интенсивность “обратного эффекта” в области коротких длин волн над неоднородностью. При этом лучше выделяется положение субгоризонтальных границ неоднородности, верхняя граница приобретает более ровную форму, нижняя граница становиться более контрастной, чем при облучении только волнами рэлеевского типа.
В обоих рассмотренных вариантах основная аномалия, интерпретируемая в ММЗ как искомый объект, имеет близкие к заданной скоростной неоднородности форму, “знак” и размеры. Она проявляется в одном и том же частотном диапазоне как в поле только вертикально падающих P-волн, так и при облучении только R-волнами. Этот результат сохраняется независимо от горизонтального размера и характера неоднородности. Видно, что любое содержание объемных P-волн в модельном микросейсмическом сигнале в основном сохраняет главную аномалию, но при этом могут возникать артефакты, не связанные со строением среды.
В рамках настоящего исследования авторы ограничились рассмотрением сред и включений с одинаковым коэффициентом Пуассона, равным 0.25. В дальнейших исследованиях может оказаться интересным случай, когда коэффициент Пуассона в неоднородности отличается от значения во вмещающей среде, либо он существенно отклоняется от значения 0.25.
ЗАКЛЮЧЕНИЕ
Результаты моделирования на основе первых принципов для взаимодействия упругих P- и R-волн в линейном изотропном полупространстве с заглубленной скоростной неоднородностью позволяют в дальнейшем полагать, что в случае, когда вертикальная компонента микросейсмического поля помимо волн типа Рэлея содержит объемные продольные волны, использование метода микросейсмического зондирования для оценки строения геологической среды допустимо. Даже присутствие объемных P-волн вплоть до 100% по энергии не ограничивает возможности применения ММЗ без каких-либо процедурных изменений для оценки структуры среды. При этом ожидаемый результат может осложняться более интенсивными искусственными аномалиями в высокочастотной области, чем в случае, когда микросейсмическое поле состоит только из волн Рэлея. Оценка по ММЗ скорости в обнаруженном включении также будет искажена по сравнению с чисто рэлеевским полем. Это следует принимать во внимание при геологической интерпретации результатов ММЗ.
Представляется, что полученный результат не может быть автоматически обобщен на случаи выраженной контрастной слоистости и среды с сильными анизотропными свойствами. Эти аспекты остаются задачей для будущих исследований.
Работа выполнена с использованием оборудования Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами МГУ имени М.В. Ломоносова [23, 24].
Список литературы
Горбатиков А.В., Цуканов А.А. Моделирование волн Рэлея вблизи рассеивающих скоростных неоднородностей. Исследование возможностей метода микросейсмического зондирования // Физика Земли. 2011. Т. 4. С. 96–112.
Цуканов А.А., Горбатиков А.В. Метод микросейсмического зондирования: влияние аномальных значений коэффициента Пуассона и оценка величины нелинейных искажений // Физика Земли. 2015. Т. 4. С. 94.
Горбатиков А.В., Степанова М.Ю., Кораблев Г.Е. Закономерности формирования микросейсмического поля под влиянием локальных геологических неоднородностей и зондирование среды с помощью микросейсм // Физика Земли. 2008. № 7. С. 66–84.
Nakamura Y. A method for dynamic characteristic estimation of subsurface using microtremor on the ground surface // Quarterly Report of Railway Technical Research Institute. 1989. V. 30. №1. P. 25–33.
Винник Л.П., Денисков А.С., Коньков Т.Д. Структура микросейсм в области частот около 1 Гц // Изв. АН СССР. Физика Земли. 1967. № 8.
Винник Л.П. Структура микросейсм и некоторые вопросы методики группирования в сейсмологии. М: Наука, 1968. 104 с.
Claerbout J.F. Detection of P-waves from weak sources at great distances // Geophysics. 1964. V. 29(2). P. 197–211.
Gerstoft P., Fehler M.C., Sabra K.G. When Katrina hit California // Geophys. Res. Lett. 2006. V. 33. P. L17308. https://doi.org/10.1029/2006GL027270
Gerstoft P., Shearer P.M., Harmon N., Zhang J. Global P, PP, and PKP wave microseisms observed from distant storms // Geophys. Res. Lett. 2008. V. 35. P. L23306. https://doi.org/10.1029/2008GL036111
Koper K.D., De Foy B. Seasonal anisotropy in short-period seismic noise recorded in South Asia // Bull. Seismological Soc. Am. V. 98(6). P. 3033–3045.
Landes M., Hubans F., Shapiro N.M., Paul A., Campillo M. Studying the origin of deep ocean microseisms using teleseismic body waves // In AGU Fall Meeting Abstracts. 2008. V. 1. P. 1893.
Яновская Т.Б. К теории метода микросейсмического зондирования // Физика Земли. 2017. № 6. С. 18–23.
Menke W. Geophysical data analysis: Discrete inverse theory // Academic press. 2012. V. 45.
Wiggins R.A. The general linear inverse problem: Implication of surface waves and free oscillations for earth structure // Reviews of Geophysics. 1972. V. 10(1). P. 251–285.
Аки К., Ричардс П. Количественная сейсмология: теория и методы. Т. 1. М.: Мир, 1983. 520 с.
Лурье А.И. Теория упругости. М.: Наука, 1970. 940 с.
Viktorov I.A. Rayleigh and Lamb waves: Physical theory and applications // New York, Plenum Press, 1967. 154 p.
Malischewsky P.G. Comment to “A new formula for the velocity of Rayleigh waves” by D. Nkemzi [Wave Motion. 1997. V. 26. P. 199–205] // Wave Motion. 2000. V. 31(1). P. 93–96.
Калиткин Н.Н. Численные методы. М.: Наука, 1978. 512 с.
Цуканов А.А. Исследование и развитие метода микросейсмического зондирования. Дисс. на соиск. уч. ст. к. ф.-м. н. МГУ, Москва, 2010. 152 с.
Цуканов А.А., Горбатиков А.В. Использование горизонтальных компонент микросейсмического поля для выявления протяженных низкоскоростных тел // Geomodel 2016–18th Science and Applied Research Conference on Oil and Gas Geological Exploration and Development. 2016. https://doi.org/10.3997/2214-4609.201602198 http://www.earthdoc.org/publication/publicationdetails/?publication=86769
Цуканов А.А., Горбатиков А.В. Влияние заглубленных неоднородностей на спектральное отношение горизонтальных компонент случайного поля волн Рэлея // Акуст. журн. 2018. Т. 64. № 1. С. 63–70.
Sadovnichy V., Tikhonravov A., Voevodin Vl., Opanasenko V. “Lomonosov”: Supercomputing at Moscow State University // In: Contemporary High Performance Computing: From Petascale toward Exascale (Chapman & Hall/CRC Computational Science). Boca Raton, USA, CRC Press, 2013. P. 283–307.
Adinets A.V., Bryzgalov P.A., Voevodin V.V., Zhumatii S.A.E., Nikitenko D.A., Stefanov K.S. Job digest: An approach to dynamic analysis of job characteristics on supercomputers // Numerical methods and programming: Advanced Computing. 2012. V. 13(4). P. 160–166.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал


