Акустический журнал, 2020, T. 66, № 4, стр. 453-462
О методе электроакустического преобразования, основанном на электрокинетических явлениях
Б. П. Шарфарец a, *, В. Е. Курочкин a, **, В. А. Сергеев b, Ю. В. Гуляев c
a Институт аналитического приборостроения Российской академии наук
198095 Санкт-Петербург, ул. Ивана Черных 31–33, Россия
b АО “АКВАМАРИН”
198097 Санкт-Петербург, Баррикадная ул. 17, Россия
c Институт радиотехники и электроники имени В.А. Котельникова Российской академии наук
125009 Москва, ул. Моховая 11, стр. 7, Россия
* E-mail: sharb@mail.ru
** E-mail: lavrovas@yandex.ru
Поступила в редакцию 04.09.2019
После доработки 16.12.2019
Принята к публикации 24.12.2019
Аннотация
Предложены в линейном и нелинейном приближении (ламинарный режим) физическая и математическая модели для описания механизма функционирования нового вида акустического преобразователя. Кратко даны сведения о таком электрокинетическом явлении, как электроосмос. Приведены необходимые уравнения для описания акустических полей, вызываемых электрокинетическими явлениями: наличием двойного электрического слоя и приложенного суммарного электрического поля, состоящего из постоянного поля и поля, несущего акустическую информацию. Уравнения рассматриваются для жидкости в круговом цилиндрическом капилляре применительно к расчету гидродинамики стационарного электроосмотического процесса и гармонического акустического процесса. Теоретически, на вычислительной модели и экспериментально показано, что учет нелинейности стационарного процесса приводит, в отличие от линейного стационарного процесса, к перекачке энергии постоянного электрического поля в акустическое поле, вызываемого переменным электрическим полем. Полученные результаты при некоторых ограничениях верны для широкого класса пористых структур. Экспериментально для бумажной мембраны в качестве капиллярно-пористой структуры с помощью накачки получено усиление первой гармоники акустического давления от 5.9 до 28 раз для различных значений амплитуды переменного электрического поля. Полученные в работе теоретические и экспериментальные результаты позволяют решить приоритетную научно-техническую проблему проектирования и создания акустических излучателей нового типа.
ВВЕДЕНИЕ
В работе [1] предложен оригинальный способ электроакустического преобразования, основанный на подходе, заключающемся в том, что к пористому телу, заполненному жидкостью или газом, подается сумма постоянного напряжения и переменного напряжения, связанного с амплитудой акустического сигнала. Этот подход отличается от стандартного электрокинетического преобразования, основанного на явлении электроосмоса и изложенного, например, в работе [2] или обзорах [3, 4] (см., также библиографию в этих работах), тем, что существенную роль в электроакустическом преобразовании играет обязательное наличие наряду с переменной (акустической) составляющей прикладываемого к жидкости напряжения еще и постоянного напряжения (называемого в дальнейшем напряжением накачки). Причиной накачки, как будет показано в работе, является нелинейность возникающей гидродинамической части задачи. Аналогичные явления возникают при изучении нелинейных течений жидкости вблизи диэлектрических и идеально поляризованных частиц при воздействии на них внешнего электрического поля [5], но в этом случае нелинейность возникает в электрической части физической модели проблемы.
Отметим, что отдаленно похожие процессы в смысле одновременного воздействия постоянных и переменных магнитных или электрических полей описаны в работах [6, 7]. Так, при создании магнитогидродинамического генератора псевдозвука, описанного в работе [6], показано, что при возбуждении в некотором объеме периодических движений проводящей жидкости, помещенной в постоянное магнитное поле, при прохождении через эту жидкость переменного тока возникают звуковые волны вследствие отражения от границ объема псевдозвуковых течений, возбуждаемых МГД генератором. Течение жидкости при этом рассмотрено в рамках линейной системы уравнений Эйлера. В работе [7] описан вибрационный преобразователь, вынуждающее усилие в котором создается системой катушек с переменным током, магнитное поле которых поляризуется полем постоянных магнитов и взаимодействует с индуцированными в системе токами.
Приведенное в [1] описание принципа действия преобразователя никак не увязано с электрогидродинамикой (ЭГД), предметом которой является данная проблематика. Кроме того, никак не учтено такое электрокинетическое явлением, как электроосмос, неизбежно возникающий при подаче разности потенциалов к пористому телу, наполненному жидкостью, где на границе раздела фаз имманентно присутствует двойной электрический слой (ДЭС), в котором нарушается электронейтральность жидкости.
В настоящей работе подробно излагаются детали, предложенных кратко в [8] физической и математической моделей, описывающих принцип действия этого электроакустического преобразователя на примере одиночного цилиндрического капилляра, заполненного жидкостью. Уравнения движения жидкости здесь рассматриваются и на основе линеаризованной системы уравнений Навье–Стокса, изложенной в [8], и на основе ее нелинейной версии применительно к ламинарному движению жидкости.
Учитывая пограничный характер научных явлений, лежащих в основе принципа действия рассматриваемого акустического преобразователя, целесообразно изложить основные положения такой неакустической дисциплины, как электроосмос.
СТАЦИОНАРНЫЙ ЭЛЕКТРООСМОС
К настоящему времени теория стационарного электроосмоса устоялась и опубликована в солидном количестве источников, из которых упомянем работы [9–11]. Электроосмос является одним из электрокинетических явлений, т.е. явлений, происходящих в системах, содержащих капилляры или пористые мембраны, размещенные в электролите при наложении электрического поля, и обратных им эффектов [12, с. 534]. Основную роль в электрокинетических явлениях играет ДЭС, формирующийся на границе раздела фаз, одна из которых должна обязательно быть жидкой или газообразной, и его поляризация. Таким образом, электроосмос – это движение жидкости (газа) через капилляры или пористые среды при наложении внешнего электрического поля. В силу различных причин безотносительно к тому, присутствует или нет внешний электрический потенциал, на поверхности раздела твердой и жидкой (газообразной) фаз образуется ДЭС (см., например, [9, глава 1; 10, глава 7]). На поверхности твердой фазы образуется слой потенциал-определяющих ионов одного знака, имеющий молекулярные размеры. Вследствие законов электростатики противоионы в жидкости при контакте с твердой фазой притягиваются к твердой границе; ионы жидкости, заряженные одноименно заряду границы, отталкиваются от границы. Часть противоионов (адсорбционная плотная, неподвижная часть ДЭС) остаются неподвижными даже при движении жидкости. Остальные противоионы и коионы остаются подвижными и образуют подвижную (диффузную) часть ДЭС. Область, где касаются адсорбционный и диффузный слои, называется поверхностью скольжения, которая получается несколько отодвинутой от реальной границы. Диффузный слой имеет толщину, равную дебаевской длине ${{\lambda }_{{\text{D}}}}$. Подвижная часть ДЭС за небольшое время переходного процесса приходит к стационарной концентрации. Концентрации противоионов и коионов в ДЭС и значение образовавшегося распределения электрического потенциала $\varphi $ в ДЭС связаны между собой распределением Больцмана [9, с. 15]. Потенциал $\varphi $ вектора электрической напряженности является электрической характеристикой ДЭС. Выделяют несколько характерных потенциалов, важнейшим из которых является электрокинетический потенциал (дзета-потенциал или $\zeta $-потенциал; во избежание путаницы в обозначениях с динамической вязкостью дзета-потенциал далее обозначаем $\tilde {\zeta }$), соответствующий поверхности скольжения. Часть диффузного слоя не является электронейтральной, что в конечном итоге и приводит к движению жидкости под воздействием стороннего электрического поля, т.е. к явлению электроосмоса.
В ДЭС формируется электростатическое поле, электрический потенциал $\varphi $ которого при заданном распределении свободных зарядов удовлетворяет уравнению Пуассона [9, с. 16; 10, с. 220]
(1)
$\Delta \varphi = - \frac{{{{\rho }_{{{\text{el}}}}}}}{{\varepsilon {{\varepsilon }_{0}}}}\,\,\,\,({\text{в}}\,\,{\text{СИ}}),\,\,\,\,\Delta \varphi = - \frac{{4\pi {{\rho }_{{{\text{el}}}}}}}{\varepsilon }\,\,\,\,\,({\text{в}}\,\,{\text{СГСЭ}}).$Здесь ${{\varepsilon }_{0}}$ – электрическая постоянная; $\varepsilon $ – относительная диэлектрическая проницаемость среды; ${{\rho }_{{{\text{el}}}}}$ – объемная плотность электрического заряда. В случае, когда тепловая энергия превосходит электрическую энергию [10, с. 97; 11, с. 147] $Ze\tilde {\zeta } \ll {{k}_{{\text{B}}}}T$ ($Z$ – заряд иона в единицах заряда протона; ${{k}_{{\text{B}}}}$ – постоянная Больцмана; $T$ – абсолютная температура; $e$ – элементарный электрический заряд (заряд протона)), уравнение (1) переходит в линейное уравнение Дебая–Хюккеля $\Delta \varphi \left( {\mathbf{r}} \right) = \frac{1}{{\lambda _{{\text{D}}}^{2}}}\varphi \left( {\mathbf{r}} \right).$ Длина Дебая определяется выражением [10, с. 97; 11, с. 147] ${{\lambda }_{{\text{D}}}} = \sqrt {\frac{{\varepsilon {{\varepsilon }_{0}}{{k}_{{\text{B}}}}T}}{{2{{{\left( {Ze} \right)}}^{2}}{{c}_{0}}}}} ,$ где ${{c}_{0}}$ – равновесная концентрация ионов вне ДЭС. Решение $\varphi \left( {\mathbf{r}} \right)$, полученное из уравнения Дебая–Хюккеля, позволяет рассчитать объемную плотность электрического заряда ${{\rho }_{{{\text{el}}}}}$ из уравнения (1), например, в СИ в виде ${{\rho }_{{{\text{el}}}}} = - \varepsilon {{\varepsilon }_{0}}\Delta \varphi .$
УРАВНЕНИЯ ДВИЖЕНИЯ ЖИДКОСТИ. ЛИНЕЙНЫЙ СЛУЧАЙ
Поскольку здесь рассматриваются акустические процессы, закон сохранения импульса принимаем в виде уравнения Навье–Стокса для движения вязкой сжимаемой однородной жидкости [13, с. 73]
(2)
$\begin{gathered} {{\rho }_{\Sigma }}\left( {\frac{{\partial {{v}_{\Sigma }}}}{{\partial t}} + \left( {{{v}_{\Sigma }}\nabla } \right){{v}_{\Sigma }}} \right) = \\ = - \nabla {{p}_{\Sigma }} + \eta \Delta {{v}_{\Sigma }} + \left( {\zeta + \frac{\eta }{3}} \right)\nabla \nabla {{v}_{\Sigma }} + {{\rho }_{{{\text{el}}}}}{{E}_{\Sigma }}. \\ \end{gathered} $В (2) учтено внешнее электрическое поле [10, с. 309; 11, с. 141] напряженностью ${{E}_{\Sigma }} = {{E}_{0}} + E$, где постоянное электрическое поле ${{E}_{0}} = {\text{const}}$ модулируется коллинеарным ему электрическим вектором $E$, зависящим от времени ($E \times {{E}_{0}} = 0$). В (2) $\eta $, $\zeta $ – динамическая и объемная вязкости соответственно; ${{p}_{\Sigma }}$ – давление, ${{v}_{\Sigma }}$ – вектор скорости в среде; ${{\rho }_{\Sigma }}$ – плотность среды. Величины, помеченные индексом $\Sigma $, обозначают поля, возбужденные полем ${{E}_{\Sigma }}$. Пометим поля, вызванные электрическим полем ${{E}_{0}}$, нижним индексом 0: ${{p}_{0}}$, ${{{\mathbf{v}}}_{0}}$. Кроме того, обозначим через ${{\rho }_{0}}$ невозмущенное значение плотности, имеющее место в том числе и при воздействии только стационарного поля ${{E}_{0}}$. Соответственно, акустические поля обозначим через $v$, $p$, $\rho $.
Если принять допущение о том, что скорости процессов ${{{\mathbf{v}}}_{0}}$ и $v$ соответствуют малым значениям числа Рейнольдса $\operatorname{Re} \ll 1$, то в (2) можно пренебречь конвективным членом [13, с. 89], что делает уравнение (2) линейным
(3)
${{\rho }_{\Sigma }}\frac{{\partial {{v}_{\Sigma }}}}{{\partial t}} = - \nabla {{p}_{\Sigma }} + \eta \Delta {{v}_{\Sigma }} + \left( {\zeta + \frac{\eta }{3}} \right)\nabla \nabla {{v}_{\Sigma }} + {{\rho }_{{{\text{el}}}}}{{E}_{\Sigma }}.$Поскольку в этом случае справедлив принцип суперпозиции, то можно записать ${{\rho }_{\Sigma }} = {{\rho }_{0}} + \rho ,$ ${{p}_{\Sigma }} = {{p}_{0}} + p,$ ${{{\mathbf{v}}}_{\Sigma }} = {{{\mathbf{v}}}_{0}} + {\mathbf{v}}.$
При описании стационарного электроосмоса пользуются усеченной версией уравнения (3) [9, с. 33; 10, с. 220]
которое формально следует из (3) при выполнении условий $\nabla {{p}_{0}} = 0,$ $\frac{{\partial {{v}_{0}}}}{{\partial t}} = 0.$ Уравнение (4) описывает стационарное электроосмотическое течение под воздействием постоянного электрического поля ${{E}_{0}}$ при рассмотрении баланса электрических сил и сил трения.Далее рассматриваем случай кругового цилиндрического капилляра. Отличным от нуля решением (4) при условии ${{\left. {{{{\mathbf{v}}}_{0}}} \right|}_{{r = a}}} = 0$ для капилляра с осью, совпадающей с $Oz$, и ${{E}_{0}} = \left( {0,0,{{E}_{0}}} \right)$, является составляющая ${{v}_{{0z}}}\left( r \right)$ скорости ${{v}_{0}}$ [10, с. 220; 11, с. 161]
(5)
${{v}_{{0z}}}\left( r \right) = {{E}_{0}}\frac{{\varepsilon {{\varepsilon }_{0}}}}{\eta }\tilde {\zeta }\left( {1 - \frac{{{{I}_{0}}\left( {{r \mathord{\left/ {\vphantom {r {{{\lambda }_{{\text{D}}}}}}} \right. \kern-0em} {{{\lambda }_{{\text{D}}}}}}} \right)}}{{{{I}_{0}}\left( {{a \mathord{\left/ {\vphantom {a {{{\lambda }_{{\text{D}}}}}}} \right. \kern-0em} {{{\lambda }_{{\text{D}}}}}}} \right)}}} \right).$Здесь $a$ – радиус поверхности скольжения; ${{I}_{0}}$ – модифицированная функция Бесселя первого рода нулевого порядка. Асимптотика (5) при $r \to 0$ называется электроосмотической скоростью и равна ${{U}_{0}}\left( r \right) = $ ${{E}_{0}}\frac{{\varepsilon {{\varepsilon }_{0}}}}{\eta }\tilde {\zeta } = {\text{const}}$. Известно, что при выполнении соотношения ${{\lambda }_{{\text{D}}}} \ll a$, практически для всех $r \in \left[ {0,a} \right)$ будет справедливо соотношение ${{v}_{{0z}}}\left( r \right) \approx {{U}_{{eo}}}$ [11, с. 162].
На долю возмущенного решения приходится остающаяся часть уравнения (3), которое с точностью до акустических величин второго порядка малости имеет следующий вид
(6)
${{\rho }_{0}}\frac{{\partial v}}{{\partial t}} = - \nabla p + \eta \Delta v + \left( {\zeta + \frac{\eta }{3}} \right)\nabla \nabla v + {{\rho }_{{{\text{el}}}}}E.$К уравнению движения (6) необходимо добавить линеаризованное уравнение непрерывности
Принимая среду баротропной, выписываем уравнение состояния в линеаризованном виде
(8)
$p = \left( {{{{\left. {\frac{{\partial {{p}_{\Sigma }}}}{{\partial {{\rho }_{\Sigma }}}}} \right|}}_{{{{\rho }_{\Sigma }} = {{\rho }_{0}}}}}} \right)\rho = {{с}^{2}}\rho ,$Принимая представление вектора скорости $v$ в виде суммы потенциальной ${{v}_{l}}$ и соленоидальной ${{v}_{t}}$ частей
(9)
$v = {{v}_{l}} + {{v}_{t}},\,\,\,\,{{v}_{l}} = \nabla \Phi ,\,\,\,\,{{v}_{t}} = \nabla \times {\mathbf{\Psi }},\,\,\,\,\nabla {\mathbf{\Psi }} = 0,$(10)
$\begin{gathered} \left[ {{{\rho }_{0}}\frac{{\partial {{{\mathbf{v}}}_{l}}}}{{\partial t}} + \nabla p - \left( {\zeta + \frac{4}{3}\eta } \right)\Delta {{{\mathbf{v}}}_{l}} - {{\rho }_{{{\text{el}}}}}E} \right] + \\ + \,\,\left[ {{{\rho }_{0}}\frac{{\partial {{{\mathbf{v}}}_{t}}}}{{\partial t}} - \eta \Delta {{{\mathbf{v}}}_{t}}} \right] = 0. \\ \end{gathered} $В (10) учтено, что $E = - \nabla \psi $ – потенциальный вектор, где $\psi $ – скалярный потенциал поля $E$. Из (10) получаем для потенциального течения
(11)
${{\rho }_{0}}\frac{{\partial {{{\mathbf{v}}}_{l}}}}{{\partial t}} = - \nabla p + \left( {\zeta + \frac{4}{3}\eta } \right)\Delta {{{\mathbf{v}}}_{l}} + {{\rho }_{{{\text{el}}}}}E$(12)
${{\rho }_{0}}\frac{{\partial {{{\mathbf{v}}}_{t}}}}{{\partial t}} = \eta \Delta {{{\mathbf{v}}}_{t}}.$Подстановка в (11), (12) значений для ${{{\mathbf{v}}}_{l}}$ и ${{{\mathbf{v}}}_{t}}$ из (9) преобразует их к виду
(13)
$\begin{gathered} {{\rho }_{0}}\frac{{\partial \Phi }}{{\partial t}} = - p + \left( {\zeta + \frac{4}{3}\eta } \right)\Delta \Phi - {{\rho }_{{{\text{el}}}}}\psi , \\ {{\rho }_{0}}\frac{{\partial {\mathbf{\Psi }}}}{{\partial t}} = \eta \Delta {\mathbf{\Psi }}. \\ \end{gathered} $Далее при условии, что глубина проникновения вязких волн $\delta $ мала, соленоидальным течением пренебрегаем (см., например, [14, с. 63]).
По предположению векторы ${{E}_{0}}$ и $E$ направлены вдоль оси $Oz$ (${{E}_{0}} = \left( {0,0,{{E}_{0}}} \right)$, $E = \left( {0,0,E} \right)$) и вектор $E$, вызывающий акустические колебания, имеет гармоническую зависимость от времени $E = \bar {E}{{e}^{{ - i\omega t}}}$, где $\bar {E} = {\text{const}}$ – амплитуда колебаний. Тогда потенциал $\psi $ вектора $E$ определяется из соотношения $\nabla \psi = \frac{{\partial \psi }}{{\partial z}} = - \bar {E}{{e}^{{ - i\omega t}}}$. Интегрируя последнее равенство, имеем при условии $\psi \left( 0 \right) = {{\left. {\psi \left( z \right)} \right|}_{{z = 0}}} = 0$
Преобразуем уравнение (13). Для этого воспользуемся условием непрерывности (7) и соотношением $p = {{с}^{2}}\rho $. Получаем $\frac{{\partial p}}{{\partial t}} = - {{\rho }_{0}}{{c}^{2}}\nabla v$ или через скалярный потенциал $\frac{{\partial p}}{{\partial t}} = - {{\rho }_{0}}{{c}^{2}}\Delta \Phi $. В гармоническом случае, сохраняя те же обозначения для амплитуд, для амплитуды давления $p$ получаем
С учетом (14) и (15) выражение (13) для гармонического сигнала примет вид
(16)
$\begin{gathered} - i\omega {{\rho }_{0}}\Phi = - \frac{{{{\rho }_{0}}{{c}^{2}}}}{{i\omega }}\Delta \Phi + \\ + \,\,\left( {\zeta + \frac{4}{3}\eta } \right)\Delta \Phi + {{\rho }_{{{\text{el}}}}}z\bar {E}. \\ \end{gathered} $В круговом капилляре в дебаевском приближении справедливо выражение [11, с. 149] ${{\rho }_{{{\text{el}}}}}\left( r \right) = - \frac{{\varepsilon {{\varepsilon }_{0}}\tilde {\zeta }}}{{\lambda _{D}^{2}}}\frac{{{{I}_{0}}\left( {{r \mathord{\left/ {\vphantom {r {{{\lambda }_{{\text{D}}}}}}} \right. \kern-0em} {{{\lambda }_{{\text{D}}}}}}} \right)}}{{{{I}_{0}}\left( {{a \mathord{\left/ {\vphantom {a {{{\lambda }_{{\text{D}}}}}}} \right. \kern-0em} {{{\lambda }_{{\text{D}}}}}}} \right)}}.$ С учетом этого уравнение (16) преобразуется к виду
(17)
$\begin{gathered} \left\{ {\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{\partial }{{\partial r}}} \right) + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right] + {{k}^{2}}} \right\}\Phi = \\ = - \frac{{i{{k}^{2}}}}{{\omega {{\rho }_{0}}}}\frac{{\varepsilon {{\varepsilon }_{0}}\tilde {\zeta }}}{{\lambda _{D}^{2}}}\frac{{{{I}_{0}}\left( {{r \mathord{\left/ {\vphantom {r {{{\lambda }_{{\text{D}}}}}}} \right. \kern-0em} {{{\lambda }_{{\text{D}}}}}}} \right)}}{{{{I}_{0}}\left( {{a \mathord{\left/ {\vphantom {a {{{\lambda }_{{\text{D}}}}}}} \right. \kern-0em} {{{\lambda }_{{\text{D}}}}}}} \right)}}\bar {E}z. \\ \end{gathered} $Здесь $k = {{\frac{\omega }{c}} \mathord{\left/ {\vphantom {{\frac{\omega }{c}} {{{{\left( {1 - i\omega {{\left( {\zeta + \frac{4}{3}\eta } \right)} \mathord{\left/ {\vphantom {{\left( {\zeta + \frac{4}{3}\eta } \right)} {{{\rho }_{0}}{{c}^{2}}}}} \right. \kern-0em} {{{\rho }_{0}}{{c}^{2}}}}} \right)}}^{{1/2}}}}}} \right. \kern-0em} {{{{\left( {1 - i\omega {{\left( {\zeta + \frac{4}{3}\eta } \right)} \mathord{\left/ {\vphantom {{\left( {\zeta + \frac{4}{3}\eta } \right)} {{{\rho }_{0}}{{c}^{2}}}}} \right. \kern-0em} {{{\rho }_{0}}{{c}^{2}}}}} \right)}}^{{1/2}}}}}$ – волновое число потенциальных волн.
Таким образом, для амплитуды скалярного потенциала скорости $\Phi $ получено неоднородное уравнение Гельмгольца (17). Правая часть этого уравнения, как и скорость (5) в случае стационарного электроосмоса, пропорциональна амплитуде электрического потенциала $\bar {E}$ и величине $\tilde {\zeta }$-потенциала и обратно пропорциональна величине динамической вязкости $\eta $, а также, в отличие от стационарного электроосмоса, еще и объемной вязкости $\zeta $. Кроме того, $\Phi $, как и в стационарном случае, пропорциональна произведению диэлектрической проницаемости среды и электрической постоянной $\varepsilon {{\varepsilon }_{0}}$. Разумеется, эти зависимости в силу линейности уравнения (17) сохраняются для скорости потока ${\mathbf{v}}$.
Формально при сделанных выше допущениях задача считается решенной, если определен скалярный потенциал $\Phi $. Скалярный потенциал определяется выражением (17). Вектор колебательной скорости ${\mathbf{v}} = {{v}_{l}}$ определяется после этого из (9). Поле давления определяется из (15). В случае пренебрежения вихревым течением на скалярный потенциал $\Phi $ на поверхности скольжения можно наложить краевое условие ${{\left. {\mathbf{v}} \right|}_{a}} \approx {{\left. {{{{\mathbf{v}}}_{l}}} \right|}_{a}} = {{\left. {\nabla \Phi } \right|}_{a}} = 0$. Краевые условия для стационарного электроосмоса приведены в [9, с. 34; 10, с. 218].
УРАВНЕНИЯ ДВИЖЕНИЯ ЖИДКОСТИ. НЕЛИНЕЙНЫЙ СЛУЧАЙ, ЛАМИНАРНЫЙ РЕЖИМ
Далее снимается допущение о возможности линеаризации уравнения (2), но сохраняется допущение о ламинарности потоков жидкости в рассматриваемом процессе.
За основу вновь берется уравнение движения Навье–Стокса (2). Примем, что стационарное электрическое поле много больше переменного $\left| {{{E}_{0}}} \right| \gg \left| E \right|$. Число Рейнольдса ${{\operatorname{Re} }_{{{{v}_{0}}}}}$ для скорости ${{{\mathbf{v}}}_{0}}$ уже не считаем пренебрежимо малым, и конвективным членом слева в (2) для скорости ${{{\mathbf{v}}}_{0}}$ пренебрегать нельзя. Уравнение (4) в этом случае приводится к виду (как и выше, полагаем величину стационарного давления постоянной $\nabla {{p}_{0}} = 0$)
(18)
${{\rho }_{0}}\left( {{{v}_{0}}\nabla } \right){{v}_{0}} = \eta \Delta {{v}_{0}} + {{\rho }_{{{\text{el}}}}}{{E}_{0}}.$Вычтем из уравнения (2) для суммарных полей уравнение движения из (18) для стационарного потока. Получившееся уравнение для акустических полей линеаризуем. В результате получаем линеаризованную версию уравнения Навье–Стокса для акустических полей (см. также рассуждения в работе [13, § 26])
(19)
$\begin{gathered} {{\rho }_{0}}\left( {\frac{{\partial v}}{{\partial t}} + \left( {{{v}_{0}} \cdot \nabla } \right)v + \left( {v\nabla } \right){{v}_{0}}} \right) = \\ = - \nabla p + \eta \Delta v + \left( {\zeta + \frac{\eta }{3}} \right)\nabla \nabla v + {{\rho }_{{{\text{el}}}}}E{\kern 1pt} {\text{.}} \\ \end{gathered} $К уравнению движения (19) следует добавить линеаризованное уравнение непрерывности (7).
Как и выше, рассматриваем безвихревое акустическое движение. Тогда, после подстановки выражения $v = \nabla \Phi $ в уравнение (19), получаем уравнение для потенциала $\Phi $
(20)
$\begin{gathered} {{\rho }_{0}}\left( {\frac{{\partial \nabla \Phi }}{{\partial t}} + \left( {{{v}_{0}}\nabla } \right)\nabla \Phi + \left( {\nabla \Phi \nabla } \right){{v}_{0}}} \right) = \\ = - \nabla p + \eta \Delta \nabla \Phi + \left( {\zeta + \frac{\eta }{3}} \right)\nabla \Delta \Phi - {{\rho }_{{{\text{el}}}}}\nabla \psi . \\ \end{gathered} $Из (20) после простых преобразований получаем
(21)
${{\rho }_{0}}\left( {\frac{{\partial \Phi }}{{\partial t}} + 2\left( {{{v}_{0}}\nabla \Phi } \right)} \right) = - p + \left( {\zeta + \frac{4}{3}\eta } \right)\Delta \Phi - {{\rho }_{{{\text{el}}}}}\psi .$Выражение (21) следует из (20), если учесть, что скорость ${{v}_{0}}$ электроосмотического течения потенциальна [9, с. 38] и в члене $\left( {\nabla \Phi \nabla } \right){{v}_{0}}$ из (20) сделать замену ${{v}_{0}} = \nabla {{\Phi }_{0}}$, а затем опустить во всех членах (20) правый оператор градиента $\nabla $.
Рассматриваем далее гармонический процесс с множителем ${{e}^{{ - i\omega t}}}$ (амплитуды полей вновь обозначаем теми же буквами). Вектора ${{E}_{0}}$ и $E$ по прежнему являются коллинеарными и направлены вдоль оси $Oz$ (${{E}_{0}} = \left( {0,0,{{E}_{0}}} \right),$ $E = \left( {0,0,E} \right)$), а модуль вектора $E$ имеет гармоническую зависимость от времени $E = \bar {E}{{e}^{{ - i\omega t}}},$ где $\bar {E} = {\text{const}}{\text{.}}$ Тогда амплитудa потенциала $\psi $ вектора $E$ равна $\psi = - \bar {E}z$. После подстановки амплитуды давления и потенциала в (21) имеем в гармоническом случае
(22)
$\Delta \Phi + {{k}^{2}}\Phi = \frac{{2{{k}^{2}}}}{{i\omega }}\left( {{{v}_{0}}\nabla \Phi } \right) - \frac{{{{k}^{2}}}}{{i\omega {{\rho }_{0}}}}{{\rho }_{{{\text{el}}}}}\bar {E}z.$Уравнение (22) представляет собой подобие неоднородного уравнения Гельмгольца относительно скалярного потенциала $\Phi $ акустической составляющей осмотической скорости $v$, однако, с тем отличием, что в правую часть уравнения (22) входит искомая величина $\nabla \Phi $. Решение таких уравнений сводится к линейному интегральному уравнению с ядром, представляющим собой функцию Грина соответствующего уравнения Гельмгольца, которое здесь подробно не рассматривается. Проделаем лишь качественное рассуждение, касающееся того, что справа в (22) стоит скалярное произведение $\left( {{{v}_{0}}\nabla \Phi } \right)$ вектора стационарной осмотической скорости ${{v}_{0}}$ и вектора $\nabla \Phi $, а следовательно, искомое решение $\Phi $ скалярного потенциала акустической составляющей осмотической скорости $v$ прямо пропорционально модулю $\left| {{{v}_{0}}} \right|$ скорости ${{v}_{0}}$ стационарного осмотического течения. Поскольку имеет место линейная связь между потенциалом $\Phi $ и скоростью $v$, а также давлением $p$ (см. (9) и (15)), то при росте амплитуды $\left| {{{v}_{0}}} \right|$ будет расти и акустическое давление $p$ и модуль $\left| v \right|$ акустической составляющей осмотической скорости, а следовательно, и интенсивность звука $I \sim p\left| {\mathbf{v}} \right|$.
Подставляя в (22) соответствующее значение для ${{{\rho }}_{{{\text{el}}}}}\left( r \right)$, получаем
(23)
$\begin{gathered} \left\{ {\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{\partial }{{\partial r}}} \right) + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right] + {{k}^{2}}} \right\}\Phi = \\ = \frac{{{{k}^{2}}}}{{i\omega }}\left( {2\left( {{{v}_{0}}\nabla \Phi } \right) + \frac{1}{{{{\rho }_{0}}}}\frac{{\varepsilon {{\varepsilon }_{0}}\widetilde \zeta {{I}_{0}}\left( {{r \mathord{\left/ {\vphantom {r {{{\lambda }_{{\text{D}}}}}}} \right. \kern-0em} {{{\lambda }_{{\text{D}}}}}}} \right)}}{{\lambda _{D}^{2}{{I}_{0}}\left( {{a \mathord{\left/ {\vphantom {a {{{\lambda }_{{\text{D}}}}}}} \right. \kern-0em} {{{\lambda }_{{\text{D}}}}}}} \right)}}\bar {E}z} \right). \\ \end{gathered} $Выражение (23) отличается от выражения (17) только стоящим справа членом $\frac{{2{{k}^{2}}}}{{i\omega }}\left( {{{v}_{0}}\nabla \Phi } \right)$, появившимся в результате учета нелинейности в уравнении Навье–Стокса (2). Таким образом, с ростом числа Рейнольдса для скорости стационарного электроосмотического потока ${{v}_{0}}$ уравнения движения для стационарного потока и нестационарного акустического потока перестают быть несвязанными, как в линейном случае при получении уравнения (17). Это выражается в появлении в уравнениях (22), (23), описывающих акустический поток $v$, члена $\frac{{2{{k}^{2}}}}{{i\omega }}\left( {{{v}_{0}}\nabla \Phi } \right),$ непосредственно связанного со скоростью ${{v}_{0}}$ стационарного электроосмотического потока. В этом и состоит возможность увеличения мощности акустического процесса за счет энергии стационарного процесса, т.е. возникает эффект накачки энергии из стационарного потока в энергию акустического процесса.
Остановимся на оценке члена $\frac{{2{{k}^{2}}}}{{i\omega }}\left( {{{v}_{0}}\nabla \Phi } \right)$ в выражении (23). Стационарная электроосмотическая скорость ${{v}_{0}}$ является решением уравнения (18), которое отличается от уравнения, рассматриваемого в классическом электроосмосе (см., например в [9, с. 33, 34]
Уравнение (18) преобразуется в (24) при пренебрежении конвективным членом ${{\rho }_{0}}\left( {{{v}_{0}}\nabla } \right){{v}_{0}}$. Это возможно при условии $\left| {{{\rho }_{0}}\left( {{{v}_{0}}\nabla } \right){{v}_{0}}} \right| \ll \left| {{{\rho }_{{{\text{el}}}}}{{E}_{0}}} \right|.$ Если это условие справедливо, то можно воспользоваться оценкой для скорости ${{v}_{0}}$ при условии $a \gg {{\lambda }_{{\text{D}}}}$ [11, с. 161, 162]: ${{v}_{0}} \approx {{U}_{{eo}}}{{{\mathbf{e}}}_{z}}$, где ${{U}_{{eo}}}$ – электроосмотическая скорость; ${{E}_{0}} = \left| {{{E}_{0}}} \right|$; ${{{\mathbf{e}}}_{z}}$ – единичный орт оси $Oz$, совпадающей с осью капилляра. С учетом приведенных рассуждений уравнение (23) переписывается в следующем виде
(25)
$\begin{gathered} \left\{ {\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{\partial }{{\partial r}}} \right) + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right] + {{k}^{2}}} \right\}\Phi = \\ = \frac{{{{k}^{2}}}}{{i\omega }}\varepsilon {{\varepsilon }_{0}}\tilde {\zeta }{{E}_{0}}\left( {\frac{2}{\eta }\left( {{{e}_{z}}\nabla \Phi } \right) + \frac{1}{{{{\rho }_{0}}}}\frac{{{{I}_{0}}\left( {{r \mathord{\left/ {\vphantom {r {{{\lambda }_{{\text{D}}}}}}} \right. \kern-0em} {{{\lambda }_{{\text{D}}}}}}} \right)}}{{\lambda _{D}^{2}{{I}_{0}}\left( {{a \mathord{\left/ {\vphantom {a {{{\lambda }_{{\text{D}}}}}}} \right. \kern-0em} {{{\lambda }_{{\text{D}}}}}}} \right)}}\frac{{\bar {E}}}{{{{E}_{0}}}}z} \right), \\ \end{gathered} $При решении задачи (25) следует наложить специфичные для электроосмотических задач краевые условия (см., например, [9, с. 33, 34; 10, с. 220]). После вычисления потенциала $\Phi $ вектор колебательной скорости и давления определяются стандартно, как описано выше. Плотность определяется из условия баротропности жидкости $\rho = \frac{p}{{{{с}^{2}}}}$.
Замечание 1. Уравнения (3) и (10) описывают процессы линейной акустики. В случае, когда нельзя пренебречь нелинейным слагаемым $\left( {v\nabla } \right)v$, опущенным слева в (19), уравнение (25) трансформируется к нелинейному, что, в частности, объясняет появление кратных гармоник, которые в процессе эксперимента и сигнализируют о возникновении нелинейности акустического процесса.
МОДЕЛЬНЫЙ ЭКСПЕРИМЕНТ
Для проверки рассмотренной теории был проведен модельный эксперимент в вычислительном пакете COMSOL. В качестве пористой структуры был выбран круговой стеклянный капилляр, заполненный воздухом с параметрами: радиус капилляра 10 мкм, длина капилляра 0.1 мм, амплитуда переменной разности потенциалов сохранялась в эксперименте постоянной $U = 1000$ В (переменное напряжение $u\left( t \right)$ определялось так $u\left( t \right)$ $ = U\sin \left( {2\pi 1000t} \right)$), частота 1000 Гц, дзета-потенциал был принят равным 100 мВ.
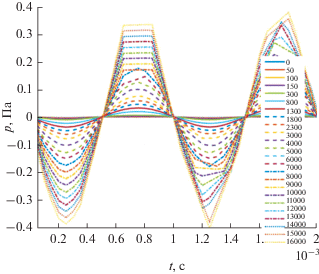
На сетке фиксированных значений постоянного напряжения ${{U}_{{0i}}}$, $i = \overline {1,N} $ решалась задача расчета уровня акустического давления p = f $\left( {{{U}_{{0i}}},U = {\text{const}}} \right)$ на торце капилляра в случае наиболее общего уравнения движения (2). На рис. 1 представлены зависимости ${{p}_{i}}\left( t \right)$ $ = f\left( {{{U}_{{0i}}},U = {\text{const}}} \right)$ при дискретной вариации величины ${{U}_{{0i}}}$ в интервале $i \in \overline {1,N} $. С правой стороны рисунка отдельно приведены дискретные значения ${{U}_{{0i}}}$. Из рис. 1 видно, что начиная с некоторых значений ${{U}_{{0i}}}$, функции давления ${{p}_{i}}\left( t \right)$ становятся нелинейными вследствие нелинейности задачи (2), на что указывает отклонение их формы от синусоидальной. Кроме того, видна прямая зависимость амплитуд колебаний ${{p}_{i}}\left( t \right)$ от величины амплитуды накачки ${{U}_{{0i}}}$.
Рис. 1.
Поведение результирующего акустического давления $p$ на торце капилляра в зависимости от времени $t$ при различных напряжениях накачки ${{U}_{0}}$ при значении величины амплитуды переменного напряжения $U = 1000$ В. Значения ${{U}_{0}}$, В приведены в правой стороне графика.
Далее с помощью разложений в ряд Фурье кривых ${{p}_{i}}\left( t \right)$ были получены амплитуды ${{p}_{{1i}}}$ первых гармоник функций ${{p}_{i}}\left( t \right)$. На рис. 2, 3 приведены в режиме линейной интерполяции зависимости величины $20{\text{lg}}\left( {{{p}_{1}}} \right)$ от напряжения накачки ${{U}_{0}}$ в интервале соответственно ${{U}_{0}} \in \left[ {0,150} \right]$ и ${{U}_{0}} \in \left[ {0,16\,000} \right]$ В при значении величины амплитуды переменного напряжения $U = 1000$ В. Здесь ${{p}_{1}}$ – первая гармоника давления $p(t)$.
Рис. 2.
Зависимость величины $20{\text{lg}}\left( {{{p}_{1}}} \right)$ от напряжения накачки ${{U}_{0}}$ в интервале ${{U}_{0}} \in \left[ {0,\,\,150} \right]$ В при значении величины амплитуды переменного напряжения $U = 1000$ В. Здесь ${{p}_{1}}$ – первая гармоника давления $p$ (см. рис. 1).
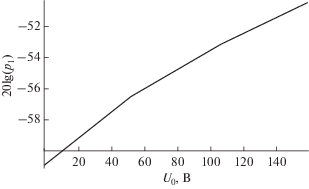
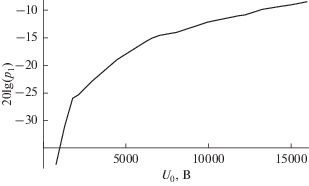
Рис. 3.
Зависимость величины $20{\text{lg}}\left( {{{p}_{1}}} \right)$ от напряжения накачки ${{U}_{0}}$ в интервале ${{U}_{0}} \in \left[ {0,\,\,16\,000} \right]$ В при значении величины амплитуды переменного напряжения $U = 1000$ В. Здесь ${{p}_{1}}$ – первая гармоника давления $p$ (см. рис. 1).
Замечание 2. Полученный выше теоретически и на модельном эксперименте результат, заключающийся в том, что в нелинейном режиме при подаче постоянного и переменного электрических полей к электродам электроакустического преобразователя происходит перекачка энергии от постоянного электрического поля непосредственно к энергии акустического поля, был получен применительно к пористой структуре в виде кругового капилляра. Прежде чем переходить к описанию натурных экспериментов, приведем условия, когда эти результаты можно экстраполировать на достаточно широкий класс пористых структур. В § 2.2 работы [9] показано подобие системы уравнений электроосмотического течения применительно к капиллярно-пористой среде со сколь угодно сложной геометрией внутренней поверхности системе уравнений для простейших случаев границ (плоскость, плоский слой, капилляр) при выполнении следующих условий:
1. толщина двойного слоя достаточно мала, а радиусы кривизны внутренней поверхности пор больше некоторой величины, значительно превышающей длину Дебая ${{\lambda }_{{\text{D}}}}$, обычно принимаемую за толщину ДЭС;
2. минимальный линейный размер пор существенно превышает толщину двойного слоя.
В экспериментах, описанных ниже, в качестве капиллярно-пористой структуры используется писчая бумага. Согласно [15, с. 67], средний радиус пор бумаги составляет от 20–30 нм для мелованной бумаги, 270 нм для газетной бумаги и до 450 нм для фильтровальной бумаги. Для обычной писчей бумаги средний радиус пор лежит внутри интервала (30 нм, 270 нм). Порядок величины длины Дебая составляет ${{\lambda }_{{\text{D}}}} \sim 10$ нм [11, с. 47]. Таким образом, для обычной писчей бумаги выполняются условия подобия, описанные в замечании 2.
НАТУРНЫЙ ЭКСПЕРИМЕНТ
Для проверки описанной теории был проведен ряд экспериментов. В качестве излучающей системы использовалась расположенная в воздушной среде пачка писчей бумаги постоянной толщины $\Delta $ (15 листов толщиной по ~ 0.1 мм каждый) формата А4, помещенная между двумя соразмерными бумаге перфорированными алюминиевыми пластинами-электродами. К электродам подводились постоянное ${{E}_{0}}$ и гармоническое $E$ электрические поля, направленные по нормали к электродам. При постоянной величине $\Delta $ далее вместо полей ${{E}_{0}}$ и $E$ оперируем соответствующими величинами приложенных к электродам разностей потенциалов ${{U}_{0}}$ и $U{{e}^{{ - i\omega t}}}$. Частота колебаний переменного электрического поля в опытах составляла $f = 3$ кГц. В волновой зоне описываемого преобразователя в точке на оси, проходящей нормально к его центру, был установлен микрофон, измерявший излучаемое давление, которое фиксировалось на анализаторе спектра в условных дБ11.
В процессе экспериментов был получен ряд зависимостей давления первой гармоники давления ${{p}_{1}}$ на входе микрофона от напряжения накачки ${{p}_{1}} = {{f}_{i}}\left( {{{U}_{0}},{{U}_{i}}} \right)$ при фиксированных значениях величины амплитуды гармонической составляющей электрического поля $U = {{U}_{i}}$, $i = \overline {1,8} $, равных соответственно ${{U}_{1}} = 30{\text{ В}}$; ${{U}_{2}} = 60{\text{ В}}$; ${{U}_{3}} = 105{\text{ В}}$; ${{U}_{4}} = 150{\text{ В}}$; ${{U}_{5}} = 210{\text{ В}}$; ${{U}_{6}} = 270{\text{ В}}$; ${{U}_{7}} = 300{\text{ В}}$; ${{U}_{8}} = 412.5{\text{ В}}$. Кривые зависимостей ${{p}_{1}} = {{f}_{i}}\left( {{{U}_{0}},{{U}_{i}}} \right)$ представлены на рис. 4 под соответствующими номерами. На приведенных графиках значения уровня первой гармоники давления ${{p}_{1}}$ в дБ являются относительными, показывающими только соотношение его амплитуд в процессе эксперимента при различных значениях амплитуд $U$ и ${{U}_{0}}$. Напряжение накачки ${{U}_{0}}$ при фиксированной величине $U = {{U}_{i}}$, $i = \overline {1,8} $ варьировалось на дискретном множестве точек от 20 до 3000 В с переменным шагом: 30 В на интервале ${{U}_{0}} \in [20,500]$ В и с шагом 100 В на интервале ${{U}_{0}} \in (500,3000]$ В.
Рис. 4.
Амплитуда давления первой гармоники ${{p}_{1}}$ в некоторой фиксированной точке волновой зоны излучателя в зависимости от изменения напряжения накачки ${{U}_{0}}$ при дискретных постоянных значениях $U$ (кривые 1–8; маркеры на кривых 1 и 7 служат для идентификации кривых).
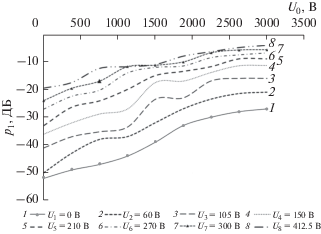
Из рис. 4 следует, что кривые ${{p}_{1}} = {{f}_{i}}({{U}_{0}},{{U}_{i}} = $ $ = {\text{const}})$ имеют сходный характер поведения в зависимости от напряжения накачки ${{U}_{0}}$ (т.е. от величины осмотической скорости ${{{\mathbf{v}}}_{0}}$, пропорциональной величине ${{U}_{0}}$): вначале все кривые достаточно монотонно возрастают с ростом величины ${{U}_{0}}$. В интервале значений ${{U}_{0}} \in \left[ {2600,3000} \right]{\text{ В}}$ наступает режим насыщения.
Фаза нарастания давления ${{p}_{1}}$ с ростом накачки ${{U}_{0}}$ прогнозировалась выше в теоретической части работы. Фаза насыщения давления ${{p}_{1}}$ с ростом напряжения накачки требует дополнительного пояснения. Участок насыщения кривых ${{p}_{1}} = {{f}_{i}}\left( {{{U}_{0}},{{U}_{i}} = {\text{const}}} \right)$ можно объяснить тремя факторами. Во-первых, суммарная энергия при входе в нелинейный режим излучения начинает перераспределяться от первой гармоники акустических колебаний к появляющимся кратным гармоникам. Это отчетливо проявилось и при проведении модельного эксперимента в вычислительном пакете, что выразилось во все большем отклонении формы акустического давления $p$ от синусоидальной при росте напряжения накачки ${{U}_{0}}$. Во-вторых, как будет показано в следующей работе авторов, при некоторых значениях ${{U}_{0}}$, зависящих от размера пор, ламинарный режим течения жидкости (газа) в порах преобразователя переходит в турбулентный режим течения, который сопровождается появлением паразитных широкополосных пульсационных шумов, на что также идут затраты энергии. В-третьих, как показано в работе [16], с ростом ${{U}_{0}}$ возрастают диссипативные потери в теле преобразователя. Этим и объясняется поведение представленных на рисунке кривых.
Из результатов эксперимента, представленных на рис. 4, следует, что величины давления без накачки ${{p}_{1}} = {{f}_{i}}\left( {{{U}_{0}},{{U}_{i}}} \right)$ при ${{U}_{0}} = 0$ (т.е. соответствующие значения давления ${{p}_{1}}$ на оси ${{U}_{0}} = 0$ для $i = \overline {1,8} $) при фиксированных значениях ${{U}_{i}}$ по мере увеличения накачки ${{U}_{0}}$ возрастают по-разному. Рост составляет от 15.4 дБ при ${{U}_{i}} = 412.5$ В (в 5.9 раза) до 29 дБ при ${{U}_{i}} = 60$ В (в 28.2 раза). Эти результаты с учетом замечания 2 подтверждают теоретические прогнозы данной работы.
Замечание 3. Сравнение результатов модельного (рис. 2) и натурного (рис. 4) экспериментов в совпадающем интервале напряжения накачки ${{U}_{0}} \in [0,150]$ В показывает, что при изменении напряжения накачки в этом интервале амплитуда давления растет на $ \sim 10.4$ дБ для модельного эксперимента и на 1‑3 дБ для натурного эксперимента. Объяснить это можно следующим образом. При проведении модельного эксперимента задавалось возможное верхнее предельное значение электрокинетического потенциала $\widetilde \zeta = 0.1$ В (интервал принимаемых значений на практике составляет $\widetilde \zeta \in \left[ {0.001,0.1} \right]$ В [15, с. 320]). Как видно из выражения (25), снижение величины дзета-потенциала в 2 раза до $\widetilde \zeta = 0.05$ В по сравнению с принятым в модельном эксперименте влечет к уменьшению скалярного потенциала $\Phi $ и связанного с ним линейно давления $p$ на ~ 6 дБ. Реально в натурном эксперименте дзета-потенциал вероятно был еще меньше, однако в настоящей работе он специально не измерялся.
Замечание 4. Получение идентичных результатов качественной зависимости величины первой гармоники давления ${{p}_{1}}$, получаемого в преобразователе, от величины напряжения накачки ${{U}_{0}}$ при разных частотах переменного напряжения (соответственно 1000 и 3000 Гц для модельного и натурного экспериментов) лишь подчеркивает общий характер предложенной теоретической модели процесса.
ЗАКЛЮЧЕНИЕ
В работе предложены в линейном и нелинейном приближении (ламинарный режим движения жидкости) необходимые уравнения и краевые условия для описания акустических полей, вызываемых электрокинетическими явлениями: наличием двойного электрического слоя и приложенного электрического поля, являющегося суммой постоянного поля и электрического поля, несущего акустическую информацию. Уравнения рассматриваются применительно к цилиндрическому капилляру.
В линейном режиме электроосмотических явлений наличие стационарного электроосмоса не оказывает влияния на протекание электроосмоса, вызванного переменным электрическим полем. В нелинейном ламинарном режиме происходит перекачка энергии постоянного электрического поля в энергию акустического поля. Результаты модельного эксперимента на капилляре качественно подтверждают верность проведенных теоретических исследований. Различие степени накачки в модельном и натурном экспериментах можно объяснить меньшим значением дзета-потенциала в натурном эксперименте.
Результаты натурного эксперимента на такой нетривиальной пористой структуре, как бумага, также подтверждают верность развитой в работе для кругового капилляра теории в части ее основного прогноза – возникновения процесса перекачки энергии постоянного электрического поля в акустическую энергию и демонстрируют правомерность ее экстраполяции на сложные пористые структуры. В натурном эксперименте усиление первой гармоники давления с помощью накачки составляло для различных значений переменного давления от 5.9 до 28 раз. В модельном эксперименте, в отличие от натурного эксперимента не происходит режима насыщения даже при изменении напряжения накачки до величины 16 000 В. Причины этого будут вскрыты в следующей публикации авторов.
Полученные результаты могут быть использованы при проектировании и оптимизации преобразователей нового типа.
Авторы благодарны С.П. Дмитриеву и С.Г. Телятнику за содействие в проведении экспериментов.
Работа выполнена в ИАП РАН в рамках Государственного задания 075-00780-20-00 по теме № 0074-2019-0013 Министерства науки и высшего образования.
Список литературы
Shishov S.V., Andrianov S.A., Dmitriev S.P., Ruchkin D.V. Method of converting electric signals into acoustics oscillations and an electric gas-kinetic transducer. United States Patent # US 8,085,957,B2. Dec. 27, 2011.
Касимзаде М.С., Халилов Р.Ф., Балашов А.Н. Электрокинетические преобразователи информации. М.: Энергия, 1973. 136 с.
O’Brien R.W. Electro-acoustic effects in a dilute suspension of spherical particles // J. Fluid Mech. 1988. V. 190. P. 71–86.
Hunter R.J. Review. Recent developments in the electroacoustic characterization of colloidal suspensions and emulsions // Colloids and Surfaces A: Physicochemical and Engineering Aspects. 1998. V. 14. P. 37–65.
Мурцовкин В.А. Нелинейные течения вблизи поляризованных дисперсных частиц // Коллоидн. журн. 1996. Т. 58. № 3. С. 358–367.
Данилян А.В., Дорофеев Д.Л., Наскидашвили В.И., Пахомов Г.В., Зон Б.А. Магнитогидродинамический генератор псевдозвука // Акуст. журн. 2005. Т. 51. № 5. С. 694–696.
Гладилин А.В., Пирогов В.А., Голямина И.П., Кулаев Ю.В. Вибрационный преобразователь с магнитной левитацией // Акуст. журн. 2015. Т. 61. № 3. С. 409–415.
Курочкин В.Е., Сергеев В.А., Шарфарец Б.П., Гуляев Ю.В. Теоретическое обоснование нового метода электроакустического преобразования. Линейное приближение // Докл. Акад. наук. 2018. Т. 483. № 3. С. 265–268.
Духин С.С., Дерягин Б.В. Электрофорез. М.: Наука, 1976. 332 с.
Ньюмен Дж. Электрохимические системы. М.: Мир, 1977. 464 с.
Bruus H. Theoretical Microfluidics. Oxford University Press, 2008. 346 p.
Физическая энциклопедия. Т. 5. М.: БРЭ, 1998. 760 с.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 6. Гидродинамика. М.: Наука, 1988. 736 с.
Исакович М.А. Общая акустика. М.: Наука, 1973. 496 с.
Шахкельдян Б.Н., Загаринская Л.А. Полиграфические материалы. М.: “Книга”, 1988. 328 с.
Шарфарец Б.П. О диссипации энергии в электроосмотическом процессе // Научное приборостроение. 2019. Т. 29. № 3. С. 30–40.
Глинка Н.Л. Общая химия. Л.: Химия. 702 с.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал


