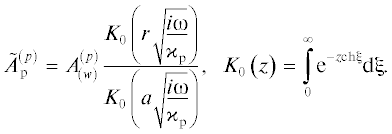Акустический журнал, 2020, T. 66, № 6, стр. 669-674

О динамике гармонических фильтрационных волн в гидроразрывной трещине, расположенной перпендикулярно к скважине

В. Ш. Шагапов^a, *, Е. П. Аносова^b, **, З. М. Нагаева^b, ***

^a Институт механики им. Р.Р. Малютова Уфимского федерального исследовательского центра Российской академии наук
450054 Уфа, Проспект Октября 71, Россия

^b Уфимский государственный нефтяной технический университет
450062 Уфа, ул. Космонавтов 1, Россия

^* E-mail: shagapov@rambler.ru
^** E-mail: ae0809@mail.ru
^*** E-mail: Nagaeva_Zilya@mail.ru

Поступила в редакцию 23.07.2019
После доработки 28.05.2020
Принята к публикации 07.07.2020

DOI: 10.31857/S0320791920060106

Полный текст (PDF)

Аннотация

Изучено распространение низкочастотных гармонических волн давления в трещине, образованной гидроразрывом пласта и расположенной перпендикулярно к скважине в пористой и проницаемой среде. Проанализировано влияние коллекторских характеристик пласта и трещины (например, их проницаемости, ширины трещины). Установлено, что при распространении волн от скважины по радиальным трещинам характерные расстояния проникания возмущений давления могут быть значительно выше по сравнению с глубиной проникания возмущений от открытой скважины в пласте, когда трещина отсутствует.

Ключевые слова: гидроразрыв пласта, трещина, гармонические волны давления, интегродифференциальное уравнение, аналитическое решение

ВВЕДЕНИЕ

Одним из основных способов интенсификации добычи нефти из низкопроницаемых пластов является гидравлический разрыв пласта (ГРП). Большое количество работ посвящено математическому моделированию процессов фильтрации в окрестности скважин с трещинами гидроразрыва. Впервые описание течения флюида в трещине и окружающей ее пористой среде было дано в работах M. Muskat [1]. И.А. Чарным [2], Г.И. Баренблатом [3], Р.Д. Каневской [4] и другими исследователями достаточно подробно были изучены вопросы фильтрации флюида в трещине и окружающем пласте в стационарном случае. В связи с тем, что растет доля месторождений, где проницаемость пластов низкая, а вязкость флюида высокая, время выхода распределения давления на стационарный режим становится соизмеримым со временем работы скважины. Модель нестационарной фильтрации билинейного потока была предложена H. Cinco-Ley, V.F. Samaniego [5]. Наиболее детальное изучение динамики волн давления в вертикальной гидроразрывной трещине с учетом притока флюида через стенки трещины рассмотрено в работах В.Ш. Шагапова и З.М. Нагаевой [6, 7]. Следует также отметить работы И.Л. Хабибуллина и А.А. Хисамова [8], в которых изучено распределение давления в трещине ГРП при постоянном перепаде давления в скважине и постоянном расходе. В работе [9] приведены результаты численного моделирования распределения давления в зоне действия горизонтальной скважины, пересеченной вертикальными трещинами гидроразрыва в зависимости от технических и природных показателей. В [10] исследуется распределение притоков в скважину с горизонтальным стволом после проведения поинтервального гидроразрыва пласта, рассматривается влияние на распределение давления проводимости трещины, геометрии трещины, угла перекоса между трещиной и скважиной. В работах [11, 12] представлены результаты исследования эволюции акустических волн в цилиндрических каналах в случае, когда вокруг канала имеются радиальные трещины, изучены количественные и качественные особенности динамики волн в зависимости от состояния неоднородной пористой среды.

Представляется, что контроль качества гидроразрыва, расположение трещин в пласте можно в значительной степени осуществлять акустическим зондированием, гидропрослушиванием и гидродинамическим испытанием скважин (ГДИС).

В настоящей работе рассмотрено в радиальной постановке распространение гармонических волн давления в трещине, расположенной перпендикулярно к скважине, сопровождаемое фильтрационными потоками между трещиной и пористым пластом.

ОСНОВНЫЕ УРАВНЕНИЯ

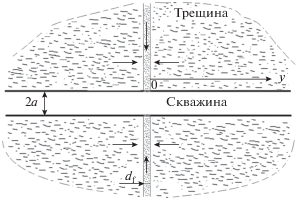
Пусть трещина ширины ${{d}_{{\text{f}}}},$ образованная гидроразрывом пласта, находится между плоскостями, перпендикулярными к цилиндрической скважине (рис. 1). Примем, что течение в трещине, инициированное функционированием скважины, радиально симметричное. Тогда уравнение неразрывности для флюида в трещине запишем в виде

(1.1)

${{\left. {\frac{{\partial \left( {{{m}_{{\text{f}}}}{{{\rho }}_{{\text{f}}}}} \right)}}{{\partial t}} + \frac{1}{r}\frac{{\partial \left( {r{{{\rho }}_{{\text{f}}}}{{{v}}_{{\text{f}}}}} \right)}}{{\partial r}} = - 2\frac{{\left( {{{{\rho }}_{{\text{p}}}}{{{v}}_{{\text{p}}}}} \right)}}{{{{d}_{{\text{f}}}}}}} \right|}_{{y = 0}}}\,\,\,\,(a < r),$

где ${{m}_{i}}$ и ${{{\rho }}_{i}}$ – пористость и плотность флюида (здесь и в дальнейшем нижние индексы ${\text{f}}$ и ${\text{p}}$ соответствуют значениям параметров в трещине и окружающей ее пористой среде), ${{{v}}_{i}}$ – скорость фильтрации жидкости, $a$ – радиус скважины. Отметим, что слагаемое в правой части (1.1) выражает приток флюида из пласта в трещину. Чтобы определить это слагаемое, в свою очередь, необходимо параллельно решить сопряженную фильтрационную задачу в пласте вне трещины. Для этого запишем уравнение неразрывности в пористой среде, как

(1.2)

$\frac{{\partial \left( {{{m}_{{\text{p}}}}{{{\rho }}_{{\text{p}}}}} \right)}}{{\partial t}} + \frac{{\partial \left( {{{{\rho }}_{{\text{p}}}}{{{v}}_{{\text{p}}}}} \right)}}{{\partial y}} = 0\,\,\,\,{\text{\;}}(0 < y < \infty ).$

Здесь ось $Oy$ отсчитывается от стенки трещины.

Рис. 1.

Схема трещины ГРП, расположенной перпендикулярно к скважине.

Для процесса фильтрации в трещине и в пласте примем закон Дарси

(1.3)

$\begin{gathered} {{{v}}_{{\text{f}}}} = - \frac{{{{k}_{{\text{f}}}}}}{{\mu }}\frac{{\partial {{P}_{{\text{f}}}}}}{{\partial r}}\left( {a < r < \infty } \right), \\ {{{v}}_{{\text{p}}}} = - \frac{{{{k}_{{\text{p}}}}}}{{\mu }}\frac{{\partial {{P}_{{\text{p}}}}}}{{\partial y}}\,\,\,\,\left( {a < r < \infty ,~\,\,0 < y < \infty } \right), \\ \end{gathered} $

где ${{k}_{i}}~\left( {i = {\text{f}},{\text{p}}} \right)$ – коэффициент проницаемости, ${\mu }$ – динамическая вязкость флюида. Сжимаемость жидкости будем учитывать в акустическом приближении

(1.4)

${{P}_{i}} - {{P}_{0}} = {{C}^{2}}\left( {{{{\rho }}_{i}} - {{{\rho }}_{0}}} \right)\,\,\,\,\left( {i = {\text{f}},{\text{p}}} \right),$

где $C$ – скорость звука для жидкости, нижний индекс 0 у давления и плотности соответствует их невозмущенным значениям. Флюид будем считать слабо сжимаемым $\left( {\left| {{{{\rho }}_{i}} - {{{\rho }}_{0}}} \right| \ll {{{\rho }}_{i}} \approx {{{\rho }}_{0}}} \right).$ Тогда уравнения (1.1) и (1.2) с учетом (1.3) и (1.4) можно привести к виду

(1.5)

${{\left. {\frac{{\partial {{P}_{{\text{f}}}}}}{{\partial t}} = \frac{{{{\varkappa }_{{\text{f}}}}}}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{P}_{{\text{f}}}}}}{{\partial r}}} \right)\, + \,2\frac{{{{m}_{{\text{p}}}}}}{{{{m}_{{\text{f}}}}}}\frac{{{{\varkappa }_{{\text{p}}}}}}{{{{d}_{{\text{f}}}}}}\left( {\frac{{\partial {{P}_{{\text{p}}}}}}{{\partial y}}} \right)} \right|}_{{y = 0}}}\,\,\left( {a\, < \,r\, < \,\infty } \right),$

(1.6)

$\frac{{\partial {{P}_{{\text{p}}}}}}{{\partial t}} = {{\varkappa }_{{\text{p}}}}\frac{{{{\partial }^{2}}{{P}_{{\text{p}}}}}}{{\partial {{y}^{2}}}}\,\,\,\,(a < r < \infty ,~\,\,0 < y < \infty ),$

где

${{\varkappa }_{i}} = \frac{{{{k}_{i}}{{{\rho }}_{0}}{{C}^{2}}}}{{{{m}_{i}}{\mu }}}\left( {i = {\text{f}},{\text{p}}} \right).$

Отметим, что ${{P}_{{\text{f}}}}$ является функцией от переменных $t$ и $r$, а ${{P}_{{\text{p}}}}$ – функция от переменных $t,$ $r$ и $y.$ Система уравнений (1.5) и (1.6) может быть сведена к одному интегро-дифференциальному уравнению для ${{P}_{{\text{f}}}}.$ Действительно, величина давления ${{P}_{{\text{p}}}}$ на поверхности стенки трещины $\left( {y = 0} \right)$ должна быть равна ${{P}_{{\text{f}}}}.$ Запишем это условие:

(1.7)

${{P}_{{\text{p}}}} = {{P}_{{\text{f}}}}\,\,\,\,(a < r < \infty ,\,\,~y = 0).$

Вдали от трещины будем считать, что в пористой среде давление однородное и равно ${{P}_{0}},$ т.е.

(1.8)

${{P}_{{\text{p}}}} = {{P}_{0}}\left( {a < r < \infty ,\,\,~y = \infty } \right).$

Согласно принципу Дюамеля [13] решение уравнения (1.6), удовлетворяющее начальному и граничному условиям

(1.9)

$\begin{gathered} {{P}_{{\text{p}}}} = {{P}_{0}}\left( {t \leqslant {{t}_{0}},\,\,0 < y < \infty } \right), \\ ~{{P}_{{\text{p}}}} = {{P}_{{\text{f}}}}\,\,\,\,(t > {{t}_{0}},~\,\,y = 0), \\ \end{gathered} $

может быть записано в виде

(1.10)

${{P}_{{\text{p}}}} - {{P}_{0}} = \int\limits_{{{t}_{0}}}^t {\frac{{\partial u\left( {y,t - {\tau }} \right)}}{{\partial t}}} \left( {{{P}_{{\text{f}}}}\left( {{\tau },r} \right) - {{P}_{0}}} \right)d\tau ,$

где

(1.11)

$\begin{gathered} u\left( {y,t - {\tau }} \right) = 1 - {\text{Ф}}\left( {{y \mathord{\left/ {\vphantom {y {\left( {2\sqrt {{{\varkappa }_{{\text{p}}}}\left( {t - {\tau }} \right)} } \right)}}} \right. \kern-0em} {\left( {2\sqrt {{{\varkappa }_{{\text{p}}}}\left( {t - {\tau }} \right)} } \right)}}} \right) = \\ = \frac{2}{{\sqrt {\pi } }}\int\limits_{{y \mathord{\left/ {\vphantom {y {\left( {2\sqrt {{{\varkappa }_{{\text{p}}}}\left( {t - {\tau }} \right)} } \right)}}} \right. \kern-0em} {\left( {2\sqrt {{{\varkappa }_{{\text{p}}}}\left( {t - {\tau }} \right)} } \right)}}}^{ + \infty } {{{e}^{{ - {{{\alpha }}^{2}}}}}d{\alpha }} {\text{.}} \\ \end{gathered} $

После несложных преобразований с учетом условий (1.9) решение (1.10) можно привести к виду

(1.12)

${{P}_{{\text{p}}}} - {{P}_{0}} = \int\limits_{{{t}_{0}}}^t {\frac{{\partial \left( {{{P}_{{\text{f}}}}\left( {{\tau },r} \right) - {{P}_{0}}} \right)}}{{\partial {\tau }}}} u\left( {y,t - {\tau }} \right)d{\tau }{\text{.}}$

Подставляя (1.12) в уравнение (1.5) и полагая ${{t}_{0}} = - \infty ,$ получим следующее линейное интегро-дифференциальное уравнение для ${{P}_{{\text{f}}}}{\text{:}}$

(1.13)

$\begin{gathered} \frac{{\partial {{P}_{{\text{f}}}}}}{{\partial t}} = \frac{{{{\varkappa }_{{\text{f}}}}}}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{P}_{{\text{f}}}}}}{{\partial r}}} \right) - 2\frac{{{{m}_{{\text{p}}}}}}{{{{m}_{{\text{f}}}}}}\frac{{{{\varkappa }_{{\text{p}}}}}}{{{{d}_{{\text{f}}}}}} \times \\ \times \,\,\int\limits_{ - \infty }^t {\frac{{\partial \left( {{{P}_{{\text{f}}}}\left( {{\tau },r} \right) - {{P}_{0}}} \right)}}{{\partial {\tau }}}} \frac{{d{\tau }}}{{\sqrt {{\pi }{{\varkappa }_{{\text{p}}}}\left( {t - {\tau }} \right)} }}. \\ \end{gathered} $

Для нахождения решений уравнения могут быть использованы методы конечных элементов (МКЭ) или конечных разностей, широко применяемые при решении подобных задач (см., например, [14, 15]). В рамках данной работы нас интересуют решения типа гармонических волн.

2. РАСПРОСТРАНЕНИЕ ГАРМОНИЧЕСКИХ ВОЛН

Уравнение (1.13) является линейно-однородным для функции

(2.1)

$\Delta {{P}_{{\text{f}}}} = {{P}_{{\text{f}}}} - {{P}_{0}}.$

Пусть возмущение давления в скважине меняется по гармоническому закону:

(2.2)

${{P}_{{\left( w \right)}}} - {{P}_{0}} = A_{{\left( w \right)}}^{{\left( p \right)}}\cos \left( {{\omega }t} \right) = {\text{Re}}\left( {A_{{\left( w \right)}}^{{\left( p \right)}}{{e}^{{ - i{\omega }t}}}} \right).$

Полагаем, что источник гармонических волн функционирует достаточно долгое время, так что в трещине и в пористой среде вблизи нее устанавливаются периодические колебания (начальные условия в трещине и в пласте “забываются”). Тогда на основе полученных выше теоретических построений можно искать решение, описывающее распространение давления в трещине и удовлетворяющее граничному условию (2.2) при $r = a.$

Будем искать решение в виде

(2.3)

$\Delta {{P}_{{\text{f}}}} = {\text{Re}}\left( {A_{{\text{f}}}^{{\left( p \right)}}\left( r \right){{e}^{{ - i{\omega }t}}}} \right).$

Подставляя (2.3) в (1.13), получим

(2.4)

$\begin{gathered} \frac{1}{r}\frac{d}{{dr}}\left( {r\frac{d}{{dr}}A_{{\text{f}}}^{{\left( p \right)}}} \right) = {{z}^{2}}A_{{\text{f}}}^{{\left( p \right)}}~, \\ ~{{z}^{2}} = - i\left( {\frac{{\omega }}{{{{\varkappa }_{{\text{f}}}}}} + \frac{2}{{{{d}_{{\text{f}}}}}}\frac{{{{m}_{{\text{p}}}}}}{{{{m}_{{\text{f}}}}}}\frac{{\sqrt {{{\varkappa }_{{\text{p}}}}} }}{{{{\varkappa }_{{\text{f}}}}}}\sqrt {i{\omega }} } \right). \\ \end{gathered} $

Здесь параметр ${{z}^{2}}$ выражает упругоемкость системы “трещина–пласт”.

Из анализа зависимости этого параметра от круговой частоты следует, что упругоемкость флюида, находящегося в трещине, не существенна $\left( {\frac{{\omega }}{{{{\varkappa }_{{\text{f}}}}}} \ll \left| {{{z}^{2}}} \right|} \right)$ в плане распространения гармонических колебаний для частот, удовлетворяющих условию

(2.5)

${\omega } \ll {\omega }*,\,\,\,\,{\omega }* = 4\frac{{m_{{\text{p}}}^{2}}}{{m_{{\text{f}}}^{2}}}\frac{{{{\varkappa }_{{\text{p}}}}}}{{d_{{\text{f}}}^{2}}}.$

В большинстве случаев, представляющих практический интерес, это условие всегда выполняется, и поэтому в дальнейшем для ${{z}^{2}}$ будем использовать выражение

(2.6)

${{z}^{2}} = \frac{2}{{{{d}_{{\text{f}}}}}}\frac{{{{m}_{{\text{p}}}}}}{{{{m}_{{\text{f}}}}}}\frac{{\sqrt {{{\varkappa }_{{\text{p}}}}} }}{{{{\varkappa }_{{\text{f}}}}}}\sqrt { - i{\omega }} .$

Из (2.6) следует

(2.7)

$z = \sqrt A {{{\omega }}^{{\frac{1}{4}}}}{{e}^{{\frac{{3{\pi }}}{8}i}}},\,\,\,\,A = \frac{2}{{{{d}_{{\text{f}}}}}}\frac{{{{m}_{{\text{p}}}}}}{{{{m}_{{\text{f}}}}}}\frac{{\sqrt {{{\varkappa }_{{\text{p}}}}} }}{{{{\varkappa }_{{\text{f}}}}}}.$

Давление на бесконечности равно невозмущенному значению, т.е.

(2.8)

${{P}_{{\text{f}}}} = {{P}_{0}}\,\,\,\,{\text{или}}\,\,\,\,~\Delta {{P}_{{\text{f}}}} = 0~~~\left( {r = \infty } \right).$

Тогда решение уравнения (2.4), которое в соответствии с (2.2) и (2.8) должно удовлетворить следующим граничным условиям

(2.9)

$A_{{\text{f}}}^{{\left( p \right)}} = A_{{\left( w \right)}}^{{\left( p \right)}}\,\,\,\,\left( {r = a} \right)\,\,\,\,{\text{и}}\,\,\,\,A_{{\text{f}}}^{{\left( p \right)}} = 0\,\,\,\,\left( {r = \infty } \right),$

будет иметь вид [16]

(2.10)

$\begin{gathered} A_{{\text{f}}}^{{\left( p \right)}} = A_{{\left( w \right)}}^{{\left( p \right)}}\frac{{{{K}_{0}}\left( {zr} \right)}}{{{{K}_{0}}\left( {za} \right)}}~, \\ {{K}_{0}}\left( {zr} \right) = \int\limits_0^\infty {\exp \left( { - zr{\text{ch}}\left( \xi \right)} \right)d\xi } . \\ \end{gathered} $

Здесь ${{K}_{0}}\left( {zr} \right)$ – функция Макдональда нулевого порядка.

С учетом (2.10) решение (2.3) можно записать как

(2.11)

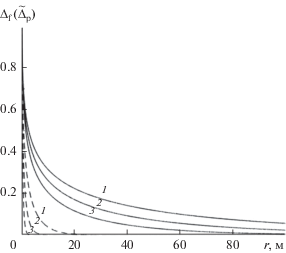
$\Delta {{P}_{{\text{f}}}} = A_{{\text{f}}}^{{'\left( p \right)}}\cos \left( {{\omega }t - \Delta {{{\varphi }}_{{\text{f}}}}} \right),$

где

$A_{{\text{f}}}^{{'\left( p \right)}} = A_{{\left( w \right)}}^{{\left( p \right)}}\left| {\frac{{{{K}_{0}}\left( {zr} \right)}}{{{{K}_{0}}\left( {za} \right)}}} \right|,\,\,\,\,\Delta {\varphi } = {\text{arg}}\left( {\frac{{{{K}_{0}}\left( {zr} \right)}}{{{{K}_{0}}\left( {za} \right)}}} \right).$

На рис. 2 сплошными линиями представлено распределение безразмерной амплитуды ${{\Delta }_{{\text{f}}}} = \frac{{A_{{\text{f}}}^{{'\left( p \right)}}}}{{A_{{\left( w \right)}}^{{\left( p \right)}}}}$ по радиальной координате $r.$ Для параметров трещины, пласта и радиуса скважины здесь и в дальнейшем (если специально не оговорено) приняты следующие величины: ${{d}_{{\text{f}}}} = {{10}^{{ - 2}}}$ м, ${{k}_{{\text{f}}}} = {{10}^{{ - 10}}}\,\,{{{\text{м}}}^{2}},$ $~{{k}_{{\text{p}}}} = {{10}^{{ - 15}}}\,\,{{{\text{м}}}^{2}},~$ ${{m}_{{\text{f}}}} = 3 \times {{10}^{{ - 1}}},$ ${{m}_{{\text{p}}}} = {{10}^{{ - 1}}},$ $a = {{10}^{{ - 1}}}~\,\,{\text{м}}.$ В качестве флюида принята нефть: ${{{\rho }}_{0}} = 860\,\,\frac{{{\text{кг}}}}{{{{{\text{м}}}^{{\text{3}}}}}},$ ${\mu } = {{10}^{{ - 2}}}\,\,~{\text{Па}}\,\,{\text{с}}.$ Линии 1, 2 и 3 соответствуют значениям круговой частоты ${\omega } = {{10}^{{ - 4}}},$ ${{10}^{{ - 3}}}\,{\text{и}}\,~{{10}^{{ - 2}}}\,{{{\text{с}}}^{{ - 1}}}.$

Рис. 2.

Распределение безразмерной амплитуды колебаний давления ${{\Delta }_{{\text{f}}}}$ по трещине (сплошные линии) и ${{\Delta }_{{\text{p}}}}$ в пласте при отсутствии трещины (пунктирные линии) при различных значениях круговой частоты: 1 – ${\omega } = {{10}^{{ - 4}}},$ 2 – ${\omega } = {{10}^{{ - 3}}},$ 3 – ${\omega } = {{10}^{{ - 2}}}\,\,{{{\text{с}}}^{{ - 1}}}.$

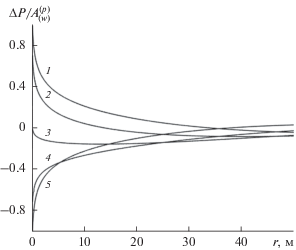
На рис. 3 показана эволюция безразмерных полей давления $\frac{{\Delta {{P}_{{\text{f}}}}}}{{A_{{\left( w \right)}}^{{\left( p \right)}}}}$ в трещине в соответствии с решением (2.11) при ${\omega } = {{10}^{{ - 3}}}\,\,{{{\text{с}}}^{{ - 1}}}.$ Линии 1, 2, 3, 4 и 5 соответствуют фазам колебаний давления в скважине ${\omega }t = 0,\frac{{\pi }}{4},\frac{{\pi }}{{~2}},\frac{{3{\pi }}}{4}~\,\,{\text{и}}\,\,{\pi }{\text{.}}$

Рис. 3.

Эволюция безразмерных полей возмущений давления в трещине $\frac{{\Delta {{P}_{{\text{f}}}}}}{{A_{{\left( w \right)}}^{{\left( p \right)}}}}$ в течение полупериода колебаний давления в скважине: 1 – ${\omega }t = 0,$ 2 – ${\omega }t = \frac{{\pi }}{4},$ 3 – ${\omega }t = \frac{{\pi }}{{~2}},$ 4 – ${\omega }t = \frac{{3{\pi }}}{4},$ 5 – ${\omega }t = {\pi }.$

На основе системы (1.5), (1.6) с учетом решения (2.11) можно получить решение, описывающее поле давления в пористой среде вблизи трещины:

(2.12)

${{P}_{{\text{p}}}} = {{P}_{0}} + A_{{\left( w \right)}}^{{\left( p \right)}}\left| {\frac{{{{K}_{0}}\left( {zr} \right)}}{{{{K}_{0}}\left( {za} \right)}}} \right|{{e}^{{ - {\delta }y}}}\cos \left( {{\omega }t - \Delta {{{\varphi }}_{{\text{f}}}} - ky} \right),$

где

$k = \delta = \sqrt {\frac{{\omega }}{{2{{\varkappa }_{{\text{p}}}}}}} .$

Следовательно, в каждой точке пористой среды $(r > a,~\,\,y > 0)$ давление флюида будет совершать гармонические колебания с амплитудой

(2.13)

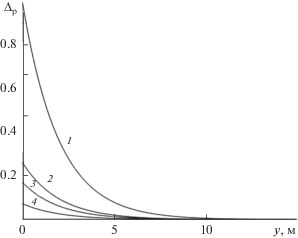
$A_{{\text{p}}}^{{'\left( p \right)}} = A_{{\left( w \right)}}^{{\left( p \right)}}\left| {\frac{{{{K}_{0}}\left( {zr} \right)}}{{{{K}_{0}}\left( {za} \right)}}} \right|{{e}^{{ - {\delta }y}}}$

и со сдвигом по фазе от колебаний давления в скважине

(2.14)

$\Delta {{{\varphi }}_{{\text{p}}}} = \Delta {{{\varphi }}_{{\text{f}}}} + ky.$

На рис. 4 представлено распределение безразмерной амплитуды давления ${{\Delta }_{{\text{p}}}} = \frac{{A_{{{\text{p}}~~}}^{{'\left( p \right)}}}}{{A_{{\left( w \right)}}^{{\left( p \right)}}}}$ по координате $y$ при ${\omega } = {{10}^{{ - 3}}}\,\,{{{\text{c}}}^{{ - 1}}}.$ Линии 1, 2, 3 и 4 соответствуют значениям радиальной координаты $r = 0.1,\,\,10,\,\,20,\,\,50~\,\,{\text{м}},$ где $r$ – расстояние от скважины.

Рис. 4.

Распределение безразмерной амплитуды колебаний давления ${{\Delta }_{{\text{p}}}}$ в пласте в зависимости от расстояния до трещины $y$ при различных значениях $r$ – расстояния от скважины: 1 – $r = 0.1,$ 2 – $r = 10,$ 3 – $r = 20,$ 4 – $r = 50~\,\,{\text{м}}.$

Для сравнительного анализа рассмотрим также расходящиеся от скважины гармонические волны в однородной пористой и проницаемой среде (трещины отсутствуют). В этом случае основное уравнение фильтрации для осесимметричного упругого режима фильтрационного течения запишется, как

(2.15)

$\frac{{\partial {{P}_{{\text{p}}}}}}{{\partial t}} = \frac{{{{\varkappa }_{{\text{p}}}}}}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{P}_{{\text{p}}}}}}{{\partial r}}} \right)\,\,\,\,\left( {a < r < \infty } \right).$

Пусть давление в скважине меняется по закону, аналогичному (2.2), а на бесконечности удовлетворяет условию (2.8). Решение ищем в виде

(2.16)

$\Delta \widetilde {{{P}_{{\text{p}}}}} = \widetilde {{{P}_{{\text{p}}}}} - {{P}_{0}} = {\text{Re}}\left( {\tilde {A}_{{{\text{\;p}}}}^{{\left( p \right)}}\left( r \right){{{\text{e}}}^{{ - i{\omega }t}}}} \right)\,\,\,\,\left( {a < r < \infty } \right).$

Подставляя (2.16) в (2.15), получим уравнение для $\tilde {A}_{{\text{p}}}^{{\left( p \right)}}$в виде

(2.17)

$ - \frac{{i{\omega }}}{{{{\varkappa }_{{\text{p}}}}}}\tilde {A}_{{{\text{\;p}}}}^{{\left( p \right)}} = \frac{1}{r}\frac{d}{{dr}}\left( {r\frac{{d\tilde {A}_{{{\text{\;p}}}}^{{\left( p \right)}}}}{{dr}}} \right).$

Его решение, удовлетворяющее выше отмеченным граничным условиям, имеет вид

(2.18)

Подставляя (2.18) в (2.16), получим решение, описывающее распространение давления вокруг скважины, в виде

(2.19)

$\Delta \widetilde {{{P}_{{\text{p}}}}} = \tilde {A}_{{\text{p}}}^{{{\text{'}}\left( p \right)}}\cos \left( {{\omega }t - \Delta {{{{\tilde {\varphi }}}}_{{\text{p}}}}} \right),$

где

$\tilde {A}_{{\text{p}}}^{{{\text{'}}\left( p \right)}} = A_{{\left( w \right)}}^{{\left( p \right)}}\left| {\frac{{{{K}_{0}}\left( {r\sqrt {\frac{{i{\omega }}}{{{{\varkappa }_{{\text{p}}}}}}} } \right)}}{{{{K}_{0}}\left( {a\sqrt {\frac{{i{\omega }}}{{{{\varkappa }_{{\text{p}}}}}}} } \right)}}} \right|,\,\,\,\,\Delta {{{\tilde {\varphi }}}_{{\text{p}}}} = {\text{arg}}\left( {\frac{{{{K}_{0}}\left( {r\sqrt {\frac{{i{\omega }}}{{{{\varkappa }_{{\text{p}}}}}}} } \right)}}{{{{K}_{0}}\left( {a\sqrt {\frac{{i{\omega }}}{{{{\varkappa }_{{\text{p}}}}}}} } \right)}}} \right).$

На рис. 2 пунктирными линиями представлены распределения безразмерной амплитуды ${{\tilde {\Delta }}_{{\text{p}}}} = \frac{{\tilde {A}_{{\text{p}}}^{{'\left( p \right)}}}}{{A_{{\left( w \right)}}^{{\left( p \right)}}}}$ колебаний давления в пористой среде. Для параметров пласта и круговой частоты колебаний давления в скважине использованы выше принятые значения. Линии 1, 2 и 3 соответствуют значениям круговой частоты ${\omega } = {{10}^{{ - 4}}},\,\,~{{10}^{{ - 3}}}\,\,~{\text{и}}\,\,~{{10}^{{ - 2}}}\,\,{{{\text{с}}}^{{ - 1}}}.$

Из сравнения графиков, представленных на рис. 2, следует, что характерное расстояние затухания гармонических возмущений давления, распространяющихся вдоль трещины, может значительно превышать аналогичное расстояние от скважины при отсутствии радиальной трещины. В частности, из анализа графиков затухания амплитуд колебаний давления, приведённых на рис. 2, видно, что если амплитуда волны с круговой частотой ${\omega } = {{10}^{{ - 4}}}\,\,{{{\text{с}}}^{{ - 1}}}$ в пласте при отсутствии трещины составляет 10% от амплитуды волны на скважине на расстоянии около 5 м, то в случае распространения волны по трещине амплитуда волны составляет 10% от амплитуды волны на скважине на расстоянии около 80 м.

ЗАКЛЮЧЕНИЕ

На основе анализа решений типа гармонических волн в трещинах, находящихся в низкопроницаемых пластах и расположенных перпендикулярно скважине, показано, что трещины для низкочастотных колебаний давления в скважине являются своеобразным волновым каналом. Таким образом, характерное расстояние затухания волн в трещинах, а также в пласте вблизи нее может быть значительно выше, чем в однородной пористой среде при отсутствии трещины.

Список литературы

Muskat M. The Flow of Homogeneous Fluids Through Porous Media. New–York City: McGraw–Hill Book Co. Inc., 1937. 763 p.
Чарный И.А. Подземная гидрогазодинамика. М.: Гостоптехиздат, 1948. 196 с.
Баренблат Г.И., Ентов В.М., Рыжик М.В. Движение жидкостей и газов в природных пластах. М.: Недра, 1984. 211 с.
Каневская Р.Д. Математическое моделирование разработки месторождений нефти и газа с применением гидравлического разрыва пласта. М.: Недра, 1999. 212 с.
Cinco-Ley H., Samaniego V.F. Transient pressure analysis for fractured wells // J. Petroleum Technology. 1981. V. 33. № 9. C. 1749–1766.
Шагапов В.Ш., Нагаева З.М. К теории фильтрационных волн давления в трещине, находящейся в пористой проницаемой среде // ПМТФ.2017.Т. 58. № 5(345). С. 121–130.
Шагапов В.Ш., Нагаева З.М. Гармонические волны давления в трещинах, находящихся в нефтяных и газовых пластах // ИФЖ. 2017. Т. 90. № 5. С. 1109–1117.
Хабибуллин И.Л., Хисамов А.А. К теории билинейного режима фильтрации в пластах с трещинами гидроразрыва // Вестник БашГУ. 2018. Т.23. № 4. С. 958–963.
Васильев В.А., Верисокин А.Е. Гидроразрыв пласта в горизонтальных скважинах // Вестник ПНИПУ. Геология. Нефтегазовое и горное дело. 2013. № 6. С. 101–110.
Feng Q., Xia T., Wang S., Singh H. Pressure transient behavior of horizontal well with time-dependent fracture conductivity in tight oil reservoirs // Geofluids. 2017. V. 2017. Article ID 5279792. 19 p.
Булатова З.А., Гумерова Г.А., Шагапов В.Ш. Об эволюции акустических волн в каналах, имеющих участки с проницаемыми стенками и окруженных неоднородной пористой средой // Акуст. журн. 2002. Т. 48. № 3. С. 300–308.
Шагапов В.Ш., Булатова З.А. К теории акустического зондирования прискважинных областей пористых и проницаемых горных пород // Геофизический журн. 2002. Т. 24. № 2. С. 79–91.
Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1977. 736 с.
Глушков Е.В., Глушкова Н.В., Евдокимов А.А. Гибридная численно-аналитическая схема для расчета дифракции упругих волн в локально неоднородных волноводах // Акуст. журн. 2018. Т. 64. № 1. С. 3–12.
Рыбянец А.Н., Наседкин А.В., Щербинин С.А., Петрова Е.И., Швецова Н.А., Швецов И.А., Луговая М.А. Конечно-элементное моделирование низкочастотных биморфных преобразователей для диагностики и активации нефтяных скважин // Акуст. журн. 2017. Т. 63. № 6. С. 685–691.
Зайцев В.Ф., Полянин А.Д. Справочник по обыкновенным дифференциальным уравнениям. М.: Физматлит, 2001. 576 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал