1. На главную
  2. Электронные версии
  3. Журнал аналитической химии
  4. T. 78, № 6, 2023

Журнал аналитической химии, 2023, T. 78, № 6, стр. 528-537

Особенности линейной корреляции газохроматографических индексов удерживания соединений различных таксономических групп

И. Г. Зенкевич *

Санкт-Петербургский государственный университет, Институт химии
198504 Санкт-Петербург, Университетский просп., 26, Россия

* E-mail: izenkevich@yandex.ru

Поступила в редакцию 02.09.2022
После доработки 10.09.2022
Принята к публикации 10.09.2022

Полный текст (PDF)

Аннотация

Несмотря на постоянное совершенствование сложных компьютерных алгоритмов вычисления газохроматографических индексов удерживания, сохраняют свое значение простейшие способы их оценки на основании линейных корреляционных соотношений между индексами структурных аналогов разных таксономических групп, RI1 ≈ aRI2 + b. Показано, что условием корректности подобных корреляций в простейших группах (замещенные метаны) являются симбатные вариации первых конечных разностей индексов удерживания, $\Delta _{{{\text{RI}}}}^{1}$ = RIn+ 1 – RIn (эквивалентны первым производным индексов удерживания по варьируемому в группе структурному параметру). Монотонные вариации $\Delta _{{{\text{RI}}}}^{1}$ в одной из групп при наличии экстремумов в другой – однозначный признак отсутствия линейной корреляции индексов удерживания. Если в одной из групп значения $\Delta _{{{\text{RI}}}}^{1}$ возрастают, а в другой – убывают, то порядок ранжирования соединений в какой-либо одной их них должен быть заменен обратным. Показано, что простейшее соотношение RI1 ≈ aRI2 + b также применимо в более сложных таксономических группах (замещенные этаны, бензолы и нафталины) и позволяет не только оценивать значения RI еще не охарактеризованных в настоящее время соединений, но и уточнять известные справочные данные.

Ключевые слова: газохроматографические индексы удерживания, таксономические группы структурных аналогов, линейная корреляция, контроль корректности индексов, оценка неизвестных значений.

Возможности хромато-масс-спектрометрической идентификации следов органических соединений в сложных смесях могут быть эффективно реализованы только при совместном использовании масс-спектров с ионизацией электронами и газохроматографических индексов удерживания (RI). Однако если судить по содержанию современных баз данных (в том числе [1]), число соединений, охарактеризованных масс-спектрами, существенно уступает числу соединений, для которых известны значения RI на стандартных неподвижных фазах. Например, база данных NIST [1] (версия 2020 г.) содержит 350643 масс-спектров с ионизацией электронами 306869 соединений, но значения RI имеются только для 139 498 соединений. Из них лишь для части (111768) объектов одновременно известны как масс-спектры, так и индексы удерживания.

Лимитирующей стадией формирования баз справочных значений RI является доступность объектов. Наибольших затрат времени требует, при необходимости, их целенаправленный синтез. По этой причине быстрое увеличение объема массивов справочных данных маловероятно, что придает особую актуальность совершенствованию способов расчета индексов удерживания на основании структур молекул. Известно огромное число методов расчета RI, рассмотрение которых является самостоятельной задачей. В последнее время “популярны” алгоритмы, предполагающие использование различных топологических дескрипторов (QSRR) [2–4], но все большее распространение приобретают самообучающиеся алгоритмы на принципах нейронных сетей [5–8] и более сложные (например, Gene Expression Programming [9]). Вместе с тем нельзя утверждать, что исчерпаны возможности известных и широко применяемых аддитивных схем [10, 11].

Преимущества современных компьютерных методов расчета RI [5–9] проявляются при обработке максимально больших выборок данных, что не всегда рационально. Дело в том, что по мере накопления новых данных известные справочные значения RI могут быть уточнены или даже исправлены (в том числе это относится к базе [1]), что ведет к необходимости обработки массива информации для всех соединений заново. Кроме этого, в подобных алгоритмах точность оценок индексов удерживания фактически усреднена для всех рассматриваемых объектов. Это затрудняет выявление менее надежных данных, что часто приходится проводить вручную. Кроме того, в практике хроматографического анализа актуальна необходимость решения более “локальных” задач оценки RI единичных соединений более простыми способами. При этом характеристики точности таких оценок должны относиться к конкретным результатам, а не представлять собой средние значения для метода расчетов в целом. В таких случаях эффективны алгоритмы, применимые именно для малых таксономических групп, в том числе:

1. На основании корреляции RI с положением характеризуемого соединения в соответствующей группе гомологов, конгенеров или структурных аналогов, RI = f(nx);

2. В результате корреляции значений RI соединений выбранной таксономической группы с их физико-химическими характеристиками, RI = = f(Ax);

3. В результате корреляции RI соединений некоторой таксономической группы (1) с известными значениями RI соединений другой группы (2) (структурных аналогов), RI1 = f(RI2).

Алгоритмы первой группы представляют собой расширенный вариант аддитивных схем, так что их возможности сопоставимы двух с другом. Наибольшую точность оценки газохроматографических индексов удерживания обеспечивают методы второй группы, особенно предполагающие использование нормальных температур кипения гомологов или конгенеров [12, 13]. Причина этого в том, что число соединений, для которых с высокой точностью определены значения Ткип, существенно превышает число соединений, охарактеризованных значениями RI. Однако некоторая сложность таких корреляций состоит в том, что используемые для вычислений соотношения нелинейны (линейно-логарифмические) [12, 13], что несколько затрудняет вычисления:

(1)
$\lg {\text{RI}} = a\lg {{T}_{{{\text{кип}}}}} + bA + c,$
где А – параметр, фиксирующий положение конкретного соединения в соответствующей таксономической группе (например, число атомов углерода в молекуле, число циклов, формальная непредельность, и т.п.); a, b, c – коэффициенты, вычисляемые методом наименьших квадратов.

Вычисление индексов удерживания на основании корреляции их значений для структурных аналогов различных групп (третья группа; в общем случае такие зависимости нелинейны) предполагает использование аналогичных линейно-логарифмических соотношений [14]:

(2)
$\lg {\text{R}}{{{\text{I}}}^{1}} = a\lg {\text{R}}{{{\text{I}}}^{2}} + bA + c,$
при этом смысл параметров A, a, b, c – такой же, как и формуле (1).

Говоря о возможностях корреляции газохроматографических индексов удерживания структурных аналогов различных таксономических групп, нельзя не отметить практически важный частный случай. Дело в том, что для некоторых сочетаний структурных аналогов различных классов зависимость RI1 = f(RI2) с приемлемой точностью может быть аппроксимирована простейшим уравнением линейной регрессии:

(3)
${\text{R}}{{{\text{I}}}^{1}} \approx aR{{I}^{2}} + b.$

В подобных случаях получение оценок RI существенно упрощается, так как не требует применения нестандартных методов вычислений. Однако до настоящего времени не сформулированы какие-либо априорные правила выявления групп конгенеров, для которых этот вариант обеспечивает приемлемую точность результатов.

Для иллюстрации в качестве примера на рис. 1а приведена зависимость индексов удерживания бромзамещенных метанов CH4 –xBrx с числом атомов брома от одного до четырех (1 ≤ х ≤ 4) от значений RI структурно аналогичных хлорзамещенных метанов CH4 –xClx (1 ≤ х ≤ 4). Казалось бы, не следует ожидать больших различий свойств таких галогенопроизводных; они характеризуются близкими значениями диэлектрических проницаемостей и дипольных моментов, а атомные радиусы брома и хлора близки (1.00 и 1.15 ангстрем). Однако зависимость RI(CH4 –xBrx) = = f[RI(CH4 –xClx)] нелинейна, так что вычисления в таких условиях возможны только с использованием уравнения (2). При этом аналогичная зависимость индексов удерживания йодметанов и бромметанов (рис. 1б) близка к линейной (коэффициент корреляции R = 0.9989), хотя различия атомных радиусов йода и брома больше (1.40 и 1.15 ангстрем). Таким образом, уже из этого примера следует, что линейность или нелинейность корреляций RI1 = f(RI2) определяется не физико-химическими характеристиками сравниваемых структурных аналогов, а какими-то иными причинами.

Рис. 1.

Иллюстрация типичной нелинейной и практически линейной зависимостей индексов удерживания соединений разных таксономических групп: (а) – бромметаны и хлорметаны, 1 ≤ х ≤ 4; (б) – йодметаны и бромметаны, 1 ≤ х ≤ 4. При использовании уравнения (2) нелинейная зависимость (а) может быть приведена к линейному виду. Параметры линейной регрессии (б): a = 1.49 ± 0.05, b = –101 ± 39, R = 0.9989, S0 = 23.

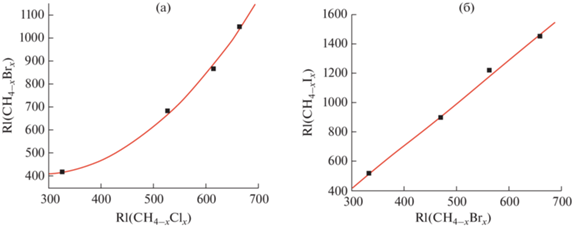
Комментируя рис. 1б, следует заметить, что значение RI тетрайодметана (1862) непропорционально завышено по сравнению с другими йодпроизводными: 516 ± 7 (CH3I), 899 ± 9 (CH2I2) и 1209 ± 24 (CHI3). В базу [1] оно включено на основании двух публикаций [15, 16], но, скорее всего, ошибочно. Дело в том, что CI4 плавится при 168–171°С с разложением, следовательно, его газохроматографический анализ невозможен из-за деструкции в испарителе хроматографа. Поэтому значение RI, принадлежащее какому-то другому соединению (продукту разложения CI4), было заменено экстраполированной теоретически ожидаемой оценкой 1446, вычисленной по линейно-логарифмическому соотношению (2) на основании данных для трех остальных йодметанов. Как отмечено в работе [17], проверка надежности исходных данных – необходимая стадия корреляций “свойство–свойство”.

Цель настоящей работы состоит в выявлении критериев применимости простейших линейных соотношений (3) для оценки газохроматографических индексов удерживания конгенеров различных таксономических групп на основании значений индексов для конгенеров других групп. Решаемые при этом задачи включают оценку неизвестных значений RI, проверку их правильности и, в отдельных случаях, идентификацию аналитов.

ВЫБОР ИСХОДНЫХ ДАННЫХ И ИХ ОБРАБОТКА (ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ)

Источником газохроматографических индексов удерживания рассматриваемых соединений на стандартных неполярных полидиметилсилоксановых неподвижных фазах служила база NIST [1]. Значения RI этоксисиланолов (C2H5O)4 –xSi(OH)x (1 ≤ х ≤ 3) заимствовали из работы [18] (там же указаны условия газохроматографического анализа).

Для вычислений методом наименьших квадратов использовали программное обеспечение Excel (Microsoft 2007) и Origin (версии 8.1 и 4.1). В качестве критериев корректности линейных зависимостей RI1 ≈ aRI2 + b выбирали а) значения коэффициентов корреляции R > 0.99 и б) результаты сравнения минимальных разностей RI гомологов характеризуемой группы со значениями генеральных дисперсий S0. Величины S0 в первом приближении характеризуют надежность значений, вычисляемых по уравнению линейной регрессии (для более точных оценок используют так называемые коридоры ошибок [19]). Результаты аппроксимации RI по соотношениям вида (3) значимы, если минимальные разности индексов удерживания соседних структурных аналогов превышают удвоенные значения S0:

(4)
${\text{min}}\left| {{\text{R}}{{{\text{I}}}_{i}}--{\text{R}}{{{\text{I}}}_{i}}_{{ \pm 1}}} \right| > 2{{S}_{0}}.$

Невыполнение неравенства (4) соответствует ненадежным оценкам RI, которые нецелесообразно использовать для решения аналитических задач.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Таксономические группы структурных аналогов. Особенности линейной корреляции газохроматографических индексов удерживания структурных аналогов выявляли на примерах соединений нескольких таксономических типов, в том числе следующих:

1. Замещенные метаны: CH4 → CH3X → CH2X2 → → CHX3 → CX4. Поскольку в таких группах первый член (СН4, RI = 100) одинаков, то его исключали из рассмотрения. В результате в них остается всего по четыре объекта, что снижает практическую ценность таких корреляций RI, но упрощает выявление их закономерностей и особенностей.

2. Замещенные этаны: C2H6 → C2H5X → → CH3CHX2 → XCH2CH2X → XCH2CHX2 → → XCH2CX3 → X2CHCHX2 → X2CHCX3 → X3C-CX3. После исключения незамещенного этана (RI = 200) в таких группах остается по восемь соединений, часть из которых (в зависимости от природы Х) не охарактеризована значениями RI, что делает решение подобных задач более актуальным, чем соединений первого типа.

3. Замещенные бензолы: C6H6 → C6H5X → → C6H4X2 (три изомера) → С6Н3Х3 (три изомера) → → С6Н2Х4 (три изомера) → С6НХ5 → С6Х6. Без незамещенного бензола (RI = 654 ± 7 [1]) число объектов в таких группах равно 13. Для многих из них получение оценок RI является актуальной задачей из-за отсутствия экспериментальных данных.

4. Замещенные нафталины: С10Н8 → С10Н7Х (два изомера) → С10Н6Х2 (10 изомеров). Эти группу чаще всего приходится ограничивать дизамещенными соединениями, так как для многих изомеров с тремя даже простейшими заместителями (метильные группы) надежные значения RI неизвестны [1].

Особенности корреляции газохроматографических индексов удерживания в группе замещенных метанов и родственных соединений11. Проверка взаимной корреляции значений RI замещенных метанов при разных Х (Х = Cl, Br, I, OCH3, OC2H5, CH3, C6H5 и др.) позволяет выявить примеры как нелинейности зависимостей RI1 = f(RI2) (рис. 1а), так и (реже) их линейности (как на рис. 1б). Для характеристики рассматриваемого подхода необходимо выяснить причины подобных различий, которые, как отмечено выше, не связаны с химической природой фрагментов Х.

Необходимым, но не достаточным условием взаимной линейной корреляции индексов удерживания структурных аналогов являются их симбатные изменения в обеих сравниваемых группах. Если в одной из групп значения RI монотонно возрастают или убывают, а во второй имеется экстремум, то применение соотношений вида (3) не может обеспечить необходимую точность оценок. Экстремумы индексов удерживания (максимумы) наблюдаются, например, в группах метоксиметанов CH3O → … → C(OCH3)4, фторметанов CH3F → … → CF4, метилсиланов CH3SiH3 → … → → Si(CH3)4 и других.

Для получения более определенных заключений об особенностях вариации значений RI в разных группах необходимо сопоставить не просто значения индексов удерживания, а их первых конечных разностей, $\Delta _{{{\text{RI}}}}^{1}$ = RIi+ 1 – RIi (табл. 1). Так, для рассмотренного выше примера бром- и хлорметанов (рис. 1) индексы удерживания монотонно возрастают в каждой из групп. Однако разности $\Delta _{{{\text{RI}}}}^{1}$ в ряду CH3Cl → CCl4 монотонно убывают от 201 до 48, тогда как в ряду CH3Br → CBr4 последнее значение $\Delta _{{{\text{RI}}}}^{1}$ (186) несколько больше предыдущего (181), т.е. набор значений $\Delta _{{{\text{RI}}}}^{1}$ характеризуется незначительным экстремумом (минимумом). В математическом смысле первые конечные разности $\Delta _{{{\text{RI}}}}^{1}$ эквивалентны первой производной функции RI = f(nX) по числу варьируемых фрагментов структуры, однако выявление причин вариаций ее знака (появления экстремумов) даже на феноменологическом уровне представляет собой сложную задачу. Наиболее вероятным представляются стерические взаимодействия фрагментов Х в молекулах, аналогичные эффектам, выявленным в работе [20] на примере метилбензолов.

Таблица 1.

Индексы удерживания бром- и хлорметанов [1] и их разности

Бромметан RI ΔRI1 Хлорметан RI ΔRI1
CH3Br 415 ± 5   CH3Cl 327 ± 3  
    268     201
CH2Br2 683 ± 6   CH2Cl2  528 ± 10  
     181*      87
CHBr3   864 ± 11   CHCl3 615 ± 6  
    186      48
CBr4 1050 ± 5   CCl4 663 ± 16  

*  Минимум значений $\Delta _{{{\text{RI}}}}^{1}.$

Таким образом, если в одной из сопоставляемых таксономических групп первые разности индексов удерживания $\Delta _{{{\text{RI}}}}^{1}$ изменяются монотонно, а во второй характеризуются экстремумами, то корреляция таких значений RI не может обеспечить приемлемой точность их оценок. К таким примерам относятся сочетания набора данных CH3Cl → CCl4 (значения $\Delta _{{{\text{RI}}}}^{1}$ монотонно убывают) с наборами данных CH3OCH3 → C(OCH3)4, CCl3Br → CBr4, (CH3)3SiCl → SiCl4 (во всех случаях существуют максимумы значений $\Delta _{{{\text{RI}}}}^{1}$) и другими.

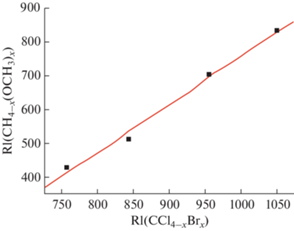
С другой стороны, если оба сравниваемых набора значений RI характеризуются экстремумами $\Delta _{{{\text{RI}}}}^{1},$ то можно полагать, что их корреляция окажется вполне приемлемой по критерию точности оценок индексов удерживания. В табл. 2 сопоставлены индексы удерживания серии метоксиметанов CH3OCH3 → C(OCH3)4 (данные для которых недостаточно надежны [1] и заслуживают уточнения), рассматриваемые как функция индексов удерживания хлорбромметанов CCl3Br → CBr4. В обеих группах регистрируются максимумы $\Delta _{{{\text{RI}}}}^{1},$ однако корреляция значений RI этих совокупностей структурных аналогов, иллюстрируемая рис. 2, вполне пригодна для получения практически полезных оценок индексов. Все значения $\Delta _{{{\text{RI}}}}^{1}$ превышают удвоенную генеральную дисперсию S0 = 23. Параметры уравнения линейной регрессии и расчетные значения RI указаны в табл. 2; среднее значение абсолютного отклонения расчетных и справочных величин составляет всего 15 ± 5 ед. индекса.

Таблица 2.

Индексы удерживания хлорбром- и метоксиметанов [1] и их разности

Метоксиметан RI ΔRI1 Аппроксимированное значение RI Хлорбромметан RI ΔRI1
CH3OCH3 427 ± 19   408 CCl3Br 757 ± 5  
    81       87
CH2(OCH3)2 508 ± 2   531 CCl2Br2 844 ± 1  
    194*       111*
CH(OCH3)3 702   689 CClBr3 955  
    128       95
C(OCH3)4 830 ± 4   824 CBr4 1050 ± 5  

* Максимумы значений $\Delta _{{{\text{RI}}}}^{1}.$

Рис. 2.

Корреляция индексов удерживания метоксиметанов и хлорбромметанов (1 ≤ х ≤ 4). Параметры линейной регрессии: a = 1.42 ± 0.10, b = –667 ± 95, R = 0.995, S0 = 23.

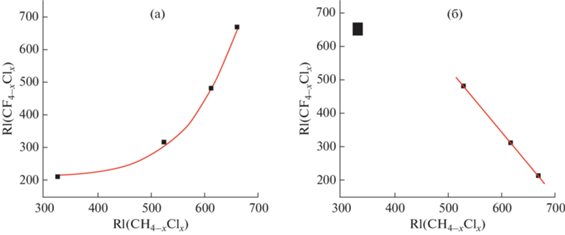
Значения $\Delta _{{{\text{RI}}}}^{1}$ в двух сравниваемых таксономических группах должны либо одновременно возрастать, либо убывать. Поэтому еще одной причиной отсутствия линейной корреляции RI1 = = f(RI2) являются антибатные изменения ΔRI1, что эквивалентно разным знакам первой производной dRI/dnX. В качестве примера можно привести корреляцию индексов удерживания фторхлорметанов CF4 –xClx и хлорметанов CH4 –xClx (1 ≤ х ≤ 4), результаты которой иллюстрирует рис. 3а, б. Если обе группы структурных аналогов сформированы по увеличению числа атомов хлора в молекуле, т.е. CF3Cl → … → CCl4 и CH3Cl → … → CCl4, то зависимость RI1 = f(RI2) нелинейна (рис. 3а). Причина этого в том, что в первой из этих серий значения ΔRI1 возрастают, а во второй – убывают. Чтобы преобразовать данные к линейной зависимости последовательность структурных аналогов в первой из этих групп (целевой) нужно изменить на противоположную, т.е. ранжировать по уменьшению значений $\Delta _{{{\text{RI}}}}^{1},$ CCl4 → … → CF3Cl. Однако в результате этого преобразовании данных на графике появляется точка (показана на рис. 3б в увеличенном масштабе слева вверху), отвечающая паре соединений CH3Cl – CCl4, которые не содержат фтора и, следовательно, по химическим признакам не соответствуют остальным фторпроизводным. Поэтому вполне закономерно, что она выпадает из общей линейной регрессии; коэффициент корреляции для трех оставшихся пар соединений составляет R = 0.9995.

Рис. 3.

Корреляция индексов удерживания фторхлорметанов и хлорметанов (1 ≤ х ≤ 4). (а): Нелинейная зависимость: обе группы структурных аналогов ранжированы по увеличению числа атомов хлора в молекуле: CF3Cl → CCl4 и CH3Cl → CCl4; (б): группы аналогов ранжированы по увеличению значений $\Delta _{{{\text{RI}}}}^{1}{\text{:}}$ CF3Cl → CCl4 и CCl4 → CF3Cl и CH3Cl → CCl4. После исключения точки CH3Cl – CCl4 (слева вверху) параметры линейной регрессии для трех оставшихся пар: a = –2.00 ± 0.06, b = 1536 ± 38, R = 0.9995, S0 = 6.

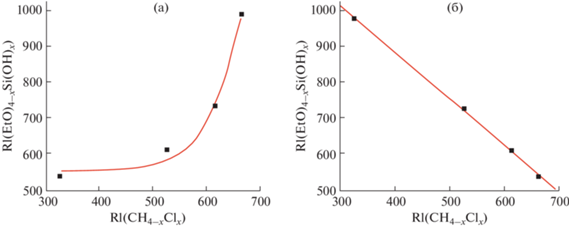
В качестве примера применения обсуждаемых особенностей корреляции значений RI в группе замещенных метанов и их аналогов (в том числе кремнийсодержащих) небезынтересно рассмотреть газохроматографическую идентификацию необычных продуктов частичного гидролиза тетраэтоксисилана (C2H5O)4Si (RI 978 ± ± 10). В их числе обнаружены триэтоксисиланол (C2H5O)3SiOH (RI 727 ± 3), диэтоксисиландиол (C2H5O)2Si(OH)2 (RI 608 ± 1) и этоксисилантриол (C2H5O)Si(OH)3 (RI 537 ± 2) [18]. Если сравнивать значения RI таких этоксисиланолов, ранжированные “естественным образом” по увеличению числа этоксигрупп в молекулах (соответствует возрастанию значений $\Delta _{{{\text{RI}}}}^{1}$), с данными для хлорметанов CH3Cl → CCl4 (соответствует уменьшению $\Delta _{{{\text{RI}}}}^{1}$), то зависимость RI1 = f(RI2) оказывается нелинейной (рис. 4а). Для ее линеаризации одну из этих последовательностей необходимо заменить обратной, например, рассматривать совокупность этоксисиланолов по увеличению числа ОН-групп в молекуле, (C2H5O)4Si → … → → (C2H5O)Si(OH)3. В результате получаем практически “идеальную” линейную регрессию (коэффициент корреляции R достигает 0.9995), график которой изображен на рис. 4б. Примечательно, что разметка осей рис. 4а и 4б, естественно, одинакова, и для того чтобы различить два рассматриваемых варианта, необходимы специальные комментарии.

Рис. 4.

Корреляция индексов удерживания этоксисиланолов (C2H5O)4 –xSi(OH)x и хлорметанов (1 ≤ х ≤ 4). (а): Нелинейная зависимость: значения RI этоксисиланолов ранжированы по увеличению молекулярных масс (или, иначе, числа этоксигрупп в молекуле), что соответствует возрастанию $\Delta _{{{\text{RI}}}}^{1};$ (б): обе группы ранжированы по убыванию значений $\Delta _{{{\text{RI}}}}^{1},$ что приводит к обращению последовательности алкоксисиланолов: (C2H5O)4Si → (C2H5O)Si(OH)3. Параметры регрессии (б): a = 1.30 ± 0.03, b = 1408 ± 16, R = –0.9995, S0 = 8.

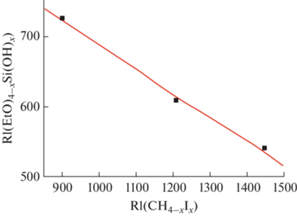
Для дополнительного подтверждения того, что продукты частичного гидролиза тетраэтоксисилана образуют совокупность конгенеров, можно рассмотреть еще одну корреляцию их значений RI с данными для какой-либо иной совокупности структурных аналогов, например йодалканов CI4 (RI 1446) → CHI3 (1209 ± 24) → CH2I2 (899 ± 9) → → CH3I (516 ± 7). Бромалканы для этого использовать нельзя из-за присущего им небольшого максимума значений $\Delta _{{{\text{RI}}}}^{1}$ (см. табл. 1). График линейной зависимости RI1 ≈ aRI2 + b приведен на рис. 5. После исключения точки, соответствующей паре соединений CH3I–(C2H5O)4Si, значение R для трех оставшихся пар структурных аналогов равно –0.998 при S0 = 9.

Рис. 5.

Корреляция индексов удерживания этоксисиланолов (C2H5O)4 –xSi(OH)x и йодметанов (2 ≤ х ≤ 4). Обе группы структурных аналогов ранжированы по убыванию значений $\Delta _{{{\text{RI}}}}^{1}.$ Параметры линейной регрессии: a = –0.35 ± 0.02, b = 1038 ± 29, R = –0.998, S0 = 9.

Рассматриваемые корреляции RI1 ≈ aRI2 + b рекомендуется использовать не только для оценки, но и для проверки надежности справочных значений индексов удерживания наименее подробно охарактеризованных “экзотических” соединений. При этом в качестве реперных объектов (с которыми проводят сравнение) целесообразно выбирать соединения с хорошо известными и воспроизводимыми значениями RI, например подробно охарактеризованные углеводороды. Следующий пример относится именно к такому типу: необходимо проверить известные значения RI метилсиланов CH3SiH3 → Si(CH3)4. Данные для простейшего монометилсилана в базе [1] отсутствуют, а следующие два гомолога охарактеризованы в единственной работе [21], поэтому их приходится дополнять расчетными величинами на основании температур кипения [12–14]. Значения RI метилсиланов можно сопоставлять с данными для изоструктурных алканов С2–С5, что иллюстрирует табл. 3.

Таблица 3.

Индексы удерживания метилсиланов и алканов С2–С5 [1]

Метилсилан RI ΔRI1 Аппроксимированное значение RI Алкан RI ΔRI1
CH3SiH3 243 ± 8   240 C2H6 200  
    94       100
(CH3)2SiH2 337 ± 8   342 C3H8 300  
    71        62
(CH3)3SiH 408   402 изо-C4H10 362 ± 7  
    48        51
(CH3)4Si 456 ± 16   413 нео-C5H12 413 ± 2  

График зависимости RI1 = f(RI2) в данном случае настолько близок к линейному, что его вполне можно не приводить и ограничиться только параметрами линейной регрессии: a = 1.01 ± 0.03, b = 39 ± 9, R = 0.9992, S0 = 4.5. Таким образом, подтверждено, что известные значения RI метилсиланов достаточно надежны.

При соответствующем контроле вариаций $\Delta _{{{\text{RI}}}}^{1}$ в сравниваемых группах структурных аналогов рассмотренный подход не имеет принципиальных ограничений и отличается исключительной простотой.

Корреляция газохроматографических индексов удерживания в других таксономических группах (большего объема) существенно расширяет возможности рассматриваемого подхода. С другой стороны, можно ожидать непредсказуемого усложнения зависимостей RI1 = f(RI2), например, за счет проявления трудно формализуемых стерических эффектов, заметных лишь для отдельных соединений в пределах таких групп. В качестве примера целесообразно рассмотреть группу замещенных этанов (9 конгенеров), значения RI которых сопоставлены с данными для изоструктурных алканов (табл. 4). Из их графического представления (рис. 6) следует, что весь набор точек “распадается” на две подгруппы, соответствующие двум линейным участкам: (I) для соединений №№ 1–6 (содержат от одного до четырех атомов хлора) и (II) для соединений №№ 6–9 (от четырех до шести атомов хлора). Параметры двух уравнений линейной регрессии, соответствующие каждому из этих участков, приведены в подписи к рисунку. Объяснение причин появления двух линейных участков в настоящий момент представляется затруднительным, и к этому факту следует относиться как к феноменологически выявленной закономерности. Аналогично два линейных участка зависимости RI1 = f(RI2) наблюдаются при корреляции значений RI хлор- и бромэтанов.

Таблица 4.

Индексы удерживания хлорэтанов С2Н6 –xСlx и алканов С3–С8 [1]

Номер
соединения 		Хлорэтан RI Аппроксимированное значение RI (номер подгруппы) Алкан
(структурный аналог) 		RI
1 C2H5Cl 422 ± 8 436 (I) C3H8 300
2 ClCH2-CH2Cl 642 ± 7 624 (I) C4H10 400
3 CH3-CHCl2  558 ± 19 553 (I) Изобутан 362 ± 7
4 ClCH2-CHCl2 768 ± 4 761 (I) Изопентан 473 ± 4
5 CH3-CCl3 641 ± 7 648 (I) Неопентан 413 ± 2
6 ClCH2-CCl3  869 882 (I), 876 (II) 2,2-Диметилбутан 537 ± 2
7 Cl2CH-CHCl2  916 905 (II) 2,3-Диметилбутан 566 ± 3
8 C2HCl5  969 974 (II) 2,2,3-Триметилбутан 635 ± 4
9 C2Cl6 1064 1063 (II) 2,2,3,3-Тетраметилбутан 724 ± 9
Рис. 6.

Корреляция индексов удерживания хлорэтанов C2H6 –xClx (1 ≤ х ≤ 6) и алканов С3–С8. Параметры линейной регрессии участка (I): a = 1.88 ± 0.08, b = = 128 ± 32, R = 0.997, S0 = 14; участка (II): a = 1.00 ± ± 0.07, b = 339 ± 43, R = 0.995, S0 = 10.

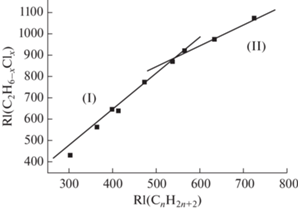
Средняя точность оценок индексов удерживания хлорэтанов по данным для изоструктурных углеводородов составляет 9 ± 5 ед. индекса, что вполне достаточно для практических целей и не уступает возможностям гораздо более сложных методов. Поскольку атомы хлора могут находиться при двух атомах углерода, это усложняет использование первых конечных разностей индексов удерживания $\Delta _{{{\text{RI}}}}^{1}$ (массив $\Delta _{{{\text{RI}}}}^{1}$ становится двумерным).

Проверку возможностей рассматриваемого подхода в группах замещенных бензолов целесообразно начать с сопоставления индексов удерживания бром- и хлорбензолов. Справочные данные приведены в табл. 5; для некоторых бромбензолов значения RI неизвестны, что объясняет актуальность их оценки. Поскольку значение коэффициента корреляции R достигает 0.9989, график зависимости RI1 = f(RI2) (рис. 7) подтверждает ее линейность.

Таблица 5.

Индексы удерживания бромбензолов С6Н6 –xBrx и хлорбензолов С6Н6 –xClx [1]

Хлорбензол RI Бромбензол RI Расчетное значение RI
Монохлор- 839 ± 7 Монобром- 839 ± 7  
1,2-Дихлор- 1016 ± 11 1,2-Дибром- 1216 ± 5  
1.3-Дихлор- 989 ± 10 1.3-Дибром- 1190 ± 7  
1,4-Дихлор- 995 ± 10 1,4-Дибром- 1193  
1,2,3-Трихлор- 1199 ± 12 1,2,3-Трибром- –* 1530
1,2,4-Трихлор- 1160 ± 13 1,2,4-Трибром- –     1464**
1,3,5-Трихлор- 1117 ± 14 1,3,5-Трибром- 1390  
1,2,3,4-Тетрахлор- 1364 ± 11 1,2,3,4-Тетрабром- – 1808
1,2,3,5-Тетрахлор- 1322 ± 11 1,2,3,5-Тетрабром- – 1737
1,2,4,5-Тетрахлор- 1326 ± 18 1,2,4,5-Тетрабром- 1697  
Пентахлор- 1501 ± 5 Пентабром- – 2039
Гексахлор- 1691 ± 5 Гексабром- 2379  

*  Прочерк означает отсутствие справочных данных в базе [1]; ** оценка RI по аддитивной схеме [10] равна 1460.

Рис. 7.

Корреляция индексов удерживания бромбензолов C6H6 –xBrx (1 ≤ х ≤ 6) и соответствующих хлорбензолов. Параметры линейной регрессии: a = 1.68 ± ± 0.03, b = –489 ± 40, R = 0.9989, S0 = 24.

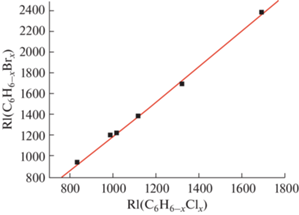
Объективным ограничением такого способа оценки индексов удерживания является невозможность различить некоторые изомеры положения, характеризующиеся относительно небольшими различиями RI, например орто-, мета- и пара-дибромбензолы с индексами 1216, 1190 и 1193 соответственно. Их попарные разности меньше удвоенной величины S0 = 24 (см. уравнение (4)). Примечательно, что для изомерных трибромбензолов таких совпадений уже нет: 1530 (1,2,3-изомер), 1464 (1,2,4-изомер) и 1390 (1,3,5-изомер).

Аналогичные оценки RI на основании их взаимных корреляций для соединений различных таксономических групп получены для Br- и Cl-бензолов C6H6 –xHalx (1 ≤ x ≤ 6) в результате их сравнения с данными для метилбензолов. Для индексов удерживания йодбензолов C6H6 –xIx (1 ≤ x ≤ 3) эффективным оказалось их сравнение с данными для соответствующих хлорбензолов, метиловых эфиров бензолкарбоновых кислот C6H6 –x(CO2CH3)x (1 ≤ x ≤ 4) – с хлорбензолами, хлорнафталинов C10H8 –xClx (1 ≤ x ≤ 4) – с метилнафталинами) и т.д.

* * *

Таким образом, анализ возможностей и особенностей простейшей линейной корреляции газохроматографических индексов удерживания соединений разных таксономических групп структурных аналогов, RI1 ≈ aRI2 + b позволил установить следующее:

– Если каждое соединение в соответствующей группе однозначно задано молекулярной формулой, т.е. не имеет изомеров (это возможно для простейших замещенных метанов, CH3X → … → → CX4), то условием линейной корреляции индексов удерживания в таких группах являются симбатные вариации первых конечных разностей индексов удерживания, $\Delta _{{{\text{RI}}}}^{1}$ = RIn+ 1 – RIn. Наличие экстремумов $\Delta _{{{\text{RI}}}}^{1}$ в одной из групп при их монотонном изменении в другой – однозначный признак отсутствия линейной корреляции RI1 ≈ ≈ aRI2 + b. Если в одной из групп значения $\Delta _{{{\text{RI}}}}^{1}$ возрастают, а в другой – убывают, то в любой из групп порядок ранжирования соединений должен быть заменен обратным.

– Показано, что корреляции индексов удерживания возможны в таких группах структурных аналогов, как замещенные этаны, бензолы, нафталины и других. Во всех случаях использование простейшего соотношения RI1 ≈ aRI2 + b позволяет не только оценивать значения RI еще не охарактеризованных в настоящее время соединений, но и уточнять ненадежные справочные данные.

Список литературы

  1. The NIST Mass Spectral Library (NIST/EPA/NIH EI MS Library, 2020 Release). Software/Data Version; NIST Standard Reference Database, Number 69, May 2020. National Institute of Standards and Technology, Gaithersburg, MD 20899: http://webbook.nist.gov (дата обращения: сентябрь 2022 г.).

  2. Pompe M., Novic M. Prediction of gas-chromatographic retention indices using topological descriptors // J. Chem. Inf. Comput. Sci. 1999. V. 39. № 1. P. 59. https://doi.org/10.1021/ci980036z

  3. Farkas O., Heberger K., Zenkevich I.G. Quantitative structure-retention relationships XIV. Prediction of GC retention indices for saturated O-, N-, and S-heterocyclic compounds // Chemometr. Intel. Lab. Systems. 2004. V. 72. P. 173.

  4. Heberger K. Quantitative structure – (chromatographic) retention relationships (QSRR) // J. Chromatogr. A. 2007. V. 1158. P. 273. https://doi.org/10.1016/chroma.2007.03.108

  5. Matyushin D., Buryak A. Gas chromatographic retention index prediction using multimodal machine learning // IEEE Access. 2020. V. 8. P. 223140. https://doi.org/10.1109/ACCESS.2020.3045047

  6. Matyshin D.D., Sholokhova A.Yu., Buryak A.K. Deep learning based prediction of gas chromatographic retention indices for a wide variety of polar and mid-polar liquid stationary phases // Int. J. Mol. Sci. 2021. V. 22. 13 p. https://doi.org/10.3390/ijms22179194

  7. Idroes R., Noviandy T.R., Maulana A., Syhendra R., Sasmita N.R., Muslem M., Idroes G.M., Kemala P., Irvanizam I. Application of genetic algorithm – multiple linear regression and artificial newral network determination for prediction of Kovats retention index // Int. Rev. Model. Simulat. 2021. V. 14. № 2. 137 p. https://doi.org/10.15866/iremos.v14i2.20460

  8. Qu C., Schneider B.I., Kearsley A.J., Keyrouz W., Allison T.C. Predicting Kovats retention indices using graph neural networks // J. Chromatogr. A. 2021. V. 1646. Art. 462100. https://doi.org/10.1016/jchroma.2021.462100

  9. Zhang X., Shi L., Ding L., Sun Z., Song L., Qu H., Sun T. Study on quantitative structure – retention relationships (QSRR) for oxygen-containing organic compounds based on gene expression programming (GEP) // J. Chromatogr. Sep. Tech. 2015. V. 6. № 7. 7 p. https://doi.org/10.4172/2157-7064.1000306

  10. Stein S.E., Babushok V.I., Brown R.L., Linstrom P.J. Estimation of Kovats retention indices using group contribution // J. Chem. Inf. Model. 2007. V. 47. P. 975. https://doi.org/10.1021/ci600548y

  11. Зенкевич И.Г., Елисеенков Е.В., Касаточкин А.Н. Идентификация продуктов органических реакций при отсутствии аддитивности хроматографических индексов удерживания. Хлорпроизводные метил-трет-бутилкетона // Журн. структ. химии. 2013. Т. 54. № 3. С. 453. https://doi.org/10.1134/S0022476613030050

  12. Зенкевич И.Г. Формирование таксономических групп органических соединений для расчета газохроматографических индексов удерживания по физико-химическим константам // Журн. структ. химии. 1994. Т. 35. № 6. С. 176.

  13. Zenkevich I.G. Reciprocally unambiguous conformity between GC retention indices and boiling points within two- and multidimensional taxonomic groups of organic compounds // J. High Resolut. Chromatogr. Chromatogr. Commun. 1998. V. 21. № 10. P. 565.

  14. Зенкевич И.Г. Принцип структурной аналогии при оценке газохроматографических индексов удерживания // Журн. структ. химии. 1996. Т. 37. № 4. С. 793.

  15. Waggott A., Davies I.W. Identification of organic pollutants using linear temperature programmed retention indices (LTPRIs) – Part II // 1984. http://dwi.defra.gov.uk/research/completed/research/ reports/dwi0383.pdf (дата обращения: август 2022 г.).

  16. Yasuhara A., Morita M., Fuwa K. Temperature-programmed retention indices of 221 halogenated organic compounds with 1-bromoalkanes as references // J. Chromatogr. 1985. V. 328. P. 35. https://doi.org/10.1016/S0021-9673(01)87374-X

  17. Зенкевич И.Г. Контроль, коррекция и восстановление значений физико-химических свойств органических соединений с использованием рекуррентных зависимостей // Журн. физ. химии. 2021. Т. 95. № 5. С. 700. https://doi.org/10.1134/S0036024421040294

  18. Зенкевич И.Г., Баранов Д.А. Газохроматографическая идентификация необычных нестабильных продуктов частичного гидролиза тетраэтоксисилана // Журн. аналит. химии. 2023. Т. 78. № 1. С. .

  19. Линник Ю.В. Метод наименьших квадратов и основы теории обработки наблюдений. М.: Физматгиз, 1958. 334 с.

  20. Зенкевич И.Г. Выявление аномалий газохроматографических индексов удерживания гомологов на основании их гомологических инкрементов // Журн. физ. химии. 2021. Т. 95. № 8. С. 1269. https://doi.org/10.1134/S003602442107030X

  21. Szekely T., Nefedov O.M., Gazzo G., Shinyayav V.I., Fritz D. Gas chromatographic investigation of the thermal decomposition of polydimethylsilylene // Acta Chem. Acad. Sci. Hung. 1967. V. 54. № 3–4. P. 241.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал аналитической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал