Астрономический журнал, 2021, T. 98, № 5, стр. 407-422

R-тороид как трехмерное обобщение кольца Гaусса и его применение в астрономии

Б. П. Кондратьев^{1, 2, 3, *}, В.С. Корноухов^1, 2

¹ Московский государственный университет им. М.В. Ломоносова, Физический факультет
Москва, Россия

² Московский государственный университет им. М.В. Ломоносова, Государственный астрономический институт им. П.К. Штернберга
Москва, Россия

³ Главная (Пулковская) Астрономическая обсерватория РАН
Санкт-Петербург, Россия

^* E-mail: work@boris-kondratyev.ru

Поступила в редакцию 26.11.2020
После доработки 22.12.2020
Принята к публикации 30.12.2020

DOI: 10.31857/S0004629921050042

Полный текст (PDF)

Аннотация

Построена новая аналитическая модель (R-тороид) для изучения вековых возмущений в небесной механике, представляющая 3D обобщение прецессирующего кольца Гаусса. Наш подход основан на тройном усреднении движения материальной точки и сводится к цепочке преобразований: 1D кольцо Гаусса–2D R-кольцо–3D R-тороид. Изучаются форма, структура и гравитационный потенциал R-тороида. Для исследования движения тел в гравитационном поле модели, в двух формах (в интегральной и в виде степенного ряда) получено выражение взаимной энергии R-тороида и внешнего кольца Гаусса. С помощью взаимной энергии выводятся две системы уравнений вековой эволюции оскулирующих орбит (колец Гаусса): в гравитационном поле R-тороида и в поле центральной прецессирующей звезды. Найдены периоды нодальной T_Ω и апсидальной T_ω прецессии орбит. Рассмотрены примеры трех горячих юпитеров с известным периодом нодальной прецессии. Для экзопланеты Kepler-413b R-тороид описывает эволюцию любой орбиты с a ≥ 5.48 а.е., а для экзопланеты PTFO 8-8695b критическое значение большой полуоси оказалось равным всего a_min ≈ 0.2 а.е. Рассчитан профиль частот прецессии пробной орбиты в поле звезды и планеты PTFO 8-8695b. Минимальное значение периода нодальной прецессии оказалось равным T_Ω ≈ (26.1 ± 3.0) × 10³ лет.

1. ВВЕДЕНИЕ

В небесной механике для изучения вековых эффектов активно применяются методы усреднения по “быстрым” переменным. В арсенал этих методов входит кольцо Гаусса, идею которого предложил К.Ф. Гаусс в 1818 г. Метод колец Гаусса был создан для изучения вековых возмущений первого порядка. Среди других аналитических методов этот выделяется наглядностью и основан на том предположении, что возмущающее действие тела с массой $\,{{M}_{1}}$ на другое тело массой$\,{{M}_{2}}$ эквивалентно влиянию силового поля материального гравитирующего кольца (кольца Гаусса), полученного при специальном распределении первой массы по эллиптической орбите.

Напомним, что кольцо Гаусса получается при “размазывании” точечной массы M по кеплеровскому эллипсу орбиты с плотностью, обратной скорости движения на данном участке траектории. После усреднения получается неоднородный эллипс с законом плотности

(1)

$\mu ({v}) = \frac{{M\sqrt {1 - {{e}^{2}}} }}{{2\pi a}}{{(1 + {{e}^{2}} + 2e\cos {v})}^{{ - 1/2}}}.$

Здесь ${v}$ – угол истинной аномалии, a и e – большая полуось и эксцентриситет орбиты соответственно. Элемент массы на угловом интервале $d{v}$ кольца равен

(2)

$dM = \frac{M}{{2\pi }}\frac{{{{{(1 - {{e}^{2}})}}^{{3/2}}}}}{{{{{(1 + e\cos {v})}}^{2}}}}d{v}.$

Потенциал кольца Гаусса в конечном аналитическом виде недавно был найден методами, развитыми в [1] и [2], см. также [3]. Возможности метода колец Гаусса были расширены в работе [4] и особенно в аналитическом подходе, основанном на вычислении энергии взаимодействия двух колец Гаусса [1, 5, 6].

Однако для решения многих задач в астрономии одного усреднения оказывается недостаточно, и тогда следует изыскивать дополнительные возможности для усреднения по быстрым переменным. Так, при отличии потенциала центрального тела от закона $\varphi = \frac{\mu }{r}$ линия апсид возмущенной орбиты будет совершать дополнительное вращение (апсидальная прецессия эллипса). Тогда, как показано в [7], возможно второе усреднение, которое приводит к “размазыванию” массы кольца Гаусса за счет равномерного движения его линии апсид. В итоге получается плоское неоднородное 2D кольцо, названное в [8] R-кольцом. Структура и гравитационный потенциал R-кольца изучались в работах [1, 7, 8].

Кольцо Гаусса и его двумерное обобщение (R-кольцо) вошли в арсенал современных методов динамической астрономии. Но на практике встречаются задачи, когда в инерциальной системе отсчета плоскость R-кольца прецессирует вокруг некоторого направления; тогда появляется возможность дополнительного азимутального усреднения изучаемой орбиты спутника. В результате этого дополнительного азимутального усреднения получается $3D$ фигура тороидального типа (R-тороид), изучению которой и посвящена данная статья.

В разделе 2 даны необходимые сведения о двумерном R-кольце. В разделе 3 методом тройного усреднения получена фигура R-тороида, изучаются его форма и внутренняя структура. Гравитационный потенциал новой модели исследуется в разделах 4 и 5. В разделе 6 найдена взаимная энергия R-тороида и кольца Гаусса. В разделе 7.1 тремя способами вычисляется отношение периодов нодальной и апсидальной прецессий орбиты. В разделе 7.2 результаты теории используются для оценки параметров R-тороидов для Юпитера и Сатурна. В разделе 7.3 рассматривается возможность применения теории для изучения вековых эффектов в движении экзопланет. В разделе 7.4 развит метод вычисления суммарного влияния несферичности прецессирующей центральной звезды и возмущений от R-тороида на прецессию внешних орбит.

2. R-КОЛЬЦО КАК ДВУМЕРНОЕ ОБОБЩЕНИЕ КОЛЬЦА ГАУССА

Розеточное кольцо (R-кольцо) представляет обобщение эллиптического кольца Гаусса на двумерный случай [7, 8]. Такие розеточные кольца (рис. 1) конструируются или из многих симметрично расположенных одиночных колец Гаусса, или заполняются розеточными орбитами, прецессирующими вокруг центральной массы. Пространственный потенциал R-кольца изучался в работах [1, 7, 8]. Важность модели R-кольца определяется тем, что такие кольца естественным образом могут формироваться в планетных системах и в центральных областях плоских галактик.

Рис. 1.

Прецессия линии апсид создает розеточное кольцо. Взяты параметры $a = 1$, $e = 0.5$. Показаны внутренний $q$ и внешний $Q$ радиусы R-кольца.

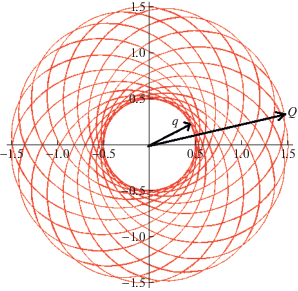
В частном случае $e \to 1$ получается полный круговой диск. Распределение поверхностной плотности в R-кольце дается формулой

(3)

$\sigma (r) = \frac{C}{{\sqrt {(Q - r)(r - q)} }},\quad C = \frac{M}{{{{\pi }^{2}}(q + Q)}}.$

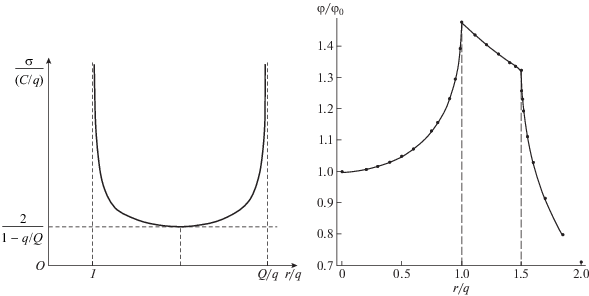
Здесь M – масса кольца, $Q = a(1 + e)$ и $q = a(1 - e)$ – расстояния от активного фокуса до точек апоцентра и перицентра в эллипсе соответственно, a – большая полуось, e – эксцентриситет кольца Гаусса. На рис. 2 показан график распределения плотности в R-кольце. Средняя поверхностная плотность в кольце будет равна $\bar {\sigma } = \frac{M}{{\pi ({{Q}^{2}} - {{q}^{2}})}}.$

Рис. 2.

Распределение нормированной плотности (панель слева) и потенциала в плоскости R-кольца (панель справа, φ₀ дано в (5)). Вертикальными штриховыми линиями отмечены точки входа и выхода из кольца.

Потенциал R-кольца в интегральном виде дается формулой [1]

(4)

$\begin{gathered} \varphi (r,{{x}_{3}}) = \frac{2}{{{{\pi }^{2}}}}{{\varphi }_{0}}\mathop \smallint \limits_{ - \pi /2}^{\pi /2} \frac{{z(\gamma )}}{{\sqrt {{{R}^{2}}(\gamma ,r) + x_{3}^{2}} }} \times \\ \times \;K\left( {2\sqrt {\frac{{rz(\gamma )}}{{{{R}^{2}}(\gamma ,r) + x_{3}^{2}}}} } \right){\text{d}}\gamma , \\ \end{gathered} $

где $K\left( {2\sqrt {\frac{{rz(\gamma )}}{{{{R}^{2}}(\gamma ,r) + x_{3}^{2}}}} } \right)$ – полный эллиптический интеграл первого рода, φ₀ – потенциал в центре розеточного кольца

(5)

${{\varphi }_{0}} = \varphi (0,0) = \frac{{2MG}}{{q + Q}} = \frac{{MG}}{a} = 2\pi G\bar {\sigma }(Q - q),$

а вспомогательные величины

(6)

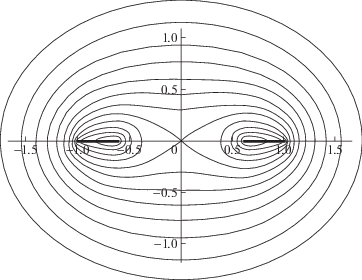
$z(\gamma ) = \frac{{Q - q}}{2}\sin \gamma + \frac{{Q + q}}{2};\quad R(\gamma ,r) = z(\gamma ) + r.$

Пример расчета потенциала R-кольца по формуле (4) показан на рис. 2 (панель справа). Из него видно, что потенциал кольца возрастает от центра вплоть до его внутренней границы и на входе в кольцо, в точке ${{x}_{3}} = 0$, $r = q$, потенциал имеет абсолютный максимум; в самом кольце потенциал почти линейно убывает вплоть до его внешней границы $r = Q$; затем, в области вне кольца $r \geqslant Q$ потенциал быстро спадает.

Отметим, что расчеты потенциала по форму-ле (4) сталкиваются с некоторыми трудностями; дело в том, что при $r = z(\gamma )$ модуль $k = 1$ и, как известно, эллиптический интеграл первого рода K(1) логарифмически расходится. Но эти технические трудности удалось преодолеть, и в [1] была построена система эквипотенциальных поверхностей (см. рис. 3). На этом рисунке видно, что сепаратриса в форме лемнискаты разделяет эквипотенциали на две разные системы кривых.

Рис. 3.

Линии равного потенциала розеточного кольца (жирной линией показано сечение самого R-кольца). Отношение внутреннего радиуса кольца $q$ к внешнему $Q$ равно $3:5.$ Потенциал нормирован на $\frac{2}{{{{\pi }^{2}}}}{{\varphi }_{0}}\left( {1 - \frac{q}{Q}} \right)$. Двенадцать изолиний (от внешних к внутренним) рассчитаны для потенциала, начиная со значения $6.127$ и кончая значением $15.886$ с интервалом $0.8871$ (по монографии [1]).

В работе [8] модель R-кольца применялась для изучения движения газа и звезд в плоских галактиках. В этой же работе с помощью R-кольца изучалась также динамика звездного диска вокруг сверхмассивной черной дыры в центре Галактики (clockwise stellar disk).

3. ПОСТАНОВКА ЗАДАЧИ И ФИГУРА R-ТОРОИДА

Если плоскость R-кольца прецессирует (прецессия узлов) вокруг некоторого направления, в движении тела появляется еще одна степень свободы и становится возможным следующее – третье усреднение орбиты спутника. Таким образом, метод получения новой модели включает в себя тройное усреднение движения материальной точки по быстрым переменным. Первое усреднение дает 1D кольцо Гаусса, на следующем этапе делается усреднение вращающегося кольца Гаусса по углу прецессии его линии апсид (это дает 2D R‑диск); наконец, на третьем этапе мы проводим азимутальное усреднение прецессирующего R-кольца, что и дает в итоге трехмерный R-тороид.

Поясним сказанное. Начнем с изучения пространственной формы R-тороида. Как уже говорилось, модель R-тороида получается методом усреднения движения прецессирующего R-кольца по долготе; в результате получается особая $3D$фигура тороидального типа. Для описания области пространства, которую занимает R-тороид, обратимся к сферическим координатам $(r,\theta ,\varphi )$, где угол широты θ отсчитывается от экваториальной плоскости. Находим, что фигура тороида описывается ограничениями (см. рис. 4, справа)

(7)

$\left\{ {\begin{array}{*{20}{c}} {q \leqslant r \leqslant Q,} \\ { - i \leqslant \theta \leqslant i.} \end{array}} \right.$

Фигура R-тороида показана на рис. 4 и 5 .

Рис. 4.

R-тороид: слева – 3D изображение, справа – меридиональное сечение R-тороида (показано синим цветом). OT – ось симметрии. Внешняя (ABC и A’B’C’) и внутренняя (abc и a’b’c') границы справа и слева есть части кругов, которые соединяются прямыми отрезками $(aA,cC)$ и $(a{\kern 1pt} {\text{'}}A{\kern 1pt} {\text{'}},c{\kern 1pt} {\text{'}}C{\kern 1pt} {\text{'}})$. Обозначен угол $i$ наклона плоских боковых сторон.

Рис. 5.

Трехмерное изображение структуры R-тороида.

Объем R-тороида, как легко убедиться, равен

(8)

$\begin{gathered} V = \mathop \smallint \limits_0^{2\pi } {\kern 1pt} \mathop \smallint \limits_{ - i}^i {\kern 1pt} {\kern 1pt} \mathop \smallint \limits_q^Q \,{{r}^{2}}\cos \theta drd\theta d\varphi = \frac{4}{3}\pi ({{Q}^{3}} - {{q}^{3}})\sin i = \\ = \frac{8}{3}\pi {{a}^{3}}e(3 + {{e}^{2}})\sin i. \\ \end{gathered} $

Здесь e – эксцентриситет исходного кольца Гаусса.

Далее находим распределение плотности ρ(x) в R-тороиде. Для этого “размажем” прецессирующее R-кольцо с плотностью (3) по объему (7), в итоге получим

(9)

$\rho (r,\theta ) = \frac{M}{{2{{\pi }^{3}}ar{\kern 1pt} \sqrt {{{{\sin }}^{2}}i - {{{\sin }}^{2}}\theta } \sqrt {(Q - r)(r - q)} }},$

где M – масса, i – угол наклона боковых сторон R-тороида. Для проверки легко убедиться, что распределение плотности (9) действительно дает массу R-тороида

(10)

$\mathop \smallint \limits_0^{2\pi } {\kern 1pt} \mathop \smallint \limits_{ - i}^i {\kern 1pt} {\kern 1pt} \mathop \smallint \limits_q^Q \,\rho (r,\theta ){{r}^{2}}\cos \theta drd\theta d\varphi = M.$

Зная из (8) объем и массу новой фигуры, находим среднюю плотность $\bar {\rho }$, что позволит представить закон плотности (9) в нормированном виде

(11)

$\frac{{\rho (r,\theta )}}{{\bar {\rho }}} = \frac{{4{{a}^{2}}e(3 + {{e}^{2}})\sin i}}{{3{{\pi }^{2}}r{\kern 1pt} \sqrt {{{{\sin }}^{2}}i - {{{\sin }}^{2}}\theta } \sqrt {(Q - r)(r - q)} }}.$

Обратим внимание на то, что поверхность R-тороида представляет собой “скорлупу” с аномально высокой плотностью. Действительно, при заданном угле θ плотность (11) при r = Q обращается в бесконечность как на внешних ABC и A'B'C' (см. рис. 4 и 5 ), так (при r = q) и на внутренних (abc и a'b'c') фронтальных участках поверхности. “Скорлупа” появляется не только из-за особенностей распределения плотности в самом R-диске (см. рис. 2, панель слева), но также из-за обращения в нуль члена ${{\sin }^{2}}i - {{\sin }^{2}}\theta = 0$ в точках на плоских сторонах самого R-тороида. На рис. 6 показаны два графика плотности, демонстрирующие указанные особенности в структуре R-тороида. На рис. 6 видно, что в большей части объема R-тороида плотность мало зависит от координат, причем оказывается там меньше средней по объему плотности.

Рис. 6.

Нормированная плотность R-тороида (слева – в экваториальной плоскости, справа – при заданном r = 0.5Q). Для расчетов взяты параметры эллипса $a = 1$, $e = 0.5$. Штрихами показано значение средней плотности.

4. ПОТЕНЦИАЛ R-ТОРОИДА В ИНТЕГРАЛЬНОМ ВИДЕ

Особенности формы и сингулярность плотности на поверхности R-тороида делают его гравитационный потенциал сложной функцией координат. Рассмотрим этот потенциал подробнее.

При законе плотности (9), потенциал R-тороида будет представлен тройным интегралом

(12)

${{\Phi }}(r,\theta ,\varphi ) = \frac{{GM}}{{2{{\pi }^{3}}a}}\mathop \smallint \limits_0^{2\pi } {\kern 1pt} \mathop \smallint \limits_{ - i}^i {\kern 1pt} {\kern 1pt} \mathop \smallint \limits_q^Q \frac{{r{\kern 1pt} {\text{'}}\cos \theta {\kern 1pt} {\text{'}}dr{\kern 1pt} {\text{'}}d\theta {\kern 1pt} {\text{'}}d\varphi {\kern 1pt} {\text{'}}}}{{\sqrt {{{{\sin }}^{2}}i - {{{\sin }}^{2}}\theta {\kern 1pt} {\text{'}}} {\kern 1pt} \sqrt {(Q - r{\kern 1pt} {\text{'}})(r{\kern 1pt} {\text{'}} - q)} \sqrt {{{r}^{2}} + r{\kern 1pt} {{{\text{'}}}^{2}} - 2rr{\kern 1pt} {\text{'}}\cos \psi } }},$

где ψ – угол между r и r', равный

(13)

$\begin{gathered} \cos \psi = (\begin{array}{*{20}{c}} {\cos \varphi \cos \theta }&{\sin \varphi \cos \theta }&{\sin \theta } \end{array}) \times \\ \times \;\left( {\begin{array}{*{20}{c}} {\cos \varphi {\kern 1pt} {\text{'}}\cos \theta {\kern 1pt} {\text{'}}} \\ {\sin \varphi {\kern 1pt} {\text{'}}\cos \theta {\kern 1pt} {\text{'}}} \\ {\sin \theta {\kern 1pt} {\text{'}}} \end{array}} \right) = \cos (\varphi {\kern 1pt} {\text{'}} - \varphi )\cos \theta {\kern 1pt} {\text{'}}\cos \theta + \\ + \;\sin \theta {\kern 1pt} {\text{'}}\sin \theta . \\ \end{gathered} $

Из-за наличия в (12) тройного интеграла и сингулярности в самой подынтегральной функции расчеты потенциала по этой формуле требуют определенных затрат машинного времени; подобные технические трудности существуют и в частных случаях (14) и (17). Однако это не помешало рассчитать необходимые графики.

На оси симметрии R-тороида, где $\theta = \frac{\pi }{2}$ и $\cos \psi = \sin \theta {\kern 1pt} {\text{'}}$, потенциал (12) будет представлен однократным интегралом

(14)

$\begin{gathered} {{\Phi }}(r) = \frac{{2GM}}{{{{\pi }^{2}}a}} \times \\ \times \;\mathop \smallint \limits_q^Q \frac{{K\left( k \right)r{\kern 1pt} {\text{'}}dr{\kern 1pt} {\text{'}}}}{{\sqrt {(Q - r{\kern 1pt} {\text{'}})(r{\kern 1pt} {\text{'}} - q)} \sqrt {{{r}^{2}} + r{\kern 1pt} {{{\text{'}}}^{2}} + 2rr{\kern 1pt} {\text{'}}\sin i} }}, \\ \end{gathered} $

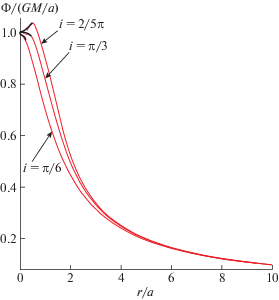
где $K(k)$ – полный эллиптический интеграл первого рода

(15)

$\begin{gathered} K(k) = \mathop \smallint \limits_0^{\pi /2} \frac{{d\alpha }}{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}\alpha } }}; \\ k = 2{\kern 1pt} \sqrt {\frac{{rr{\kern 1pt} {\text{'}}\sin i}}{{{{r}^{2}} + r{\kern 1pt} {{{\text{'}}}^{2}} + 2rr{\kern 1pt} {\text{'}}\sin i}}} {\kern 1pt} {\kern 1pt} {\kern 1pt} . \\ \end{gathered} $

Графики потенциала на оси симметрии у R-тороидов с разными углами наклона $i$ плоских сторон показаны на рис. 7. Отметим, что для углов $i > \frac{\pi }{{3}},$ потенциал при малых $\frac{r}{a}$ ведет себя немонотонно и есть области, где сила притяжения направлена от центра фигуры.

Рис. 7.

Зависимость нормированного потенциала R-тороида на оси симметрии от ${r \mathord{\left/ {\vphantom {r {a.}}} \right. \kern-0em} {a.}}$ Расчеты по формуле (14) для параметров эллипса $a = 1$, $e = 0.5$ и разных углов наклона сторон $i.$

В центре симметрии R-тороида, где r = 0, потенциал равен

(16)

$\begin{gathered} {{{{\Phi }}}_{0}} = \frac{{GM}}{{{{\pi }^{2}}a}}\mathop \smallint \limits_{ - i}^i \frac{{\cos \theta {\kern 1pt} {\text{'}}d\theta {\kern 1pt} {\text{'}}}}{{\sqrt {{{{\sin }}^{2}}i - {{{\sin }}^{2}}\theta {\kern 1pt} {\text{'}}} }} \times \\ \times \;\mathop \smallint \limits_q^Q \frac{{dr{\kern 1pt} {\text{'}}}}{{\sqrt {(Q - r{\kern 1pt} {\text{'}})(r{\kern 1pt} {\text{'}} - q)} }} = \frac{{GM}}{a}. \\ \end{gathered} $

Кроме того, из формулы (12) следует, что потенциал R-тороида в экваториальной плоскости дается двойным интегралом

(17)

$\begin{gathered} \Phi (r,\theta ) = \frac{{GM}}{{2{{\pi }^{3}}a}}\int\limits_q^Q {\frac{{r{\kern 1pt} {\text{'}}dr{\kern 1pt} {\text{'}}}}{{\sqrt {(Q - r{\kern 1pt} {\text{'}})(r{\kern 1pt} {\text{'}} - q)} }} \times } \\ \times \;\int\limits_{ - i}^i {\frac{{\cos \theta {\kern 1pt} {\text{'}}}}{{\sqrt {{{{\sin }}^{2}}i - {{{\sin }}^{2}}\theta {\kern 1pt} {\text{'}}} }}} \frac{{K\left( {\sqrt {\frac{{2{{b}_{1}}}}{{{{b}_{1}} + {{b}_{2}}}}} } \right)}}{{\sqrt {{{b}_{1}} + {{b}_{2}}} }}d\theta {\kern 1pt} {\text{'}}, \\ \end{gathered} $

где

(18)

${{b}_{1}} = {{r}^{2}} + r{\kern 1pt} {{'}^{2}};\quad {{b}_{2}} = 2rr{\kern 1pt} '\cos \theta {\kern 1pt} '.$

Результаты расчетов по формуле (17) в экваториальной плоскости R-тороида для разных углов $i$ показаны на рис. 8.

Рис. 8.

Зависимость нормированного потенциала R-тороида в его экваториальной плоскости от ${r \mathord{\left/ {\vphantom {r {a.}}} \right. \kern-0em} {a.}}$ Расчет выполнен для параметров эллипса $a = 1$, $e = 0.5$ и углов наклона $i = 0,\;{\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6},\;{\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}$ (последовательность графиков сверху вниз). Верхний график представляет потенциал в плоскости R-кольца. Вертикальными штриховыми линиями отмечены точки входа и выхода из фигуры.

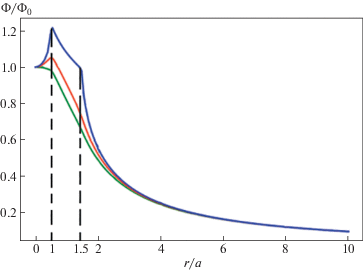
Из рис. 7 и 8 следует, что при малых углах наклона сторон $i$ потенциал (17) вблизи центра фигуры ведет себя немонотонно: сила притяжения в экваториальной плоскости монотонно возрастает от центра к внутренней границе фигуры (однако на оси симметрии потенциал будет всюду убывать). Вместе с тем для R-тороидов с большими углами наклона $i,$ потенциал на оси симметрии в указанной области изменяется немонотонно, но в плоскости симметрии фигуры монотонно убывает. В связи с этим напомним, что как раз на эффекте возрастания потенциала от центра к нижней границе кольца основывалась та модель, с помощью которой в [8] объяснялся эффект существования резких локальных минимумов на кривых вращения у многих плоских галактик.

Заметим, что в предельном случае $i = \frac{\pi }{2}$ R-тороид превращается в толстый сферический слой.

На рис. 9 показаны сечения эквипотенциальных поверхностей R-тороида. Эти сечения отличаются от окружностей и немного вытянуты вдоль оси симметрии фигуры $Oz.$

Рис. 9.

Меридиональное сечение R-тороида (красным цветом) и сечение двух его эквипотенциальных поверхностей (синим цветом). Расчет выполнен для параметров эллипса $a = 1$, $e = 0.5$ и угла наклона $i = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}$.

5. ПРЕДСТАВЛЕНИЕ ПОТЕНЦИАЛА R-ТОРОИДА В ДРУГОЙ ФОРМЕ

Преобразуем формулу (12) для потенциала R‑тороида, положив в ней

(19)

$\sin \theta {\kern 1pt} ' = \sin u\sin i,\quad r{\kern 1pt} ' = x + a.$

Тем самым вместо (r', θ') вводятся новые переменные (x, u)$.$ Тогда

(20)

$\begin{gathered} \cos \theta {\kern 1pt} 'd\theta {\kern 1pt} ' = \cos u\sin idu, \\ \sqrt {{{{\sin }}^{2}}i - {{{\sin }}^{2}}\theta {\kern 1pt} '} = \cos u\sin i, \\ \sqrt {(Q - r{\kern 1pt} ')(r{\kern 1pt} ' - q)} = \sqrt {{{a}^{2}}{{e}^{2}} - {{x}^{2}}} , \\ \end{gathered} $

и интеграл (12) примет вид

(21)

$\Phi (r,\theta ) = \frac{{2GM}}{{{{\pi }^{3}}a}}\int\limits_{ - \pi /2}^{\pi /2} {\int\limits_{ - ae}^{ae} {\frac{{(x + a)K(\bar {k})dxdu}}{{\Delta (x,u)\sqrt {{{a}^{2}}{{e}^{2}} - {{x}^{2}}} }}} } ,$

где

(22)

$\Delta (x,u) = \sqrt {{{R}^{2}} + {{z}^{2}} + {{{(x + a)}}^{2}} + 2(x + a)[R\sqrt {1 - {{g}^{2}}(u)} - zg(u)]} ,$

(23)

$\begin{gathered} R = r\cos \theta ,\quad z = r\sin \theta ,\quad g(u) = \sin i\sin u, \\ \\ {{{\bar {k}}}^{2}}\, = \,\frac{{4(x + a)R\sqrt {1 - {{g}^{2}}(u)} }}{{{{R}^{2}}\, + \,{{z}^{2}}\, + \,{{{(x\, + \,a)}}^{2}}\, + \,2(x\, + \,a)[R\sqrt {1\, - \,{{g}^{2}}(u)} \, - \,zg(u)]}}. \\ \end{gathered} $

Внешний потенциал R-тороида (21) можно представить и в виде ряда. После некоторых преобразований (см. Приложение) получим

(24)

$\begin{gathered} {{\Phi }_{{{\text{out}}}}}(R,z) = \frac{{2GM}}{{{{\pi }^{3}}}} \times \\ \times \;\sum\limits_{n,m = 0}^\infty {\left[ {{{{\left. {\frac{{{{a}^{n}}{{e}^{n}}(e{{P}_{{n + 1}}} + {{P}_{n}})}}{{n!}}\frac{{{{P}_{m}}{{{\sin }}^{m}}i}}{{m!}}\frac{{{{\partial }^{{n + m}}}\bar {F}(R,z,a,g)}}{{\partial {{a}^{n}}\partial {{g}^{m}}}}} \right|}}_{{g = 0}}}} \right]} , \\ \end{gathered} $

где введены коэффициенты с целочисленным неотрицательным индексом

(25)

${{P}_{n}} = \left\{ \begin{gathered} 1,\quad n = 0; \hfill \\ 0,\quad n = 2l - 1\quad (l = 1,\;2,\;3,\;...); \hfill \\ \frac{{(n - 1){\kern 1pt} !{\kern 1pt} !}}{{n{\kern 1pt} !{\kern 1pt} !}},\quad n = 2l\quad (l = 1,\;2,\;3,\;...). \hfill \\ \end{gathered} \right.$

Так как на внешней поверхности R-тороида (где r = Q) плотность (9) имеет сингулярность $\rho (r = Q) \to \infty $, то при приближении пробной точки к веществу R-тороида ряд (24) будет сходиться все медленнее, и внутри вещества этот ряд вообще неприменим.

Формулу (24) можно представить в более наглядном виде, если рассматривать ее как ряд для потенциала R-тороида по степеням малых $e$ и $i$. Тогда, с точностью до второй степени $e$ и $\sin i$, этот ряд примет вид

(26)

$\begin{gathered} \Phi (R,z) = \frac{{2GM}}{{\pi \sqrt {{{{(R + a)}}^{2}} + {{z}^{2}}} }}({{\varphi }_{0}} + {{\varphi }_{2}}); \\ {{\varphi }_{0}} = K(k);\quad k = 2\sqrt {\frac{{Ra}}{{{{{(R + a)}}^{2}} + {{z}^{2}}}}} ; \\ \end{gathered} $

(27)

${{\varphi }_{2}} = \frac{{{{e}^{2}} - {{{\sin }}^{2}}i}}{{8({{{(R + a)}}^{2}} + {{z}^{2}})({{{(R - a)}}^{2}} + {{z}^{2}})}}\left( {\frac{{({{R}^{2}} + {{a}^{2}} + {{z}^{2}})({{{(R - a)}}^{2}} + z(z + 2a))({{{(R - a)}}^{2}} + z(z - 2a))}}{{{{{(R - a)}}^{2}} + {{z}^{2}}}} \times } \right.$

$\left. {\mathop { \times \;E(k) - (({{R}^{2}} - {{a}^{2}}) + {{z}^{2}}(2{{R}^{2}} + {{z}^{2}}))K(k)}\limits_{_{{_{{}}}}} } \right).$

Обратим внимание на присутствие в числителе φ₂ выражения ${{e}^{2}} - {{\sin }^{2}}i;$ так как члены этой комбинации имеют разные знаки, эксцентриситет кольца и его наклон во втором приближении могут взаимно компенсировать вклад друг друга в потенциал.

В частном случае i = 0, когда R-тороид превращается в плоское широкое R-кольцо, усеченный потенциал (26) в точках главной плоскости (при z = 0) примет вид

(28)

$\begin{gathered} \Phi (R) = \frac{{2GM}}{{\pi (R + a)}} \times \\ \times \;\left\{ {K(k) + \frac{{{{e}^{2}}}}{8}\left( {\frac{{{{R}^{2}} + {{a}^{2}}}}{{{{{(R - a)}}^{2}}}}E(k) - K(k)} \right)} \right\}, \\ k = \frac{{2\sqrt {Ra} }}{{R + a}}. \\ \end{gathered} $

Здесь R – расстояние от центра R-кольца до пробной точки, a – внешний радиус R-кольца (большая полуось исходного кольца Гаусса), e – эксцентриситет исходного кольца Гаусса. Отметим, что полный потенциал R-кольца в главной плоскости ранее был получен в [8].

Кроме того, потенциал R-тороида можно представить в виде ряда по малым величинам обратных расстояний $\frac{a}{r}$. Для этого заметим, что подынтегральный множитель в (12) есть производящая функция для полиномов Лежандра ${{\bar {P}}_{n}}(\cos \psi )$

(29)

$\begin{gathered} \frac{1}{{\sqrt {{{r}^{2}} + {{{(x + a)}}^{2}} - 2r(x + a)\cos \psi } }} = \\ = \frac{1}{r}\sum\limits_{n = 0}^\infty {{{{\bar {P}}}_{n}}(\cos \psi ){{{\left( {\frac{{x + a}}{r}} \right)}}^{n}}} ; \\ \end{gathered} $

подставляя тогда (29) в интегральное выражение (12), в итоге получим требуемый ряд

(30)

$\begin{gathered} {{\Phi }_{{{\text{out}}}}}(r,\theta ) = \\ = \frac{{GM}}{r}\sum\limits_{n = 0}^\infty {\left\{ {{{{( - 1)}}^{n}}{{P}_{{2n}}}{\kern 1pt} \sum\limits_{k = 0}^n {\left[ {\frac{{(2n + 1){\kern 1pt} !{{P}_{{2k}}}{{e}^{{2k}}}}}{{(2(n - k) + 1){\kern 1pt} !(2k){\kern 1pt} !}}} \right]} } \right. \times } \\ \times \;\left. {{{{\bar {P}}}_{{2n}}}(\cos i){{{\bar {P}}}_{{2n}}}(\sin \theta ){{{\left( {\frac{a}{r}} \right)}}^{{2n}}}} \right\}. \\ \end{gathered} $

В частности, с точностью до 4-й степени по $\frac{a}{r}$ включительно ряд (30) имеет вид

${{\Phi }_{{{\text{out}}}}}\left( {r,\theta } \right) = \frac{{GM}}{r} \times $

(31)

$\begin{gathered} \times \;\left\{ {1 - \frac{1}{2}\left( {1 + \frac{3}{2}{{e}^{2}}} \right){{{\bar {P}}}_{2}}(\cos i){{{\bar {P}}}_{2}}(\sin \theta ){{{\left( {\frac{a}{r}} \right)}}^{2}} + } \right. \\ + \;\frac{3}{8}\left( {1 + 5{{e}^{2}} + \frac{{15}}{8}{{e}^{4}}} \right) \times \\ \end{gathered} $

$\left. { \times \;{{{\bar {P}}}_{4}}(\cos i){{{\bar {P}}}_{4}}(\sin \theta ){{{\left( {\frac{a}{r}} \right)}}^{4}} + O\left( {{{{\left( {\frac{a}{r}} \right)}}^{6}}} \right)} \right\},$

где полиномы Лежандра 2-й и 4-й степеней в явном виде

(32)

${{\bar {P}}_{2}}(x) = \frac{{3{{x}^{2}} - 1}}{2};\quad {{\bar {P}}_{4}}(x) = \frac{{35{{x}^{4}} - 30{{x}^{2}} + 3}}{8}.$

6. ВЗАИМНАЯ ЭНЕРГИЯ “R-ТОРОИД–КОЛЬЦО ГАУССА”. УРАВНЕНИЯ ЭВОЛЮЦИИ КОЛЬЦА

Для вывода уравнений вековой эволюции внешней орбиты в гравитационном поле R-тороида необходимо знать взаимную (потенциальную) энергию R-тороида и кольца Гаусса, представляющего орбиту. Интегрируя выражение внешнего потенциала R-тороида (31) по внешней оскулирующей орбите с распределением массы (2), получим указанную взаимную энергию тел в виде

(33)

${{W}_{{{\text{mut}}}}} = - \frac{{M{\kern 1pt} '{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{2\pi }}\int\limits_0^{2\pi } {\frac{{{{\Phi }_{{{\text{out}}}}}(r{\kern 1pt} ',\varphi {\kern 1pt} ',\theta {\kern 1pt} ')d{v}{\kern 1pt} '}}{{{{{(1 + e{\kern 1pt} '\cos {v}{\kern 1pt} ')}}^{2}}}}} ,$

где верхний штрих $(\,){\kern 1pt} '$ обозначает параметры, которые относятся к кольцу Гаусса. Сделаем в (33) замены

(34)

$\begin{gathered} r{\kern 1pt} ' = \frac{{a{\kern 1pt} '(1 - e{\kern 1pt} {{'}^{2}})}}{{1 + e{\kern 1pt} '\cos {v}{\kern 1pt} '}},\quad \sin \theta {\kern 1pt} ' = \sin ({v}{\kern 1pt} {\text{'}} + \omega {\kern 1pt} ')\sin i{\kern 1pt} ', \\ \cos \theta {\kern 1pt} ' = \sqrt {1 - {{{\sin }}^{2}}({v}{\kern 1pt} {\text{'}} + \omega {\kern 1pt} '){{{\sin }}^{2}}i{\kern 1pt} '} . \\ \end{gathered} $

Интегрируя (33) с учетом (31) и замен (34), получим взаимную энергию ${{W}_{{{\text{mut}}}}}$ R-тороида и кольца Гаусса в виде усеченного ряда

$\begin{gathered} {{W}_{{{\text{mut}}}}} = - \frac{{GMM{\kern 1pt} '}}{{a{\kern 1pt} '}}\left\{ {1 + \frac{1}{{4{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{{3/2}}}}}\left( {1 + \frac{3}{2}{{e}^{2}}} \right)} \right. \times \\ \times \,{{{\bar {P}}}_{2}}(\cos i){{{\bar {P}}}_{2}}\left( {\cos i{\kern 1pt} '} \right){{\left( {\frac{a}{{a'}}} \right)}^{2}} + \frac{9}{{64{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{{7/2}}}}} \times \\ \end{gathered} $

(35)

$ \times \;\left( {1 + 5{{e}^{2}} + \frac{{15}}{8}{{e}^{4}}} \right){{\bar {P}}_{4}}(\cos i){{\left( {\frac{a}{{a{\kern 1pt} '}}} \right)}^{4}} \times $

$\begin{gathered} \times \;\left[ {\left( {1 + \frac{1}{2}e{\kern 1pt} {{'}^{2}}} \right){{{\bar {P}}}_{4}}(\cos i{\kern 1pt} ') + \frac{{e{\kern 1pt} {{'}^{2}}}}{4}(5{{{\cos }}^{2}}i{\kern 1pt} '\; - 1) - } \right. \\ \left. {\mathop - \limits_{}^{} \;\left. {\frac{{5e{\kern 1pt} {{'}^{2}}{{{\sin }}^{2}}i{\kern 1pt} '{{{\sin }}^{2}}\omega {\kern 1pt} '}}{4}(7{{{\cos }}^{2}}i{\kern 1pt} ' - 1)} \right]} \right\} \\ \end{gathered} $

Рассмотрим теперь эволюцию гауссова кольца в силовом поле R-тороида. При этом исходим из известных уравнений Лагранжа эволюции оскулирующего эллипса. Важной особенностью данной задачи является то, что функция возмущения у нас заменяется (с точностью до коэффициента пропорциональности, см. статью [6]) найденной выше функцией взаимной энергии колец Гаусса (35):

(36)

$R(e{\kern 1pt} ',i{\kern 1pt} ',\omega {\kern 1pt} ') = - \frac{{{{W}_{{{\text{mut}}}}}}}{{M{\kern 1pt} '}}.$

Обратим внимание: так как функция $R(e{\kern 1pt} ',i{\kern 1pt} ',\omega {\kern 1pt} ')$ зависит только от трех параметров кольца Гаусса, сами уравнения Лагранжа заметно упрощаются и принимают вид

$\frac{{de{\kern 1pt} '}}{{dt}} = - \frac{{\sqrt {1 - e{\kern 1pt} {{'}^{2}}} }}{{e{\kern 1pt} 'n{\kern 1pt} 'a{\kern 1pt} {{'}^{2}}}}\frac{{\partial R}}{{\partial {\kern 1pt} '\omega }},$

(37)

$\begin{gathered} \frac{{di{\kern 1pt} '}}{{dt}} = \frac{{\cos i{\kern 1pt} '}}{{n{\kern 1pt} 'a{\kern 1pt} {{'}^{2}}\sqrt {1 - e{\kern 1pt} {{'}^{2}}} \sin i{\kern 1pt} '}}\frac{{\partial R}}{{\partial \omega {\kern 1pt} '}}, \\ \frac{{d\omega {\kern 1pt} '}}{{dt}} = \frac{{\sqrt {1 - e{\kern 1pt} {{'}^{2}}} }}{{e{\kern 1pt} 'n{\kern 1pt} 'a{\kern 1pt} {{'}^{2}}}}\frac{{\partial R}}{{\partial e{\kern 1pt} '}} - \cos i{\kern 1pt} '\frac{{d\Omega {\kern 1pt} '}}{{dt}}, \\ \end{gathered} $

$\frac{{d\Omega {\kern 1pt} '}}{{dt}} = \frac{1}{{n{\kern 1pt} 'a{\kern 1pt} {{'}^{2}}\sqrt {1 - e{\kern 1pt} {{'}^{2}}} \sin i{\kern 1pt} '}}\frac{{\partial R}}{{\partial i{\kern 1pt} '}}.$

Отметим, что в (37) есть только четыре уравнения, так как большая полуось a' = const.

Используя теперь ${{W}_{{{\text{mut}}}}}$ из (36) и (35), после многих выкладок из (37) получим требуемые уравнения эволюции кольца Гаусса в силовом поле R-тороида:

(38)

$\begin{gathered} {{\left( {\frac{{de{\kern 1pt} '}}{{dt}}} \right)}_{p}} = \frac{{15n{\kern 1pt} '}}{{16}}C_{{40}}^{p}\frac{M}{{{{M}_{*}}}}{{\left( {\frac{a}{{a{\kern 1pt} '}}} \right)}^{4}} \times \\ \times \;\frac{{{{{\sin }}^{2}}i{\kern 1pt} '(7{{{\cos }}^{2}}i{\kern 1pt} '\; - 1)e{\kern 1pt} '\sin \omega {\kern 1pt} '\cos \omega {\kern 1pt} '}}{{{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{3}}}}; \\ \end{gathered} $

(39)

$\begin{gathered} {{\left( {\frac{{di{\kern 1pt} '}}{{dt}}} \right)}_{p}} = - \frac{{15n{\kern 1pt} '}}{{16}}C_{{40}}^{p}\frac{M}{{{{M}_{*}}}}{{\left( {\frac{a}{{a{\kern 1pt} '}}} \right)}^{4}} \times \\ \times \;\frac{{\sin i{\kern 1pt} '\cos i{\kern 1pt} '(7{{{\cos }}^{2}}i{\kern 1pt} '\; - 1)e{\kern 1pt} {{'}^{2}}\sin \omega {\kern 1pt} '\cos \omega {\kern 1pt} '}}{{{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{4}}}}; \\ \end{gathered} $

(40)

${{\left( {\frac{{d\Omega {\kern 1pt} '}}{{dt}}} \right)}_{p}} = \frac{{3n{\kern 1pt} '}}{2}C_{{20}}^{p}\frac{M}{{{{M}_{*}}}}{{\left( {\frac{a}{{a{\kern 1pt} '}}} \right)}^{2}}\frac{{\cos i{\kern 1pt} '}}{{{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{2}}}};$

(41)

${{\left( {\frac{{d\omega {\kern 1pt} '}}{{dt}}} \right)}_{p}} = - \frac{{3n{\kern 1pt} '}}{4}C_{{20}}^{p}\frac{M}{{{{M}_{*}}}}{{\left( {\frac{a}{{a{\kern 1pt} '}}} \right)}^{2}}\frac{{5{{{\cos }}^{2}}i{\kern 1pt} '\; - 1}}{{{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{2}}}},$

где ${{M}_{*}}$ – масса центральной звезды, M – масса планеты (R-тороида). Уравнения (38)–(41) даны в системе отсчета, где главной плоскостью является плоскость Лапласа для системы звезда–планета.

Кроме того, в той ситуации, когда надо учитывать также влияние центральной звезды, уравнения эволюции кольца Гаусса следует записать в потенциале этой звезды, разложенном по сферическим гармоникам:

(42)

$\begin{gathered} {{\left( {\frac{{de{\kern 1pt} '}}{{dt}}} \right)}_{c}} = \frac{{15n{\kern 1pt} '}}{{16}}C_{{40}}^{c}{{\left( {\frac{{{{R}_{*}}}}{{a{\kern 1pt} '}}} \right)}^{4}} \times \\ \times \;\frac{{{{{\sin }}^{2}}i{\kern 1pt} '(7{{{\cos }}^{2}}i{\kern 1pt} '\; - 1)e{\kern 1pt} '\sin \omega {\kern 1pt} '\cos \omega {\kern 1pt} '}}{{{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{3}}}}; \\ \end{gathered} $

(43)

$\begin{gathered} {{\left( {\frac{{di{\kern 1pt} '}}{{dt}}} \right)}_{c}} = - \frac{{15n{\kern 1pt} '}}{{16}}C_{{40}}^{c}{{\left( {\frac{{{{R}_{*}}}}{{a{\kern 1pt} '}}} \right)}^{4}} \times \\ \times \;\frac{{\sin i{\kern 1pt} '\cos i{\kern 1pt} '(7{{{\cos }}^{2}}i{\kern 1pt} '\; - 1)e{\kern 1pt} {{'}^{2}}\sin \omega {\kern 1pt} '\cos \omega {\kern 1pt} '}}{{{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{4}}}}; \\ \end{gathered} $

(44)

${{\left( {\frac{{d\Omega {\kern 1pt} '}}{{dt}}} \right)}_{c}} = \frac{{3n{\kern 1pt} '}}{2}C_{{20}}^{c}{{\left( {\frac{{{{R}_{*}}}}{{a{\kern 1pt} '}}} \right)}^{2}}\frac{{\cos i{\kern 1pt} '}}{{{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{2}}}};$

(45)

${{\left( {\frac{{d\omega {\kern 1pt} '}}{{dt}}} \right)}_{c}} = - \frac{{3n{\kern 1pt} '}}{4}C_{{20}}^{c}{{\left( {\frac{{{{R}_{*}}}}{{a{\kern 1pt} '}}} \right)}^{2}}\frac{{5{{{\cos }}^{2}}i{\kern 1pt} ' - 1}}{{{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{2}}}},$

где ${{R}_{*}}$ – среднеобъемный радиус центрального тела. Подчеркнем: в (42)–(45) главная плоскость проходит через экватор центральной звезды.

Коэффициенты гармоник поля R-тороида при нормировочном радиусе $R = a$ равны (см. (31)):

(46)

$\begin{gathered} C_{{20}}^{p} = - \frac{1}{2}\left( {1 + \frac{3}{2}{{e}^{2}}} \right){{{\bar {P}}}_{2}}(\cos i); \\ C_{{40}}^{p} = \frac{3}{8}\left( {1 + 5{{e}^{2}} + \frac{{15}}{8}{{e}^{4}}} \right){{{\bar {P}}}_{4}}(\cos i). \\ \end{gathered} $

Коэффициенты (46) понадобятся в разделе 7.4 для вычисления частот прецессии орбиты экзопланеты.

7. ПРИМЕРЫ ПРИМЕНЕНИЯ МОДЕЛИ R-ТОРОИДА

7.1. Отношение периодов нодальной и апсидальной прецессии орбиты

С помощью уравнений (40) и (41) находим отношение периодов прецессии для внешней орбиты пробной планеты (оскулирующего кольца Гаусса)

(47)

$\frac{{T_{\Omega }^{'}}}{{T_{\omega }^{'}}} = \frac{{\dot {\omega }{\kern 1pt} '}}{{\dot {\Omega }{\kern 1pt} '}} = - \frac{{5{{{\cos }}^{2}}i{\kern 1pt} '\; - 1}}{{2\cos i{\kern 1pt} '}} \approx - 2\left( {1 - \frac{3}{4}i{\kern 1pt} {{'}^{2}}\; + O(i{\kern 1pt} {{'}^{6}})} \right).$

Из (47) следует, что модуль отношения периодов нодальной и апсидальной прецессий кольца Гаусса, находящегося в гравитационном поле R-тороида, оказывается чуть меньше 2:

(48)

$\left| {\frac{{T_{\Omega }^{'}}}{{T_{\omega }^{'}}}} \right| \leqslant 2.$

Для сравнения заметим, что если экзопланета находится на орбите, близкой к центральной звезде и влиянием других тел можно пренебречь, отношение периодов прецессии орбиты можно оценить по формуле (см. [9])

(49)

$\frac{{{{T}_{\Omega }}}}{{{{T}_{\omega }}}} = \frac{{5{{{\cos }}^{2}}i - 1}}{{2\cos i}}.$

В частности, при $i = 0$ уравнение (49) дает ${{{{T}_{\Omega }}} \mathord{\left/ {\vphantom {{{{T}_{\Omega }}} {{{T}_{\omega }}}}} \right. \kern-0em} {{{T}_{\omega }}}} = 2$. Этот результат подтвержден при моделировании экзопланеты KOI 120.01 [10].

Полезными являются также выражения для отношений периодов прецессии ${{{{T}_{\Omega }}} \mathord{\left/ {\vphantom {{{{T}_{\Omega }}} {{{T}_{\omega }}}}} \right. \kern-0em} {{{T}_{\omega }}}}$ для двух колец, полученные в рамках известной двупланетной задачи. В этом случае возмущение движения происходит от взаимодействия орбит, представленных кольцами Гаусса. Тогда, согласно [6], для модулей отношения периодов прецессии первого и второго кольца в линейном приближении находим $\left( {\kappa = \frac{{{{a}_{2}}}}{{{{a}_{1}}}}} \right)$:

(50)

$\begin{gathered} \frac{{{{T}_{{1\Omega }}}}}{{{{T}_{{1\omega }}}}} = \frac{{{{M}_{1}} + 2{{M}_{2}}\sqrt \kappa }}{{{{M}_{1}} + {{M}_{2}}\sqrt \kappa }}; \\ \frac{{{{T}_{{2\Omega }}}}}{{{{T}_{{2\omega }}}}} = \frac{{2{{M}_{1}} + {{M}_{2}}\sqrt \kappa }}{{{{M}_{1}} + {{M}_{2}}\sqrt \kappa }}. \\ \end{gathered} $

Например, для Юпитера и Сатурна наблюдения дают [11]

(51)

$\begin{gathered} {{M}_{J}} = {\text{1}}{\text{.9096}} \times {{10}^{{30}}}\;{\text{г}},\quad {{a}_{1}} = 7.783 \times {{10}^{{13}}}\;{\text{см}},{\text{ }} \\ {{M}_{S}} = {\text{ 5}}{\text{.71674 }} \times {{10}^{{29}}}\;{\text{г}}, \\ {{a}_{2}} = 1.4294 \times {{10}^{{14}}}\;{\text{см}}. \\ \end{gathered} $

Тогда первое из уравнений (50) для Юпитера дает ${{{{T}_{{J\Omega }}}} \mathord{\left/ {\vphantom {{{{T}_{{J\Omega }}}} {{{T}_{{J\omega }}}}}} \right. \kern-0em} {{{T}_{{J\omega }}}}} \approx {\text{1}}{\text{.181}}$. Это величина действительно близка к той, которую дают современные расчеты ${{{{T}_{{J\Omega }}}} \mathord{\left/ {\vphantom {{{{T}_{{J\Omega }}}} {{{T}_{{J\omega }}}}}} \right. \kern-0em} {{{T}_{{J\omega }}}}} \approx {\text{1}}{\text{.219}}$, что подтверждает адекватность применения метода в двупланетной задаче.

7.2. Планеты-гиганты Солнечной системы

Как отмечалось, модель R-тороида предназначена для изучения вековой эволюции внешних орбит, большие полуоси которых превышают некоторое критическое (минимальное) значение ${{a}_{{{\text{min}}}}}$. При известном периоде узловой прецессии орбиты возмущающего тела ${{T}_{\Omega }}$, значение ${{a}_{{{\text{min}}}}}$ рассчитывается по формуле

(52)

${{a}_{{\min }}} \approx {{\left( {\frac{{\sqrt \mu }}{{2\pi }}{{T}_{\Omega }}} \right)}^{{2/3}}}.$

Здесь $\mu = G({{M}_{*}} + {{M}_{p}})$ – гравитационный параметр системы.

Вначале рассмотрим модель R-тороида для двух планет-гигантов Солнечной системы. Начнем с Юпитера. Требуется знать два периода: период движения планеты вокруг Солнца ${{T}_{{{\text{orb}}}}} \approx $ $ \approx 11.86233\;{\text{лет}}$ и период прецессии узла орбиты Юпитера ${{T}_{{J\Omega }}}$. По данным [12], в линейном приближении частота движения узла орбиты Юпитера равна:

(53)

$\frac{d}{{dt}}{{\Omega }_{J}} \approx 6362_{.}^{{''}}03561.$

(время в столетиях). Следовательно, соответствующий период прецессии будет примерно равен ${{T}_{{J\Omega }}} \approx 20370.84\;{\text{лет}}$. Угол наклона орбиты Юпитера к эклиптике в настоящее время мал и равен $i \approx 1_{.}^{^\circ }30327,$ но в прошлом, согласно расчетам в рамках двупланетной задачи [9, 11], он мог достигать и больших значений $i \approx 2_{.}^{^\circ }5.$ Ширина R-кольца для Юпитера равна $2ea \approx 0.50\;{\text{а}}.{\text{е}}.$ Так как характерное время создания R-тороида для Юпитера равно ${{T}_{\Omega }} \approx 20370.84\;{\text{лет}}$, то на меньших масштабах времени фигура R-тороида для Юпитера не будет полной. Отсюда следует, что можно рассматривать вековое влияние R-тороида Юпитера только на те небесные тела, большие полуоси орбит у которых удовлетворяют неравенству $a \geqslant \;747$ а.е. Аналогичные расчеты для Сатурна приводятся в табл. 1.

Таблица 1.

Периоды узловой прецессии и соответствующие ${{a}_{{{\text{min}}}}}$ для R-тороидов двух планет-гигантов

Планета	${{T}_{\Omega }}$, годы	${{a}_{{{\text{min}}}}}$, а.е.
Юпитер	20 370.84	747
Сатурн	14 025.67	582.4

Для Сатурна величина ${{a}_{{\min }}} \geqslant 582$ а.е. оказывается даже меньше, чем для Юпитера. Следовательно, модели R-тороидов для Юпитера и Сатурна позволяют рассчитать вековые эффекты не только на движение гипотетической Планеты 9 (с принятыми для нее параметрами $a \approx 400{\kern 1pt} - $ 800 а.е. [13, 14]), но также на движение седноидов [15] и некоторых экстремальных транснептуновых объектов (eTNO).

7.3. Экзопланеты

В последние годы исследование внесолнечных планетных систем идет бурными темпами, и постоянный приток новых данных ставит новые задачи.

Для решения этих задач перспективным является применение модели R-тороида к экзопланетам. Особый интерес вызывает класс горячих юпитеров, имеющих тесные орбиты и большие массы [16]. В литературе уже появились некоторые данные, указывающие, что некоторые из таких планет, в отличие от планет Солнечной системы, могут иметь быструю узловую прецессию. Приведем некоторые примеры.

Kepler-413b

Планета Kepler-413b согласно работе Kostov et al. [17] относится к классу циркумбинарных экзопланет; она обращается с периодом ${{T}_{{{\text{orb}}}}} \approx 66.262~$ д. вокруг тесной пары звезд классов K и M с массами ${{M}_{1}} = 0.{\text{82}}0 \pm 0.0{\text{15\;}}\,{{M}_{ \odot }}$ и ${{M}_{2}} = 0.{\text{542}} \pm 0.00{\text{8}}\,{{M}_{ \odot }}$. Сами звезды обращаются вокруг центра масс всего за ${\text{1}}0.{\text{11615}} \pm 0.0000{\text{1}}$ дней по почти круговым $(e = 0.0{\text{37}} \pm 0.00{\text{2}})$ орбитам. Радиус и масса экзопланеты равны $R \approx 0.388{{R}_{J}}$, $M \approx 0.2110{{M}_{J}}.$ По этим характеристикам данная экзопланета близка к горячим Сатурнам. Параметры ее орбиты равны $e = 0.118$, $q \approx 0.3553$ а.е., $i \approx 30^\circ $. Для орбиты этой планеты известен также период узловой прецессии ${{T}_{\Omega }} \approx 11\;{\text{лет}}$ [17]. Следовательно, для данной планеты $\frac{{{{T}_{\Omega }}}}{{{{T}_{{{\text{orb}}}}}}} \approx 60.83$. По этим данным можно рассчитать критическое значение большой полуоси орбиты, которое оказывается равным ${{a}_{{\min }}} \approx 5.48$ а.е. Таким образом, для Kepler-413b модель R-тороида позволяет описывать эволюцию орбит, расположенных на умеренных (несколько астрономических единиц) расстояниях от центральной звезды.

WASP-33b

Эта планета классифицируется как ретроградный горячий юпитер [18] – одна из самых горячих известных экзопланет. Обращается вокруг звезды с массой $M \approx 1.5\,{{M}_{ \odot }}$ по очень тесной почти полярной орбите с полуосью $a = 0.02$ а.е. и исключительно малым периодом ${{T}_{{{\text{orb}}}}} \approx 1.22$ д. Вместе с тем частота движения восходящего узла довольна умеренная и равна $\dot {\Omega } \approx 0.373^\circ $ лет^–1, что соответствует периоду нодальной прецессии ${{T}_{\Omega }} \approx 965$ лет. Следовательно, для этой экзопланеты ${{a}_{{\min }}} \approx 112$ а.е., т.е. модель R-тороида позволяет описывать эволюцию только орбит, далеких от центральной звезды.

7.4. Расчет суммарного эффекта влияния несферичности прецессирующей звезды и возмущения от R-тороида планеты. Пример экзопланеты PTFO 8-8695b

Рассмотрим подробнее комбинированную модель, в которой на орбиту внешней (пробной) планеты учитывается возмущающее влияние от R-тороида внутренней планеты и гравитационное поле центральной прецессирующей звезды.

Согласно Raetz et al. [19] и Barnes et al. [20], экзопланета PTFO 8-8695b (горячий юпитер) движется по сильно наклоненной орбите вокруг центральной звезды. Параметры орбиты таковы: $a = 0.0084$ а.е. и ${{T}_{{{\text{orb}}}}} \approx 10.76$ ч., поэтому PTFO 8-8695b является одной из самых близко расположенных к своей звезде экзопланет. Критическое значение большой полуоси орбиты ${{a}_{{\min }}}$ для этой планеты (см. форм. (52)) составляет всего ${{a}_{{\min }}} \approx 0.2{\kern 1pt} - {\kern 1pt} 0.7$ а.е. Таким образом, модель R-тороида для планеты PTFO 8-8695b позволяет описывать эволюцию орбит даже тех тел, которые очень близко подходят к центральной звезде. Ирония в том, что вторая из известных планет в этой системе PTFO 8-8695с находится столь далеко от центральной звезды ($a = 662\;{\text{а}}.{\text{е}}.$), что влиянием внутренней планеты на нее вполне можно пренебречь.

Однако в системе PTFO-8-8695 мы можем рассмотреть эволюцию пробной внешней орбиты в гравитационном поле центральной звезды и R‑тороида планеты b. В статье [20] даны два максимально правдоподобных набора параметров (табл. 2).

Таблица 2.

Данные из статьи [20]. ${{M}_{}}$ – масса звезды; $M$ – масса планеты b; ${{R}_{}}$ – радиус звезды; $C_{{20}}^{c}$ – коэффициент второй зональной гармоники поля звезды; ${{\varphi }_{p}}$ – наклон орбитального момента планеты b к суммарному моменту звезды и планеты b; ${{\varphi }_{*}}$ – наклон спинового момента звезды к суммарному моменту звезды и планеты b; $\varphi $ – угол между моментами звезды и планеты b. Коэффициент $C_{{20}}^{c} = - Cf$ рассчитан нами, в [20] аналогичный коэффициент ${{j}_{2}} = 0.012.$

${{M}_{*}}$ [${{M}_{ \odot }}$]	$0.34$	$0.44$
$M$ [${{M}_{J}}$]	$3.0 \pm 0.2$	$3.6 \pm 0.3$
${{R}_{*}}$ [${{R}_{ \odot }}$]	$1.04 \pm 0.01$	$1.03 \pm 0.01$
$C_{{20}}^{c}$	$ - 0.0064$	$ - 0.0049$
${{\varphi }_{p}}\;[^\circ ]$	$51$	$52.9$
${{\varphi }_{*}}\;[^\circ ]$	$18$	$20.2$
$\varphi \;[^\circ ]$	$69 \pm 3$	$73.1 \pm 0.6$

Далее рассмотрим только прецессию линии узлов и линии апсид пробной планеты. Напомним, что уравнения (40) и (41) записаны для случая, когда главной плоскостью является плоскость Лапласа для системы звезда–планета b, а уравнения (44) и (45) – когда главная плоскость проходит через экватор центрального тела. Чтобы найти суммарный эффект влияния несферичности звезды и возмущения от планеты b, нужно привести уравнения к единой главной плоскости, в качестве которой выберем плоскость Лапласа уравнений (40) и (41).

Введем, согласно [9], дополнительное уравнение

(54)

$\begin{gathered} {{\left( {\frac{{d\omega {\kern 1pt} '{\kern 1pt} '}}{{dt}}} \right)}_{c}} + \cos i{\kern 1pt} '{\kern 1pt} '{{\left( {\frac{{d\Omega {\kern 1pt} '{\kern 1pt} '}}{{dt}}} \right)}_{c}} = \\ = \; - {\kern 1pt} \frac{{3n{\kern 1pt} '}}{4}C_{{20}}^{c}{{\left( {\frac{R}{{a{\kern 1pt} '}}} \right)}^{2}}\frac{{3{{{\cos }}^{2}}i{\kern 1pt} '{\kern 1pt} '\; - 1}}{{{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{2}}}}, \\ \end{gathered} $

где с помощью верхних штрихов $(\,){\kern 1pt} '{\kern 1pt} '$ обозначаются углы в системе с экваториальной плоскостью звезды в качестве главной. Как показано в [9], значение левой и правой частей уравнения (54) при переходе в другую главную плоскость не меняется, т.е.

(55)

${{\left( {\frac{{d\omega {\kern 1pt} '}}{{dt}}} \right)}_{c}} + \cos i{\kern 1pt} '{{\left( {\frac{{d\Omega {\kern 1pt} '}}{{dt}}} \right)}_{c}} = {{\left( {\frac{{d\omega {\kern 1pt} '{\kern 1pt} '}}{{dt}}} \right)}_{c}} + \cos i{\kern 1pt} '{\kern 1pt} '{{\left( {\frac{{d\Omega {\kern 1pt} '{\kern 1pt} '}}{{dt}}} \right)}_{c}}$

и, кроме того, согласно той же работе [9],

(56)

$\begin{gathered} \cos i{\kern 1pt} '{\kern 1pt} ' = \cos i{\kern 1pt} '\cos {{\varphi }_{*}} + \sin i{\kern 1pt} '\sin {{\varphi }_{*}}\cos \Delta \Omega ; \\ \cos \Delta \bar {\omega } = \frac{{\sin i{\kern 1pt} '\cos {{\varphi }_{*}} - \cos i{\kern 1pt} '\sin {{\varphi }_{*}}\cos \Delta \Omega }}{{\sin i{\kern 1pt} '{\kern 1pt} '}}; \\ {{\left( {\frac{{d\Omega {\kern 1pt} '}}{{dt}}} \right)}_{c}} = \frac{{\cos \Delta \bar {\omega }}}{{\sin i{\kern 1pt} '}}\sin i{\kern 1pt} '{\kern 1pt} '{{\left( {\frac{{d\Omega {\kern 1pt} '{\kern 1pt} '}}{{dt}}} \right)}_{c}}. \\ \end{gathered} $

Используя (54)–(56), приводим уравнения (44) и (45) к виду

(57)

$\begin{gathered} {{\left( {\frac{{d\Omega {\kern 1pt} '}}{{dt}}} \right)}_{c}} = \frac{{3n{\kern 1pt} '}}{2}C_{{20}}^{c}{{\left( {\frac{{{{R}_{*}}}}{{a{\kern 1pt} '}}} \right)}^{2}} \times \\ \times \;\frac{{\cos i{\kern 1pt} '\cos {{\varphi }_{*}} + \sin i{\kern 1pt} '\sin {{\varphi }_{*}}\cos \Delta \Omega }}{{{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{2}}}} \times \\ \times \;\left( {\cos {{\varphi }_{*}} - \frac{{\cos i{\kern 1pt} '}}{{\sin i{\kern 1pt} '}}\sin {{\varphi }_{*}}\cos \Delta \Omega } \right); \\ \end{gathered} $

(58)

$\begin{gathered} {{\left( {\frac{{d\omega {\kern 1pt} '}}{{dt}}} \right)}_{c}} = - \frac{{3n{\kern 1pt} '}}{4}C_{{20}}^{c}{{\left( {\frac{{{{R}_{*}}}}{{a{\kern 1pt} '}}} \right)}^{2}} \times \\ \times \;\frac{{3{{{(\cos i{\kern 1pt} '\cos {{\varphi }_{*}} + \sin i{\kern 1pt} '\sin {{\varphi }_{*}}\cos \Delta \Omega )}}^{2}} - 1}}{{{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{2}}}} - \\ - \;\cos i{\kern 1pt} '{{\left( {\frac{{d\Omega {\kern 1pt} '}}{{dt}}} \right)}_{c}}. \\ \end{gathered} $

Учитывая, что ось вращения звезды прецессирует очень быстро (~45 д.) по сравнению с прецессией орбиты пробной планеты (~10⁶ лет), уравнения (57) и (58) следует усреднить по быстрой переменной $\Delta \Omega $; тогда получим

(59)

${{\left( {\frac{{d\Omega {\kern 1pt} '}}{{dt}}} \right)}_{c}} = \frac{{3n{\kern 1pt} '}}{2}C_{{20}}^{c}{{\left( {\frac{{{{R}_{*}}}}{{a{\kern 1pt} '}}} \right)}^{2}}\frac{{3{{{\cos }}^{2}}{{\varphi }_{*}} - 1}}{2}\frac{{\cos i{\kern 1pt} '}}{{{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{2}}}};$

(60)

${{\left( {\frac{{d\omega {\kern 1pt} '}}{{dt}}} \right)}_{c}} = - \frac{{3n{\kern 1pt} '}}{4}C_{{20}}^{c}{{\left( {\frac{{{{R}_{*}}}}{{a{\kern 1pt} '}}} \right)}^{2}}\frac{{3{{{\cos }}^{2}}{{\varphi }_{*}} - 1}}{2}\frac{{5{{{\cos }}^{2}}i{\kern 1pt} '\; - 1}}{{{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{2}}}}.$

Из формул (40), (41), (49), (59) и (60) получим уравнения для прецессии линий узлов и линии апсид под влиянием несферичности звезды совместно с влиянием планеты b

(61)

$\begin{gathered} \frac{{d\Omega {\kern 1pt} '}}{{dt}} = \frac{{3n{\kern 1pt} '}}{2}\left[ {C_{{20}}^{c}{{{\left( {\frac{{{{R}_{*}}}}{{a{\kern 1pt} '}}} \right)}}^{2}}\frac{{3{{{\cos }}^{2}}{{\varphi }_{*}} - 1}}{2} + } \right. \\ + \;\left. {C_{{20}}^{p}\frac{M}{{{{M}_{*}}}}{{{\left( {\frac{a}{{a{\kern 1pt} '}}} \right)}}^{2}}} \right]\frac{{\cos i{\kern 1pt} '}}{{{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{2}}}}; \\ \end{gathered} $

(62)

$\begin{gathered} \frac{{d\omega {\kern 1pt} '}}{{dt}} = - \frac{{3n{\kern 1pt} '}}{4}\left[ {C_{{20}}^{c}{{{\left( {\frac{{{{R}_{*}}}}{{a{\kern 1pt} '}}} \right)}}^{2}}\frac{{3{{{\cos }}^{2}}{{\varphi }_{*}} - 1}}{2} + } \right. \\ + \;\left. {C_{{20}}^{p}\frac{M}{{{{M}_{*}}}}{{{\left( {\frac{a}{{a{\kern 1pt} '}}} \right)}}^{2}}} \right]\frac{{5{{{\cos }}^{2}}i{\kern 1pt} '\; - 1}}{{{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{2}}}}. \\ \end{gathered} $

Представим решение для угловых частот в таком виде

(63)

$\begin{gathered} \frac{{d\Omega {\kern 1pt} '}}{{dt}} = {{A}_{{\Omega {\kern 1pt} '}}}{{\left( {\frac{{1\;{\text{а}}{\text{.е}}{\text{.}}}}{{a{\kern 1pt} '}}} \right)}^{{7/2}}}\frac{{\cos i{\kern 1pt} '}}{{{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{2}}}}; \\ \frac{{d\omega {\kern 1pt} '}}{{dt}} = {{A}_{{\omega {\kern 1pt} '}}}{{\left( {\frac{{1\;{\text{а}}{\text{.е}}{\text{.}}}}{{a{\kern 1pt} '}}} \right)}^{{7/2}}}\frac{{5{{{\cos }}^{2}}i{\kern 1pt} '\; - 1}}{{4{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{2}}}}. \\ \end{gathered} $

Тогда периоды прецессии даются формулами

(64)

$\begin{gathered} {{T}_{{\Omega {\kern 1pt} '}}} = T_{{\Omega {\kern 1pt} '}}^{0}{{\left( {\frac{{a{\kern 1pt} '}}{{1\;{\text{а}}{\text{.е}}{\text{.}}}}} \right)}^{{7/2}}}\frac{{{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{2}}}}{{\left| {\cos i{\kern 1pt} '} \right|}}; \\ {{T}_{{\omega {\kern 1pt} '}}} = T_{{\omega {\kern 1pt} '}}^{0}{{\left( {\frac{{a{\kern 1pt} '}}{{1\;{\text{а}}{\text{.е}}{\text{.}}}}} \right)}^{{7/2}}}\frac{{4{{{(1 - e{\kern 1pt} {{'}^{2}})}}^{2}}}}{{\left| {5{{{\cos }}^{2}}i{\kern 1pt} '\; - 1} \right|}}, \\ \end{gathered} $

где коэффициенты даны в табл. 3. Результаты расчета по формулам (64) показаны на рис. 10.

Таблица 3.

Результаты расчета прецессии орбиты пробной планеты: величины $A_{{\omega {\kern 1pt} '}}^{c} = {{\left( {\frac{{d\omega {\kern 1pt} '}}{{dt}}} \right)}_{c}}$; $A_{{\Omega '}}^{c} = {{\left( {\frac{{d\Omega {\kern 1pt} '}}{{dt}}} \right)}_{c}}$; $A_{{\omega {\kern 1pt} '}}^{p} = {{\left( {\frac{{d\omega {\kern 1pt} '}}{{dt}}} \right)}_{p}}$; $A_{{\Omega {\kern 1pt} '}}^{p} = {{\left( {\frac{{d\Omega {\kern 1pt} '}}{{dt}}} \right)}_{p}}$; ${{A}_{{\omega {\kern 1pt} '}}} = \frac{{d\omega {\kern 1pt} '}}{{dt}}$; ${{A}_{{\Omega {\kern 1pt} '}}} = \frac{{d\Omega {\kern 1pt} '}}{{dt}}$; вычислены при а' = 1 а.е., e' = 0, i' = 0; $T_{{\omega {\kern 1pt} '}}^{0} = \frac{{2\pi }}{{\left| {{{A}_{{\omega {\kern 1pt} '}}}} \right|}}$; $T_{{\Omega {\kern 1pt} '}}^{0} = \frac{{2\pi }}{{\left| {{{A}_{{\Omega {\kern 1pt} '}}}} \right|}}$; $C_{{20}}^{p}$ и $C_{{40}}^{p}$ – коэффициенты 2-й и 4-й зональной гармоники поля R‑тороида планеты b

$A_{{\omega '}}^{c}\;\left[ {{{{10}}^{{ - 14}}}\;\frac{{{\text{рад}}}}{{\text{с}}}} \right]$	$4.5 \pm 0.1$	$3.66 \pm 0.07$
$A_{{\Omega '}}^{c}\;\left[ {{{{10}}^{{ - 14}}}\;\frac{{{\text{рад}}}}{{\text{с}}}} \right]$	$ - 2.25 \pm 0.05$	$ - 1.83 \pm 0.04$
$A_{{\omega '}}^{p}\;\left[ {{{{10}}^{{ - 14}}}\;\frac{{{\text{рад}}}}{{\text{с}}}} \right]$	$1.0 \pm 0.6$	$0.5 \pm 0.2$
$A_{{\Omega '}}^{p}\;\left[ {{{{10}}^{{ - 14}}}\;\frac{{{\text{рад}}}}{{\text{с}}}} \right]$	$ - 0.5 \pm 0.3$	$ - 0.25 \pm 0.08$
${{A}_{{\omega '}}}\;\left[ {{{{10}}^{{ - 14}}}\;\frac{{{\text{рад}}}}{{\text{с}}}} \right]$	$5.5 \pm 0.6$	$4.2 \pm 0.2$
${{A}_{{\Omega '}}}\;\left[ {{{{10}}^{{ - 14}}}\;\frac{{{\text{рад}}}}{{\text{с}}}} \right]$	$ - 2.7 \pm 0.3$	$ - 2.1 \pm 0.1$
$T_{{\omega '}}^{0}\;[{{10}^{6}}\;{\text{лет}}]$	$3.6 \pm 0.4$	$4.8 \pm 0.2$
$T_{{\Omega '}}^{0}\;[{{10}^{6}}\;{\text{лет}}]$	$7.3 \pm 0.8$	$9.6 \pm 0.4$
$C_{{20}}^{p}$	$ - 0.047 \pm 0.028$	$ - 0.023 \pm 0.005$
$C_{{40}}^{p}$	$ - 0.159 \pm 0.004$	$ - 0.154 \pm 0.002$

Рис. 10.

График зависимости периода прецессии долготы узла орбиты пробной планеты ${{\left. {\mathop {{{T}_{{\Omega {\kern 1pt} '}}}(a{\kern 1pt} ')}\limits_{} } \right|}_{\begin{subarray}{l} e{\kern 1pt} ' = 0 \\ i{\kern 1pt} ' = 0 \end{subarray} }}$, измеряемого в годах, от ее полуоси, измеряемой в a.e., в вырожденном случае $e{\kern 1pt} ' = 0$ и $i{\kern 1pt} ' = 0$. График представлен в логарифмической шкале по обеим осям. Сплошной линией показан результат для первого варианта ${{M}_{*}} = 0.34\,{{M}_{ \odot }}$, штрихованной линией – для второго варианта ${{M}_{*}} = 0.44\,{{M}_{ \odot }}$. Указаны границы оценки периода в пределах $1\sigma .$

График на рис. 10 построен от минимального значения полуоси пробной планеты a_min = 0.2 а.е. При таком значении полуоси орбиты оценка периода прецессии долготы восходящего узла для двух наборов входных параметров из табл. 2 ${{\left. {\mathop {{{T}_{{\Omega {\kern 1pt} '}}}}\limits_{} } \right|}_{\begin{subarray}{l} a{\kern 1pt} ' = {{a}_{{\min }}} \\ e{\kern 1pt} ' = 0 \\ i{\kern 1pt} ' = 0 \end{subarray} }} = $ [(26.1 ± 3.0 × 10³ лет; (34.3 ± 1.5) × × 10³ лет].

Так, в гравитационном поле прецессирующей несферичной звезды PTFO 8-8695 и R-тороида ближайшей к ней планеты PTFO 8-8695b минимальное значение периода нодальной прецессии пробной орбиты равно ${{T}_{\Omega }} \approx (26.1 \pm 3.0) \times {{10}^{3}}$ лет.

8. РЕЗУЛЬТАТЫ И ВЫВОДЫ

В этой статье построена новая модель для изучения вековых возмущений в небесной механике, названная R-тороидом. Метод построения R-тороида состоит из трех этапов: вначале движение усредняется по кеплеровскому эллипсу и получается одномерное кольцо Гаусса, затем усреднение прецессирующего кольца Гаусса по углу вращения линии апсид дает 2D R-кольцо; наконец, выполняя азимутальное усреднение прецессирующего R-кольца, получаем трехмерный R-тороид.

Распределение плотности внутри R-тороида является уникальным – его поверхность напоминает скорлупу с аномально высокой плотностью. Мы подробно изучаем гравитационный потенциал новой фигуры. Этот потенциал представлен не только в интегральной форме, но и в виде ряда как по степеням малых $e$ и $i,$ так и по обратным расстояниям пробной точки. Это позволило изучить зоны монотонного и немонотонного поведения потенциала и найти эквипотенциали. Методом интегрирования внешнего потенциала тороида по оскулирущей орбите была получена взаимная (потенциальная) энергия R-тороида и кольца Гаусса. Важность нахождения ${{W}_{{{\text{mut}}}}}$ объясняется тем, что именно она используется затем в качестве возмущающей функции для вывода системы уравнений эволюции оскулирующих колец в гравитационном поле R-тороида, а также в поле центральной прецессирующей звезды. Были найдены периоды нодальной ${{T}_{\Omega }}$ и апсидальной ${{T}_{\omega }}$ прецессии кольца; доказано, что при малом наклоне отношение ${{{{T}_{\Omega }}} \mathord{\left/ {\vphantom {{{{T}_{\Omega }}} {{{T}_{\omega }}}}} \right. \kern-0em} {{{T}_{\omega }}}}$ равно 2. Именно такое отношений для частот прецессий дают современные модели для экзопланет [10].

Рассмотрены примеры применения R-тороида. Установлено, что вековое влияние R-тороидов Сатурна и Юпитера распространяется на орбиты тел с полуосями, большими ${{a}_{{\min }}} \approx 582$ а.е. и ${{a}_{{\min }}} \approx 747$ а.е. соответственно. Следовательно, модель R-тороида можно применять для изучения вековой эволюции орбит тел в рассеянном диске Солнечной системы. Кроме того, эта модель позволяет изучать влияние планет-гигантов на движение гипотетической девятой планеты.

Перспективным является использование новой модели для изучения вековых эффектов в движении экзопланет, например, горячих юпитеров. Здесь параметры модели R-тороида были конкретизированы для трех экзопланет, время нодальной прецессии у которых известно. Показано, что среди огромного разнообразия внесолнечных систем существуют такие экзопланеты, для которых модель R-тороида позволяет описывать эволюцию орбит на умеренных, или даже близких расстояниях от центральной звезды. Так, для экзопланеты Kepler-413b R-тороид позволяет описывать эволюцию всех орбит с $a \geqslant 5.48$ а.е., а для экзопланеты PTFO 8-8695b критическое значение большой полуоси орбиты равно всего ${{a}_{{\min }}} \approx 0.20$ а.е.

В разделе 7.4 развит метод вычисления суммарного влияния гравитационного поля от центральной прецессирующей несферичной звезды и R-тороида ближней планеты PTFO 8-8695b на движение пробного тела. В частности, минимальное значение периода нодальной прецессии пробной орбиты оказалось равным ${{T}_{\Omega }} \approx (26.1 \pm 3.0) \times {{10}^{3}}$ лет.

Важно заметить, что модель R-тороида можно применять не только к планетам, но и к орбитам центральных звезд, вокруг которых эти планеты движутся. В следующей работе мы покажем, что для циркумбинарных планет действительно можно построить систему из трех моделей R-тороида.

Список литературы

Б. П. Кондратьев, Теория потенциала. Новые методы и задачи с решениями (М.: Мир, 2007).
B. P. Kondratyev, Solar Syst. Res. 46, 352 (2012).
В. А. Антонов, И. И. Никифоров, К. В. Холшевников, Элементы теории гравитационного потенциала и некоторые случаи его явного выражения (Изд-во СПбГУ, 2008).
М. А. Вашковьяк, С. Н. Вашковьяк, Астрон. вестник 46, 69 (2012).
J. R. Touma, S. Tremaine, and M. V. Kazandjian, Monthly Not. Roy. Astron. Soc. 394, 1085 (2009).
B. P. Kondratyev and V. S. Kornoukhov, Astron. Rep. 64, 434 (2020).
B. P. Kondratyev, N. G. Trubitsyna, and E. Sh. Mukha-metshina, ASP Conf. Ser. 316, 326 (2004).
B. P. Kondratyev, Monthly Not. Roy. Astron. Soc. 442, 1755 (2014).
B. P. Kondratyev and V. S. Kornoukhov, Astron. Rep. 64, 870 (2020).
Y. Judkovsky, A. Ofir, and O. Aharonson, Astron. J. 160, id.195 (2020).
C. D. Murray and S. F. Dermott, Solar System Dynamics (Cambridge, UK: Cambridge University Press, 2000).
J. L. Simon, P. Bretagnon, J. Chapront, M. Chapront-Touze, G. Francou, and J. Laskar, Astron. and Astrophys. 282, 663 (1994).
K. Batygin and M. E. Brown, Astron. J. 151, 22 (2016).
K. Batygin, F. C. Adams, M. E. Brown, and J. C. Becker, Physics Reports. 805, 1 (2019).
JPL Small-Body Database.
R. A. Wittenmyer, M. Endl, W. D. Cochran, and H. F. Levison, Astron. J. 134, 1276 (2007).
V. B. Kostov, P. R. McCullough, J. A. Carter, M. Deleuil, et al., Astrophys. J. 784, 14 (2014).
M. C. Johnson, W. D. Cochran, A. Collier Cameron, and D. M. Bayliss, Astrophys. J. Lett. 810, 23 (2015).
St. Raetz, T. O. B. Schmidt, S. Czesla, T. Klocová, et al., Monthly Not. Roy. Astron. Soc. 460, 2834 (2016).
J. W. Barnes, J. C. van Eyken, B. K. Jackson, D. R. Ciardi, and J. J. J. W. Fortney, Astrophys. J. 774, 53 (2013).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал