Астрономический журнал, 2022, T. 99, № 12, стр. 1264-1271
Использование обобщенных экспоненциальных функций при анализе статистических характеристик межзвездных мерцаний пульсаров
М. В. Попов *
Астрокосмический центр Физического института им. П.Н. Лебедева РАН
Москва, Россия
* E-mail: popov069@asc.rssi.ru
Поступила в редакцию 09.10.2022
После доработки 20.10.2022
Принята к публикации 24.10.2022
- EDN: SPBPLA
- DOI: 10.31857/S0004629922110160
Аннотация
Предлагается аппроксимировать частотные и временны́е сечения двумерных автокорреляционных функций динамических спектров мерцаний пульсаров универсальной экспоненциальной функцией с произвольным показателем $m$. Эта аппроксимация существенно лучше описывает форму корреляционной функции, чем гауссовская или простая экспоненциальная функции. Путем численного моделирования проведено исследование связи формы автокорреляционных функций с формой исходного профиля средней частотной структуры дифракционных мерцаний. Показано, что истинная ширина этого среднего частотного профиля значительно отличается от ширины самой автокорреляционной функции, что приводит к смещению оценок некоторых эффектов, обусловленных мерцаниями. Представлены примеры таких искаженных оценок для скорости пульсаров (${{V}_{{{\text{iss}}}}}$) и для перехода от ширины полосы декорреляции $\Delta f$ к времени рассеяния $\Delta {{\tau }_{s}}$.
1. ВВЕДЕНИЕ
Размеры области радиоизлучения пульсаров не могут превышать размеры магнитосферы нейтронной звезды, ограниченной световым цилиндром радиусом ${{R}_{L}} = Pc{\text{/}}2\pi $, что составит для периода повторения импульсов пульсара $P$ в одну секунду величину около $5 \times {{10}^{9}}$ см. Угловой размер такой области при типичном расстоянии до пульсаров в несколько сотен парсек оказывается меньше угловой микросекунды. На самом деле размеры области радиоизлучения ${{R}_{{{\text{em}}}}}$ гораздо меньше размеров светового цилиндра: при типичной длительности субимпульсов пульсаров $\delta t$ в несколько миллисекунд ${{R}_{{{\text{em}}}}} \approx c\delta t$ = $3 \times {{10}^{7}}$ см. Таким образом, пульсары являются точечными радиоисточниками, удобными для изучения эффектов рассеяния радиоизлучения на неоднородностях межзвездной плазмы, так как нет необходимости учитывать собственную структуру источника радиоизлучения. Поэтому интенсивные исследования эффектов рассеяния начались именно после открытия пульсаров. Изложение основных теоретических представлений можно найти в обзорной статье Риккета [1]. Основными параметрами рассеяния являются: характерное время мерцаний ${{t}_{{{\text{scint}}}}}$, время размытия импульса $\Delta {{\tau }_{s}}$, частотный масштаб дифракционных искажений радиоспектра $\Delta f$, называемый полосой декорреляции, и видимое угловое расширение источника ${{\theta }_{{{\text{sc}}}}}$. Для оценки параметров рассеяния ${{t}_{{{\text{scint}}}}}$ и $\Delta f$ обычно анализируют динамические спектры на временнóм интервале ${{T}_{{{\text{obs}}}}} > {{t}_{{{\text{scint}}}}}$, для достижения некоторой статистической значимости ([2–4]). На таком наблюдательном интервале вычисляются двумерные корреляционные функции (АКФ) от динамических спектров. Подробности вычисления и нормировки АКФ изложены в цитированных выше публикациях [2–4]. Время размытия импульса $\Delta {{\tau }_{s}}$ определяется путем анализа формы среднего профиля импульса (см., напр., статью Кузьмина и Лосовского [5]). Такие “прямые” измерения величины $\Delta {{\tau }_{s}}$ возможны для пульсаров с большой мерой дисперсии и/или на низких радиочастотах, где величина уширения превосходит несколько микросекунд. Меньшие значения $\Delta {{\tau }_{s}}$ получаются путем пересчета из измеренной полосы декорреляции $\Delta f$ через соотношение неопределенности $2\pi \Delta {{\tau }_{s}}\Delta f = 1$; мы рассмотрим ограничения на использование такого способа в разделе 4.2. В разделе 2 мы сформулируем исходные положения для дальнейшего анализа, затем в разделе 3 представим результаты численного моделирования основных типов автокорреляционных функций и установим связь между параметрами этих функций. В разделе 4 проведем сравнение наших результатов с наблюдательными данными.
2. ИСХОДНЫЕ ПОЛОЖЕНИЯ
Видимое угловое расширение источника ${{\theta }_{{{\text{sc}}}}}$ измеряется путем интерферометрических наблюдений со сверхдлинными базами (РСДБ). Большой прогресс в этой области был достигнут в ходе реализации проекта наземно-космического интерферометра Радиоастрон [6]. Некоторые итоги таких измерений рассмотрены в работе Попова и соавт. [7]. В этой работе проведен анализ формы интерферометрического отклика в зависимости от временнóй задержки (амплитуда функции видности $V(\tau )$). Оказалось, что усредненная автокорреляционная функция от функции видности хорошо описывается функцией Лоренца $ACF(V(\tau ))$ = = $L(\delta \tau )$ = ${{A}_{l}}{\text{/}}(\delta {{\tau }^{2}} + {{d}^{2}})$, где параметр $d$ равен полуширине этой функции на уровне 1/2, а ${{A}_{l}}$ – масштабный множитель. Введем несколько математических соотношений, полезных для дальнейшего изложения. Запишем выражение для функции Лоренца:
Автокорреляционная функция для функции Лоренца дается следующей формулой:
т.е. полуширина автокорреляционной функции вдвое превышает полуширину самой функции. Фурье преобразование от функции Лоренца является двухсторонней экспоненциальной функциейЗдесь полуширина функции $FT$ по уровню $1{\text{/}}e$ составляет величину $W_{{1/e}}^{F} = 1{\text{/}}(2\pi d)$, так что именно в этом случае точно выполняется соотношение неопределенности $2\pi W_{{1/e}}^{F}W_{{1/2}}^{L} = 1$. Как уже упоминалось выше, согласно результатам анализа, представленным в работе Попова и соавт. [7], $ACF$ от функции видности $V(\tau )$ для всех исследованных пульсаров хорошо аппроксимируется функцией Лоренца. В соответствии с выражением (2) и сама функция видности $V(\tau )$ должна описываться функцией Лоренца. Функция видности $V(\tau )$ получается в результате обратного Фурье преобразования от кросс-корреляционного спектра $S(f)$, т.е. $V(\tau ) = F{{T}^{{ - 1}}}(S(f))$. Следовательно, в соответствии с уравнением (3), средняя структура кросс-корреляционного (или автокорреляционного) спектра представляет собой набор двухсторонних экспонент. В отличие от среднего профиля импульса пульсара, накопить средний профиль частотной дифракционной структуры не представляется возможным, так как эта структура меняется со временем случайным образом, что и представляет собой явление мерцаний. Однако можно сразу накопить автокорреляционную функцию частотной структуры мерцаний или двумерную АКФ от динамических спектров для измерения временны́х и частотных сечений. Такой подход использовался многими исследователями (см., напр., [2–4]. При этом временны́е и частотные сечения АКФ аппроксимировались гауссианами. Другие исследователи, использующие корреляционные функции для анализа данных [8–10], указывали на отклонения этих функций от гауссовой формы. Согласно представлениям, изложенным выше, частотное сечение АКФ должно соответствовать автокорреляционной функции от двухсторонней экспоненты:
Эта функция уже объявлялась в соотношении (3). Приведем выражение для $ACF$ от двухсторонней экспоненты,
(5)
$ACF(E(b,f)) = {{A}_{{ACF}}}({\text{|}}\delta f{\text{|}} + b)\exp \left( { - \frac{{{\text{|}}\delta f{\text{|}}}}{b}} \right),$(6)
$U(\nu ) = {{A}_{u}}\exp \left( { - {\kern 1pt} \frac{{{\text{|}}\nu {{{\text{|}}}^{m}}}}{b}} \right),$3. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ АВТОКОРРЕЛЯЦИОННЫХ ФУНКЦИЙ
Как уже было упомянуто во Введении, в ходе анализа наблюдательных данных (динамических спектров) вычисляются двумерные корреляционные функции (АКФ), усредненные за время ${{T}_{{{\text{obs}}}}}$, значительно превышающее характерное время мерцаний ${{t}_{{{\text{scint}}}}}$. Из временны́х и частотных сечений этих АКФ получаются важные параметры мерцаний. Однако, как уже было показано в предыдущем разделе, полуширина автокорреляционной функции не совпадает с полушириной исходной функции, присущей процессу рассеяния. Получить из наблюдаемого сечения АКФ форму этой исходной функции (деконволюция) невозможно без предварительных условий. Поэтому в нашем численном моделировании мы в качестве исходного сигнала задавали средний профиль частотной структуры мерцаний в виде функции $U(\nu )$ с различными показателями степени ${{m}_{0}}$, а затем вычисляли соответствующие автокорреляционные функции в виде свертки
(7)
$A(\Delta \nu ) = \frac{1}{{B - \Delta \nu }}\int\limits_0^{B - \Delta \nu } U(\nu ){\kern 1pt} U(\nu + \Delta \nu )d\nu {\kern 1pt} .$Здесь $B$ – спектральный интервал, на котором задана функция $U(\nu )$. На самом деле интеграл в выражении (7) определялся путем вычисления суммы произведений на этом частотном интервале $B$. Для ясности укажем, что полуширина всех модельных функций была одинакова и принята равной 100 кГц, а спектральный интервал $T$ составил 32.768 MГц (N = 32 768). Такая конкретизация необходима для перехода к функции видности $V(\tau )$.
Таким образом, исходные функции $U(\nu )$ задают среднюю форму дифракционных частотных (или временны́х) искажений радиоспектра пульсара. Эти функции являются действительными и четными. По смыслу они имитируют структуру спектра мощности в предположении, что существует некий средний частотный профиль спектральных искажений, что подтверждается существованием устойчивых и повторяющихся форм усредненных $ACF$ от динамических спектров. Естественным условием, которое всегда принималось, было предположение, что этот средний частотный профиль описывается функцией Гаусса. Тогда и $ACF$ от динамических спектров имели бы форму гауссианы. На практике наблюдается большое разнообразие форм средних $ACF$. Наш анализ носит чисто математический характер. Никаких шумовых составляющих исходные функции $U(\nu )$ не содержат. Результаты моделирования даны в табл. 1. В первом столбце указан показатель степени ${{m}_{0}}$ функции $U(\nu )$; во втором столбце приведены значения показателя степени ${{m}_{1}}$ для автокорреляционной функции $A(\Delta \nu )$ при ее аппроксимации универсальной экспоненциальной функцией $U(\Delta \nu )$; в третьем столбце содержится показатель степени ${{m}_{2}}$, полученный в результате аппроксимации функции видности $V(\tau )$, которая была вычислена через обратное преобразование Фурье от исходной функции $U(\nu )$: $V(\tau ) = F{{T}^{{ - 1}}}(U(\nu ))$. Временнóе разрешение функции видности составляет для наших условий величину $\delta \tau = 1{\text{/}}B = 0.0305 \mu s$. В четвертом столбце дан фактор $R$ увеличения полуширины автокорреляционной функции $A(\Delta \nu )$ по отношению к полуширине исходной функции $U(\nu )$. В пятом столбце мы поместили значения полуширины функции видности, а в двух последних столбцах приведены значения произведения $2\pi \Delta \nu \Delta \tau $, ${{K}_{1}}$ и ${{K}_{2}}$. На рис. 1 показаны примеры модельных функций дифракционной частотной структуры $U(\nu )$ (слева), и соответствующие им автокорреляционные функции $A(\Delta \nu )$ (справа). Штриховая линия соответствует случаю, когда спектральный профиль частотной структуры $U(\nu )$ задается двухсторонней экспонентой (${{m}_{0}} = 1.0$); для такой функции автокорреляционная функция описывается модифицированной экспонентой (5), полуширина которой примерно в 2 раза превышает полуширину частотного профиля. Пунктирная линия соответствует гауссову частотному профилю. Известно, что автокорреляционная функция от гауссианы также является гауссианой с полушириной в $\sqrt 2 $ раз превышающей исходную полуширину. Наконец, третий пример, изображенный сплошной линией, соответствует случаю, когда автокорреляционная функция имеет вид чистой экспоненты. Такой автокорреляционной функции соответствует частотный профиль в виде модифицированной функции Бесселя второго рода нулевого порядка, формально стремящейся к бесконечности при нулевом сдвиге [11]. В нашем численном моделировании ближе всего к этому случаю подходит вариант с показателями ${{m}_{0}} = 0.60$ и ${{m}_{1}} = 0.98$. Именно этот случай показан на рис. 1 сплошной линией, так что автокорреляционная функция не выглядит чистой экспонентой, а функция частотного профиля не стремится к бесконечности.
Таблица 1.
Результаты моделирования
| Показатель степени | Фактор $R$ уширения АКФ | Полуширина $V(\tau )$, μs | ${{K}_{1}}$ | ${{K}_{2}}$ | ||
|---|---|---|---|---|---|---|
| $U(\nu )({{m}_{0}})$ | АКФ от $U(\nu )$ (${{m}_{1}}$) | $V(\tau )$ (${{m}_{2}}$) | ||||
| 0.45 | 0.77 | 0.61 | 9.32 | 0.197 | 0.124 | 1.155 |
| 0.50 | 0.84 | 0.67 | 6.87 | 0.298 | 0.187 | 1.284 |
| 0.55 | 0.91 | 0.73 | 5.42 | 0.415 | 0.261 | 1.414 |
| 0.60 | 0.98 | 0.80 | 4.48 | 0.552 | 0.346 | 1.515 |
| 0.65 | 1.05 | 0.87 | 3.80 | 0.689 | 0.433 | 1.662 |
| 0.70 | 1.11 | 0.94 | 3.38 | 0.836 | 0.525 | 1.744 |
| 0.75 | 1.17 | 1.01 | 3.04 | 0.976 | 0.613 | 1.863 |
| 0.80 | 1.22 | 1.08 | 2.77 | 1.113 | 0.699 | 1.936 |
| 0.85 | 1.28 | 1.16 | 2.56 | 1.241 | 0.780 | 1.997 |
| 0.90 | 1.33 | 1.23 | 2.40 | 1.363 | 0.856 | 2.054 |
| 0.95 | 1.38 | 1.30 | 2.26 | 1.476 | 0.929 | 2.099 |
| 1.00 | 1.43 | 1.36 | 2.15 | 1.560 | 0.992 | 2.133 |
| 1.05 | 1.48 | 1.43 | 2.05 | 1.678 | 1.054 | 2.161 |
| 1.10 | 1.52 | 1.49 | 1.97 | 1.766 | 1.109 | 2.185 |
| 1.15 | 1.56 | 1.54 | 1.90 | 1.848 | 1.161 | 2.206 |
| 1.20 | 1.60 | 1.60 | 1.84 | 1.928 | 1.211 | 2.228 |
| 1.25 | 1.64 | 1.64 | 1.78 | 1.998 | 1.255 | 2.234 |
| 1.30 | 1.67 | 1.69 | 1.74 | 2.062 | 1.295 | 2.253 |
| 1.35 | 1.71 | 1.73 | 1.70 | 2.126 | 1.336 | 2.271 |
| 1.40 | 1.74 | 1.77 | 1.66 | 2.181 | 1.370 | 2.274 |
| 1.45 | 1.77 | 1.80 | 1.63 | 2.236 | 1.404 | 2.288 |
| 1.50 | 1.80 | 1.83 | 1.60 | 2.284 | 1.435 | 2.296 |
| 1.55 | 1.83 | 1.86 | 1.57 | 2.330 | 1.464 | 2.298 |
| 1.60 | 1.85 | 1.88 | 1.55 | 2.376 | 1.493 | 2.314 |
| 1.65 | 1.88 | 1.90 | 1.53 | 2.416 | 1.518 | 2.328 |
| 1.70 | 1.90 | 1.92 | 1.52 | 2.455 | 1.542 | 2.434 |
| 1.75 | 1.92 | 1.94 | 1.49 | 2.489 | 1.564 | 2.330 |
| 1.80 | 1.94 | 1.95 | 1.47 | 2.525 | 1.587 | 2.333 |
| 1.85 | 1.96 | 1.97 | 1.46 | 2.556 | 1.606 | 2.344 |
| 1.90 | 1.97 | 1.98 | 1.44 | 2.586 | 1.625 | 2.340 |
| 1.95 | 1.99 | 1.99 | 1.43 | 2.614 | 1.642 | 2.348 |
| 2.00 | 2.00 | 2.00 | 1.41 | 2.641 | 1.660 | 2.349 |
Рис. 1.
Сравнение синтезированных средних профилей частотных искажений (слева) и формы соответствующих автокорреляционных функций (справа). Штриховая линия – спектральный профиль $U(\nu )$ задается двухсторонней экспонентой (${{m}_{0}} = 1.0$). Пунктирная линия соответствует гауссову частотному профилю. Сплошная линия – автокорреляционная функция имеет вид чистой экспоненты.

На рис. 2 представлена зависимость множителя $R$, определяющего расширение автокорреляционной функции по отношению к исходной функции профиля частотной дифракционной структуры, от показателя степени $m$ универсальной экспоненциальной функции, аппроксимирующей данную АКФ. В отдельных случаях этот фактор указывает на десятикратное уширение, а в минимальных случаях он оказывается около 1.4.
4. СРАВНЕНИЕ С НАБЛЮДАТЕЛЬНЫМИ ДАННЫМИ
Сравнение с наблюдательными данными мы начнем с рассмотрения табл. 2, в которой представлены измеренные показатели степени $\beta $, определенные по сечениям двумерных автокорреляционных функций для 11 пульсаров, представленных в работе [12]. В отношении частотной структуры наименьшее значение показателя ${{m}_{1}}$ обнаружено у пульсара В0823+26 (${{m}_{1}} = 0.76$), что соответствует уширению АКФ почти в 10 раз. Наибольшее(трехкратное) уширение АКФ сечения по времени имеем у пульсара В1933+16 (${{m}_{1}} = 1.18$). Хотя статистику из десятка пульсаров нельзя считать убедительной, мы все же приведем средние величины уширения АКФ по частоте и по времени, которые составили 3.0 и 2.0 соответственно с надежностью в 30%. Эта оценка пригодится нам в следующем параграфе.
Таблица 2.
Сводка результатов измерений показателей степени универсальной экспоненциальной функции
| Имя пульсара | Показатель степени | |
|---|---|---|
| ${{m}_{f}}$ | ${{m}_{t}}$ | |
| B0329+54 | 1.14 | 1.67 |
| B0525+21 | 1.11 | – |
| B0809+74 | – | 1.33 |
| B0823+26 | 0.76 | 1.66 |
| B0834+06 | 1.11 | 1.53 |
| B0919+06 | 0.83 | 1.57 |
| B1133+16 | 1.45 | 1.86 |
| B1237+16 | 1.47 | 1.39 |
| B1749–28 | 1.26 | 1.82 |
| B1929+10 | 1.26 | 1.65 |
| B1933+16 | 0.98 | 1.18 |
| B2016+28 | 1.38 | 1.36 |
4.1. Сцинтилляционные скорости
В 1986 г. Кордс [3] опубликовал большую статью, посвященную определению пространственных скоростей для 71 пульсара на основе измерения параметров мерцания $\Delta f$ и ${{t}_{{{\text{scint}}}}}$. Эти величины автор определял по временны́м и частотным сечениям двумерных автокорреляционных функций, используя аппроксимацию гауссианами. Основное выражение, по которому вычислялись пространственные скорости, имеет следующий вид
(8)
${{V}_{{{\text{iss}}}}} = {{A}_{V}}\frac{{\sqrt {\Delta f{{D}_{{{\text{kpc}}}}}} }}{{({{\nu }_{{{\text{GHz}}}}}{\kern 1pt} {{t}_{{{\text{scint}}}}})}}.$Так как параметры $\Delta f$ и ${{t}_{{{\text{scint}}}}}$ определялись по автокорреляционным функциям, то их величины оказались завышенными в 3 раза по $\Delta f$ и в 2 раза по ${{t}_{{{\text{scint}}}}}$. При переходе к действительны значениям $\Delta f$ и ${{t}_{{{\text{scint}}}}}$ оценки ${{V}_{{{\text{iss}}}}}$ следует исправить на коэффициент $2{\text{/}}\sqrt 3 $ = 1.15. В данном случае поправочные множители в числителе и знаменателе дроби скомпенсировали друг друга, и оценки скорости в работе [3] можно считать состоятельными.
4.2. Сотношение неопределенности
При сравнении параметров $\Delta f$ и $\Delta {{\tau }_{s}}$ часто используется соотношение неопределенности $2\pi \Delta f\Delta {{\tau }_{s}} = K$ (см., напр., [1, 13–15]. В большинстве случаев коэффициент $K$ полагается равным единице. Правда, Риккет [1] замечает, что этот коэффициент зависит от формы автокорреляционной функции и от передаточной функции среды, и только для тонкого фазового экрана с Гауссовым спектром неоднородностей можно считать $K = 1$. В 6-м столбце табл. 1 приведены значения ${{K}_{1}}$, полученные в результате численного моделирования для различной формы заданного частотного профиля спектральных искажений, в предположении, что нам удалось каким-то образом измерить истинные ширины частотного профиля и истинную величину $\Delta {{\tau }_{s}}$, например, по анализу рассеянного среднего профиля. Видно, что даже в этом идеальном эксперименте коэффициент ${{K}_{1}}$ близок к единице только для формы частотного профиля в виде двухсторонней экспоненты, что отмечалось еще в разделе 2. В общем случае коэффициент ${{K}_{1}}$ меняется от 0.124 до 1.66. В последнем столбце табл. 1 приведены рассчитанные значения коэффициента ${{K}_{2}}$ для более реального случая, когда $\Delta {{\tau }_{s}}$ определены по измерению уширения импульса, а $\Delta f$ берется как полуширина частотного сечения АКФ. В таком варианте ${{K}_{2}}$ изменяется от 1.15 до 2.35. Именно этот вариант используется часто для пересчета измеренного времени уширения импульса $\Delta {{\tau }_{s}}$ в величину полосы декорреляции $\Delta f$ и наоборот.
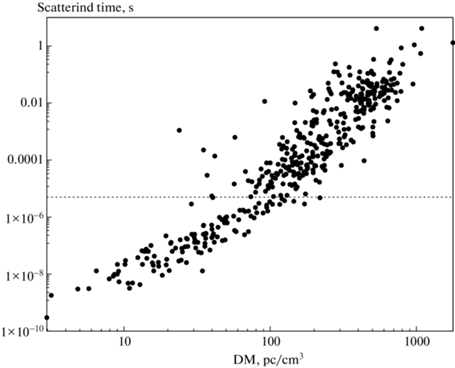
Рассмотрим, например, представленные в австралийском каталоге пульсаров [16] значения $\Delta {{\tau }_{s}}$, которые были получены двумя способами: 1) по измерению уширения среднего профиля импульса из-за рассеяния и 2) путем пересчета от $\Delta f$, измеренной по частотной корреляционной функции, по соотношению неопределенности $2\pi \Delta f\Delta {{\tau }_{s}} = K$ с $K = 1$. На рис. 3 показана зависимость $\Delta {{\tau }_{s}}$ от величины меры дисперсии по данным австралийского каталога [16]. Можно заметить, что на рисунке выделяются две зоны, разделенные пунктирной линией по величине $\Delta {{\tau }_{s}} = 10$ μs. Бóльшие значения $\Delta {{\tau }_{s}}$ определены по измерениям уширения импульса, а меньшие значения получены путем пересчета из $\Delta f$. Но из нашего анализа следует, что величина $K$ в среднем равна примерно 2! Значит, пересчитанные значения $\Delta {{\tau }_{s}}$ уменьшены примерно в 2 раза. На наш взгляд, это объясняет наблюдаемое нарушение непрерывного распределения точек на рисунке.
Рис. 3.
Зависимость уширения импульса $\Delta {{\tau }_{s}}$ на частоте 1 ГГц от меры дисперсии по данным каталога пульсаров [16]. Пунктирная линия соответствует $\Delta {{\tau }_{s}} = 10 \mu s$. Бóльшие значения $\Delta {{\tau }_{s}}$ определены по измерениям уширения импульса, а меньшие значения получены путем пересчета из $\Delta f$.
5. ЗАКЛЮЧЕНИЕ
При оценке основных параметров рассеяния радиоизлучения пульсаров на неоднородностях межзвездной плазмы $\Delta f$ (полоса декорреляции) и ${{t}_{{{\text{scint}}}}}$ (характерное время мерцаний) принято их измерять по ширинам частотных и временны́х автокорреляционных функций, взятых по уровню 1/2 и $1{\text{/}}e$ соответственно. Такое соглашение удобно при сравнении результатов, полученных разными авторами в разные эпохи и на разных частотах. Выполненное в данной работе численное моделирование указывает на то, что оценки параметров мерцаний по автокорреляционным функциям дают смещенные значения по отношению к истинным характеристикам процессов рассеяния, а именно, завышенные величины в среднем в 3 раза для полосы декорреляции $\Delta f$, и в 2 раза для времени мерцаний ${{t}_{{{\text{scint}}}}}$. Такие значительные переоценки параметров могут иметь существенное значение при построении статистических зависимостей и при сравнении наблюдений с теоретическими предсказаниями. Для перехода от измеренных параметров АКФ к истинным значениям мы рекомендуем аппроксимировать сечения АКФ с помощью универсальной экспоненциальной функции $U(x)$ (6), измерить полуширину этой функции $W_{{1/e}}^{U} = {{b}^{{1/m}}}$, по величине показателя ${{m}_{1}}$ (второй столбец табл. 1) найти соответствующий множитель $R$ увеличения ширины АКФ (четвертый столбец табл. 1) и получить оценку истинного значения параметра $W_{{1/e}}^{{{\text{cor}}}} = W_{{1/e}}^{{{\text{obs}}}}{\text{/}}R$.
Для перехода от значений полосы декорреляции $\Delta f$ к величине уширения импульса из-за рассеяния $\Delta {{\tau }_{s}}$ (и наоборот) повсеместно используется соотношение $2\pi \Delta f\Delta {{\tau }_{s}} = K$. В большинстве случаев принимается, что $K = 1$. Риккет (1977) высказал замечание, что величина $K$ может зависеть теоретически от передаточной функции среды. В табл. 1 в двух последних столбцах даются значения коэффициентов ${{K}_{1}}$ и ${{K}_{2}}$ для идеального случая измерений (${{K}_{1}}$) и для реальных условий перехода от измеренной по сечению АКФ ширине полосы декорреляции $\Delta f$ к значению временнóго уширения импульса $\Delta {{\tau }_{s}}$. Если частотное сечение АКФ аппроксимировалось универсальной экспоненциальной функцией $U(x)$, то можно выбрать значение ${{K}_{2}}$ в соответствующей строке табл. 1. В среднем величина множителя ${{K}_{2}} = 2.2$.
Список литературы
B. J. Rickett, Ann. Rev. Astron. Astrophys. 15, 479 (1977).
J. M. Cordes, J. M. Weisberg, and V. Boriakoff, Astrophys. J. 288, 221 (1985).
J. M. Cordes, Astrophys. J. 311, 183 (1986).
N. D. R. Bhat, A. P. Rao, and Y. Gupta, Astrophys. J. Suppl. 121, 483 (1999).
A. D. Kuzmin and B. Ya. Losovsky, Astron. Astrophys. Trans. 26, 597 (2007).
В. В. Андреянов, Н. С. Кардашев, В. В. Хартов, Космич. исслед. 52, 353, (2014).
M. V. Popov, N. Bartel, M. S. Burgin, C. R. Gwinn, T. V. Smirnova, and V. A. Soglasnov, Astrophys. J. 888, id. 57 (2020).
V. I. Shishov, Soviet Astron. 17, 598 (1974).
J. M. Armstrong and B. J. Rickett, Monthly Not. Roy. Astron. Soc. 194, 623 (1981).
A. Wolszczan, Monthly Not. Roy. Astron. Soc. 204, 591 (1983).
W. Feller, An Introduction to Probability Theory and its Application. Vol.2, 2nd ed. (John Wiley and Sons, 1971).
М. В. Попов, Т. В. Смирнова, Астрон. журн. 98, 929 (2021).
O. B. Slee, G. A. Dulk, and R. E. Otrupchek, Proc. Astron. Soc. Australia 4(1), 100 (1980).
J. M. Sutton, Monthly Not. Roy. Astron. Soc. 155, 51 (1971).
D. C. Backer, Astrophys. J. 190, 667 (1974).
R. N. Manchester, G. B. Hobbs, A. Teoh, and M. Hobbs, Astron. J. 129, 1993 (2005).
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал



