Астрономический журнал, 2022, T. 99, № 7, стр. 531-536

1. ВВЕДЕНИЕ

В пионерских работах [1–3] и других было замечено, что вывод о нестационарности Вселенной и закон ее динамической эволюции могут быть получены из Ньютоновской теории без обращения к теории Эйнштейна. С тех пор изложение космологической проблемы в популярных книжках (см., напр., [4–6]), как правило, делается с использованием именно Ньютоновской теории. Более того, даже профессиональные монографии начинают изложения космологии часто с Ньютоновской теории (см., напр., [7–10]). При таком подходе подчеркивается, что закон тяготения Ньютона, описывающий ускорение, создаваемое гравитацией, является асимптотически правильным выражением закона Эйнштейна в случае слабых полей тяготения и сферических распределений вещества и скорости движения элементов объема, где скорости должны быть малыми по сравнению со световой. Как правило, при сравнении законов Эйнштейна и Ньютона этим и ограничиваются. В данной работе мы показываем, что такое ограничение недостаточно для понимания сути дела и, более того, ведет к ошибкам.

2. НЬЮТОНОВСКАЯ КОСМОЛОГИЯ

Как уже было сказано, начиная с пионерских работ [1–3] и других, Ньютоновская космология используется для “простого” введения в современную космологию. Чтобы выделить основные идеи, рассмотрим простейшую идеальную космологическую модель. Пусть однородное вещество без давления равномерно заполняет всю Вселенную. В подобной модели галактики рассматриваются в большом объеме как точки в таком веществе. Выделим мысленно в этом веществе шар произвольного радиуса с центром в произвольной точке. Рассмотрим сначала силы тяготения, создаваемые на поверхности этого шара только веществом самого шара, и не будем пока рассматривать все остальное вещество Вселенной. Пусть радиус шара выбран не слишком большим, так что поле тяготения, создаваемое веществом шара, относительно слабо, и для вычисления силы тяготения применима теория Ньютона. Тогда точки, находящиеся на граничной сфере, будут притягиваться к центру шара с силой, пропорциональной массе шара $M$ и обратно пропорциональной квадрату его радиуса $R$.

Теперь вспомним о всем остальном веществе Вселенной вне шара, и попытаемся учесть создаваемые им силы тяготения. Для этого будем рассматривать последовательно сферические оболочки все большего и большего радиуса, охватывающие шар. Но известно, что сферически-симметричные слои вещества никаких гравитационных сил внутри полости не создают. Следовательно, все эти сферически-симметричные оболочки (т.е. все остальное вещество Вселенной) ничего не добавят к силе притяжения, которое испытывает точка $A$ на поверхности шара к его центру $O$.

Итак, можно вычислить ускорение одной точки $A$ по отношению к другой точке $O$. Мы приняли $O$ за центр шара, а точка $A$ находится на расстоянии $R$ от $O$. Это ускорение обусловлено тяготением только вещества шара радиусом $R$. Согласно закону Ньютона оно есть

Знак минус означает, что ускорение соответствует притяжению, а не отталкиванию. Итак, любые две точки, находящиеся в однородной Вселенной на расстоянии $R$, испытывают относительное ускорение (отрицательное) $\ddot {R}$, задаваемое формулой (1). Это и означает, что Вселенная должна быть нестационарной. Действительно, если бы мы представили, что в некоторый момент времени галактики покоятся, т.е. $\dot {R} = 0$, и плотность вещества во Вселенной не меняется, то в следующий момент галактики получили бы скорости под действием взаимного тяготения всего вещества, так как имеется ускорение тяготения, даваемое формулой (1). Итак, покой галактик друг относительно друга возможен лишь на мгновение. В начальный момент времени можно выбрать не покой, а расширение друг относительно друга. В общем же случае галактики должны двигаться – они должны или удаляться, или сближаться, радиус шара $R$ должен меняться со временем, плотность вещества также должна изменяться со временем.

Вселенная должна быть нестационарной, ибо в ней действует тяготение – таков основной вывод теории. Формулу (1) можно переписать, заменив в ней массу выражением $M = \frac{4}{3}\pi {{R}^{3}}\rho $, тогда получим силу тяготения на единицу массы в виде

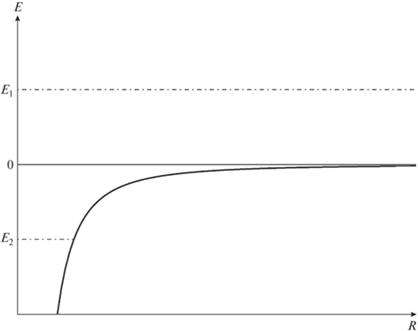
Точка означает производную по времени, $\rho $ – плотность вещества. Выбор точки $O$ был произволен. Наша модель однородна, следовательно, формула (2) справедлива для любой точки пространства Вселенной. Формула (2) описывает закон изменения радиуса произвольного шара со временем и также описывает закон изменения плотности вещества со временем, так как плотность вещества $\rho \sim \frac{1}{{{{R}^{3}}}}$ для пыли, когда давление $P = 0$. С учетом этого соотношения уравнение (2) можно проинтегрировать: где $E$ – произвольная константа интегрирования. Формула (3) позволяет легко анализировать динамику эволюции разных масштабов и эволюцию плотности Вселенной. Выражение (3) можно рассматривать как закон сохранения энергии при эволюции поверхности шара: $E$ – полная энергия, равная сумме кинетической (член с ${{\dot {R}}^{2}}$) и потенциальной (член с постоянной $G$). Отрицательное слагаемое в выражении $E = \left( {\frac{1}{2}} \right){\kern 1pt} {{\dot {R}}^{2}} - \left( {\frac{4}{3}} \right){\kern 1pt} \pi G\rho {{R}^{2}}$ называют потенциалом, он изображен на рис. 1. Эволюция модели происходит с постоянной энергией $E = {\text{const}}$, изображенной на рис. 1 горизонтальной линией. Если ${{E}_{1}} > 0$, то расширение происходит от $R = 0$ до $R = \infty $. Если ${{E}_{2}} < 0$, то расширение происходит от $R = 0$ до встречи с потенциальной кривой, и затем происходит сжатие до $R = 0$. Величина $E = {\text{const}}$ может выбираться произвольно, так как начальные условия в Ньютоновской теории никак не связаны с уравнением тяготения. К сказанному еще добавляют, что шар достаточно мал, чтобы не только силы тяготения на его поверхности были малы, но и скорости вещества тоже малы по сравнению со световой $c$. Сказанное составляет суть Ньютоновской космологии, которая, как утверждается, совпадает локально с релятивистской космологией. Но как мы увидим, это утверждение требует существенных уточнений.

3. УРАВНЕНИЯ ЭЙНШТЕЙНА

Механика релятивистской космологии (теория Фридмана) основана на уравнениях Эйнштейна. Уравнения Эйнштейна описывают структуру и эволюцию геометрии пространства-времени с помощью метрического тензора ${{g}_{{ik}}}$ (см., напр., [11]) совместно с эволюцией физических свойств материи [11], описываемых тензором ${{T}_{{ik}}}$. В отличие от уравнения тяготения Ньютона, уравнения Эйнштейна содержат в себе уравнение движения. Вся система является системой дифференциальных уравнений частных производных второго порядка компонент метрического тензора по координатам ${{x}^{0}},\;{{x}^{1}},\;{{x}^{2}},\;{{x}^{3}}$. Система может быть записана в виде

Здесь $G$ – постоянная тяготения; $i,k = 0,{\kern 1pt} 1,{\kern 1pt} 2,{\kern 1pt} 3$; $G_{i}^{k}$ – тензор кривизны Эйнштейна; $T_{i}^{k}$ – тензор энергии$ - $импульса материи. Эти уравнения делятся на две группы.

1) Уравнения, не содержащие вторых производных по времени ${{x}^{0}}$. Это уравнения на начальные условия при ${{x}^{0}} = 0$:

2) Уравнения эволюции, содержащие вторые производные по ${{x}^{0}}$:

При этом, если уравнения (5) выполняются при ${{x}^{0}} = 0$, а уравнения (6) выполняются при всех ${{x}^{0}},\;{{x}^{1}},\;{{x}^{2}},\;{{x}^{3}}$, то уравнения (5) так же выполняются при всех ${{x}^{0}},\;{{x}^{1}},\;{{x}^{2}},\;{{x}^{3}}$. Мы считаем, что $\Lambda $ – член релятивистской теории, включен в выражение для тензора $T_{i}^{k}$. В данной статье полагаем, что $\Lambda = 0$.

4. НАЧАЛЬНЫЕ УСЛОВИЯ В РЕЛЯТИВИСТСКОЙ КОСМОЛОГИИ

Мы будем рассматривать однородные изотропные релятивистские модели. Их строение и эволюция описываются радиусом кривизны трехмерного пространства $a(t)$. Будем считать давление $P = 0$. Для таких моделей уравнения Эйнштейна переписываются в виде

где $k$ может принимать значение $k = 0,\; \pm {\kern 1pt} 1$. Случай $k = 0$ является вырожденным и мы его здесь не рассматриваем. В нашем случае $P = 0$ и $\rho = {{\rho }_{0}}{{\left( {\frac{{{{a}_{0}}}}{a}} \right)}^{3}}$. Уравнения (7), (8) похожи на (2), (3), но вместо произвольного радиуса шара $R$ здесь стоит конкретный радиус кривизны $a$, характеризующий масштаб всей Вселенной. 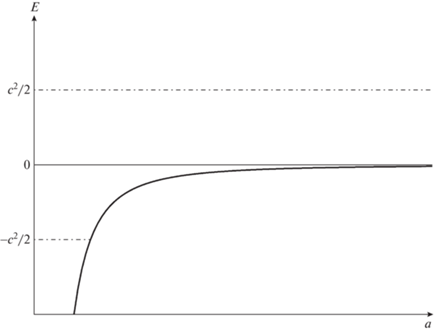Вдобавок к этому заметим, что уравнение (8) похоже на интеграл (3) теории Ньютона, отличаясь лишь тем, что вместо произвольной константы $E$ здесь стоит $ - \frac{{k{{c}^{2}}}}{2}$. Отличие весьма существенное, т.к. без произвольной $E$ уравнение (8) является ограничением на начальные условия, чего принципиально нет в теории Ньютона.

Для сравнения с Ньютоновской теорией введем функцию $E = \frac{{{{{\dot {a}}}^{2}}}}{2} - \frac{{4\pi G}}{3}{{a}^{2}}\rho $, $\rho \sim \frac{1}{{{{a}^{3}}}}$ для пыли, когда $P = 0$. Эту функцию будем называть энергией. Величину $E = E(a)$ при $\frac{{{{{\dot {a}}}^{2}}}}{2} = 0$ будем называть потенциалом, он изображен на рис. 2. Похожесть систем (2), (3) и (7), (8) позволяла заменять вторую систему первой для анализа локальных величин. При этом различию между (3) и (8) значение не придавалось и не обсуждалось. А принципиальное различие состоит в том, что теперь в уравнении (8) речь идет не о шаре произвольного выбранного размера $R$, а о конкретной величине $a$ – радиусе кривизны трехмерного сечения Вселенной, и выражение (8) становится условием на начальные значения параметров задачи.

5. НАЧАЛЬНЫЕ ДАННЫЕ В РЕЛЯТИВИСТСКОЙ ТЕОРИИ И НЬЮТОНОВСКАЯ КОСМОЛОГИЯ

Для того чтобы обсудить разницу в подходе двух теорий – Ньютоновской и релятивистской – к описанию даже локальных свойств Вселенной, давайте выполним в релятивистской теории операцию выделения небольшого шара, как мы делали в Ньютоновской теории в разделе 2, и затем проанализируем возникающие различия. В Ньютоновской теории мы мысленно выделили в однородном веществе Вселенной небольшой шар произвольного радиуса $R$ в произвольный момент времени ${{t}_{0}}$, когда плотность вещества равна ${{\rho }_{0}}$ с центром в произвольной точке $O$. При этом требовалось, чтобы ускорение $\ddot {R}$, вычисляемое согласно уравнению (1), мало отличалось от ускорения по релятивистской формуле (7). Для этого, как известно, необходимо уравнение (8), чтобы гравитационный радиус ${{r}_{g}}$ шара массой $M$ был много меньше физического радиуса $R$:

При этом иногда добавлялось или предполагалось, что скорости движения вещества $R$ должны быть нерелятивистскими, Из (9) следует

В Ньютоновской теории для построения конкретной космологической модели, т.е. для интегрирования единственного уравнения модели (2), требуется задать начальные условия в момент времени ${{t}_{0}}$:

После этого решение находится однозначно. Модель построена. Обратимся к релятивистской теории. Обозначим, насколько выбранный нами радиус шара $R$ меньше $a$:

Это отношение $N \equiv \frac{a}{R}$ постоянно по времени. Прежде всего для нашего маленького шарика должно выполняться динамическое уравнение (7), переписанное для поверхности шара $R$. Подставим (13) в (7):

Но помимо этого уравнения во Фридмановской теории должно еще выполняться уравнение для начальных данных (8), переписанное снова для поверхности шара $R$. Подставим (14) в (8), получаем: Это условие накладывает на начальные данные в момент $t = {{t}_{0}}$ жесткие соотношения. Начальные данные связаны условиями (16). Это то, чего нет в Ньютоновской теории. Из проведенного рассмотрения следует, что для того, чтобы сделать Ньютоновскую теорию близкой к релятивистской, недостаточно взять шар малым и задать скорость его однородного расширения много меньше световой. Надо еще, чтобы при заданных ${{R}_{0}}$ и ${{\rho }_{0}}$ скорость на поверхности шара удовлетворяла соотношению (16). Пренебрежение этим условием ведет к ошибкам. Для иллюстрации рассмотрим шар в начальный момент времени ${{t}_{0}}$. Зададим $N\frac{a}{R}$, т.е. выберем размер шара по отношению к $a$. Пусть этот выбор удовлетворяет необходимым условиям малости. Но теперь мы не можем произвольно выбрать достаточно малую скорость расширения. Она должна быть такой, чтобы полная энергия была равна $\frac{{ - k{{c}^{2}}}}{{2{{N}^{2}}}}$ (см. (16)). На диаграмме рис. 1 это соответствует движению точки, представляющей решение уравнений эволюции, по горизонтальной линии постоянной энергии

Становится понятной причина существенной разницы рис. 1 и 2. На рис. 2 горизонтали $E = \pm \frac{{{{c}^{2}}}}{2},\;0$ изображают эволюцию всей Вселенной при $k = \pm 1,{\kern 1pt} 0$ соответственно. На рис. 1 горизонтали $E = {\text{const}}$ изображают эволюцию шаровой части. При этом ${{E}_{{1,2}}} = {\text{const}}$ может принимать не любые значения, а только указанные нами значения, определяемые необходимыми начальными условиями релятивистской теории, даваемые выражением (16).

Таким образом, следует помнить, что правильное приближение Ньютоновской космологии к релятивистской теории требует учет не только близкого значения ускорения согласно обоим теориям, т.е. условия (11), но и обязательного выполнения условий (16). При построении динамики однородной, изотропной космологической модели без релятивистской теории Эйнштейна не обойтись. Невыполнение условий (16) ведет к совсем другой неправильной картине эволюции.