Астрономический вестник, 2019, T. 53, № 6, стр. 423-427
Учет релятивистских эффектов во вращении Марса и его спутников
В. В. Пашкевич a, *, А. В. Вершков a
a Главная (Пулковская) астрономическая обсерватория РАН
Санкт-Петербург, Россия
* E-mail: apeks@gaoran.ru
Поступила в редакцию 11.02.2019
После доработки 13.03.2019
Принята к публикации 26.03.2019
Аннотация
Данное исследование посвящено учету релятивистских эффектов (геодезической прецессии и нутации, вместе составляющих геодезическое вращение) во вращении Марса и его спутников (Фобоса и Деймоса). Для их вычисления использовался метод, разработанный в статье (Пашкевич, 2016), который применим для изучения любых тел Солнечной системы, имеющих долгосрочные эфемериды. В результате для спутников Марса впервые определены наиболее существенные вековые и периодические члены их геодезического вращения в возмущающих членах физической либрации и в углах Эйлера.
ВВЕДЕНИЕ
Геодезическое вращение, впервые рассмотренное Виллемом де Ситтером в 1916 г. (De Sitter, 1916), включает в себя два эффекта: систематический – геодезической прецессии – и периодический – геодезической нутации. Эти эффекты являются наиболее существенными в релятивистском вращении и имеют формальное сходство с известными в классической механике явлениями прецессии и нутации. Их появление не связано с действием на тело каких-либо сил, в отличие от вышеупомянутых эффектов классической механики, а обусловлено изменением направления его оси вращения в результате параллельного переноса вектора углового момента тела вдоль его орбиты в искривленном пространстве-времени.
Основной целью данного исследования является определение наиболее существенных вековых и периодических членов геодезического вращения Марса в углах Эйлера и его спутников в углах Эйлера и в возмущающих членах их физической либрации.
Для этого будем использовать, разработанный в статье (Пашкевич, 2016) метод для вычисления величин геодезического вращения любых тел Солнечной системы, для которых имеется долгосрочная эфемерида.
ОПИСАНИЕ МЕТОДА РЕШЕНИЯ ЗАДАЧИ
Суть применяемого метода (Пашкевич, 2016) состоит в следующем:
1) Задача о геодезическом (релятивистском) вращении Марса и его спутников изучается относительно кинематически невращающейся (Kopeikin и др., 2011) собственной координатной системы исследуемых тел (Archinal и др., 2018). Положения, скорости и орбитальные элементы для Фобоса и Деймоса берутся из Horizons On-Line Ephemeris System (Giorgini и др., 2001). Для Солнца, Луны, Плутона и больших планет положения и скорости вычисляются с помощью фундаментальной эфемериды JPL DE431/LE431 (Folkner и др., 2014).
2) Для каждого исследуемого тела в углах Эйлера, а для марсианских спутников еще и в возмущающих членах физической либрации, с шагом в 57 мин на 900-летнем интервале времени (от AD1600 01 января 00 ч 00 мин до AD2499 14 октября 14 ч 03 мин) получаются значения скоростей их геодезического вращения.
Вид вектора угловой скорости геодезического вращения для любых тел солнечной системы определяется следующей формулой (Eroshkin, Pashkevich, 2007):
(1)
${{\bar {\sigma }}_{i}} = \frac{1}{{{{c}^{2}}}}\sum\limits_{j \ne i} {\frac{{G{{m}_{j}}}}{{{{{\left| {{{{\bar {R}}}_{i}} - {{{\bar {R}}}_{j}}} \right|}}^{3}}}}} \left( {{{{\bar {R}}}_{i}} - {{{\bar {R}}}_{j}}} \right) \times \left( {\frac{3}{2}{{{\dot {\bar {R}}}}_{i}} - 2{{{\dot {\bar {R}}}}_{j}}} \right).$Здесь c – скорость света в вакууме; G – гравитационная постоянная; индекс i соответствует исследуемым телам (Марсу и его спутникам), а j – возмущающим телам; ${{\bar {R}}_{i}},\;{{\dot {\bar {R}}}_{i}},{{\bar {R}}_{j}},\;{{\dot {\bar {R}}}_{j}}$ – барицентрические векторы положений и скоростей i-го и j-го тела, соответственно; mj – масса j-го тела; символ × означает векторное произведение. Далее в формулах индекс i будет опущен.
С помощью формул (3)–(5) (Пашкевич, 2016) производится редукция компонент вектора угловой скорости геодезического вращения спутников Марса от геоцентрической системы координат (координатная система эфемериды DE431/LE431) к планетоцентрической координатной системе (Archinal и др., 2018).
Скорости геодезического вращения тел Солнечной системы определяются для спутников Марса в углах Эйлера и в возмущающих членах физической либрации с использованием следующих выражений (Пашкевич, 2016):
(2)
$\begin{gathered} \left. \begin{gathered} \Delta \dot {\psi } = - \frac{{{{\sigma }_{1}}\sin \varphi + {{\sigma }_{2}}\cos \varphi }}{{\sin \theta }} \hfill \\ \Delta \dot {\theta } = - {{\sigma }_{1}}\cos \varphi + {{\sigma }_{2}}\sin \varphi \hfill \\ \Delta \dot {\varphi } = {{\sigma }_{3}} - \Delta \dot {\psi }\cos \theta , \hfill \\ \end{gathered} \right\} \\ {\text{ }}\left. {\begin{array}{*{20}{c}} {\sin \theta {\text{ }}\Delta \dot {\psi } = - {{\sigma }_{1}}\sin \varphi - {{\sigma }_{2}}\cos \varphi = \Delta ({\text{I}}\dot {\sigma })} \\ {\Delta \dot {\theta } = - {{\sigma }_{1}}\cos \varphi + {{\sigma }_{2}}\sin \varphi = \Delta \dot {\rho }} \\ {\Delta \dot {\psi } + \Delta \dot {\varphi } = {{\sigma }_{3}} - ({{\sigma }_{1}}\sin \varphi + {{\sigma }_{2}}\cos \varphi ){\text{tg}}\frac{\theta }{2} = \Delta \dot {\tau }.} \end{array}} \right\} \\ \end{gathered} $Здесь ψ, θ, φ – углы Эйлера (ψ – угол долготы нисходящего узла экватора тела на эклиптике эпохи J2000; θ – угол наклона экватора тела к неподвижной эклиптике эпохи J2000; φ – угол собственного вращения тела между нисходящим узлом эпохи J2000.0 и главной осью минимального момента инерции тела); τ, ρ, и σ – возмущающие члены физической либрации исследуемого тела для неподвижной эклиптики эпохи J2000.0 в долготе, в наклоне и в долготе узла, соответственно; I – постоянный угол наклона экватора исследуемого тела к плоскости Лапласа; $\Delta \dot {\psi } = {{\dot {\psi }}_{r}} - \dot {\psi },$ $\Delta \dot {\theta } = {{\dot {\theta }}_{r}} - \dot {\theta }$ и $\Delta \dot {\varphi } = {{\dot {\varphi }}_{r}} - \dot {\varphi }$ – разности релятивистских и ньютоновых углов Эйлера исследуемого тела, соответственно; $\Delta ({\text{I}}\dot {\sigma }) = {\text{I}}{{\dot {\sigma }}_{r}} - {\text{I}}\dot {\sigma },$ $\Delta \dot {\rho } = {{\dot {\rho }}_{r}} - \dot {\rho }$ и $\Delta \dot {\tau } = {{\dot {\tau }}_{r}} - \dot {\tau }$ – разности релятивистских и ньютоновых возмущающих членов физической либрации исследуемого тела, соответственно; точка означает дифференцирование по времени.
3) Наиболее существенные составляющие скорости геодезического вращения исследуемого тела находятся методами наименьших квадратов и спектрального анализа. В результате вычисляются значения коэффициентов основных систематических и периодических членов скорости геодезического вращения тела.
Выражения для систематических и периодических членов скорости геодезического вращения тела имеют вид, соответствующий формуле (7) из (Пашкевич, 2016):
(3)
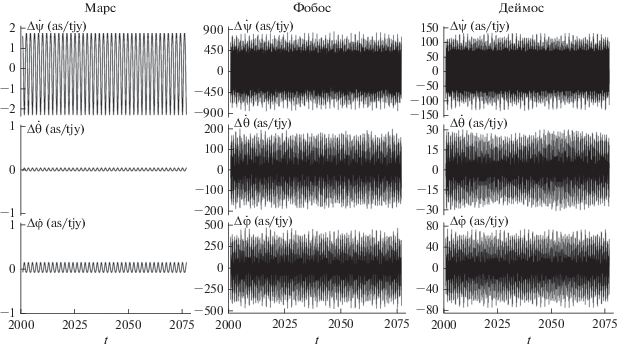
$\begin{gathered} \Delta \dot {x} = \sum\limits_{n = 1}^N {\Delta {{{\dot {x}}}_{n}}{{t}^{{n - 1}}}} + \\ + \,\,\sum\limits_j {\sum\limits_{k = 0}^M {(\Delta {{{\dot {x}}}_{{Cjk}}}\cos } } ({{\nu }_{{j0}}} + {{\nu }_{{j1}}}t) + \\ + \,\,\Delta {{{\dot {x}}}_{{Sjk}}}\sin ({{\nu }_{{j0}}} + {{\nu }_{{j1}}}t)){{t}^{k}}, \\ \end{gathered} $На рис. 1 в углах Эйлера представлена скорость изменения геодезической нутации Марса и его спутников на 75-летней части исследуемого интервала.
После их аналитического интегрирования вычисляются систематические и периодические члены геодезического вращения тела:
(4)
$\begin{gathered} \Delta x = \sum\limits_{n = 1}^N {\Delta {{x}_{n}}{{t}^{n}}} + \sum\limits_j {\sum\limits_{k = 0}^M {(\Delta {{x}_{{Cjk}}}} } \cos ({{\nu }_{{j0}}} + {{\nu }_{{j1}}}t) + \\ + \,\,\Delta {{x}_{{Sjk}}}\sin ({{\nu }_{{j0}}} + {{\nu }_{{j1}}}t)){{t}^{k}}, \\ \end{gathered} $(5)
$\begin{gathered} \Delta {{x}_{{SjM}}} = \frac{{\Delta {{{\dot {x}}}_{{CjM}}}}}{{{{\nu }_{{j1}}}}},\,\,\,\,\Delta {{x}_{{CjM}}} = \frac{{ - \Delta {{{\dot {x}}}_{{SjM}}}}}{{{{\nu }_{{j1}}}}}, \\ \Delta {{x}_{{SjM - 1}}} = \frac{{\Delta {{{\dot {x}}}_{{CjM - 1}}} - m\Delta {{x}_{{CjM}}}}}{{{{\nu }_{{j1}}}}}, \\ \Delta {{x}_{{CjM - 1}}} = \frac{{m\Delta {{x}_{{SjM}}} - \Delta {{{\dot {x}}}_{{SjM - 1}}}}}{{{{\nu }_{{j1}}}}},\,\,... \\ \Delta {{x}_{{Sj1}}} = \frac{{\Delta {{{\dot {x}}}_{{Cj1}}} - 2\Delta {{x}_{{Cj2}}}}}{{{{\nu }_{{j1}}}}},\,\,\,\,\Delta {{x}_{{Cj1}}} = \frac{{2\Delta {{x}_{{Sj2}}} - \Delta {{{\dot {x}}}_{{Sj1}}}}}{{{{\nu }_{{j1}}}}}, \\ \Delta {{x}_{{Sj0}}} = \frac{{\Delta {{{\dot {x}}}_{{Cj0}}} - \Delta {{x}_{{Cj1}}}}}{{{{\nu }_{{j1}}}}},\,\,\,\,\Delta {{x}_{{Cj0}}} = \frac{{\Delta {{x}_{{Sj1}}} - \Delta {{{\dot {x}}}_{{Sj0}}}}}{{{{\nu }_{{j1}}}}}. \\ \end{gathered} $В результате исследований методом наименьших квадратов были определены значения величин N и M для различных объектов, обеспечивающие наилучшую аппроксимацию параметров геодезического вращения. Соответственно, для Фобоса и Деймоса N = 2, M = 4, а для Марса N = = 3, M = 4.
РЕЗУЛЬТАТЫ
Для Фобоса и Деймоса в углах Эйлера и в возмущающих членах физической либрации вычислены их систематические (табл. 1) и периодические члены их геодезического вращения (табл. 2).
Таблица 1.
Систематические члены геодезического вращения Марса и его спутников
| Марс | Фобос | Деймос | |||
|---|---|---|---|---|---|
| Δψ1 (угл. мкс) | Δψ1 (угл. мкс) | Δτ1 (угл. мкс) | Δψ1 (угл. мкс) | Δτ1 (угл. мкс) | |
| T | –7113935.67 | –209314536.65 | –95713029.32 | –27680041.88 | –15836786.70 |
| T2 | 9758.66 | 41131.73 | 20886.67 | 14513.92 | 2090.37 |
| T3 | 1328.31 | ||||
| Δθ1 (угл. мкс) | Δθ1 (угл. мкс) | Δρ1 (угл. мкс) | Δθ1 (угл. мкс) | Δρ1 (угл. мкс) | |
| T | 119866.55 | 109622.21 | 109622.21 | 118920.67 | 118920.67 |
| T2 | –1065.60 | –80000.14 | –80000.14 | –5747.68 | –5747.68 |
| T3 | –57.96 | ||||
| Δφ1 (угл. мкс) | Δφ1 (угл. мкс) | Δ(Iσ)1 (угл. мкс) | Δφ1 (угл. мкс) | Δ(Iσ)1 (угл. мкс) | |
| T | 405134.49 | 113601507.33 | 94088355.88 | 11843255.18 | 12076373.96 |
| T2 | –11482.61 | –20245.06 | 33091.62 | –12423.55 | 602.99 |
| T3 | –280.34 | ||||
Таблица 2.
Периодические члены геодезического вращения Марса и его спутников
| Название тела | Угол | Период | Аргумент | Коэффициент
при sin(Аргумент) (угл. мкс) |
Коэффициент
при cos(Аргумент) (угл. мкс) |
|---|---|---|---|---|---|
| Марс | Δψ2 | 1.881 лет | λ4 | –543.44 – 22.46T +… | –241.42 + 40.43T + … |
| Δθ2 | 1.881 лет | λ4 | 9.16 + 0.24T + … | 4.07 – 0.74T + … | |
| Δφ2 | 1.881 лет | λ4 | 30.95 – 0.39T + … | 13.75 – 3.05T + … | |
| Фобос | Δψ2 | 7.657 ч | D41 | –58.68 + 0.20T + 0.88T 2 + … | 59.45 – 0.02T + 0.78T 2 + … |
| Δθ2 | 7.657 ч | D41 | –8.48 + 0.02T –0.10T 2 + … | –9.23 – 0.04T – 0.39T 2 + … | |
| Δφ2 | 7.657 ч | D41 | 21.36 – 0.13T – 1.00T 2 + … | –22.72 – 0.04T – 0.32T 2 + … | |
| Δ(Iσ)2 | 7.657 ч | D41 | 26.38 – 0.04T – 0.41T 2 + … | –26.72 – 0.03T – 0.36T 2 + … | |
| Δρ2 | 7.657 ч | D41 | –8.48 + 0.02T – 0.10T 2 + … | –9.23 – 0.04T – 0.39T 2 + … | |
| Δτ2 | 7.657 ч | D41 | –37.32 + 0.07T – 0.12T 2 + … | 36.73 – 0.06T + 0.46T 2 + … | |
| Деймос | Δψ2 | 1.265 дней | D42 | –51.78 + 0.14T – 1.00T 2 + … | 11.01 + 00.01T + 0.53T 2 + … |
| Δθ2 | 1.265 дней | D42 | –1.21 + 0.01T + 0.23T 2 + … | –7.57 – 0.09T + 0.67T 2 + … | |
| Δφ2 | 1.265 дней | D42 | 19.15 – 0.05T – 0.07T 2 + … | –4.58 – 0.04T – 0.31T 2 + … | |
| Δ(Iσ)2 | 1.265 дней | D42 | 22.60 + 0.17T – 1.92T 2 + … | –4.80 – 0.05T + 0.26T 2 + … | |
| Δρ2 | 1.265 дней | D42 | –1.21 + 0.01T + 0.23T 2 + … | –7.57 – 0.09T + 0.67T 2 + … | |
| Δτ2 | 1.265 дней | D42 | –32.63 + 0.10T – 1.07T 2 + … | 6.43 – 0.04T + 0.22T 2 + … |
Для Марса в углах Эйлера определены новые высокоточные, динамически согласованные с эфемеридой DE431/LE431, наиболее существенные систематические (табл. 1) и периодические члены его геодезического вращения (табл. 2).
Введем обозначения для углов, приведенных в выражении (4), для данных табл. 1 и 2:
(6)
$\begin{gathered} \Delta {{x}_{1}} = \sum\limits_{n = 1}^N {\Delta {{x}_{n}}{{t}^{n}}} , \\ \Delta {{x}_{2}} = \sum\limits_j {\sum\limits_{k = 0}^M {(\Delta {{x}_{{Cjk}}}} } \cos ({{\nu }_{{j0}}} + {{\nu }_{{j1}}}t) + \\ + \,\,\Delta {{x}_{{Sjk}}}\sin ({{\nu }_{{j0}}} + {{\nu }_{{j1}}}t)){{t}^{k}}, \\ \end{gathered} $Заметим, что в похожих таблицах предыдущей работы (Пашкевич, 2016) приведены разности ньютоновых и релятивистских углов $(\Delta x = {{x}_{{{\text{ньютоновое}}}}} - {{x}_{{{\text{релятивистское}}}}}),$ поэтому полученные в данном исследовании величины членов геодезического вращения для Марса в таблицах имеют противоположный знак.
В табл. 1 и 2: D41 = λ41 – λ4 + 180°, D42 = λ42 – λ4 + + 180° – средние элонгации Фобоса и Деймоса от Солнца; λ4 – средняя долгота Марса; λ41, λ42 – средние марсоцентрические долготы Фобоса и Деймоса; T – Динамическое Барицентрическое Время (Dynamical Barycentric Time) (TDB) измеряется в юлианских тысячелетиях (tjy) (365250 дней) от эпохи J2000. Средняя долгота Марса взята из работы (Brumberg, Bretagnon, 2000). Средние долготы спутников Марса и их средние элонгации от Солнца вычислены с использованием данных Horizons On-Line Ephemeris System (Giorgini и др., 2001).
Поскольку масса Солнца является доминирующей в Солнечной системе, основная часть вектора угловой скорости геодезического вращения ${{\bar {\sigma }}_{i}}$ для каждого тела Солнечной системы является результатом его гелиоцентрического орбитального движения. Марс и его спутники Фобос и Деймос находятся в среднем на одном расстоянии от Солнца и движутся относительно него в среднем с одной скоростью. Вследствие этого величины их геодезического вращения, вызванные влиянием Солнца, подобно Земле и Луне (Пашкевич, 2016), должны быть достаточно близки между собой. В то же время, величины полного геодезического вращения Фобоса и Деймоса значительно превосходят величину геодезического вращения Марса. Поэтому величины их коэффициентов в Δψ и Δτ при вековых составляющих (табл. 1) заметно отличаются друг от друга. Это связано с тем, что из-за близкого к ним расстояния Марс оказывает большее влияние на их геодезическое вращение, чем Солнце. Так же из табл. 1 и 2 видно, что величина геодезического вращения спутников Марса убывает с увеличением их расстояния от Марса.
В данной работе также было проведено исследование взаимного релятивистского влияния спутников Марса друг на друга (т.е. включение другого спутника в число возмущающих тел). Так изменение величины геодезической прецессии Деймоса от релятивистского влияния Фобоса в долготе узла составляет –6.9 × 10–17 мкс дуги за 1000 лет, в наклоне –5.5 × 10–18 мкс дуги за 1000 лет и в угле собственного вращения –6.7 × 10–17 мкс дуги за 1000 лет; а изменение величины геодезической прецессии Фобоса от релятивистского влияния Деймоса: в долготе узла составляет ‒7.3 × 10–17 мкс дуги за 1000 лет, в наклоне –6.4 × × 10–18 мкс дуги за 1000 лет и в угле собственного вращения –6.9 × 10–17 мкс дуги за 1000 лет.
ЗАКЛЮЧЕНИЕ
В данном исследовании впервые в углах Эйлера и в возмущающих членах физической либрации для спутников Марса вычислены их систематические (табл. 1) и периодические (табл. 2) члены геодезического вращения. Взаимное релятивистское влияние спутников Марса друг на друга по сравнению с влиянием Марса является несущественным. Полученные аналитические значения для геодезического вращения Фобоса и Деймоса могут быть использованы для численного исследования их вращения в релятивистском приближении.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-02-00811.
Список литературы
Пашкевич В.В. Геодезическое (релятивистское) вращение тел Солнечной системы // Вестн. СПбГУ. 2016. Сер. 1. Т. 3(61). Вып. 3. С. 506–516.
Archinal B.A., Acton C.H., A’Hearn M.F., Conrad A., Consolmagno G.J., Duxbury T., Hestroffer D., Hilton J.L., Kirk R.L., Klioner S.A., McCarthy D., Meech K., Oberst J., Ping J., Seidelmann P.K., Tholen D.J., Thomas P.C., Williams I.P. Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements: 2015 // Celest. Mech. and Dyn. Astr. 2018. V. 130. № 22. P. 1–46.
Brumberg V.A., Bretagnon P. Kinematical relativistic corrections for Earth’s rotation parameters // Proc. IAU Colloq. 180 / Eds Johnston K., McCarthy D., Luzum B., Kaplan G., U.S. Naval Observatory. 2000. P. 293–302.
De Sitter W. On Einstein’s theory of gravitation and its astronomical consequences // Mon. Notic. Roy. Astron. Soc. 1916. № 77. P. 155–184.
Eroshkin G.I., Pashkevich V.V. Geodetic rotation of the Solar system bodies // Artificial Satellites. 2007. V. 42. № 1. P. 59–70.
Giorgini J.D., Chodas P.W., Yeomans D.K. Orbit uncertainty and close-approach analysis capabilities of the Horizons On-Line Ephemeris System // 33rd AAS/DPS Meeting in New Orleans. LA. Nov 26. 2001–Dec 01. 2001.
Kopeikin S., Efroimsky M., Kaplan G. Relativistic Celestial Mechanics in the Solar System // NY: John Wiley & Sons, 2011. P. 1–894.
Folkner W.M., Williams J.G., Boggs D.H., Park R.S., Kuchynka P. The Planetary and Lunar Ephemerides DE430 and DE431 // IPN Progress Report 42-196. 2014. P. 1–81.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник