1. На главную
  2. Электронные версии
  3. Астрономический вестник
  4. T. 54, № 4, 2020

Астрономический вестник, 2020, T. 54, № 4, стр. 337-348

Динамическая структура околоземного орбитального пространства в области резонанса 1 : 2 со скоростью вращения Земли

И. В. Томилова a, *, Д. С. Красавин a, **, Т. В. Бордовицына a, ***

a Томский госуниверситет
Томск, Россия

* E-mail: irisha_tom@mail.ru
** E-mail: iosfixed@gmail.com
*** E-mail: tvbord@sibmail.com

Поступила в редакцию 06.08.2019
После доработки 30.12.2019
Принята к публикации 29.01.2020

Полный текст (PDF)

Аннотация

В работе представлены результаты исследования динамической структуры околоземного орбитального пространства в области резонанса 1 : 2 со скоростью вращения Земли. Излагаются результаты обширного численно-аналитического эксперимента по исследованию орбитальной эволюции объектов, движущихся в диапазоне больших полуосей от 26 550 до 26 570 км, с наклонениями от 0° до 180°. В этой области выявлены зоны действия пяти компонент орбитального резонанса и апсидально-нодальных вековых резонансов низких порядков. Построены карты распределения выявленных резонансов. Динамическая структура орбитального пространства исследована также с использованием быстрой ляпуновской характеристики MEGNO и представлена MEGNO-картой области в сечении плоскостью {наклонение орбиты, большая полуось}. Показано, что особенностью динамической эволюции большинства исследованных орбит является хаотичность, возникающая под действием наложения резонансов различных типов.

Ключевые слова: динамика околоземных объектов, орбитальный резонанс, вековые апсидально-нодальные резонансы, MEGNO-анализ

ВВЕДЕНИЕ

В настоящей статье представлены результаты, которые продолжают исследования, опубликованные в (Томилова и др., 2018), где были описаны данные анализа динамической структуры только той части орбитального пространства области МЕО (Medium Earth Orbits), где функционируют навигационные системы ГЛОНАСС и GPS. Следует сказать, что исследованию динамики объектов систем ГЛОНАСС и GPS и изучению структуры орбитального пространства, где эти системы функционируют, посвящено немало работ (Chao, Gick, 2004; Rossi, 2008; Rosengren и др., 2015; Daquin и др., 2016; Томилова, Бордовицына, 2017; Томилова и др., 2018). Здесь же мы даем динамическую структуру всей области резонанса 1 : 2 со скоростью вращения Земли в диапазоне больших полуосей от 26 550 до 26 570 км и в диапазоне наклонений от 0° до 180°.

В работе (Томилова и др., 2019) было отмечено, что группа авторов из Томского университета планирует построить динамическую структуру всего околоземного орбитального пространства и это третья работа запланированной серии. Все работы объединены общим подходом. Мы используем численное моделирование для построения орбитальной эволюции объектов, а аналитическую методику для выявления действующих на объекты резонансов. Это позволяет нам рассматривать совместное влияние не только вековых резонансов различных типов, но и вековых, и орбитального резонансов, что очень существенно для объектов рассматриваемой зоны околоземного орбитального пространства.

МЕТОДИКА ИССЛЕДОВАНИЯ

Для исследования динамических особенностей движения объектов, находящихся в окрестности резонанса 1 : 2 со скоростью вращения Земли, применялась методика, изложенная в (Томилова и др., 2018; 2019). Методика состоит из нескольких этапов:

– построение динамической карты области с использованием быстрой ляпуновской характеристики MEGNO (Cincotta, Simo, 2000; Cincotta и др., 2003; Valk и др., 2009);

– анализ структуры всех резонансных возмущений, действующих на движение объектов рассматриваемой орбитальной области;

– изучение особенностей долговременной эволюции орбит.

Численное моделирование движения объектов осуществлялось на кластере “СКИФ Cyberia” НИ ТГУ с использованием программного комплекса “Численная модель движения систем ИСЗ” (Александрова и др., 2017), построенного с использованием высокоточного интегратор Гаусса–Эверхарта (Авдюшев, 2010). В процессе моделирования учитывались возмущения от гармоник геопотенциала до 4 порядка и степени, а также возмущения от Луны и Солнца. Совместно с уравнениями движения интегрировались уравнения для вычисления параметров MEGNO (Бордовицына и др., 2010), по методике, которая была предложена в (Volk и др., 2009).

Выявление орбитальных резонансов производилось с использованием методики предложенной Allan (1967a; 1967b) и уточненной Кузнецовым (Кузнецов и др., 2012). Подробно методика изложена также в (Томилова и др., 2019).

В соответствии с этой методикой для рассматриваемого в данной работе резонанса 1 : 2 со скоростью вращения Земли резонансные (критические) аргументы будут иметь вид (Кузнецов и др., 2012)

(1)
$\begin{gathered} {{\Phi }_{1}} = (M + \Omega + \omega ) - 2\theta ,\,\,\,{{\Phi }_{2}} = (M + \omega ) + 2(\Omega - \theta ), \\ {{\Phi }_{3}} = M + 2(\Omega + \omega - \theta ), \\ {{\Phi }_{4}} = M - \Omega + \omega - 2\theta ,\,\,\,{{\Phi }_{5}} = M + 2( - \omega + 2\Omega - \theta ), \\ \end{gathered} $
а их резонансные соотношения запишутся как
(2)
$\begin{gathered} {{{\dot {\Phi }}}_{1}} = (\dot {M} + \dot {\Omega } + \dot {\omega }) - 2\dot {\theta }, \\ {{{\dot {\Phi }}}_{2}} = (\dot {M} + \dot {\omega }) + 2(\dot {\Omega } - \dot {\theta }), \\ {{{\dot {\Phi }}}_{3}} = \dot {M} + 2(\dot {\Omega } + \dot {\omega } - \dot {\theta }), \\ {{{\dot {\Phi }}}_{4}} = \dot {M} - \dot {\Omega } + \dot {\omega } - 2\dot {\theta }, \\ {{{\dot {\Phi }}}_{5}} = \dot {M} + 2( - \dot {\omega } + 2\dot {\Omega } - \dot {\theta }), \\ \end{gathered} $
где $\Omega ,{\text{ }}\omega ,{\text{ }}M$ – долгота восходящего узла, аргумент перигея, средняя аномалия орбиты спутника, $\theta $ – гринвичское звездное время.

Для вековых резонансов также изучается эволюция во времени резонансных аргументов, полученных из аргументов разложения возмущающей функции (Murray, Dermott, 2000) для однократно (3) и двукратно (4) осредненной ограниченной задачи трех тел

(3)
$\begin{gathered} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } = (l - 2p{\kern 1pt} '\,\, + q{\kern 1pt} ')M{\kern 1pt} '\,\, + (l - 2p)\omega - \\ - \,\,(l - 2p{\kern 1pt} ')\omega {\kern 1pt} '\,\, + \bar {m}(\Omega - \Omega {\kern 1pt} '), \\ \end{gathered} $
(4)
$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } = (l - 2p)\omega - (l - 2p{\kern 1pt} ')\omega {\kern 1pt} '\,\, + \bar {m}(\Omega - \Omega {\kern 1pt} '),$
и оценивается степень близости к нулю резонансных соотношений
(5)
$\dot {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } \approx 0,\,\,\,\,\dot {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } } \approx 0,$
причем

(6)
$\begin{gathered} M{\kern 1pt} ' = M_{0}^{'} + n{\kern 1pt} '\left( {t - {{t}_{0}}} \right),\,\,\,\,\omega {\kern 1pt} ' = \omega _{0}^{'} + \dot {\omega }{\kern 1pt} '\left( {t - {{t}_{0}}} \right), \\ \Omega {\kern 1pt} ' = \Omega _{0}^{'} + \dot {\Omega }{\kern 1pt} '\left( {t - {{t}_{0}}} \right), \\ \omega = {{\omega }_{0}} + \dot {\omega }\left( {t - {{t}_{0}}} \right),\,\,\,\,\Omega = {{\Omega }_{0}} + \dot {\Omega }\left( {t - {{t}_{0}}} \right). \\ \end{gathered} $

Вековые частоты в движении спутника $\dot {\Omega } = {{\dot {\Omega }}_{{{{J}_{2}}}}} + {{\dot {\Omega }}_{L}} + {{\dot {\Omega }}_{S}},$ $\dot {\omega } = {{\dot {\omega }}_{J}} + {{\dot {\omega }}_{L}} + {{\dot {\omega }}_{S}}$ определяются влиянием второй зональной гармоники с коэффициентом ${{J}_{2}}$, а также влиянием Луны (L) и Солнца (S) и вычисляются по известным формулам (Бордовицына, Авдюшев, 2007).

Полагая индексы, содержащиеся в формулах (5) равными l = 2, $p,p{\kern 1pt} ',\bar {m} = 0,1,2,$ $q{\kern 1pt} ' = - 1,0,1,$ получим резонансные соотношения для вековых резонансов низких порядков. Типы рассматриваемых в настоящей работе вековых апсидально-нодальных резонансов первого-шестого порядков приведены в таблице. Соотношение 20 представляет собой резонанс Лидова‒Козаи (Лидов, 1961; Kozai, 1962).

Таблица 1.

   Типы апсидально-нодальных резонансов низких порядков

№ Тип резонансного
соотношения 		№ Тип резонансного
соотношения 		№ Тип резонансного
соотношения
1 $\left( {\dot {\Omega } - \Omega _{{S,L}}^{'}} \right) + \dot {\omega } - \dot {\omega }_{{S,L}}^{'}$ 8 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - 2\dot {\omega } - 2\dot {\omega }_{{S,L}}^{'}$ 15 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + 2\dot {\omega }_{{S,L}}^{'}$
2 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - \dot {\omega } + \dot {\omega }_{{S,L}}^{'}$ 9 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + \dot {\omega }$ 16 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - 2\dot {\omega }_{{S,L}}^{'}$
3 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + \dot {\omega } + \dot {\omega }_{{S,L}}^{'}$ 10 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - \dot {\omega }$ 17 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right)$
4 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - \dot {\omega } - \dot {\omega }_{{S,L}}^{'}$ 11 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + 2\dot {\omega }$ 18 $\dot {\omega } - \dot {\omega }_{{S,L}}^{'}$
5 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + 2\dot {\omega } - 2\dot {\omega }_{{S,L}}^{'}$ 12 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - 2\dot {\omega }$ 19 $\dot {\omega } + \dot {\omega }_{{S,L}}^{'}$
6 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - 2\dot {\omega } + 2\dot {\omega }_{{S,L}}^{'}$ 13 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + \dot {\omega }_{{S,L}}^{'}$ 20 $\dot {\omega }$
7 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + 2\dot {\omega } + 2\dot {\omega }_{{S,L}}^{'}$ 14 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - \dot {\omega }_{{S,L}}^{'}$    

Классификация основной части вековых резонансов, действующих на движение ИСЗ, была впервые дана Куком (Cook, 1962), а аналитическая теория вековых спутниковых резонансов представлена в работах (Breiter, 2001a; 2001b).

Следует отметить, что характер изменения резонансных аргументов (1), (3) и (4) играет важную роль в оценке устойчивости резонанса (Murray, Dermott, 1999). Если резонансный аргумент либрирует, резонанс устойчив, если резонансный аргумент в процессе эволюции меняет изменение с либрационного характера на циркуляционный, резонанс неустойчив. В том случае, когда резонансный аргумент циркулирует на всем рассматриваемом интервале времени, считается, что резонанс отсутствует.

Действие вековых резонансов со скоростью движения возмущающего тела в процессе исследования динамической структуры рассматриваемой области орбитального пространства выявлено не было, поэтому мы не будем на них останавливаться.

ОПИСАНИЕ ДИНАМИЧЕСКОЙ СТРУКТУРЫ ОБЛАСТИ РЕЗОНАНСА 1 : 2 СО СКОРОСТЬЮ ВРАЩЕНИЯ ЗЕМЛИ

Для общей оценки динамической структуры области орбитального резонанса 1 : 2 со скоростью вращения Земли был проведен обширный численный эксперимент. Принимались во внимание только гравитационные возмущения, определяемые влиянием несферичности гравитационного поля Земли, а также притяжением Луны и Солнца. Особенности динамики объектов рассматривались в орбитальном пространстве $\left\{ {a{{,}_{{}}}e,{\text{ }}i} \right\}$. Это сделано для того, чтобы выявить общие закономерности в динамической структуре орбитального пространства, не связанные с особенностями строения самого аппарата и условиями вывода его в точку стояния.

Вопросы совместного влияния гравитационных возмущений и светового давления рассмотрены в работе Томилова, Бордовицына, 2018), оценки влияния начальных значений параметров $\Omega ,{\text{ }}\omega $ на эволюцию орбит в области МЕО под действием вековых возмущений представлены в работе (Бордовицына и др., 2012).

В работе (Томилова и др., 2018) было показано, что область рассматриваемого орбитального резонанса ограничивается диапазоном больших полуосей 26550–26570 км, поэтому в настоящей работе был выполнен MEGNO-анализ области орбитального пространства, расположенного в указанном диапазоне больших полуосей и в диапазоне наклонений от 0° до 180° для почти круговых орбит с начальным эксцентриситетом ${{e}_{0}} = 0.01$. В работе (Томилова и др., 2018) рассматривался диапазон наклонений 50°–70°, охватывающий области размещения навигационных систем ГЛОНАСС и GPS.

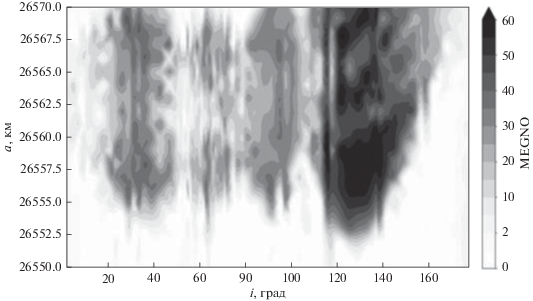
На рис. 1 приведена MEGNO-карта данной области орбитального пространства. Модельные объекты выбирались с шагом 1 км по большой полуоси и 2° по наклонению. Здесь и во всех остальных рассматриваемых в данной работе численных экспериментах начальный эксцентриситет принимался равным 0.001. Орбитальная эволюция прослеживалась на интервале времени 100 лет. На графике приведены значения усредненного параметра MEGNO ${{\bar {Y}}_{\phi }}\left( t \right)$. Как известно (Cincotta и др., 2003), эволюция этого параметра во времени позволяет определить характер движения. Так, например, для квазипериодических (регулярных) орбит ${{\bar {Y}}_{\phi }}\left( t \right)$ осциллирует около 2. Причем для квазипериодических орбит ${{\bar {Y}}_{\phi }}\left( t \right) \to 2$, а для устойчивых орбит типа гармонического осциллятора ${{\bar {Y}}_{\phi }}\left( t \right) \to 0$.

Рис. 1.

MEGNO-карта области орбитального резонанса 1 : 2 со скоростью вращения Земли.

Как показывают данные, приведенные на рис. 1, область очень неоднородна по степени хаотизации движения рассмотренных объектов. Источником возникновения хаотичности в движении околоземных объектов может являться наложение резонансов различных типов, поэтому структура всех действующих резонансов была исследована очень тщательно.

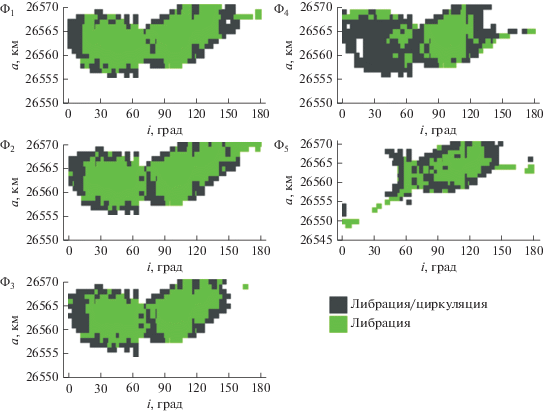
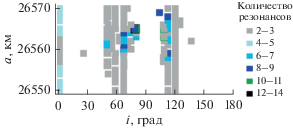
Обратимся к результатам исследования структуры резонансов, действующих на объекты, движущиеся в рассматриваемой области околоземного орбитального пространства. На рис. 2 показана локализация зон действия мультиплетов орбитального резонанса 1 : 2 со скоростью вращением Земли. В области околоэкваториальных наклонений орбит все пять компонент показывают либо неустойчивое действие резонанса, либо его отсутствие. В области больших наклонений компоненты с устойчивым и неустойчивым действием распределены неравномерно. Симметрии в распределении резонансов по наклонению между прямым и обратным движением не наблюдается.

Рис. 2.

Зоны действия мультиплетов орбитального резонанса 1 : 2 со скоростью вращения Земли.

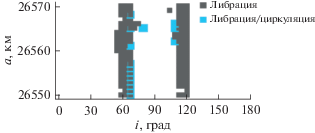
На рис. 3 представлено распространение векового резонанса Лидова–Козаи в рассматриваемой области орбитального пространства. На рис. 4 показаны все устойчивые вековые резонансы, связанные с Луной, на рис. 5 – неустойчивые резонансы того же типа. На рис. 6 приведены все устойчивые вековые резонансы, связанные с Солнцем, действующие на объекты изучаемой области орбитального пространства, а на рис. 7 – все неустойчивые вековые резонансы, связанные с Солнцем.

Рис. 3.

Распространенность резонанса Лидова–Козаи в рассматриваемой области.

Рис. 4.

Распределение всех устойчивых лунных вековых резонансов. Цветом показано количество резонансов, резонансный аргумент которых либрирует на всем интервале исследования.

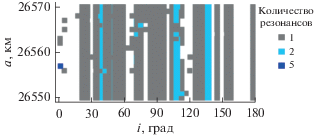
Рис. 5.

Распределение всех неустойчивых лунных вековых резонансов. Цветом показано количество резонансов, резонансный аргумент которых на интервале исследования переходит от либрации к циркуляции.

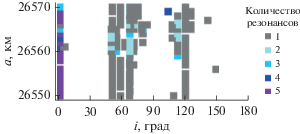
Рис. 6.

Распределение всех устойчивых солнечных вековых резонансов. Цветом показано количество резонансов, резонансный аргумент которых либрирует на всем интервале исследования.

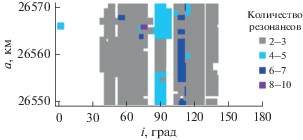
Рис. 7.

Распределение всех неустойчивых солнечных вековых резонансов. Цветом показано количество резонансов, резонансный аргумент которых на интервале исследования переходит от либрации к циркуляции.

На рис. 3 показаны полосы проявления резонанса Лидова–Козаи11 ${{\dot {\psi }}_{{L{\text{ - }}K}}} = \dot {\omega } \approx 0$ в динамике объектов рассматриваемой зоны околоземного орбитального пространства. Резонанс устойчив, неустойчивые островки очень малы.

Устойчивые вековые резонансы, связанные с Луной, покрывают рассматриваемую область орбитального пространства в диапазоне наклонений от 20° до 160° (рис. 4), а неустойчивые концентрируются в околоэкваториальной области (рис. 5). Вековые резонансы, связанные с Солнцем, концентрируются в области, ограниченной наклонениями от 40° до 140° (рис. 6 и 7).

Если объединить данные о распространенности резонансов, приведенные на рис. 2–7, то практически вся область орбитального резонанса 1 : 2 будет покрыта резонансами, причем с большим количеством наложений резонансов различных типов. Это не может не сказываться на орбитальной эволюции объектов.

ОСОБЕННОСТИ ОРБИТАЛЬНОЙ ЭВОЛЮЦИИ ОБЪЕКТОВ

Перейдем теперь к рассмотрению динамической эволюции объектов зоны орбитального резонанса 1 : 2 со скоростью вращения Земли. Рассмотрим движение около-экваториальных объектов, орбиты которых имеют малые наклонения. На рис. 8 показана динамическая эволюция объекта под действием только орбитального резонанса. А на рис. 9 орбитальная эволюция такого же типа объекта, но под влиянием как орбитального, так и вековых резонансов.

Рис. 8.

Динамическая эволюция околоэкваториального объекта под действием только орбитального резонанса: (а) эволюция основных орбитальных элементов и параметров MEGNO; (б) эволюция ${{\dot {\Phi }}_{1}},$${{\Phi }_{1}}$; (в) эволюция ${{\dot {\Phi }}_{2}},$${{\Phi }_{2}}$; (г) эволюция ${{\dot {\Phi }}_{3}},$${{\Phi }_{3}}$.

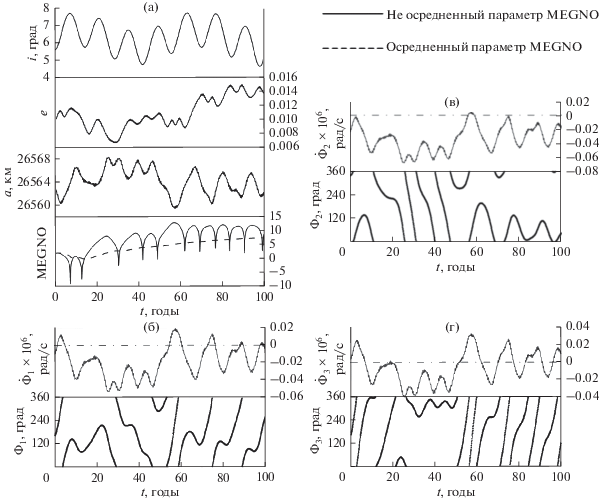
Рис. 9.

Динамическая эволюция околоэкваториального объекта под действием резонансов различных типов: (а) эволюция основных орбитальных элементов и параметров MEGNO; (б) эволюция ${{\dot {\Phi }}_{1}},$${{\Phi }_{1}}$; (в) эволюция ${{\dot {\Phi }}_{2}},$${{\Phi }_{2}}$; (г) эволюция ${{\dot {\Phi }}_{3}},$${{\Phi }_{3}};$ (д) эволюция ${{\dot {\psi }}_{L}} = \left( {\dot {\Omega } - \dot {\Omega }{{{_{L}^{'}}}_{{}}}} \right) + 2\dot {\omega } - 2\dot {\omega }_{L}^{'} \approx 0$ и соответствующего резонансного аргумента.

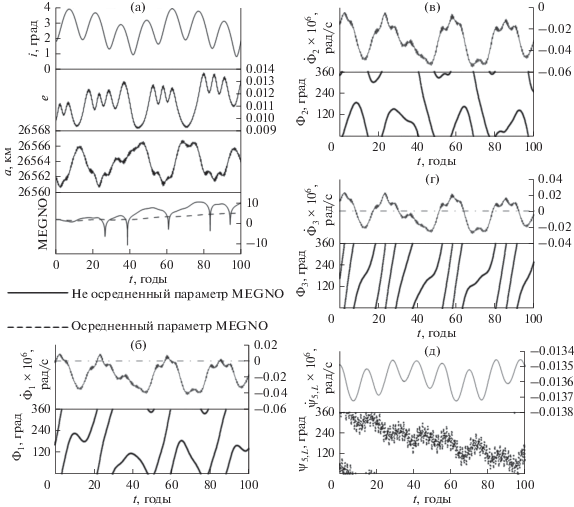
Следует отметить, что компоненты ${{\Phi }_{4}}$ и ${{\Phi }_{5}}$ мультиплета (1) циркулируют на всем рассматриваемом интервале времени и не оказывают влияния на исследуемые объекты, поэтому их эволюция не представлена на рис. 8 и 9.

И в том, и в другом случаях появление слабой хаотичности движения объясняется действием неустойчивых компонент орбитального резонанса.

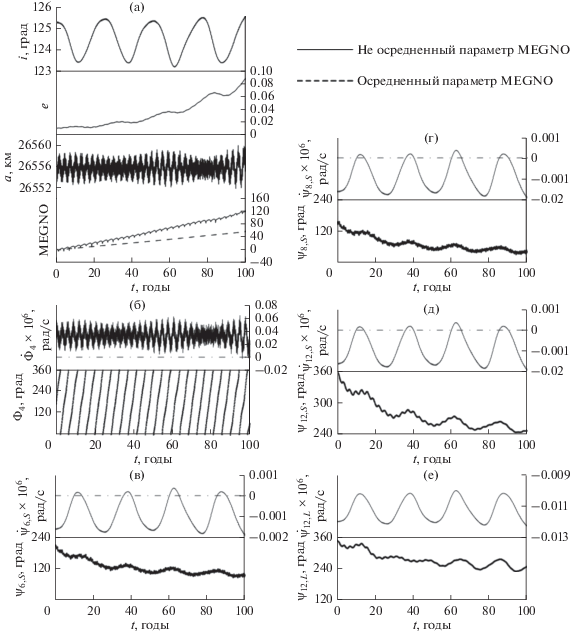
Объект, орбитальная эволюция которого показана на рис. 10, имеет обратное движение и подвержен действию устойчивых вековых апсидально-нодальных резонансов: ${{\dot {\psi }}_{{6,S}}} = (\dot {\Omega } - \dot {\Omega }{{_{S}^{'}}_{{}}})$ – $ - \,\,2\dot {\omega } + 2\dot {\omega }_{S}^{'} \approx 0$, ${{\dot {\psi }}_{{{\text{8,}}S}}}$ = $(\dot {\Omega } - \dot {\Omega }_{S}^{'}) - 2\dot {\omega } - 2\dot {\omega }_{S}^{'} \approx 0,$ ${{\dot {\psi }}_{{12,S}}} = (\dot {\Omega } - \dot {\Omega }_{S}^{'}) - 2\dot {\omega } \approx 0$ и ${{\dot {\psi }}_{{12,L}}} = (\dot {\Omega } - \dot {\Omega }{{_{L}^{'}}_{{}}})$ – $ - \,\,2\dot {\omega } \approx 0.$ Этим объясняется непрерывный рост его эксцентриситета на всем рассматриваемом интервале времени. Хаотичность же возникает из-за действия неустойчивых, проходящих через нулевое значение компонент орбитального резонанса.

Рис. 10.

Орбитальная эволюция объекта с обратным орбитальным движением под действием преимущественно апсидально-нодальных резонансов, связанных с Солнцем и Луной: (а) эволюция основных орбитальных элементов и параметров MEGNO; (б) эволюция ${{\dot {\Phi }}_{1}},$${{\Phi }_{1}}$; эволюция резонансных соотношений и соответствующих резонансных аргументов вековых резонансов: (в) ${{\dot {\psi }}_{{6,S}}}$, (г) ${{\dot {\psi }}_{{{\text{8,}}S}}}$, (д) ${{\dot {\psi }}_{{12,S}}},$ (е) ${{\dot {\psi }}_{{12,L}}}$.

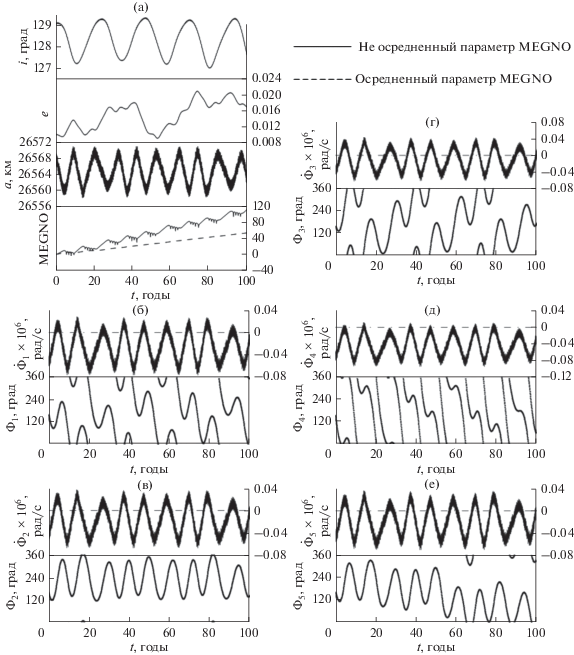
На рис. 11 приведена орбитальная эволюция объекта с обратным движением под действием мультиплета орбитального резонанса. Вековые резонансы в движении объекта отсутствуют. Объект показывает высокую хаотичность движения, поскольку три из пяти компонент мультиплета неустойчивы.

Рис. 11.

Динамическая эволюция объекта с обратным орбитальным движением под действием мультиплета орбитального резонанса: (а) эволюция основных орбитальных элементов и параметров MEGNO; (б)–(е) эволюция $\dot {\Phi },\Phi $ орбитального резонанса.

Интересно отметить, что анализ орбитальной эволюции всей совокупности модельных объектов рассматриваемой области на 100-летнем интервале времени показал отсутствие заметного проявления в динамике объектов эффекта Лидова–Козаи, связанного с перекачкой энергии между эксцентриситетом и наклонением.

Рассмотрим этот вопрос более подробно на примере одного из объектов, принадлежащих левой резонансной полосе на рис. 3. Орбитальная эволюция выбранного объекта в деталях представлена на рис. 12.

Рис. 12.

Динамическая эволюция объекта под действием механизма Лидова–Козаи, орбитальная эволюция объекта: (а) на 100-летнем интервале времени под действием возмущений от сжатия Земли, притяжения Луны и Солнца относительно экватора Земли; далее на 300-летнем интервале относительно эклиптики: (б) под действием притяжения Луны; (в) притяжения Солнца; (г) под действием притяжения Луны и Солнца; (д) под действием возмущений от сжатия Земли, притяжения Луны и Солнца; (е) сверху вниз: с учетом возмущений от Луны, (пункт (б)) изменения резонансного соотношения, полученные по аналитическим формулам, те же изменения, полученные путем численного моделирования, изменения резонансного аргумента, (ж) интеграл Лидова–Козаи ${{c}_{1}} = \sqrt {1 - {{e}^{2}}} \cos i.$

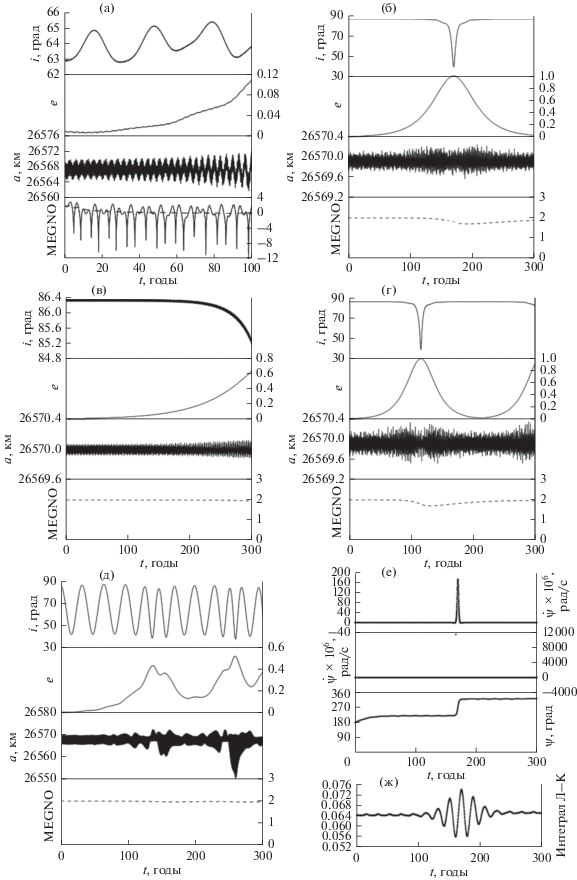
Начальные параметры объекта: большая полуось составляет 26 565 км, наклонение к экваториальной плоскости равно 62.8°, эксцентриситет равен 0.01, долготы восходящего узла и перицентра от узла равны 180°. На 100-летнем интервале времени (рис. 12а) движение устойчиво на всем интервале времени, хаотичность нулевая. Заметен рост эксцентриситета от начального значения 0.01 до 0.12 и связанный с этим рост амплитуды колебаний большой полуоси. Чтобы понять причину возрастания эксцентриситета, была рассмотрена эволюция объекта на 300-летнем интервале времени в системе координат, связанной с эклиптикой. Как известно, действие механизма Лидова–Козаи зависит от наклонения объекта к орбите возмущающего тела. Эклиптика совпадает с орбитой Солнца в геоцентрической системе координат и достаточно близка к орбите Луны. Кроме того, было рассмотрено влияние каждого из возмущающих факторов отдельно. Поскольку влияние сжатия вызывает только небольшие долгопериодические колебания в эксцентриситете и наклонении, мы его здесь не приводим. Источником возникновения эффекта Лидова–Козаи является, прежде всего, действие Луны (рис. 12б). Солнце также вносит свой вклад в действие этого механизма (рис. 12в). Интересно, что совместное действие Луны и Солнца приводит к уменьшению периода долгопериодических колебаний, но не меняет их амплитуду (рис. 12г). В то же время совместное влияние трех возмущающих факторов: двух внешних тел и сжатия Земли искажает картину влияния механизма Лидова–Козаи. Еще М.Л. Лидовым было замечено (Вашковьяк, Тесленко, 2016), что влияние сжатия способно нивелировать открытый им эффект. Интеграл Лидова‒Козаи сохраняется на всем 300-летнем интервале прогнозирования (рис. 12ж). Острый резонанс Лидова–Козаи и соответственно максимальное возрастание эксцентриситета появляется при прохождении долготы перицентра $\omega $ через значения $ \pm {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$.

Механизм Лидова–Козаи, как было показано в (Александрова и др., 2016) начинает проявляться в динамике околоземных объектов, начиная с 20 000 км по большой полуоси, и вполне естественно, что он впервые проявляется в районе критических наклонений (рис. 3), где вековое влияние сжатия Земли минимально.

ЗАКЛЮЧЕНИЕ

В настоящей работе представлены результаты численного эксперимента по построению динамической структуры орбитального пространства резонанса 1 : 2 со скоростью вращения Земли в диапазоне больших полуосей от 26 550 до 26 570 км и в диапазоне наклонений от 0° до 180°. Исследования показали, что в рассматриваемой области присутствуют все пять компонент мультиплета орбитального резонанса 1 : 2 со скоростью вращения Земли. Однако четвертая и пятая компоненты мультиплета устойчивы только в области обратного движения.

Кроме того, на объекты рассматриваемой области действует большое количество вековых апсидально-нодальных резонансов, включая резонанс Лидова–Козаи.

Области с высокой хаотизацией движения приходятся на зоны совместного влияния устойчивых и неустойчивых резонансов различных типов. Особенно выделяется по хаотичности зона между наклонениями 120°–160° в области обратного движения. На эту зону приходятся неустойчивые участки действия мультиплетов орбитального резонанса и большое количество устойчивых и неустойчивых вековых апсидально-нодальных резонансов.

Совместное действие устойчивых апсидально-нодальных резонансов приводит к значительному росту эксцентриситета.

Механизм Лидова–Козаи, связанный с характерной перекачкой энергии между эксцентриситетом и наклонением, в движении объектов этой области орбитального пространства заметно проявляется только на больших интервалах времени. Объекты, подверженные влиянию механизма Лидова–Козаи, при отсутствии других резонансов сохраняют устойчивое движение с незначительным ростом эксцентриситета на больших интервалах времени.

Работа выполнена при финансовой поддержке гранта РФФИ 18-32-00735 мол_а “Исследование особенностей динамики околоземных космических объектов в условиях наложения резонансов различных типов”.

Список литературы

  1. Авдюшев В.А. Интегратор Гаусса–Эверхарта // Вычисл. технологии. 2010. Т. 15. № 4. С. 31–47.

  2. Александрова А.Г., Бордовицына Т.В., Чувашов И.Н. Численное моделирование в задачах динамики околоземных объектов // Изв. вузов. Физика. 2017. Т. 60. С. 69–76.

  3. Александрова А.Г., Бордовицына Т.В., Томилова И.В. Резонанс Лидова–Козаи и его влияние на орбитальную эволюцию околоземных космических объектов // М.Л. Лидов – яркое имя в космической науке. Сб. докл. / Ред. Вашковьяка М.А. М.: ИПМ им. М.В. Келдыша, 2016. С. 49–66.

  4. Александрова А.Г., Бордовицына Т.В., Томилова И.В. Особенности совместного влияния вековых резонансов низких порядков и светового давления на движение околоземных космических объектов // Изв. вузов. Физика. 2018. Т. 61. № 4. С. 75–80.

  5. Бордовицына Т.В., Авдюшев В.А. Теория движения искусственных спутников Земли. Аналитические и численные методы. Томск: Изд-во Том. ун-та, 2007. 220 с.

  6. Бордовицына Т.В., Александрова А.Г., Чувашов И.Н. Комплекс алгоритмов и программ для исследования хаотичности в динамике искусственных спутников Земли // Изв. вузов. Физика. 2010. Т. 53 № 8/2. С. 14–21.

  7. Бордовицына Т.В., Томилова И.В., Чувашов И.Н. Влияние вековых резонансов на долговременную орбитальную эволюцию неуправляемых объектов спутниковых радионавигационных систем в области МЕО // Астрон. вестн. 2012. Т. 46. № 5. С. 356–368. (Bordovitsyna T.V., Tomilova I.V., Chuvashov I.N. The effect of secular resonances on the long-term orbital evolution of uncontrollable objects on satellite radio navigation systems in the MEO region // Sol. Syst. Res. 2012. V. 46. Is. 5. P. 329–340.)

  8. Вашковьяк М.А., Тесленко Н.М. Михаил Львович Лидов – яркое имя в космической науке С. 9–38 // М.Л. Лидов – яркое имя в космической науке. Сб. докл. / Ред. Вашковьяк М.А. М.: ИПМ им. М.В. Келдыша, 2016. С. 9–38.

  9. Кузнецов Э.Д., Захарова П.Е., Гламазда Д.В., Шагабутдинов А.И., Кудрявцев С.О. О влиянии светового давления на орбитальную эволюцию объектов, движущихся в окрестности резонансов низких порядков // Астрон. вестн. 2012. Т. 46. № 6. С. 480–488. (Kuznetsov E.D., Zakharova P.E., Glamazda D.V., Shagabutdinov A.I., Kudryavtsev S.O. Light pressure effect on the orbital evolution of objects moving in the neighborhood of low-order resonances // Sol. Syst. Res. 2012. V. 46. Is 6. P. 442–449.)

  10. Лидов М.Л. Эволюция искусственных спутников планет под действием гравитационных возмущений от внешнего тела // Искусственные спутники Земли. 1961. Т. 8. С. 5–45.

  11. Томилова И.В., Блинкова Е.В., Бордовицына Т.В. Особенности динамики объектов, движущихся в окрестности резонанса 1 : 3 с вращением Земли // Астрон. вестн. 2019. Т. 53. № 5. С. 1–16. (Tomilova I.V., Blinkova E.V. Bordovitsyna T.V. Features of the Dynamics of Objects Moving in the Neighborhood of the 1 : 3 Resonance with the Earth’s Rotation //Sol. Syst. Res. 2019. V. 53. № 5. Р. 1–15.)

  12. Томилова И.В., Бордовицына Т.В. Особенности структуры резонансных возмущений неуправляемых объектов навигационных систем ГЛОНАСС и GPS. Влияние на орбитальную эволюцию // Изв. вузов. Физика. 2017. Т. 60. № 4. С. 119–125.

  13. Томилова И.В., Бордовицына Т.В., Красавин Д.С. Динамическая структура орбитального пространства ГЛОНАСС и GPS. Проблема утилизации отработавших объектов // Астрон. вестн. 2018. Т. 52. № 5. С. 1–17. (Tomilova I.V., Bordovitsyna T.V., Krasavin D.S. Dynamical structure of the GLONASS and GPS orbital space: Problem of disposal of retired objects // Sol. Syst. Res. 2018. V. 52. Is. 5. P. 450–465.)

  14. Allan R.R. Resonance effects due to the longitude dependence of the gravitational field of a rotating primary // Planet. and Space Sci. 1967a. V. 15. P. 53–76.

  15. Allan R.R. Satellites resonance with the longitude dependent gravity. II. Effects involving the eccentricity // Planet. and Space Sci. 1967b. V. 15. P. 1829–1845.

  16. Breiter S. On the coupling of lunisolar resonances for Earth satellite orbits // Celest. Mech. Dyn. Astron. 2001a. V. 80. P. 1–20.

  17. Breiter S. Lunisolar resonances revisited // Celest. Mech. Dyn. Astr. 2001b. V. 81. P. 81–91.

  18. Chao C., Gick R. Long-term evolution of navigation satellite orbits // Adv. Space Res. 2004. V. 34. P. 1221–1226.

  19. Cincotta P.M., Simó C. Simple tools to study global dynamics in non-axisymmetric galactic potentials – I // Astron. and Astrophys. Suppl. 2000. V. 147. P. 205–228.

  20. Cincotta P.M., Girdano C.M., Simo C. Phase space structure of multi-dimensional systems by means of the mean exponential growth factor of nearby orbits // Physica D. 2003.V. 182. P. 151–178.

  21. Cook G.E. Luni-Solar Perturbations of the Orbit of an Earth Satellite // Geophys. J. 1962. V. 6. № 3. P. 271–291.

  22. Daquin J., Rosengren A.J., Alessi E.M., Deleflie F., Valsecchi G.B., Rossi A. The dynamical structure of the MEO region: long-term stability, chaos, and transport // Celest. Mech. and Dyn. Astron. 2016. V. 124(4). P. 335–336.

  23. Kozai Y. Secular perturbations of asteroids with high inclination and eccentricity // Astron. J. 1962. V. 67. P. 591–598.

  24. Murray C.D., Dermott S.F. Solar System Dynamics. Cambridge: Cambridge Univ. Press, 1999. XIII+592 p.

  25. Rosengren A.J., Alessi E.M., Rossi A., Valsecchi G.B. Chaos in navigation satellite orbits caused by the perturbed motion of the Moon // Mon. Notic. Roy. Astron. Soc. 2015. V. 449. P. 3522–3526.

  26. Rossi A. Resonant dynamics of Medium Earth Orbits: space debris // Celest. Mech. Dyn. Astron. 2008. V. 100. P. 267–286.

  27. Takashi Ito, Katsuhito Ohtsuka. The Lidov–Kozai Oscillation and Hugo von Zeipel // Monogr. Environ. Earth Planets. 2019. V. 7. № 1. P. 1–113.

  28. Valk S., Delsate N., Lemaitre A., Carletti T. Global dynamics of high area-to-mass ratios GEO space debris by means of the MEGNO indicator // Adv. Space Res. 2009. V. 43. P. 1509–1526.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический вестник

Архивы выпусков Информация о журнале Отправить рукопись в журнал