Астрономический вестник, 2020, T. 54, № 4, стр. 349-359
Адаптивные методы построения перелетов в системе Юпитера с выходом на орбиту спутника галилеевой Луны
Ю. Ф. Голубев a, *, А. В. Грушевский a, **, В. В. Корянов a, ***, С. М. Лавренов a, А. Г. Тучин a, ****, Д. А. Тучин a, *****
a ИПМ им. М.В. Келдыша РАН
Москва, Россия
* E-mail: golubev@keldysh.ru
** E-mail: alexgrush@rambler.ru
*** E-mail: korianov@keldysh.ru
**** E-mail: tag@kiam1.rssi.ru
***** E-mail: den@kiam1.rssi.ru
Поступила в редакцию 09.01.2020
После доработки 10.02.2020
Принята к публикации 13.02.2020
Аннотация
Рассматриваются космические экспедиции с долгосрочным нахождением КА около исследуемого небесного тела (искусственные спутники малых тел Солнечной системы), либо экспедиции с возможной посадкой КА на поверхность небесного тела (например – миссия ESA Jovian Icy Moon Explorer “JUICE”, Российский перспективный проект “Лаплас‑П”). Предложен эффективный формализм создания сценариев адаптивного поиска малозатратных комбинированных траекторий КА, ориентированный на возможность привлечения высокопроизводительных вычислительных средств компьютерного экспериментирования. Приводятся примеры реализации указанного формализма для поиска комбинаций межлунных гравитационных маневров в системе Юпитера с целью выхода на орбиту искусственного спутника юпитерианской луны.
ВВЕДЕНИЕ
Формальные адаптивные методы построения “экстенсивных” межпланетных перелетов с использованием гравитационных маневров (ГМ) в окрестности массивных тел Солнечной системы к настоящему времени достаточно хорошо разработаны (Labunsky и др., 1998; Minovitch, 1963; Campagnola и др., 2010; Келдыш и др., 1988; Энеев и др., 2010; Boutonnet и др., 2012). Базовые алгоритмы предполагают увеличение орбитальной скорости космического аппарата (КА) (Minovitch, 1963; Келдыш и др., 1988), либо обеспечение сближения с заданным небесным телом и его пролет (Labunsky и др., 1998; Келдыш и др., 1988; Голубев и др., 2014). Тем не менее, существует целый класс космических миссий, не укладывающихся в формат подобных методик. Это космические экспедиции с долгосрочным нахождением около исследуемого небесного тела – “мишени” (искусственные спутники малых небесных тел, в западной литературе – orbiters), либо экспедиции с посадкой КА на поверхность небесного тела (в западной литературе – landers, descent modules) (Boutonnet и др., 2012; Golubev и др., 2014). Для указанного класса задач требуется обеспечить экономичное уменьшение скорости КА относительно малого тела. Такое условие практически невыполнимо при использовании гравитационных маневров около одного этого тела в силу существования обобщенного интеграла энергии Якоби в круговой ограниченной задаче трех тел. Для подобных космических проектов необходим адаптивный поиск малозатратных сценариев комбинированных перелетов КА, максимально формализованный для возможности привлечения высокопроизводительных вычислительных средств компьютерного экспериментирования. В данной работе предложен эффективный формализм создания сценариев адаптивного поиска малозатратных комбинированных траекторий КА. Даны примеры применения разработанного формализма для поиска межлунных перелетов в системе Юпитера с выходом КА на орбиту искусственного спутника юпитерианской луны (Golubev и др., 2014; 2015; Голубев и др., 2014; Grushevskii и др., 2018; Тучин и др., 2018) при выполнении стандартных требований к длительности проведения миссии и комфортных значениях накопленной КА дозы радиации.
ГАЛИЛЕЕВЫ СПУТНИКИ В СИСТЕМЕ ЮПИТЕРА
Поиск малозатратных туров в системе Юпитера подразумевает использование многократных ГМ около галилеевых юпитерианских лун. Каждый ГМ позволяет уменьшить или увеличить орбитальную энергию КА путем вращения вектора асимптотической скорости КА относительно вектора орбитальной скорости малого тела на некоторый угол. Галилеевы луны Ио, Европа, Ганимед и Каллисто, названные в честь пассий Зевса, получили условные обозначения ${{J}_{1}}$, ${{J}_{2}}$, ${{J}_{3}}$ и ${{J}_{4}}$ соответственно. В табл. 1 представлены возможные изменения абсолютной скорости КА после выполнения ГМ в окрестности спутников Юпитера, Сатурна и Земли соответственно в зависимости от высот пролета ${{h}_{{GM}}}$ КА над поверхностью спутника.
Таблица 1.
Предельные возможности изменения величины абсолютной скорости КА при совершении ГМ, км/с
| Спутник планеты | Высота пролета | ||
|---|---|---|---|
| 0.3 тыс. км | 1 тыс. км | 5 тыс. км | |
| Ио | 1.81 | 1.45 | 0.93 |
| Европа | 1.43 | 1.11 | 0.70 |
| Ганимед | 1.94 | 1.65 | 1.14 |
| Каллисто | 1.73 | 1.46 | 0.98 |
| Титан | 1.87 | 1.43 | 1.10 |
| Луна | 1.68 | 1.34 | 0.85 |
Из таблицы видно, что помимо очевидной возможности изменения направления скорости при гравитационном маневре имеют место ощутимые вариации величины абсолютной траекторной скорости.
ПУЧКОВЫЕ АЛГОРИТМЫ В АСТРОДИНАМИКЕ
Поиск точных межпланетных траекторий КА в сложных гравитационных полях представляет собой актуальную задачу современной астродинамики. Решение классической задачи перелета Эйлера–Ламберта для попадания в окрестность целевого тела может значительно отличаться от траектории КА, найденной с учетом эфемерид и возмущающих факторов (нецентральности гравитационного поля основного тела, гравитационных полей других небесных тел, сил светового давления и т.д.). Это, в конечном итоге, может приводить к существенному промаху при управлении КА согласно закону движения невозмущенной задачи. Для соответствующей коррекции номинала в астродинамике используются итерационные методы, которые не всегда сходятся. Такое часто бывает при использовании гравитационных маневров. По этой причине использование трубок виртуальных траекторий, первоначально слабо отличающихся друг от друга, с продолжением по времени в уточненных эфемеридах, оказывается весьма эффективным приемом для поиска реальных траекторий перелета (Golubev и др., 2014; Голубев и др., 2014). Успех обеспечивается, когда в заданную окрестность планеты попадает хотя бы одна виртуальная траектория КА из трубки, и только одна из них затем перейдет из разряда виртуальных в траекторию реального полета. Подобный метод анализа виртуальных траекторий разрабатывался в ИПМ им. М.В. Келдыша РАН с самого начала активного освоения космоса. Так было, например, при построении В.А. Егоровым (Энеев и др., 2010) лунных траекторий, численном моделировании Т.М. Энеевым и Н.Н. Козловым процесса образования планет из протопланетного облака с использованием метода виртуальных контактов (Энеев и др., 1979) и т.д.
Пучки пролетных траекторий относительно небесных тел с целью проведения пассивных ГМ формируются с помощью малых виртуальных коррекций скорости КА загодя, имея некоторый временной интервал до проведения ГМ. Возможности ГМ будем исследовать, исходя из предположения о том, что имеется трубка допустимых траекторий с одним и тем же вектором асимптотической скорости. Метод ${\text{Л}}{{\Pi }_{\tau }}$‑последовательностей И.М. Соболя (Соболь, 1976) является наиболее эффективным при формировании равномерно распределенного по пространству множества начальных условий (Golubev и др., 2014; Голубев и др., 2014). Каждый виртуальный вариант, отобранный для дальнейшего поиска, переводится в разряд перспективных и фиксируется.
С использованием эфемеридных моделей JPL NASA (NAIF, 2019) проводится моделирование рассеяния сформированного пучка при прохождении им сферы действия малого тела (спутника Юпитера). Каждая траектория попадает в свой, однозначно определенный сегмент картинной плоскости ${{{\mathbf{V}}}_{\infty }}$ $({{R}_{\xi }},{{R}_{\eta }})$ (Тучин и др., 2018), что приводит к гравитационному рассеянию – отклонению траектории от соседних вариантов трубки изначально почти параллельных траекторий. Проводится интегрирование и селекция удовлетворительных вариантов согласно представленным ниже критериям. Используя современные возможности для высокопроизводительного компьютерного моделирования в Баллистическом центре ИПМ им. М.В. Келдыша РАН, с указанной целью применяются методы адаптивного поиска малозатратных сценариев, не привязанные жестко к конкретной эпохе прилета и максимально формализованные для эффективного массового счета. Эти методы позволяют за приемлемое время просчитывать десятки миллионов вариантов, требующих дальнейшей селекции.
МАЛОЗАТРАТНОСТЬ И УМЕНЬШЕНИЕ ОРБИТАЛЬНОГО ПЕРИОДА
Ставится задача формализации целевого малозатратного уменьшения орбитальной энергии КА (что, очевидно, приводит к уменьшению орбитального периода КА и уменьшению большой полуоси его орбиты и эксцентриситета) с помощью проведения серии ГМ около массивных тел системы галилеевых лун. В результате можно обеспечить ограничение на время проведения миссии. Пусть ${{N}_{{{\text{ГМ}}}}}$ – общее число гравитационных маневров из некоторой выбранной серии. Будем обозначать гравитационный маневр из этой серии около произвольной галилеевой луны ${{J}_{i}}$, $i \in \{ 1,2,3,4\} $ символом ${{G}_{n}} = {{J}_{{{{i}_{n}}}}}$, ${{i}_{n}} \in \{ 1,2,3,4\} ,$ $n = 1,...,{{N}_{{{\text{ГМ}}}}}$. Тогда для галилеевых лун многовариантный поиск малозатратного уменьшения периода обращения и орбитальной энергии с использованием гравитационных маневров можно формально записать в виде цепочки (Golubev и др., 2014; 2015):
Поиск ${{\Psi }_{t}}$ осуществляется с помощью последовательного решения задач Эйлера–Ламберта (Labunsky и др., 1998; Энеев и др., 2010; Golubev и др., 2014; Тучин А. и др., 2018), обеспечивающих попадание в заданную окрестность следующей галилеевой луны после проведения текущего ГМ, а затем краевых задач с использованием эфемеридных моделей.
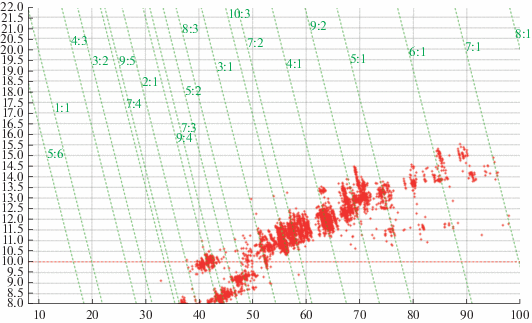
Пример поиска цепочек ГМ ${{\Psi }_{{{{t}_{1}}}}}\left\{ {{{J}_{3}} \circ {{J}_{3}} \circ {{J}_{3}} \circ } \right.$ $\left. { \circ \,\,{{J}_{3}} \circ {{J}_{3}} \circ {{J}_{3}}} \right\}$, уменьшающих орбитальную энергию КА и его орбитальный период, приведен на рис. 1 на диаграмме Тиссерана, показывающей зависимость перийовия ${{R}_{\pi }}$ от апойовия ${{R}_{\alpha }}$. По оси абсцисс отложены расстояние ${{R}_{\alpha }}$ апоцентра орбиты КА, по оси ординат – расстояние перицентра ${{R}_{\pi }}$ (в радиусах Юпитера ${{R}_{{\text{Ю}}}}$). Зеленым нанесены изолинии орбитального периода КА, резонансные с периодом обращения Ганимеда. Любой ГМ можно представить на диаграмме Тиссерана как мгновенный вектор‑перескок с одного фазового состояния $({{R}_{{\alpha 1}}},{{R}_{{\pi 1}}})$ на новую точку $({{R}_{{\alpha 2}}},{{R}_{{\pi 2}}})$. Для наглядности на рис. 1 красными точками для пучка цепочек ГМ нанесены только концы векторов-перескоков ГМ.
СОЛЬНЫЕ ГРАВИТАЦИОННЫЕ МАНЕВРЫ. РЕЗОНАНСНОЕ ПОНИЖЕНИЕ ОРБИТАЛЬНОГО ПЕРИОДА
Учет ограничения на время проведения миссии в системе Юпитера (в западной литературе – TOF, Time of flight) может обеспечиваться с большой надежностью посредством уменьшения орбитального периода КА с помощью сольных ГМ, когда в качестве партнера используется фиксированная галилеева луна ${{J}_{{\bar {i}}}}$. В этом случае из всевозможных найденных серий ГМ $\{ {{J}_{{{{i}_{n}}}}}\} ,{{i}_{n}} \in \{ 1,2,3,4\} ,$ $n = 1,...,{{N}_{{{\text{ГМ}}}}}$необходимо выделить цепочки специального вида $\{ {{J}_{{\bar {i}}}} \circ ... \circ {{J}_{{\bar {i}}}}\} $ с фиксированным значением $\bar {i}$ такие, что в каждом их элементе сохраняется резонансность между орбитальными периодами КА ${{T}_{n}}$ и орбитальным периодом ${{T}_{{{{J}_{{\bar {i}}}}}}}$ луны ${{J}_{{\bar {i}}}}$:
(2)
$\begin{gathered} \Psi _{t}^{*}\{ {{J}_{{\bar {i}}}} \circ ... \circ {{J}_{{\bar {i}}}}\} ,\,\,\,\,\bar {i} \in \{ 1,2,3,4\} , \\ {{M}_{{{{N}_{{{\text{ГМ}}}}}}}} < {{M}_{{{{N}_{{{\text{ГМ}}}}} - 1}}} < {{M}_{{{{N}_{{{\text{ГМ}}}}} - 2}}} < ... < {{M}_{1}}. \\ \end{gathered} $Множество цепочек, порождаемых правилом (2), является подмножеством цепочек, порождаемых правилом (1). Поисковая формула $\Psi _{t}^{*}$ является суженной модификацией ${{\Psi }_{t}}$, поскольку выделяет подмножество резонансных цепочек сольных гравитационных маневров среди множества цепочек с прохождением произвольных лун.
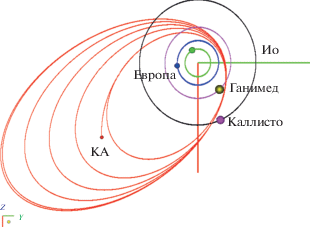
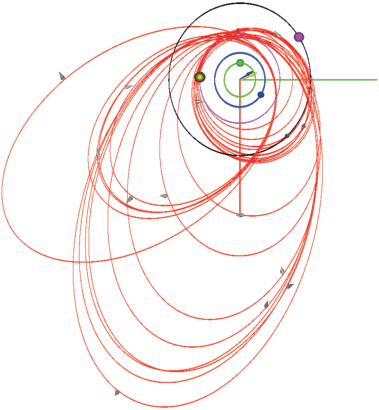
Фрагмент малозатратного типового тура в системе Юпитера с сокращением времени проведения миссии, найденный с применением формального правила $\Psi _{t}^{*}$ (2) в случае ${{J}_{{\bar {i}}}} = {{J}_{3}}$, представлен на рис. 2 в проекции на среднюю плоскость системы. Квазирезонансность периодов КА и спутника-мишени ${{J}_{3}}$ обеспечивает новую встречу со спутником в малой окрестности истинной аномалии последней встречи. Сценарий представлен в табл. 2.
КОМФОРТАБЕЛЬНОСТЬ ПО ПОГЛОЩЕННОЙ ДОЗЕ РАДИАЦИИ
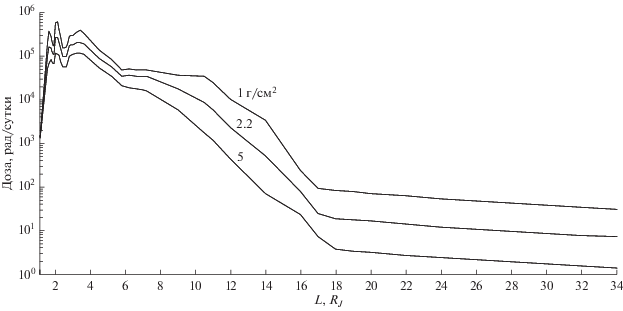
Рассмотрим радиационную обстановку в системе Юпитера с учетом данных, полученных в ходе проведения миссии “Galileo” (Divine и др., 1983). В ходе ее проведения КА получил суммарную поглощенную дозу радиации (в англоязычной литературе TID – Total Ionizing Doze), превышающую 275 Крад, при наличии противорадиационной защиты 8 мм Al, 2.2 г/см2. Вследствие этого КА частично потерял свою функциональность. Уровень радиации в юпитерианской системе чрезвычайно высок (Podzolko и др., 2013) (рис. 3) и представляет серьезную проблему, требующую учета при проектировании сценариев полета к спутникам Юпитера. По оси абсцисс отложено расстояние до центра Юпитера в его радиусах, а по оси ординат − доза радиации, полученная КА за сутки.
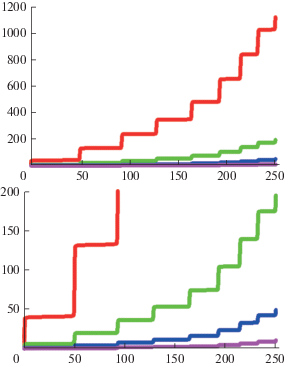
Согласно проведенным расчетам (Golubev и др., 2014; Голубев и др., 2014), на околоюпитерианской эллиптической орбите КА характер накопления радиационной дозы носит скачкообразный характер и происходит в районе перийовия. На рис. 4 показана динамика накопления радиации в дебюте миссии к спутникам Юпитера (в стандартном и увеличенном масштабе). По оси абсцисс отложено время в земных сутках, а по оси ординат − доза накопленной радиации в Крад. Защита: 0.27 г/см2 – красный, 1 г/см2 – зеленый, 2.2 г/см2 – синий, 5 г/см2 – фиолетовый.
Суммарная доза накопленной КА радиации, получаемая в течение всей миссии около планеты Юпитер, может достигать очень больших величин, обусловленных не столько общей длительностью миссии, сколько числом и высотой наиболее низких перийовиев тура. Любой пролет спутников Ио и Европа нарушает модельное ограничение на эту дозу, характерное для миссий класса “Galileo” (150–260 Крад при стандартной защите 2.2 г/см2). К подобным миссиям относятся перспективный российский проект “Лаплас‑П” и проект ESA “JUICE”.
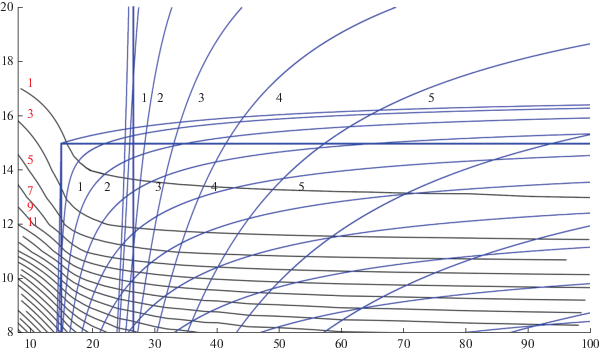
На обобщенной диаграмме Тиссерана (рис. 5) (Голубев и др., 2014; Golubev и др., 2015; Grushevskii и др., 2018; Тучин А. и др., 2018) дополнительно нанесены соответствующие изолинии дозы радиации “изорады”, полученной на одном витке с шагом 2 Крад (доза обозначена красными цифрами). Голубыми нанесены изолинии интеграла Якоби локальных круговых ограниченных задач трех тел (Ганимед, Каллисто). Черными числами обозначены значения асимптотической скорости КА в км/с.
Рассмотрим космические миссии, для которых КА имеют противорадиационную защиту класса “Galileo” (8 мм Al). Будем называть комфортабельным туром по полученной дозе радиации такой сценарий проведения ГМ, для которого полученная доза радиации не превышает половины дозы КА “Galileo”: 140 Крад. Анализ результатов (Golubev и др., 2014; 2015; Голубев и др., 2014; Grushevskii и др., 2018; Тучин А. и др., 2018) показывает, что для комфортабельных туров необходимое условие обеспечения комфортабельности состоит в выполнении ограничения по минимальной высоте перийовия:
Таким образом, должны быть исключены варианты с проведением ГМ около Ио и Европы. Соответствующее формализованное ограничение селекции может быть записано в следующем виде:
УМЕНЬШЕНИЕ АСИМПТОТИЧЕСКОЙ СКОРОСТИ КА ОТНОСИТЕЛЬНО ЦЕЛЕВОГО СПУТНИКА
Процесс уменьшения асимптотической скорости КА относительно спутника-мишени ${{J}_{i}}$ является сложной процедурой при использовании сольного маневрирования (Golubev и др., 2014; 2015; Голубев и др., 2014; Grushevskii и др., 2018; Тучин А. и др., 2018), приемлемого при реализации формализованных правил (1),(2),(4). Причина этих трудностей проявляется при анализе модельной круговой ограниченной задачи трех тел, для которой справедлив обобщенный интеграл энергии Якоби (Labunsky и др., 1998; Campagnola и др., 2010; Tisserand, 1986; Miller и др., 2002). Соответствующая, “изощренная” комбинация может быть записана в виде правила:
(5)
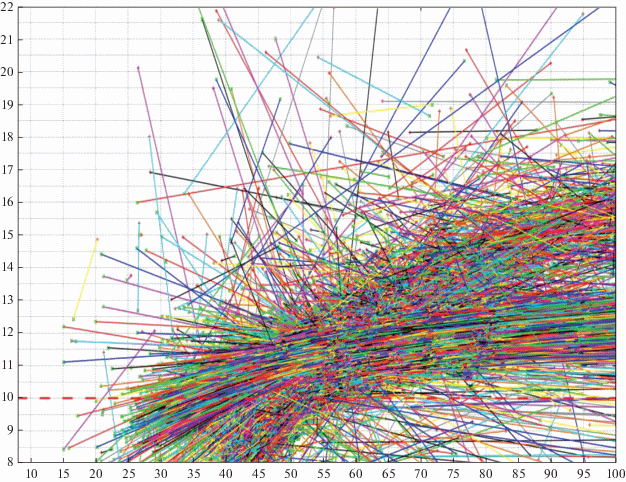
$\begin{gathered} {{\Psi }_{{v\infty }}}\{ {{J}_{l}} \circ ... \circ {{J}_{l}} \circ {{J}_{m}} \circ ... \circ {{J}_{m}} \circ {{J}_{l}} \circ {{J}_{l}} \ldots \circ {{J}_{l}}\} , \\ l,m \in \{ 3,4\} ,\,\,\,\,l \ne m. \\ \end{gathered} $На рис. 6 представлены результаты моделирования гравитационного рассеяния пучка виртуальных траекторий КА на одном ГМ около ${{J}_{3}}$ в формате диаграммы Тиссерана $({{R}_{\alpha }},{{R}_{\pi }})$ (Campagnola и др., 2010) в юпитерианских радиусах ${{R}_{J}}$. Красная пунктирная линия на рисунке соответствует границе возможности обеспечения формализованного правила (3). Число моделируемых вариантов – порядка 2.5 миллионов. Как уже указывалось, любой ГМ можно представить на диаграмме Тиссерана как мгновенный вектор‑перескок с одного фазового состояния $({{R}_{{\alpha 1}}},{{R}_{{\pi 1}}})$ на новую точку $({{R}_{{\alpha 2}}},{{R}_{{\pi 2}}})$. Нанесены соответствующие векторы-перескоки моделируемых ГМ.
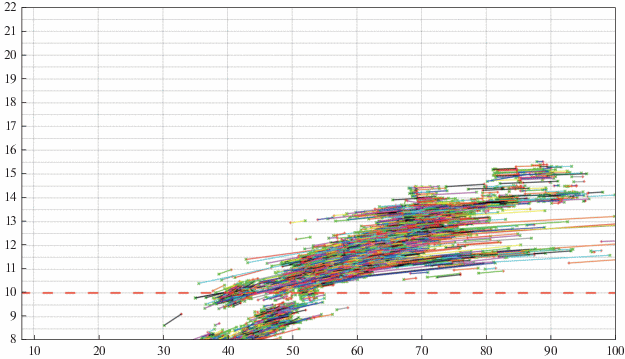
На рис. 7 представлены результаты моделирования кратного гравитационного рассеяния пучка виртуальных траекторий КА луной ${{J}_{3}}$ с повторным ГМ около другой луны ${{J}_{4}}$, отобранных согласно формальному правилу $\Psi _{{v\infty }}^{{343}}\{ {{J}_{3}} \circ {{J}_{4}} \circ {{J}_{3}}\} $. При использовании этого правила число вариантов сокращается на несколько порядков – до нескольких тысяч.
РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ ФОРМАЛИЗОВАННЫХ ПРАВИЛ
Представим результаты комплексного применения представленных формализованных правил (1)–(5): $\{ \Psi _{t}^{*},{{\Psi }_{{{\text{TID}}}}},{{\Psi }_{{V\infty }}}\} $. Их использование позволяет оперативно строить “лоции” – динамические области достижимости в пространстве параметров КА при использовании гравитационных маневров на диаграмме Тиссерана, что сопоставимо по эффективности и наглядности с картами окон старта (Porkchop plots) (Minovitch, 1963; Golubev и др., 2014; Тучин А. и др., 2018).
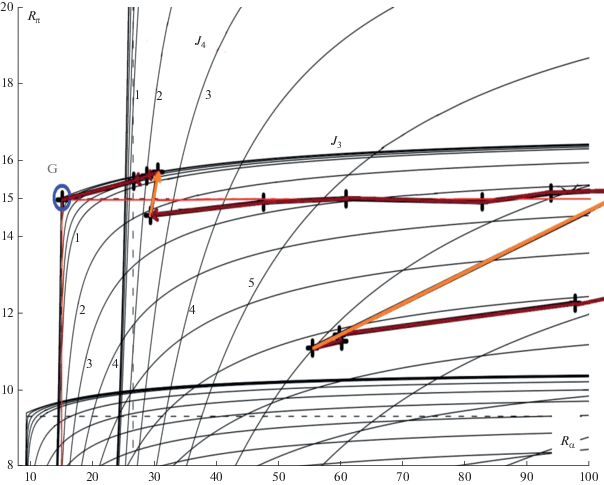
В результате проведенных в ИПМ им. М.В. Келдыша РАН массовых расчетов с применением $\{ \Psi _{t}^{*},{{\Psi }_{{{\text{TID}}}}},{{\Psi }_{{V\infty }}}\} $ найден класс траекторий с комфортабельным уровнем полученной дозы радиации 55 Крад для КА с радиационным корпусом, соответствующим классической защите КА миссии “Галилео” (7–8 мм Al) (Golubev и др., 2014; 2015; Голубев и др., 2014; Grushevskii и др., 2018; Тучин А. и др., 2018). Типовой сценарий тура, комфортабельного по TID, представлен на рис. 8, 9. Числа соответствуют значениям асимптотической скорости КА в км/с для изолиний интеграла Якоби локальной круговой ограниченной задачи трех тел.
Затраты характеристической скорости, общее время маневрирования и число ГМ в найденном классе варьируются незначительно и сопоставимы с параметрами классических сценариев миссий “JUICE” ESA и “Galileo” NASA. Основное преимущество представленных сценариев – снижение до комфортабельного уровня суммарной накопленной дозы радиации TID. Для КА “JUICE” (Boutonnet и др., 2012) TID превышает 258 Крад при той же толщине защиты.
Для резонансного случая будем записывать проведенный $n$-й резонансный ГМ с луной ${{J}_{i}}$ при наличии соотношения между их орбитальными периодами ${{{{T}_{n}}} \mathord{\left/ {\vphantom {{{{T}_{n}}} {{{T}_{{{{J}_{i}}}}}}}} \right. \kern-0em} {{{T}_{{{{J}_{i}}}}}}} = {{{{K}_{n}}} \mathord{\left/ {\vphantom {{{{K}_{n}}} {{{M}_{n}}}}} \right. \kern-0em} {{{M}_{n}}}}$ в виде $J_{i}^{*}\{ {{{{K}_{n}}} \mathord{\left/ {\vphantom {{{{K}_{n}}} {{{M}_{n}}}}} \right. \kern-0em} {{{M}_{n}}}}\} $.
Таблица 3 содержит характеристики траекторий, которые обеспечивают сближение с Ганимедом (J3) с выравниванием орбитального периода. Начало тура – 07.03.2030 05:10:45 UTC с исходной дозой радиации 2.1 Крад. Первый столбец таблицы содержит время проведения коррекции tкор, соответствующие суммарные затраты характеристической скорости Δv, приведены во втором столбце. В третьем столбце содержится суммарная TID за время проведения всех ГМ. Четвертый столбец содержит идентификатор галилеевой луны, с которой происходит сближение. Два последних столбца содержат момент времени минимального сближения и орбитальный период КА $T_{{{\text{КА}}}}^{{{{J}_{3}}}}$ в единицах периода обращения Ганимеда вокруг Юпитера. Длительность проведения всех ГМ составляет 748.8 сут с суммарными затратами на коррекции 680.73 м/c, что приблизительно в два раза меньше, чем затраты характеристической скорости при торможении КА непосредственно с помощью двигательной установки.
Таблица 3.
Параметры типового комфортабельного тура по радиации
| ${{t}_{{{\text{кор}}}}}$, UTC | Δν, м/с | TID, Крад | луна | ${{t}_{{{\text{сбл}}}}}$ , UTC | $T_{{{\text{КА}}}}^{{{{J}_{3}}}}$ |
|---|---|---|---|---|---|
| 15.03.2030 13:26:01 | 0.67 | 3.4 | J3 | 25.04.2030 16:41:56 | 4.01 |
| 03.06.2030 21:32:04 | 9.89 | 9.2 | J3 | 24.05.2030 06:33:18 | 3.69 |
| 21.07.2030 09:09:29 | 8.56 | 15.9 | J3 | 10.08.2030 22:06:16 | 3.32 |
| 24.08.2030 21:10:14 | 8.78 | 20.2 | J4 | 06.09.2030 17:42:13 | 9.39 |
| 03.10.2030 18:57:56 | 4.69 | 24.6 | J4 | 12.11.2030 11:17:27 | 8.53 |
| 10.01.2031 06:07:07 | 1.79 | 25.0 | J3 | 08.03.2031 09:25:48 | 8.47 |
| 23.04.2031 17:27:21 | 77.59 | 25.4 | J3 | 04.05.2031 09:02:43 | 7.09 |
| 10.06.2031 07:53:31 | 56.97 | 25.7 | J3 | 23.06.2031 15:32:16 | 6.05 |
| 25.07.2031 13:45:08 | 79.91 | 26.1 | J3 | 05.08.2031 12:04:10 | 4.01 |
| 12.08.2031 16:19:09 | 97.86 | 26.5 | J3 | 03.09.2031 10:53:56 | 3.03 |
| 12.09.2031 21:55:54 | 35.40 | 26.9 | J3 | 24.09.2031 23:51:20 | 1.75 |
| 03.10.2031 04:50:00 | 99.21 | 27.7 | J4 | 04.10.2031 01:51:00 | 1.79 |
| 11.12.2031 03:49:53 | 80.48 | 29.8 | J4 | 19.11.2031 08:42:11 | 1.92 |
| 09.02.2032 04:09:22 | 48.68 | 31.2 | J3 | 22.03.2032 12:33:36 | 1.54 |
| 24.03.2032 23:51:11 | 70.23 | 32.6 | J3 | 13.04.2032 10:29:12 | 0.99 |
На рис. 9 показаны направления импульсов. Их величины приведены в табл. 3.
С учетом введенных обозначений, этот тур формально можно описать правилом:
(6)
$\begin{gathered} J_{3}^{*}\left\{ {\frac{4}{1};\frac{{11}}{3};\frac{{10}}{3}} \right\} \circ J_{3}^{*}\left\{ {\frac{4}{1}} \right\} \circ {{J}_{4}} \circ J_{3}^{*}\left\{ {\frac{{17}}{2};\frac{7}{1};\frac{6}{1};\frac{4}{1};\frac{3}{1}} \right\} \circ \\ \circ \,\,{{J}_{3}} \circ {{J}_{4}} \circ {{J}_{4}} \circ J_{3}^{*}\left\{ {\frac{9}{5};\frac{3}{2};\frac{1}{1}} \right\}. \\ \end{gathered} $ЗАКЛЮЧЕНИЕ
Феноменальный успех ряда ранних космических проектов с использованием гравитационных маневров (советский проект “Луна-3”, миссии Вояджеров NASA) практически открыл для современной астродинамики возможность освоения ранее недоступных областей космического пространства. В первую очередь речь идет о внешней области Солнечной системы. Плодами этих разработок современная наука пользуется и по сей день, получая, например, снимки планеты Земля с границы внутренней гелиосферы.
К настоящему времени возник целый ряд разработок по поиску максимально эффективных способов полуавтоматического проектирования космических миссий с использованием разгоняющих гравитационных маневров для экстенсивного исследования дальнего космоса. Эти разработки активно эксплуатируют современные возможности высокопроизводительного математического моделирования. Однако, при этом подчас за бортом остается целый класс космических проектов, которые предполагают прибытие к целевому небесному телу Солнечной системы и его исследование, но подразумевают терминальное торможение КА. Для таких проектов требуется экономичное уменьшение с помощью ГМ скорости КА относительно целевого малого тела. Вместе с тем существует небесно-механическое ограничение, заключающееся в невозможности реализации этого условия посредством совершения гравитационного маневра только около одного целевого тела (указанное ограничение есть следствие обобщенного интеграла энергии Якоби в круговой ограниченной задаче трех тел).
В статье представлен адаптированный для массовых расчетов методический инструментарий, обеспечивающий оперативный поиск сценариев проведения малозатратных гравитационных маневров в системе Юпитера с выходом на орбиту его галилеева спутника. Предложенный инструментарий обладает несомненной общностью для целого класса актуальных задач астродинамики. При численном анализе формируемых в условиях массовых расчетов пучков траекторий оказывается эффективным разработанный состав формализованных правил поиска и отбора цепочек гравитационных маневров $\{ {{\Psi }_{{{\text{Res\_VP}}}}},{{\Psi }_{{{\text{TID}}}}},{{\Psi }_{{V\infty }}}\} $. Конкретный набор применяемых правил формируется из указанного состава в зависимости от проектных требований.
Приведенные примеры использования представленного подхода показали его высокую эффективность для адаптивного построения межлунных перелетов в системе Юпитера с выходом КА на орбиту искусственного спутника юпитерианской луны при выполнении стандартных требований к длительности проведения миссии и комфортабельных (по сравнению с известными зарубежными аналогами) значениях накопленной дозы радиации.
Список литературы
Боровин Г.К., Голубев Ю.Ф., Грушевский А.В., Заславский Г.С., Захваткин М.В., Корянов В.В., Лавренов С.М., Морской И.М., Симонов А.В., Степаньянц В.А., Тучин А.Г., Тучин Д.А., Ярошевский В.С. Баллистико-навигационное обеспечение полетов автоматических космических аппаратов к телам Солнечной системы / Ред. Тучин А.Г. М., Химки: “НПО Лавочкина”, 2018. 336 с.
Голубев Ю.Ф., Грушевский А.В., Корянов В.В., Тучин А.Г. Синтез сценариев космических миссий в системе Юпитера с использованием гравитационных маневров // Докл. АН. 2014. Т. 456. № 1. С. 39–41.
Келдыш М.В., Власова З.П., Лидов М.Л., Охоцимский Д.Е., Платонов А.К. Исследование траекторий облета Луны и анализ условий фотографирования и передачи информации / Келдыш М.В. Избранные труды. Ракетная техника и космонавтика. М.: Наука, 1988. С. 261–309.
Прикладная небесная механика и управление движением. Сборник статей, посвященный 90-летию со дня рождения Д.Е. Охоцимского / Сост. Т.М. Энеев, М.Ю. Овчинников, А.Р. Голиков. М.: Институт прикладной математики им. М.В. Келдыша РАН. 2010. 368 с.
Соболь И.М. Равномерно распределенные последовательности с дополнительным свойством равномерности // Журн. вычисл. матем. и матем. физ. 1976. Т. 16. № 5. С. 1332–1337.
Энеев Т.М., Козлов Н.Н. Принцип виртуальных контактов. Метод расчета процесса аккумуляции планет для новой космогонической модели // Препр. ИПМ им. М.В. Келдыша. 1979. № 78.
Boutonnet A., Schoenmaekers J. Mission Analysis for the JUICE Mission. AAS/AIAA Space Flight Mechanics Meeting, Charleston, SC, 2012. AAS 12-207 // Adv. Astron. Sci. 2012. V. 143. P. 1561–1578.
Campagnola S., Russell R. Endgame Problem Part 2: Multi-Body Technique and the Tisserand-Poincaré Graph // J. Guidance, Control, and Dynamics. 2010. V. 33. № 2. P. 476–486.
Divine N., Garrett H.B. Charged Particle Distribution in Jupiter’s Magnetosphere // J. Geophys. Res. 1983. V. 88. № A9. P. 6889–6903.
Golubev Yu., Grushevskii A., Koryanov V., Tuchin A. Gravity Assist Maneuvers of a Spacecraft in Jupiter System // J. Comput. Syst. Sci. Int. 2014. V. 53. № 3. P. 445–463.
Golubev Yu., Grushevskii A., Koryanov V., Tuchin A., Tuchin D. Bifurcation Points During Gravity Assist Tours in the Jovian System // Dokl. Phys. 2015. V. 60. № 5. P. 210–213.
Grushevskii A., Golubev Yu., Koryanov V., Tuchin A., Tuchin D. Advanced Methods of Low Cost Mission Design for Jovian Moons Exploration // Transactions of the Japan Society for Aeronautical and Space Sciences, Aerospace Technology. 2018. V. 16. № 7. P. 679–686.
Labunsky A.V., Papkov O.V., Sukhanov K.G. Multiple Gravity Assist Interplanetary Trajectories. London: Gordon and Breach Science Publishers, 1998. vi + 285 p.
Miller J.K., Weeks C.J. Application of Tisserand’s Criterion to the Design of Gravity Assist Trajectories // AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Monterey, USA. 2002. 7 p.
Minovitch M.A. The Determination and Characteristics of Ballistic Interplanetary Trajectories Under the Influence of Multiple Planetary Attractions. Tech. Rep. № 32–464. Jet Propulsion Lab., Pasadena, CA, 1963. 40 p.
NAIF – Navigation and Ancillary Information Facility. http://naif.jpl.nasa.gov/ Ephemeris of Jupiter’s Galilean satellites. ftp://naif.jpl.nasa.gov/pub/naif/generic_kernels/ (дата обращения 20.12.2019).
Podzolko M.V., Getselev I.V. Radiation Conditions of Mission to Jupiter’s Moon Ganymede // Int. Colloq. and Workshop Ganymede Lander: scientific goals and experiments. Moscow, March 4–8, 2013.
Tisserand F.F. Traité de Mecanique céléste. V. 4. Paris: Gauthier-Villars et fils., 1896. P. 203–205.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник