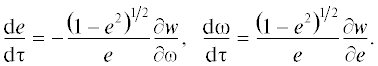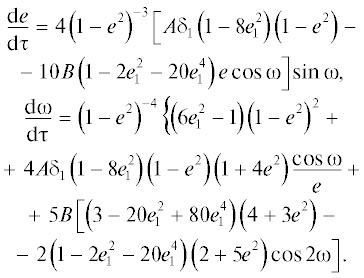Астрономический вестник, 2020, T. 54, № 4, стр. 360-375
Об эволюции орбит во внешнем варианте ограниченной эллиптической двукратно осредненной задачи трех тел
М. А. Вашковьяк *
Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия
* E-mail: vashkov@keldysh.ru
Поступила в редакцию 28.10.2019
После доработки 26.12.2019
Принята к публикации 27.02.2020
Аннотация
Рассмотрен внешний вариант ограниченной эллиптической задачи трех тел, когда возмущаемое тело пренебрежимо малой массы удалено от двух близких друг к другу тел конечных масс (основного и возмущающего), а его орбита расположена целиком вне орбиты возмущающего тела. В разложении возмущающей функции задачи сохранены слагаемые до четвертой степени включительно по отношению больших полуосей орбит возмущающего и возмущаемого тел. Приведены явные аналитические выражения двукратно осредненной возмущающей функции и ее производных по элементам орбиты, входящих в правые части эволюционных уравнений. Исследованы интегрируемые случаи двукратно осредненной эллиптической задачи: плоские и ортогонально-апсидальные орбиты. Указаны качественные отличия по сравнению с внутренним (спутниковым) вариантом. В общем (неинтегрируемом) случае проведено численное интегрирование эволюционной системы для ряда специальных начальных условий, гипотетически соответствующих орбитальной эволюции тел малой массы (планетезималей, маломассивных планет) в экзопланетной системе GJ 3512.
ВВЕДЕНИЕ И ПОСТАНОВКА ЗАДАЧИ
Исследования эволюции орбит в ограниченной задаче трех тел, как правило, опираются на ее двукратно осредненную постановку, а также на интегрируемый случай круговой орбиты возмущающего тела. Основы этих исследований, заложенные известными учеными Х. фон Цейпелем (von Zeipel, 1910) и Н.Д. Моисеевым (Моисеев, 1945), были существенно развиты М.Л. Лидовым (Лидов, 1961) и И. Козаи (Kozai, 1962).
Заметным событием в небесно-механической литературе в 2019 г. явилась монография (в двух незначительно различающихся версиях) Ito и Ohtsuka “The Lidov-Kozai Oscillation and Hugo von Zeipel”, представляющая собой фундаментальное научно-историческое исследование. Написание этой монографии, по словам ее авторов, инициировано статьей (Baily, Emel’yanenko, 1996), в которой цитирована долгое время остававшаяся неизвестной работа (von Zeipel, 1910). О версии (Ito, Ohtsuka, 2019a) автору стало известно из сообщений директора ГАИШ МГУ проф. К.А. Постнова и проф Н.В. Емельянова, а о более полной версии (Ito and Ohtsuka, 2019b) ему любезно сообщил проф. И.И. Шевченко (ГАО РАН). В указанной монографии проведено тщательное фактическое и хронологическое сопоставление результатов, полученных в ограниченной круговой двукратно осредненной задаче трех тел вышеуказанными авторами вместе с предоставлением обширнейшей библиографии, подробным изложением теоретических аспектов проблемы и оценкой вклада каждого из ученых в ее исследование.
В работе (von Zeipel, 1910), в частности, выделены и качественно изучены три основных случая расположения орбиты возмущаемого тела в двукратно осредненной круговой задаче: внутренний, внешний и случай так называемых “зацепленных” орбит. Эти варианты могут быть непосредственно распространены и на эллиптическую задачу.
В данной работе исследуется внешний вариант ограниченной эллиптической двукратно осредненной задачи, когда орбита возмущающего тела целиком находится внутри сферы радиуса, равного расстоянию перицентра орбиты возмущаемого тела. Методически – это продолжение работы (Вашковьяк, 2020), в которой рассмотрен спутниковый или внутренний вариант задачи. Поэтому структуры обеих статей весьма сходны, а некоторые небольшие текстовые фрагменты идентичны. Среди методически близких необходимо отметить недавние работы (Vinson, Chiang, 2017; Naoz и др., 2017; de Elía и др., 2019), которые посвящены инверсии резонанса Лидова–Козаи для внешнего варианта эллиптической задачи.
Рассмотрим движение материальной точки Р пренебрежимо малой массы под действием притяжения центральной точки S массы m и возмущающей точки J массы m1$ \ll $ m, движущейся относительно S по эллиптической орбите с большой полуосью а1 и эксцентриситетом е1. Введем прямоугольную систему координат Oxyz c началом в точке S, основная плоскость xOy которой совпадает с плоскостью орбиты точки J. Ось Ox пусть направлена в перицентр орбиты точки J, ось Oy – в сторону ее движения от перицентра в основной плоскости, а ось Oz дополняет систему координат до правой. Возмущенная орбита точки P характеризуется оскулирующими кеплеровскими элементами: большой полуосью а, эксцентриситетом е, наклонением i, аргументом перицентра ω и долготой восходящего узла Ω. Внешний вариант задачи предполагает, что расстояние перицентра орбиты точки Р в процессе ее эволюции остается бóльшим расстояния апоцентра орбиты точки J, т.е. а(1 – е) > a1(1 + e1).
Для исследования эволюции орбиты точки Р используется вековая часть W полной возмущающей функции
Здесь, кроме уже введенных обозначений элементов орбит, Δ = |r – r1| – расстояние между возмущаемой и возмущающей точками, λ и λ1 – суть средние долготы этих точек, f – гравитационная постоянная. Собственно процедура подобного (независимого) двукратного осреднения по быстрым переменным носит название схемы Гаусса, в которой предполагается отсутствие соизмеримостей низких порядков между средними движениями точек J и P. Как следствие, в двукратно осредненной задаче появляются первые интегралы уравнений возмущенного движения в элементах
а в случае е1 = 0 существует еще один первый интеграл (1 – e2)cos2i = const (Моисеев, 1945). В функции W a1 и e1 играют роль параметров эволюционной задачи.УПРОЩЕННОЕ ВЫРАЖЕНИЕ ОСРЕДНЕННОЙ ВОЗМУЩАЮЩЕЙ ФУНКЦИИ И ЭВОЛЮЦИОННЫЕ УРАВНЕНИЯ ВНЕШНЕГО ВАРИАНТА ЗАДАЧИ
В аналитических исследованиях нередко используется и другое равносильное выражение функции W с помощью известных формул
(2)
$W = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {V\left( \lambda \right){\text{d}}\lambda ,} \,\,\,\,V\left( \lambda \right) = \frac{{f{{m}_{1}}}}{{2\pi }}\int\limits_0^{2\pi } {\frac{{{\text{d}}{{\lambda }_{1}}}}{{\Delta \left( {{{\lambda }_{1}},\lambda } \right)}}} ,$(3)
$\begin{gathered} V\left( \lambda \right) = \frac{{f{{m}_{1}}}}{{2\pi r}}\int\limits_0^{2\pi } {\sum\limits_{n = 0}^4 {{{{\left( {\frac{{{{r}_{1}}}}{r}} \right)}}^{n}}} {{P}_{n}}\left( {\cos H} \right)} {\text{d}}{{\lambda }_{1}}, \\ \cos H = \frac{1}{{r{{r}_{1}}}}\left( {x{{x}_{1}} + y{{y}_{1}}} \right). \\ \end{gathered} $Выполняя стандартные процедуры интегрирования в (2), получим явное выражение функции V
(4)
$\begin{gathered} V = \frac{{f{{m}_{1}}}}{r}\left\{ {1 - \frac{{3{{a}_{1}}{{e}_{1}}x}}{{2{{r}^{2}}}} + \frac{1}{4}{{{\left( {\frac{{{{a}_{1}}}}{r}} \right)}}^{2}}\left[ {3\left( {1 + 4e_{1}^{2}} \right){{{\left( {\frac{x}{r}} \right)}}^{2}}} \right. + } \right. \\ \left. { + \,\,3\left( {1 - e_{1}^{2}} \right){{{\left( {\frac{y}{r}} \right)}}^{2}} - \left( {2 + 3e_{1}^{2}} \right)} \right] + \frac{5}{{16}}{{\left( {\frac{{{{a}_{1}}}}{r}} \right)}^{3}}\frac{x}{r}{{e}_{1}} \times \\ \times \,\,\left[ {3\left( {4 + 3e_{1}^{2}} \right) - 5\left( {3 + 4e_{1}^{2}} \right){{{\left( {\frac{x}{r}} \right)}}^{2}} - 15\left( {1 - e_{1}^{2}} \right){{{\left( {\frac{y}{r}} \right)}}^{2}}} \right] + \\ + \,\,\frac{3}{{64}}{{\left( {\frac{{{{a}_{1}}}}{r}} \right)}^{4}}\left[ {35\left( {1 + 12e_{1}^{2} + 8e_{1}^{4}} \right){{{\left( {\frac{x}{r}} \right)}}^{4}} + } \right. \\ + \,\,35{{\left( {1 - e_{1}^{2}} \right)}^{2}}{{\left( {\frac{y}{r}} \right)}^{4}} + 70\left( {1 - e_{1}^{2}} \right)\left( {1 + 6e_{1}^{2}} \right){{\left( {\frac{x}{r}\frac{y}{r}} \right)}^{2}} - \\ - \,\,10\left( {4 + 41e_{1}^{2} + 18e_{1}^{4}} \right){{\left( {\frac{x}{r}} \right)}^{2}} - 10\left( {1 - e_{1}^{2}} \right) \times \\ \left. { \times \,\,\left. {\left( {4 + 3e_{1}^{2}} \right){{{\left( {\frac{y}{r}} \right)}}^{2}} + 8 + 40e_{1}^{2} + 15e_{1}^{4}} \right]} \right\} \\ \end{gathered} $(5)
$\begin{gathered} W\left( {e,i,\omega ,\Omega ,\alpha ,{{e}_{1}}} \right) = \frac{{3f{{m}_{1}}{{\alpha }^{3}}}}{{8{{a}_{1}}}}w,\,\,\,\,w = {{w}_{0}} + A{{w}_{1}} + B{{w}_{2}}, \\ {{w}_{0}} = {{\left( {1 - {{e}^{2}}} \right)}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}\left[ {\left( {\frac{2}{3} + e_{1}^{2}} \right){{A}_{0}} + e_{1}^{2}{{A}_{2}}\cos 2\Omega } \right], \\ {{w}_{1}} = e{{\left( {1 - {{e}^{2}}} \right)}^{{{{ - 5} \mathord{\left/ {\vphantom {{ - 5} 2}} \right. \kern-0em} 2}}}}\left[ {{{b}_{1}}\left( {{{A}_{1}}\cos \Omega + {{B}_{1}}\sin \Omega } \right)} \right. + \\ \left. { + \,\,{{b}_{3}}\left( {{{A}_{3}}\cos 3\Omega + {{B}_{3}}\sin 3\Omega } \right)} \right],\,\,\,\,{{w}_{2}} = {{\left( {1 - {{e}^{2}}} \right)}^{{{{ - 7} \mathord{\left/ {\vphantom {{ - 7} 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,\left[ {{{b}_{0}}{{C}_{0}} + {{b}_{2}}\left( {{{C}_{2}}\cos 2\Omega + {{B}_{2}}\sin 2\Omega } \right)} \right. + \\ \left. { + \,\,{{b}_{4}}\left( {{{C}_{4}}\cos 4\Omega + {{B}_{4}}\sin 4\Omega } \right)} \right],\,\,\,\,\alpha = \frac{{{{a}_{1}}}}{a}, \\ A = \frac{{5\alpha {{e}_{1}}}}{{32}},\,\,\,\,B = \frac{{3{{\alpha }^{2}}}}{{128}},\,\,\,\,\alpha \left( {1 + {{e}_{1}}} \right) < 1 - e, \\ {{b}_{0}} = 2 + 10e_{1}^{2} + \frac{{15}}{4}e_{1}^{4},\,\,\,\,{{b}_{1}} = 4 + 3e_{1}^{2}, \\ {{b}_{2}} = \left( {2 + e_{1}^{2}} \right){{b}_{3}},\,\,\,\,{{b}_{3}} = 35e_{1}^{2},\,\,\,\,{{b}_{4}} = \frac{{21}}{8}e_{1}^{2}{{b}_{3}}. \\ \end{gathered} $Здесь коэффициенты А0,1,2,3, В1,2,3,4 и С0,2,4, зависящие от элементов e, i, ω и не зависящие от Ω, определяются формулами
(6)
$\begin{gathered} {{A}_{0}} = 1 - \frac{3}{2}{{\sin }^{2}}i,\,\,\,\,{{A}_{1}} = \left( {5{{{\sin }}^{2}}i - 4} \right)\cos \omega , \\ {{A}_{2}} = \frac{5}{2}{{\sin }^{2}}i,\,\,\,\,{{A}_{3}} = - {{\sin }^{2}}i\cos \omega , \\ {{B}_{1}} = \left( {4 - 15{{{\sin }}^{2}}i} \right)\sin \omega \cos i, \\ {{B}_{2}} = {{e}^{2}}\left( {7{{{\sin }}^{2}}i - 2} \right)\sin 2\omega \cos i, \\ {{B}_{3}} = {{\sin }^{2}}i\sin \omega \cos i,\,\,\,\,{{B}_{4}} = - 4{{e}^{2}}{{\sin }^{2}}i\sin 2\omega \cos i, \\ {{C}_{0}} = \left( {1 + \frac{3}{2}{{e}^{2}}} \right)\left( {8 - 40{{{\sin }}^{2}}i + 35{{{\sin }}^{4}}i} \right) + \\ + \,\,5{{e}^{2}}{{\sin }^{2}}i\left( {6 - 7{{{\sin }}^{2}}i} \right)\cos 2\omega , \\ {{C}_{2}} = \left( {1 + \frac{3}{2}{{e}^{2}}} \right){{\sin }^{2}}i\left( {6 - 7{{{\sin }}^{2}}i} \right) + \\ + \,\,{{e}^{2}}\left( {2 - 8{{{\sin }}^{2}}i + 7{{{\sin }}^{4}}i} \right)\cos 2\omega , \\ {{C}_{4}} = \left( {2 + 3{{e}^{2}}} \right){{\sin }^{4}}i + 2{{e}^{2}}{{\sin }^{2}}i\left( {2 - {{{\sin }}^{2}}i} \right)\cos 2\omega . \\ \end{gathered} $Слагаемое Аw1 содержит величины, пропорциональные е1 и $e_{1}^{3}$, а функция w2 содержит слагаемые нулевой, второй и четвертой степени относительно е1. При е1 = 0 приведенная формула для W совпадает с начальными слагаемыми (с точностью до α5 включительно) существенно более полного (до α15) разложения, полученного в работе (Ito, 2016). При е1 > 0 формулы (5), (6) дают более точное (и совпадающее при В = 0) выражение двукратно осредненной возмущающей функции для внешнего варианта ограниченной эллиптической задачи по сравнению с полученным в работе (Naoz и др., 2017), посвященной эксцентрическому механизму Козаи–Лидова.
Отметим еще, что в кубичном приближении относительно параметра α, т.е. при А = В = 0, функция W не зависит от аргумента перицентра ω, сама эволюционная задача, как это было показано С.Л. Зиглиным, становится интегрируемой. При этом эксцентриситет е оказывается постоянной величиной, связь наклонения и времени определяется с помощью неполных эллиптических интегралов первого рода, а долгота восходящего узла находится из интеграла w0 = const (Зиглин, 1975). В этой же работе отмечается неинтегрируемость эллиптической задачи при учете слагаемых порядком выше, чем α3, когда появляется зависимость функции W от ω.
Таблица 1 дает сравнительное представление о характере зависимости возмущающей функции W от параметров α, e1 и элементов орбиты для обоих вариантов двукратно осредненной ограниченной эллиптической задачи трех тел – внутреннего и внешнего.
Таблица 1.
Характерные компоненты функции W
| Внутренний вариант | Внешний вариант | |
|---|---|---|
| α | a/a1 | a1/a |
| Wα→0 | $\frac{{3f{{m}_{1}}{{\alpha }^{2}}}}{{8{{a}_{1}}{{{\left( {1 - e_{1}^{2}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{w}_{0}}$ | $\frac{{3f{{m}_{1}}{{\alpha }^{3}}}}{{8{{a}_{1}}}}{{w}_{0}}$ |
| w0 | ${{e}^{2}} - {{\sin }^{2}}i + {{e}^{2}}{{\sin }^{2}}i\left( {1 - 5{{{\sin }}^{2}}\omega } \right)$ | ${{\left( {1 - {{e}^{2}}} \right)}^{{ - 3/2}}}\left[ {\left( {\frac{2}{3} + e_{1}^{2}} \right)\left( {1 - \frac{3}{2}{{{\sin }}^{2}}i} \right) + \frac{5}{2}e_{1}^{2}{{{\sin }}^{2}}i\cos 2\Omega } \right]$ |
| Aw1 | $\frac{{5\alpha {{e}_{1}}}}{{8\left( {1 - e_{1}^{2}} \right)}}{{w}_{1}}\left( { - ,e,i,\omega ,\Omega } \right)$ | $\frac{{5\alpha {{e}_{1}}}}{{32}}{{w}_{1}}\left( {e_{1}^{2},e,i,\omega ,\Omega } \right)$ |
| Bw2 | $\frac{{15{{\alpha }^{2}}}}{{64{{{\left( {1 - e_{1}^{2}} \right)}}^{2}}}}{{w}_{2}}\left( {e_{1}^{2},e,i,\omega ,\Omega } \right)$ | $\frac{{3{{\alpha }^{2}}}}{{128}}{{w}_{2}}\left( {e_{1}^{2},e,i,\omega ,\Omega } \right)$ |
Тире в функции w1 для внутреннего варианта означает отсутствие ее зависимости от параметра е1. При α → 0 эволюционная задача является интегрируемой в обоих вариантах, что обусловлено существованием (кроме w = const) дополнительных первых интегралов:
(1 – е2)cos2i = const для внутреннего варианта (Лидов, 1961; Lidov, 1962; Kozai, 1962), е = const – для внешнего варианта, причем постоянство эксцентриситета сохраняется не только в ограниченной, но и в неограниченной задаче (Зиглин, 1975). Далее будет удобно ввести новую независимую переменную – “безразмерное время” τ, согласно формуле
где $n = \frac{{\sqrt {fm} }}{{{{a}^{{3/2}}}}}$ – среднее движение точки Р. Отметим, что в рассматриваемом внешнем варианте нормирование времени и формулы для функции W, естественно, отличаются от соответствующих формул внутреннего варианта (Вашковьяк, 2020), но их структуры весьма похожи.Для описания эволюции орбит будут использованы уравнения Лагранжа в элементах с нормированной функцией w, являющейся их первым и единственным интегралом
(8)
$\begin{gathered} \frac{{de}}{{d\tau }} = - \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial \omega }},\,\,\,\,\frac{{di}}{{d\tau }} = \frac{{{\text{ctg}}i}}{{\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial \omega }} - \\ - \,\,\frac{1}{{{\text{sin}}i\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial \Omega }},\,\,\,\,\frac{{d\omega }}{{d\tau }} = \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial e}} - \\ - \,\,\frac{{{\text{ctg}}i}}{{\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial i}},\,\,\,\,\frac{{d\Omega }}{{d\tau }} = \frac{{{\text{cosec}}i}}{{\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial i}}. \\ \end{gathered} $В общем случае для произвольных орбит точки Р решение уравнений (8) может быть найдено лишь численным методом, а процесс вычислений может контролироваться постоянством функции w вдоль этого решения. Для полноты совокупности формул мы приводим выражения для производных функций w0,1,2 по элементам. Они необходимы для вычисления правых частей эволюционных уравнений (8).
Производные функции w0
Производные функции w1
Производные функции w2
ИНТЕГРИРУЕМЫЕ СЛУЧАИ ЗАДАЧИ
Плоские орбиты
Если sini = 0, орбита точки Р постоянно располагается в основной координатной плоскости, причем данное плоское решение оказывается устойчивым относительно наклонения (Neishtadt и др., 2018). С введением долготы перицентра орбиты точки Р
где δ = sign(cosi), эволюционная система упрощается и принимает вид(10)
$\frac{1}{\delta }\frac{{de}}{{d\tau }} = - \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial g}},\,\,\,\,\frac{1}{\delta }\frac{{dg}}{{d\tau }} = \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial e}}.$При этом очевидно, что эволюция прямых (δ = 1) и обратных (δ = –1) орбит происходит одинаковым образом с инверсией времени, а наличие первого интеграла
делает плоскую эволюционную задачу интегрируемой как систему с одной степенью свободы. Напомним, что внутренний вариант плоской эллиптической задачи был впервые аналитически исследован в работах Е.П. Аксенова (Аксенов, 1979а; 1979б).В рассматриваемом внешнем варианте из формул (5), (6) при sini → 0 получим
(12)
$\begin{gathered} w\left( {e,g} \right) = {{\left( {1 - {{e}^{2}}} \right)}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}\left( {\frac{2}{3} + e_{1}^{2}} \right) - \\ - \,\,4Ae{{\left( {1 - {{e}^{2}}} \right)}^{{{{ - 5} \mathord{\left/ {\vphantom {{ - 5} 2}} \right. \kern-0em} 2}}}}{{b}_{1}}\cos g + 2B{{\left( {1 - {{e}^{2}}} \right)}^{{{{ - 7} \mathord{\left/ {\vphantom {{ - 7} 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,\left[ {4{{b}_{0}}\left( {1 + \frac{3}{2}e_{1}^{2}} \right) + {{b}_{2}}{{e}^{2}}\cos 2g} \right] = h, \\ \end{gathered} $а уравнения (10) примут вид
(13)
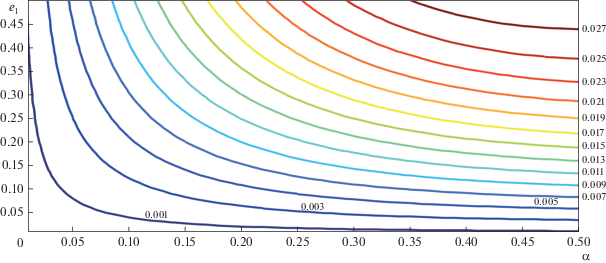
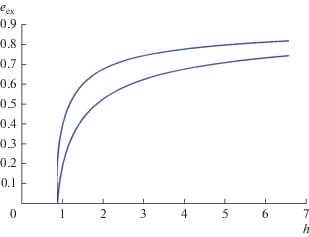
$\begin{gathered} \frac{{de}}{{\delta d\tau }} = - 4{{\left( {1 - {{e}^{2}}} \right)}^{{ - 3}}}\left[ {A{{b}_{1}}\left( {1 - {{e}^{2}}} \right) - 2B{{b}_{2}}e\cos g} \right]\sin g, \\ \frac{{dg}}{{\delta d\tau }} = {{\left( {1 - {{e}^{2}}} \right)}^{{ - 4}}}\left[ {\left( {{{b}_{1}} - 2} \right){{{\left( {1 - {{e}^{2}}} \right)}}^{2}}} \right. - \\ - \,\,4A{{b}_{1}}\left( {1 - {{e}^{2}}} \right)\left( {1 + 4{{e}^{2}}} \right)\frac{{\cos g}}{e} + \\ \left. {_{{^{{^{{}}}}}}^{{^{{^{{}}}}}} + \,\,2B\left[ {10{{b}_{0}}\left( {4 + 3{{e}^{2}}} \right) + {{b}_{2}}\left( {2 + 5{{e}^{2}}} \right)\cos 2g} \right]} \right]. \\ \end{gathered} $При фиксированных значениях параметров α и е1 интеграл (12) определяет h-семейство интегральных кривых в плоскости (g, e). Одно из таких семейств показано на рис. 1 для α = 0.26 и е1 = = 0.4356. Как будет ясно из последнего раздела данной работы, числовые значения приведенных параметров имеют отношение к недавно открытой экзосистеме GJ 3512.
Рис 1.
Семейство интегральных кривых (12) в плоскости (g, e) для α = 0.26, е1 = 0.4356 (А = 0.0177, В = 0.0016, $e_{1}^{*}$ = 0.627, $e_{2}^{*}$ = 0.853, е* = 0.107, es = 0.213).
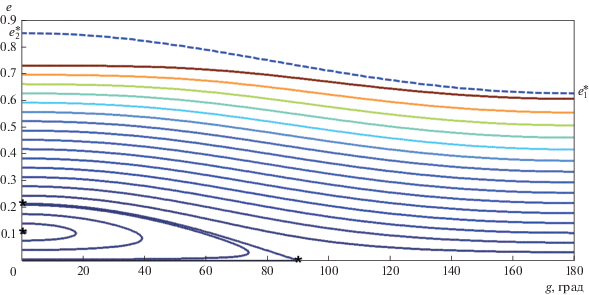
В силу имеющейся симметрии, фазовые траектории изображены лишь в области 0° < g < 180°. Звездочками отмечены стационарная точка (g = 0, e = e*), а также точки (g = 0, e = es) и (g = 90°, e = 0) на интегральной кривой, ограничивающей зону либрации долготы перицентра.
Штриховая линия, называемая в дальнейшем “сепаратрисой”, определяется уравнением
Указанная область лежит ниже штриховой линии, причем в рамках применимости двукратно осредненной схемы реальный физический смысл имеют лишь фазовые траектории, расположенные ниже и не слишком близко к данной границе непересекающихся орбит. Поэтому рассматриваемая в данной работе область лежит ниже горизонтальной прямой $e = e_{1}^{*} < e_{2}^{*}$, а само семейство фазовых траекторий разделяется на две области с качественно различным изменением аргумента перицентра: либрационным и циркуляционным. Значения параметров α, е1, принятые для построения данного семейства, принадлежат области 4 на рис. 1 работы (Вашковьяк, 1982).
Напомним, что во внутреннем (спутниковом) варианте, кроме указанных типов, существуют так называемые вырожденные траектории, отвечающие падению спутника на центральное тело (Аксенов, 1979а).
Стационарные решения системы (13) находятся приравниванием нулю правых частей обоих уравнений. Из первого уравнения (13) имеем g = 0, или g = π. Очевидно, для g = π правая часть второго уравнения (13) не обращается в нуль и положительна при любом е. Поэтому стационарным значением переменной g является
Замечание: Строго говоря, стационарное значение долготы перицентра g*, отличное от 0 для некоторой области значений параметров α, е1, может определяться из условия $A{{b}_{1}}\left( {1 - {{e}^{2}}} \right) - 2B{{b}_{2}}e\cos g = 0$, также получающегося из первого уравнения (13). Однако ввиду возможного влияния слагаемых, неучтенных в функции W, мы пока оставляем в стороне вопрос о существовании подобных стационарных решений, которые можно было бы назвать “внутренними”. Отметим только, что при α → 0 таких решений не существует.
При g* = 0 стационарное значение эксцентриситета находится как соответствующий действительный корень (0 < е* < 1) полинома пятой (при В = 0 третьей) степени
(15)
${{c}_{5}}{{e}^{{*{\kern 1pt} 5}}} + {{c}_{4}}{{e}^{{*{\kern 1pt} 4}}} + {{c}_{3}}{{e}^{{*{\kern 1pt} 3}}} + {{c}_{2}}{{e}^{{*{\kern 1pt} 2}}} + {{c}_{1}}e{\text{*}} + {{c}_{0}} = 0,$(16)
$\begin{gathered} {{c}_{0}} = - 4A{{b}_{1}},\,\,\,{{c}_{1}} = {{c}_{5}} + 4B\left( {{{b}_{2}} + 20{{b}_{0}}} \right), \\ {{c}_{2}} = 3{{c}_{0}},\,\,\,\,{{c}_{3}} = - 2{{c}_{5}} + 10B\left( {{{b}_{2}} + 6{{b}_{0}}} \right), \\ {{c}_{4}} = - 4{{c}_{0}},\,\,\,\,{{c}_{5}} = {{b}_{1}} - 2. \\ \end{gathered} $Анализ его коэффициентов (с использованием теорем Декарта и Бюдана–Фурье) показывает, что для 0 < e1 < 1 и умеренных значений α < 0.5 уравнение (15) имеет один корень, находящийся в диапазоне 0 < e* < 1.
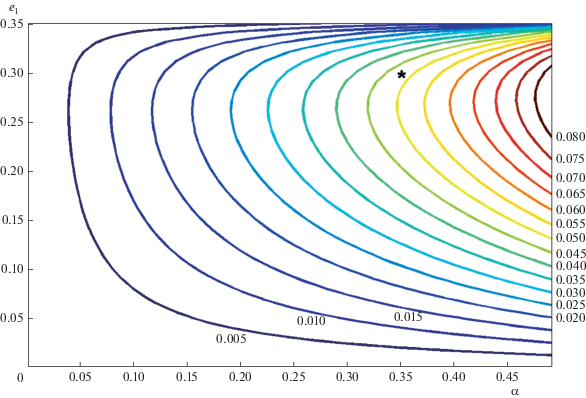
Поскольку А и В зависят от параметров задачи – отношения α = a1/a и е1, – то для наглядности естественно представить результаты решения уравнения (15) в виде семейства изолиний e*(α, е1) = const (рис. 2). Численные значения e* нанесены внутри области и по вертикали у правых концов соответствующих линий.
Рис. 2.
Семейство изолиний стационарных значений эксцентриситета е*(α, е1) = const для плоских орбит.
Отметим, что в рассматриваемой области значений параметров α, е1 величины e* относительно невелики и не превышают примерно 0.15.
Аналогично семейству изолиний для e* строится семейство еs(α, е1) = const (рис. 3), характеризующее размер либрационной зоны. Для определения еs служит уравнение
(17)
$\begin{gathered} f\left( {\alpha ,{{e}_{1}},{{e}_{s}}} \right) = \left( {\frac{2}{3} + e_{1}^{2}} \right){{\left( {1 - e_{s}^{2}} \right)}^{2}} \times \\ \times \,\,\left[ {1 - {{{\left( {1 - e_{s}^{2}} \right)}}^{{3/2}}}} \right] - 4A{{b}_{1}}{{e}_{s}}\left( {1 - e_{s}^{2}} \right) + \\ + \,\,2B\left\{ {\left( {6{{b}_{0}} + {{b}_{2}}} \right)e_{s}^{2} + 4{{b}_{0}}\left[ {1 - {{{\left( {1 - e_{s}^{2}} \right)}}^{{7/2}}}} \right]} \right\} = 0. \\ \end{gathered} $Что касается нахождения нулей непрерывной функции одной переменной (так же, как и полинома), то оно может быть выполнено практически в любой вычислительной системе, например, в системе MATLAB (функции fzero и roots). При этом существенным является выбор начального приближения к искомому решению. Для уравнения (17) оно может быть получено для малых еs ее сведением к соответствующему квадратному уравнению, решение которого дается формулой
(18)
$\begin{gathered} e_{s}^{{(0)}} = \frac{1}{2}\left( {\sqrt {{{b}^{2}} + 4} - b} \right), \\ b = \frac{{{{b}_{1}} - 2 + 4B\left( {20{{b}_{0}} + {{b}_{2}}} \right)}}{{8A{{b}_{1}}}}. \\ \end{gathered} $Для последующего “движения” по изолинии еs(α, е1) = const в качестве начального приближения используется значение еs в “предыдущей” точке. Отметим, что величины еs, естественно, превышают соответствующие значения e* и в рассматриваемой области значений параметров α, е1 не превосходят примерно 0.03.
Кроме вышеуказанных специальных значений эксцентриситета, представляет интерес нахождение его экстремальных значений для каждого из характерных диапазонов значений постоянной интеграла (12) h. Как показывает анализ для 0 ≤ е ≤ $e_{1}^{*}$, величина h может принимать значения в пределах
Эти значения определяются следующим образом:
(19)
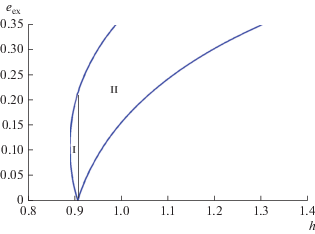
$\begin{gathered} h* = F\left( {e{\text{*}}} \right),\,\,\,\,{{h}_{s}} = F\left( {{{e}_{s}}} \right),\,\,\,\,h{\text{**}} = F\left( {e_{1}^{*}} \right), \\ F\left( e \right) = \left( {\frac{2}{3} + e_{1}^{2}} \right){{\left( {1 - {{e}^{2}}} \right)}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}} - 4A{{b}_{1}}e{{\left( {1 - {{e}^{2}}} \right)}^{{{{ - 5} \mathord{\left/ {\vphantom {{ - 5} 2}} \right. \kern-0em} 2}}}} + \\ + \,\,2B\left[ {4{{b}_{0}}\left( {1 - \frac{3}{2}{{e}^{2}}} \right) + {{b}_{2}}{{e}^{2}}} \right]{{\left( {1 - {{e}^{2}}} \right)}^{{{{ - 7} \mathord{\left/ {\vphantom {{ - 7} 2}} \right. \kern-0em} 2}}}}. \\ \end{gathered} $На рис. 4 представлены зависимости от h экстремальных значений эксцентриситета, построенные для тех же значений α = 0.26, е1 = 0.4356.
В большем масштабе на рис. 5 представлен фрагмент, позволяющий явно выделить области либрации (I) и циркуляции (II) долготы перицентра g.
Экстремальные значения эксцентриситета получаются с помощью нахождения нулей функций с соответствующими начальными приближениями е(0):
φ1(еmax) = F(еmax) – h для всего диапазона значений h* ≤ h ≤ h** (области I, II, $e_{{\max }}^{{(0)}}$ = es),
φ1(еmin) = F(еmin) – h для h* ≤ h ≤ hs (либрация g, область I, $e_{{\min }}^{{(0)}}$ = es),
φ2(еmin) = Φ(еmin) – h для hs < h ≤ h** (циркуляция g, область II, $e_{{\min }}^{{(0)}}$ = es), где Φ(е, A) = F(e, –A).
К сожалению, в отличие от внутреннего варианта задачи, получение строгого аналитического решения уравнений (13) даже при В = 0 наталкивается на трудности обращения квадратур, к которым эти уравнения приводятся с использованием первого интеграла (12).
ОРТОГОНАЛЬНО-АПСИДАЛЬНЫЕ ОРБИТЫ
Если cosi = 0 и sinΩ = 0, то орбита точки Р постоянно располагается ортогонально орбитальной плоскости возмущающей точки J (di/dτ = 0, dΩ/dτ = 0). Общее качественное исследование этого случая с учетом возможных пересечений орбит точек Р и J было проведено с помощью численно-аналитического метода в работе (Вашковьяк, 1984) для произвольных значений α. Здесь внешний вариант задачи изучается для α, не превосходящих примерно 0.4 с уточнением некоторых качественных результатов и количественных оценок.
В рассматриваемом случае эволюционные уравнения (8) упрощаются и принимают вид
Здесь
(21)
$\begin{gathered} w\left( {e,{\omega },\alpha ,{{e}_{1}}} \right) = {{\left( {1 - {{e}^{2}}} \right)}^{{ - 3/2}}}\left( { - \frac{1}{3} + 2e_{1}^{2}} \right) + \\ + \,\,4A{{\delta }_{1}}\left( {1 - 8e_{1}^{2}} \right){{\left( {1 - {{e}^{2}}} \right)}^{{ - 5/2}}}e\cos {\omega } + \\ + \,\,B{{\left( {1 - {{e}^{2}}} \right)}^{{ - 7/2}}}\left[ {\left( {2 + 3{{e}^{2}}} \right)\left( {3 - 20e_{1}^{2} + 80e_{1}^{4}} \right)} \right. - \\ \left. { - \,\,10\left( {1 - 2e_{1}^{2} - 20e_{1}^{4}} \right){{e}^{2}}\cos 2{\omega }} \right] = h = {\text{const}}, \\ {{\delta }_{1}} = {\text{sign}}({\text{cos}}\Omega ){\text{ }} = \pm 1, \\ \end{gathered} $так что
При фиксированных значениях параметров α и е1 интеграл (21) определяет h-семейство интегральных кривых в плоскости (ω, e). Структуры этого семейства отличаются бóльшим разнообразием, чем в предыдущем интегрируемом случае. Они характеризуются как присутствием специальных кривых – “сепаратрис”, соответствующих пересечениям орбит точек P и J, так и числом и расположением стационарных особых точек. Отметим, что существуют два специальных значения параметра е1 = 6–1/2 и 8–1/2, при которых возможно качественное изменение структуры семейств интегральных кривых. Далее мы ограничимся приведением примеров наиболее типичных семейств для δ1 = 1, α = 0.35 и различных значений е1.
На рис. 6 в плоскости (ω, e) две штриховые линии – “сепаратрисы” – соответствуют пересечениям орбит точек P и J, причем области с криволинейными границами, расположенные между этими линиями, отвечают так называемым “зацепленным” орбитам этих точек. Пространственное расположение таких (в данном случае – ортогональных) орбит характеризуется тем, что одна из точек пересечения орбиты Р с плоскостью орбиты J находится внутри нее, а другая – вне. Такая классификация ограниченной круговой двукратно осредненной задачи трех тел была предложена в работе (von Zeipel, 1910) для общего случая и в работе (Lidov, Ziglin, 1974) для равномерно близких орбит. В данной статье мы рассматриваем лишь фазовые траектории, соответствующие “не зацепленным” орбитам умеренного эксцентриситета, для которых обе указанные точки пересечения находятся вне орбиты J. Эти фазовые траектории заполняют на рис. 6 область ниже штриховых линий, а звездочками отмечены стационарные особые точки различных типов. Символами $e_{1}^{*}$ и $e_{2}^{*}$ отмечены граничные значения е на “сепаратрисах” в их точках пересечения с прямыми ω = π и ω = 0, соответственно.
Рис. 6.
Семейство интегральных кривых (21) в плоскости (ω, e) для α = 0.35, е1 = 0.3 (А = 0.0164, В = 0.00287, $e_{1}^{*}$ = 0.545, $e_{2}^{*}$ = 0.755).
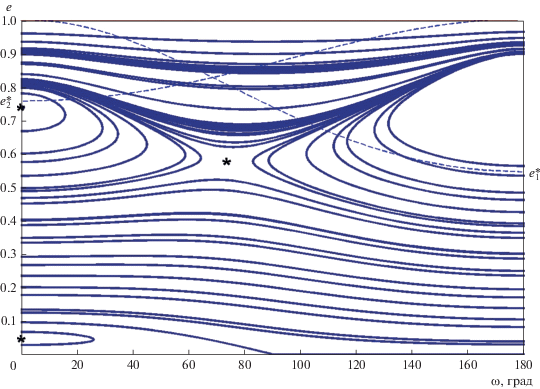
Для принятого значения α = 0.35 стационарные значения e* могут соответствовать “зацепленным орбитам”. Одно из них, не отмеченное на рис. 6, неявно присутствует при ω* = π. Семейство, представленное на рис. 6, характеризуется наличием внутренней особой седловой точки, также отмеченной звездочкой, наряду с двумя граничными точками типа центр ω* = 0.
Семейство, показанное на рис. 7, отличается от предыдущего наличием только одной стационарной точки типа “центр” и отсутствием седловой точки.
Рис. 7.
То же самое, что и на рис. 6, но для α = 0.35, е1 = 0.4 (А = 0.0219, В = 0.00287, $e_{1}^{*}$ = 0.510, $e_{2}^{*}$ = 0.790).
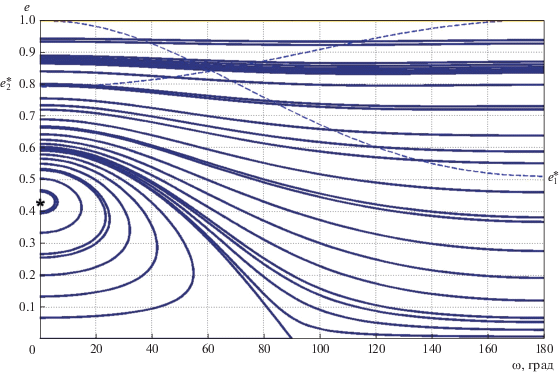
Анализ показывает, в плоскости параметров α, е1 существует достаточно узкая область 8–1/2 < е1 < 6–1/2 , в которой на границе ω = π существуют две особые точки е* < $e_{1}^{*}$. Семейство, представленное на рис. 8, характеризуется как наличием внутренней особой седловой точки, также отмеченной звездочкой, наряду с тремя граничными точками типа центр, две из которых принадлежат прямой ω = π.
Рис. 8.
То же самое, что и на рис. 6, но для α = 0.35, е1 = 0.37 (А = 0.0202, В = 0.00287, $e_{1}^{*}$ = 0.520, $e_{2}^{*}$ = 0.780).
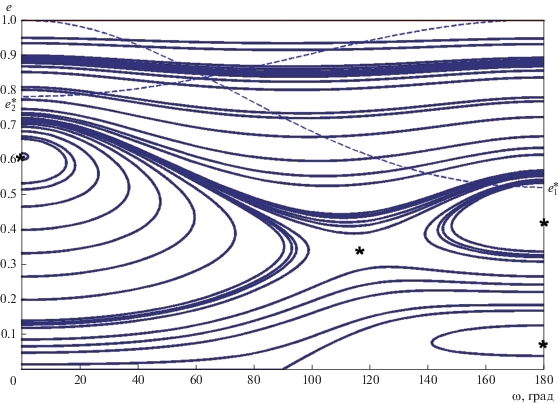
Стационарные решения системы (22) e = e*, ω = ω* или координаты особых точек в фазовой плоскости (ω, е), находятся приравниванием нулю правых частей обоих уравнений.
Выделим вначале граничные решения sinω* = 0, следующие из первого уравнения (22) и принадлежащие вертикальным границам рассматриваемой области т.е.
(23)
$\omega * = 0,~\,\,\,{\text{или}}\,\,\,~\omega * = \pi ,~\,\,{{\delta }_{2}} = {\text{sign}}({\text{cos}}\omega *) = \pm 1.$Стационарные значения эксцентриситета находятся как соответствующие положительные корни полинома пятой степени
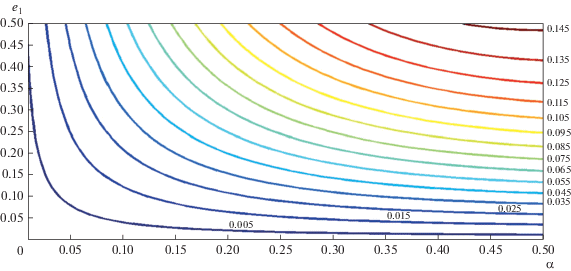
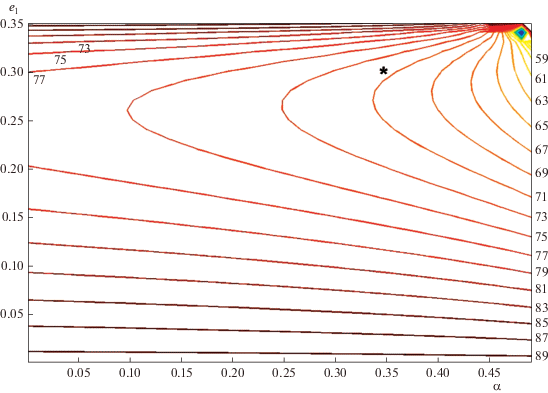
С помощью анализа этих коэффициентов (с привлечением теорем Декарта и Бюдана–Фурье) можно показать, что для 0 < e1 < 1 и умеренных значений α ≤ 0.4 число его корней, находящихся в интервале 0 < е* < 1, может изменяться от 0 до 3. Для иллюстрации на рис. 9, аналогичном рис. 2, в плоскости параметров (α, е1) показаны семейства изолиний стационарных значений эксцентриситета, соответствующих граничным решениям с ω* = 0 для δ1δ2 = 1. Звездочкой отмечено значение, отвечающее граничной стационарной точке е* ≈ 0.048 на рис. 6. Приведенные лишь для умеренных значений е1 < 8–1/2 стационарные значения е* не превышают примерно 0.1.
Численные значения е* нанесены внутри области и по вертикали у правых концов соответствующих линий. Расчеты показывают, что для е1 > 6–1/2 стационарные значения е* могут составлять около 0.3.
Как следует из рис. 6 и 8, при произвольных значениях постоянных А и В не исключено существование особых точек внутри рассматриваемой прямоугольной области. Координаты этих точек удовлетворяют системе, получающейся приравниванием нулю выражений в квадратной и фигурной скобках двух уравнений (22), и определяются следующими формулами
На рис. 10 и 11 численные значения $e_{{{\text{in}}}}^{*}$ и ${\omega }_{{{\text{in}}}}^{*}$ нанесены внутри области и у концов соответствующих линий, а звездочками отмечены значения, отвечающие внутренней стационарной точке рис. 6.
Рис. 10.
Семейства изолиний стационарных значений эксцентриситета $e_{{{\text{in}}}}^{*}$ (α, е1) = const для ортогонально-апсидальных орбит (внутренние решения).
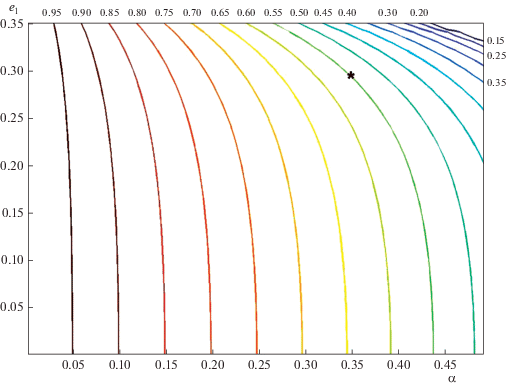
Рис. 11.
Семейства изолиний стационарных значений аргумента перицентра $\omega _{{{\text{in}}}}^{*}$(α, е1) = const для ортогонально-апсидальных орбит (внутренние решения).
К сожалению, получение строгого аналитического решения уравнений (21) даже при В = 0 связано с такими же трудностями, что и в интегрируемом случае, плоских орбит.
ОЦЕНКИ ПАРАМЕТРОВ ГИПОТЕТИЧЕСКИХ ОРБИТ В ЭКЗОСИСТЕМЕ GJ 3512 С ПОМОЩЬЮ ЧИСЛЕННОГО РЕШЕНИЯ ЭВОЛЮЦИОННЫХ УРАВНЕНИЙ
Использование внешнего варианта рассматриваемой двукратно осредненной эллиптической задачи для уточненного описания орбитальной эволюции каких-либо астрономических объектов Солнечной системы достаточно ограничено. Это связано с тем, что эксцентриситеты планетных орбит относительно невелики – для наиболее массивной планеты Юпитера, как правило, вносящего основной вклад в возмущения движения малых небесных тел, величина е1 составляет примерно 0.05. Тем не менее можно надеяться, что влияние эллиптичности его орбиты может оказаться заметным в орбитальной эволюции некоторых далеких малых тел, в том числе, еще не открытых.
Вместе с тем априори, вообще говоря, нельзя было бы полностью исключить существования экзопланетных систем с более выраженной орбитальной эксцентричностью. Именно такой пример представляет совсем недавнее открытие в созвездии Большой Медведицы планеты-гиганта около М-карлика GJ 3512. В статье (Morales и др., 2019) обсуждаются вопросы образования такой необычной системы на основе данных о ее физических и орбитальных параметрах:
| масса центральной звезды GJ 3512 | m0 = 0.123M☉ |
| минимальная масса планеты GJ 3512b | m1 = 0.463MJ |
| большая полуось ее орбиты | a1 = 0.338 а. е. |
| эксцентриситет | e1 = 0.4356. |
Кроме того, приведены нижние оценки параметров вероятно существующей в системе второй планеты-кандидата GJ 3512с минимальной массы m2 > 0.17 MJ с большой полуосью орбиты a2 > 1.2 а. е. (α = a1/a2 < 0.28). Угловые элементы орбиты этой гипотетической планеты i, ω, Ω, пока не определены.
Наряду с вопросами происхождения подобной экзосистемы, с небесно-механической точки зрения интересно само ее реально наблюдаемое существование. В этом плане рассматриваемый в данной работе внешний вариант осредненной задачи оказывается полезным для получения приближенных оценок характеристик орбитальной эволюции в системе GJ 3512. Конечно, ограниченность рассматриваемой задачи (m2 → 0) позволяет использовать эти оценки, в основном, для возможно существующих в системе объектов достаточно малой массы c a2> a1, но в некоторой степени и для гипотетической планеты GJ 3512c (m2/m1 ~ 0.37).
В рамках плоской модели (i = 0) и с принятыми значениями параметров a =1.3 а. е. (α = 0.26 < 0.28) и е1 = 0.4356 эволюционные характеристики будут соответствовать полученным для первого из интегрируемых случаев. Поэтому семейство на рис. 1 и зависимости на рис. 4 и 5, построенные для параметров рассматриваемой экзосистемы, дают некоторое представление (хотя и приближенное) о возможном изменении эксцентриситета орбиты GJ 3512с под влиянием GJ 3512b. В частности, для орбиты с большой полуосью a2= = 1.3 а. е. (α = 0.26), незначительно превышающей минимальную, его характерные значения (по данным рис. 2 и 3) составляют, соответственно, е* ≈ 0.107 и еs ≈ 0.212.
Интересно не только само существование стационарной особой точки в плоской модели, но и ее трансформация для возможных в системе ненулевых орбитальных наклонений. Результаты выполненного с этой целью численного интегрирования эволюционной системы (8) приведены в табл. 2. В каждом из ее элементов представлены пары экстремальных на интервале времени 1 млн лет значений эксцентриситета emin, emax (верхние строки) и наклонения imin, imax (град, нижние строки) для заданных параметров α = 0.26, е1 = 0.4356 (А ≈ 0.018, В ≈ 0.0016). Начальные значения элементов орбиты гипотетического тела е0 = е* и ω0 = 0, а для ее пространственных угловых переменных принят ряд значений из диапазонов: 5°–45° по i0 и 0°–180° по Ω0.
Таблица 2.
Оценки экстремальных значений эксцентриситета и наклонения орбит в системе GJ 3512
| Ω0, град |
i0, град | |||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 15 | 30 | 45 | |||||
| 0 | 0.107 | 0.108 | 0.10 | 0.11 | 0.09 | 0.13 | 0.07 | 0.15 |
| 3.3 | 5.0 | 10.0 | 15.0 | 19.5 | 30.0 | 28.1 | 45.0 | |
| 30 | 0.05 | 0.16 | 0.05 | 0.17 | 0.05 | 0.17 | 0.04 | 0.18 |
| 3.8 | 5.8 | 11.4 | 17.4 | 22.5 | 35.1 | 32.6 | 54.4 | |
| 60 | 0.002 | 0.21 | 0.001 | 0.22 | 0.001 | 0.23 | 0.005 | 0.20 |
| 4.7 | 7.0 | 13.9 | 21.4 | 27.6 | 44.6 | 40.72 | 84.0 | |
| 90 | 0.04 | 0.26 | 0.03 | 0.26 | 0.01 | 0.28 | 0.008 | 0.26 |
| 5.00 | 7.6 | 14.9 | 23.1 | 29.8 | 49.4 | 44.5 | 135.5 | |
| 120 | 0.08 | 0.29 | 0.07 | 0.29 | 0.05 | 0.31 | 0.0 | 0.29 |
| 4.6 | 7.0 | 13.7 | 21.4 | 27.3 | 44.7 | 40.1 | 85.1 | |
| 150 | 0.10 | 0.31 | 0.10 | 0.32 | 0.09 | 0.33 | 0.08 | 0.37 |
| 3.7 | 5.8 | 11.2 | 17.5 | 22.0 | 35.3 | 31.8 | 4.8 | |
| 180 | 0.11 | 0.32 | 0.11 | 0.32 | 0.11 | 0.34 | 0.11 | 0.37 |
| 3.3 | 5.1 | 9.6 | 15.2 | 19.1 | 30.3 | 27.4 | 45.4 | |
Во всех представленных вариантах эксцентриситет орбит изменяется в ограниченных пределах, слабо зависящих от i0, и не превосходит величины примерно 0.4. Аргумент периастра изменяется вековым образом с частичным наложением периодических колебаний с периодами порядка сотен тысяч лет. Для небольших начальных наклонений циркуляционное изменение долготы узла сопровождается колебаниями наклонения в пределах 10°–15°.
При Ω0 = 90° и начальном наклонении 45° размах его колебаний составляет более 90° (выделено жирным шрифтом), а изменение долготы узла также носит колебательный характер. Для указанных выше ненулевых значений параметров А и В это обстоятельство согласуется с результатами работы (Зиглин, 1975), в которой, в частности, определена зависимость от е1 ширины зоны либрации наклонения $\Delta i = 2\arccos \sqrt {\frac{{1 - e_{1}^{2}}}{{1 + 4e_{1}^{2}}}} $ при А = В = 0. С принятым значением е1 ее полуширина Δi/2 = = 47°.3, а соответствующее предельное наклонение при Ω = 90°, когда долгота узла еще изменяется циркуляционным образом, составляет 90° – Δi/2 = 42°.7 < 45°. Именно поэтому эволюция орбит с Ω0 = 90° и начальным наклонением 45° (и бóльшим) происходит в режиме либрации обеих пространственных переменных i и Ω со значительным размахом колебаний наклонения с переходом через значение i = 90°. Это своего рода “флип”, но в рассматриваемом внешнем варианте эллиптической задачи (в отличие от внутреннего) такой переход не сопровождается приближением эксцентриситета к единице.
Представленные оценки диапазонов изменения орбитальных элементов дают лишь некоторые ориентиры для областей поиска возможных неизвестных объектов в системе GJ 3512. Но, конечно, надежность этих оценок могла бы быть повышена их получением в более реалистичной модели. С этой точки зрения будет полезно выполнить исследование неограниченной эллиптической двукратно осредненной задачи трех тел в принятом приближении по отношению к параметру α, причем как для внутреннего, так и для внешнего вариантов.
В заключение позволим себе один комментарий к упомянутой во Введении монографии. В связи с дополнительной информацией к первой версии монографии (Ito, Ohtsuka, 2019а, на стр. 183) и, следуя по Интернет-ссылке Supplementary Information is available from the publisher’s webpage до стр. S25, п. 7.3, находим утверждение “… it seems that there are no asteroids named after Nikolay Dmitriyevich Moiseev …”. Вместе с проф. Н.В. Емельяновым (ГАИШ МГУ) мы считаем своим долгом развеять необоснованное сомнение авторов монографии – астероид, названный в честь Н.Д. Моисеева, существует и имеет номер (3080) https://www.minorplanetcenter.net/db_search/show_ object?object_id=3080.
Список литературы
Аксенов Е.П. Двукратно осредненная эллиптическая ограниченная задача трех тел // Астрон. журн. 1979а. Т. 56. 2. С. 419–426 (Aksenov E.P. The doubly averaged, elliptical, restricted three-body problem // Sov. Astron. 1979a. 23(2). P. 236–240).
Аксенов Е.П. Траектории в двукратно-осредненной эллиптической ограниченной задаче трех тел // Астрон. журн. 1979б. 56. 3. С. 623–631 (Aksenov E.P. Trajectories in the doubly averaged, elliptical, restricted three-body problem // Sov. Astron. 1979b. 23(3). P. 351–355).
Вашковьяк М.А. Эволюция орбит в плоской ограниченной эллиптической двукратно осредненной задаче трех тел // Космич. исслед. 1982. Т. 20. Вып. 3. С. 332–341 (Vashkov’yak M.A. Evolution of orbits in the two-dimensional restricted elliptical twice-averaged three-body problem // Cosmic Research. 1982. V. 20. № 3. P. 236–244).
Вашковьяк М.А. Об интегрируемых случаях ограниченной двукратно осредненной задачи трех тел // Космич. исслед. 1984. Т. 22. Вып. 3. С. 327–334 (Vashkov’yak M.A. Integrable cases of the restricted twice-averaged three-body problem // Cosmic Research. 1984. V. 22. № 3. P. 260–267).
Вашковьяк М.А. Некоторые особенности эволюции орбит в спутниковой ограниченной эллиптической двукратно осредненной задаче трех тел // Астрон. вестн. 2020. Т. 54. № 1. С. 57–73 (Vashkov’yak M.A. Solar System Research. 2020. V. 54. № 1. P. 49–63.
Зиглин С.Л. О вековой эволюции орбиты планеты в системе двойной звезды // Письма в Астрон. журн. 1975. Т. 1. № 9. С. 45–47 (Ziglin S.L. Secular evolution of the orbit of a planet in a binary-star system. Sov. Astron. Lett. 1975. V. 1. № 5. Sept.–Oct. P. 194–195).
Лидов М.Л. Эволюция орбит искусственных спутников планет под действием гравитационных возмущений внешних тел // Искусственные спутники Земли. 1961. Вып. 8. С. 5–45.
Моисеев Н.Д. О некоторых основных упрощенных схемах небесной механики, получаемых при помощи осреднения ограниченной круговой проблемы трех точек. 2. Об осредненных вариантах пространственной ограниченной круговой проблемы трех точек // Тр. Гос. Астрон. Ин-та им. П.К. Штернберга. 1945. Т. 15. Вып. 1 С. 100–117.
Bailey M.E., Emel’yanenko V.V. Dynamical evolution of Halley-type comets // Mon. Notic. Roy. Astron. Soc. 1996. 278. P. 1087–1110.
de Elía G.C., Zanardi M., Dugaro A., Naoz S. The inverse Lidov-Kozai resonance for an outer test particle due to an eccentric perturber. 2019. arXiv:1904.12062v1 [astro-ph.EP] (Astron. and Astrophys. 2019. V. 627. P. 15).
Ito T. High-Order Analytic Expansion of Disturbing Function for Doubly Averaged Circular Restricted Three-Body Problem // Adv. Astron. V. Hindawi Publish. Corp. 2016. 23 p.
Ito T., Ohtsuka K. The Lidov-Kozai oscillation and Hugo von Zeipel // Environ. Earth Planets. Suppl. Information. 2019a. P. S1–S26. arXiv:1911.03984v1[astro-ph.EP] 10 Nov2019. P. 1–183.
Ito T., Ohtsuka K. The Lidov-Kozai oscillation and Hugo von Zeipel // Environ. Earth Planets. 2019b. V. 7. № 1. P. 1–113. https://doi.org/10.5047/meep.2019.00701.0001
Kozai Y. Secular perturbations of asteroids with high inclination and eccentricity // Astron. J. 1962. V. 67. P. 591–598.
Lidov M.L. The evolution of orbits of artificial satellites of planets under the action of gravitational perturbations of external bodies // Planet. and Space Sci. 1962. № 9. P. 719–759.
Lidov M.L., Ziglin S.L. The analysis of restricted circular twice-averaged three body problem in the case of close orbits // Celest. Mech. 1974. V. 10. № 2. P. 151.
Morales J.C., Mustill A.J., Ribas I. (список всех авторов и аффиляций см. https://science.sciencemag.org/content/365/6460/1441?intcmp=trendmd-sci. A giant exoplanet orbiting a very-low-mass star challenges planet formation models // Science. 2019. V. 365. Is. 6460. P. 1441–1445. https://arxiv.org/ftp/arxiv/papers/1909/1909.12174.pdf
Naoz S., Li G., Zanardi M., de Elía G.C., Di Sisto R.P. The eccentric Kozai–Lidov mechanism for outer test particle // Astron. J. 2017. V. 154. P. 18. https://doi.org/10.3847/1538-3881/aa6fb0
Neishtadt A.I., Sheng K., Sidorenko V.V. On stability of planar solution of double averaged restricted elliptic three-body problem. arXiv:1803.08847v2 [math.DS] 4 Apr 2018. 7 pp.
Vinson B.R., Chiang E. Secular dynamics of an exterior test particle: The inverse Kozai and other eccentricity-inclination resonances // Mon. Notic. Roy. Astron. Soc. 2018. V. 474. Iss. 4. P. 4855–4869.
von Zeipel H. Sur l’application des séries de M. Lindstedt à l′etude du mouvement des comètes périodiques // Astron. Nachr. 1910. V. 183. P. 345–418. https://doi.org/10.1002/asna.19091832202 ]. A full-text open access PDF file is available from ADS, https://ui.adsabs.harvard.edu/abs/1910AN….183..345V
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник