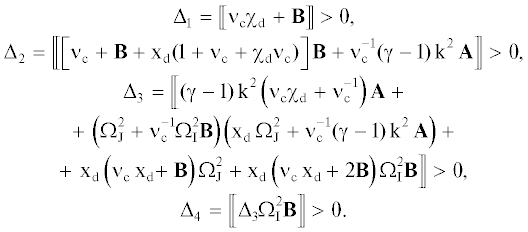Астрономический вестник, 2022, T. 56, № 6, стр. 427-441
Влияние черного излучения на критерий гравитационной неустойчивости Джинса в околозвездном плазменном диске при учете неизоэнтропических эффектов
А. В. Колесниченко *
Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия
* E-mail: kolesn@keldysh.ru
Поступила в редакцию 26.01.2022
После доработки 27.02.2022
Принята к публикации 04.04.2022
- EDN: NLYWQH
- DOI: 10.31857/S0320930X22050036
Аннотация
В рамках проблемы моделирования эволюции околозвездного газопылевого облака обсуждается влияние черного излучения на джинсовскую магнито-гравитационную неустойчивость для самогравитирующего намагниченного плазменного диска, с учетом эффектов воздействия вращения, крупномасштабного магнитного поля, диссипативных процессов магнитной вязкости и лучевого теплопереноса. С использованием анализа нормального режима выведено общее дисперсионное соотношение. На его основе получены модифицированные критерии джинсовской неустойчивости для ряда частных случаев, связанных с различными относительными ориентациями магнитного поля, оси вращения и вектора распространения волны возмущения. Условие гравитационной устойчивости системы обсуждается с использованием критерия Рауса−Гурвица. Показано, что в случае как продольного, так и поперечного направления распространения волны возмущения критерии нестабильности Джинса существенно модифицируются за счет лучевых теплопотерь и стоксовой коррекции. Полученные результаты позволяют, в частности, лучше понять проблему, связанную с эволюцией околозвездных плазменных дисков.
ВВЕДЕНИЕ
Заключительным этапом эволюции маломассивного протозвездного объекта является звезда типа T Tau, окруженная газопылевым диском. Изучение этих дисков вызывает особый интерес, поскольку в них, по современным представлениям, происходит образование планетных систем, подобных Солнечной системе. При этом критерии магнито-гравитационной неустойчивости во вращающемся горячем газе (плазме) имеют ключевое значение в понимании процессов эволюции подобных околозвездных дисков. Именно гравитационная неустойчивость Джинса играет главную роль в процессе фрагментации дискового вещества. В частности, экзопланетные диски формируются из самогравитирующих околозвездных дисков в результате потери ими гравитационной устойчивости. Однако полной ясности в том, какие физико-механические свойства звездной системы доминируют при их формировании, до сих пор нет. Большинство обнаруженных на сегодня экзопланетных дисков вокруг галактических звезд заметно отличаются от протопланетного диска Солнца. По этой причине теория, которая используется для описания эволюции Солнечной системы, является, по-видимому, одной из многих, и для адекватного моделирования эволюции экзопланетных дисков она должна быть частично видоизменена и дополнена.
Классическая теория гравитационной неустойчивости Джинса предполагает, что среда однородна и изотропна и характеризуется баротропным уравнением состояния (Jeans, 1902). Существенное усовершенствование этой теории при учете различных предположений о вращении системы и магнитном поле было выполнено Чандрасекхаром (Chandrasekhar, 1961). В дальнейшем многочисленные исследователи обсуждали гравитационную неустойчивость в линейном и нелинейном приближениях для вращающихся газа и плазмы в разных аспектах относительной ориентации магнитного поля, оси вращения и вектора распространения волны возмущения, а также с учетом влияния разнообразных физических процессов и явлений (см., например, Bhatia, 1967; Aggarwal, Talwar, 1969; Sharma, 1974; Михайловский, 1977; Fridman, Polyachenko, 1984; Sharma, Singh, 1988; Bora, Nayyar, 1991; Bora, Talwar, 1993; Хоперсков, Храпов, 1999; Jacobs, Shukla, 2005; Borah, Sen, 2007; Shaikh и др., 2007; 2008; Prajapati и др., 2010; Dhiman, Dadwal, 2010; 2011; 2012; Фридман, Хоперсков, 2011; Kaothekar, Chhajlani, 2012; Prajapati и др., 2012; Argal и др., 2014; Jain и др., 2015; Kaothekar, 2016; Joshi, Pensia, 2017; Kumar и др., 2017; Pensia и др., 2018; Колесниченко, 2020).
Существует также относительно небольшое число работ, в которых при различных предположениях относительно направления магнитного поля и режимов распространения волны возмущения было исследовано влияние взвешенных частиц и процессов теплопроводности на магнито-гравитационную нестабильность вращающейся плазмы (см., например, Chhajlani, Vaghela, 1987; Tsintsadze и др., 2008; Prajapati, Chhajlani, 2011; Prajapati, Bhakta, 2015; Sharma, Patidar, 2017; Kumar и др., 2018; Dolai, Prajapati, 2018). Во всех перечисленных публикациях показано, что критерий неустойчивости Джинса сохраняется с некоторыми модификациями, связанными с учетом различных параметров.
И совсем немного на сегодняшний день имеется в литературе работ, в которых исследуется неустойчивость самогравитирующих астрофизических объектовв приближении чернотельного излучения (см., например, Vranješ, Čadež, 1990; Vranješ, 1990; Vaghela, Shrivastava, 1994; Prajapati, Chhajlani, 2011; Kumar и др., 2017; Kolesnichenko, 2020; 2021). Обычно, температура газа в околозвездных дисках растет с приближением к аккрецирующему объекту. С ростом температуры увеличивается значимость давления излучения в эволюции диска по сравнению с газовым давлением. Впервые анализ устойчивости дисковой аккреции на черную дыру звездной массы относительно возмущений с учетом давления излучения был поставлен в работах (Lightman, 1974; Lightman, Eardley, 1974). Подробный анализ устойчивости относительно осесимметричных возмущений с учетом давления излучения был проведен Шакурой и Сюняевым в работе (Shakura, Sunyaev, 1976), в которой моделирование эволюции диска разбивается на несколько областей, в которых преимущественную роль играет то, или иное давление (${{P}_{g}}$ или ${{P}_{r}}$), а поток излучения может быть представлен (если исключить из рассмотрения внешние области плазменного диска, близкие к поверхности) в диффузионном приближении. В ряде последующих немногочисленных работ также рассматривалась гравитационная неустойчивость аккреционных дисков с излучением при учете тепловой, вязкой и акустической мод, а также некоторых других физических процессов (см., например, Фридман, Хоперсков, 2011; Хоперсков, Храпов, 1999).
Вместе с тем, почти во всех цитируемых выше работах по неустойчивости радиационно-доминирующей области диска рассматривались только изоэнтропические волновые возмущения, при которых энтропия каждого элемента массы на всем его пути сохраняется. В этом случае мелкомасштабные эйлеровы вариации давления ${{P{\kern 1pt} {\kern 1pt} '} \mathord{\left/ {\vphantom {{P{\kern 1pt} {\kern 1pt} '} P}} \right. \kern-0em} P}$, плотности ${{\rho {\kern 1pt} {\kern 1pt} '} \mathord{\left/ {\vphantom {{\rho {\kern 1pt} {\kern 1pt} '} \rho }} \right. \kern-0em} \rho }$ и температуры ${{T{\kern 1pt} {\kern 1pt} '} \mathord{\left/ {\vphantom {{T{\kern 1pt} {\kern 1pt} '} T}} \right. \kern-0em} T}$ в линеаризованном уравнении сохранения энергии определялись, как правило, на основе известных адиабатических соотношений Эддингтона−Чандрасекхара (см. Тассуль, 1982). И хотя для большинства астрофизических приложений эти соотношения представляют собой достаточно разумное приближение, во многих более реалистических ситуациях необходимо учитывать отклонение от изоэнтропичности, при которой элементы массы приобретают или теряют тепло (например, в звездах верхней части главной последовательности, в которых давление излучения преобладает над газовым давлением). В этом случае относительно простые адиабатические соотношения Эддингтона−Чандрасекхара (см. Тассуль, 1982) более не применимы и следует использовать другие соотношения (Cox, Giuli, 1968; Ch 9), усложненные за счет учета вектора потока энергии, обусловленного всеми возможными механизмами переноса (излучение, теплопроводность, конвекция, нейтринные потери, потеря массы и т.п.). Как уже говорилось выше, вопрос о неустойчивости самогравитирующего плазменного облака, с учетом чернотельного излучения в неизоэнтропическом случае почти не обсуждался в литературе. Насколько известно автору, только в двух публикациях (Kaneko и др., 2005; Kaneko, Morita, 2006) методом радиационной акустики Уитхема (см. Cogley, Vincent, 1969) было исследовано распространение одномерных малоамплитудных возмущений в излучающей и рассеивающей серой среде совершенного газа с учетом лучистых теплопотерь.
В связи с этим представляется вполне оправданным появление работ, целью которых является детальное исследование того, как классический критерий гравитационной неустойчивости Джинса во вращающейся пылевой намагниченной плазме модифицируется для астрофизических оптически тонких11 дисков в случае неизоэнтропичности возмущений совокупных параметров вещества и черного излучения при наличии динамически значимого давления излучения, лучистой вязкости и теплопроводности, а также крупномасштабных магнитных полей и турбулентности.
БАЗИСНАЯ СИСТЕМА УРАВНЕНИЙ ДЛЯ НАМАГНИЧЕННОЙ ИЗЛУЧАЮЩЕЙ ПЫЛЕВОЙ ПЛАЗМЫ
В представленной работе мы обсудим в рамках предельно простой модели проблему влияния силы Кориолиса, однородного магнитного поля и чернотельного излучения на динамическую неустойчивость самогравитирующего околозвездного диска, вещество которого, являющееся смесью пылевой плазмы и черного излучения, вращается вокруг фиксированной в пространстве оси с некоторой постоянной угловой скоростью ${\mathbf{\Omega }}.$ Далее будем предполагать, что пылевая фаза в каждом элементарном объеме присутствует в виде сферических включений одинакового радиуса $r$, причем объемная концентрация дисперсной фазы $\alpha = ({4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3})\pi {{r}^{3}}n$ не очень велика. По этой причине можно пренебречь силовым взаимодействием (в частности, столкновениями) между пылевыми частицами. Будем также предполагать, что плазменное облако в значительной мере обладает осевой симметрией, что является следствием его вращения вокруг центральной звезды. Исходная система уравнений для химически однородной облачной среды, записанная при отсутствии некоторых диссипативных эффектов, состоит в этом случае из уравнений звездной гидродинамики, уравнения Пуассона и уравнения магнитной индукции, которые имеют следующий вид:
(2)
$\begin{gathered} \rho \left\{ {\frac{{\partial {\kern 1pt} {\mathbf{u}}}}{{\partial t}} + ({\mathbf{u}} \cdot \nabla ){\mathbf{u}}} \right\} = - \nabla P + \nabla \cdot {{{\mathbf{\tau }}}_{\Sigma }} + \\ + \,\,{\mathbf{j}} \times {\mathbf{H}} + \rho \nabla \Phi + {{\rho }_{\operatorname{d} }}{{\nu }_{\operatorname{c} }}({{{\mathbf{u}}}_{\operatorname{d} }} - {\mathbf{u}}), \\ \end{gathered} $(3)
${{\rho }_{\operatorname{d} }}\left( {\frac{{\partial {\kern 1pt} {{{\mathbf{u}}}_{\operatorname{d} }}}}{{\partial t}} + ({\mathbf{u}} \cdot \nabla ){{{\mathbf{u}}}_{\operatorname{d} }}} \right) = {{\rho }_{\operatorname{d} }}{{\nu }_{\operatorname{c} }}({\mathbf{u}} - {{{\mathbf{u}}}_{\operatorname{d} }}),$(4)
$\rho \left\{ {\frac{{\partial E{\mathbf{e}}}}{{\partial t}} + {\mathbf{u}} \cdot \nabla E} \right\} + P\nabla \cdot {\mathbf{u}} = - \nabla \cdot ({{{\mathbf{J}}}_{g}} + {{{\mathbf{J}}}_{r}}),$(5)
${{\partial {\kern 1pt} {\mathbf{H}}} \mathord{\left/ {\vphantom {{\partial {\kern 1pt} {\mathbf{H}}} {\partial t}}} \right. \kern-0em} {\partial t}} = \nabla \times ({\mathbf{u}} \times {\mathbf{H}}),\,\,\,\,\nabla \cdot {\mathbf{H}} = 0{\text{,}}$(7)
$P(\rho ,T): = {{P}_{{{\text{gas}}}}} + {{P}_{{{\text{rad}}}}} \equiv {{P}_{{{\text{gas}}}}} + {{a{{T}^{4}}} \mathord{\left/ {\vphantom {{a{{T}^{4}}} {3,}}} \right. \kern-0em} {3,}}$(8)
$E(\rho ,T) = {{e}_{{{\text{gas}}}}} + {{e}_{{{\text{rad}}}}} \equiv {{e}_{{{\text{gas}}}}} + {{a{{T}^{4}}} \mathord{\left/ {\vphantom {{a{{T}^{4}}} \rho }} \right. \kern-0em} \rho }$Дивергенция $\nabla \cdot ({{{\mathbf{J}}}_{{{\text{gas}}}}} + {{{\mathbf{J}}}_{{{\text{rad}}}}})$ в уравнении (4) описывает приток тепла от соседних элементов плазменного облака. Далее считается, что Jgas = $ = - {{\lambda }_{{{\text{gas}}}}}\nabla T,$ где ${{\lambda }_{{{\text{g}}{\kern 1pt} {\text{as}}}}}$ − коэффициент теплопроводности, являющийся мерой необратимого переноса тепловой энергии между частицами плазмы от областей облака, температура которых выше, к областям с более низкой температурой. Если исключить из рассмотрения внешние области плазменного диска, близкие к поверхности, то вектор потока излучения также может быть записан в диффузионном приближении в виде:
(9)
${{{\mathbf{J}}}_{{{\text{rad}}}}} = - {{\lambda }_{{{\text{rad}}}}}\nabla T,\,\,\,\,{{\lambda }_{{{\text{rad}}}}} = {4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}({{ac} \mathord{\left/ {\vphantom {{ac} {\kappa \rho }}} \right. \kern-0em} {\kappa \rho }}){{T}^{3}},$При написании системы уравнений (1)−(6) были сделаны часто используемые в астрофизической литературе предположения. В частности, не учитывались токи смещения и предполагалось, что магнитная проницаемость плазменного вещества равна единице. В уравнении магнитной индукции (6) не учитывалась диффузия магнитного поля, поскольку для больших астрофизических масс крупномасштабное магнитное поле очень медленно просачивается сквозь вещество (т.е. далее рассматривается идеально проводящая среда с нулевой магнитной вязкостью, ${{\nu }_{H}} = 0$). По этой же причине в законе сохранения тепловой энергии (4) опущен член уравнения $({{{{\nu }_{H}}} \mathord{\left/ {\vphantom {{{{\nu }_{H}}} {4\pi }}} \right. \kern-0em} {4\pi }}){{\left| {\nabla \times {\mathbf{H}}} \right|}^{2}}$. Кроме этого, в энергетическом уравнении (4) не учитывался внутренний нагрев плазменного облака, описываемый так называемой диссипативной функцией ${{\Phi }_{v}}: = {{{{\tau }_{{ij}}}{{\tau }_{{ij}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{ij}}}{{\tau }_{{ij}}}} {2{{\mu }_{\Sigma }},}}} \right. \kern-0em} {2{{\mu }_{\Sigma }},}}$ которая пропорциональна полному коэффициенту сдвиговой вязкости
(10)
$\begin{gathered} {{\mu }_{\Sigma }}: = {{\mu }_{{{\text{gas}}}}} + {{\mu }_{{{\text{rad}}}}} = \\ = ({2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-0em} 5}){{m}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{{{{({{k}_{\operatorname{B} }}T)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}} \mathord{\left/ {\vphantom {{{{{({{k}_{\operatorname{B} }}T)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}} {({{e}^{4}}\ln \Lambda )}}} \right. \kern-0em} {({{e}^{4}}\ln \Lambda )}} + ({4 \mathord{\left/ {\vphantom {4 {15}}} \right. \kern-0em} {15}}){{a{{T}^{4}}} \mathord{\left/ {\vphantom {{a{{T}^{4}}} {(c\kappa \rho ),}}} \right. \kern-0em} {(c\kappa \rho ),}} \\ \end{gathered} $Изоэнтропические процессы в среде, содержащей газ и излучение
Уравнение баланса полной внутренней энергии излучающей плазмы (4) удобно переписать, используя уравнение неразрывности (1), в форме первого начала термодинамики (тождества Гиббса)22
(11)
$\begin{gathered} {{dE} \mathord{\left/ {\vphantom {{dE} {dt}}} \right. \kern-0em} {dt}} + Pd{{({1 \mathord{\left/ {\vphantom {1 \rho }} \right. \kern-0em} \rho })} \mathord{\left/ {\vphantom {{({1 \mathord{\left/ {\vphantom {1 \rho }} \right. \kern-0em} \rho })} {dt}}} \right. \kern-0em} {dt}} = {{dQ} \mathord{\left/ {\vphantom {{dQ} {dt}}} \right. \kern-0em} {dt}} = {{TdS} \mathord{\left/ {\vphantom {{TdS} {dt,}}} \right. \kern-0em} {dt,}} \\ \left( {{d \mathord{\left/ {\vphantom {d {dt}}} \right. \kern-0em} {dt}}: = {\partial \mathord{\left/ {\vphantom {\partial {\partial t}}} \right. \kern-0em} {\partial t}} + {\mathbf{u}} \cdot \nabla } \right), \\ \end{gathered} $Для адиабатического (изоэнтропического) движения дивергенция $\nabla \cdot ({{{\mathbf{J}}}_{{{\text{gas}}}}} + {{{\mathbf{J}}}_{{{\text{rad}}}}})$ равна нулю во всех точках, т.е. теплота не течет через поверхность внутри жидкой среды. В этом случае уравнение энергии (11) принимает вид
(12)
${{\rho dE} \mathord{\left/ {\vphantom {{\rho dE} {dt}}} \right. \kern-0em} {dt}} - ({P \mathord{\left/ {\vphantom {P \rho }} \right. \kern-0em} \rho }){{d\rho } \mathord{\left/ {\vphantom {{d\rho } {dt}}} \right. \kern-0em} {dt}} = 0,$(13)
$\frac{d}{{d{\kern 1pt} t}}\ln P = {{\Gamma }_{1}}\frac{d}{{d{\kern 1pt} t}}\ln \rho ,\,\,\,\,\frac{d}{{dt}}\ln T = ({{\Gamma }_{3}} - 1)\frac{d}{{dt}}\ln \rho ,$(14)
$\begin{gathered} {{\Gamma }_{1}}: = {{\left( {\frac{{\partial {\kern 1pt} \ln {\kern 1pt} P}}{{\partial {\kern 1pt} \ln {\kern 1pt} \rho }}} \right)}_{{{\text{ad}}}}} = \beta + \frac{{{{{(4 - 3\beta )}}^{2}}(\gamma - 1)}}{{\beta + 12(\gamma - 1)(1 - \beta )}}, \\ {{\Gamma }_{3}} - 1: = {{\left( {\frac{{\partial {\kern 1pt} \ln {\kern 1pt} T}}{{\partial {\kern 1pt} \ln {\kern 1pt} \rho }}} \right)}_{{{\text{a}}{\kern 1pt} {\text{d}}}}} = \frac{{(4 - 3\beta )(\gamma - 1)}}{{\beta + 12(\gamma - 1)(1 - \beta )}} = \frac{{{{\Gamma }_{1}} - \beta }}{{4 - 3\beta }}. \\ \end{gathered} $Если ${{P}_{{{\text{gas}}}}} \gg {{P}_{{{\text{rad}}}}}$, то $\beta \simeq 1$ и все обобщенные показатели адиабаты для смеси “плазма + излучение” совпадают с показателем адиабаты идеального газа ${{\Gamma }_{1}} = {{\Gamma }_{3}} = \gamma ,$ а когда присутствует одно лишь излучение абсолютно черного тела (${{P}_{{{\text{gas}}}}} \ll {{P}_{{{\text{rad}}}}}$), то они равны 4/3. Таким образом, для рассматриваемой астрофизической системы обобщенные показатели адиабаты принимают промежуточные значения от 4/3 до 5/3.
Неизоэнтропические процессы в излучающей среде
Далее будет исследована гравитационная неустойчивость вращающегося с постоянной угловой скоростью околозвездного облака с учетом лучевого давления и крупномасштабного магнитного поля в более общем случае неизоэнтропических возмущений параметров состояния, связанных с лучевым переносом тепла (в диффузионном приближении) и магнитной вязкостью. В этом случае вместо уравнений (13) нужно использовать другие формы энергетического уравнения (4) (см., например, Cox, 1979)
(15)
$\frac{d}{{dt}}\ln {\kern 1pt} P = \left\{ {\begin{array}{*{20}{c}} {{{{{\Gamma }_{1}}d{\kern 1pt} \ln {\kern 1pt} \rho } \mathord{\left/ {\vphantom {{{{\Gamma }_{1}}d{\kern 1pt} \ln {\kern 1pt} \rho } {dt}}} \right. \kern-0em} {dt}} + ({{\Gamma }_{3}} - 1){{P}^{{ - 1}}}\rho \frac{{dQ}}{{dt}},\quad (a)} \\ {{{{{\Gamma }_{1}}d{\kern 1pt} \ln {\kern 1pt} {\kern 1pt} \rho } \mathord{\left/ {\vphantom {{{{\Gamma }_{1}}d{\kern 1pt} \ln {\kern 1pt} {\kern 1pt} \rho } {dt}}} \right. \kern-0em} {dt}} + ({{{{\chi }_{T}}} \mathord{\left/ {\vphantom {{{{\chi }_{T}}} {{{C}_{V}}T}}} \right. \kern-0em} {{{C}_{V}}T}})\frac{{dQ}}{{dt}},\quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (b)} \end{array}} \right.$(16)
$\begin{gathered} \frac{d}{{dt}}\ln {\kern 1pt} T = \\ = \left\{ \begin{gathered} ({{\Gamma }_{3}} - 1){{d\ln {\kern 1pt} \rho } \mathord{\left/ {\vphantom {{d\ln {\kern 1pt} \rho } {dt}}} \right. \kern-0em} {dt}} + ({1 \mathord{\left/ {\vphantom {1 {{{C}_{{V\Sigma }}}\rho T}}} \right. \kern-0em} {{{C}_{{V\Sigma }}}\rho T}})\frac{{dQ}}{{dt}},\quad \quad {\kern 1pt} (a) \hfill \\ \left[ {{{({{\Gamma }_{3}} - 1)} \mathord{\left/ {\vphantom {{({{\Gamma }_{3}} - 1)} {{{\Gamma }_{1}}}}} \right. \kern-0em} {{{\Gamma }_{1}}}}} \right]{{d\ln {\kern 1pt} P} \mathord{\left/ {\vphantom {{d\ln {\kern 1pt} P} {dt}}} \right. \kern-0em} {dt}} + ({1 \mathord{\left/ {\vphantom {1 {{{C}_{{P\Sigma }}}T}}} \right. \kern-0em} {{{C}_{{P\Sigma }}}T}})\frac{{dQ}}{{dt}}.\quad (b) \hfill \\ \end{gathered} \right. \\ \end{gathered} $ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ
Для изучения мелкомасштабных возмущений линеаризуем систему уравнений (1)−(6) представим магнитогидродинамические переменные в виде сумм невозмущенных ${{\rho }_{0}},{{T}_{0}},{{P}_{0}}$${\mathbf{u}}{{{\kern 1pt} }_{0}}$,${\mathbf{u}}{{{\kern 1pt} }_{{\operatorname{d} 0}}}$, ${{{\mathbf{H}}}_{0}}$, ${{\Phi }_{0}}$ и возмущенных $\rho {\kern 1pt} {\kern 1pt} ',T{\kern 1pt} ',P{\kern 1pt} {\kern 1pt} '$, ${\mathbf{u}}{\kern 1pt} '$, ${\mathbf{u}}_{{\text{d}}}^{{\text{'}}}$, ${\mathbf{H}}{\kern 1pt} '$, $\Phi {\kern 1pt} '$33 величин. Невозмущенные величины описывают по предположению некоторое равновесное состояние плазменного облака, а возмущенные − суть малые возмущения параметров, слабо нарушающие невозмущенное состояние. При этом будем считать, что невозмущенное состояние соответствует равновесному состоянию однородного диска с ${{{\mathbf{u}}}_{0}} = 0$, ${\mathbf{u}}{{{\kern 1pt} }_{{\operatorname{d} 0}}}\, = 0$ ${{{\mathbf{H}}}_{0}} = \operatorname{H} {{{\mathbf{i}}}_{z}}$ и используем так называемое “мошенничество” Джинса ${{\Phi }_{0}} \cong 0$,44 согласно которому уравнение Пуассона (6) применяется лишь к возмущениям плотности. Кроме этого будем, для простоты, предполагать, что характерная длина волны возмущения мала по сравнению с характерным размером изменения параметров ${{P}_{0}}$, ${{T}_{0}}$, ${{\rho }_{0}}$ и с некоторыми другими характерными длинами задачи (т.е. ограничимся так называемым приближением коротковолновой акустики); тогда в линеаризованных уравнениях можно пренебречь пространственными производными для этих величин. Далее индекс “0” у невозмущенных величин будем опускать.
С учетом сделанных упрощающих предположений дифференциальные уравнения (1)−(6), при выполнении необходимых разложений и удержании только членов первого порядка относительно малых возмущений, принимают следующий линеаризованный вид (здесь энергетическое уравнение (3) записано в форме (15а)):
(17)
$\frac{{\partial \rho {\kern 1pt} '}}{{\partial t}} + \rho \nabla \cdot {\mathbf{u}}{\kern 1pt} ' = 0,$(18)
$\begin{gathered} \rho \frac{{\partial {\kern 1pt} {\mathbf{u}}{\kern 1pt} '}}{{\partial t}} = - \nabla P{\kern 1pt} '\,\, + \nabla \cdot {\mathbf{\tau }}_{\Sigma }^{'} + \frac{1}{{4\pi }}(\nabla \times {\mathbf{H}}{\kern 1pt} ') \times {\mathbf{H}} + \\ + \,\,\rho \nabla \Phi {\kern 1pt} '\,\, + {{\rho }_{\operatorname{d} }}{{\nu }_{c}}({\mathbf{u}}_{\operatorname{d} }^{'} - {\mathbf{u}}{\kern 1pt} '), \\ \end{gathered} $(19)
$\frac{{\partial {\mathbf{u}}_{\operatorname{d} }^{{\text{'}}}}}{{\partial t}} = - {{\nu }_{c}}({\mathbf{u}}_{\operatorname{d} }^{{\text{'}}} - {\mathbf{u}}{\kern 1pt} '),$(20)
$\frac{{\partial P{\kern 1pt} '}}{{\partial t}} = {{\Gamma }_{1}}\frac{P}{\rho }\frac{{\partial \rho {\kern 1pt} '}}{{\partial t}} + ({{\Gamma }_{3}} - 1){{\lambda }_{\Sigma }}{{\nabla }^{2}}T{\kern 1pt} ',$(21)
$\frac{{\partial {\mathbf{H}}{\kern 1pt} '}}{{\partial t}} = \nabla \times ({\mathbf{u}}{\kern 1pt} '\,\, \times {\mathbf{H}}),\,\,\,\,\nabla \cdot {\mathbf{H}}{\kern 1pt} ' = 0,$(23)
$\begin{gathered} \tau _{{\Sigma xx}}^{'} = - {{\mu }_{\Sigma }}\left( {\frac{{\partial u_{y}^{'}}}{{\partial x}} + \frac{{\partial u_{x}^{'}}}{{\partial y}}} \right),\,\,\,\,{{{\tau '}}_{{\Sigma yy}}} = {{\mu }_{\Sigma }}\left( {\frac{{\partial u_{y}^{'}}}{{\partial x}} + \frac{{\partial u_{x}^{'}}}{{\partial y}}} \right), \\ \tau _{{\Sigma xy}}^{'} = \tau _{{\Sigma yx}}^{'} = {{\mu }_{\Sigma }}\left( {\frac{{\partial u_{x}^{'}}}{{\partial x}} - \frac{{\partial u_{y}^{'}}}{{\partial y}}} \right), \\ \tau _{{\Sigma xz}}^{'} = \tau _{{\Sigma zx}}^{'} = - 2{{\mu }_{\Sigma }}\left( {\frac{{\partial u_{y}^{'}}}{{\partial z}} + \frac{{\partial u_{z}^{'}}}{{\partial y}}} \right), \\ \tau _{{\Sigma yz}}^{'} = \tau _{{\Sigma zy}}^{'} = 2{{\mu }_{\Sigma }}\left( {\frac{{\partial u_{z}^{'}}}{{\partial x}} + \frac{{\partial u_{x}^{'}}}{{\partial z}}} \right),\,\,\,\,\tau _{{\Sigma zz}}^{'} = 0. \\ \end{gathered} $(24)
$\begin{gathered} P{\kern 1pt} ' = ({\mathcal{R} \mathord{\left/ {\vphantom {\mathcal{R} {\bar {\mu }}}} \right. \kern-0em} {\bar {\mu }}})T\rho {\kern 1pt} '\,\, + \left\{ {({\mathcal{R} \mathord{\left/ {\vphantom {\mathcal{R} {\bar {\mu }}}} \right. \kern-0em} {\bar {\mu }}})\rho + \frac{4}{3}a{{T}^{3}}} \right\}T{\kern 1pt} ' = \\ = \beta P\left\{ {\frac{{\rho {\kern 1pt} '}}{\rho } + \frac{{(4 - 3\beta )}}{\beta }\frac{{T{\kern 1pt} '}}{T}} \right\}. \\ \end{gathered} $Комбинируя записанное для возмущений уравнение (20) и соотношение (24), получим ключевую для дальнейшего связь между пульсациями полного давления $P{\kern 1pt} '$ и объемной плотности среды $\rho {\kern 1pt} '$:
(25)
$P{\kern 1pt} {\kern 1pt} ' = \left[ {{{\left( {\omega c_{{({\text{gas}},{\text{rad}})}}^{2} + {\mathbf{A}}} \right)} \mathord{\left/ {\vphantom {{\left( {\omega c_{{({\text{gas}},{\text{rad}})}}^{2} + {\mathbf{A}}} \right)} {\left( {\omega + {\mathbf{B}}} \right)}}} \right. \kern-0em} {\left( {\omega + {\mathbf{B}}} \right)}}} \right]\rho {\kern 1pt} '.$(26)
$\begin{gathered} {\mathbf{A}}: = ({{\Gamma }_{3}} - 1){\kern 1pt} \beta \frac{{{{\lambda }_{\Sigma }}T}}{{\rho (4 - 3\beta )}}{{{\mathbf{k}}}^{2}}, \\ {\mathbf{B}}: = ({{\Gamma }_{3}} - 1)\frac{{{{\lambda }_{\Sigma }}T}}{{P(4 - 3\beta )}}{{{\mathbf{k}}}^{2}}, \\ c_{{({\text{gas}},{\text{rad)}}}}^{{}}: = \sqrt {\frac{\operatorname{P} }{\rho }{{\Gamma }_{1}}} = \\ = \sqrt {({\mathcal{R} \mathord{\left/ {\vphantom {\mathcal{R} {\bar {\mu }}}} \right. \kern-0em} {\bar {\mu }}})T\left[ {1 + \frac{{{{{(4 - 3\beta )}}^{2}}(\gamma - 1)}}{{\beta \left[ {\beta + 12(\gamma - 1)(1 - \beta )} \right]}}} \right]} {\kern 1pt} , \\ \end{gathered} $Фурье-гармоники возмущений магнитного поля получим, используя линеаризованные уравнения (21); в результате будем иметь
(27)
$\begin{gathered} \omega {\kern 1pt} Н_{x}^{'}\,\, - i\operatorname{H} {{\operatorname{k} }_{\parallel }}u_{x}^{'} = 0,\,\,\,\,\omega Н_{y}^{'}\,\, - i\operatorname{H} {{\operatorname{k} }_{\parallel }}u_{y}^{'} = 0, \\ \omega Н_{z}^{'}\,\, - i\operatorname{H} {{\operatorname{k} }_{ \bot }}{{{u'}}_{x}} = 0,\,\,\,\,\operatorname{H} _{x}^{'}{{\operatorname{k} }_{ \bot }}\,\, + \operatorname{H} _{z}^{'}{{\operatorname{k} }_{\parallel }} = 0. \\ \end{gathered} $Из уравнений (17) и (21) следуют еще два соотношения для фурье-гармоник возмущений скорости и плотности
(28)
$\omega \rho {\kern 1pt} '\,\, + i\rho ({{\operatorname{k} }_{ \bot }}u_{x}^{'} + {{\operatorname{k} }_{\parallel }}u_{y}^{'}) = 0,\,\,\,\,{{{\mathbf{k}}}^{2}}{\kern 1pt} \Phi {\kern 1pt} ' = 4\pi G\rho {\kern 1pt} '.$(29)
$\begin{gathered} \left( {{\mathbf{C}} + \frac{{{{{\mathbf{k}}}^{2}}c_{\operatorname{A} }^{2}}}{\omega }} \right)u_{x}^{'} + \left[ {{{\nu }_{\Sigma }}\left( {{{{\mathbf{k}}}^{2}} + \operatorname{k} _{\parallel }^{2}} \right) - 2{{\Omega }_{\parallel }}} \right]u_{y}^{'} + \\ + \,\,i\frac{{{{\operatorname{k} }_{ \bot }}}}{{{{{\mathbf{k}}}^{2}}}}\Omega _{\operatorname{T} }^{2}\left( {\frac{{\rho {\kern 1pt} '}}{\rho }} \right) = 0, \\ \end{gathered} $(30)
$\begin{gathered} \left[ {2{{\Omega }_{\parallel }} - {{\nu }_{\Sigma }}\left( {{{{\mathbf{k}}}^{2}} + \operatorname{k} _{\parallel }^{2}} \right)} \right]u_{x}^{'} + \left( {{\mathbf{C}} + \frac{{\operatorname{k} _{\parallel }^{2}c_{\operatorname{A} }^{2}}}{\omega }} \right)u_{y}^{'} - \\ - \,\,2\left( {{{\nu }_{\Sigma }}{{\operatorname{k} }_{ \bot }}{{\operatorname{k} }_{\parallel }}\, + {{\Omega }_{ \bot }}} \right)u_{z}^{'} = 0, \\ \end{gathered} $(31)
$2\left( {{{\nu }_{\Sigma }}{{\operatorname{k} }_{ \bot }}{{\operatorname{k} }_{\parallel }}\, + {{\Omega }_{ \bot }}} \right)u_{y}^{'} + {\mathbf{C}}u_{z}^{'} + i\frac{{{{\operatorname{k} }_{\parallel }}}}{{{{{\mathbf{k}}}^{2}}}}\Omega _{\operatorname{T} }^{2}\left( {\frac{{\rho {\kern 1pt} '}}{\rho }} \right) = 0.$(32)
$\begin{gathered} i\frac{{c_{\operatorname{A} }^{2}{{\operatorname{k} }_{ \bot }}{{{\mathbf{k}}}^{2}}}}{\omega }u_{x}^{'} + \\ + \,\,i\left[ {{{\nu }_{\Sigma }}{{\operatorname{k} }_{ \bot }}\left( {{{{\mathbf{k}}}^{2}} + 3\operatorname{k} _{\parallel }^{2}} \right) + 2\left( {{{\operatorname{k} }_{\parallel }}{{\Omega }_{ \bot }} - {{\operatorname{k} }_{ \bot }}{{\Omega }_{\parallel }}} \right)} \right]u_{y}^{'} - \\ - \,\,\left( {\omega {\mathbf{C}} + \Omega _{\operatorname{T} }^{2}} \right)\left( {\frac{{\rho {\kern 1pt} '}}{\rho }} \right) = 0. \\ \end{gathered} $(33)
$\begin{gathered} \Omega _{\operatorname{T} }^{2}: = \frac{{\Omega _{\operatorname{I} }^{2} + \omega \Omega _{\operatorname{J} }^{2}}}{{\omega + {\mathbf{B}}}},\,\,\,\,{\mathbf{C}}: = \omega \left( {1 + \frac{{{{\nu }_{\operatorname{c} }}}}{{\omega + {{\nu }_{\operatorname{c} }}}}{{{\text{x}}}_{\operatorname{d} }}} \right), \\ \Omega _{\operatorname{I} }^{2}\,\,: = {{\operatorname{k} }^{2}}{\mathbf{A}} - 4\pi G\rho {\mathbf{B}},\,\,\,\,\Omega _{\operatorname{J} }^{2}: = {{{\mathbf{k}}}^{2}}c_{{({\text{gas,rad}})}}^{2} - 4\pi G\rho , \\ \end{gathered} $Система уравнений (29)−(32) для пульсаций скорости и плотности является исходной для дальнейшего анализа динамики малых плоских возмущений в модели вращающегося плазменного облака с чернотельной радиацией.
ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ В НЕИЗОЭНТРОПИЧЕСКОМ ПЛАЗМЕННОМ ОБЛАКЕ
Вводя для удобства обозначения
(34)
$\begin{gathered} {{R}_{1}}: = \left[ {{{\nu }_{\Sigma }}\left( {\operatorname{k} _{ \bot }^{2}\,\, + 2\operatorname{k} _{\parallel }^{2}} \right) - 2{{\Omega }_{\parallel }}} \right], \\ {{R}_{2}}: = - 2\left( {{{\nu }_{\Sigma }}{{\operatorname{k} }_{ \bot }}{{\operatorname{k} }_{\parallel }}\,\, + {{\Omega }_{ \bot }}} \right),\,\,\,\,{{R}_{3}}: = {{R}_{{{\kern 1pt} 1}}}{{\operatorname{k} }_{ \bot }} - {{R}_{2}}{{\operatorname{k} }_{\parallel }} \\ \end{gathered} $(35)
$\left( {\begin{array}{*{20}{c}} {{\mathbf{C}} + \frac{{c_{\operatorname{A} }^{2}{{{\mathbf{k}}}^{2}}}}{\omega }}&{{{R}_{1}}}&0&{i\frac{{{{\operatorname{k} }_{\parallel }}}}{{{{{\mathbf{k}}}^{2}}}}{\kern 1pt} \Omega _{\operatorname{T} }^{2}} \\ { - {{R}_{1}}}&{{\mathbf{C}} + \frac{{c_{\operatorname{A} }^{2}\operatorname{k} _{ \bot }^{2}}}{\omega }}&{{{R}_{2}}}&0 \\ 0&{ - {{R}_{2}}}&{\mathbf{C}}&{i\frac{{{{\operatorname{k} }_{ \bot }}}}{{{{{\mathbf{k}}}^{2}}}}{\kern 1pt} \Omega _{\operatorname{T} }^{2}} \\ {i\frac{{c_{\operatorname{A} }^{2}{\kern 1pt} {{\operatorname{k} }_{\parallel }}{\kern 1pt} {{{\mathbf{k}}}^{2}}}}{\omega }}&{i{{R}_{3}}}&0&{ - \left( {\omega {\mathbf{C}} + \Omega _{\operatorname{T} }^{2}} \right)} \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} {u_{x}^{'}} \\ {u_{y}^{'}} \\ {u_{z}^{'}} \\ {\frac{{\rho {\kern 1pt} '}}{\rho }} \end{array}} \right){\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} 0.$Получим теперь на основе дисперсионного соотношения (36) несколько модифицированных критериев джинсовской гравитационной неустойчивости для ряда специальных случаев, связанных с различными относительными ориентациями магнитного поля, оси вращения и вектора распространения волны возмущения.
Соотношение (36) состоит из двух сомножителей, приравнивание каждого из которых к нулю приводит к двум независимым режимам распространения волны возмущения. С равенством
(37)
${\mathbf{C}} \equiv \omega \left( {1 + \frac{{{{\nu }_{\operatorname{c} }}}}{{\omega + {{\nu }_{\operatorname{c} }}}}\frac{{{{\rho }_{\operatorname{d} }}}}{\rho }} \right) = 0$(38)
${{\omega }^{2}} + \omega {{\nu }_{\operatorname{c} }}(1 + {{{\text{x}}}_{\operatorname{d} }}) = 0.$Первый корень ${{\omega }_{{{\kern 1pt} 1}}} = 0$ этого уравнения описывает минимально устойчивый режим распространения волны возмущения, а второй отрицательный корень
соответствует устойчивой затухающей волне возмущения, модифицируемой силой Стокса, действующей на пылевые частицы со стороны несущей жидкости. Он не зависит от самогравитации системы и эффектов, связанных с диссипативными процессами и магнитным полем.Второй сомножитель уравнения (36) приводит к дисперсионному соотношению
(40)
$\begin{gathered} \omega \left[ {{\mathbf{C}}\left\{ {\left( {{\mathbf{C}} + \frac{{c_{\operatorname{A} }^{2}{{{\mathbf{k}}}^{2}}}}{\omega }} \right)\left( {{\mathbf{C}} + \frac{{c_{\operatorname{A} }^{2}\operatorname{k} _{\parallel }^{2}}}{\omega }} \right) + R_{2}^{2} + R_{1}^{2}} \right\} + R_{2}^{2}\frac{{c_{\operatorname{A} }^{2}{{{\mathbf{k}}}^{2}}}}{\omega }} \right] + \\ + \,\,\Omega _{T}^{2}\left\{ {{{{\left( {{\mathbf{C}} + \frac{{c_{\operatorname{A} }^{2}\operatorname{k} _{\parallel }^{2}}}{\omega }} \right)}}^{2}} + R_{2}^{2} + R_{1}^{2} - \frac{1}{{{{{\mathbf{k}}}^{2}}}}R_{3}^{2}} \right\} = 0, \\ \end{gathered} $ПОПЕРЕЧНОЕ РАСПРОСТРАНЕНИЕ ВОЛНЫ ВОЗМУЩЕНИЯ
В случае поперечного распространения мелкомасштабной волны возмущения, когда ${{\operatorname{k} }_{ \bot }} = \operatorname{k} $, ${{\operatorname{k} }_{\parallel }} = 0$, а параметры ${{R}_{i}}$ равны
(41)
$\begin{gathered} {{R}_{{{\kern 1pt} 1}}} = \left( {{{\nu }_{\Sigma }}\operatorname{k} _{{}}^{2}\, - 2{{\Omega }_{\parallel }}} \right),\,\,\,\,{{R}_{2}}: = - 2{{\Omega }_{ \bot }}, \\ {{R}_{3}} = \operatorname{k} \left( {{{\nu }_{\Sigma }}\operatorname{k} _{{}}^{2}\, - 2{{\Omega }_{\parallel }}} \right), \\ \end{gathered} $(42)
$\begin{gathered} \omega \left[ {{\mathbf{C}}\left\{ {\left( {{\mathbf{C}} + \frac{{c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}}}{\omega }} \right){\mathbf{C}} + 4\Omega _{ \bot }^{2} + {{{\left( {{{\nu }_{\Sigma }}\operatorname{k} _{{}}^{2}\, - 2{{\Omega }_{\parallel }}} \right)}}^{2}}} \right\} + 4\Omega _{ \bot }^{2}\frac{{c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}}}{\omega }} \right] + \\ + \,\,\Omega _{T}^{2}\left( {{{{\mathbf{C}}}^{2}} + 4\Omega _{ \bot }^{2}} \right) = 0. \\ \end{gathered} $Проанализируем это соотношение для двух расположений оси вращения системы − вдоль и поперек магнитного поля.
Ось вращения параллельна магнитному полю, ${\mathbf{\Omega }}\parallel {\mathbf{H}}$
Подставляя $\Omega _{ \bot }^{{}} = 0$ в уравнение (42), в результате получим следующее алгебраическое уравнение
(43)
${\mathbf{C}}\left\{ {\omega \left[ {{\mathbf{C}}\left( {{\mathbf{C}} + \frac{{c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}}}{\omega }} \right) + {{{\left( {{{\nu }_{\Sigma }}\operatorname{k} _{{}}^{2}\, - 2\Omega } \right)}}^{2}}} \right] + \Omega _{T}^{2}{\mathbf{C}}} \right\} = 0,$(44)
${\mathbf{C}} = \omega \left( {1 + \frac{{{{\nu }_{\operatorname{c} }}}}{{\omega + {{\nu }_{\operatorname{c} }}}}{{{\text{x}}}_{\operatorname{d} }}} \right) = 0,$Второе соотношение приводит к алгебраическому уравнению 5-ой степени
(45)
$\begin{gathered} \left( {\omega + \frac{{\omega {{\nu }_{\operatorname{c} }}}}{{\omega + {{\nu }_{\operatorname{c} }}}}{{\operatorname{x} }_{\operatorname{d} }}} \right) \times \\ \times \,\,\left[ {\omega \left( {\omega + \frac{{\omega {{\nu }_{\operatorname{c} }}}}{{\omega + {{\nu }_{\operatorname{c} }}}}{{\operatorname{x} }_{\operatorname{d} }}\, + \frac{{c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}}}{\omega }} \right) + \frac{{\Omega _{\operatorname{I} }^{2} + \omega \Omega _{\operatorname{J} }^{2}}}{{\omega + {\mathbf{B}}}}} \right] + \\ + \,\,\omega {{\left( {{{\nu }_{\Sigma }}\operatorname{k} _{{}}^{2} - 2\Omega } \right)}^{2}} = 0. \\ \end{gathered} $(46)
$\begin{gathered} {{\omega }^{3}}\left\{ {\omega \left( {\omega + \frac{{c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}}}{\omega }} \right)} \right. + \\ \left. {^{{^{{^{{^{{^{{^{{}}}}}}}}}}}} + \,\,{{{\left( {{{\nu }_{\Sigma }}\operatorname{k} _{{}}^{2} - 2\Omega } \right)}}^{2}} + \frac{{\Omega _{{\text{I}}}^{2} + \omega \Omega _{{\text{J}}}^{2}}}{{\omega + {\mathbf{B}}}}} \right\} = 0. \\ \end{gathered} $Решение $\omega = 0$ уравнения (46) описывает минимально устойчивый режим распространения волны возмущения. Другие корни уравнения (46) являются решениями кубического (по параметру стабильности $\omega \,)$ алгебраического уравнения:
(47)
$\begin{gathered} {{\omega }^{3}} + {\mathbf{B}}{{\omega }^{2}} + \\ + \,\,\left[ {{{{\left( {2\Omega - \nu _{\Sigma }^{{}}{\kern 1pt} {{\operatorname{k} }^{2}}} \right)}}^{2}} + \left( {c_{{({\text{gas}},{\text{rad}})}}^{2}{\kern 1pt} {{\operatorname{k} }^{2}} + c_{\operatorname{A} }^{2}{\kern 1pt} {{\operatorname{k} }^{2}}{\kern 1pt} {\kern 1pt} - 4\pi G\rho } \right)} \right]{\kern 1pt} \omega + \\ + \,\,{{\operatorname{k} }^{2}}{\mathbf{A}} + \left[ {\left( {c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}} - 4\pi G\rho } \right) + {{{\left( {2\Omega - \nu _{\Sigma }^{{}}{{\operatorname{k} }^{2}}} \right)}}^{2}}} \right]{\mathbf{B}} = 0. \\ \end{gathered} $Пренебрегая далее для простоты анализа вязкими эффектами, ($\nu _{\Sigma }^{{}} = 0$), запишем соотношение (47) в виде
(48)
$\begin{gathered} {{\omega }^{3}} + {\mathbf{B}}{{\omega }^{2}} + \left[ {4{{\Omega }^{2}} + c_{\operatorname{A} }^{2}{\kern 1pt} {{\operatorname{k} }^{2}} + \left( {c_{{({\text{gas}},{\text{rad}})}}^{2}{\kern 1pt} {{\operatorname{k} }^{2}} - 4\pi G\rho } \right)} \right]{\kern 1pt} \omega + \\ + \,\,{\mathbf{A}}{{\operatorname{k} }^{2}} + {\mathbf{B}}\left[ {4{{\Omega }^{2}} + \left( {c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}} - 4\pi G\rho } \right)} \right] = 0. \\ \end{gathered} $(49)
${{\operatorname{k} }^{2}}{\mathbf{A}} + {\mathbf{B}}\left[ {4{{\Omega }^{2}} + \left( {c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}\, - 4\pi G\rho } \right)} \right] \leqslant 0.$(50)
$\frac{{4\pi G\rho }}{{c_{{({\text{gas}},{\text{rad}})}}^{2}}} < {{\operatorname{k} }^{2}} \leqslant 4\frac{{\pi G\rho - {{\Omega }^{2}}}}{{c_{{{\text{gas}}}}^{{'2}} + c_{\operatorname{A} }^{2}}} = \operatorname{k} _{{\text{J}}}^{2}\frac{{1 - {{{{\Omega }^{2}}} \mathord{\left/ {\vphantom {{{{\Omega }^{2}}} {\pi G\rho }}} \right. \kern-0em} {\pi G\rho }}}}{{{{\gamma }^{{ - 1}}} + {{c_{\operatorname{A} }^{2}} \mathord{\left/ {\vphantom {{c_{\operatorname{A} }^{2}} {c_{{{\text{gas}}}}^{2}}}} \right. \kern-0em} {c_{{{\text{gas}}}}^{2}}}}}.$Из неравенства (50), представляющего собой модификацию критерия Джинса, можно сделать вывод, что в случае поперечного распространения волны возмущения, направленной перпендикулярно к оси вращения плазменного облака $({\mathbf{k}} \bot {\mathbf{\Omega }}$), и при условии $\nu _{\Sigma }^{{}} = 0,$ вращение и магнитное поле стабилизируют гравитационную неустойчивость; при этом лучистая теплопроводность влияет на стандартный критерий Джинса в излучающей плазменной среде, приводя к замене адиабатической скорости на изотермическую.
Покажем теперь, что если выполняется неравенство
(51)
${{\operatorname{k} }^{2}}{\mathbf{A}} + {\mathbf{B}}\left[ {4{{\Omega }^{2}} + \left( {c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}\, - 4\pi G\rho } \right)} \right] > 0,$Обратимся теперь к полному уравнению (45), которое запишем в развернутом виде:
(52)
${{\omega }^{5}} + {{\mathfrak{L}}_{1}}{{\omega }^{4}} + ... + {{\mathfrak{L}}_{4}}\omega + {{\mathfrak{L}}_{5}} = 0,$Уравнение (52) является уравнением пятой степени по параметру $\omega $ и, следовательно, имеет пять корней. Когда свободный член ${{\mathfrak{L}}_{5}}$ уравнения (52) отрицателен, т.е. когда $\Omega _{\operatorname{I} }^{2} + c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}} < 0$, то один из корней этого уравнения будет положительным действительным числом или комплексным числом с положительной действительной частью. В этом случае система, представленная уравнением (52), будет нестабильной. Следовательно, условие неустойчивости имеет вид
(53)
${\mathbf{A}} < 4\pi G\rho {\mathbf{B}}{{\operatorname{k} }^{{ - 2}}}\, - c_{\operatorname{A} }^{2}.$(54)
${{\operatorname{k} }^{2}} < \gamma \operatorname{k} _{\operatorname{J} }^{2}\left( {1 - c_{\operatorname{A} }^{2}\frac{{{{С}_{{V{\kern 1pt} \Sigma }}}}}{{{{\lambda }_{\Sigma }}4\pi G}}} \right) = \gamma \operatorname{k} _{\operatorname{J} }^{2}\left( {1 - c_{\operatorname{A} }^{2}\frac{{{{С}_{{V{\kern 1pt} \Sigma }}}}}{{{{\lambda }_{\Sigma }}4\pi G}}} \right).$(55)
$\begin{gathered} {\mathbf{B}}: = \frac{{({{\Gamma }_{3}} - 1){{\lambda }_{\Sigma }}T}}{{(4 - 3\beta )}}\frac{{{{\operatorname{k} }^{2}}}}{P} = \frac{{{{C}_{{V,{\text{gas}}}}}}}{{{{С}_{{V\,\Sigma }}}}}(\gamma - 1)\frac{{{{\lambda }_{\Sigma }}{{\operatorname{k} }^{2}}}}{{{{\left( {{\mathcal{R} \mathord{\left/ {\vphantom {\mathcal{R} {\bar {\mu }}}} \right. \kern-0em} {\bar {\mu }}}} \right)} \mathord{\left/ {\vphantom {{\left( {{\mathcal{R} \mathord{\left/ {\vphantom {\mathcal{R} {\bar {\mu }}}} \right. \kern-0em} {\bar {\mu }}}} \right)} \rho }} \right. \kern-0em} \rho }}} = \\ = \frac{{{{\lambda }_{\Sigma }}{{\operatorname{k} }^{2}}}}{{\rho {{С}_{{V\Sigma }}}}} = \frac{{{{\Gamma }_{1}}}}{\beta }\frac{{{{\lambda }_{\Sigma }}{{\operatorname{k} }^{2}}}}{{\rho {{С}_{{P\,\Sigma }}}}}, \\ \end{gathered} $(56)
$\begin{gathered} {\mathbf{A}}: = \frac{{({{\Gamma }_{3}} - 1)}}{{(4 - 3\beta )}}\beta \frac{{{{\lambda }_{\Sigma }}T}}{\rho }{{\operatorname{k} }^{2}} = \frac{1}{{{{С}_{{V\Sigma }}}}}\frac{{{{\lambda }_{\Sigma }}{{P}_{{{\text{gas}}}}}}}{{{{\rho }^{2}}}}{{\operatorname{k} }^{2}} = \\ = \frac{{{{\Gamma }_{1}}}}{\beta }\frac{{{{\lambda }_{\Sigma }}{\text{c}}_{{{\text{gas}}}}^{{'2}}}}{{\rho {{С}_{{P\Sigma }}}}}{{\operatorname{k} }^{2}} = {\mathbf{B}}\operatorname{c} _{{{\text{gas}}}}^{{'2}}, \\ \end{gathered} $Таким образом, из неравенства (54) можно сделать вывод, что, в случае поперечного распространения волны возмущения перпендикулярного к оси вращения плазменного облака (${\mathbf{k}} \bot {\mathbf{\Omega }}$), магнитное поле и лучевая теплопроводность также модифицируют критерий неустойчивости Джинса, увеличивая размер ${{\lambda }_{{{\text{cr}}}}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{\operatorname{k} }_{{{\text{cr}}}}}}}} \right. \kern-0em} {{{\operatorname{k} }_{{{\text{cr}}}}}}}$ мельчайших “капель” рассматриваемой среды, которые могут удерживаться вместе собственным гравитационным притяжением.
Ось вращения перпендикулярна к магнитному полю, ${\mathbf{\Omega }} \bot {\mathbf{H}}$
Подставляя в уравнение (42) коэффициенты ${{R}_{{{\kern 1pt} 1}}}: = {{\nu }_{\Sigma }}\operatorname{k} _{ \bot }^{2}$, ${{R}_{2}}: = - 2{{\Omega }_{ \bot }}$ и ${{R}_{3}} = {{R}_{1}}{{\operatorname{k} }_{ \bot }}$, в результате получим следующее дисперсионное соотношение
(57)
$\begin{gathered} \omega \left[ {{\mathbf{C}}\left\{ {\left( {{\mathbf{C}} + \frac{{c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}}}{\omega }} \right){\mathbf{C}} + 4\Omega _{{}}^{2} + \nu _{\Sigma }^{2}{{\operatorname{k} }^{4}}} \right\} + 4\Omega _{{}}^{2}\frac{{c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}}}{\omega }} \right] + \\ + \,\,\Omega _{T}^{2}\left( {{{{\mathbf{C}}}^{2}} + 4\Omega _{{}}^{2}} \right) = 0, \\ \end{gathered} $(58)
${{\omega }^{8}} + {{\mathfrak{L}}_{1}}{{\omega }^{7}} + ... + {{\mathfrak{L}}_{7}}\omega + {{\mathfrak{L}}_{8}} = 0,$(59)
${{\operatorname{k} }^{2}}{\mathbf{A}} - 4\pi G\rho {\mathbf{B}} + c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}} < 0,$(60)
${{\operatorname{k} }^{2}} < \operatorname{k} _{\operatorname{J} }^{2}\gamma \left( {1 - \frac{{c_{\operatorname{A} }^{2}}}{{4\pi G{{\lambda }_{\Sigma }}}}{{C}_{{V,{\text{gas}}}}}\frac{{(\gamma - 1){{{(4 - 3\beta )}}^{2}}}}{{\beta ({{\Gamma }_{1}} - \beta )}}} \right).$Когда одновременно справедливы неравенства $\Omega _{\operatorname{I} }^{2} > 0$ и $\Omega _{\operatorname{J} }^{2} > 0$, все коэффициенты уравнения (58) будут положительными. В этом случае выполняется необходимое условие устойчивости системы, но не достаточное. Следовательно, можно сделать вывод, что система, представленная уравнением (58), дает устойчивые режимы распространения волны возмущения только с учетом указанных необходимых условий.
Заметим, что если пренебречь наличием пыли (${{\nu }_{\operatorname{c} }} = 0$) и эффектами вязкости $(\nu _{\Sigma }^{{}} = 0)$ в уравнении (57), то оно приобретает более простой вид
(61)
$\begin{gathered} {{\omega }^{3}} + {\mathbf{B}}{{\omega }^{2}} + \left[ {c_{{({\text{gas}},{\text{rad}})}}^{2}{{\operatorname{k} }^{2}} + \left( {c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}\, - 4\pi G\rho } \right)} \right]\omega + \\ + \,\,\left( {{{\operatorname{k} }^{2}}c_{\operatorname{A} }^{2} - 4\pi G\rho } \right){\mathbf{B}} + {{\operatorname{k} }^{2}}{\mathbf{A}} = 0, \\ \end{gathered} $(62)
$\left( {{\mathbf{A}}{{\operatorname{k} }^{2}} + c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}{\mathbf{B}}} \right) - 4\pi G\rho {\mathbf{B}} \leqslant 0,$(63)
${{\operatorname{k} }^{2}} \leqslant \frac{{4\pi G\rho }}{{{{\mathbf{A}} \mathord{\left/ {\vphantom {{\mathbf{A}} {\mathbf{B}}}} \right. \kern-0em} {\mathbf{B}}} + c_{\operatorname{A} }^{2}}} = \frac{{4\pi G\rho }}{{c_{{{\text{gas}}}}^{{'2}} + c_{\operatorname{A} }^{2}}} = \operatorname{k} _{{\text{J}}}^{2}\gamma \frac{1}{{1 + {{c_{\operatorname{A} }^{2}} \mathord{\left/ {\vphantom {{c_{\operatorname{A} }^{2}} {c_{{{\text{gas}}}}^{{'2}}}}} \right. \kern-0em} {c_{{{\text{gas}}}}^{{'2}}}}}},$ПРОДОЛЬНОЕ РАСПРОСТРАНЕНИЕ ВОЛНЫ ВОЗМУЩЕНИЯ
Если ${{\operatorname{k} }_{\parallel }} = \operatorname{k} $, ${{\operatorname{k} }_{ \bot }} = 0$, то коэффициенты ${{R}_{i}}$ равны ${{R}_{{{\kern 1pt} 1}}} = 2\left( {{{\nu }_{\Sigma }}\operatorname{k} _{\parallel }^{2}\, - {{\Omega }_{\parallel }}} \right)$, ${{R}_{2}} = - 2{{\Omega }_{ \bot }}$ и ${{R}_{3}} = - {{R}_{2}}{{\operatorname{k} }_{\parallel }} = $ $ = 2{{\Omega }_{ \bot }}{{\operatorname{k} }_{\parallel }}$; в этом случае дисперсионное соотношение (40) принимает вид
(64)
$\begin{gathered} \omega \left[ {{\mathbf{C}}\left\{ {{{{\left( {{\mathbf{C}} + \frac{{c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}}}{\omega }} \right)}}^{2}} + 4\Omega _{ \bot }^{2} + 4{{{\left( {{{\nu }_{\Sigma }}\operatorname{k} _{{}}^{2} - {{\Omega }_{\parallel }}} \right)}}^{2}}} \right\} + 4\Omega _{ \bot }^{2}\frac{{c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}}}{\omega }} \right] + \\ + \,\,\Omega _{T}^{2}\left\{ {{{{\left( {{\mathbf{C}} + \frac{{c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}}}{\omega }} \right)}}^{2}} + 4{{{\left( {{{\nu }_{\Sigma }}\operatorname{k} _{{}}^{2} - {{\Omega }_{\parallel }}} \right)}}^{2}}} \right\} = 0. \\ \end{gathered} $Проанализируем это соотношение для двух расположений оси вращения системы − вдоль и поперек магнитного поля.
Ось вращения параллельна к магнитному полю, ${\mathbf{\Omega }}\parallel {\mathbf{H}}$
Подставляя в (64) величины ${{\Omega }_{\parallel }} = \Omega $ и ${{\Omega }_{ \bot }} = 0$, получим следующее уравнение
(65)
$\begin{gathered} \left\{ {{{{\left( {{\mathbf{C}} + \frac{{c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}}}{\omega }} \right)}}^{2}} + 4{{{\left( {{{\nu }_{\Sigma }}\operatorname{k} _{{}}^{2} - \Omega } \right)}}^{2}}} \right\} \times \\ \times \,\,\left( {{\mathbf{C}}\omega + \frac{{\Omega _{\operatorname{I} }^{2} + \omega \Omega _{\operatorname{J} }^{2}}}{{\omega + {\mathbf{B}}}}} \right) = 0, \\ \end{gathered} $(66)
$\left( {1 + \frac{{{{\nu }_{\operatorname{c} }}}}{{\omega + {{\nu }_{\operatorname{c} }}}}{{\operatorname{x} }_{\operatorname{d} }}} \right){{\omega }^{2}} + \frac{{\Omega _{\operatorname{I} }^{2} + \omega \Omega _{\operatorname{J} }^{2}}}{{\omega + {\mathbf{B}}}} = 0$(67)
${{\left( {\omega + \frac{{\omega {{\nu }_{\operatorname{c} }}}}{{\omega + {{\nu }_{\operatorname{c} }}}}{{\operatorname{x} }_{\operatorname{d} }}\, + \frac{{c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}}}{\omega }} \right)}^{2}} + 4{{\left( {{{\nu }_{\Sigma }}\operatorname{k} _{{}}^{2} - \Omega } \right)}^{2}} = 0.$Дисперсионное соотношение (66) при разложении сводится к уравнению
(68)
$\begin{gathered} {{\omega }^{4}} + \left( {{{\nu }_{c}}{{\chi }_{\operatorname{d} }} + {\mathbf{B}}} \right){{\omega }^{3}} + \left[ {{{\nu }_{c}}{{\chi }_{\operatorname{d} }}{\mathbf{B}} + \Omega _{\operatorname{J} }^{2}} \right]{{\omega }^{2}} + \\ + \left( {{{\nu }_{c}}\Omega _{\operatorname{J} }^{2} + \Omega _{\operatorname{I} }^{2}} \right)\omega + {{\nu }_{c}}\Omega _{\operatorname{I} }^{2}{\mathbf{B}} = 0. \\ \end{gathered} $(69)
${{\operatorname{k} }^{2}} < \frac{{\mathbf{B}}}{{\mathbf{A}}} = \frac{{4\pi G\rho }}{{\operatorname{c} _{{{\text{gas}}}}^{{'2}}}} = \operatorname{k} _{{\text{J}}}^{2}\frac{{{\text{c}}_{{{\text{gas}}}}^{2}}}{{\operatorname{c} _{{{\text{gas}}}}^{{'2}}}} = \gamma \operatorname{k} _{{\text{J}}}^{2}.$В случае, когда справедливо неравенство $\Omega _{\operatorname{I} }^{2} > 0$, все коэффициенты уравнения (68) будут положительными. Это означает, что многочлен, заданный уравнением (68), будет иметь все корни с отрицательными вещественными частями (или комплексные корни с отрицательными действительными частями) тогда и только тогда, когда все главные диагональные миноры матрицы Гурвица будут также положительными. Для того чтобы убедиться в выполнении критерий Рауса−Гурвица выпишем все главные миноры для многочлена, заданного уравнением (68):
Поскольку все миноры положительны, то критерий Рауса−Гурвица удовлетворяется. Это означает, что система, представленная уравнением (68), будет всегда устойчивой.
Обратимся теперь к уравнению (67), которое при разложении принимает вид:
(70)
$\begin{gathered} {{\omega }^{6}} + 2\nu _{\operatorname{c} }^{{}}{{\chi }_{\operatorname{d} }}{{\omega }^{5}} + \left[ {\nu _{\operatorname{c} }^{2}{{\chi }_{\operatorname{d} }} + 2c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}} + {{{\left( {\Omega - \nu _{\Sigma }^{{}}{{\operatorname{k} }^{2}}} \right)}}^{2}}} \right]{{\omega }^{4}} + \\ + \,\,2\nu _{\operatorname{c} }^{{}}\left[ {c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}\left( {1 + {{\chi }_{\operatorname{d} }}} \right) + 4{{{\left( {\Omega - \nu _{\Sigma }^{{}}{{\operatorname{k} }^{2}}} \right)}}^{2}}\nu _{\operatorname{c} }^{{}}} \right]{{\omega }^{3}} + \\ + \,\,\nu _{\operatorname{c} }^{{}}\left[ {c_{\operatorname{A} }^{2}{{\operatorname{k} }^{2}}\left( {1 + 2\nu _{\operatorname{c} }^{{}}{{\chi }_{\operatorname{d} }}} \right) + 4\nu _{\operatorname{c} }^{{}}{{{\left( {\Omega - \nu _{\Sigma }^{{}}{{\operatorname{k} }^{2}}} \right)}}^{2}}} \right]{{\omega }^{2}} + \\ + \,\,\left( {2\nu _{\operatorname{c} }^{{}}c_{\operatorname{A} }^{4}{{\operatorname{k} }^{4}}} \right)\omega + \nu _{\operatorname{c} }^{2}c_{\operatorname{A} }^{4}{{\operatorname{k} }^{4}} = 0. \\ \end{gathered} $Ось вращения перпендикулярна к магнитному полю, ${\mathbf{\Omega }} \bot {\mathbf{H}}$
Подставляя в уравнение (64) величины ${{\Omega }_{\parallel }} = 0$ и ${{\Omega }_{ \bot }} = \Omega $, получим дисперсионное соотношение
(71)
$\begin{gathered} \left\{ {{{{\left( {{\mathbf{C}} + \frac{{{{\operatorname{k} }^{2}}c_{\operatorname{A} }^{2}}}{\omega }} \right)}}^{2}} + 4\nu _{\Sigma }^{2}{{\operatorname{k} }^{4}}} \right\}\left( {\omega {\mathbf{C}} + \Omega _{T}^{2}} \right) + \\ + \,\,4\Omega _{{}}^{2}\omega \left( {{\mathbf{C}} + \frac{{{{\operatorname{k} }^{2}}c_{\operatorname{A} }^{2}}}{\omega }} \right) = 0, \\ \end{gathered} $ЗАКЛЮЧЕНИЕ
Основные этапы эволюции экзопланетных дисков в настоящее время все более проясняются и уточняются. Однако проблема построения непротиворечивой картины образования самих звезд и околозвездных газопылевых дисков до сих пор полностью не решена. Большинство обнаруженных на сегодня экзопланетных дисков вокруг солнечноподобных звезд сильно отличаются от протопланетного диска Солнца. По этой причине современная теория происхождения Солнечной системы является лишь одной из многих, и для моделирования эволюции любой другой протозвездной туманности подходящая теория может оказаться более сложной. Об этом, в частности, свидетельствует коллекция обнаруженных во Вселенной экзопланет, которые весьма разнообразны. В связи со сказанным возникла, по мнению автора, необходимость в разработке нестандартного подхода, объясняющего (до известной степени) многообразие открытых экзопланетных дисков вокруг звезд.
В данной работе в рамках проблемы моделирования эволюции околозвездного диска обсуждается влияние чернотельного излучения на неустойчивость Джинса для намагниченной вращающейся пылевой плазмы с учетом влияния на критическую длину волны возмущения таких диссипативных процессов как магнитная вязкость и лучистая теплопроводность. Принимается, что ось вращения системы параллельна либо перпендикулярна к магнитному полю как для продольного, так и для поперечного режима распространения волны возмущения. На основе выведенного полного дисперсионного соотношения получены модифицированные критерии джинсовой неустойчивости для ряда специальных случаев, связанных с различными относительными ориентациями магнитного поля, оси вращения и вектора распространения возмущающей волны. Устойчивость среды обсуждается с помощью использования критерия Рауса−Гурвица.
Важно отметить, что эффект от совместного влияния черного излучения, магнитного поля, вращения системы, вязкости и теплопередачи на неустойчивость Джинса самогравитирующей намагниченной пылевой плазмы в литературе все еще недостаточно изучен. С учетом значимости подобного рассмотрения в астрофизическом контексте, в работе было проведено исследование неустойчивости самогравитирующего намагниченного плазменного пылевого облака при неизоэнтропичности распространения волны возмущения. Было показано, что во всех случаях критерий неустойчивости Джинса остается справедливым, но с небольшими модификациями, вызванными включением различных параметров. Вместе с тем, полученные в работе модифицированные критерии нестабильности Джинса существенно отличаются от некоторых известных в литературе критериев. В частности, было показано, что чернотельное излучение за счет лучевой теплопроводности подавляет флуктуации температуры в волне возмущения (вследствие чего волна затухает), сделав режим ее распространения изотермическим вместо адиабатического. Показано также, что для продольного распространения волны возмущения, в случае, когда ось вращения плазменного облака перпендикулярна к магнитному полю, эффекты, связанные с вращением системы и наличием взвешенных пылевых частиц, не влияют на критерий Джинса в присутствии магнитного поля. Для поперечного режима распространения волны возмущения, когда ось вращения параллельна магнитному полю, было установлено, что вращение системы и магнитное поле стабилизируют гравитационную неустойчивость, причем стабилизирующий эффект вращения сравнительно более эффективен.
Результаты проведенного исследования позволяют, в частности, лучше понять проблемы, связанные с эволюцией околосолнечных экзопланетных дисков в результате потери ими устойчивости.
Работа выполнена в рамках Госзадания, а также частично поддержана грантом Минобрнауки № 075-15-2020-780 от 07.10.2020 г.
Список литературы
Гантмахер Ф.Р. Теория матриц. М.: Физматлит, 2010. 463 с.
де Гроот С., Мазур П. Неравновесная термодинамика. М.: Мир, 1964. 456 с.
Колесниченко А.В. Вывод в рамках неэкстенсивной кинетики критерия гравитационной неустойчивости Джинса для допланетного вращающегося облака с учетом радиации и магнитного поля // Mathematica Montisnigri. 2020. V. XLVII. P. 176−200.
Колесниченко А.В. Роль черного излучения в модификации критериев неустойчивости Джинса для экзопланетного пылевого плазменного диска при учете магнитной вязкости и лучевого теплообмена // Препр. ИПМ им. М.В. Келдыша. 2022. № 3. 40 с.
Михайловский А.Б. Теория плазменных неустойчивостей. Т. 2. Неустойчивости неоднородной плазмы. М.: Атомиздат, 1977. 360 с.
Тассуль Ж.-Л. Теория вращающихся звезд. М.: Мир, 1982. 472 с.
Шапиро С., Тьюколски С. Черные дыры, белые карлики и нейтронные звезды. Физика компактных объектов (в двух частях). М.: Мир, 1985. 635 с.
Фридман А.М., Хоперсков А.В. Физика галактических дисков. М.: Физматлит, 2011. 640 с.
Хоперсков А.В., Храпов С.С. Неустойчивость тепловой, вязкой и акустических мод в тонких аккреционных дисках // Астрон. журн. 1999. Т. 76. № 4. С. 256−269.
Aggarwal M., Talwar S.P. Magnetothermal instability in a rotating gravitating fluid // Mon. Notic. Roy. Astron. Soc. 1969. V. 146. P. 235−242.
Argal S., Tiwari A., Sharma P.K. Jeans instability of a rotating self-gravitating viscoelastic fluid // Europhys. Lett. 2014. V. 108. id. 35003.
Bhatia P.K. Gravitational instability of a rotating anisotropic plasma // Phys. Fluids. 1967. V. 10. № 8. P. 1652− 1653.
Bora M.P., Talwar S.P. Magnetothermal instability with generalized Ohm’s law // Phys. Fluids. B. 1993. V. 5. P. 950−955.
Bora M.P., Nayyar N.K. Gravitational instability of a heat-conducting plasma // Astrophys. and Space Sci. 1991. V. 179. P. 313−320.
Borah A.C., Sen A.K. Gravitational instability of partially ionized molecular clouds // J. Plasma Phys. 2007. V. 73. № 6. P. 831−838.
Chandrasekhar S. Hydrodynamics and Hydromagnetic Stability. Oxford: Clarendon Press, 1961. 588 p.
Chhajlani R.K., Vaghela D.S. Gravitational stability of finitely conducting two-component plasma through porous medium // Astrophys. and Space Sci. 1987. V. 139. P. 337−352.
Cogley A.C., Vincent W.G. Application to radiative acoustics of Whitham’s method for the analysis of non-equilibrium wave phenomena // J. Fluid Mech. 1969. V. 39. № 4. P. 641−866.
Cox J.P. Theory of stellar pulsation. Princeton, New Jersey: Princeton Univ. Press, 1979. 378 p.
Cox J.P., Giuli R.T. Principles of Stellar Structure. New York: Gordon and Dreach, 1968. 568 p.
Dhiman J.S., Dadwal R. On the gravitational instability of a medium in non-uniform rotation and magnetic field // Astrophys. and Space Sci. 2010. V. 325. № 2. P. 195− 200.
Dhiman J.S., Dadwal R. The gravitational instability of a non-uniformly rotating heat conducting medium in the presence of non-uniform magnetic field // Astrophys. and Space Sci. 2011. V. 332. № 2. P. 373−378.
Dhiman J.S., Dadwal R. On the Jeans criterion of a stratified heat conducting gaseous medium in the presence of non-uniform rotation and magnetic field // J. Astrophys. and Astron. (Indian Acad. of Sci.). 2012. V. 33. P. 363−373.
Dolai B., Prajapati R.P. The rotating Rayleigh-Taylor instability in a strongly coupled dusty plasma // Physics of Plasmas.
Fridman A.M., Polyachenko V.L. Physics of gravitating system. N.Y.: Springer-Verlag, 1984. V. 1. 468 p. V. 2. 358 p.
Jacobs G., Shukla P.K. Stability of molecular clouds in partially ionized self-gravitating space plasmas // J. Plasma Phys. 2005. V. 71. № 04. P. 487−493.
Jain S., Sharma P., Chhajlani R.K. Jeans instability of magnetized quantum plasma: effect of viscosity, rotation and finite Larmor radius corrections // AIP Conf. Proc. 2015. V. 1670. id. 030013.
Jeans J.H. The stability of spherical nebulae // Philosoph. Transact. Roy. Soc. 1902. V. 199. P. 1−53.
Joshi H., Pensia R.K. Effect of rotation on Jeans instability of magnetized radiative quantum plasma // Physics of Plasmas. 2017. V. 24. № 3. id. 032113.
Kaneko N., Morita K., Satoh T., Hayasaki K. Small-amplitude disturbances in a radiating and scattering grey medium II. Solutions of given real wave number k // Astrophys. and Space Sci. 2005. V. 299. P. 263−306.
Kaneko N., Morita K. Small-amplitude disturbances in a radiating and scattering grey medium III. Gravitational effects on the solutions of given real wave number k // Astrophys. and Space Sci. 2006. V. 305. P. 349−376.
Kaothekar S. Star formation through thermal instability of radiative plasma with finite electron inertia and finite Larmor radius corrections // AIP Advances. 2016. V. 6. id. 085020 (1−14).
Kaothekar S., Chhajlani R.K. Effect of radiative heat-loss function and finite Larmor radius corrections on Jeans instability of viscous thermally conducting self-gravitating astrophysical plasma // ISRN Astron. and Astrophys. 2012. V. 2012. id. 420938 (1−14).
Kolesnichenko A.V. Jeans instability of a protoplanetary gas cloud with radiation in nonextensive Tsallis kinetics // Sol. Syst. Res. 2020. V. 54. № 2. P. 137−149.
Kolesnichenko A.V. Jeans instability of a protoplanetary circular disk taking into account the magnetic field and radiation in nonextensive Tsallis kinetics // Sol. Syst. Res. 2021. V. 55. № 2. P. 132−149.
Kumar A., Sutar D.L., Pensia R.K., Sharma S. Effect of fine dust particles and finite electron inertia of rotating magnetized plasma // AIP Conf. Proc. 2018. V. 1953. № 1. id. 060036 (1−4).
Kumar A., Sutar D.L., Pensia R.K. Jeans instability of a monatomic gas in the presence of thermal radiation // J. Physics: Conf. Ser. 2017. V. 836. id. 012012 (1−3).
Lightman A.P. Time-dependent accretion disks around compact objects. I. Theory andbasic equations // Astrophys. J. 1974. V. 194. id. 419427.
Lightman A.P., Eardley D.M. Black holes in binary systems: instability of disk accretion // Astrophys. J. 1974. V. 187. P. 1−35.
Pensia R.K., Sutar D.L., Sharma S. Analysis of Jeans instability of optically thick quantum plasma under the effect of modified Ohms law // AIP Conf. Proc. 2018. V. 1953. № 1. id. 060044 (1−4).
Prajapati R.P., Chhajlani R.K. Gravitational instability of dusty plasma with radiative process // AIP Conf. Proc. 2011. V. 1397. P. 267−268.
Prajapati R.P., Pensia R.K., Kaothekar S., Chhajlani R.K. Self-gravitational instability of rotating viscous Hall plasma with arbitrary radiative heat-loss functions and electron inertia // Astrophys. and Space Sci. 2010. V. 327. P. 139−154.
Prajapati R.P., Sharma P.K., Sanghvi R.K., Chhajlani R.K. Jeans instability of self-gravitating magnetized strongly coupled plasm // J. Physics: Conf. Ser. 2012. V. 365. id. 012040 (1−4).
Prajapati R.P., Bhakta S. Influence of dust charge fluctuation and polarization force on radiative condensation instability of magnetized gravitating dusty plasma // Phys. Lett. A. 2015. V. 379. № 42. P. 2723−2729.
Roberts K.V., Taylor J.B. Magnetohydrodynamic equations for finite Larmor radius // Phys. Rev. Lett. 1962. V. 8. № 5. P. 197−198.
Shaikh S., Khan A., Bhatia P.K. Jeans’ gravitational instability of a thermally conducting plasma // Phys. Lett. A. 2008. V. 372. № 9. P. 1451−1457.
Shaikh S., Khan A., Bhatia P.K. Stability of thermally conducting plasma in a variable magnetic field // Astrophys. and Space Sci. 2007. V. 312. P. 35−40.
Shakura N.I., Sunyaev R.A. A theory of the instability of disk accretion onto black holes and the variability of binary X-ray sources, galactic nuclei and quasars // Mon. Notic. Roy. Astron. Soc. 1976. V. 175. P. 613−632.
Sharma R.C. Gravitational instability of a rotating plasma // Astrophys. and Space Sci. 1974. V. 29. P. L1−L4.
Sharma R.C., Patidar A. Effect of ion radiative cooling on Jeans instability of partially ionized dusty plasma with dust charge fluctuation // Physics of Plasmas. 2017. V. 24. id. 013705 (1−13).
Sharma R.C., Singh B. Gravitational instability of a rotating and partially-ionized plasma in the presence of variable magnetic field // Astrophys. and Space Sci. 1988. V. 143. P. 233−239.
Tsintsadze N.L., Chaudhary R., Shah H.A., Murtaza G. Jeans instability in a magneto-radiative dusty plasma // J. Plasma Physics. 2008. V. 74. № 06. P. 847−853.
Vaghela D.S., Shrivastava H.S.P. Magnetogravitational instability of a rotating homogeneous gas cloud with radiation // Czechoslovak J. Physics. 1994. V. 44. № 10. P. 905−911.
Vranješ J. Gravitational instability of a quasi-homogeneous plasma cloud with radiation // Astrophys. and Space Sci. 1990. V. 173. № 2. P. 293−298.
Vranješ J., Čadež V. Gravitational instability of a homogeneous gas cloud with radiation // Astrophys. and Space Sci. 1990. V. 164. № 2. P. 329−331.
Vyas M.K., Chhajlani R.K. On the gravitational instability of an ionized magnetized rotating plasma flowing through a porous medium with other transport processes and the suspended particles // Contrib. Plasma Phys. 1989. V. 29. № 2. P. 135−151.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник