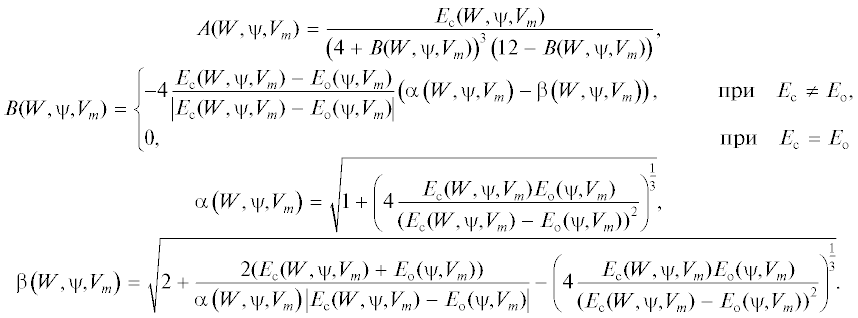Биологические мембраны: Журнал мембранной и клеточной биологии, 2019, T. 36, № 1, стр. 53-62
Моделирование механизма влияния электрического трансмембранного потенциала на показатели Херста в последовательности времен жизни одиночного ионного канала
А. А. Гриневич a, b, *, М. Е. Асташев a
a Институт биофизики клетки РАН
142290 Московской обл., Пущино, ул. Институтская, 3, Россия
b Институт теоретической и экспериментальной биофизики РАН
142290 Московской обл., Пущино, ул. Институтская, 3, Россия
* E-mail: grin_aa@mail.ru
Поступила в редакцию 16.04.2018
После доработки 27.06.2018
Принята к публикации 21.06.2018
Аннотация
Из экспериментальных исследований известно, что показатель Херста, характеризующий степень скоррелированности событий в последовательности времен жизни канала в открытом и закрытом состояниях, зависит от электрического трансмембранного потенциала. Однако механизм этого явления остается не ясным. В настоящей работе построена модель, позволяющая описать это явление. При помощи модели рассчитаны зависимости показателя Херста от электрического трансмембранного потенциала. Показано, что наилучшее согласие теоретических и экспериментальных данных наблюдается при учете зависимости гидрофобного фактора от электрического трансмембранного потенциала.
ВВЕДЕНИЕ
Ионные каналы представляют собой крупные гликопротеиновые комплексы, встроенные в липидный бислой биологической мембраны. В структуре канала имеются модули, ответственные за управление ионным током, текущим через канал – воротный механизм. Частицы воротного механизма совершают конформационные переходы между двумя функциональными состояниями, соответствующими открытому (ионный ток течет через канал) и закрытому каналу (ионный ток не течет через канал). В результате этого формируются импульсы ионного тока приблизительно одной и той же амплитуды, но различной длительности (τo), перемежающиеся закрытыми состояниями канала (τс). Функциональная характеристика индивидуального канала может быть экспериментально получена в экспериментах пэтч-методом в виде записи тока через канал. Последовательности времен $\left\{ {{{\tau }_{{\text{o}}}}} \right\}$ и $\left\{ {{{\tau }_{{\text{c}}}}} \right\}$ жизни канала в открытом и закрытом состояниях, соответственно, характеризуют кинетику активности канала, и являются его кинетическими параметрами.
Экспериментальное исследование активности K+-каналов методами анализа нестационарных временны́х рядов (метод Херста, бестрендовый флуктуационный анализ (БФА)) показало, что в последовательностях открытых и закрытых состояний каналов наблюдается высокая степень корреляции между событиями на больших временах (от нескольких секунд до десятков секунд) [1–12]. Эти корреляции характеризуются показателем Херста H, безразмерным параметром, который изменяется от 0 до 1. При этом значение $H = 0.5$ свидетельствует об отсутствии корреляций в последовательности событий и такой процесс считается абсолютно случайным, если $H < 0.5$, то процесс считается антиперсистентным, напротив, если $H > 0.5$, то процесс считается персистентным. Эксперименты на K+-каналах также показали, что показатель Херста зависит от электрического трансмембранного потенциала, приложенного к мембране [5, 9].
Сильные корреляции на временах порядка десятков секунд наблюдались и в других биологических системах, например, в спайковой активности слухового нерва. Этот феномен объясняется результатами корреляционных соотношений в активности ионных каналов слуховых волосковых клеток [13]. При этом моделирование спайковой активности слухового нерва на основе Марковской кинетики ионных каналов не воспроизводит экспериментально наблюдаемые корреляции [14].
Вопрос, связанный с механизмом формирования корреляционных соотношений в событиях открытых и закрытых состояний ионных каналов и зависимости этих соотношений от трансмембранного потенциала, до сих пор во многом остается открытым.
Эффективным методом исследования кинетики активности ионных каналов считается математическое моделирование. Существует несколько математических моделей, описывающих кинетику ионных каналов или работу их воротного механизма. К ним относятся стохастические Марковские модели [15–19], диффузионные модели [20–26], детерминистические модели [27–30], полноатомные модели [31–33].
На базе предложенной ранее простой схемы одиночного ионного канала (рис. 1) нами построена математическая модель воротного механизма одиночного ионного канала [34]. Схема основана на рентгеноструктурных данных бактериального K+-канала (KcsA-канала) [35, 36]. В этой схеме подвижные части трансмембранных сегментов ТМ2, являющиеся воротными частицами, моделируются жесткими стержнями. Динамика этих стержней описывается конформационной переменной $\varphi \left( t \right)$, соответствующей углу отклонения воротных частиц во время открывания/закрывания канала. Зависимость угла $\varphi $ от времени моделируется уравнением Ланжевена:
(1)
$\begin{gathered} {{I}_{g}}\frac{{{{d}^{2}}\varphi \left( t \right)}}{{d{{t}^{2}}}} = - \frac{\gamma }{3}\frac{{d\varphi \left( t \right)}}{{dt}} - \\ - \,\,\frac{d}{{d\varphi }}U\left( {\varphi \left( t \right),W\left( t \right),\psi \left( t \right),{{V}_{m}}} \right) + \sqrt {\frac{{\gamma kT}}{2}} \varsigma \left( t \right), \\ \end{gathered} $Рис. 1.
KcsA-канал (вид сбоку) (а) и схема модельного ионного канала, построенного на основе структуры KcsA-канала (б). Маленькие серые шарики – ионы K+, маленькие черные цилиндры внутри поры – молекулы воды, серая стрелка показывает направление движения ионов. $\varphi $ – угол отклонения подвижных частей трансмембранных сегментов ТМ2 канального белка при его открывании и закрывании.
БАЗОВАЯ МОДЕЛЬ И ЕЕ МОДИФИКАЦИИ
Базовая модель. Базовой моделью будем называть модель, представленную уравнением (1). Рассмотрим эту модель более подробно. Для численного анализа базовой модели и нахождения численного решения уравнения (1) удобно перейти к безразмерному времени $\tau = \tilde {\gamma }t$, где $\tilde {\gamma } = \frac{\gamma }{{3{{I}_{g}}}}$ – приведенный коэффициент трения, а потенциальную функцию $U$ выразить через безразмерную потенциальную функцию $\tilde {U}$ следующим образом: $U = {{E}_{g}}\tilde {U}$, где ${{E}_{g}}$ – максимальная величина энергетического барьера между открытым и закрытым положением воротных частиц, соответствующих открытому и закрытому состояниям канала. Тогда уравнение (1) перепишется следующим образом:
(2)
$\begin{gathered} \frac{{{{d}^{2}}\varphi \left( \tau \right)}}{{d{{\tau }^{2}}}} = - \frac{{d\varphi \left( \tau \right)}}{{d\tau }} - \frac{{{{E}_{g}}}}{{{{{\tilde {\gamma }}}^{2}}{{I}_{g}}}}\frac{d}{{d\varphi }} \times \\ \times \,\,\tilde {U}\left( {\varphi \left( \tau \right),W\left( \tau \right),\psi \left( \tau \right),{{V}_{m}}} \right) + \sqrt {\frac{{3kT}}{{2{{{\tilde {\gamma }}}^{3}}{{I}_{g}}}}} \varsigma \left( \tau \right), \\ \end{gathered} $(3)
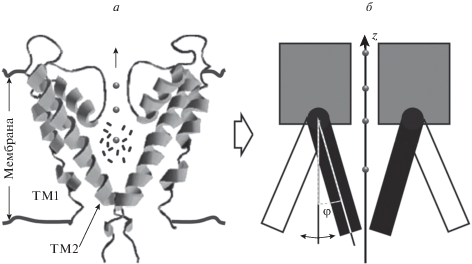
$\begin{gathered} \tilde {U}(\varphi ,W,\psi ,{{V}_{m}}) = A\left( {W,\psi ,{{V}_{m}}} \right) \times \\ \times \,\,\left( {\frac{{{{{\left( {\tilde {L}\sin (\varphi )} \right)}}^{4}}}}{4} - B\left( {W,\psi ,{{V}_{m}}} \right)\frac{{{{{\left( {\tilde {L}\sin (\varphi )} \right)}}^{3}}}}{3} - } \right. \\ \left. { - \,\,\frac{{{{{\left( {\tilde {L}\sin (\varphi )} \right)}}^{2}}}}{2} + B\left( {W,\psi ,{{V}_{m}}} \right)\tilde {L}\sin (\varphi )} \right). \\ \end{gathered} $Здесь $\tilde {L} = \frac{L}{{{{{{D}_{{\max }}}} \mathord{\left/ {\vphantom {{{{D}_{{\max }}}} 4}} \right. \kern-0em} 4}}}$, ${{D}_{{\max }}}$ – максимальный диаметр поры канала в открытом состоянии. Функции $A\left( {W,\psi ,{{V}_{m}}} \right)$ и $B\left( {W,\psi ,{{V}_{m}}} \right)$ выражаются через глубины потенциальных ям закрытого ${{E}_{{\text{c}}}}\left( {W,\psi ,{{V}_{m}}} \right)$ и открытого ${{E}_{{\text{o}}}}\left( {\psi ,{{V}_{m}}} \right)$ состояний канала (рис. 2) следующим образом:
Рис. 2.
Профиль безразмерного потенциала, определяющего конформационные переходы канала во время воротного процесса. Здесь ${{\varphi }_{{\max }}}$ – угол отклонения подвижной части сегмента ТМ2 от оси симметрии одной субъединицы при максимально открытой поре, ${{E}_{{\text{c}}}}$ и ${{E}_{{\text{o}}}}$ – величины глубин потенциальных ям закрытого и открытого состояний канала соответственно.
Глубины потенциальных ям ${{E}_{{\text{c}}}}\left( {W,\psi ,{{V}_{m}}} \right)$ и ${{E}_{{\text{o}}}}\left( {\psi ,{{V}_{m}}} \right)$ являются безразмерными величинами и изменяются от 0 до 1. Они определяют форму профиля конформационной энергии в области ворот, который, в свою очередь, определяет динамику воротных частиц и их переходы между положениями, соответствующими закрытому и открытому состояниям канала. Выражения для ${{E}_{{\text{c}}}}\left( {W,\psi ,{{V}_{m}}} \right)$ и ${{E}_{{\text{o}}}}\left( {\psi ,{{V}_{m}}} \right)$ имеют вид:
(4)
$\begin{gathered} {{E}_{{\text{c}}}}(W,\psi ,{{V}_{m}}) = \frac{1}{{1 + {{e}^{{{{a}_{{\text{c}}}}({{V}_{m}} - {{V}_{{\text{c}}}})}}}}}\frac{1}{2}\left( {1 + {{\varepsilon }_{W}}W(\tau ) + {{\varepsilon }_{\psi }}\psi (\tau )} \right), \\ {{E}_{{\text{o}}}}(\psi ,{{V}_{m}}) = \frac{1}{{1 + {{e}^{{ - {{a}_{{\text{o}}}}({{V}_{m}} - {{V}_{{\text{o}}}})}}}}}\frac{1}{2}\left( {1 - {{\varepsilon }_{\psi }}\psi (\tau )} \right). \\ \end{gathered} $Здесь учитывается зависимость от электрического трансмембранного потенциала ${{V}_{m}}$, которая носит сигмоидный характер с параметрами ${{a}_{{\text{c}}}},{{V}_{{\text{c}}}},{{a}_{{\text{o}}}},{{V}_{{\text{o}}}}$. Кроме того, учитывается влияние гидрофобного $W$ фактора, определяемого взаимодействием гидрофобной выстилки поры канала с молекулами воды, и инерционного $\psi $ фактора, описывающего медленные, по сравнению с переходами канала между состояниями проводимости, и низкоамплитудные, по сравнению с конформационной динамикой воротных частиц, конформационные изменения канала во время воротного процесса.
Изменение во времени гидрофобного фактора определяется уравнением:
(5)
$\begin{gathered} \frac{d}{{d\tau }}W(\tau ) = \frac{{{{\alpha }_{W}}}}{{\tilde {\gamma }}}\left( {{{g}_{W}}(\varphi ) + {{\beta }_{W}}\left( {1 - {{g}_{W}}(\varphi )} \right)} \right) \times \\ \times \,\,\left( { - W(\tau ) - 2{{g}_{W}}(\varphi ) + 1} \right), \\ \end{gathered} $Изменение во времени инерционного фактора определяется уравнением:
(6)
$\frac{d}{{d\tau }}\psi (\tau ) = - \frac{{{{\alpha }_{\psi }}}}{{\tilde {\gamma }}}\left( {\psi (\tau ) + \tilde {L}\sin (\varphi )} \right),$Модель, учитывающая зависимость фактора инерционности от ${{V}_{m}}$. Ранее нами было показано, что корреляционные соотношения в последовательностях закрытых и открытых времен жизни канала во многом определяются скоростью изменения инерционного фактора ${{\alpha }_{\psi }}$ [34]. Таким образом, мы предположили, что модификация базовой модели, учитывающая зависимость ${{\alpha }_{\psi }}$ от ${{V}_{m}}$, может позволить нам описать зависимость корреляционных соотношений от ${{V}_{m}}$. Чтобы сделать это, на основе базовой модели мы подбирали реперные значения параметра ${{\alpha }_{\psi }}$ для различных значений ${{V}_{m}}$ так, чтобы значения показателя Херста ${{H}_{2}}$ приблизительно соответствовали экспериментальным значениям ${{H}_{2}}$ для Kv-канала, взятым из работы [5]. Затем мы провели регрессионный анализ полученных реперных значений с помощью следующей зависимости:
(7)
${{\alpha }_{\psi }}({{V}_{m}}) = {{\alpha }_{{\psi ,1}}}{{e}^{{ - {{b}_{{\psi ,1}}}{{V}_{m}}}}} + {{\alpha }_{{\psi ,2}}}{{e}^{{{{b}_{{\psi ,2}}}{{V}_{m}}}}}.$Параметры ${{\alpha }_{{\psi ,1}}}$, ${{b}_{{\psi ,1}}}$, ${{\alpha }_{{\psi ,2}}}$, ${{b}_{{\psi ,2}}}$, полученные при помощи регрессионного анализа представлены в табл. 1. Коэффициент детерминации регрессии ${{R}^{2}} = 0.98$.
Таблица 1.
Коэффициенты формулы (7)
| ${{\alpha }_{{\psi ,1}}}$, с–1 | ${{b}_{{\psi ,1}}}$, мВ–1 | ${{\alpha }_{{\psi ,2}}}$, с–1 | ${{b}_{{\psi ,2}}}$, мВ–1 |
|---|---|---|---|
| 2.6056 | 0.1833 | 0.1989 | 0.3873 |
Модель, учитывающая зависимость гидрофобного фактора от ${{V}_{m}}$. Кроме вышеописанной модификации, зависимость корреляционных соотношений от ${{V}_{m}}$ можно учесть, введя в базовую модель зависимость относительной скорости вытеснения молекул воды ${{\beta }_{W}}$ из гидрофобной поры канала в закрытом состоянии от ${{V}_{m}}$. Основанием для этого является то, что кинетика ионного тока через модельный канал существенно зависит от параметра ${{\beta }_{W}}$, в частности, он обуславливает формирование пачечной активности. Для выбора зависимости ${{\beta }_{W}}$ от ${{V}_{m}}$ мы использовали подход, аналогичный уже описанному, только в качестве функции регрессии выбирали 4-параметрическую сигмоиду:
(8)
${{\beta }_{W}}({{V}_{m}}) = {{\beta }_{{W,\min }}} + \frac{{{{\beta }_{{W,\max }}}}}{{1 + {{e}^{{ - {{\left( {{{V}_{m}} - {{V}_{{0,W}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{V}_{m}} - {{V}_{{0,W}}}} \right)} {{{b}_{W}}}}} \right. \kern-0em} {{{b}_{W}}}}}}}}},$Параметры ${{\beta }_{{W,\min }}}$, ${{\beta }_{{W,\max }}}$, ${{V}_{{0,W}}}$, ${{b}_{W}}$, полученные при помощи регрессионного анализа представлены в табл. 2. Коэффициент детерминации регрессии ${{R}^{2}} = 0.995$.
Таблица 2.
Коэффициенты формулы (8)
| ${{\beta }_{{W,\min }}}$ | ${{\beta }_{{W,\max }}}$ | ${{V}_{{0,W}}}$, мВ | ${{b}_{W}}$, мВ |
|---|---|---|---|
| 0.089 | 0.9178 | 7.8861 | 6.8907 |
МЕТОДЫ
Для сравнения модели с экспериментальными данными необходимо корректно рассчитать измеряемый ток через канал. Этот ток мы описывали уравнением, учитывающим наличие фильтра низких частот и шум измерительной установки:
(9)
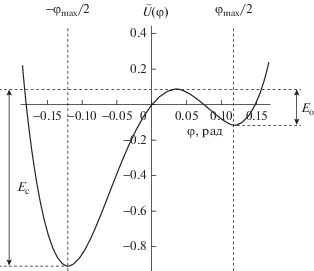
$\frac{d}{{d\tau }}I(\tau ) = \frac{f}{{\tilde {\gamma }}}\left( { - I(\tau ) + {{g}_{i}}\left( {\varphi (\tau )} \right)(V - {{V}_{0}}) + \delta \varsigma (\tau )} \right),$Численно решая уравнения базовой модели или уравнения модифицированных моделей, с учетом уравнения (9), мы получали записи модельного тока, из которых методом полуамплитудного уровня получали кинетические параметры $\left\{ {{{\tau }_{{\text{c}}}}} \right\}$ и $\left\{ {{{\tau }_{{\text{o}}}}} \right\}$ (рис. 3).
Рис. 3.
Фрагмент записи ионного тока через модельный канал (черная линия) и аппроксимация последовательности импульсов тока методом полуамплитудного уровня (белая линия). ${{\tau }_{{{\text{c}},i}}}{{\tau }_{{{\text{o}},i}}}$ – времена жизни канала $i$-го участка последовательности в закрытом и открытом состоянии соответственно.
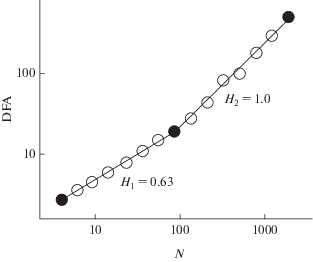
Для анализа кинетических параметров модельного и экспериментального тока использовали метод БФА [37]. В результате получали зависимости усредненной вариации от длины отрезков разбиения исследуемых последовательностей времен жизни канала, которые аппроксимировали одним или несколькими прямыми отрезками (рис. 4). Наклоны отрезков определяют искомые показатели Херста.
Рис. 4.
Показатели Херста, полученные методом БФА. Кружки – анализ кинетических параметров ионного тока через модельный канал, прямые линии – линейная аппроксимация методом наименьших квадратов.
Численные расчеты проводили в среде Matlab с использованием пакета Simulink и численной схемы Рунге–Кутта 4-го порядка с фиксированным шагом интегрирования. Использованные параметры базовой модели приведены в табл. 3. В модифицированной модели, учитывающей зависимость инерционного фактора от ${{V}_{m}}$, используются такие же параметры, как в табл. 3, кроме ${{\varepsilon }_{W}}$ и ${{\beta }_{W}}$, значения которых приведены в табл. 4. В модифицированной модели, учитывающей зависимость гидрофобного фактора от ${{V}_{m}}$, использованы такие же параметры, как в табл. 3, кроме ${{\varepsilon }_{W}}$, ${{\varepsilon }_{\psi }}$, ${{\alpha }_{W}}$ и ${{\alpha }_{\psi }}$, значения которых приведены в табл. 5. Параметры уравнения (9) для тока приведены в табл. 6.
Таблица 3.
Параметры базовой модели
| Параметр | Значение |
|---|---|
| $\tilde {\gamma } = {{\tilde {\gamma }}_{{{\text{calc}}}}}$ | $1 \times {{10}^{6}}\,{{{\text{c}}}^{{ - 1}}}$ ($1 \times {{10}^{9}}\,{{{\text{c}}}^{{ - 1}}}$) |
| ${{E}_{g}}$ | $9.28 \times {{10}^{{ - 28}}}\,{\text{Д ж }}$ ($1 \times {{10}^{{ - 19}}}\,{\text{Д ж }}$) |
| $M$ | ${\text{3}}{\text{.5}} \times {\text{1}}{{{\text{0}}}^{{ - {\text{24}}}}}\,{\text{к г }}$ |
| $L$ | $2.5 \times {{10}^{{ - 9}}}\,{\text{м }}$ |
| $k$ | $1.38 \times {{10}^{{ - 23}}}\,{\text{Д ж }}\,{{{\text{К }}}^{{ - 1}}}$ |
| $T = {{T}_{{{\text{calc}}}}}$ | $1 \times {{10}^{{ - 3}}}\,{\text{К }}$ ($300\,\,{\text{К }}$) |
| ${{D}_{{\max }}}$ | $1.2 \times {{10}^{{ - 9}}}\,{\text{м }}$ |
| ${{a}_{{\text{c}}}}$ | $1.9 \times {{10}^{{ - 5}}}\,\,{{{\text{В }}}^{{ - 1}}}$ |
| ${{V}_{{\text{c}}}}$ | $ - 1.1 \times {{10}^{{ - 1}}}\,\,{\text{В }}$ |
| ${{a}_{{\text{o}}}}$ | $1.3 \times {{10}^{{ - 5}}}\,\,{{{\text{В }}}^{{ - 1}}}$ |
| ${{V}_{{\text{o}}}}$ | $1.7 \times {{10}^{{ - 1}}}\,\,{\text{В }}$ |
| ${{\varepsilon }_{W}}$ | $4 \times {{10}^{{ - 1}}}$ |
| ${{\varepsilon }_{\psi }}$ | $5 \times {{10}^{{ - 2}}}$ |
| ${{\alpha }_{W}}$ | $5 \times {{10}^{2}}\,\,{{{\text{с }}}^{{ - 1}}}$ |
| ${{\beta }_{W}}$ | $5.45 \times {{10}^{{ - 1}}}$ |
| ${{\alpha }_{\psi }}$ | $2\,\,{{{\text{с }}}^{{ - 1}}}$ |
| ${{\tilde {\mu }}_{W}}$ | $1.36 \times {{10}^{1}}$ |
| ${{\varphi }_{W}} = \frac{1}{2}({{\varphi }_{{\max }}} + {{\varphi }_{{\min }}})$ | 0 |
Таблица 4.
Параметры модифицированной модели, учитывающей зависимость инерционного фактора от ${{V}_{m}}$
| Параметр | Значение |
|---|---|
| ${{\varepsilon }_{W}}$ | $3 \times {{10}^{{ - 1}}}$ |
| ${{\beta }_{W}}$ | $5 \times {{10}^{{ - 1}}}$ |
Таблица 5.
Параметры модифицированной модели, учитывающей зависимость гидрофобного фактора от ${{V}_{m}}$
| Параметр | Значение |
|---|---|
| ${{\varepsilon }_{W}}$ | $3.5 \times {{10}^{{ - 1}}}$ |
| ${{\varepsilon }_{\psi }}$ | $7.5 \times {{10}^{{ - 2}}}$ |
| ${{\alpha }_{W}}$ | $1 \times {{10}^{3}}\,\,{{{\text{с }}}^{{ - 1}}}$ |
| ${{\alpha }_{\psi }}$ | $8\,\,{{{\text{с }}}^{{ - 1}}}$ |
Таблица 6.
Параметры уравнения (9) для тока
| Параметр | Значение |
|---|---|
| $f$ | $2.5 \times {{10}^{3}}\,{\text{Г ц }}$ |
| $\delta $ | 2 |
| ${{g}_{{\max }}}$ | 1 |
| ${{\mu }_{i}}$ | $1.36 \times {{10}^{1}}$ |
| ${{\varphi }_{i}} = \frac{1}{2}({{\varphi }_{{\max }}} + {{\varphi }_{{\min }}})$ | 0 |
| $V$ | $4 \times {{10}^{{ - 3}}}\,{\text{В }}$ |
| ${{V}_{0}}$ | $ - 6 \times {{10}^{{ - 2}}}\,{\text{В }}$ |
Для уменьшения времени счета мы перенормировали значения некоторых основных параметров уравнения (2), а именно $\tilde {\gamma }$ и $T$, согласно следующему алгоритму. Известно, что характерное время релаксации участков полипептидной цепи $t \sim {{10}^{{ - 9}}}\,{\text{с }}$, следовательно $\tilde {\gamma } = \frac{1}{t} \sim {{10}^{9}}\,{{{\text{c}}}^{{ - 1}}}$. Обычный температурный диапазон, при котором были получены экспериментальные данные, используемые в данной статье, соответствовал: $T = 290{\kern 1pt} - {\kern 1pt} 295\,\,{\text{K}}$. Время перехода канала из одного состояния в другое составляет $ \sim {\kern 1pt} {{10}^{{ - 5}}}\,{\text{c}}$. В расчетах же $\tilde {\gamma }$ и $T$ были заменены на расчетные параметры, равные соответственно ${{\tilde {\gamma }}_{{{\text{calc}}}}} = {{10}^{6}}\,\,{{{\text{c}}}^{{ - 1}}}$ и ${{T}_{{{\text{calc}}}}} = 0.001\,\,{\text{K}}$ так, чтобы время перехода канала из одного состояния в другое не изменилось, т.е. составляло $ \sim {\kern 1pt} {{10}^{{ - 5}}}\,{\text{c}}$. Параметр ${{E}_{g}}$ также подбирали таким образом, чтобы выполнялось описанное выше условие, и среднее значение закрытых времен $\left\langle {{{\tau }_{{\text{c}}}}} \right\rangle $ и среднее значение открытых времен $\left\langle {{{\tau }_{{\text{o}}}}} \right\rangle $ были $ \sim {\kern 1pt} {{10}^{{ - 3}}}$ с при вероятности открытого состояния ${{P}_{{\text{o}}}} \approx 0.5$. Таким образом, ускорение расчетов заключается в том, что для расчета 1 с размерного времени в случае не перенормированных параметров необходимо провести вычисления в интервале от 0 до ${{10}^{9}}$ у.е. в безразмерном времени, а в случае перенормированных параметров это время сокращается до 106 у.е.
Отметим, что ранее нами были сделаны тестовые расчеты для не перенормированных значений параметров $\tilde {\gamma } = {{10}^{9}}\,\,{{{\text{с }}}^{{ - 1}}}$, $T = 300\,\,{\text{K}}$. При этом для корректности расчетов мы использовали безразмерную случайную силу $\tilde {\varsigma }\left( \tau \right) = {{\varsigma \left( \tau \right)} \mathord{\left/ {\vphantom {{\varsigma \left( \tau \right)} {\sqrt {\tilde {\gamma }} }}} \right. \kern-0em} {\sqrt {\tilde {\gamma }} }}$. В результате тестовых расчетов подобранное значение максимального энергетического барьера было ${{E}_{g}} = {{10}^{{ - 19}}}\,{\text{Д ж }}$. Если учесть, что расчеты проводили для случая, когда вероятность открытого состояния модельного канала приблизительно была равна 0.5, что в модели соответствует ${{V}_{m}} = 4\,\,{\text{м В }}$, а ${{E}_{{\text{c}}}} = {{E}_{{\text{o}}}} = 0.1$, то фактическое значение энергетического барьера соответствовало ${{10}^{{ - 20}}}\,{\text{Д ж }}$. При этом надо отметить, что в тестовых расчетах изменялись только $\tilde {\gamma },\,\,T$ и ${{E}_{g}}$, все остальные параметры оставались такими же, как в случае с перенормированными $\tilde {\gamma },\,\,T$, ${{E}_{g}}$.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
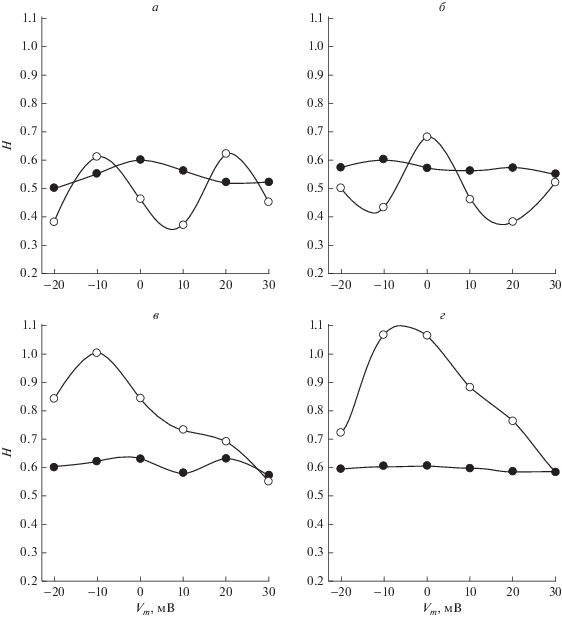
Результаты расчетов на основе базовой модели и ее модификаций представлены на рис. 5а, 5б, 5в. Экспериментальные данные [5, 9] по зависимости показателей Херста (${{H}_{1}}$, ${{H}_{2}}$) от величины трансмембранного потенциала ${{V}_{m}}$ показаны на рис. 5г. Из рис. 5а, 5б, 5в видно, что в модельных данных зависимость показателя Херста ${{H}_{1}}$ от ${{V}_{m}}$ во всех случаях принимает значения, близкие к 0.6, что соответствует экспериментальным значениям (рис. 5г) и говорит о почти абсолютно случайном характере воротного процесса на малых временах (несколько секунд). Вместе с тем, зависимости показателей Херста ${{H}_{2}}$ от ${{V}_{m}}$ имеют значимые различия для трех моделируемых случаев. При этом наиболее близкое поведение к экспериментальным данным соответствует модифицированной модели, учитывающей зависимость гидрофобного фактора от ${{V}_{m}}$ (рис. 5в). Это говорит о важной роли гидрофобного фактора в воротном процессе.
Рис. 5.
Сравнение модельных (а, б, в) и экспериментальных (г) зависимостей показателей Херста от трансмембранного потенциала ${{V}_{m}}$. Модельные расчеты выполнены на основе: а – базовой модели с постоянными параметрами; б – модели, учитывающей зависимость фактора инерционности от ${{V}_{m}}$; в – модели, учитывающей зависимость гидрофобного фактора от ${{V}_{m}}$; г – экспериментальные данные [5]. Белые кружки – ${{H}_{2}}$, черные кружки – ${{H}_{1}}$. На всех графиках кружки соответствуют значениям ${{V}_{m}}$ для экспериментальных кривых.
Важную роль гидрофобного фактора в воротном процессе отмечают и другие исследователи. Так, при помощи метода молекулярной динамики изучен воротный процесс и движение ионов K+ через селективный фильтр Kv1.2-канала [31]. Утверждается, что обнаружен новый фундаментальный механизм “гидрофобных ворот”, который позволяет коллапсировать открытой поре канала в закрытое состояние при обезвоживании ее внутренней гидрофобной полости.
Известно, что гидрофобные взаимодействия обусловлены изменением свободной энергии системы за счет изменения энтропийной составляющей, поэтому можно предположить, что влияние электрического трансмембранного потенциала на скоррелированность событий открывания или закрывания канала во время воротного процесса осуществляется именно через гидрофобный фактор. Действительно, если посмотреть на модель (уравнение (5)), то видно, что гидрофобный фактор зависит от скорости (коэффициент ${{\beta }_{W}}$) вытеснения молекул воды из закрытой поры канала за счет гидрофобных взаимодействий воды с гидрофобной выстилкой поры. Включение электрического поля приводит к поляризации молекул воды и их ориентации по силовым линиям поля за счет наведенного дипольного момента, что, в свою очередь, снижает энтропию системы и увеличивает ее свободную энергию. Это может приводить к увеличению скорости вытеснения молекул воды из поры канала в закрытом состоянии, так как системе не выгодно находиться в состоянии с повышенной свободной энергией, и она стремится перейти в состояние с более низкой свободной энергией.
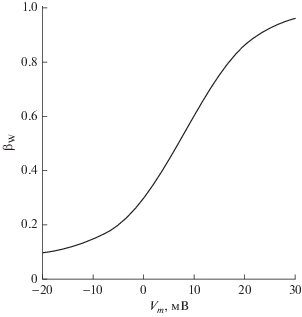
На рис. 6 показана зависимость ${{\beta }_{W}}$ от ${{V}_{m}}$, описываемая уравнением (8). Видно, что эта зависимость носит сигмоидный характер. Изменение ${{V}_{m}}$ от отрицательных значений к положительным ведет к увеличению скорости выхода молекул воды из гидрофобной полости канала, что согласуется с данными [31]. В этой работе при помощи метода молекулярной динамики показано, что при отрицательных значениях трансмембранного электрического потенциала обезвоживание поры Kv1.2-канала происходит за несколько микросекунд, в то время как при значениях ${{V}_{m}} = 0$ мВ и выше, это время сокращается до десятков наносекунд.
Рис. 6.
Зависимость относительной скорости ${{\beta }_{W}}$ (уравнения (5), (8)) вытеснения молекул воды из гидрофобной поры канала в закрытом состоянии от трансмембранного электрического потенциала Vm.
В рамках представленной модифицированной модели, учитывающей зависимость гидрофобного фактора от ${{V}_{m}}$, удалось показать связь между интегральной характеристикой кинетики ионного тока через одиночный ионный канал – показателем Херста, и внутримолекулярным свойством канала – гидрофобностью ионной поры. Ранее мы показывали связь между гидрофобностью ионной поры и полиэкспоненциальностью распределений последовательностей $\left\{ {{{\tau }_{{\text{o}}}}} \right\}$ и $\left\{ {{{\tau }_{{\text{c}}}}} \right\}$ [34]. Сейчас мы показали, что зависимость гидрофобного фактора от ${{V}_{m}}$ может определять зависимость корреляционных соотношений в активности ионного канала от ${{V}_{m}}$. Это является основным отличием наших результатов от результатов, полученных методом молекулярной динамики [31].
Заметим, однако, что наши результаты получены при целом ряде ограничений. Во-первых, ионный канал представляет собой сложный гликопротеиновый комплекс, который имеет модульную структуру. Эта структура включает в себя селективный фильтр, сенсоры электрического потенциала, воротный механизм и цитоплазматическую часть. Однако при моделировании мы упростили структуру канала и рассмотрели только воротный механизм, так как он напрямую участвует в регуляции ионного тока через пору канала.
Мы моделируем работу воротного механизма на основе данных рентгеноструктурного анализа KcsA-канала, состоящего из четырех субединиц. При этом подвижные части (воротные частицы) трансмембранных сегментов каждой субъединицы моделируются жесткими стержнями, т.е. не учитываются их внутренние деформации. Для упрощения расчетов мы также предполагаем, что воротные частицы движутся синхронно и симметрично в радиальных направлениях от центральной оси поры канала. В результате, это позволило рассматривать динамику только одной воротной частицы. Более того, при описании динамики воротной частицы мы учитываем только одну степень свободы.
Известно, что переход канала в открытое состояние, когда проникающие ионы свободно двигаются через пору канала, определяется пороговым значением угла отклонения воротных частиц от центральной оси поры. Мы предположили, что это значение соответствует половине максимального угла отклонения воротных частиц от центральной оси поры канала (приблизительно 6.8°).
Отметим, однако, что все приведенные ограничения не являются принципиальными, и снятие этих ограничений не изменит существенно полученные результаты.
Таким образом, на модифицированной модели воротного механизма одиночного ионного канала показано, что корреляционные соотношения в последовательностях событий открывания ионного канала зависят от электрического трансмембранного потенциала, эта зависимость определяется гидрофобным фактором, что говорит о важности гидрофобных взаимодействий в воротном процессе.
Авторы благодарят Л.В. Якушевич за ценные советы и помощь при написании рукописи.
Список литературы
Varanda W.A., Liebovitch L.S., Figueiroa J.N., Nogueira R.A. 2000. Hurst analysis applied the study of single calcium-activated potassium channel kinetics. J. Theor. Biol. 206, 343–353.
Nogueira R.A., Varanda W.A., Liebovitch L.S. 1995. Hurst analysis in the study of ion current kinetics. Brasilian J. Med. Biol. 28, 491–496.
Kochetkov K.V., Kazachenko V.N., Aslanidi O.V., Chemeris N.K. Gapeev A.B. 1999. Non-Markovian gating of Ca2+-activated K+-channels kidney cells Vero. Rescaled range analysis. J. Biol. Phys. 25, 211–222.
Кочетков К.В., Казаченко В.Н., Асланиди О.В. 2001. Временнáя корреляция событий в “воротном” процессе ионных каналов. Метод нормированного размаха. Биол. мембраны. 18, 51—66.
Казаченко В.Н., Кочетков К.В., Асташев М.Е., Гриневич А.А. 2004. Фрактальные свойства воротного механизма потенциалозависимых K+-каналов в нейронах L. stagnalis. Биофизика. 49, 852–865.
Казаченко В.Н., Кочетков К.В., Асланиди О.В., Гриневич А.А. 2001. Исследование фрактальных свойств “воротного” механизма одиночных ионных каналов методом быстрого Фурье-преобразования. Биофизика. 46, 1062–1070.
Кочетков К.В., Казаченко В.Н., Асланиди О.В. 2003. Применение вейвлет-преобразования для анализа активности одиночных ионных каналов. Биол. мембраны. 20, 359–368.
Кочетков К.В., Казаченко В.Н., Асланиди О.В. 2001. Временнáя корреляция событий в “воротном” процессе ионных каналов. Метод нормированного размаха. Биол. мембраны. 18, 51–66.
Гриневич А.А., Асташев М.Е. 2010. Фрактальные свойства ионных каналов. Saarbrucken: LAP Lambert Acad. Publ. 148 с.
Liebovitch L.S., Fischbarg J., Koniarek J. 1987. Ion channel kinetics: a model based on fractal scaling rather than multistate Markov process. Math. Biosci. 84, 37–68.
Liebovitch L.S., Lullivan J.M. 1987. Fractal analysis of a voltage-dependent potassium channel from cultured mouse hippocampal neurons. Biophys. J. 52, 979–988.
Varanda W.A., Liebovitch L.S., Figueiroa J.N., Nogueira R.A. 2000. Hurst analysis applied the study of single calcium-activated potassium channel kinetics. J. Theor. Biol. 206, 343–353.
Moezzi B., Iannella N., McDonnell M.D. 2016. Ion channel noise can explain firing correlation in auditory nerves. J. Comput. Neurosci. 41, 193–206.
Moezzi B., Iannella N., McDonnell M.D. 2014. Modelling the influence of short term depression in vesicle release and stochastic calcium channel gating on auditory nerve spontaneous firing statistics. Front. Comput. Neurosci. 8, 163.
Colquhoun D., Hawkes A.G. 1977. Relaxation and fluctuations of membrane currents that flow through drug-operated channels. Proc. R. Soc. London Ser. B. 199, 231–262.
Croxton T.L. 1988. A model of the gating of ion channels. Biochim. Biophys Acta. 946, 19–24.
Horn R. 1987. Statistical methods for model discrimination. Applications to gating kinetics and permeation of the acetylholine receptor channel. Biophys. J. 51, 255–263.
McManus O.B., Magleby K.L. 1994. Accounting for the Ca2+-dependet kinetics of single large-conductance Ca2+-activated K+-channels in rat skeletal muscle. J. Physiol. (London). 443, 739–777.
Казаченко В.Н., Кочетков К.В. 2003. Макси-Са2+-активируемые К+-каналы: структура и воротный механизм. Биол. мембраны. 20, 99–120
Liebovitch L.S., Fischbarg J., Koniarek J. 1987. Ion channel kinetics: a model based on fractal scaling rather than multistate Markov process. Math. Biosci. 84, 37–68.
Liebovitch L.S. 1989. Analysis of fractal ion channel gating kinetics: Kinetics rates energy levels and activation energies. Math. Biosci. 93, 97–115.
Liebovitch L.S., Toth T.I. 1990. Fractal activity in cell membrane ion channels. Math. Approach. Cardiac. Arrythmias. 591, 375–391.
Millhauser G.L., Salpeter E.E., Oswald R.E. 1988. Diffusion models of ion channel gating and the origin of power-law distributions from single channel recording. Proc. Natl. Acad. Sci. USA. 85, 1503–1507.
Oswald R.E., Millhause G.L., Carter A.A. 1991. Diffusion model in ion channel gating. Extension to agonist-activated ion channels. Biopys. J. 59, 1136–1142.
Liebovitch L.S., Yang W. 1997. Transition from persistent to antipersistent correlation in biological systems. Phys. Rev. E. 56, 4557–4566.
Kurzynski M., Palacz K., Chelminiak P. 1998. Time course of reactions controlled and gated by intramolecular dynamics of proteins: predictions of the model of random walk on fractal lattices. Proc. Natl. Acad. Sci. USA. 95, 11685–11690.
Liebovitch L.S., Toth T.I. 1991. A model of ionic channel kinetics using deterministic chaotic rather than stochastic processes. J. Theor. Biol. 148, 243–267.
Liebovitch L.S., Czegledy F. 1992. A model of ion channel kinetics based on deterministic motion in a potential with two local minima. Ann. Biomed. Engr. 84, 37–68.
Cavalcanti S., Fontanazzi F. 1999. Deterministic model of ion channel flipping with fractal scaling of kinetics rates. Ann. Biomed. Engr. 27, 682–695.
Liebovitch L.S., Krekora P. 2002. The physical basis of ion channel kinetics: the impotance of dynamics. Proc. Inst. Math. and its Appl. Univ. Minnessota. 129, 27–52.
Jensen M.O., Borhani D.W., Lindorff-Larsen K., Maragakis P., Jogini V., Eastwood M.P., Dror R.O., Shaw D.E. 2010. Principles of conduction and hydrophobic gating in K+ channels. Proc. Natl. Acad. Sci. USA. 107 (13), 5833–5838.
Jensen M.O., Jogini V., Borhani D.W., Leffler A.E., Dror R.O., Shaw D.E. 2012. Mechanism of voltage gating in potassium channels. Science. 336 (6078), 229–233.
Sigg D. 2014. Modeling ion channels: Past, present, and future. J. Gen. Physiol. 144 (1), 7–26.
Гриневич А.А., Асташев М.Е., Казаченко В.Н. 2007. Мультифрактальная кинетика воротного механизма ионных каналов в биологических мембранах. Биол. мембраны. 24 (3), 234–250.
Gazzarrini S., Severino M., Lombardi M., Morandi M., DiFrancesco D., Etten J.L.V., Thiel G., Moroni A. 2003. The viral potassium channel Kcv: structural and functional features. FEBS Letters. 552 (1), 12–16.
Doyle D.A., Morais Cabral J., Pfuetzner R.A., Kuo A., Gulbis J.M., Cohen S.L., Chait B.T., MacKinnon R. 1998. The structure of the potassium channel: Molecular basis of K+ conduction and selectivity. Science. 280 (5360), 69–77.
Peng C.-K., Buldyrev S.V., Halvin S., Simons M., Stanley H.E., Goldberger A.L. 1994. Mosaic organization of DNA nucleotides. Phys. Rev. 49, 1685–1689.
Дополнительные материалы отсутствуют.
Инструменты
Биологические мембраны: Журнал мембранной и клеточной биологии