Биологические мембраны: Журнал мембранной и клеточной биологии, 2022, T. 39, № 3, стр. 186-194

ВВЕДЕНИЕ

Бислойные липидные мембраны являются основным структурным элементом клеточных мембран. За счет чрезвычайно низкой проницаемости, мембраны выполняют в клетках барьерную функцию, изолируя содержимое клеточных органелл от цитоплазмы и цитоплазмы от окружающей среды. Барьерные свойства мембран позволяют поддерживать неравномерное пространственное распределение различных веществ и электрических потенциалов, необходимое для жизнедеятельности клеток, являющихся открытыми неравновесными системами.

Обмен клетки с окружающей средой небольшими молекулами и ионами обеспечивается встроенными в мембрану специализированными каналами и обменниками (пассивный транспорт) или насосами (активный транспорт). Проникновение в клетку или выход из нее крупных молекул или надмолекулярных объектов происходит посредством эндоцитоза и экзоцитоза, соответственно. Примечательно, что при экзоцитозе и эндоцитозе барьерная функция мембран не нарушается: как правило, в этих процессах цитоплазма и окружающая среда ни в какой момент времени не бывают непрерывно связаны, т.е. слияние (экзоцитоз) и деление (эндоцитоз) мембран в норме происходят без утечки [1–3]. Отсутствие утечки подразумевает тонкую перестройку липидного матрикса в этих процессах, сопровождающуюся сильными деформациями мембран [1–5]. Энергия, необходимая для реализации деформаций, обеспечивается работой специализированных белков слияния и деления. Характерная величина энергии деформаций, как правило, настолько велика, что именно она определяет высоты активационных барьеров и, соответственно, скорость протекания процессов [1, 3, 6].

Энергия деформации может быть количественно оценена в рамках адекватной теории упругости. По-видимому, первая теория упругости липидных мембран была разработана Хельфрихом в 1973 году [7]. В ней учитывалась только деформация, аналогичная поперечному изгибу в смектических жидких кристаллах, а также вклад гауссовой кривизны, являющийся топологическим инвариантом. Деформации считались малыми, и энергия вычислялась в квадратичном приближении (закон Гука). По мере развития экспериментальной техники становились доступны для наблюдения дополнительные деформационные моды. Оказалось, что для описания промежуточных структур процесса слияния мембран необходимо учитывать деформацию наклона, при которой оси липидных молекул отклоняются от нормали к поверхности липидного монослоя. Деформация наклона была введена в теорию упругости мембран в работе Хамма и Козлова [8]. Более строгий учет вкладов деформаций во втором порядке был сделан в работе Терци и Дезерно [9], в которой было введено перекрестное слагаемое по деформациям наклона и поперечному изгибу. Однако полученный функционал энергии не мог описывать стабильную упругую систему, поскольку он не являлся положительно определенной квадратичной формой малых деформаций [10], и упругая энергия, в принципе, могла понижаться при бесконечном увеличении амплитуды деформаций. Для получения функционала упругой энергии, стабильного в указанном смысле, необходимо дополнительно учитывать вклад, квадратичный по градиенту деформации поперечного изгиба [10]. При использовании функционалов упругой энергии различной степени полноты и точности вычисляется энергия деформаций липидных монослоев. При этом деформирующие мембрану белки и пептиды сами, как правило, считаются твердыми и недеформируемыми. В рамках теории упругости белки и пептиды учитываются через условия на их границе с липидным монослоем, которые налагаются на деформации мембраны, например на толщину бислоя, ориентацию липидных молекул, краевой угол поверхности липидного монослоя на границе с белком и т.д. [5, 11, 12].

Периферические белки и амфипатические пептиды частично встраиваются в липидный монослой, раздвигая в стороны полярные головки липидов [13, 14]. Трансмембранные белки и пептиды с приблизительно цилиндрической формой трансмембранной части деформируют липидный бислой, если длина трансмембранного участка не совпадает с толщиной гидрофобной части мембраны [15–17]. Когда твердые мембранные включения расположены далеко друг от друга, вызываемые ими деформации мембраны независимы, и их энергия аддитивна. При сближении включений деформации перекрываются, что приводит к эффективному латеральному взаимодействию; характерная длина затухания деформаций в мембране составляет несколько нанометров [12, 18, 19].

Для расчета энергии деформаций обычно используются квадратичные функционалы упругой энергии, применимые лишь в случае малых деформаций [7–10]. Для нахождения пространственного распределения деформаций функционал упругой энергии минимизируется, что приводит к системе линейных дифференциальных уравнений, которая решается в заданных граничных условиях. Для систем, обладающих трансляционной или вращательной симметрией, т.е. являющихся практически одномерными, минимизация функционала упругой энергии приводит к системе обыкновенных линейных дифференциальных уравнений, решение которой может быть получено в аналитическом виде [11, 12]. Однако в случае низкой симметрии рассматриваемой системы получаются уравнения в частных производных, которые, как правило, не удается решить аналитически. В частности, даже простейшая задача о нахождении энергии взаимодействия двух цилиндрических трансмембранных пептидов аналитически не решается [11]. В таких случаях функционал упругой энергии может быть минимизирован численно для каждого заданного набора граничных условий.

Ранее было показано, что латеральное взаимодействие двух частично встроенных в мембрану амфипатических пептидов может быть с хорошей точностью описано в рамках одномерного приближения [12]. В этом приближении предполагается, что оси пептидов параллельны друг другу, длина пептидов бесконечна и система обладает трансляционной симметрией вдоль направления осей пептидов. В такой эффективно одномерной системе энергия деформаций мембраны, отнесенная к единице длины вдоль направления трансляционной симметрии, может быть рассчитана аналитически. Для получения абсолютной величины энергии деформаций мембраны, индуцируемых пептидами конечной длины, необходимо погонную энергию, рассчитанную в одномерном приближении, умножить на эффективную “деформационную” длину пептида. Если оси пептидов практически параллельны друг другу, то “деформационная” длина превышает фактическую длину пептида приблизительно на 1 нм [12]. Если же оси пептидов существенно не параллельны и пересекаются под значительным углом, условно от π/4 до 3π/4, то эффективная “деформационная” длина приблизительно равна размеру (диаметру) пептида в направлении, перпендикулярном его продольной оси. Данное одномерное приближение оказывается близко к подходу Дерягина для расчета энергии взаимодействия, опосредованного быстро (экспоненциально) монотонно убывающими силами в конфигурациях с относительно низкой симметрией [20].

В настоящей работе мы рассмотрели латеральное взаимодействие двух цилиндрических трансмембранных пептидов, опосредованное упругими деформациями мембраны. В данной системе распределение деформаций и их энергия не могут быть получены в аналитическом виде, поэтому мы находили их путем численной минимизации функционала упругой энергии. Энергия взаимодействия двух трансмембранных пептидов была рассчитана аналитически в одномерном приближении в предположении, что система обладает трансляционной симметрией в направлении, перпендикулярном отрезку, соединяющему центры двух пептидов. Мы показали, что взаимодействие цилиндрических трансмембранных пептидов достаточно точно описывается в одномерном приближении.

ПОСТАНОВКА И РЕШЕНИЕ ЗАДАЧИ

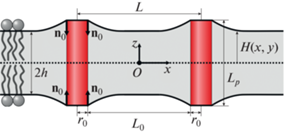
Энергию деформаций мембраны будем рассчитывать в рамках теории упругости Хамма–Козлова [8], обобщенной для учета дополнительных деформационных мод [11, 12]. Состояние деформированного участка липидного монослоя определяется векторным полем единичных векторов n, называемых директорами, характеризующими среднюю ориентацию липидных молекул. Поле директоров задается на некоторой поверхности, называемой нейтральной, проходящей внутри монослоя параллельно его границе с водой в области сочленения полярных головок с гидрофобными цепями липидов. Форма нейтральной поверхности характеризуется векторным полем ее единичных нормалей N. Введем декартову систему координат Oxyz таким образом, чтобы плоская межмонослойная поверхность в исходном недеформированном состоянии совпадала с плоскостью Oxy, ось Oz была перпендикулярна плоскости недеформированной мембраны, начало координат O было расположено в середине отрезка, соединяющего центры трансмембранных пептидов, а ось Ox была направлена вдоль этого отрезка (рис. 1). Монослой, находящийся в области z > 0 будем называть верхним, а в области z < 0 – нижним. Форму нейтральной поверхности верхнего монослоя будем задавать z-координатами ее точек, функцией H(x, y) (рис. 1). Будем учитывать следующие деформации: 1) поперечный изгиб, характеризующийся дивергенцией директора вдоль нейтральной поверхности, div(n); 2) наклон, характеризующийся вектором наклона t = n – N; 3) латеральное растяжение-сжатие, характеризующееся относительным изменением площади нейтральной поверхности, α = (a – a₀)/a₀, где a, a₀ – текущая и исходная площади нейтральной поверхности, приходящиеся на одну липидную молекулу, соответственно; 4) гауссову кривизну $K = \frac{{\partial {{n}_{x}}}}{{\partial x}}\frac{{\partial {{n}_{y}}}}{{\partial y}} - \frac{{\partial {{n}_{x}}}}{{\partial y}}\frac{{\partial {{n}_{y}}}}{{\partial x}}$ где n_x, n_y – проекции директора на соответствующие оси; 5) кручение, характеризующееся ротором директора, rot(n); 6) латеральное натяжение, определяющее работу, которую необходимо совершить для увеличения площади липидного монослоя, пропорциональную [grad(H(x, y))]². Деформации считаются малыми, и энергия записывается во втором порядке по ним следующим образом [11, 12]:

где B, K_t, K_a, K_G, K_rot – модули поперечного изгиба, наклона, латерального растяжения–сжатия, гауссовой кривизны и кручения, соответственно; J₀ – спонтанная кривизна липидного монослоя; σ – латеральное натяжение липидного монослоя; интегрирование ведется по нейтральной поверхности. Мембрана со встроенными в нее трансмембранными цилиндрическими пептидами обладает зеркальной симметрией относительно межмонослойной поверхности, которая при деформации остается плоской. В связи с этим все описание можно относить к одному монослою, для определенности, верхнему, а затем получаемые значения энергии умножить на два. Модуль объемного сжатия мембран очень велик (∼10¹⁰ Дж/м³ ≈ ≈ 3 × 10³k_BT/нм³ [21], где k_BT ≈ 4.14 × 10^–21 Дж), поэтому гидрофобную часть липидного монослоя можно считать локально объемно несжимаемой. Условие объемной несжимаемости налагает связь на возможные деформации. С требуемой точностью оно может быть записано в виде [8]: где h – толщина гидрофобной части липидного монослоя (рис. 1), которую далее будем называть просто толщиной монослоя. Это условие позволяет выразить относительное изменение площади нейтральной поверхности α через дивергенцию директора и форму нейтральной поверхности H(x, y). Вектор единичной нормали к нейтральной поверхности может быть выражен через ее форму: ${\mathbf{N}} = {{\left( {{{\partial H} \mathord{\left/ {\vphantom {{\partial H} {\partial x,}}} \right. \kern-0em} {\partial x,}}{{\partial H} \mathord{\left/ {\vphantom {{\partial H} {\partial y,}}} \right. \kern-0em} {\partial y,}} - {\kern 1pt} 1} \right)}^{T}}$, где T обозначает транспонирование. Таким образом, функционал упругой энергии (1) может быть записан в следующем виде [12, 22]: Функционал энергии необходимо дополнить граничными условиями. Вдали от трансмембранных пептидов мембрана считается плоской и невозмущенной; соответственно, директоры и нормали параллельны друг другу и оси Oz: На границе каждого вертикального цилиндрического трансмембранного пептида ставятся следующие условия: где r₀ – радиус пептида; n_n, n_t – нормальная и касательная к границе пептида компоненты граничного директора n₀ соответственно; L_p – длина трансмембранного пептида (рис. 1).

Вариация функционала (3) по директору и форме нейтральной поверхности монослоя приводит к системе линейных уравнений в частных производных, которая не может быть решена аналитически при граничных условиях (4), (5). Поэтому минимизация функционала проводилась численно с использованием метода конечных элементов с адаптивной расчетной сеткой, аналогично работам [12, 22, 23]. Плоскость Oxy разбивалась на элементарные треугольники. В каждом треугольнике поля деформаций, определяемые функциями n(x, y) = (n_x(x, y), n_y(x, y), –1)^T и H(x, y), аппроксимировались линейными функциями координат (x, y), т.е. поля деформаций заменялись их линейными интерполянтами, заданными на узлах расчетной сетки (вершинах элементарных треугольников). Линейные интерполянты деформаций подставлялись в функционал упругой энергии (3), и поверхностная плотность энергии аналитически интегрировалась по площади каждого элементарного треугольника. Далее бралась сумма энергий по всем треугольным ячейкам расчетной сетки, т.е. по всей нейтральной поверхности липидного монослоя, и получалась полная упругая энергия монослоя W_total. В это выражение для W_total квадратично входят неизвестные значения деформационных полей в узлах расчетной сетки. Чтобы получить численное значение полной упругой энергии, функция W_total аналитически минимизировалась по значениям полей деформации в узлах сетки, за исключением тех, которые задаются граничными условиями. Граничные условия (4) при x, y → ∞ фактически задавались на расстоянии не менее 25 нм от трансмембранных пептидов. Это расстояние существенно превышает характерные длины затухания деформаций мембраны, которые обычно составляют несколько нанометров [12, 22].

Для повышения точности приближенного расчета энергии использовались неоднородные сетки: поверхностная плотность узлов расчетной сетки в окрестности трансмембранных пептидов была повышенной. Границы трансмембранных пептидов в верхнем и нижнем монослоях представлялись в виде кусочно-линейных функций. Окрестность границы пептида разделялась на пять областей; каждая область определялась неравенством r_{i – 1} ≤ d ≤ r_i, где d – расстояние до границы пептида; r_{i – 1}, r_i – константы, определяющие внутреннюю и внешнюю границы областей соответственно для i = 1, 2, 3, 4, 5. Численные значения r_i были следующими: r₀ = 0; r₁ = 1 нм; r₂ = = 1.5 нм; r₃ = 4 нм; r₄ = 11 нм; r₅ = ∞. Максимальная площадь элементарного треугольника расчетной сетки ограничивалась величиной 0.5 γ (в нм²). Введенные пять областей разбивались на элементарные треугольники, площадь которых не превышала γ θ_i, где θ₁ = 0.01, θ₂ = 0.02, θ₃ = 0.04, θ₄ = = 0.05, θ₅ = 0.5. Этот алгоритм позволяет получить численное значение W_total для каждого конкретного значения γ, устанавливаемого вручную. Для повышения точности расчетов величина энергии W_total рассчитывалась при пяти последовательно уменьшающихся значениях γ = 1.5; 1.25; 1.05; 0.85; 0.62. Затем полученная таким образом зависимость W_total от γ аппроксимировалась полиномом второй степени и экстраполировалась на нулевой размер ячейки расчетной сетки, γ → 0. Однако оказалось, что значение W_total, рассчитанное для самой грубой сетки, соответствующей γ = 1.5, отличается от величины W_total, получаемой в результате экстраполяции при γ → 0, не более чем на 1.5%. В связи с этим большая часть расчетов проводились на самой грубой сетке γ = 1.5. В результате были получены зависимости энергии деформаций мембраны от расстояния между двумя цилиндрическими трансмембранными пептидами.

В одномерном приближении в предположении о трансляционной симметрии системы вдоль оси Oy все деформации зависят только от координаты x, и функционал упругой энергии (3) может быть переписан в следующем виде:

где n = n_x – проекция директора на ось Ox. Вариация этого функционала по функциям n(x) и H(x) приводит к двум линейным уравнениям Эйлера–Лагранжа: где штрих обозначает производную по координате x. Из первого уравнения выражается H ′ через n и n ″. Второе уравнение дифференцируется один раз по x, и в получившееся уравнение подставляется H ′, выраженное из первого уравнения. В результате получается изолированное линейное уравнение на n(x) четвертого порядка: где A = K_a/K_t; l ² = B/K_t; s = σ/K_t. Общее решение этого уравнения записывается в виде: где c₁, c₂, c₃, c₄ – постоянные комплексные коэффициенты, которые следует определить из граничных условий, Решение n(x) в виде (9) подставляем в первое уравнение системы (7), откуда, интегрируя по x, находим решение H(x) в виде: Выражения (9) и (11) подставляются в функционал упругой энергии (6). Интегрирование по нейтральной поверхности липидного монослоя позволяет получить аналитическое выражение для упругой энергии мембраны, однако это выражение слишком громоздко и поэтому здесь не приводится.

Четыре комплексных коэффициента c₁, c₂, c₃, c₄ эквивалентны восьми действительным. Однако при наложении условия вещественности функций n(x) и H(x) при любом действительном x остается только четыре независимых действительных коэффициента, которые следует определить из граничных условий. В одномерном приближении граничные условия ставятся следующим образом:

где L₀ — расстояние между границами трансмембранных пептидов; начало координат расположено посередине между пептидами в точке x = 0 (рис. 1). Три граничных условия (12) позволяют найти три неопределенных коэффициента; оставшийся четвертый коэффициент находится путем минимизации по нему полной упругой энергии мембраны. Полученная зависимость упругой энергии в одномерном приближении W(L₀) преобразовывалась в энергию взаимодействия пептидов путем вычитания энергии при L₀ → ∞. Кроме того, для аппроксимации энергии взаимодействия, полученной методом конечных элементов, энергия в одномерном приближении приводилась к тому же аргументу, т.е. к расстоянию между центрами пептидов, а не расстоянию между их границами. Окончательно энергия взаимодействия пептидов в одномерном приближении получалась в следующем виде: Рассчитанная методом конечных элементов энергия взаимодействия аппроксимировалась энергией в одномерном приближении согласно соотношению: где D_eff – эффективный “деформационный” диаметр трансмембранного пептида, α и β – коэффициенты, учитывающие изменения характерных длин деформаций в одномерном приближении по сравнению с реальной низкосимметричной системой. Аппроксимация проводилась методом наименьших квадратов, однако расчетные точки, соответствующие малым расстояниям между пептидами, брались с уменьшенным в 10 раз весом, поскольку при малых расстояниях в области между пептидами теория упругости сплошной среды, вообще говоря, неприменима.

РЕЗУЛЬТАТЫ

Расчеты энергии деформаций мембраны, индуцированных двумя трансмембранными цилиндрическими пептидами, были проведены при следующих параметрах мембран и пептидов. Длина трансмембранной части пептидов считалась равной L_p = 3.6 нм; радиус трансмембранного пептида – r₀ = 0.65 нм, что приблизительно соответствует радиусу α-спирали. Были рассмотрены бислои четырех различных толщин: 2h = 3.0, 3.2, 4.0, 4.2 нм; при 2h = L_p = 3.6 нм пептиды не деформируют мембрану. При каждой толщине бислоя были рассмотрены случаи “мягкой” (обозначаемой индексом “s”) и “жесткой” (обозначаемой индексом “r”) мембран, характеризующихся двумя различными наборами модулей упругости: модули поперечного изгиба B_s = 10 k_BT [23], B_r = = 5B_s = 50 k_BT; модули латерального растяжения-сжатия K_s = 133 мН/м [23], K_r = 5K_s = 665 мН/м. Модули гауссовой кривизны и кручения выражались через модуль поперечного изгиба: K_G = –B/2 [24], K_rot = B/2 [12, 22]. Модуль наклона определяется величиной поверхностного натяжения границы раздела вода – гидрофобные цепи липидов и должен слабо зависеть от конкретной химической структуры и состояния липида; он считался равным K_t = 40 мН/м [8]. Латеральное натяжение считалось равным σ = 0.1 мН/м; получаемые результаты слабо зависят от его конкретной величины. Спонтанная кривизна дает постоянный вклад в упругую энергию, не зависящий от расстояния между пептидами [22]. Поскольку мы рассматриваем энергии взаимодействия, отсчитываемые от энергии состояния бесконечно удаленных друг от друга пептидов (см. (13)), постоянные вклады в упругую энергию не учитывались. Функционал упругой энергии (3) минимизировался методом конечных элементов при следующих дискретных расстояниях между центрами пептидов: L = {1.4, 1.7, 2.0, 2.4, 2.8, 3.2, 3.6, 4.0, 4.5, 5.0, 5.5, 6.0, 6.5, 7.0, 7.5, 8.0, 8.5, 9.0, 9.5, 10.0, 11.0, 12.0, 13.0, 14.0, 15.0, 16.0, 18.0, 20.0, 24.0, 28.0} нм. При аппроксимации расчетные энергии при первых трех расстояниях брались с уменьшенным весом.

Результаты расчетов энергии взаимодействия двух цилиндрических трансмембранных пептидов методом конечных элементов и в рамках одномерного приближения приведены на рис. 2. Значения энергии, полученные численно методом конечных элементов, аппроксимировались кривыми, рассчитанными в одномерном приближении согласно соотношению (14). В случае, когда L_p = 2h = 3.6 нм, пептиды не деформируют мембрану и энергия взаимодействия пептидов постоянна и равна нулю. При L_p ≠ 2h возникают упругие деформации мембраны, которые опосредуют латеральное взаимодействие пептидов. При всех значениях параметров пептиды отталкиваются (энергия взаимодействия положительна) на больших расстояниях (L > 4–6 нм) и притягиваются (энергия взаимодействия отрицательна) на малых расстояниях (L < 4 нм) (рис. 2). Индуцируемые пептидами деформации затухают на расстояниях порядка нескольких нанометров, и при L > > 10 нм энергия взаимодействия становится пренебрежимо малой (рис. 2). Таким образом, для сближения пептидов необходимо преодолеть некоторый энергетический барьер, высота которого практически не зависит от жесткости мембраны (ср. соответствующие кривые на рис. 2а и 2б), но зависит от разности (L_p – 2h). Положение вершины барьера смещается вправо приблизительно на 1 нм при увеличении толщины бислоя с 2h = = 3.0 нм до 2h = 4.2 нм (рис. 2).

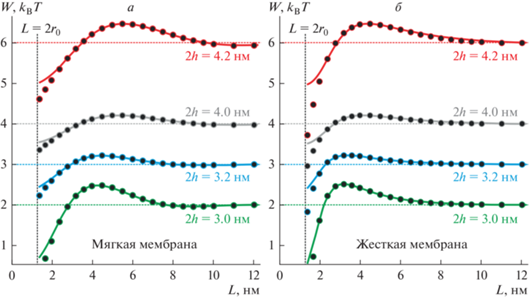
Из графиков (рис. 2) видно, что одномерное приближение достаточно хорошо описывает взаимодействие цилиндрических трансмембранных пептидов при расстояниях между центрами пептидов L ≥ 2 нм независимо от жесткости и толщины мембраны. При расстоянии между центрами L = 2 нм расстояние между границами пептидов составляет L₀ = L – 2r₀ = 0.7 нм, что приблизительно соответствует латеральному размеру одной липидной молекулы. Применение теории упругости сплошной среды для описания состояния участка мембраны между пептидами при меньших расстояниях между ними, вообще говоря, не вполне корректно, особенно в одномерном приближении. Параметры D_eff , α и β аппроксимации энергий взаимодействия, полученных численно методом конечных элементов, кривыми, рассчитанными в одномерном приближении согласно соотношению (14), приведены в табл. 1.

Из табл. 1 видно, что параметры аппроксимации D_eff и α практически не зависят от толщины бислоя. В настоящей работе мы фиксировали длину трансмембранного пептида (L_p = 3.6 нм) и варьировали толщину бислоя. Независимость D_eff и α от h позволяет применять разработанный подход в другой постановке: при фиксированной толщине бислоя можно аналогичным образом рассматривать взаимодействие цилиндрических трансмембранных пептидов различной длины. При увеличении жесткости мембраны в 5 раз параметр α меняется слабо (с ∼0.9 до ∼1.1), однако D_eff уменьшается приблизительно в 2 раза, c ∼0.70 до ∼0.33. В подходе Дерягина [20] для приближенного расчета энергии взаимодействия кривых поверхностей на основе одномерного приближения эффективная длина l_eff, по которой взаимодействуют кривые поверхности, в наших обозначениях определяется выражением:

где l_d – характерная длина затухания сил, опосредующих взаимодействие. В табл. 1 приведены значения длин затухания (l_d) и осцилляций (l_o) деформаций мембраны, полученные из (10) как l_d = 1/|Re(q)|, l_o = 1/|Im(q)|. Из таблицы видно, что D_eff не связано напрямую с l_d, например, потому, что l_d сильно зависит от толщины липидного монослоя, в то время как D_eff от нее практически не зависит. Таким образом, несмотря на то что одномерное приближение позволяет достаточно точно находить энергии взаимодействия цилиндрических трансмембранных пептидов (рис. 2), эффективный “деформационный” диаметр пептидов D_eff не может быть определен в рамках подхода Дерягина согласно соотношению (15). Это, по-видимому, связано с тем, что l_eff в виде (15) получается в предположении r₀ ⪢ l_d, что в нашем случае заведомо не выполняется. Кроме того, подход Дерягина был обоснован для монотонно затухающих с расстоянием сил, опосредующих взаимодействие [20], в то время как деформации мембраны затухают и осциллируют, т.е. затухают немонотонно, поскольку |Im(q)| = 1/l_o ≠ 0 (табл. 1).

Отметим, однако, что при увеличении жесткости мембраны в 5 раз эффективный “деформационный” диаметр пептидов уменьшился приблизительно в (0.72/0.32) = 2.25 ≈ $\sqrt 5 $ раз, причем практически независимо от толщины бислоя. Таким образом, на основании результатов расчетов, приведенных в табл. 1, можно предварительно предположить, что эффективный диаметр пептидов, определяющий их латеральное взаимодействие в одномерном приближении, должен быть обратно пропорционален корню квадратному из жесткости мембраны. При этом наиболее вероятно, что деформацией, определяющей величину D_eff, является поперечный изгиб. Модули поперечного изгиба и латерального растяжения–сжатия имеют разную размерность. Для сравнения “жесткостей” этих деформаций необходимо привести их модули к одной размерности. Можно модуль поперечного изгиба разделить на квадрат характерного параметра липидного монослоя, имеющего размерность длины, т.е., например, на его толщину h. Тогда B/h² ≈ (10 k_BT)/(2 нм)² = = 0.625 k_BT/нм², в то время как K_a = 133 мН/м ≈ ≈ 32 k_BT/нм², т.е. K_a ⪢ B/h². Таким образом, деформация латерального растяжения–сжатия значительно более “жесткая”, и ее энергия, соответственно, существенно меньше, чем энергия деформации поперечного изгиба.

Таким образом, в настоящей работе мы обосновали применение одномерного приближения для расчета энергии взаимодействия цилиндрических трансмембранных пептидов в липидных бислоях различной толщины и жесткости. Величины энергии, рассчитанные в одномерном приближении, значительно отклоняются от точных значений, когда расстояние между границами пептидов становится меньше латерального размера липидной молекулы. Однако в таких условиях применение теории упругости сплошной среды в целом не вполне корректно. При больших расстояниях между пептидами одномерное приближение достаточно хорошо воспроизводит результаты точного (численного) расчета. Эффективный “деформационный” диаметр трансмембранного пептида практически не зависит от толщины бислоя и, по-видимому, обратно пропорционален корню квадратному из модуля поперечного изгиба.

Работа выполнена при поддержке Российского научного фонда (грант № 22-24-00834).