1. На главную
  2. Электронные версии
  3. Биологические мембраны: Журнал мембранной и клеточной биологии
  4. T. 39, № 5, 2022

Биологические мембраны: Журнал мембранной и клеточной биологии, 2022, T. 39, № 5, стр. 384-397

Возможность формирования пор в липидных мембранах несколькими молекулами амфипатических пептидов

О. В. Кондрашов a, С. А. Акимов a, *

a Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
119071 Москва, Россия

* E-mail: akimov_sergey@mail.ru

Поступила в редакцию 04.05.2022
После доработки 02.06.2022
Принята к публикации 03.06.2022

Полный текст (PDF)

Аннотация

Антимикробная активность некоторых амфипатических пептидов связана с образованием сквозных пор в бактериальных мембранах. Антимикробные пептиды (АМП) специфически связываются с плазматической мембраной, встраивая в наружный липидный монослой свои гидрофобные участки. Мембрана при этом неизбежно деформируется. Многие АМП формируют так называемые тороидальные поры, кромка которых частично выстлана пептидными молекулами. Кромка поры характеризуется значительными деформациями. В настоящей работе мы рассчитали энергию кромки поры, на экваторе которой расположены амфипатические пептиды, а также энергию деформаций, индуцируемых АМП в плоском липидном бислое. Было показано, что при определенных физико-химических и геометрических характеристиках молекулы АМП энергия поры, на экваторе которой расположены две и более пептидные молекулы, может быть ниже, чем энергия деформаций плоского бислоя, индуцированных тем же количеством пептидных молекул. Таким образом, две молекулы АМП, в принципе, могут образовать сквозную пору в мембране, хотя это возможно лишь в достаточно узком диапазоне физико-химических и геометрических характеристик пептидов.

Ключевые слова: антимикробный пептид, теория упругости, пора, линейное натяжение, амфипатический пептид

ВВЕДЕНИЕ

Липидные бислои являются структурной основой плазматических мембран клеток. Липидные молекулы амфифильны, что обуславливает чрезвычайно низкую проницаемость мембран [1] и позволяет мембранам выполнять их основную – барьерную – функцию в клетках. За счет барьерной функции мембран поддерживаются значительные перепады химических и электрических потенциалов, а также концентраций различных веществ, необходимые для нормального функционирования клеток, которые являются открытыми неравновесными системами. Даже кратковременное и локальное нарушение барьерной функции мембран вследствие образования в них сквозных пор, как правило, приводит к гибели клетки, на чем основывается действие перспективных антимикробных препаратов пептидной природы [2–4]. Антимикробные пептиды (АМП) содержат в своем составе как гидрофильные, так и гидрофобные аминокислоты, т.е. являются амфипатическими, и при взаимодействии с мембраной частично встраиваются в нее, погружая внутрь свои гидрофобные участки [2–7]. Встраивание неизбежно сопровождается деформациями мембраны [8–11]. Затем по не вполне понятному механизму в мембране образуется сквозная пора, что приводит к гибели патогенной клетки [2–4, 6, 11, 12]. Интенсивная порация происходит при превышении некоторой пороговой поверхностной концентрации молекул АМП, связанных с мембраной, что может указывать на то, что образование поры требует участия нескольких пептидных молекул [2, 4, 12–14]. Предполагается, что латеральное взаимодействие молекул АМП, необходимое для обеспечения их кооперативного действия в процессе порации, может быть опосредовано упругими деформациями мембраны [10, 15, 16]. Когда деформирующие мембрану частично встроенные в нее пептиды расположены далеко друг от друга, деформации независимы, и их энергия аддитивна. При сближении деформации перекрываются, что приводит к эффективному латеральному взаимодействию пептидов [15–17]. При неглубоком встраивании твердой амфипатической молекулы в липидный монослой полярные головки липидов раздвигаются в разные стороны, и монослой локально становится выпуклым, т.е. его поверхность приобретает положительную кривизну (рис. 1а). Такую же кривизну индуцируют лизоформы липидов [18], которые способствуют образованию в мембранах сквозных пор [19].

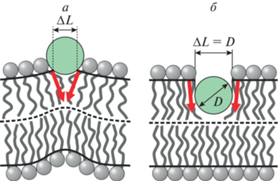
Рис. 1.

Деформации мембраны, индуцированные частично встроенным в липидный монослой амфипатическим пептидом. Пептид показан зеленым кругом, граничные директоры – красными стрелками, нейтральные поверхности монослоев – сплошными черными кривыми, межмонослойная поверхность – штриховыми кривыми. а – Неглубокое встраивание пептида. Ширина встроенной области ΔL на нейтральной поверхности меньше диаметра пептида D. Индуцируется значительный скачок граничного директора (большой угол между красными стрелками); поверхность мембраны становится выпуклой. б – Глубокое встраивание пептида. Ширина встроенной области ΔL на нейтральной поверхности равна диаметру пептида D. Индуцируется небольшой скачок граничного директора (красные стрелки почти параллельны друг другу); поверхность мембраны остается практически плоской.

Кромка поры характеризуется значительными деформациями мембраны [19–21]. Как правило, их энергия настолько велика, что в немодифицированной мембране, липидный состав которой близок к составу плазматических мембран бактериальных или эукариотических клеток, поры спонтанно (без внешнего воздействия) не образуются. Для качественного анализа особенностей процесса порации используется модель разрыва тонких пленок, разработанная Дерягиным и Гутопом [22]. В этой модели предполагается, что к тонкой бесструктурной пленке приложено некоторое внешнее латеральное натяжение σ. Кромка поры характеризуется избыточной энергией материала пленки по сравнению с энергией вдали от кромки. Эта избыточная энергия, отнесенная к периметру поры, называется линейным натяжением γ. В таких обозначениях, энергия создания круглой поры радиуса R может быть записана в виде: E(R) = 2πRγ – πR2σ [22]. Первое слагаемое описывает изменение внутренней энергии пленки, а второе слагаемое учитывает работу внешних сил в процессе порации. Зависимость энергии поры от радиуса имеет максимум при критическом радиусе R* = γ/σ. Поры, радиус которых меньше критического, самопроизвольно закрываются. Закритические поры (R > R*) неограниченно растут, что приводит к необратимому разрыву пленки. Для образования закритической поры необходимо преодолеть энергетический барьер высотой ΔE = E(R*) = πγ2/σ. Высота барьера может быть понижена за счет увеличения латерального натяжения либо за счет уменьшения линейного натяжения. Применительно к мембранам, для образования пор, как правило, прикладывается напрямую латеральное натяжение [23–25] либо подается трансмембранная разность электрических потенциалов, что также приводит к увеличению латерального натяжения [26–29]. Однако натяжения, возникающие при связывании и частичном встраивании в замкнутые мембраны молекул АМП, оказываются недостаточными для эффективной порации. Кроме того, АМП эффективно образуют поры в модельных мембранах Мюллера–Рудина или Монтала, которые принципиально связаны с липидным резервуаром [30]. В этих мембранах латеральное натяжение определяется резервуаром и практически не меняется при адсорбции пептидов. Из качественной модели Дерягина–Гутопа, таким образом, следует, что для образования пор АМП должны понижать линейное натяжение. В серии работ было экспериментально показано, что АМП формируют два основных типа пор: 1) “бочкообразные” поры, в которых кромка полностью образована пептидными молекулами; 2) “тороидальные” поры, в которых кромка частично выстлана АМП [11–13, 31–33]. Исходя из того, что АМП индуцируют положительную кривизну поверхности монослоев, схожую со спонтанной кривизной лизоформ липидов, способствующих образованию пор, можно заключить, что АМП могут снижать линейное натяжение за счет релаксации упругих напряжений на кромке поры. Отметим, что значительная положительная кривизна индуцируется только при неглубоком встраивании пептидной молекулы в липидный монослой (рис. 1а). Если же при встраивании помимо липидных головок расходятся в стороны также и углеводородные цепи липидных молекул, то мембрана остается практически плоской, т.е. ее поверхность имеет приблизительно нулевую кривизну (рис. 1б). Кроме того, пептидные молекулы, по-видимому, значительно тверже углеводородных цепей липидов, и при деформации мембраны сами пептидные молекулы практически не деформируются. В этом случае АМП могут снижать линейное натяжение просто за счет частичного или полного замещения сильно деформированного липидного материала на кромке поры на твердую недеформируемую среду (пептид). Для такого механизма уменьшения линейного натяжения не важно, насколько глубоко встроена в мембрану молекула АМП.

Молекулярные механизмы кооперативного формирования пор в мембранах молекулами АМП в настоящее время не выяснены. Однако известно, что образованию поры предшествует адсорбция и частичное встраивание молекул АМП в липидный монослой [2, 4–6]. В конце концов, формируется сквозная пора, кромка которой частично выстлана молекулами АМП [31–33], либо кромка находится в поле деформаций, индуцированных молекулами АМП [34]. Таким образом, известны начальное и конечное состояния процесса порации. Для спонтанного протекания этого процесса необходимо (хотя и не достаточно), чтобы энергия конечного состояния по крайней мере не превышала значительно энергию начального состояния. В настоящей работе мы рассчитали энергию деформаций мембраны, индуцированных встроенными в липидный монослой молекулами АМП. Рассмотрены α-спиральные амфипатические пептиды, у которых одна боковая поверхность спирали гидрофильна, а противоположная боковая сторона спирали гидрофобна. Далее была рассчитана энергия кромки поры, на экваторе которой расположены молекулы АМП. Расчеты проделаны для случаев неглубокого и глубокого встраивания пептидов в липидный монослой. Глубина встраивания определяется соотношением гидрофобной и гидрофильной площадей боковой поверхности спирали: более гидрофобные спиральные пептиды должны глубже встраиваться в липидный монослой. Получено, что лишь в случае неглубокого встраивания пептидов энергии начального и конечного состояний процесса образования пор могут быть близки. При глубоком встраивании пептидов уменьшение линейного натяжения кромки оказывается недостаточным для эффективной порации.

ПОСТАНОВКА И РЕШЕНИЕ ЗАДАЧИ

Функционал упругой энергии. Для расчета энергии и пространственного распределения деформаций мембраны использовался функционал упругой энергии, полученный Хаммом и Козловым [35]. Этот функционал учитывает деформации поперечного изгиба, седлового изгиба и наклона. Кроме того, мы дополнительно учли приложенное к мембране латеральное натяжение, а также деформацию латерального растяжения–сжатия [15, 17, 19, 34, 36]. Все деформации считались малыми, и энергия вычислялась в квадратичном порядке по ним. Для формального описания изгибовых деформаций вводится векторное поле единичных векторов n, называемых директорами. Это поле характеризует среднюю ориентацию липидных молекул. Поле директоров задается на так называемой нейтральной поверхности, проходящей внутри липидного монослоя в области сочленения полярных головок и углеводородных цепей липидов [37]. На нейтральной поверхности деформации поперечного изгиба и латерального растяжения–сжатия энергетически независимы в том смысле, что в функционале упругой энергии отсутствует слагаемое, перекрестное по этим деформациям [35, 37]. Форма нейтральной поверхности характеризуется векторным полем ее единичных нормалей N. Деформация поперечного изгиба описывается дивергенцией директора вдоль нейтральной поверхности, div(n). Деформация наклона характеризуется вектором наклона t; для малых деформаций t = n – N [35]. Седловой изгиб равен произведению слагаемых, входящих в дивергенцию директора. В частности, если нейтральная поверхность лежит в плоскости Oxy некоторой декартовой системы координат, то седловой изгиб $K = \frac{{\partial {{n}_{x}}}}{{\partial x}}\frac{{\partial {{n}_{y}}}}{{\partial y}} - \frac{{\partial {{n}_{x}}}}{{\partial y}}\frac{{\partial {{n}_{y}}}}{{\partial x}}$, где nx, ny – соответствующие проекции директора [17]. Латеральное растяжение–сжатие описывается относительным изменением площади нейтральной поверхности α = (a – a0)/a0, где a и a0 – текущая и начальная площади нейтральной поверхности соответственно, приходящиеся на липидную молекулу. Энергия, связанная с латеральным натяжением, пропорциональна изменению (увеличению) площади исходно плоской нейтральной поверхности в результате деформации. Это увеличение площади происходит не вследствие растяжения нейтральной поверхности, а за счет вытягивания дополнительной площади из липидного резервуара. Формально латеральное натяжение может быть приложено к латерально нерастяжимой поверхности. В введенных обозначениях энергия деформированного участка монослоя записывается в следующем виде [17, 34, 35]:

(1)
$\begin{gathered} W = \int {dS\left( {\frac{{{{K}_{c}}}}{2}{{{\left( {{\text{div}}{\kern 1pt} \left( {\mathbf{n}} \right) + {{J}_{0}}} \right)}}^{2}} - \frac{{{{K}_{c}}}}{2}J_{0}^{2} + \frac{{{{K}_{t}}}}{2}{{{\mathbf{t}}}^{2}} + } \right.} \\ \left. { + \,\,\frac{{{{K}_{a}}}}{2}{{\alpha }^{2}} + {{K}_{G}}K} \right) + \int {{{\sigma }_{0}}dS} - {{\sigma }_{0}}{{A}_{0}}, \\ \end{gathered} $
где интегрирование ведется по нейтральной поверхности; J0 – спонтанная кривизна монослоя; A0 – площадь нейтральной поверхности в исходном недеформированном состоянии; Kc, Kt, Ka, KG – модули поперечного изгиба, наклона, латерального растяжения-сжатия и седлового изгиба соответственно; σ0 – латеральное натяжение. Дифференциальные уравнения, получающиеся при вариации (минимизации) функционала упругой энергии (1) по полям деформаций, вообще говоря, являются уравнениями в частных производных и, как правило, не могут быть решены аналитически. Решение может быть получено лишь в случае достаточно высокой симметрии рассматриваемой системы, например, трансляционной или вращательной. В этих случаях вариационные уравнения становятся обыкновенными линейными дифференциальными уравнениями и могут быть решены аналитически.

Энергия деформаций мембраны, индуцированных одиночным пептидом. Для расчета энергии деформаций, индуцированных частично встроенным в мембрану одиночным пептидом, рассмотрим горизонтальный липидный бислой, в верхний монослой которого встроена молекула АМП. Для определенности будем считать, что амфипатический пептид имеет α-спиральную вторичную структуру и ось спирали параллельна плоскости мембраны. Введем декартову систему координат Oxyz, ось Oy которой параллельна оси спирали, ось Ox перпендикулярна оси спирали, ось Oz перпендикулярна плоскости мембраны и проходит через ось спирали. Ранее мы показали, что энергия и пространственное распределение деформаций, индуцированных частично встроенным в липидный монослой амфипатическим пептидом, достаточно точно описываются в одномерном приближении, в предположении о трансляционной симметрии системы вдоль направления продольной оси α-спирали [15], т.е. оси Oy в введенной декартовой системе координат. В этом случае вычисляется погонная упругая энергия, т.е. отнесенная к единице длины вдоль направления трансляционной симметрии. Для получения абсолютной величины энергии деформаций, индуцируемых пептидом конечной длины, погонную энергию необходимо умножить на эффективную “деформационную” длину пептида, которая приблизительно на 1 нм превосходит фактическую длину α-спирали [15]. При трансляционной симметрии формально оказывается равным нулю седловой изгиб. Однако по теореме Гаусса–Боне интеграл по поверхности от седлового изгиба дает константу, зависящую только от связности области интегрирования. Таким образом, энергия, связанная с седловым изгибом, может быть вычислена напрямую, без предположения о трансляционной симметрии системы, и соответствующая величина может быть добавлена к упругой энергии, вычисленной в рамках этого предположения.

В предположении о трансляционной симметрии все поля деформаций зависят только от координаты x, и все векторные величины в (1) могут быть заменены их проекциями на ось Ox: n → nx = n, N → Nx = N, t → tx = t. Форму нейтральной поверхности будем описывать z-координатами ее точек, функцией H(x); форму межмонослойной поверхности – функцией M(x). Ниже все величины, относящиеся к верхнему монослою, будем обозначать индексом “u”, к нижнему монослою – индексом “l”. С требуемой точностью Nu = dHu(x)/dx; Nl = –dHl(x)/dx; div(nu) = = dnu(x)/dx; div(nl) = dnl(x)/dx; изменение площади нейтральной поверхности (единичной ширины вдоль оси Oy) вследствие отклонения ее от плоскости $\int {dS} - {{A}_{0}}$ → $\int {\left( {\sqrt {1 + {{{\left[ {{\mathbf{grad}}\left( H \right)} \right]}}^{2}}} - 1} \right)dx} $ ≈ ≈ $\int {\frac{1}{2}{{{\left( {{{dH} \mathord{\left/ {\vphantom {{dH} {dx}}} \right. \kern-0em} {dx}}} \right)}}^{2}}dx} $. Модуль объемного сжатия мембран очень велик, ∼1010 Дж/м3 [38], и с высокой точностью гидрофобная часть липидного монослоя может считаться локально объемно несжимаемой. В рамках линейной теории условие локальной объемной несжимаемости для верхнего и нижнего монослоев, соответственно, записывается в виде [15, 35]:

(2)
$\begin{gathered} {{H}_{u}} - M = h - \frac{{{{h}^{2}}}}{2}\frac{{d{{n}_{u}}}}{{dx}} - h{{\alpha }_{u}}, \hfill \\ M - {{H}_{l}} = h - \frac{{{{h}^{2}}}}{2}\frac{{d{{n}_{l}}}}{{dx}} - h{{\alpha }_{l}}, \hfill \\ \end{gathered} $
где h – толщина гидрофобной части липидного монослоя, ниже для простоты называемая просто толщиной монослоя. Из условий (2) выражаются формы нейтральных поверхностей монослоев Hu, Hl. через которые выражаются проекции Nu, Nl единичных нормалей на ось Ox, входящие в проекции вектора наклона tu = nu – Nu, tl = nl – Nl. Таким образом, функционал упругой энергии участка деформированного бислоя (единичной ширины в направлении оси Oy) в предположении о трансляционной симметрии и малости всех деформаций может быть записан в следующем виде:
(3)
$\begin{gathered} W = \frac{{{{K}_{t}}}}{2}\int {\left\{ {{{l}^{2}}{{{\left( {n_{u}^{'} + {{J}_{0}}} \right)}}^{2}} - {{l}^{2}}J_{0}^{2} + } \right.} \\ + \,\,{{\left( {{{n}_{u}} - M{\kern 1pt} ' + \frac{{{{h}^{2}}}}{2}n_{u}^{{''}} + h\alpha _{u}^{'}} \right)}^{2}} + \\ \left. { + \,\,A\alpha _{u}^{2} + \sigma {{{\left( {M{\kern 1pt} ' - \frac{{{{h}^{2}}}}{2}n_{u}^{{''}} - h\alpha _{u}^{'}} \right)}}^{2}}} \right\}dx + \\ + \,\,\frac{{{{K}_{t}}}}{2}\int {\left\{ {{{l}^{2}}{{{\left( {n_{l}^{'} + {{J}_{0}}} \right)}}^{2}} - {{l}^{2}}J_{0}^{2} + } \right.} \\ + \,\,{{\left( {{{n}_{l}} + M{\kern 1pt} '\,\, + \frac{{{{h}^{2}}}}{2}n_{l}^{{''}} + h\alpha _{l}^{'}} \right)}^{2}} + \\ \left. { + \,\,A\alpha _{l}^{2} + \sigma {{{\left( {M{\kern 1pt} '\,\, + \frac{{{{h}^{2}}}}{2}n_{l}^{{''}} - h\alpha _{l}^{'}} \right)}}^{2}}} \right\}dx, \\ \end{gathered} $
где l2 = Kc/Kt, A = Ka/Kt, σ = σ0/Kt; штрих обозначает производную по координате x. Вариация функционала (3) по функциям nu(x), nl(x), αu(x), αl(x), M(x) приводит к пяти уравнениям Эйлера–Лагранжа:

(4)
$\left\{ \begin{gathered} \frac{{{{h}^{4}}}}{4}\left( {1 + \sigma } \right)n_{u}^{{\left( 4 \right)}} + \left( {{{h}^{2}} - {{l}^{2}}} \right)n_{u}^{{''}} + {{n}_{u}} - \,\,\frac{{{{h}^{2}}}}{2}\left( {1 + \sigma } \right)M{\kern 1pt} '''\,\, - M{\kern 1pt} '\,\, + \frac{{{{h}^{3}}}}{2}\left( {1 + \sigma } \right){{\alpha }_{u}} + h\alpha _{u}^{'} = 0, \hfill \\ \frac{{{{h}^{4}}}}{4}\left( {1 + \sigma } \right)n_{l}^{{\left( 4 \right)}} + \left( {{{h}^{2}} - {{l}^{2}}} \right)n_{l}^{{''}} + {{n}_{l}} + \frac{{{{h}^{2}}}}{2}\left( {1 + \sigma } \right)M{\kern 1pt} '''\,\, - M{\kern 1pt} '\,\, + \frac{{{{h}^{3}}}}{2}\left( {1 + \sigma } \right){{\alpha }_{l}} + h\alpha _{l}^{'} = 0, \hfill \\ \frac{{{{h}^{2}}}}{2}\left( {1 + \sigma } \right)\left( {n_{u}^{{'''}} - n_{l}^{{'''}}} \right) + n_{u}^{'} - n_{l}^{'} - \,\,2\left( {1 + \sigma } \right)M{\kern 1pt} ''\,\, + h\left( {1 + \sigma } \right)\left( {\alpha _{u}^{{''}} - \alpha _{l}^{{''}}} \right) = 0, \hfill \\ \frac{{{{h}^{2}}}}{2}\left( {1 + \sigma } \right)n_{u}^{{'''}} + n_{u}^{'} - \,\,\left( {1 + \sigma } \right)M{\kern 1pt} '' + h\left( {1 + \sigma } \right)\alpha _{u}^{{''}} - \frac{A}{h}{{\alpha }_{u}} = 0, \hfill \\ \frac{{{{h}^{2}}}}{2}\left( {1 + \sigma } \right)n_{l}^{{'''}} + n_{l}^{'} + \,\,\left( {1 + \sigma } \right)M{\kern 1pt} '' + h\left( {1 + \sigma } \right)\alpha _{l}^{{''}} - \frac{A}{h}{{\alpha }_{l}} = 0. \hfill \\ \end{gathered} \right.$

Общее решение линейной системы уравнений (4) для проекций директора и формы межмонослойной поверхности имеет вид:

(5)
$\begin{gathered} {{n}_{u}}\left( x \right) = {{c}_{1}}{{e}^{{ - {{p}_{1}}x}}} + {{c}_{2}}{{e}^{{{{p}_{1}}x}}} + {{c}_{3}}{{e}^{{ - {{p}_{2}}x}}} + \,\,{{c}_{4}}{{e}^{{{{p}_{2}}x}}} + {{c}_{5}}{{e}^{{\sqrt {\frac{\sigma }{{1 + \sigma }}} \frac{x}{l}}}} + {{c}_{6}}{{e}^{{ - \sqrt {\frac{\sigma }{{1 + \sigma }}} \frac{x}{l}}}} + {{c}_{7}}, \\ {{n}_{l}}\left( x \right) = {{c}_{1}}{{e}^{{ - {{p}_{1}}x}}} + {{c}_{2}}{{e}^{{{{p}_{1}}x}}} + {{c}_{3}}{{e}^{{ - {{p}_{2}}x}}} + \,\,{{c}_{4}}{{e}^{{{{p}_{2}}x}}} - {{c}_{5}}{{e}^{{\sqrt {\frac{\sigma }{{1 + \sigma }}} \frac{x}{l}}}} - {{c}_{6}}{{e}^{{ - \sqrt {\frac{\sigma }{{1 + \sigma }}} \frac{x}{l}}}} - {{c}_{7}}, \\ M\left( x \right) = {{c}_{5}}\frac{{2{{l}^{2}} + {{h}^{2}}\sigma }}{{2l\sqrt {\sigma \left( {1 + \sigma } \right)} }}{{e}^{{\sqrt {\frac{\sigma }{{1 + \sigma }}} \frac{x}{l}}}} - \,\,{{c}_{6}}\frac{{2{{l}^{2}} + {{h}^{2}}\sigma }}{{2l\sqrt {\sigma \left( {1 + \sigma } \right)} }}{{e}^{{ - \sqrt {\frac{\sigma }{{1 + \sigma }}} \frac{x}{l}}}} + {{c}_{7}}x + {{c}_{8}}, \\ \end{gathered} $
где c0, c1, …, c8 – комплексные постоянные коэффициенты, которые следует определить из граничных условий,

(6)
${{p}_{{1,2}}} = \sqrt {\frac{{2{{h}^{2}}\sigma - 2A\left( {{{h}^{2}} - {{l}^{2}}} \right) \pm 2\sqrt {{{h}^{4}}{{\sigma }^{2}} - 2A{{h}^{2}}\left( {\sigma \left( {{{h}^{2}} + {{l}^{2}}} \right) + 2{{l}^{2}}} \right) - {{A}^{2}}\left( {\sigma {{h}^{2}}\left( {{{h}^{2}} + 2{{l}^{2}}} \right) - {{l}^{4}}} \right)} }}{{{{h}^{2}}\left( {1 + \sigma } \right)\left( {A{{h}^{2}} + 4{{l}^{2}}} \right)}}} .$

Относительное изменение площади нейтральной поверхности записывается в виде:

(7)
$\begin{gathered} {{\alpha }_{u}}\left( x \right) = {{\alpha }_{l}}\left( x \right) = {{D}_{1}}{{c}_{1}}{{e}^{{ - {{p}_{1}}x}}} + {{D}_{2}}{{c}_{2}}{{e}^{{{{p}_{1}}x}}} + \\ + \,\,{{D}_{3}}{{c}_{3}}{{e}^{{ - {{p}_{2}}x}}} + {{D}_{4}}{{c}_{4}}{{e}^{{{{p}_{2}}x}}}, \\ \end{gathered} $
где D1, D2, D3, D4 – известные комбинации параметров системы, которые очень громоздки и здесь не приводятся. Из условий локальной объемной несжимаемости (2) находятся формы нейтральных поверхностей монослоев Hu(x), Hl(x). Полученные выражения для проекций директора, формы межмонослойной поверхности и относительного изменения площади нейтральной поверхности подставляются в функционал упругой энергии (3), и в результате интегрирования по нейтральным поверхностям монослоев получается энергия деформаций мембраны, отнесенная к единице длины вдоль оси Oy.

В области встроенного в липидный монослой пептида не существует нейтральной поверхности. Таким образом, состояние противоположного липидного монослоя непосредственно под встроенным пептидом отличается от состояния липидного монослоя в составе бислоя. Обозначим величины, относящиеся к этому монослойному участку, индексом “m”. Для этого участка монослоя функционал упругой энергии может быть записан в следующем виде:

(8)
$\begin{gathered} {{W}_{m}} = \frac{{{{K}_{t}}}}{2}\int {\left\{ {{{l}^{2}}{{{\left( {n_{m}^{'} + {{J}_{0}}} \right)}}^{2}} - {{l}^{2}}J_{0}^{2} + } \right.} \\ + \,\,{{\left( {{{n}_{m}} + M{\kern 1pt} '\,\, + \frac{{{{h}^{2}}}}{2}n_{m}^{{''}} + h\alpha _{m}^{'}} \right)}^{2}} + \\ \left. { + \,\,A\alpha _{m}^{2} + \sigma {{{\left( {M{\kern 1pt} '\,\, + \frac{{{{h}^{2}}}}{2}n_{m}^{{''}} - h\alpha _{m}^{'}} \right)}}^{2}}} \right\}dx. \\ \end{gathered} $

Вариация функционала (8) по функциям nm(x), M(x), αm(x) приводит к трем линейным дифференциальным уравнениям Эйлера–Лагранжа, общее решение которых может быть записано в виде:

(9)
$\begin{gathered} {{\alpha }_{m}}\left( x \right) = 0, \\ {{n}_{m}}\left( x \right) = {{f}_{1}} + {{f}_{2}}{{e}^{{\sqrt {\frac{\sigma }{{1 + \sigma }}} \frac{x}{l}}}} + {{f}_{3}}{{e}^{{ - \sqrt {\frac{\sigma }{{1 + \sigma }}} \frac{x}{l}}}}, \\ M\left( x \right) = {{f}_{0}} - {{f}_{1}}x - {{f}_{2}}\frac{{2{{l}^{2}} + {{h}^{2}}\sigma }}{{2l\sqrt {\sigma \left( {1 + \sigma } \right)} }}{{e}^{{\sqrt {\frac{\sigma }{{1 + \sigma }}} \frac{x}{l}}}} + \\ + \,\,{{f}_{3}}\frac{{2{{l}^{2}} + {{h}^{2}}\sigma }}{{2l\sqrt {\sigma \left( {1 + \sigma } \right)} }}{{e}^{{ - \sqrt {\frac{\sigma }{{1 + \sigma }}} \frac{x}{l}}}}, \\ \end{gathered} $
где f0, f1, f2, f3 – вещественные коэффициенты, которые следует определить из граничных условий. Форма нейтральной поверхности монослоя находится из условия локальной объемной несжимаемости (2):

(10)
${{H}_{l}} = M - h + \frac{{{{h}^{2}}}}{2}n_{m}^{'} + h{{\alpha }_{m}}.$

Неопределенные коэффициенты, входящие в общие решения уравнений Эйлера–Лагранжа, находились из следующих условий: 1) все функции, описывающие деформации, должны быть вещественными при любом вещественном значении x; 2) эти функции должны быть всюду ограничены; 3) вдали от пептида мембрана не деформирована; 4) проекция директора, межмонослойная и нейтральная поверхности каждого монослоя должны быть всюду непрерывны, за исключением границы пептида. Кроме того, в случае неглубоко встроенного пептида, исходя из геометрического смысла директора, на значения проекции директора на правой и левой границах пептида ставилось следующее условие:

(11)
$\begin{gathered} {{n}_{u}}\left( {\Delta L{\text{/}}2} \right) - {{n}_{u}}\left( { - \Delta L{\text{/}}2} \right) \equiv \Delta {{n}_{0}} = \\ = - \frac{{\Delta L}}{{\sqrt {{{{\left( {\frac{{\Delta L}}{2}} \right)}}^{2}} + {{{\left( {h - \frac{{\Delta L}}{2}} \right)}}^{2}}} }}, \\ \end{gathered} $
где ΔL – ширина встроенной части пептида на нейтральной поверхности верхнего монослоя. В случае глубоко встроенного пептида на проекции директора ставилось условие:
(12)
${{n}_{u}}\left( {D{\text{/}}2} \right) - {{n}_{u}}\left( { - D{\text{/}}2} \right) = \Delta n,$
где D – диаметр пептида, Δn – величина скачка проекции директора, зависящая от глубины встраивания пептида и изменяющаяся от 0 (глубокое встраивание) до Δn0 (неглубокое встраивание). Встраивание на глубину меньше половины диаметра пептида считалось неглубоким, больше половины диаметра – глубоким. Коэффициенты, оставшиеся неопределенными после наложения указанных граничных условий, находились путем минимизации по ним полной упругой энергии.

К упругой энергии мембраны, рассчитываемой в рамках предположения о трансляционной симметрии системы, необходимо добавить энергию, связанную с седловым изгибом. Этот вклад может быть рассчитан, например, для круглого пептида с заданной величиной радиальной проекции директора на границе пептида, равной Δn0/2 или Δn/2. По теореме Гаусса–Боне интеграл от гауссовой кривизны по замкнутой поверхности является топологическим инвариантом, поэтому вклад седлового изгиба зависит лишь от величин директора на границе пептида и на бесконечном удалении от пептида. Для круглого пептида энергия седлового изгиба может быть записана в виде:

(13)
$\begin{gathered} {{W}_{G}} = {{K}_{G}}\int {2\pi r\frac{{d{{n}_{r}}}}{{dr}}} \frac{{{{n}_{r}}}}{r}dr = \\ = \pi {{K}_{G}}\left( {n_{r}^{2}\left( \infty \right) - n_{r}^{2}\left( {{{R}_{p}}} \right)} \right) = - \pi {{K}_{G}}n_{r}^{2}\left( {{{R}_{p}}} \right), \\ \end{gathered} $
где nr – радиальная проекция директора; Rp – радиус границы пептида; здесь учтено, что nr(∞) = 0. Таким образом, вклад седлового изгиба равен WG0 = = –πKG(Δn0/2)2 для случая неглубоко встроенного пептида и WG = –πKG(Δn/2)2, если пептид глубоко встроен в липидный монослой. Этот вклад не зависит явно от геометрических характеристик пептида и зависит только от граничного директора в предположении того, что на всей границе пептида директор нормален к поверхности границы и его проекция, нормальная к границе пептида и лежащая в плоскости мембраны, постоянна по абсолютной величине.

Энергия кромки поры. Рассмотрим круглую сквозную пору в горизонтальной мембране. Радиус нейтральной поверхности липидного монослоя на кромке поры в самом узком месте (“экваторе”) обозначим через R0. Система обладает вращательной симметрией относительно оси, проходящей через центр окружности кромки поры перпендикулярно плоскости мембраны. Введем цилиндрическую систему координат Orz с началом O, расположенным на оси вращательной симметрии в плоскости межмонослойной поверхности; ось Oz совпадает с осью вращательной симметрии; ось Or лежит в плоскости межмонослойной поверхности. Все поля деформаций зависят только от координаты r. В этом случае можно все векторные величины заменить их проекциями на ось Or: n → nr = n, N → Nr = N, t → tr = t. Кроме того, с требуемой точностью div(n) = n' + n/r; Nu = dHu(r)/dr, Nl = –dHl(r)/dr. Условия локальной объемной несжимаемости (2) переписываются для вращательно симметричной системы следующим образом:

(14)
$\begin{gathered} {{H}_{u}} - M = h - \frac{{{{h}^{2}}}}{2}\left( {\frac{{d{{n}_{u}}}}{{dr}} + \frac{{{{n}_{u}}}}{r}} \right) - h{{\alpha }_{u}}, \\ M - {{H}_{l}} = h - \frac{{{{h}^{2}}}}{2}\left( {\frac{{d{{n}_{l}}}}{{dr}} + \frac{{{{n}_{l}}}}{r}} \right) - h{{\alpha }_{l}}. \\ \end{gathered} $

Учтем, что мембрана как с чисто липидной порой, так и порой, на экваторе которой расположен амфипатический пептид, обладает зеркальной симметрией относительно плоской межмонослойной поверхности. Это означает, что M(r) = 0, M'(r) = 0; кроме того, можно все вычисления проделать для одного монослоя, для определенности верхнего, а затем полученное значение энергии умножить на два. Из условий (14) выражается функция Hu(r), через которую выражается радиальная проекция нормали Nu, и проекция вектора наклона tu = nu – Nu. Функционал упругой энергии (2) радиально симметричного бислоя записывается следующим образом:

(15)
$\begin{gathered} W = 2\frac{{{{K}_{t}}}}{2}\int\limits_{{{R}_{m}}}^\infty {2\pi r\left\{ {{{l}^{2}}{{{\left( {n_{u}^{'} + \frac{{{{n}_{u}}}}{r} + {{J}_{0}}} \right)}}^{2}} - {{l}^{2}}J_{0}^{2}} \right.} + \\ + \,\,{{\left( {{{n}_{u}} + \frac{{{{h}^{2}}}}{2}\left( {n_{u}^{{''}} + \frac{{n_{u}^{'}}}{r} - \frac{{{{n}_{u}}}}{{{{r}^{2}}}}} \right) + h\alpha _{u}^{'}} \right)}^{2}} + \\ \left. { + \,\,\sigma {{{\left( {\frac{{{{h}^{2}}}}{2}\left( {n_{u}^{{''}} + \frac{{n_{u}^{'}}}{r} - \frac{{{{n}_{u}}}}{{{{r}^{2}}}}} \right) + h\alpha _{u}^{'}} \right)}}^{2}} + A\alpha _{u}^{2}} \right\}dr - \\ - \,\,\pi {{K}_{G}}n_{u}^{2}\left( {{{R}_{m}}} \right), \\ \end{gathered} $
где множитель “2” в правой части учитывает энергию второго (нижнего) монослоя; Rm – радиус границы горизонтального бислоя, определяемый ниже; последнее слагаемое учитывает вклад седлового изгиба при условии nu(∞) = 0. Далее, обозначим nu = n, αu = α, 2σ + 1 = s. Вариация функционала (15) по n(r), α(r) приводит к следующим уравнениям Эйлера–Лагранжа:

(16)
$\begin{gathered} \frac{{{{h}^{4}}}}{4}{{n}^{{\left( 4 \right)}}} + \frac{{{{h}^{4}}}}{{2r}}n{\kern 1pt} '''\,\, + \left( {\frac{{{{h}^{2}} - {{l}^{2}}}}{s} - \frac{{3{{h}^{4}}}}{{4{{r}^{2}}}}} \right)n{\kern 1pt} '' + \\ + \,\,\left( {\frac{{{{h}^{2}} - {{l}^{2}}}}{s} + \frac{{3{{h}^{4}}}}{{4{{r}^{2}}}}} \right)\frac{{n{\kern 1pt} '}}{r} + \left( {\frac{{{{r}^{2}} - \left( {{{h}^{2}} - {{l}^{2}}} \right)}}{{s{{r}^{2}}}} - \frac{{3{{h}^{4}}}}{{4{{r}^{4}}}}} \right)n + \\ + \,\,\frac{{{{h}^{3}}}}{2}\alpha {\kern 1pt} '''\,\, + \frac{{{{h}^{3}}}}{{2r}}\alpha {\kern 1pt} '' + \left( {\frac{h}{s} - \frac{{{{h}^{3}}}}{{2{{r}^{2}}}}} \right)\alpha {\kern 1pt} ' = 0, \\ {{h}^{3}}n{\kern 1pt} '''\,\, + \frac{{2{{h}^{3}}}}{r}n{\kern 1pt} '' + \left( {\frac{{2h}}{s} - \frac{{{{h}^{3}}}}{{{{r}^{2}}}}} \right)n{\kern 1pt} ' + \left( {\frac{{2h}}{s} + \frac{{{{h}^{3}}}}{{{{\rho }^{2}}}}} \right)\frac{n}{r} + \\ + \,\,2{{h}^{2}}\alpha {\kern 1pt} '' + \frac{{2{{h}^{2}}}}{r}\alpha {\kern 1pt} ' - \frac{{2A}}{s}\alpha = 0. \\ \end{gathered} $

Общее решение этих уравнений записывается в виде:

(17)
$\begin{gathered} n\left( r \right) = {{b}_{1}}{{J}_{1}}\left( {{{q}_{1}}r} \right) + {{b}_{2}}{{J}_{1}}\left( {{{q}_{2}}r} \right) + {{b}_{3}}{{Y}_{1}}\left( {{{q}_{1}}r} \right) + {{b}_{4}}{{Y}_{1}}\left( {{{q}_{2}}r} \right), \\ \alpha \left( r \right) = \frac{{{{q}_{1}}\left( {2A{{l}^{2}} - {{h}^{2}}A + \frac{1}{2}q_{2}^{2}{{h}^{2}}\left( {{{h}^{2}}A + 4{{l}^{2}}} \right)} \right)}}{{hA\left( {2 + A} \right)}}\,\left( {{{b}_{1}}{{J}_{0}}\left( {{{q}_{1}}r} \right) + {{b}_{3}}{{Y}_{0}}\left( {{{q}_{1}}r} \right)} \right) + \\ + \,\,\frac{{{{q}_{2}}\left( {2A{{l}^{2}} - {{h}^{2}}A + \frac{1}{2}q_{1}^{2}{{h}^{2}}\left( {{{h}^{2}}A + 4{{l}^{2}}} \right)} \right)}}{{hA\left( {2 + A} \right)}}\left( {{{b}_{2}}{{J}_{0}}\left( {{{q}_{2}}r} \right) + {{b}_{4}}{{Y}_{0}}\left( {{{q}_{2}}r} \right)} \right), \\ \end{gathered} $
где J0, Y0, J1, Y1 – модифицированные функции Бесселя нулевого и первого порядков соответственно; b1, b2, b3, b4 – комплексные постоянные коэффициенты, которые следует определить из граничных условий;

(18)
${{q}_{{1,2}}} = \sqrt {\frac{{A\left( {{{h}^{2}} - {{l}^{2}}} \right) - 2{{h}^{2}}\sigma \pm \sqrt {\left( {{{l}^{4}} - 2{{h}^{4}}\sigma - 2{{h}^{2}}{{l}^{2}}} \right){{A}^{2}} - 4{{h}^{2}}\left( {{{l}^{2}} + \sigma \left( {{{h}^{2}} + {{l}^{2}}} \right)} \right)A + 4{{h}^{4}}\sigma } }}{{{{h}^{2}}\left( {2\sigma + 1} \right)\left( {{{h}^{2}}A + 4{{l}^{2}}} \right)}}} .$

Полученные решения подставляются в функционал упругой энергии (15), и после интегрирования по нейтральной поверхности получается выражение для энергии деформированного участка горизонтального бислоя. Это выражение аналитическое, однако очень громоздкое и поэтому здесь не приводится.

Выражение (15) для упругой энергии участка горизонтального бислоя применимо только в случае малых деформаций. В частности, необходимо, чтобы |n| $ \ll $ 1, |hn'| $ \ll $ 1, |h2n''| $ \ll $ 1. Первое условие означает, что в среднем оси липидных молекул в горизонтальном бислое должны слабо отклоняться от вертикали. В то же время на экваторе чисто липидной поры липидные молекулы расположены горизонтально, т.е. n(R0) = 1, и функционал (15) вблизи экватора поры, вообще говоря, неприменим. Вблизи экватора нейтральная поверхность монослоя слабо отклоняется не от горизонтальной плоскости, а от вертикальной цилиндрической поверхности, соосной с порой. Таким образом, для расчета энергии кромки в рамках линейной теории упругости мы разбиваем мембрану на две области: 1) практически горизонтальный бислой, в котором нормаль к нейтральной поверхности и директоры слабо отклоняются от вертикали; 2) практически цилиндрический монослой, соосный с порой, в котором нормаль к нейтральной поверхности и директоры слабо отклоняются от горизонтальной плоскости.

Форму нейтральной поверхности вертикального монослоя будем описывать r-координатами ее точек, функцией R(z), в введенной цилиндрической системе координат Orz. Проекцию директора на ось Oz обозначим v(z). С требуемой точностью div(n) = $v{\kern 1pt} '$(z) + 1/R(z). Будем предполагать, что нейтральная поверхность, описываемая функцией R(z), слабо отклоняется от цилиндрической поверхности, радиус которой обозначим ${{R}_{v}}$, а межмонослойная поверхность, описываемая функцией M(z), слабо отклоняется от цилиндрической поверхности радиуса ${{M}_{v}}$ т.е.: R(z) = ${{R}_{v}}$ + u(z), M(z) = ${{M}_{v}}$ + m(z), где |u(z)| $ \ll $ ${{R}_{v}}$, |m(z)| $ \ll $ ${{M}_{v}}$. Условие локальной объемной несжимаемости для вертикального монослоя записывается в виде:

(19)
$M\left( z \right) - R\left( z \right) = h - \frac{{{{h}^{2}}}}{2}\left( {v{\kern 1pt} '\,\, + \frac{1}{{R\left( z \right)}}} \right) - h\beta \left( z \right),$
где β(z) обозначает относительное латеральное растяжение-сжатие. Нейтральная и межмонослойная поверхности цилиндрического монослоя, отклонения от которого мы считаем малыми в области вертикального монослоя на кромке поры, также должны удовлетворять условию локальной объемной несжимаемости, которое записывается в следующем виде:

(20)
${{M}_{v}} - {{R}_{v}} = h - \frac{{{{h}^{2}}}}{{2R_{v}^{2}}}.$

С учетом (20) из уравнения (19) можно выразить отклонение радиуса нейтральной поверхности u(z) в первом (линейном) порядке по малым деформациям:

(21)
$u\left( z \right) = \frac{{R_{v}^{2}}}{{2R_{v}^{2} + {{h}^{2}}}}\left( {2m\left( z \right) + 2h\beta \left( z \right) + {{h}^{2}}v{\kern 1pt} '\left( z \right)} \right).$

С требуемой точностью проекция нормали на ось Oz записывается как Nz = –u'(z). Функционал упругой энергии (1) для вертикального монослоя записывается в виде:

(22)
$\begin{gathered} {{W}_{m}} = \frac{{{{K}_{t}}}}{2}\int\limits_{ - {{Z}_{m}}}^{{{Z}_{m}}} {2\pi R\sqrt {1 + {{{\left( {R{\kern 1pt} '} \right)}}^{2}}} } \left\{ {{{l}^{2}}{{{\left( {v{\kern 1pt} '\,\, + \frac{1}{R} + {{J}_{0}}} \right)}}^{2}} - } \right. \\ \left. { - \,\,{{l}^{2}}J_{0}^{2} + {{{\left( {v - {{N}_{z}}} \right)}}^{2}} + A{{\beta }^{2}} + \sigma } \right\}dz \\ - \,\,2{{\sigma }_{0}}\pi \left( {R_{m}^{2} - R_{0}^{2}} \right) + 2\pi {{K}_{G}}\left( {v\left( {{{Z}_{m}}} \right) - v\left( { - {{Z}_{m}}} \right)} \right), \\ \end{gathered} $
где {Rm, Zm} – координаты границы (“сшивки”) вертикального монослоя и горизонтального бислоя; последнее слагаемое учитывает вклад седлового изгиба. В функционал (22) подставляется выражение Nz = –u'(z), затем подставляется u(z) из (21), и функционал разлагается до второго порядка по малым величинам $v$(z), m(z), b(z) и их производным. Вариация получающегося функционала по $v$(z), m(z), b(z) приводит к трем линейным дифференциальным уравнениям Эйлера–Лагранжа. Общее решение этих уравнений записывается в следующем виде:
(23)
$\begin{gathered} \beta \left( z \right) = 0, \\ v\left( z \right) = {{d}_{1}}{{e}^{{ - {{o}_{1}}z}}} + {{d}_{2}}{{e}^{{{{o}_{1}}z}}} + {{d}_{3}}{{e}^{{ - {{o}_{2}}z}}} + {{d}_{4}}{{e}^{{{{o}_{2}}z}}}, \\ m\left( z \right) = \frac{{\left( {2R_{v}^{2} + {{h}^{2}}} \right)\left( {{{l}^{2}} - 2\sigma R_{v}^{2}} \right)}}{{4{{R}_{v}}{{l}^{2}}}} + \\ + \,\,{{D}_{1}}{{d}_{1}}{{e}^{{ - {{o}_{1}}z}}} + {{D}_{2}}{{d}_{2}}{{e}^{{{{o}_{1}}z}}} + {{D}_{3}}{{d}_{3}}{{e}^{{ - {{o}_{2}}z}}} + {{D}_{4}}{{d}_{4}}{{e}^{{{{o}_{2}}z}}}, \\ \end{gathered} $
где d1, d2, d3, d4 – комплексные постоянные коэффициенты, которые следует определить из граничных условий; D1, D2, D3, D4 – известные, но очень громоздкие комбинации упругих параметров мембраны;

(24)
$\begin{gathered} {{o}_{{1,2}}} = 2{{\left( {{{l}^{2}} + 2{{l}^{2}}{{J}_{0}}{{R}_{v}} + 2sR_{v}^{2} + 2R_{v}^{2}} \right)}^{{ - \frac{1}{2}}}} \times \\ \times \,\,\left[ {2\sigma R_{v}^{4} + 6{{l}^{2}}{{J}_{0}}R_{v}^{3} - 2{{l}^{4}}J_{0}^{2}R_{v}^{2} + {{l}^{2}}R_{v}^{2} + 2{{l}^{4}}} \right. \pm \\ \pm \,\,\left( {2\sigma R_{v}^{4} - 2{{l}^{4}} + 5{{l}^{2}}R_{v}^{2} + 6{{l}^{2}}{{J}_{0}}R_{v}^{3} - 4{{l}^{4}}{{J}_{0}}R_{v}^{4}} \right. - \\ {{\left. { - \,\,2{{l}^{4}}J_{0}^{2}R_{v}^{2}} \right)}^{{\frac{1}{2}}}} \times \left( {2\sigma R_{v}^{4} - 2{{l}^{4}} - 3{{l}^{2}}R_{v}^{2} + } \right. \\ \left. { + \,\,6{{l}^{2}}{{J}_{0}}R_{v}^{3} + 4{{l}^{4}}{{J}_{0}}R_{v}^{4} - 2{{l}^{4}}J_{0}^{2}R_{v}^{2}} \right){{\left. {^{{\frac{1}{2}}}} \right]}^{{\frac{1}{2}}}}. \\ \end{gathered} $

Решение (23) затем подставляется в функционал (22), и после интегрирования получается выражение для упругой энергии вертикального монослоя.

Распределения деформаций, получаемые для вертикального монослоя и горизонтального бислоя, сопрягаются на их общей границе {Rm, Zm}, исходя из непрерывности директора и нейтральной поверхности монослоя, с учетом малости деформаций [19]:

(25)
$\begin{gathered} H\left( {{{R}_{m}}} \right) = {{Z}_{m}},\,\,\,\,R\left( {{{Z}_{m}}} \right) = {{R}_{m}},\, \\ n\left( {{{R}_{m}}} \right)--v\left( {{{Z}_{m}}} \right) = 1. \\ \end{gathered} $

Кроме того, считалось, что вдали от поры мембрана не деформирована, и налагались следующие условия:

(26)
$n(\infty ) = 0,\,\,\,\,H(\infty ) = h.$

Для чисто липидной поры на экваторе ставилось условие $v$(0) = 0, R(0) = R0. В случае, если на экваторе поры расположен амфипатический пептид, то на вертикальном монослойном участке кромки поры налагались следующие условия:

(27)
$\begin{gathered} v\left( {\Delta L{\text{/}}2} \right) = \frac{{\Delta {{n}_{0}}}}{2} = - \frac{{\Delta L}}{{2\sqrt {{{{\left( {\frac{{\Delta L}}{2}} \right)}}^{2}} + {{{\left( {h - \frac{{\Delta L}}{2}} \right)}}^{2}}} }}, \\ R\left( {\Delta L{\text{/}}2} \right) = {{R}_{0}}, \\ \end{gathered} $
для случая неглубокого встраивания пептида и
(28)
$v\left( {{D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0em} 2}} \right) = \frac{{\Delta n}}{2},\,\,\,\,R\left( {D{\text{/}}2} \right) = {{R}_{0}},$
в случае глубоко встроенного пептида. Суммарная упругая энергия вертикального монослоя и горизонтального бислоя затем численно минимизировалась по координатам сшивки этих участков {Rm, Zm} методом спуска по градиенту.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Для получения количественных результатов и их графической иллюстрации использовались величины упругих параметров мембраны, характерные для диолеоилфосфтадилхолина (ДОФХ), типичного липида плазматических мембран бактериальных клеток. В расчете на один монослой: модуль изгиба Kc = 10 kBT (kBT ≈ 4.14 × 10–21 Дж) [39]; модуль наклона Kt = 40 мН/м ≈ 10 kBT/нм2 [35]; модуль латерального растяжения–сжатия Ka = 133 мН/м ≈ 32 kBT/нм2 [39]; модуль седлового изгиба KG = –Kc/2 = –5 kBT [40]; латеральное натяжение σ0 = 0.01 мН/м; спонтанная кривизна J0 = –0.091 нм–1 [41]; толщина гидрофобной части монослоя h = 1.45 нм [19, 39]. Предполагалось, что диаметр пептида D = 1.3 нм; длина пептида Lp = 5 нм; Rv = R0 + h/4. Если на экваторе кромки поры расположена одна пептидная молекула, то радиус поры равен R1 = Lp/(2π) = 0.8 нм; две пептидные молекулы – R2 = 2Lp/(2π) = 1.6 нм; три пептидные молекулы – R3 = 3Lp/(2π) = 2.4 нм. В случае неглубокого встраивания пептида количественные результаты были получены для ширины встроенной области ΔL = 0, 0.3, 0.5, 0.7, 1.0, 1.2, 1.3 нм, что согласно условию (11) соответствует значениям скачка директора на границе пептида |Δn0| = 0, 0.23, 0.41, 0.61, 0.93, 1.15, 1.26. Для случая глубокого встраивания пептида ширина встроенной области считалась равной диаметру пептида D = 1.3 нм, а граничный директор Δn последовательно устанавливался равным выписанным выше значениям Δn0. Величины энергии деформаций мембраны, индуцированных одиночной молекулой пептида, приведены в табл. 1.

Таблица 1.  

Величины энергии деформаций, индуцированных одиночной пептидной молекулой, в случае неглубокого и глубокого встраивания

ΔL, нм Δn0, Δn W, kBT
встраивание
неглубокое глубокое
0 0 0 0
0.3 0.23 –0.53 –0.58
0.5 0.41 –0.27 –0.39
0.7 0.61 0.66 0.49
1.0 0.93 3.59 3.36
1.2 1.15 6.53 6.37
1.3 1.26 8.21 8.21

При некоторых значениях граничного скачка директора Δn0, Δn (при неглубоком и глубоком встраивании пептида, соответственно) энергия деформаций, индуцированных одиночной пептидной молекулой, оказывается отрицательной. Это связано с тем, что спонтанная кривизна монослоя ДОФХ отрицательная, и встраивание пептида, индуцирующего положительную кривизну, энергетически выгодно, поскольку при этом уменьшается разница между спонтанной (отрицательной) и геометрической (практически нулевой) кривизнами поверхности монослоя. Формально в квадратичном по деформациям функционале (1) отрицательный вклад, связанный со спонтанной кривизной J0, обеспечивается линейным по спонтанной кривизне слагаемым:

(27)
$\begin{gathered} \frac{{{{K}_{c}}}}{2}{{\left( {{\text{div}}{\kern 1pt} \left( {\mathbf{n}} \right) + {{J}_{0}}} \right)}^{2}} - \frac{{{{K}_{c}}}}{2}J_{0}^{2} = \\ = \,\,\frac{{{{K}_{c}}}}{2}\left\{ {{{{\left[ {\operatorname{div} \left( {\mathbf{n}} \right)} \right]}}^{2}} + 2{{J}_{0}}\operatorname{div} \left( {\mathbf{n}} \right)} \right\}. \\ \end{gathered} $

Из табл. 1 видно, что энергия деформаций, индуцированных встроенной в липидный монослой молекулой АМП, определяется граничным директором Δn0, Δn: энергия практически не отличается в случаях глубокого и неглубокого встраивания, т.е. она слабо зависит от ширины встроенной области (ΔL при неглубоком встраивании по сравнению с D – при глубоком).

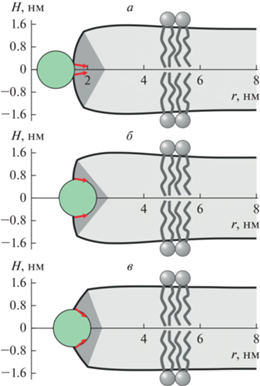
На рис. 2 приведены рассчитанные формы мембраны вблизи кромки поры радиуса R = 1.5 нм с неглубоко (рис. 2а) и глубоко (рис. 2б) встроенным пептидом, индуцирующим скачок граничного директора Δn0 = Δn = 0.23 (ΔL = 0.3 нм). В этих условиях оптимизированные координаты сопряжения вертикального монослойного и горизонтального бислойного участков кромки поры составляют Rm = 1.86 нм, Zm = 1.35 нм и Rm = 1.64 нм, Zm = 1.35 нм для случаев неглубоко и глубоко встроенного пептида соответственно. На рис. 2в приведена рассчитанная форма мембраны вблизи кромки поры радиуса R = 1.5 нм с пептидом шириной ΔL = D = 1.3 нм, индуцирующим скачок граничного директора Δn = Δn0 = 1.26. В этом случае координаты сопряжения вертикального монослойного и горизонтального бислойного участков кромки поры равны Rm = 2.02 нм, Zm = 1.38 нм. Из рисунков видно, что формы мембраны различаются для одинаковых скачков граничных директоров при разной ширине встроенной части пептида (ср. рис. 2а и 2б), а также при одинаковой ширине встроенной части пептида, но различных скачках граничных директоров (ср. рис. 2б и 2в).

Рис. 2.

Форма мембраны вблизи кромки поры радиуса R = 1.5 нм с амфипатическими пептидами, расположенными на ее экваторе. а – Неглубоко встроенные пептиды с шириной вcтроенной области ΔL = = 0.3 нм (скачок граничного директора Δn0 = 0.23); б – глубоко встроенные пептиды, индуцирующие скачок директора Δn = 0.23; в – пептиды встроенные на глубину радиуса α-спирали, индуцирующие скачок директора Δn = Δn0 = 1.26. Пептид показан зеленым кругом; граничные директоры показаны красными стрелками; область горизонтального бислоя показана светло-серым цветом, область вертикального монослоя – серым цветом. На панелях а и б угол между граничными директорами одинаков; на панелях б и в одинакова ширина встроенной в мембрану части пептида (ΔL = 1.3 нм).

На рис. 3а приведены зависимости линейного натяжения кромки поры от радиуса для случаев неглубоко (сплошные кривые) и глубоко (штриховые кривые) встроенных пептидов, расположенных на экваторе поры. Из рисунка видно, что в рассматриваемом диапазоне радиусов 0.7 нм < R < 5 нм линейное натяжение сильно зависит от радиуса поры. В частности, в случае пептида, встроенного на глубину радиуса α-спирали (ΔL = D = 1.3 нм) и индуцирующего скачок граничного директора Δn = Δn0 = 1.26 (рис. 3а, нижняя кривая) линейное натяжение изменяется приблизительно в 3 раза: от 13.7 пН при R = 0.7 нм до 4.3 пН при R = 5 нм. В целом, пептидные молекулы на экваторе поры понижают линейное натяжение кромки, причем неглубоко встроенные пептиды понижают линейное натяжение сильнее, чем глубоко встроенные АМП. Понижение линейного натяжения оказывается тем большим, чем больший скачок граничного директора индуцируют пептиды (рис. 3а). Согласно качественной модели Дерягина–Гутопа, при фиксированном латеральном натяжении понижение линейного натяжения кромки поры способствует образованию закритических пор, поскольку при этом понижается энергетический барьер порации ΔE = πγ2/σ.

Рис. 3.

Влияние амфипатических пептидов на энергию кромки поры. Сплошные кривые соответствуют случаю неглубоко встроенных пептидов, штриховые кривые – случаю глубоко встроенных пептидов. а – Зависимость линейного натяжения кромки поры с пептидами, расположенными на ее экваторе, от радиуса. Пары кривых (сплошная + штриховая), сверху вниз: Δn = Δn0 = 0, ΔL = 0 (красные кривые); Δn = Δn0 = 0.61, ΔL = 0.7 нм (зеленые кривые); Δn = Δn0 = = 0.93, ΔL = 1.0 нм (синие кривые); Δn = Δn0 = 1.15, ΔL = 1.2 нм (фиолетовые кривые); нижняя (темно-синяя) кривая – Δn = Δn0 = 1.26, ΔL = 1.3 нм. б – Зависимость энергии кромки поры от радиуса. Цвета пар кривых аналогичны их цветам на панели а. Точками показана энергия деформаций плоского бислоя, индуцированных неглубоко встроенными пептидами. Цвет точек соответствует цвету кривых. При радиусе поры R = 0.8 нм на экваторе размещается одна пептидная молекула, при R = 1.6 нм – две молекулы, при R = 2.4 нм – три молекулы и т.д. Значения скачка директора указаны у каждой пары кривых.

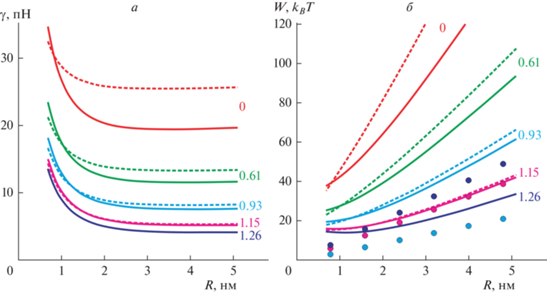
Зависимость энергии поры от радиуса приведена на рис. 3б для случаев неглубоко (сплошные кривые) и глубоко (штриховые кривые) встроенных пептидов, расположенных на экваторе поры. Из зависимостей видно, что энергия кромки понижается при последовательном увеличении скачка директора Δn0, Δn на границе пептида. При малых радиусах энергия кромки поры с глубоко встроенным пептидом несколько ниже, чем с неглубоко встроенным пептидом; однако при радиусах поры R > 1.5 нм энергия кромки поры с неглубоко встроенным пептидом оказывается ниже для всех рассмотренных величин скачка граничного директора. На рис. 3б точками показаны энергии деформаций, индуцируемых одиночными пептидами, встроенными в плоский бислой. Радиусу поры R = 0.8 нм соответствует один одиночный пептид длиной Lp = 5 нм, радиусу поры R = 1.6 нм – два пептида, радиусу поры R = 2.4 нм – три пептида и т.д. При ширине встроенной части пептида ΔL = = D = 1.3 нм и скачке граничного директора Δn = = Δn0 = 1.26 энергия деформаций, индуцированных двумя пептидами в плоском бислое, оказывается выше, чем энергия кромки поры с двумя такими же пептидами, расположенными на ее экваторе. Отсюда можно заключить, что двух пептидных молекул, встроенных в липидный монослой приблизительно на глубину радиуса α-спирали, достаточно для образования сквозной поры. В принципе, состояния двух пептидов, встроенных в плоский бислой, и поры с пептидами на экваторе могут быть разделены энергетическим барьером неизвестной высоты. Однако энергетический барьер определяет характерное время перехода из одного состояния в другое; при этом разница энергий состояний определяет их относительную вероятность возникновения. Когда энергии двух состояний сопоставимы, вероятности реализации этих состояний также сопоставимы при условии, что время ожидания достаточно для установления равновесия.

Вклад конфигураций поры с пептидами на ее экваторе в общую статистическую сумму системы значительно ниже, чем вклад свободных АМП и изолированной чисто липидной поры [34]. Это связано с тем, что площадь кромки поры, доступная для АМП, существенно меньше, чем площадь бислоя по крайней мере для малых концентраций АМП, когда взаимодействием пептидов друг с другом можно пренебречь. Таким образом, при малых концентрациях АМП порация мембраны будет редко наблюдаемым событием, хотя и формально возможным. В случае, когда поверхностная концентрация АМП достаточно велика (площадь, затронутая индуцированными АМП деформациями, сравнима с полной площадью мембраны), статистический вес АМП, расположенных на кромке поры, будет сравним с вкладом АМП, расположенных вдали от поры. Это связано с тем, что при увеличении концентрации молекул АМП и учете их взаимодействия друг с другом доступная площадь для каждой пептидной молекулы будет существенно меньше площади бислоя, – аналогично тому, как изменяется доступное для частицы число конфигураций при переходе из газовой фазы в жидкую. При измеряемой в экспериментах пороговой поверхностной концентрации АМП практически вся мембрана покрыта деформациями, индуцированными пептидными молекулами [15]; именно при этой поверхностной концентрации в мембране начинают интенсивно образовываться поры.

Отметим также, что для большего числа пептидов, встроенных в мембрану на глубину радиуса α-спирали (ΔL = D = 1.3 нм, Δn = Δn0 = 1.26), энергия кромки поры с пептидами на ее экваторе оказывается значительно ниже, чем энергия деформаций, индуцированных пептидами в плоском бислое (рис. 3б, темно-синяя кривая и темно-синие точки). Соответственно, в этом случае оказывается энергетически выгоден рост радиуса поры за счет встраивания в ее кромку дополнительных пептидов из плоской части бислоя. Для пептидов со скачком граничного директора Δn = Δn0 = 1.15 (ΔL = 1.2 нм) энергия кромки с пептидами на ее экваторе практически совпадает с энергией деформаций, индуцируемых пептидами в плоском бислое, при числе пептидов N ≥ 4 (рис. 3б фиолетовая кривая и фиолетовые точки). При меньшем скачке граничного директора (например, Δn = Δn0 = 0.93, рис. 3б, синяя кривая и синие точки) энергия кромки поры с пептидами на экваторе значительно выше, чем энергия деформаций плоского бислоя, и образование поры оказывается заведомо энергетически невыгодным независимо от высот энергетических барьеров между состояниями поры с пептидами на экваторе и пептидами, встроенными в плоский бислой.

Таким образом, формирование сквозной поры амфипатическими пептидами возможно лишь в узком диапазоне физико-химических и геометрических характеристик пептидов. Молекулы АМП должны относительно глубоко встраиваться в липидный монослой, чтобы обеспечить достаточную ширину встроенной части, ΔL. Этому же должны способствовать более объемные аминокислоты в составе пептида. В то же время встраивание не должно быть слишком глубоким, чтобы обеспечить максимальный скачок граничного директора Δn0. Это означает, что площади гидрофильной и гидрофобной частей боковой поверхности α-спирали пептидной молекулы должны быть приблизительно одинаковыми. Помимо ширины встроенной области пептида, скачок граничного директора зависит от толщины гидрофобной части монослоя, согласно (10), (25); т.е. один и тот же АМП будет индуцировать разный скачок директора в монослоях различной толщины, и, соответственно, эффективность порации мембран также будет различной. Эта особенность может быть использована для повышения избирательности действия АМП. Бактериальные мембраны содержат большое количество ненасыщенных липидов (ДОФХ, диолеоилфосфатидилглицерин, диолеоилфосфатидилэтаноламин и т.д.) и не содержат стеролы. В составе плазматических мембран эукариотических клеток значительную долю липидов составляют насыщенные липиды и холестерин [42]. Холестерин конденсирует насыщенные углеводородные цепи липидов, что приводит к увеличению толщины монослоя [43]. Различие толщин липидных бислоев, обогащенного ненасыщенными липидами и обогащенного насыщенными липидами и холестерином, может достигать 1.5 нм [43]. Таким образом, в принципе, возможно подобрать структуру АМП так, чтобы он эффективно формировал поры в более тонких бактериальных мембранах и не образовывал поры в мембранах эукариотических клеток. Кроме того, холестерин повышает жесткость мембран, содержащих насыщенные липиды [44]. Это должно приводить к увеличению как энергии деформаций, индуцированных одиночными пептидами, так и энергии кромки поры. Равновесное распределение АМП между мембраной и водной фазой определяется, в том числе, и энергией деформаций, индуцированных пептидом в липидном бислое: чем выше эта энергия, тем меньшей будет равновесная поверхностная концентрация пептида на мембране. Возможно подобрать структуру и концентрацию АМП таким образом, чтобы на мембранах эукариотических клеток не достигалась пороговая поверхностная концентрация интенсивного порообразования. В работе [2] было показано, что при объемной концентрации АМП 1 мкМ поверхностная концентрация АМП на мембране, не содержащей холестерин, оказывается в 3 раза выше, чем на мембране, в составе которой присутствует 40 мол. % холестерина. Это различие поверхностной концентрации может быть достигнуто за счет разности энергии деформаций, индуцируемых в мембране одиночными молекулами АМП, всего в 1 kBT. При объемной концентрации АМП 1 мкМ в работе [2] наблюдалась интенсивная порация мембран липосом, не содержащих холестерин, в то время как в мембранах эритроцитов поры не образовывались.

Конфликт интересов. Авторы декларируют отсутствие явных и потенциальных конфликтов интересов, связанных с публикацией настоящей статьи.

Источники финансирования. Работа выполнена при поддержке Российского научного фонда (грант № 22-24-00834).

Соответствие принципам этики. Настоящая статья не содержит описания каких-либо исследований с участием людей или животных в качестве объектов.

Список литературы

  1. Rawicz W., Smith B.A., McIntosh T.J., Simon S.A., Evans E. 2008. Elasticity, strength, and water permeability of bilayers that contain raft microdomain-forming lipids. Biophys. J. 94, 4725–4736.

  2. Pérez-Peinado C., Dias S.A., Domingues M.M., Benfield A.H., Freire J.M., Rádis-Baptista G., Gaspar D., Castanho M.A.R.B., Craik D.J., Henriques S.T., Veiga A.S., Andreu D. 2018. Mechanisms of bacterial membrane permeabilization by crotalicidin (Ctn) and its fragment Ctn (15–34), antimicrobial peptides from rattlesnake venom. J. Biol. Chem. 293, 1536–1549.

  3. Hasan M., Karal M.A.S., Levadnyy V., Yamazaki M. 2018. Mechanism of initial stage of pore formation induced by antimicrobial peptide magainin 2. Langmuir 34, 3349–3362.

  4. Parvez F., Alam J.M., Dohra H., Yamazaki M. 2018. Elementary processes of antimicrobial peptide PGLa-induced pore formation in lipid bilayers. Biochim. Biophys. Acta. 1860, 2262–2271.

  5. Pan J., Tieleman D.P., Nagle J.F., Kučerka N., Tristram-Nagle S. 2009. Alamethicin in lipid bilayers: Combined use of X-ray scattering and MD simulations. Biochim. Biophys. Acta. 1788, 1387–1397.

  6. Tamba Y., Ariyama H., Levadny V., Yamazaki M. 2010. Kinetic pathway of antimicrobial peptide magainin 2-induced pore formation in lipid membranes. J. Phys. Chem. B. 114, 12018–12026.

  7. Park S.C., Kim J.Y., Shin S.O., Jeong C.Y., Kim M.H., Shin S.Y., Cheong G.-W., Park Y., Hahm K.S. 2006. Investigation of toroidal pore and oligomerization by melittin using transmission electron microscopy. Biochem. Biophys. Res. Comm. 343, 222–228.

  8. Campelo F., McMahon H.T., Kozlov M.M. 2008. The hydrophobic insertion mechanism of membrane curvature generation by proteins. Biophys. J. 95, 2325–2339.

  9. Santo K.P., Berkowitz M.L. 2012. Difference between magainin-2 and melittin assemblies in phosphatidylcholine bilayers: results from coarse-grained simulations. J. Phys. Chem. B. 116, 3021–3030.

  10. Zemel A., Ben-Shaul A., May S. 2005. Perturbation of a lipid membrane by amphipathic peptides and its role in pore formation. Eur. Biophys. J. 34, 230–242.

  11. Huang H.W., Chen F.Y., Lee M.T. 2004. Molecular mechanism of peptide-induced pores in membranes. Phys. Rev. Lett. 92, 198304.

  12. Huang H.W. 2006. Molecular mechanism of antimicrobial peptides: The origin of cooperativity. Biochim. Biophys. Acta. 1758, 1292–1302.

  13. Huang H.W. 2000. Action of antimicrobial peptides: Two-state model. Biochemistry. 39, 8347–8352.

  14. Manzini M.C., Perez K.R., Riske K.A., Bozelli Jr.J.C., Santos T.L., da Silva M.A., Saraiva G.K.V., Politi M.J., Valente A.P., Almeida F.C.L., Chaimovich H., Rodrigues M.A., Bemquerer M.P., Schreier S., Cuccovia I.M. 2014. Peptide: Lipid ratio and membrane surface charge determine the mechanism of action of the antimicrobial peptide BP100. Conformational and functional studies. Biochim. Biophys. Acta. 1838, 1985–1999.

  15. Kondrashov O.V., Galimzyanov T.R., Jiménez-Munguía I., Batishchev O.V., Akimov S.A. 2019. Membrane-mediated interaction of amphipathic peptides can be described by a one-dimensional approach. Phys. Rev. E. 99, 022401.

  16. Kozlovsky Y., Zimmerberg J., Kozlov M.M. 2004. Orientation and interaction of oblique cylindrical inclusions embedded in a lipid monolayer: A theoretical model for viral fusion peptides. Biophys. J. 87, 999–1012.

  17. Kondrashov O.V., Galimzyanov T.R., Pavlov K.V., Kotova E.A., Antonenko Y.N., Akimov S.A. 2018. Membrane elastic deformations modulate gramicidin A transbilayer dimerization and lateral clustering. Biophys. J. 115, 478–493.

  18. Fuller N., Rand R.P. 2001. The influence of lysolipids on the spontaneous curvature and bending elasticity of phospholipid membranes. Biophys. J. 81, 243–254.

  19. Akimov S.A., Volynsky P.E., Galimzyanov T.R., Kuzmin P.I., Pavlov K.V., Batishchev O.V. 2017. Pore formation in lipid membrane I: Continuous reversible trajectory from intact bilayer through hydrophobic defect to transversal pore. Sci. Rep. 7, 12152.

  20. Awasthi N., Hub J.S. 2016. Simulations of pore formation in lipid membranes: Reaction coordinates, convergence, hysteresis, and finite-size effects. J. Chem. Theor. Comput. 12, 3261–3269.

  21. Wohlert J., den Otter W.K., Edholm O., Briels W.J. 2006. Free energy of a trans-membrane pore calculated from atomistic molecular dynamics simulations. J. Chem. Phys. 124, 154905.

  22. Дерягин Б.В., Гутоп Ю.В. 1962. Теория разрушения (прорыва) свободных пленок. Коллоидн. журн. 24, 431–437.

  23. Evans E., Heinrich V., Ludwig F., Rawicz W. 2003. Dynamic tension spectroscopy and strength of biomembranes. Biophys. J. 85, 2342–2350.

  24. Karal M.A.S., Levadnyy V., Yamazaki M. 2016. Analysis of constant tension-induced rupture of lipid membranes using activation energy. Phys. Chem. Chem. Phys. 18, 13487–13495.

  25. Evans E., Smith B.A. 2011. Kinetics of hole nucleation in biomembrane rupture. New J. Phys. 13, 095010.

  26. Abidor I.G., Arakelyan V.B., Chernomordik L.V., Chizmadzhev Y.A., Pastushenko V.F., Tarasevich M.P. 1979. Electric breakdown of bilayer lipid membranes: I. The main experimental facts and their qualitative discussion. J. Electroanal. Chem. Interfacial Electrochem. 104, 37–52.

  27. Weaver J.C., Chizmadzhev Y.A. 1996. Theory of electroporation: A review. Bioelectrochem. Bioenerg. 41, 135–160.

  28. Portet T., Dimova R. 2010. A new method for measuring edge tensions and stability of lipid bilayers: Effect of membrane composition. Biophys. J. 99, 3264–3273.

  29. Melikov K.C., Frolov V.A., Shcherbakov A., Samsonov A.V., Chizmadzhev Y.A., Chernomordik L.V. 2001. Voltage-induced nonconductive pre-pores and metastable single pores in unmodified planar lipid bilayer. Biophys. J. 80, 1829–1836.

  30. Basañez G., Shinnar A.E., Zimmerberg J. 2002. Interaction of hagfish cathelicidin antimicrobial peptides with model lipid membranes. FEBS Lett. 532, 115–120.

  31. Qian S., Wang W., Yang L., Huang H.W. 2008. Structure of transmembrane pore induced by Bax-derived peptide: Evidence for lipidic pores. Proc. Natl. Acad. Sci. USA. 105, 17379–17383.

  32. Yang L., Harroun T.A., Weiss T.M., Ding L., Huang H.W. 2001. Barrel-stave model or toroidal model? A case study on melittin pores. Biophys. J. 81, 1475–1485.

  33. Chen F.Y., Lee M.T., Huang H.W. 2003. Evidence for membrane thinning effect as the mechanism for peptide-induced pore formation. Biophys. J. 84, 3751–3758.

  34. Kondrashov O.V., Akimov S.A. 2022. Regulation of antimicrobial peptide activity via tuning deformation fields by membrane-deforming inclusions. Int. J. Mol. Sci. 23, 326.

  35. Hamm M., Kozlov M.M. 2000. Elastic energy of tilt and bending of fluid membranes. Eur. Phys. J. E. 3, 323–335.

  36. Galimzyanov T.R., Molotkovsky R.J., Cohen F.S., Pohl P., Akimov S.A. 2016. Galimzyanov et al. Reply. Phys. Rev. Lett. 116, 079802.

  37. Leikin S., Kozlov M.M., Fuller N.L., Rand R.P. 1996. Measured effects of diacylglycerol on structural and elastic properties of phospholipid membranes. Biophys. J. 71, 2623–2632.

  38. Nagle J.F., Wilkinson D.A. 1978. Lecithin bilayers. Density measurement and molecular interactions. Biophys. J. 23, 159–175.

  39. Rawicz W., Olbrich K.C., McIntosh T., Needham D., Evans E. 2000. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 79, 328–339.

  40. Hu M., de Jong D.H., Marrink S.J., Deserno M. 2013. Gaussian curvature elasticity determined from global shape transformations and local stress distributions: a comparative study using the MARTINI model. Faraday Discuss. 161, 365–382.

  41. Kollmitzer B., Heftberger P., Rappolt M., Pabst G. 2013. Monolayer spontaneous curvature of raft-forming membrane lipids. Soft Matter. 9, 10877–10884.

  42. Ingólfsson H.I., Melo M.N., Van Eerden F.J., Arnarez C., Lopez C.A., Wassenaar T.A., Periole X., de Vries A.H., Tieleman D.P., Marrink S.J. 2014. Lipid organization of the plasma membrane. J. Am. Chem. Soc. 136, 14554–14559.

  43. García-Sáez A.J., Chiantia S., Schwille P. 2007. Effect of line tension on the lateral organization of lipid membranes. J. Biol. Chem. 282, 33537–33544.

  44. Evans E., Rawicz W. 1990. Entropy-driven tension and bending elasticity in condensed-fluid membranes. Phys. Rev. Lett. 64, 2094.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Биологические мембраны: Журнал мембранной и клеточной биологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал