Биология моря, 2023, T. 49, № 2, стр. 127-134

Многомерное стохастическое обобщение модели Берталанффи

Уравнения нашей модели представлены в общем виде. Для решения реальных задач их нужно конкретизировать. Остановимся на самой популярной и простой модели Берталанффи. В этой модели скорость роста признака описывается функцией f(x) = k(a – x), где a = const – дефинитивная величина признака, к которой стремятся старые, взрослые организмы; k = const – относительная скорость затухания роста.

Функцию $g\left( x \right)$ из системы (2) зададим в следующем виде: $g\left( x \right) = {{f}^{\gamma }}\left( x \right)$, где $\gamma = {\text{const}} \geqslant 0$. Эта связь означает, что, согласно развиваемой модели, амплитуда шумовых флюктуаций у скорости роста тем выше, чем больше сама эта скорость роста. При γ = 0 шум аддитивен, и его амплитуда не зависит от f, при γ = 1 шум мультипликативен, и эта амплитуда пропорциональна f. При 0 < γ < 1 шум влияет промежуточным образом. Тогда систему (2) можно представить в следующей форме:

Решение этой системы с начальными условиями E_i = c_i = const, v_ij = v_0ij = const при t = 0 имеет следующий вид:

Здесь для компактности записи обозначено K_ij = = k_i + k_j .

Теперь систему уравнений (3) для коэффициентов чувствительности также можно конкретизировать:

В этой записи коэффициентов чувствительности вместо подстрочного индекса l, обозначающего в уравнениях (3) номер того или иного параметра модели, использовано непосредственно само буквенное обозначение этого параметра p_l. Так, например, ${{\varphi }_{{i{{k}_{i}}}}}$ представляет собой частную производную ${{\partial {{x}_{i}}} \mathord{\left/ {\vphantom {{\partial {{x}_{i}}} {\partial {{k}_{i}}}}} \right. \kern-0em} {\partial {{k}_{i}}}}$. Решения выписанных уравнений имеют вид:

При этом$~~{{\varphi }_{{i{{k}_{j}}}}} = {{\varphi }_{{i{{a}_{j}}}}} = {{\varphi }_{{i{{c}_{j}}}}} = 0,$ если i ≠ j.

Окончательное представление модели сформировано из следующих элементов. Вектор средних арифметических определяется уравнениями (6). Общая ковариационная матрица согласно (5), слагается из шумового компонента (7) и структурного компонента. Последний вычисляется подстановкой коэффициентов чувствительности (8) вместе с матрицей параметрических ковариаций ||${{S}_{{ij}}}$|| в уравнение (4).

Подгонка параметров модели по данным роста минтая

Модель иллюстрируется материалами по стохастическому росту сахалинской популяции минтая Gadus chalcogramma. Они представляют собой данные массовой промысловой статистики, собранные в научно-поисковой экспедиции Сахалинского отделения ТИНРО в 1966 г. Данные представлены измерениями длины AC и общей массы тела по 1228 особям в возрасте от 3 до 8 лет. Самцы и самки не отличались достоверно друг от друга по изучавшимся характеристикам роста, поэтому материалы по обоим полам были объединены. Связь между длиной и массой тела в исходных единицах измерения показана на рис. 2. Надо подчеркнуть, что в логарифмическом масштабе эмпирические точки группируются вдоль прямой линии. Это говорит о том, что в первоначальных координатах длины и массы тела минтая эта регрессия описывается классической степенной зависимостью.

Рис. 2.

Связь между длиной (мм) и массой (г) тела минтая. Оси координат представлены в логарифмической шкале. Каждая точка – отдельная особь.

Проведем конкретизацию модели. Обозначим через x₁ натуральный логарифм длины тела особи (мм, по Смиту), через x₂ – натуральный логарифм общей массы тела (г). Средние арифметические, среднеквадратические отклонения и коэффициент корреляции между этими переменными обозначим соответственно через E₁, E₂, σ₁, σ₂, R. В качестве базовой модели для исходных признаков (непосредственно длины и массы тела) возьмем уравнение Гомпертца, которое логарифмированием зависимой переменной превращается в нужное нам уравнение Берталанффи.

Итоговая модель после завершения подгонки описывается следующими уравнениями:

Модель имеет 11 параметров: k – константа относительной скорости затухания роста, оказавшаяся одинаковой для обоих признаков; γ – степенной параметр в функции $g\left( x \right) = {{f}^{\gamma }}\left( x \right)$ из системы (2); a₁ и a₂ – дефинитивные значения средних; c₁ и c₂ – начальные значения средних при t = 0; $\beta _{1}^{2},\,\,~\beta _{2}^{2}{\text{\;\;}}--$ интенсивности белого шума для 1-го и 2-го признаков; $A_{1}^{2},~A_{2}^{2}$ – структурные дисперсии параметров a₁ и a₂ (дисперсии дефинитивных значений признаков). Последний параметр $D_{1}^{2}$ является суммой двух слагаемых. Первое слагаемое − это начальная шумовая дисперсия, то есть параметр v₀₁₁ в уравнении (7) для признака x₁. Второе слагаемое − структурная дисперсия для параметра c₁. Характер использованного материала не позволил оценить каждое слагаемое этой суммы по отдельности.

Слагаемое $D_{2}^{2}{{e}^{{ - 2kt}}}$ отсутствует в уравнении для ${{\sigma }_{2}}$ в системе (9). Оно не отличалось достоверно от нуля по материалам для сахалинской популяции минтая. Кроме того, в представленном списке модельных коэффициентов не фигурируют также и другие структурные дисперсии и ковариации, указанные в первоначальном полном описании модели (уравнения 4–8). Их оценки, полученные на промежуточных этапах идентификации модели, оказались плохо определены, то есть с большими ошибками. Поэтому такие коэффициенты были приравнены к нулю. Коэффициент корреляции ${{\rho }_{{12}}}$ между шумами для признаков x₁ и x₂ не отличался достоверно от единицы и был принят равным ей, поэтому в уравнении для R в системе (9) он отсутствует явно.

В процессе идентификации применялось последовательное упрощение модели. Исходная модель (4−8) строилась как бы “на вырост” и поэтому сначала включала в себя избыточное количество подгоняемых параметров. Исходя из фактического материала, имевшегося в нашем распоряжении, некоторые из этих параметров были определены с неприемлемо большими ошибками, а они влияют на доверительные интервалы самой модели. Поэтому на следующей итерации эти параметры из модели исключались: заменялись нулями или очевидными не подгоняемыми константами. В результате следующая версия модели упрощалась, и это приводило к уменьшению ошибок у оставшихся для оценивания параметров (это хорошо). При этом качество подгонки модели под материал, разумеется, несколько снижалось (это плохо). После достижения субъективного компромисса между этими двумя противоречащими друг другу целями, процесс идентификации модели завершился.

Подгонка параметров модели (9) проводилась с помощью градиентной процедуры Марквардта (Бард, 1979) с использованием штрафных функций для соблюдения естественных ограничений, запрещающих получение отрицательных значений у всех параметров. В качестве целевой функции, подлежавшей минимизации, выбрана остаточная сумма квадратов – сразу по всем пяти возрастным рядам переменных E₁, E₂, σ₁, σ₂, R. Такая процедура сложения здесь допустима, поскольку все переменные имеют одинаковую размерность, точнее, они безразмерны. Напомним, что признаки x₁ и x₂ представляют собой натуральные логарифмы длины и массы тела.

Попутно заметим, что если “обезразмеривание” комплекса признаков нецелесообразно или невозможно, стоит воспользоваться обобщенным алгоритмом для системы модельных уравнений, описанным в книге Барда (1979). При этом в качестве целевой функции полезно использовать многомерное обобщение понятия дисперсии (Животовский, 1984).

Не останавливаясь на конкретных этапах многошаговой процедуры идентификации, приведем окончательный список оптимальных оценок для всех одиннадцати параметров модели:

Здесь после знаков ± указаны среднеквадратические ошибки оценок.

Анализ представленных результатов подгонки свидетельствует о следующем. Оценки коэффициентов k, γ, a₁, a₂, c₁, c₂ и β₂ получены с неплохой точностью. Оценки для β₁, A₂ и D₁ определены хуже: их ошибки составляют десятки процентов от самих оценок параметров. Коэффициент A₁ определен плохо. Несмотря на большую ошибку, мы оставили его в списке коэффициентов модели, так как без него возрастной ряд для сигмы σ₁ заметно хуже описывался модельной кривой.

Качество подгонки модели для средних арифметических оказалось неплохим. Остаточная дисперсия для переменной E₁ составляет всего лишь 0.5% от общей эмпирической дисперсии и 0.6% для переменной E₂. Качество подгонки для сигм несколько хуже: остаточная дисперсия равна 6.3% для σ₁ и 15.4% для σ₂. Возрастной ряд для коэффициента корреляции R приемлемо аппроксимируется моделью: остаточная дисперсия равна 2.0%.

Возрастная динамика модельных кривых имеет следующие характерные особенности. Средние E₁ и E₂ с замедлением растут во времени. При этом относительная скорость роста (параметр k) у них одинакова, а различия в углах наклона кривых вызваны разницей в начальных значениях c₁ и c₂ этих средних. Среднеквадратические отклонения σ₁ и σ₂ снижаются во времени, причем для σ₂ это снижение идет более круто. Для старших поколений рыб стандартные отклонения обоих признаков стабилизируются на сравнительно невысоких дефинитивных уровнях.

Нужно еще раз напомнить, что признаки x₁ и x₂ представляют собой логарифмы длины (мм) и массы (г) тела рыб. Монотонное возрастное снижение дисперсий этих признаков вовсе не означает, что и в исходных шкалах (миллиметры и граммы) будет сохраняться такая же тенденция. Дисперсии непосредственно длины тела exp(x₁) и массы тела exp(x₂) вначале относительно быстро растут во времени и только затем, перевалив через свои максимумы, снижаются и, в конце концов, устанавливаются на своих низких дефинитивных предельных уровнях. Такая же картина обнаружена и для размеров раковины у приморского гребешка Mizuchopecten yessoensis (Jay, 1857) (Суханов, Селин, 2018).

Возрастная динамика связи длины и массы тела у минтая

На примере с ростом минтая покажем необычный и редко обсуждаемый феномен. Оказывается, что связь между признаками организма не остается постоянной во времени, но демонстрирует закономерные возрастные изменения. Модель воспроизводит такие изменения и дает объяснение этому явлению.

Коэффициент корреляции R между логарифмами длины и массы тела для сеголетков (возраст 0+) близок к единице, а затем монотонно уменьшается во времени. Согласно модельным оценкам асимптотическое (дефинитивное) значение R можно считать равным нулю.

Эта тенденция наглядно изображена на рис. 3. Здесь представлен возрастной ряд корреляционных эллипсов для x₁и x₂, каждый из которых охватывает суммарную вероятность, равную 90%. Отметим неплохое сходство между эмпирическим и модельным рядами этих корреляционных эллипсов.

Рис. 3.

Возрастная последовательность 90%-х корреляционных эллипсов для связи между логарифмами длины (ось x₁) и логарифмами массы тела (ось x₂) минтая. Сплошные эллипсы – эмпирика, пунктирные – модель. Центры эллипсов: маленькие кружки – эмпирика, крестики – модель. Возраст увеличивается снизу слева, вверх направо от 3 до 8 лет.

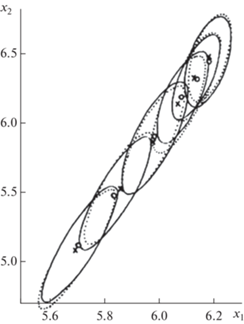
Центры эллипсов лежат на одной прямой. Эта важная особенность является следствием того, что параметр k один и тот же для обоих признаков. Точнее, различия между величинами этого параметра для обоих признаков оказались статистически недостоверными и поэтому были проигнорированы. Именно по этой причине в качестве исходной базовой модели здесь выбрано уравнение Гомпертца, а длина и масса тела представлены в логарифмических шкалах. В первоначальных арифметических шкалах эта простая линейная взаимозависимость была бы искажена нелинейностью степенной связи между непосредственно длиной и массой тела.

По мере взросления рыб корреляционные эллипсы движутся вверх направо, уменьшаются в размерах и становятся все более округлыми (рис. 3). Таким образом, в процессе роста и развития особей относительная изменчивость каждого из признаков снижается. Параллельно с этим сила связи между признаками слабеет.

Высокое значение коэффициента корреляции R на начальных этапах роста рыб и последующее его снижение объясняется следующим. Коэффициент корреляции ${{\rho }_{{12}}}$ между шумами, “раскачивающими” траектории роста признаков, практически равен единице. Это означает, что и на длину, и на массу тела рыб фактически воздействует один и тот же источник шума. По всей видимости, он непосредственно связан со случайными вариациями потока ассимилированной пищи, идущего на приросты длины и массы тела. По мере взросления рыб скорость роста каждого из этих признаков уменьшается. Вследствие этого снижается и амплитуда флюктуаций у скорости роста, поскольку параметр γ близок к единице (см. список 10). В связи с этим величина ковариации между признаками также снижается к нулю. Вместе с тем даже при полном прекращении роста обе величины дисперсий остаются ненулевыми: ${{\sigma }_{1}} \to {{A}_{1}},~\,\,{{\sigma }_{2}} \to {{A}_{2}}~$. Наличие структурных (параметрических) компонентов в общей дефинитивной изменчивости признаков, а также снижение шумовой ковариации между признаками во времени, вызванное затуханием роста приводят к возрастному падению коэффициента корреляции R.

Организм представляет собой как бы жестко образованную конструкцию, реагирующую на шумовые флюктуации внешней среды как единое целое. Эта целостность особенно ярко проявляется у быстрорастущих организмов: скорости роста отдельных признаков флюктуируют около своих средних скоростей взаимно согласованно. По мере снижения скоростей роста амплитуды этих флюктуаций снижаются, и на первый план выступает не шумовая, а структурная изменчивость параметров a₁ и a₂. При этом по крайней мере для нашего примера дефинитивная структурная коррелированность у взрослых особей практически отсутствует. Это позволяет прояснить механизм онтогенетической изменчивости и коррелированности признаков у организмов.

Величину коэффициента корреляции R можно рассматривать как меру цельности, связности организма как системы. Тогда естественно заключить, что молодые особи являются высокоинтегрированными системами с хорошо работающим механизмом гомеостаза. С возрастом целостность организмов и, вероятно, их регуляторные способности постепенно ослабевают в онтогенезе.

Похожий результат обнаружен и на примере двустворчатого моллюска приморского гребешка (Суханов, Селин, 2018). Использованная там версия модели оказалась несколько проще, чем описанная здесь. Тем не менее у приморского гребешка также обнаружено возрастное снижение коэффициента корреляции между признаками.