Ботанический журнал, 2019, T. 104, № 2, стр. 254-268
ЗАВИСИМОСТЬ СТРОЕНИЯ ПОБЕГОВ И ПОБЕГОВЫХ СИСТЕМ ОТ ИХ ПОЛОЖЕНИЯ В КРОНЕ ULMUS GLABRA (ULMACEAE)
И. С. Антонова 1, *, В. А. Барт 1
1 Санкт-Петербургский государственный университет
199034 Санкт-Петербург, Университетская наб., 7/9, Россия
* E-mail: ulmaceae@mail.ru
Поступила в редакцию 06.02.2018
После доработки 12.01.2019
Принята к публикации 15.01.2019
Аннотация
На выборке из 100 особей подроста U. glabra одного возраста и одной жизненности проведено сравнительное исследование свойств побега и двулетних побеговых систем (ДПС). На данном материале тип ДПС практически полностью соответствовал положению материнского побега в кроне. Для сравнения трижды применен двухфакторный анализ с типом местообитания (3 градации) и типом ДПС (2 градации) в качестве предикторов. В качестве отклика были последовательно выбраны признаки: длина материнского побега, длина первого сверху бокового побега и отношение длины максимального бокового побега к длине материнского побега. В первом случае признак отклика характеризовал сам побег, в то время как два последующих отклика являлись характеристиками ДПС. Во всех случаях анализ показал значимую зависимость отклика от типа ДПС. В то же время, связь с местообитанием оказалась значимой только для первого отклика. Таким образом, выявлено, что существенные метрические характеристики ДПС определенного типа, в отличие от побега, не зависят от местообитания. В этом проявляются программные свойства ДПС как основной пространственно-временной архитектурной единицы кроны. Такой взгляд подтверждается и сравнением углов ответвления боковых побегов. Он соответствует представлению о целостности живой системы по А.А. Любищеву, а именно, единство целого при свободе частей.
Изменчивость облика кроны как следствие ее развития в разных условиях давно известна. Приспособленность к условиям произрастания, которую проявляют растения, удивительна и многообразна (Halle et al., 1978). Модульный подход как будто бы позволяет описать пространственно-временную программу развития дерева, но строгая одинаковость модулей убивает жизненность и многообразие реально существующих форм кроны. Это приводит к постоянной смене парадигм: фракталы, L-системы, нейронные сети (Prusinkiewicz, Lindenmaier, 1990; Prusinkiewicz et al., 1994; Sievänen et al., 2014; Minervini et al., 2015; Minervini et al., 2017).
Вероятно, дело в соотношении стабильных и изменчивых “кирпичиков” кроны, то есть в разной устойчивости звеньев цепочки иерархических единиц. Воспользовавшись этим посылом, рассмотрим крону имматурных растений вяза на уровне строения и изменчивости побегов и двулетних побеговых систем (ДПС) двух типов, наиболее широко представленных в кроне подроста U. glabra.
Цель: определение влияния на структуру ДПС и особенности побегов факторов: положения на дереве и обитания в определенном сообществе.
МАТЕРИАЛЫ И МЕТОДЫ
В качестве объекта исследования был выбран U. glabra, входящий в состав подроста нагорной дубравы заповедника “Белогорье”, участка “Лес на Ворскле”. U. glabra широко распространен в лесных сообществах, имеет плагиотропный рост и четко выраженную структуру ветвей. Рост побегов подробно описан в работах И. А. Грудзинской (Grudzinskaya, 1962, 1968, 1974).
Древостой дубравы представлен и естественными лесонасаждениями, и лесными культурами. Помимо вяза спутниками дуба здесь являются ясень обыкновенный (Fraxinus excelsior L.), липа мелколистная (Tilia cordata Mill.), клён остролистный (Acer platanoides L.) (Neshataev, 1967, 1986). В старовозрастных насаждениях наблюдается распад 1-го яруса, образованного дубом и ясенем, и выход в верхний ярус клёна остролистного и липы мелколистной. Перекрывание крон 2-го и 3-го ярусов создает значительное затенение, сквозистость – не выше 17%. В перестойных сообществах, на вывалах старых дубов, лип и ясеней образуются окна различной величины. Особи ильма, использованные в работе, приурочены к окнам, вызванным распадом древостоя.
Высокий подрост ильма чаще встречается в мелких окнах площадью от 10 до 80 м2. В таких просветах ильм обнаруживает быстрый рост, но по мере затягивания просветов кронами соседних деревьев длина прироста сокращается. Оптимальные условия для роста и развития U. glabra складываются в северной, центральной и, частично, восточной частях окон лесного сообщества (Leonova, 1999).
Для изучения двулетних побеговых систем было исследовано 103 дерева. В местах их произрастания были проведены полные геоботанические описания по методике Ю.Н. Нешатаева трех сообществ: дубо-ясенник мертвопокровный, липо-клёно-дубняк мертвопокровный, липо-дубняк мертвопокровный. Растительность ясене-дубняка, липо-клёно-дубняка и липо-дубняка относится к зонально-климаксовым сообществам (Neshataev, 1979, 1986). Все три сообщества являются мертвопокровными, так как избыточно расплодившиеся в дубраве кабаны препятствуют естественному росту трав нижнего яруса дубравы. Клёно-липо-дубняк, представляющий собой посадку примерно столетнего возраста, приближается по своему структурно-возрастному составу к естественным насаждениям. Ясене-дубняк – искусственного происхождения, посадка в возрасте более 120 лет, на месте срубленного дубового леса, по своему структурно-возрастному составу близкая к естественным насаждениям.
Древесный ярус этих сообществ пропускает разное количество солнечного света (Gorishina, Neshataev 1974; Gorishina, Mitina 1974). Влияние факторов света и увлажнения на обитателей сообществ широколиственных лесов неоднократно обсуждалось в литературе (Evstigneev, 1988, 1996; Chistyakova, Evstigneev, 1994).
По классификации “Диагнозы и ключи возрастных состояний лесных растений” (Chistyakova, Kutina, 1986) исследованные вязы относились ко второй подгруппе растений имматурного возрастного состояния. Возраст растений, использованных в работе, 12–17 лет, высота 1.2–2.3 метра. Растения не имели видимых следов повреждений. Форма кроны всех особей зонтиковидная. На тонком стволе располагались 2–4 крупные плагиотропные ветви, с четырьмя порядками ветвления. Оси всех порядков ветвления у растений данного вида нарастают симподиально (Grudzinskaya, 1962, 1968, 1974).
Экотопические условия в местах сбора материала можно считать выровненными, что объясняется близким положением в рельефе и равными гидрологическими условиями. Почвы для всех площадей определены как серые лесные, слабо оподзоленные, на лессовидном суглинке.
Основные различия пробных площадей заключаются в структуре и составе древостоя. По мнению О.В. Смирновой и др. (Vostochnoevropeyskie..., 1994), свет в богатых, достаточно увлажненных местах, является фактором, определяющим рост и структуру древостоя.
Каждый тип ДПС определяется своим геометрическим контуром. Геометрический контур таких систем типичен для вида. Благодаря именно этому типу (с определенным количеством, длинами и углами отхождения боковых побегов) формируется характерное для вида “кружево кроны” (Antonova et al., 2012; Antonova, Fatianova, 2016).
С каждого дерева было собрано по 2 ДПС: одна “ростовая” ДПС с дистальной части оси 2-го порядка (совокупность данных ПС составила выборку группы I ) и одна “заполняющая” ДПС оси 3-го или 4-го порядков (группа этих ДПС вошла в выборку группы II) (рис. 1, табл. 2). Эти типы ДПС подробно описаны нами раньше (Antonova et al., 2016).
Рис. 1.
Схема зонтиковидного дерева подроста U. glabra. Прямоугольниками отмечены места сбора ПС группы I и группы II для каждого исследованного дерева.
Fig. 1. Scheme of umbellate tree of regrowth of U. glabra. Squares mark the gathering places of the shoot systems of the groups I and II for each tree under study.
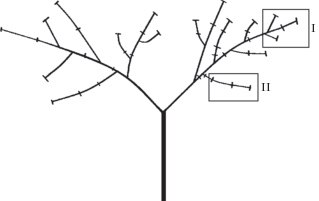
Таблица 1.
Некоторые характеристики древостоя площадей сбора материала. Table 1. Some characteristics of the forest areas of collected material
| Название сообщества Name of community |
Формула
древостоя Stand formula |
Средняя
высота 1 яруса Mean height of 1 layer |
Максимальная высота 1 яруса Max height of 1 layer | Средняя
высота 2 яруса Mean height of 2 layer |
Максимальная высота 2 яруса Max height of 2 layer |
|---|---|---|---|---|---|
| Липо-дубняк снытевый Q.robur+T.cordata –Ae.podograria | 4Д3Л2К1+И | 25 | 26–28 | 16 | 22–24 |
| Дубо-ясенник снытевый Q.robur+Fr.excelsior –Ae.podograria | 6Я2Д1К1Л+И | 26 | 25–28 | 15 | 22–24 |
| Липо-клено-дубняк снытевый Q.robur+T.cordata+A.platonoides –Ae.podograria | 6Д2Л2К+И | 25 | 26–29 | 15 | 21–25 |
Таблица 2.
Количество собранных ДПС. Table 2. The number of sampled biennial shoots systems (BSS)
| Фитоценоз/Phytocenosis | Кол-во исследованных деревьев/ Number of trees studied | Кол-во собранных ДПС/ Number of sampled BSS |
|---|---|---|
| Ясене-дубняк мертвопокровный Q. robur+Fr. excelsior – dead soil |
29 | 50 |
| Липо-клено-дубняк мертвопокровный Q. robur+T. cordata+A. platonoides – dead soil |
45 | 89 |
| Липо-дубняк мертвопокровный Q. robur+T. cordata – dead soil |
29 | 58 |
| Всего исследовано Total studied |
103 | 197 |
У “ростовой” и “заполняющей” ДПС были измерены длины всех побегов и количество листьев на них, углы ответвления боковых побегов и длины междоузлий на материнском побеге. Согласно разработанной на кафедре геоботаники Санкт-Петербургского государственного университета методике описания побеговых систем древесных растений, междоузлия всех побегов были пронумерованы сверху вниз по уже сформированному побеговому комплексу от дистального конца к начальному. Таким образом, последнее междоузлие побега получало номер 1, следующее – номер 2, и т.д. Как показали наши исследования (Antonova et al., 2004, 2008, 2012, 2016), такая нумерация позволяет адекватно описывать побеговые комплексы в кронах различных древесных растений, что было проделано на растениях более чем 30 различных семейств.
Всего было измерено 1059 побегов в 197 побеговых системах.
Двухфакторный дисперсионный анализ (two way ANOVA) был применен для оценки и сравнения влияния факторов: по 3-м градациям типов лесных сообществ и по 2‑м градациям, определяющим положение побега или ДПС на дереве, и их взаимодействия – на несколько метрических характеристик побега и ДПС в качестве откликов. Для сравнения дисперсий признаков применялись тесты Фишера и Левена. Использован пакет компьютерных программ STATISTICA 7.0 (StatSoft, Inc.).
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЯ
Первоначально в двухфакторном дисперсионном анализе в качестве отклика, был выбран признак “длина материнского побега” собранных ДПС. Так как места сбора ДПС были четко определены, то выбранный отклик характеризовал побег по его положению как внутри кроны, ветви и т. д., так и в определенном лесном сообществе.
Выборочные разделения признаков, использованных в анализе, были проверены на нормальность критериями Колмогорова–Смирнова и Лиллиефорса.
Примененный в работе дисперсионный анализ ANOVA устойчив к незначительной неоднородности дисперсий (Seber, 2003).
В таблице 3 приведены результаты такого двухфакторного анализа, показывающие, что как положение на дереве, так и тип сообщества статистически значимо влияют на длину побега. Более того, значимым является и фактор их совместного влияния, проявляющийся в разных формах кривых на рисунках (рис. 2, 3).
Рис. 2.
Длина среднего материнского побега и ее 95% доверительный интервал для двух разных позиций в кроне U. glabra, в трех различных сообществах. Штриховая линия – оси второго порядка, сплошная – третьего порядка; y – десятичный логарифм длины материнского побега; х – тип сообщества: 1 – дубо-ясенник, 2 – липо-клено-дубняк, 3 – липо-дубняк.
Fig. 2. Mean lengths of parent shoot and its 95% confidence interval for two different positions in the crown of U. glabra, in three different communities; dash line – second order, solid line – third order; y is decimal logarithm of parent shoot length. x is type of community: 1 – oak-ash forest, 2 – linden-maple-oakery, 3 – linden-oakery.
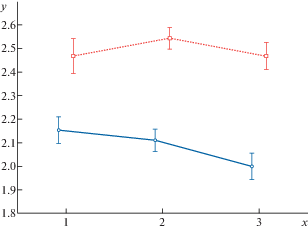
Рис. 3.
То же по градациям положения в кроне; штриховая линия – липо-дубняк, сплошная – ясене-дубняк, пунктир – липо-клено-дубняк. y – десятичный логарифм длины материнского побега. х – группы по положению побега в кроне. I – заполняющая побеговая система, II – ростовая побеговая система.
Fig. 3. The same values – by gradations of position in the crown; dash line – linden-oakery, solid line – oak-ash forest, dotted line – linden-maple-oakery; y is decimal logarithm of parent shoot length; x – position of shoot in the crown: I – the filling BSS; II – the growth BSS.
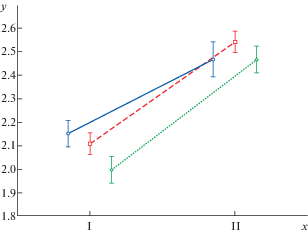
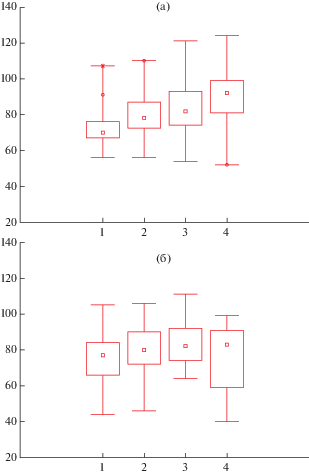
Рис. 4.
Диаграммы “ящики с усами”: медиана, 25–75%, размах выборки – для углов ответвления первых четырех сверху боковых побегов у ДПС U. glabra двух разных позиций в кроне; а) оси 2-го порядка; б) оси 3-го порядка. y – величина угла в градусах; x – номер бокового побега от верхушки.
Fig. 4. Charts “box and whiskers”: median, 25–75%, range – for angles of branching of the first four shoots from the top side of BSS U. glabra of two different positions in the crown; a) the axis of the 2nd order; b) axis 3-rd order; y – value of angle in degrees; x is the number of side shoot from the top.
Варьирование длин побегов в ответ на воздействие местообитания (табл. 3) установлено в многочисленных исследованиях (Gorishina, 1989; Zmylyev et al., 2005). Длины побегов в кроне дерева представляют собой огромный вариационный ряд без естественных дизъюнкций, ответственных за условия существования. Худшие или лучшие условия жизни ведут к изменению длины части побегов. На этом основываются работы, дающие ответ о состоянии растений в определенных условиях. При этом они никак не отвечают на вопрос, чем же собственно вся целиком кроновая система различается в разных местообитаниях. Для ответа на этот вопрос придется найти то, что в структуре кроны остается постоянным у вида. Ведь давно известно, что даже в безлистном состоянии ботаник отличает крону одного вида от кроны другого.
Таблица 3.
Значения F-статистики и статистическая значимость факторов двухфакторного дисперсионного анализа при сравнении длин групп побегов U. glabra двух разных позиций в кроне, собранных в трех разных сообществах (n = 187). Table 3. Values of F-statistics and statistical significance of factors in two-way ANOVA comparing the lengths of shoots of groups of U. glabra of two different positions in the crown, collected in three different communities (n = 187)
| Факторы/Factors | F | p |
|---|---|---|
| Тип сообщества Type of community |
F(2.187) = 6.60 | 0.0017 |
| Положение в кроне Place in crown |
F(1.187) = 297.49 | 0.0000 |
| Взаимодействие Interaction |
F(2.187) = 3.23 | 0.04 |
Примечание: F – статистика критерия с соответствующими степенями свободы, p – уровень значимости критерия; тип сообщества: липо-клено-дубняк, дубо-ясенник, липо-дубняк. Положение в кроне: группа I, группа II.
Note: F – statistics with the appropriate degrees of freedom, p – significance level of test; type of community: linden-maple-oakery, oak-ash, linden-oakery. The position in the crown: group I, group II.
Побег оси соответствующего порядка, собранный из определенного места в кроне, при сравнении растений из разных сообществ выявляет зависимость от местообитания. Выяснение же вопроса о том, что же остается неизменным в рисунке кроны, является нерешенной задачей.
Затем отклик был заменен на другой морфологический признак, характеризующий не сам побег, а развившуюся на нем ДПС. Это было сделано двумя способами. Сначала оценим длину d бокового побега на первом сверху наблюдаемом междоузлии (табл. 4). Почти во всех случаях длина первого сверху бокового побега максимальна.
Таблица 4.
Значение F-статистики и значимость факторов двухфакторного анализа при сравнении длин первого сверху бокового побега U. glabra в двух разных позициях в кроне, собранных в трех разных сообществах. Table 4. The value of F-statistics and statistical significance of factor impact in two-way ANOVA comparing the lengths of the first top lateral shoot of U. glabra in two different positions in the crown, collected in three different communities
| Факторы/Factors | F | p |
|---|---|---|
| Тип сообщества Type of community |
F(2.187) = 0.46 | 0.63 |
| Положение в кроне Place in crown |
F(1.187) = 367.53 | 0.0001 |
| Взаимодействие Interaction |
F(2.187) = 2.26 | 0.11 |
Затем в качестве отклика было выбрано отношение d/L, где L – длина материнского побега (табл. 5).
Таблица 5.
Значения F-статистики и значимость факторов двухфакторного анализа при сравнении отношений длины первого сверху бокового побега к материнскому для U. glabra в двух разных позициях в кроне, собранных в трех разных сообществах. Table 5. The value of F-statistics and statistical significance of factor impact in two-way ANOVA comparing the ratio of length of the first top lateral shoot to that of parent one of U. glabra in two different positions in the crown, collected in three different communities
| Факторы/Factors | F | p |
|---|---|---|
| Тип сообщества Type of community |
F(2.187) = 0.8 | 0.44 |
| Положение в кроне Place in crown |
F(1.187) = 153.8 | 0.0001 |
| Взаимодействие Interaction |
F(2.187) = 0.36 | 0.7 |
Отношение длины первого сверху (или какого-либо другого определенного положения) бокового побега на материнском побеге есть, несомненно, характеристика ДПС (Antonova, Fatianova, 2016). Это же относится и к признаку длины бокового побега на материнском при фиксированном номере соответствующего ему междоузлия.
Результаты анализа (табл. 4 и 5) однозначно указывают на статистическую независимость значений обоих этих откликов от изменений рассматриваемых типов лесных сообществ. Дистальная часть осей 2-го порядка, из которой была собрана группа I, как правило, представляла собой “ростовой” тип ДПС (Antonova, Fatianova, 2016). В то же время дистальная часть осей 3-го порядка соответствовала “заполняющему” типу ДПС. Если иметь в виду достаточно точное соответствие градаций положения на дереве двум выделенным типам ДПС U. glabra, то указанная независимость означает бóльшую устойчивость типа ДПС к изменению сообщества. Эта устойчивость сродни широко обсуждаемой в литературе теме соответствия устойчивости части и целого в живой природе. Так, для любой части организма по М.Д. Голубовскому (Golubovskiy, 2000) действует принцип А.А. Любищева (Lubishchev,1982) “единство целого при свободе частей”. Пример анализа в табл. 4 и 5 говорит о качественном отличии побега от ДПС в устойчивости к этому фактору.
Этот эффект основан на жесткости системы пространственно-временных единиц кроны, устойчиво закодированными для каждого вида. В этой системе структура ДПС играет роль основной единицы, и такой результат был ожидаем.
ДПС в сравнении с побегом оказывается структурно иной единицей кроны. Тип ДПС есть характеристика гораздо менее подверженная изменениям внешних условий. Крона состоит из определенных типов ДПС, присутствующих в системе в определенном количестве. Изменение внешних условий меняет именно соотношение – количество определенных типов ДПС, оставляя минимальными изменения каждого из типов.
В характеристике типа ДПС разные по положению боковые побеги играют существенно разную роль (табл. 6).
Таблица 6.
Значения F-статистики и значимость факторов двухфакторного анализа при сравнении длин и отношений к длине материнского побега для второго, третьего и четвертого сверху бокового побегов U. glabra двух разных позиций в кроне, собранных в трех разных сообществах. Table 6. The value of F-statistics and statistical significance of factor impact in two-way ANOVA comparing lengths and ratio to length of parent shoot for the second, third and fourth top lateral shoots of U. glabra of two different positions in the crown, collected in three different communities
| Положение побега Shoot position from the top |
Фактор Factor |
Длина бокового d Lateral shoot length d |
Отношение d/L Ratio d/L |
||
|---|---|---|---|---|---|
| F | p | F | p | ||
| Второй сверху Second | Тип сообщества Type of community |
F(2.187) = 1.04 | 0.36 | 0.46 | 0.63 |
| Положение в кроне Place in crown |
F(1.187) = 247.61 | 0.0001 | 163.85 | 0.0001 | |
| Взаимодействие Interaction |
F(2.187) = 2.34 | 0.10 | 1.82 | 0.17 | |
| Третий сверху Third | Тип сообщества Type of community |
F(2.187) = 0.27 | 0.76 | 0.14 | 0.87 |
| Положение в кроне Place in crown |
F(1.187) = 101.14 | 0.0001 | 69.89 | 0.0001 | |
| Взаимодействие Interaction | F(2.187) = 2.72 | 0.07 | 1.83 | 0.16 | |
| Четвертый сверху Fourth |
Тип сообщества Type of community |
F(2.187) = 0.10 | 0.90 | 0.26 | 0.77 |
| Положение в кроне Place in crown |
F(1.187) = 13.84 | 0.0001 | 7.90 | 0.0062 | |
| Взаимодействие Interaction |
F(2.187) = 0.41 | 0.66 | 0.27 | 0.76 | |
В таблице 6 представлены результаты влияния трех местообитаний и двух позиций кроны, но уже для побегов, занимающих второе, третье и четвертое положение на материнском от верхушки. Признаки, представленные в таблице, аналогичны описанным выше (табл. 4, 5): собственно длина бокового побега определенного положения на материнском и ее отношение к длине материнского побега.
Как видно из таблицы, ни по одному из этих откликов дисперсионный анализ не нашел зависимости от местообитаний, но все отклики отчетливо разделяют положение побегов в кроне. Каждый из откликов является линейным признаком или их отношением, наиболее жестко характеризующим геометрический контур ДПС. Это является подтверждением устойчивости геометрического контура, а значит, и типа ДПС, выделенного ранее на основе ее биологических и пространственно-временных свойств, и согласуется с утверждением об очень малой вариативности линейных характеристик геометрического контура ДПС в связи с изменениями внешних условий (Antonova, Gnilovskaya, 2013; Antonova, Fatianova, 2016; Antonova, Bart, 2016a, b).
Обратимся теперь к угловым характеристикам геометрического контура ДПС. Углы ответвления боковых побегов в исследованных выборках показали унимодальное распределение, согласующиеся с нормальным типом (критерии Колмогорова–Смирнова и Лиллиефорса) и, несмотря на равенство средних значений, являются ненадежными выборочными характеристиками. В частности, табл. 7 показывает, что значения углов отхождения первых двух боковых побегов имеют значимо разные дисперсии.
Таблица 7.
Значения описательных статистик и уровень значимости (p) F-критерия при сравнении дисперсий углов ответвления двух групп побегов U. glabra разных позиций в кроне. Table 7. The values of the descriptive statistics and the significance level (p) of F-test when comparing the variances of branching angles of two groups of U. glabra shoots of different positions in crown
| Угол ветвления Branching angle | Оси 3-го порядка
(Заполняющие ДПС) 3rd order axes (Filling BSS) |
Оси 2-го порядка
(Ростовые ДПС) 2rd order axes (Growth BSS) |
F | p | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Средн. Mean |
Мин Min. |
Макс Max. |
Ст. откл. SD |
Средн. Mean |
Мин Min. |
Макс. Max. |
Ст. откл. SD |
|||
| 1 побега 1 shoot |
76 | 44 | 105 | 13 | 72 | 56 | 107 | 8 | 2.24 | p < 0.0017 |
| 2 побега 2 shoot |
80 | 46 | 106 | 15 | 80 | 56 | 110 | 11 | 1.81 | p < 0.028 |
| 3 побега 3 shoot |
83 | 64 | 111 | 12 | 83 | 54 | 121 | 14 | 1.30 | нз |
| 4 побега 4 shoot |
76 | 40 | 99 | 23 | 89 | 52 | 124 | 16 | 1.94 | нз |
Это говорит, прежде всего, о разных функциональных нагрузках побегов первых верхних позиций у исследуемых групп, занимающих различное положение в кроне (по сути дела – у разных типов ДПС). У группы побегов, занимающих верхушечное положение на оси второго порядка, проявляется выраженная тенденция к захвату пространства. По-видимому, это делает этот данный признак генетически более закрепленным у вида. В то же время, группа побегов, представляющая собой верхушки третьего порядка, выполняет функцию заполнения пространства и создания листовой массы. Их верхушечные побеги отклоняются от материнского в зависимости от имеющегося в конкретной позиции свободного пространства – дисперсия углов их отклонения больше.
Третий и четвертый боковые побеги у этих групп оказываются более сходными функционально, и их углы ответвления статистически неотличимы.
Сравнение углов отклонения боковых побегов от первого до четвертого положения от верхушки материнского побега показывает, что в группе вариабельность угла первого побега существенно меньше, чем у последующих. У ростовых ДПС наблюдается отчетливое возрастание величины угла от первого к четвертому. Это, вероятно, является отражением того, что верхние углы более жестко закреплены у ДПС. У побеговых систем осей третьего порядка углы разных позиций имеют одинаковые дисперсии, а тенденции к изменению средних нет. Это означает большую функциональную однородность этих побегов, независимо от их положения на материнском.
Современные зарубежные авторы неоднократно подчеркивали мультимасштабность пространственно-временных взаимодействий внутри растительного организма (Band, King, 2012; Bucksch, 2017). По мнению Бальдацци (Baldazzi et al., 2012) в такой ситуации предпочтительно, чтобы многомасштабная модель имела определенную модульность в своей конструкции, так что отдельные модули отвечают за моделирование конкретных пространственных аспектов системы. Иными словами, предполагается наличие в системе структурных единиц.
При описании структуры кроны важным элементом является выбор основных структурных единиц.
Структурная единица должна проявлять инвариантность к внешним воздействиям в разных возрастных состояниях и иметь небольшое количество четко определенных типов. В работах (Mazurenko, Khokhriakov, 1981, 1991; Gatsuk, 2008; Getmanets, 2008; Antonova et al. 2012) представлены примеры типизаций различных единиц кроны. В данной работе на основе достаточно большой выборки определенных типов ДПС, собранных с растений одного возрастного состояния, показана устойчивость обоих типов ДПС в трех типах сообществ: липо-дубняке, ясене-дубняке, липо-клене-дубняке. При этом на признак длины материнского побега, рассмотренный отдельно от ДПС, тип сообщества оказывает статистически значимое влияние.
Несмотря на многочисленные работы, характеризующие побеги, для всей совокупности побегов дерева отсутствует типизация, приемлемая с точки зрения двух условий, приведенных выше. Несомненно, одной из причин этого является пластичность основной характеристики побега – его длины – в зависимости от внешних условий.
ЗАКЛЮЧЕНИЕ
На наш взгляд, с пространственно-временной точки зрения крону дерева целесообразно рассматривать как совокупность двулетних побеговых систем (ДПС). На внешнее воздействие система будет реагировать изменением состава ДПС по типам при минимальной внутритиповой вариабельности. Отсутствие реакции характерных боковых побегов и углов их ответвления на различия местообитаний, также проверенные в этой работе, подтверждают устойчивость всего геометрического контура, и значит, типа ДПС. Именно такая устойчивость и есть отражение принципа единства целого при свободе частей, свойственного конкретным живым системам.
Список литературы
[Antonova, Bart] Антонова И.С., Барт В.А. 2016а. Анализ метрических характеристик двулетних побеговых систем Acer negundo L. в молодом генеративном состоянии. – Вестник Тверского гос. ун-та. Сер. “Биология и Экология”. 4: 151–168.
[Antonova, Bart] Антонова И.С., Барт В.А. 2016b. К вопросу о морфологии крон некоторых видов деревьев умеренной зоны и их математического описания. В сб.: Роль ботанических садов в сохранении и мониторинге биоразнообразия Кавказа (материалы международной ботанической конференции, посвященной 175-летию сухумского Ботанического сада, 120-летию сухумского субтропического дендрапарка, 85-летию проф. Г.Г. Айба и 110-летию проф. А. А. Колоковского). Сухум, С. 42–45.
[Antonova, Belova] Антонова И.С., Белова О.А. 2008. Трансформация модулей разных уровней кроны некоторых древесных растений в связи с условиями среды и фитоценотической позицией. – Вестник Тверского гос. ун-та. Сер. “Биология и Экология”. 9: 10–16.
[Antonova, Fatianova] Антонова И.С., Фатьянова Е.В., Зайцева Ю.В., Гниловская А.А. 2012. Мультимасштабность побеговых систем некоторых деревьев умеренной зоны (разнообразие, классификация, терминология). – В кн.: Актуальные проблемы биоморфологии. Киров. С. 390–402.
[Antonova, Fatianova] Антонова И.С., Фатьянова Е.В. 2014. Необходимость использования знаний о строении и развитии кроны деревьев в различных фундаментальных и прикладных разделах геоботаники. – Бот. журн. 99 (12): 1305–1316.
[Antonova, Fatianova] Антонова И.С., Фатьянова Е.В. 2016. О системе иерархических уровней строения кроны деревьев умеренной зоны. – Бот. журн. 101 (6): 628–649.
[Antonova, Gnilovskaya] Антонова И.С., Гниловская А.А. 2013. Побеговые системы кроны Acer negundo L. (Aceraceae) в разных возрастных состояниях. – Бот. журн. 98 (1): 53–68.
[Antonova, Nikolaeva] Антонова И.С., Николаева Н.В. 2004. Элементарная побеговая система как единица структуры кроны древесных растений умеренной зоны. – В сб.: Материалы X Школы по теоретической морфологии растений “Конструкционные единицы в морфологии”. Киров. С. 10–12.
Baldazzi V., Bertin N., De Jong H., Génard M. 2012. Towards multiscale plant models: integrating cellular networks. – Trends Plant Sci. 17: 728–736. https://doi.org/10.1016/j.tplants.2012.06.012
Band L.R., King J.R. 2012. Multiscale modelling of auxin transport in the plant-root elongation zone. – J. Math. Biol. 65: 743–785. https://doi.org/10.1007/s00285-011-0472-y
Bucksch A., Atta-Boateng A., Azihou A.F. et al. (34 more authors). 2017. Morphological plant modeling: Unleashing geometric and topological potential within the plant sciences. – Frontiers in Plant Science. 8 (900): 16 DOI: http://dx.doi.org/https://doi.org/10.3389/fpls.2017.00900
[Chistyakova, Evstigneev] Чистякова А.А., Евстигнеев О.И. 1994. Популяционное поведение лиственных деревьев. – В кн.: Восточноевропейские широколиственные леса. М. С. 113–132.
[Chistyakova, Kutina] Чистякова А.А., Кутьина И.С. 1989. Вяз шершавый, ильм горный. – В кн.: Диагнозы и ключи возрастных состояний лесных растений. Деревья и кустарники Ч. I. М. С. 82–89.
[Chistyakova, Zaugolnova, Poltinkina, Kutina, Laschinskiy] Чистякова А.А., Заугольнова Л.Б., Полтинкина И.В., Кутьина И.С., Лащинский Н.Н. 1989. Диагнозы и ключи возрастных состояний лесных растений. (под ред. О.В. Смирновой.) Деревья и кустарники: методические разработки для студентов биологических специальностей. Ч. I. М. 102 с.
[Evstigneev] Евстигнеев О.И. 1988. Особенности развития широколиственных деревьев под пологом леса при различной освещенности. – Бот. журн. 73 (12): 1730–1736.
[Evstigneev] Евстигнеев О.И. 1996. Отношение лиственных деревьев к свету и водообеспеченности в связи со структурой леса. – Лесоведение. (6): 26–35.
[Gatsuk] Гацук Л.Е. 2008. Иерархическая система структурно-биологических единиц растительного организма. В кн.: Современные подходы к описанию структуры растения. Киров. С. 32–47.
[Getmanets] Гетманец И.А. 2008. Подходы к анализу биоморф вида рода Salix (на примере ив Южного Урала). – В кн.: Современные подходы к описанию структуры растения. Киров. С. 108–115.
[Golubovskiy] Голубовский М.Д. 2008. Тайный жребий профессора Любищева. – В кн.: Любищев А.А. Расцвет и упадок цивилизации. СПб. С. 5–9.
[Gorishina] Горышина Т.К. 1989. Фотосинтетический аппарат растений и условия среды. Л. 204 с.
[Gorishina, Mitina] Горышина Т.К., Митина М.В. 1974. Фотосинтез дубравных растений как физиологическая основа их продуктивности. Биологическая продуктивность и ее факторы в лесостепной дубраве. – Уч. зап. Ленинградского ун-та. Сер. “Биологические науки”. 53 (367): 93–118.
[Gorishina, Neshataev] Горышина Т.К., Нешатаев Ю.Н. 1974. О некоторых основных чертах биологической продуктивности и ее факторах в дубраве южной лесостепи. – Уч. зап. Ленинградского ун-та. Сер. “Биологические науки”. 53 (367): 209–212.
[Grudzinskaya] Грудзинская И.А. 1962. Особенности моноподиального ветвления у древесных пород на примере дуба и вяза. – Проблемы ботаники. (6): 219–231.
[Grudzinskaya] Грудзинская И.А. 1968. О строении и формировании вегетативных побегов Ulmus в связи с переходом от моноподиального к симподиальному ветвлению. – В сб.: Всесоюзная межвузовская конференция по морфологии растений. М. С. 84–85.
[Grudzinskaya] Грудзинская И.А. 1974. О гетеробластном развитии Ulmus. – Бот. журн. 59(8): 1160–1171.
Halle F., Oldeman R. A. A., Tomlinson P. B. 1978. Tropical trees and forests: an architectural analysis. Berlin. 441 p.
[Leonova] Леонова Н.А. 1999. Состояние популяций вяза шершавого (Ulmus glabra L.) в условиях разного освещения в старовозрастных широколиственных сообществах Калужской и Пензенской областей. – Лесоведение. (6): 59–64.
[Lubishchev] Любищев А.А. 1982. Проблемы формы, систематики и эволюции организмов. М. 277с.
[Mazurenko, Khokhriakov] Мазуренко М.Т., Хохряков А.П. 1981. Биоморфологическая изменчивость и ее связь с таксонообразованием у растений. – В сб.: Жизненные формы: структура, спектры и эволюция. М. С. 12–30.
[Mazurenko, Khokhriakov] Мазуренко М.Т., Хохряков А.П. 1991. Классы метамеров деревьев. – Журн. общ. биологии. 52 (3): 409–421.
Minervini M., Fischbach A., Scharr H., Tsaftaris S.A. 2015. Finely-grained annotated datasets for image-based plant phenotyping. – Pattern Recogn Lett. 81: 80–9. DOI: https://doi.org/https://doi.org/10.1016/j.patrec.2015.10.013
Minervini M., Giuffrida M.V., Perata P., Tsaftaris S.A. 2017. Phenotiki: an open software and hardware platform for affordable and easy image-based phenotyping of rosette-shaped plants. – Plant J. 90 (1): 204–16. DOI: https://doi.org/https://doi.org/10.1111/tpj.13472
[Neshataev] Нешатаев Ю.Н. 1967. Опыт крупномасштабного геоботанического картирования учлесхоза “Лес на Ворскле”. – Уч. зап. Ленинградского ун-та. Сер. “Биологические науки”. (331): 87–117.
[Neshataev] Нешатаев Ю.Н. 1986. Геоботаническая характеристика типов леса заповедника “Лес на Ворскле”. – В сб.: Комплексные исследования биогеоценозов лесостепных дубрав. Л. С. 32–48.
Prusinkiewicz P.W., Remphrey W.R., Davidson C.G., Hammel M.S. 1994. Modeling the architecture of expanding Fraxinus pennsylvanica shoots using L-systems. – Can J Bot. 72 (5): 701–14. https://doi.org/.https://doi.org/10.1139/b94-091
Prusinkiewicz P., Lindenmayer A. 1990. The algorithmic beauty of plants. New York. 240 p.
Seber G.A.F., Lee A.J. 2003. Linear Regression Analysis. Auckland. 582 p.
Sievänen R., Godin C., DeJong T.M., Nikinmaa E. 2014. Functional-structural plant models: a growing paradigm for plant studies. Ann Bot. 114 (4): 599–603. DOI: https://doi.org/https://doi.org/10.1093/aob/mcu17
[Vostochno] Восточноевропейские широколиственные леса. 1994. М. 364 с.
[Zmilyov] Жмылев П.Ю., Алексеев Ю.Е., Карпухина Е.А., Баланчин С.А. 2005. Биоморфология растений: иллюстрированный словарь. М. 256 с.
Дополнительные материалы отсутствуют.
Инструменты
Ботанический журнал


