Физиология человека, 2021, T. 47, № 5, стр. 61-66
Математическая модель регуляции показателей микрокровотока в сосудах симметричных областей парных органов человека
Л. В. Мезенцева *
ФГБНУ Научно-исследовательский институт нормальной физиологии имени П.К. Анохина
Москва, Россия
* E-mail: l.v.mezentseva@mail.ru
Поступила в редакцию 05.12.2019
После доработки 10.02.2020
Принята к публикации 01.06.2020
Аннотация
Впервые сформулирована математическая модель регуляции показателей микрокровотока в сосудах симметричных областей парных органов человека. Модель основана на экспериментально-расчетных исследованиях синхронных изменений показателей микроциркуляции (МЦР) сосудов симметричных органов у человека при асимметричных физических нагрузках на верхние конечности. Измерения проведены на здоровых добровольцах методом лазерной допплеровской флоуметрии (ЛДФ). Датчики ЛДФ-сигнала устанавливали на симметричных сторонах нижних частей правого и левого плеча в точках, расположенных на 3 см выше локтевого сгиба. Физические нагрузки представляли собой махи левой или правой рукой в положении стоя в течение 1 мин. Синхронные измерения показателей среднего значения перфузии слева и справа и их изменения под влиянием физических нагрузок выполнялись в дневное время суток через каждые 3 ч в течение 5 дней. Далее методом множественного регрессионного анализа исследовали зависимости изменений показателей МЦР от их исходных значений. Полученная регрессионная модель была положена в основу математической модели, сформулированной в виде системы линейных дифференциальных уравнений. Выведены формулы, описывающие колебательные процессы микрокровотока в симметричных областях парных органов. Сформулированы условия к диапазонам числовых значений параметров модели, при которых существуют устойчивые режимы функционирования системы МЦР симметричных областей парных органов человека.
Проблеме функциональной асимметрии периферического отдела кровообращения человека и животных посвящены многочисленные исследования [1–5]. Результаты этих исследований показали наличие морфофункциональной асимметрии в реакциях микрососудов симметричных областей парных органов млекопитающих, независимое от объекта исследования и характера тестирования. Однако физиологические механизмы, лежащие в основе этих процессов, до сих пор, не ясны. Экспериментальные подходы к исследованию физиологических процессов позволяют накапливать описательные знания об изучаемых объектах. Но для понимания физиологических механизмов, лежащих в основе изучаемых явлений, этого недостаточно. Понять механизм процесса – значит построить математическую модель, описывающую регуляцию основных параметров, описывающих этот процесс, оценивать диапазоны параметров, при которых существуют устойчивые режимы функционирования системы, а также критические точки перехода в неустойчивые состояния. В практической медицине перед исследователями стоит проблема прогнозирования течения того или оного физиологического процесса, четкой формулировки условий, при которых возможны переходы из нормы в патологию. Для этого в распоряжении исследователя должна быть не сумма разрозненных экспериментальных данных, а математическая модель изучаемого явления. Поэтому настоящее исследование посвящено разработке математической модели регуляции показателей микрокровотока в симметричных областях парных органов человека.
МЕТОДИКА
В основу исследования была положена экспериментально-расчетная методика, суть которой заключалась в том, что формулировка математической модели базируется не на абстрактных гипотезах, а на реальных параметрах, полученных в экспериментах. У 5 здоровых добровольцев (мужчины 50–55 лет) определяли синхронные измерения показателей микроциркуляции (МЦР) симметричных областей верхних конечностей при физических нагрузках на них. Измерения проводили в 2-х состояниях: 1 – исходное состояние; 2 – сразу после физических нагрузок. Физические нагрузки были асимметричные и представляли собой махи левой или правой рукой в положении стоя в течение 1 мин. Исходное положение: основная стойка, стопы на ширине плеч параллельно друг другу, руки опущены вдоль тела и расслаблены, пальцы слегка согнуты. Затем испытуемый на вдохе должен был резко поднять одну руку вперед-вверх, после чего ее свободно опустить. При этом другая рука должна была находиться опущенной вдоль тела в расслабленном состоянии. Махи совершали прямыми руками с максимальной амплитудой. Темп движений – 30 махов в мин. Первая серия экспериментов включала в себя только махи левой рукой, вторая серия – только махи правой рукой. Обе серии были независимые и проводились в разные дни. Измерения параметров МЦР проводили в положении сидя методом лазерной допплеровской флоуметрии (ЛДФ) с помощью двухканального прибора “ЛАКК-02” НПП “ЛАЗМА” (Россия). Датчики ЛДФ-сигнала фиксировали на наружной поверхности симметричных областей нижних частей правого и левого плеча в точках, расположенных на 3 см выше локтевого сгиба. Синхронные измерения показателей среднего значения перфузии слева (ПМлев) и справа (ПМпр) выполняли в дневное время суток через каждые 3 ч (5 измерений в день) в течение 5 дней. Частота дискретизации ЛДФ-сигнала 20 Гц, интервал отсчетов 0.05 с, время записи 2 мин.
Математическая обработка результатов измерений включала в себя оценку средних значений перфузии симметричных сторон наблюдения (x1 = ПМлев и x2 = ПМпр) и их изменений (∆x1 и ∆x2) под влиянием физических нагрузок. В предыдущих исследованиях [6] было показано, что степень выраженности реакции показателей МЦР на физическую нагрузку зависит от исходных значений этих показателей. Поэтому в ходе настоящего исследования провели более детальное изучение этой взаимосвязи методом множественного регрессионного анализа. Для каждого испытуемого рассчитывали параметры a0, a1, a2, b0, b1, b2 регрессионных уравнений:
(1)
$\left\{ \begin{gathered} \Delta x1 = a0 + a1x1 + a2x2 \hfill \\ \Delta x2 = b0 + b1x1 + b2x2. \hfill \\ \end{gathered} \right.$(2)
$\left\{ \begin{gathered} {{dx1} \mathord{\left/ {\vphantom {{dx1} {dt}}} \right. \kern-0em} {dt}} = a0 + a1x1 + a2x2 \hfill \\ ~{{dx2} \mathord{\left/ {\vphantom {{dx2} {dt}}} \right. \kern-0em} {dt}} = b0 + b1x1 + b2x2. \hfill \\ \end{gathered} \right.$Дальнейшее исследование решений этой системы и их устойчивости проводили с использованием известных математических методов [7]. Все расчеты проводили в условных (перфузионных) единицах с помощью программного обеспечения, входящего в пакеты прикладных программ Statistica и Excel for Windows (v. 6.0).
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ
Регрессионный анализ. Результаты исследования показали, что изменения показателей МЦР у всех испытуемых зависели не только от их исходных значений на измеряемой стороне, но и от исходных значений на противоположной стороне наблюдения, причем эти зависимости описывались системой линейных регрессионных уравнений (1):
(1)
$\left\{ \begin{gathered} \Delta x1 = a0 + a1x1 + a2x2 \hfill \\ \Delta x2 = b0 + b1x1 + b2x2. \hfill \\ \end{gathered} \right.$Применение для аппроксимации полиномов более высокого порядка или нелинейных функций (логарифмической, экспоненциальной и других) ни у одного из 5 испытуемых не потребовалось, т.к. линейная модель хорошо описывала экспериментальные зависимости (погрешность аппроксимации составляла менее 2%).
Графически зависимости (1) представляют собой плоскости в 3-мерном пространстве, где по осям X и Y отложены исходные значения ПМлев и ПМпр, а по оси Z – их изменения под влиянием физических нагрузок. На рис. 1 и 2 показаны примеры аппроксимации с помощью множественной линейной регрессии изменений показателей МЦР у одного из испытуемых. На рис. 1, А видно, что при левых махах изменения ∆ПМлев в большей степени зависят от исходных значений ПМлев и в меньшей степени от ПМпр (коэффициенты регрессии равны, соответственно –0.72 и 0.16), причем эти изменения разнонаправлены, т.к. коэффициенты регрессии имеют противоположные знаки. Совсем другая картина наблюдается для величины ∆ПМпр (рис. 1, Б). В этом случае оба коэффициента регрессии сопоставимы по величине и отрицательны, поэтому изменения ∆ПМпр зависят примерно одинаково как от исходных значений ПМлев, так и исходных значений ПМпр и эти изменения равнонаправленны. При махах правой рукой изменения ∆ПМлев (рис. 2, А) так же, как и при левых махах, разнонаправлены, но, в отличие от левых махов, оба коэффициента регрессии сопоставимы по величине (коэффициенты регрессии равны, соответственно –0.80 и 0.87). Изменения ∆ПМпр (рис. 2, Б) при правых махах, так же, как и при левых, равнонаправленны (оба коэффициента отрицательны), но, при правых махах, в отличие от левых, на изменение ∆ПМпр исходное значение ПМлев оказывает меньшее влияние, чем исходное значение ПМпр (коэффициенты регрессии равны b1 = –0.1 и b2 = –0.5). Результаты анализа показали, что величины регрессионных коэффициентов a1, a2, b1 и b2 как при левых, так и при правых махах у всех испытуемых достоверно отличались от 0, что свидетельствует о влиянии на изменения показателей МЦР исходных значений не только одноименной, но и противоположной стороны наблюдения. Однако числовые значения коэффициентов регрессии у разных испытуемых значительно отличались, что свидетельствует о большой индивидуальности реакций МЦР как по величине, так и по направленности изменений исследуемых показателей. По-видимому, это связано с тем, что коэффициенты регрессии a0, a1, a2, b0, b1, b2 не являются константами, а зависят от артериального давления (АД), частоты сердечных сокращений (ЧСС) и многих других физиологических параметров, значения которых различны для разных испытуемых.
Рис. 1.
3D-поверхности, отображающие регрессионные зависимости изменений показателей МЦР слева (А) и справа (Б) от их исходных значений при левых махах. По осям X и Y отложены исходные значения ПМлев и ПМпр, а по оси Z – их изменения (ΔПМ) под влиянием физических нагрузок. Значения всех показателей даны в перфузионных единицах. А – уравнение регрессии ΔПМлев = = 3.74–0.72ПМлев + 0.16ПМпр. Б – уравнение регрессии ΔПМпр = 6.05–0.34ПМлев – 0.4ПМпр.
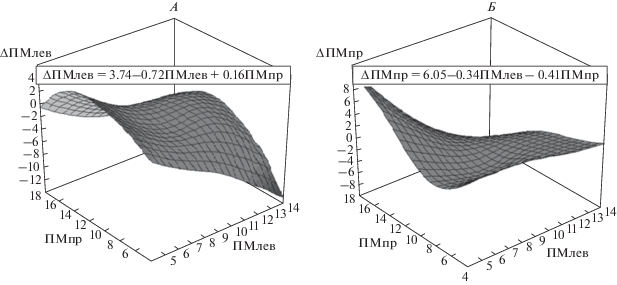
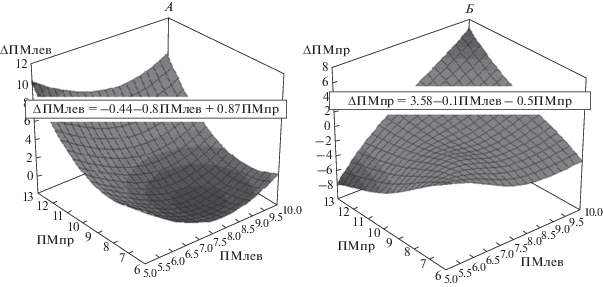
Рис. 2.
3D-поверхности, отображающие регрессионные зависимости изменений показателей МЦР слева (А) и справа (Б) от их исходных значений при правых махах. А – Уравнение регрессии ΔПМлев = –0.44–0.8ПМлев + 0.87ПМпр. Б – уравнение регрессии ΔПМпр = 3.58–0.1ПМлев – – 0.5ПМпр. Остальные обозначения см. рис. 1.
Математическая модель. Выявленные закономерности изменения показателей МЦР от их исходных значений, описываемые системой линейных регрессионных уравнений (1), дают основание полагать, что при малых отклонениях величин x1( j) и x2( j) систему линейных регрессионных уравнений (1) можно заменить на аналогичную систему линейных дифференциальных уравнений (2):
(2)
$\left\{ \begin{gathered} {{dx1} \mathord{\left/ {\vphantom {{dx1} {dt}}} \right. \kern-0em} {dt}} = a0 + a1x1 + a2x2~ \hfill \\ {{dx2} \mathord{\left/ {\vphantom {{dx2} {dt}}} \right. \kern-0em} {dt}} = b0 + b1x1 + b2x2. \hfill \\ \end{gathered} \right.$Эта система линейных дифференциальных уравнений нами была положена в основу математической модели. Известно [7], что решение линейной системы дифференциальных уравнений 1-го поряка может быть получено путем сведения этой системы к одному линейному дифференциальному уравнению более высокого порядка. Поэтому путем несложных алгебраических преобразований система (2) была сведена к одному дифференциальному уравнению 2-го порядка:
(3)
$\begin{gathered} {{{{d}^{2}}x2} \mathord{\left/ {\vphantom {{{{d}^{2}}x2} {d{{t}^{2}}}}} \right. \kern-0em} {d{{t}^{2}}}} = (b2 + a1){{dx2} \mathord{\left/ {\vphantom {{dx2} {dt}}} \right. \kern-0em} {dt}} + \\ + \,\,\left( {b1a2 - a1b2} \right)x2 + (b1a0 - a1b0), \\ \end{gathered} $(6)
$T2 = {{(b2 + a1)} \mathord{\left/ {\vphantom {{(b2 + a1)} {(b1a2 - a1b2)}}} \right. \kern-0em} {(b1a2 - a1b2)}},$(7)
$K = {{(b1a0 - a1b0)} \mathord{\left/ {\vphantom {{(b1a0 - a1b0)} {(a1b2 - b1a2).}}} \right. \kern-0em} {(a1b2 - b1a2).}}$(8)
$x2(t) = K + {\text{exp(}}\alpha t{\text{)}}\left[ {C1{\text{cos}}\beta t + C2{\text{sin}}\beta t} \right],$(9)
${{\lambda }_{{1,2}}} = {{[ - T2 \pm \surd {\text{(}}T{{2}^{2}} - 4T1{\text{)}}]} \mathord{\left/ {\vphantom {{[ - T2 \pm \surd {\text{(}}T{{2}^{2}} - 4T1{\text{)}}]} {2T1}}} \right. \kern-0em} {2T1}}$Таким образом, получили решение исходной системы дифференциальных уравнений (2) применительно к переменной x2(t), описывающей динамику изменения кровотока правой руки ПМпр(t). Аналогичное решение для переменной x1(t), описывающей динамику изменения кровотока левой руки ПМлев(t) можно получить из 2-го уравнения исходной системы дифференциальных уравнений:
(11)
$x1(t) = {{\left( {{{dx2} \mathord{\left/ {\vphantom {{dx2} {dt}}} \right. \kern-0em} {dt}} - b0 - b2x2} \right)} \mathord{\left/ {\vphantom {{\left( {{{dx2} \mathord{\left/ {\vphantom {{dx2} {dt}}} \right. \kern-0em} {dt}} - b0 - b2x2} \right)} {b1}}} \right. \kern-0em} {b1}}.$Поскольку решение для переменной x2(t) известно, а dx2/dt легко получить путем дифференцирования (8), то уравнение (11) позволяет полностью описать динамику изменения кровотока левой руки ПМлев(t). Таким образом, получили общее решение {x1(t), x2(t)} исходной системы линейных дифференциальных уравнений (2), описывающих процессы регуляции показателей микрокровотока в симметричных областях парных органов человека.
Устойчивость процессов кровообращения в микроциркуляторном русле. Одним из важных вопросов, возникающих при исследовании физиологических систем, является вопрос о механизмах, лежащих в основе обеспечения устойчивости функционирования этих систем. Результаты настоящего исследования свидетельствуют о том, что функционирование системы микроциркуляции в симметричных отделах парных органов человека подчиняется строгим математическим закономерностям, описываемым системой линейных дифференциальных уравнений первого порядка (2) относительно переменных x1(t) = = ПМлев и x2(t) = ПМпр. Поэтому исследование условий устойчивости этой системы может быть выполнено стандартными математическими методами. Под устойчивостью системы понимается, что при малых начальных возмущениях ее характеристики в последующее время мало отличаются от невозмущенных. Решение задачи исследования на устойчивость системы линейных дифференциальных уравнений n-го порядка сводится к нахождению условий отрицательности действительных частей соответствующего характеристического уравнения, т.к. только в этом случае система будет устойчивой. Для нахождения этих условий используется критерий Гурвица [7]. В нашем случае, все корни характеристического уравнения (10) будут отрицательные и система дифференциальных уравнений (2) будет иметь устойчивые решения в том случае, если
(13)
$T1 = {1 \mathord{\left/ {\vphantom {1 {(a1b2 - b1a2)}}} \right. \kern-0em} {(a1b2 - b1a2)}} > 0,$(14)
$T2 = {{ - \left( {b2 + a1} \right)} \mathord{\left/ {\vphantom {{ - \left( {b2 + a1} \right)} {\left( {a1b2 - b1a2} \right)}}} \right. \kern-0em} {\left( {a1b2 - b1a2} \right)}} > 0.$Это условие означает, что корни характеристического уравнения (10) являются комплексными. Поскольку дифференциальное уравнение (3) описывает колебательный процесс, характеристики которого зависят от конкретных числовых значений параметров a0, a1, a2, b0, b1, b2, то в зависимости от величины ζ возможны разные варианты поведения исследуемой колебательной системы. C ростом ζ колебательность переходного процесса уменьшается, исчезая совсем при ζ = 1. При дальнейшем увеличении параметра ζ происходит переход из устойчивого в неустойчивый режим функционирования системы МЦР, т.е. переход из нормы в патологию различной степени тяжести, вплоть до угрожающих жизни критических состояний. Таким образом, предложенная нами расчетно-экспериментальная методика позволяет не только получать оценки регрессионных коэффициентов а0, a1, a2, b0, b1, b2, но и оценивать устойчивость регуляторных процессов в микроциркуляторном русле. В ходе настоящих исследований было проведено тестирование всех испытуемых на устойчивость системы МЦР. С этой целью для всех испытуемых были рассчитаны числовые значения параметров T1, T2 и ζ и выполнена проверка выполнения условий (13)−(15), при которых все решения исходной системы дифференциальных уравнений являются устойчивыми. Результаты тестирования показали, что величины регрессионных коэффициентов у всех испытуемых удовлетворяли условиям устойчивости, неустойчивых состояний не обнаружено.
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Устойчивость, стабильность – универсальные понятия, используемые в различных сферах человеческой жизни. В медицине понятие “устойчивость” употребляется для обозначения степени тяжести состояния больного: “стабильное”, “стабильно тяжелое” и т.д. В психологии – для обозначения людей с “устойчивой” и “неустойчивой” психикой. В физике под “устойчивостью движения” понимается способность движущейся механической системы не отклоняться от траектории при незначительных случайных воздействиях. В отличие от механических, в большинстве физиологических систем мы сталкиваемся с невозможностью применения к ним точных математических методов оценки устойчивости, так как нам не известны дифференциальные уравнения, описывающие их состояние, т.е. отсутствует адекватная математическая модель изучаемого явления. Теоретико-методологические подходы, лежащие в основе представлений о механизмах устойчивости функционирования гемодинамической системы человека и животных, впервые были изложены в работах С.П. Ногиной [8]. Ею было показано, что гемодинамическая система представляет собой самоорганизующуюся систему, устойчивость которой обеспечивается право-левым гемодинамическим балансом и пространственно-временной организацией сосудистого русла. Сформулированный С.П. Ногиной принцип право-левого гемодинамического баланса тесно связан с другим фундаментальным свойством гемодинамической системы – свойством хиральности. Это одно из основополагающих свойств живых организмов, проявляющихся на различных уровнях их организации, как на системном, так и на регионарном. Оказалось, что хиральность регионарного кровотока у животных проявляется с самого рождения и на всех дальнейших этапах их онтогенетического развития [2]. Результаты настоящих исследований, сформулированные в виде математической модели, подтверждают теоретическую концепцию С.П. Ногиной об определяющей роли право-левого гемодинамического баланса в обеспечении устойчивости функционирования гемодинамической системы человека и животных. Результаты математического моделирования позволяют оценивать состояние регуляторных процессов в микроциркуляторной системе, рассчитывать диапазоны параметров, определяющие их устойчивость, и точки перехода системы в неустойчивые режимы и критические состояния.
ВЫВОДЫ
1. Впервые показано, что реакция показателей МЦР верхних конечностей на возмущающее воздействие в виде асимметричных физических нагрузок зависит от исходных значений показателей МЦР не только одноименной, но и противоположной стороны измерения.
2. Впервые сформулирована математическая модель регуляции показателей микрокровотока в симметричных областях парных органов человека.
3. Впервые сформулированы условия к диапазонам числовых значений параметров модели, при которых существуют устойчивые режимы функционирования системы микроциркуляции симметричных областей парных органов человека.
4. Изложенная в настоящей работе методика может найти применение в медицинской практике для оценки состояния регуляторных процессов в системе МЦР и прогнозирования возникновения неустойчивых режимов и критических состояний.
Этические нормы. Все исследования проведены в соответствии с принципами биомедицинской этики, сформулированными в Хельсинкской декларации 1964 г. и ее последующих обновлениях, и одобрены локальным биоэтическим комитетом НИИ нормальной физиологии им. П.К. Анохина (Москва).
Информированное согласие. Каждый участник исследования представил добровольное письменное информированное согласие, подписанное им после разъяснения ему потенциальных рисков и преимуществ, а также характера предстоящего исследования.
Финансирование работы. Работа выполнена за счет средств Федерального бюджета РФ в рамках выполнения Государственного задания ФГБНУ “НИИНФ им. П.К. Анохина” (Москва).
Конфликт интересов. Авторы декларируют отсутствие явных и потенциальных конфликтов интересов, связанных с публикацией данной статьи.
Список литературы
Михайличенко Л.А. Показатели микроциркуляции парных органов и тканей экспериментальных животных в норме // Регионарное кровообращение и микроциркуляция. 2007. Т. 6. № 1(21). С. 164.
Михайличенко Л.А., Мезенцева Л.В. Корреляционно-спектральный анализ регуляторных механизмов тонуса сосудов парных образований в постнатальном онтогенезе крыс // Бюлл. экспер. биол. и мед. 2014. Т. 158. № 9. С. 287. Mikhailichenko L.A., Mezentseva L.V. Correlation and spectral analysis of vascular tone regulator mechanisms in paired formations during postnatal ontogenesis in rats // Bull. Exp. Biol. Med. 2015. V. 158. № 3. P. 308.
Mezentseva L.V., Pertsov S.S., Hugaeva V.K. A Comparative Analysis of the Persistence of Capillary Blood Flow Oscillations in the Left and Right Rat Kidneys // Biophysics. 2016. V. 61. № 4. P. 656.
Benedicic M., Bernjak A., Stefanovska A., Bosnjak R. Continuous wavelet transform of laser-Doppler signals from facial microcirculation reveals vasomotion asymmetry // Microvasc. Res. 2007. V. 74. № 1. P. 45.
Ticcinelli V., Stankovski T., Iatsenko D. et al. Coherence and Coupling Functions Reveal Microvascular Impairment in Treated Hypertension // Front. Physiol. 2017. V. 8. P. 749.
Мезенцева Л.В., Перцов С.С. Синхронные изменения показателей микроциркуляции верхних конечностей при асимметричных физических нагрузках на них // Физиология человека. 2020. Т. 46. № 6. С. 101. Mezentseva L.V., Pertsov S.S. Synchronous changes in microcirculation parameters of the upper limbs in asymmetric physical loads // Human Physiology. 2020. V. 46. № 6. P. 671.
Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969. 424 с.
Мезенцева Л.В. Светлана Павловна Ногина – путь в науке // Евразийский союз ученых (ЕСУ). 2018. № 11(56). 1 ч. С. 21.
Дополнительные материалы отсутствуют.
Инструменты
Физиология человека


