Доклады Российской академии наук. Физика, технические науки, 2020, T. 490, № 1, стр. 57-62
Моделирование движения грунтовых вод в прямоугольной перемычке с экраном
Э. Н. Береславский 1, *, Я. М. Далингер 1, **, Л. М. Дудина 1, ***
1 Санкт-Петербургский государственный университет гражданской авиации
Санкт-Петербург, Россия
* E-mail: eduber@mail.ru
** E-mail: liliya_shuvalova@mail.ru
*** E-mail: iakovdalinger@gmail.com
Поступила в редакцию 23.09.2019
После доработки 23.09.2019
Принята к публикации 30.09.2019
Аннотация
В рамках плоской установившейся фильтрации несжимаемой жидкости по закону Дарси дается точное аналитическое решение задачи о течении в прямоугольной перемычке с экраном при наличии испарения со свободной поверхности грунтовых вод. Отмечаются предельные случаи рассматриваемого движения – фильтрация в безнапорном пласте к несовершенной галерее, а также течение при отсутствии испарения.
Решение задачи о притоке жидкости к несовершенной скважине с затопленным фильтром (т.е. осесимметричной задачи) в точной гидродинамической постановке связано с большими математическими трудностями (особенно для течений со свободной поверхностью) и до настоящего времени отсутствует [1–6] (здесь не рассматриваются многочисленные численные и приближенные решения). Поэтому в качестве первого приближения к решению этой проблемы были рассмотрены [1, 5–8] ее плоские аналоги – задачи о притоке жидкости к прямоугольной перемычке с экраном и к несовершенной прямолинейной галерее, которые дают определенное качественное представление о возможной зависимости фильтрационных характеристик от степени несовершенства скважины. В работе [9] приводится точное аналитическое решение задачи о движении грунтовых вод в безнапорном пласте к несовершенной галерее при наличии испарения со свободной поверхности. А также приближенное решение задачи в случае, когда область течения слева ограничивается некоторой эквипотенциалью, определяемой из решения. Показано, что картина течения вблизи непроницаемого экрана существенно зависит не только от несовершенства галереи, но и от наличия испарения, что сильно отражается на расходе галереи и ординате точки выхода кривой депрессии на непроницаемую стенку.
В представленной работе дается точное решение задачи о фильтрации в прямоугольной перемычке с экраном при наличии испарения со свободной поверхности грунтовых вод. В этом случае, как и в [9] (в отличие от [7, 8]), в области годографа скорости потока возникают не прямолинейные, а круговые многоугольники, что не позволяет воспользоваться классической формулой Кристоффеля–Шварца. Влияние испарения со свободной поверхности изучается с применением метода П.Я. Полубариновой-Кочиной [1–6]. С помощью разработанных для областей специального вида [10–12] способов конформного отображения круговых многоугольников [13] решается смешанная многопараметрическая краевая задача теории аналитических функций. Учет характерных особенностей рассматриваемого течения позволяет получить решение через элементарные функции, что делает их использование наиболее простым и удобным. Приведены результаты численных расчетов и дан гидродинамический анализ влияния всех физических параметров модели на фильтрационные характеристики. Полученные результаты решения плоской задачи дают по крайней мере некоторое качественное представление о зависимости параметров течения от степени несовершенства скважины (или трубчатого колодца).
1. На рис. 1 представлена прямоугольная перемычка с откосами A0A1 и D0B на непроницаемом горизонтальном основании длины L. Высота воды в верхнем бьефе равна H, нижний бьеф с уровнем воды H2, имеющий частично непроницаемую вертикальную стенку CD0 (экран), примыкает к подошве пласта. Если рабочая часть перемычки CB (фильтр) ширины H1 затоплена, т.е. H2 > H1, то обычный для плотин промежуток высачивания отсутствует [1]. Верхней границей области движения является свободная поверхность AD, выходящая на непроницаемый экран CD0, с которой происходит равномерное испарение интенсивности ε (0 < ε < 1). Грунт считается однородным и изотропным, течение жидкости подчиняется закону Дарси с известным коэффициентом фильтрации κ = const.
Рис. 1.
Картина течения в прямоугольной перемычке с экраном, рассчитанная при ε = 0.5, H = 3, L = 2, H1 = 1, H2 = 1.4.
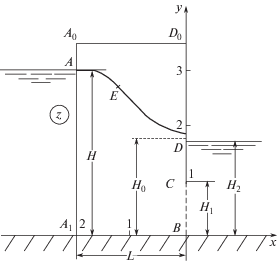
Введем комплексный потенциал движения ω = φ + iψ, где потенциал скорости, функция тока и комплексная координата z = х + iy отнесены соответственно к κH и H, где H – напор в точке A. При указанном на рис. 1 выборе системы координат и совмещении плоскости сравнения напоров с плоскостью y = 0 на границе области фильтрации выполняются следующие краевые условия:
(1)
$\begin{gathered} AD\,{\text{:}}\;\varphi = - y,\quad \psi = - \varepsilon x + Q; \\ DC\,:\;x = 0,\quad \psi = Q; \\ CB\,{\text{:}}\;x = 0,\quad \varphi = - {{H}_{2}}; \\ B{{A}_{1}}\,{\text{:}}\;y = 0,\quad \psi = 0; \\ {{A}_{1}}A\,{\text{:}}\;\varphi = - H,\quad x = - L. \\ \end{gathered} $Задача состоит в определении положения свободной поверхности AD и нахождении ординаты H0 точки выхода кривой депрессии на экран, а также фильтрационного расхода Q.
2. Для решения задачи используем метод П.Я. Полубариновой-Кочиной, который основан на применении аналитической теории линейных дифференциальных уравнений класса Фукса [1, 6, 14]. Введем вспомогательную каноническую переменную ζ и функции: z(ζ), конформно отображающую верхнюю полуплоскость ζ > 0 на область течения z при соответствии точек ζD = 0, ζE = e, ζA = 1, ${{\xi }_{{{{A}_{1}}}}}$ = a1, ζB = b (a1, b – неизвестные аффиксы точек A1 и B в плоскости ζ), ζC = ∞, а также функции $\frac{{d\omega }}{{d\zeta }}$ и $\frac{{dz}}{{d\zeta }}$. Подчеркнем, что по сравнению с [9] в области течения z здесь появляется дополнительная граничная угловая особая точка A1, что значительно осложняет решение.
Определяя характеристические показатели функций $\frac{{d\omega }}{{d\zeta }}$ и $\frac{{dz}}{{d\zeta }}$ около регулярных особых точек [1, 6, 14], найдем, что они являются линейными комбинациями двух ветвей следующей функции Римана [1, 6, 14]:
(2)
$\begin{gathered} P\left\{ {\begin{array}{*{20}{c}} 0&e&1&{{{\zeta }_{A}}}&{{{\zeta }_{B}}}&\infty \\ 0&0&{ - \frac{{1 + \nu }}{2}}&{ - \frac{1}{2}}&{ - \frac{1}{2}}&{\frac{3}{2}} \\ { - \frac{1}{2}}&2&{ - \frac{{1 - \nu }}{2}}&{\frac{1}{2}}&{\frac{1}{2}}&{ 2 } \end{array}\quad \zeta } \right\} = \\ = \;\frac{Y}{{\sqrt {\zeta {{{(1 - \zeta )}}^{{1 + \nu }}}({{\zeta }_{A}} - \zeta )({{\zeta }_{B}} - \zeta )} }}, \\ \end{gathered} $(3)
$Y{\text{''}} + \left( {\frac{1}{{2{\zeta }}} + \frac{{1 - \nu }}{{{\zeta } - 1}} - \frac{1}{{{\zeta } - e}}} \right)Y{\text{'}} + \frac{{\nu (1 + \nu ){\zeta } + \lambda }}{{4{\zeta }({\zeta } - 1)({\zeta } - e)}}Y = 0.$Хорошо известно [1–6, 14], что при интегрировании уравнений подобного рода возникают трудности принципиального характера. Они обусловлены тем, что коэффициенты уравнения (3), помимо неопределенного аффикса e, содержат еще и дополнительный, так называемый акцессорный параметр λ, также неизвестный заранее, и до сих пор не существует какого-либо эффективного способа их фактического нахождения.
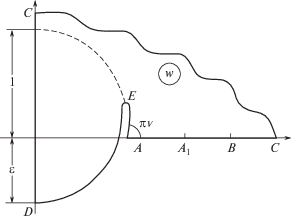
Обратимся к области комплексной скорости w, соответствующей граничным условиям (1), которая изображена на рис. 2. Эта область, представляющая собой круговой четырехугольник ABCDE с разрезом с вершиной в точке E (соответствующей точке перегиба кривой депрессии) и углом νπ при вершине A, принадлежит классу круговых многоугольников в полярных сетках и была исследована ранее [13]. Важно подчеркнуть, что подобные области, несмотря на свой частный вид, однако, весьма типичны и характерны для многих задач подземной гидромеханики: при фильтрации из каналов, оросителей и водоемов, в течениях пресных вод над покоящимися солеными водами, в задачах обтекания шпунта Жуковского при наличии соленых подпорных вод (см., например, [11–13, 15]).
Замена переменных ζ = th2t переводит верхнюю полуплоскость ζ в горизонтальную полуполосу Ret > 0, 0 < Imt < 0.5π параметрической плоскости t при соответствии точек tA = ∞, tD = 0, tC = 0.5π, tB = arcth$\sqrt b $ + 0.5πi,
а интегралы Y уравнения (3), которые построены по методике [13], преобразует к виду(4)
$\begin{gathered} {{Y}_{1}} = \frac{{{\text{ch}}t{\text{ch}}\nu t + C{\text{sh}}t{\text{sh}}\nu t}}{{{\text{c}}{{{\text{h}}}^{{1 + {\nu }}}}t}}, \\ {{Y}_{2}} = \frac{{{\text{ch}}t{\text{sh}}\nu t + C{\text{sh}}t{\text{ch}}\nu t}}{{{\text{c}}{{{\text{h}}}^{{1 + {\nu }}}}t}}, \\ \end{gathered} $Принимая во внимание соотношение (2) и учитывая, что w = $\frac{{d\omega }}{{d\zeta }}$, придем к искомым зависимостям
(5)
$\begin{gathered} \frac{{d{\omega }}}{{dt}} = iM\frac{{\sqrt {\varepsilon } ({\text{ch}}t{\text{ch}}\nu t + C{\text{sh}}t{\text{sh}}\nu t) + i({\text{ch}}t{\text{sh}}\nu t + C{\text{sh}}t{\text{ch}}\nu t)}}{{\Delta (t)}}, \\ \frac{{dz}}{{dt}} = - \frac{M}{{\sqrt {\varepsilon } }}\frac{{{\text{ch}}t{\text{ch}}\nu t + C{\text{sh}}t{\text{sh}}\nu t - i\sqrt \varepsilon ({\text{ch}}t{\text{sh}}\nu t + C{\text{sh}}t{\text{ch}}\nu t)}}{{\Delta (t)}}, \\ \Delta (t) = \sqrt {[({{a}_{1}} - 1){\text{s}}{{{\text{h}}}^{2}}t + {{a}_{1}}][(b - 1){\text{s}}{{{\text{h}}}^{2}}t + b]} , \\ \end{gathered} $Можно проверить, что функции (5) удовлетворяют граничным условиям (1), переформулированным в терминах функций $\frac{{d\omega }}{{dt}}$ и $\frac{{dz}}{{dt}}$ и, таким образом, являются параметрическим решением исходной краевой задачи. Запись представлений (5) для разных участков границы полуполосы с последующим интегрированием по всему контуру области параметрической переменной t приводит к замыканию области течения и, тем самым, служит контролем вычислений.
В результате получаем выражения для задаваемых величин: ширины L перемычки, уровней воды в верхнем H и нижнем H2 бьефах и длины H1 фильтра
(6)
$\begin{gathered} \int\limits_0^\infty {{{X}_{{DA}}}(t)dt = L,\quad \int\limits_{{\text{arcth}}\sqrt {{{a}_{1}}} }^\infty {{{Y}_{{A{{A}_{1}}}}}(t)dt = H,} } \\ \int\limits_0^{0.5\pi } {[{{\Phi }_{{DC}}}(t) + {{Y}_{{DC}}}(t)]dt + {{H}_{1}}} = {{H}_{2}}, \\ \int\limits_0^{{\text{arcth}}\sqrt b } {{{Y}_{{CB}}}(t)dt = {{H}_{1}},} \\ \end{gathered} $(7)
$x(t) = - \int\limits_0^t {{{X}_{{DA}}}(t)dt,\quad y(t) = {{H}_{0}} - } \int\limits_0^t {{{Y}_{{DA}}}(t)dt} $(8)
$Q = \int\limits_0^{{\text{arcth}}\sqrt b } {{{\Psi }_{{CB}}}} (t)dt,\quad {{H}_{0}} = H - \int\limits_0^\infty {{{\Phi }_{{DA}}}(t)dt.} $Для контроля расчетов служат другие выражения для величин Q, H0 и L:
(9)
$\begin{gathered} Q = - \varepsilon L + \int\limits_{{\text{arcth}}\sqrt {{{a}_{1}}} }^\infty {{{\Psi }_{{A{{A}_{{1}}}}}}(t)dt} , \\ {{H}_{0}} = {{H}_{2}} - \int\limits_0^{0.5\pi } {{{\Phi }_{{DC}}}(t)dt,} \\ {{H}_{0}} = {{H}_{1}} + \int\limits_0^{0.5\pi } {{{{\text{Y}}}_{{DC}}}(t)dt,} \\ \end{gathered} $(10)
$\int\limits_0^\infty {{{\Phi }_{{DA}}}(t)dt - } \int\limits_0^{0.5\pi } {{{\Phi }_{{DC}}}(t)dt + \int\limits_{{\text{arcth}}\sqrt b }^{{\text{arcth}}\sqrt {{{a}_{1}}} } {{{\Phi }_{{B{{A}_{{\text{1}}}}}}}(t)dt} } = 0,$В формулах (5)–(10) подынтегральные функции – выражения правых частей равенств (3) на соответствующих участках контура вспомогательной области t.
Предельные случаи:
1) при L → ∞, т.е. при слиянии точек A1 и A, в плоскости t, т.е. при a1 → 1 (arcth a1 = ∞), перемычка вырождается в полубесконечный слева безнапорный пласт. Таким образом, получается точное решение о течении грунтовых вод к несовершенной галерее, исследованное ранее [9];
2) при ε → 0, т.е. при малых значениях интенсивности испарения, получаются результаты работ [7, 8].
3. Представления (5)–(10) содержат четыре неизвестные постоянные M, C, a1 и b. Параметры a1, b (1 < a1 < b < ∞), C (C ≠ 1) определяются из уравнений (6) для задаваемых величин H1, H2 (H1 ≤ H2 < < H) и L, постоянная моделирования M при этом находится из второго уравнения (6), фиксирующего уровень H воды в верхнем бьефе перемычки. После определения неизвестных постоянных последовательно находятся фильтрационный расход Q и ордината H0 точки выхода кривой депрессии на непроницаемый участок DC по формулам (8) и координаты точек свободной поверхности DA по формулам (7).
На рис. 1 изображена картина течения, рассчитанная при ε = 0,5, H = 3, L = 2, H1 = 1.0, H2 = 1.4 (базовый вариант [9]). Результаты расчетов влияния определяющих физических параметров ε, H, H1, H2 и L на величины Q и H0 приведены в табл. 1, 2. На рис. 3 и 4 представлены зависимости расхода Q (кривые 1) и ординаты H0 точки выхода кривой депрессии на экран (кривые 2) от параметров H1 и H2. Анализ расчетов данных таблиц и графиков позволяет сделать следующие выводы:
Таблица 1.
Результаты расчетов величин Q и H0 при варьировании ε, H и L
| ε | Q | H0 | H | Q | H0 | L | Q | H0 |
|---|---|---|---|---|---|---|---|---|
| 0.1 | 1.3937 | 2.3003 | 2.5 | 0.5624 | 1.4074 | 1.5 | 1.6261 | 2.1424 |
| 0.2 | 1.3423 | 2.1544 | 3.0 | 1.1554 | 1.7750 | 1.7 | 1.8970 | 1.3492 |
| 0.3 | 1.2839 | 2.0179 | 3.5 | 1.5715 | 2.0883 | 2.0 | 1.1554 | 1.7755 |
| 0.4 | 1.2218 | 1.8920 | 4.5 | 2.6811 | 3.3097 | 2.5 | 0.7585 | 1.5045 |
| 0.5 | 1.1554 | 1.7755 | 5.0 | 2.9726 | 3.7528 | 2.9 | 0.4863 | 1.3727 |
Таблица 2.
Результаты расчетов величин Q и H0 при варьировании H1 и H2
| H1 | Q | H0 | H2 | Q | H0 |
|---|---|---|---|---|---|
| 0.9 | 1.1120 | 1.8292 | 1.09 | 1.3965 | 1.5533 |
| 1.0 | 1.1554 | 1.7755 | 1.19 | 1.3627 | 1.5775 |
| 1.1 | 1.1928 | 1.7161 | 1.29 | 1.2425 | 1.7051 |
| 1.2 | 1.2235 | 1.6494 | 1.39 | 1.1598 | 1.7695 |
| 1.3 | 1.2460 | 1.5728 | 1.40 | 1.1634 | 1.7694 |
Рис. 3.
Зависимость расхода перемычки Q (1) и ординаты H0 (2) точки выхода свободной поверхности от длины фильтра H1.
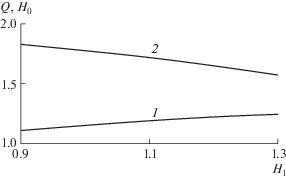
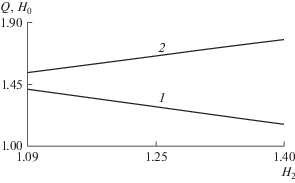
Рис. 4.
Зависимость расхода перемычки Q (1) и ординаты H0 (2) точки выхода свободной поверхности от уровня воды в нижнем бьефе H2.
1) уменьшение интенсивности испарения ε и увеличение напора H сопутствуют увеличению расхода Q и ординаты H0 точки выхода кривой депрессии на экран;
2) уменьшение заглубления экрана H1 и увеличение уровня воды в нижнем бьефе H2 сопровождаются уменьшением расхода Q и увеличением ординаты H0;
3) с ростом ширины перемычки L расход Q и ордината H0 точки выхода свободной поверхности на экран уменьшаются.
Из табл. 2 и рис. 3, 4 следует, что уменьшение параметров H1 и H2, соответственно, в 1.44 и 1.28 раза влечет изменение величины Q на 20% (при фиксировании H1) и на 12% (при фиксировании H2). Отмеченные закономерности приводят к заключению о том, что расход перемычки зависит от величины понижения уровня в несколько большей степени, чем от длины фильтра (или от несовершенства скважины или колодца).
Для базового варианта почти все зависимости величин Q и H0 от параметров ε, H, H1, H2 и L близки к линейным.
Сравнение точных значений, полученных для базового варианта Q = 1.155 и H0 = 1.776, с приближенными значениями Q = 1.141 и H0 = 1.768 для базового варианта [9], где область течения слева ограничивалась эквипотенциалью, показывает, что относительная погрешность вычислений весьма мала и составляет всего 0.5 и 1.3% соответственно.
Сопоставление точного значения расхода Q = 1.16, полученного для базового варианта, с приближенным значением Q = 1.26, которое вытекает при применении обобщенной формулы И.А. Чарного [1, c. 267] для обычной прямоугольной перемычки (без экрана) при наличии испарения
приводит к погрешности 8.3%.Для сравнения с данными H = 1, H1 = 0.05, H2 = 0.238, L = 4 работы [7] при отсутствии испарения, т.е. при ε = 0, для которых по приближенным формулам в полуобратной постановке получены значения Q = 0.118, H0 = 0.29, рассмотрим вариант ε = 0.1, H = 1, H1 = 0.05, H2 = 0.238, L = 4, приводящий к точным значениям Q = 0.42, H0 = = 0.75. Здесь относительные погрешности вычислений составляют 71 и 61% соответственно. Следовательно, как и в [9], испарение существенно влияет на картину течения.
4. Разработана методика построения точного аналитического решения задачи о движении в жидкости в прямоугольной перемычке с экраном при наличии испарения со свободной поверхности грунтовых вод. Исследование показывает, что схема фильтрации в прямоугольной перемычке с непроницаемым экраном, во-первых, весьма схожа с рассмотренной ранее [9] задачей о движении грунтовых вод к несовершенной галерее, причем одна из них является предельной по отношению к другой. Во-вторых, картина течения вблизи экрана существенно зависит не только от размера фильтра, но и от наличия испарения, что сильно отражается на величине расхода и ординате точки выхода кривой депрессии на экран. Полученные результаты дают некоторое представление (по крайней мере качественно) о возможной зависимости характеристик движения при рассмотрении задачи фильтрации уже к несовершенной скважине или трубчатому колодцу.
Список литературы
Полубаринова-Кочина П.Я. Теория движения грунтовых вод. М.: Наука, 1977. 664 с.
Аравин В.И., Нумеров С.Н. Теория движения жидкостей и газов в недеформируемой пористой среде. М.: Гостехиздат, 1953. 616 с.
Развитие исследований по теории фильтрации в СССР (1917–1967) / Под. ред. П.Я. Полубариновой-Кочиной. М.: Наука, 1967. 545 с.
Михайлов Г.К., Николаевский В.Н В кн.: Механика в СССР за 50 лет. М.: Наука, 1970. Т. 2. С. 585–648.
Полубаринова-Кочина П.Я., Пряжинская В.Г., Эмих В.Н. Математические методы в вопросах орошения. М.: Наука, 1969. 414 с.
Кочина П.Я. Избранные труды. Гидродинамика и теория фильтрации. М.: Наука, 1991. 351 с.
Пряжинская В.Г. Движение грунтовых вод в прямоугольной перемычке с непроницаемой вертикальной стенкой // Изв. АН СССР. Механика и машиностроение. 1964. № 4. С. 41–49.
Полубаринова-Кочина П.Я., Постнов В.А., Эмих В.Н. Установившаяся фильтрация к несовершенной галерее в безнапорном пласте // Изв. АН СССР. МЖГ. 1967. № 4. С. 97–100.
Береславский Э.Н., Дудина Л.М. О движении грунтовых вод к несовершенной галерее при наличии испарения со свободной поверхности // Вестник СПбГУ. Сер. 1. Математика. Механика. Астрономия. 2017. № 4. Т. 4 (62). С. 654–663.
Береславский Э.Н., Кочина П.Я. О некоторых уравнениях класса Фукса в гидро- и аэромеханике // Изв. РАН. МЖГ. 1992. № 5. С. 3–7.
Кочина П.Я., Береславский Э.Н., Кочина Н.Н. Аналитическая теория линейных дифференциальных уравнений класса Фукса и некоторые задачи подземной гидромеханики. Препринт № 567. М.: Ин-т проблем механики. РАН, 1996. Ч. 1. 122 с.
Береславский Э.Н., Кочина П.Я. О дифференциальных уравнениях класса Фукса, встречающихся в некоторых задачах механики жидкостей и газов // Изв. РАН. МЖГ. 1997. № 5. С. 9–17.
Береславский Э.Н. Об интегрировании в замкнутой форме некоторых дифференциальных уравнений класса Фукса, встречающихся в гидро-аэромеханике // ДАН. 2009. Т. 428. № 4. С. 439–443.
Голубев В.В. Лекции по аналитической теории дифференциальных уравнений. М.; Л.: Гостехиздат, 1950. 436 с.
Береславский Э.Н., Лихачева Н.В. Математическое моделирование фильтрации из каналов и оросителей // Вестник СПбГУ. Сер. 10. Прикл. матем. Информ. Проц. упр. 2012. В. 3. С. 10–22.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Физика, технические науки