Доклады Российской академии наук. Физика, технические науки, 2020, T. 490, № 1, стр. 52-56
Точное полуобратное решение для семейства геофизических задач дренирующего склона
К. Н. Анахаев 1, 2, *, В. В. Беликов 2, **
1 Институт прикладной математики и автоматизации Кабардино-Балкарского научного центра
Российской академии наук
Нальчик, Россия
2 Институт водных проблем
Российской академии наук
Москва, Россия
* E-mail: anaha13@mail.ru
** E-mail: belvv@bk.ru
Поступила в редакцию 29.07.2019
После доработки 29.07.2019
Принята к публикации 02.10.2019
Аннотация
Одной из основных причин возникновения опасных геофизических склоновых явлений является водонасыщение склонов и негативное гидродинамическое воздействие на них потока подземных вод. В работе получено точное полуобратное гидромеханическое решение для семейства геофизических задач дренирующего склона на основе теории функции комплексного переменного. Методом последовательных конформных отображений установлена аналитическая взаимосвязь между областями комплексного потенциала и комплекса Н.Е. Жуковского, позволяющая определять все необходимые параметры области фильтрации. Приведен пример расчета с определением очертаний линий водоупора, участка высачивания, депрессионной поверхности, а также линий токов и равных напоров (эквипотенциалей) с построением ортогональной и квадратичной гидродинамической сетки фильтрационного потока, высачивающегося через дренирующий склон. Дана краткая оценка влияния фильтрации на суффозионную и оползневую устойчивость грунтового массива дренирующего склона.
Как известно, одной из основных причин возникновения опасных геофизических склоновых явлений, таких как оползни, обвалы, сели и др., является водонасыщение проницаемых склонов и негативное гидродинамическое воздействие на них потока подземных (грунтовых) вод. Множественность различных форм и очертаний естественных склонов и подстилающих их непроницаемых грунтов – водоупора (скальных и полускальных пород, плотных глин и суглинков), затрудняет принятие однозначных граничных условий при гидромеханическом рассмотрении указанной задачи. В этих условиях наиболее приемлемым является использование полуобратного гидромеханическое метода на основе комплекса Н.Е. Жуковского [1–3], позволяющего получить точные решения для большого числа (семейства) задач с различными граничными очертаниями и отдельными, наперед заданными параметрами потока. Указанный полуобратный метод широко используется при рассмотрении задач свободной фильтрации из водотоков различного профиля (см. [4–7] и др.), однако для решения задач безнапорной фильтрации из прилегающих грунтовых массивов в дренирующие русла он не получил еще должного развития [3, 8].
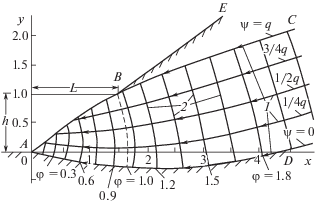
Ниже рассматривается геофизическая задача высачивания на дренирующий склон $AE$ фильтрующегося через участок $AB$ потенциального потока подземных вод по подстилаемой криволинейной поверхности водоупора $AD$ (рис. 1).
Рис. 1.
Расчетная схема высачивания подземных вод через дренирующий склон с квадратичной гидродинамической сеткой фильтрационного потока. Кривые 1 – линии тока, 2 – линии равных напоров.
Решение указанной задачи получаем полуобратным методом путем последовательных конформных отображений области комплексного потенциала $W = \psi + i\varphi $, где $\psi $ и $\varphi $ – функция тока и напорная функция соответственно (рис. 2а), на область комплекса Н.Е. Жуковского $\theta = {{\theta }_{1}} + i{{\theta }_{2}}$ (рис. 3а) [1–7]. В последней величине ${{\theta }_{2}}$ и ${{\theta }_{1}}$ – координаты указанной комплексной области, задающие линии равного давления и ортогональные им линии, значения которых
где $x$ и $y$ – текущие координаты физической области течения (рис. 1).Рис. 2.
Схема последовательных конформных отображений области комплексного потенциала $W = \psi + i\varphi $ на комплексную связующую полуплоскость $\varsigma = \xi $ + iη.
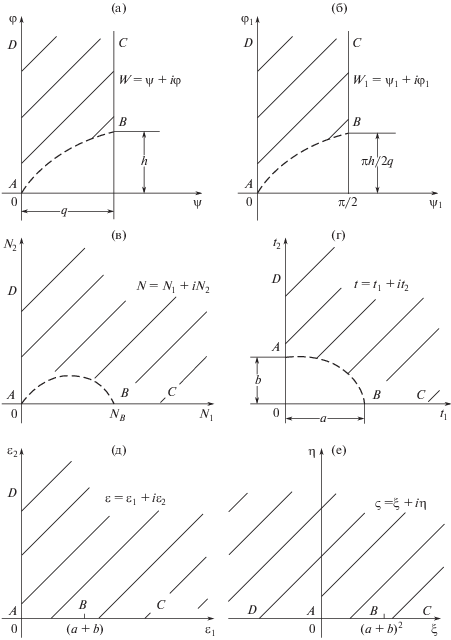
Рис. 3.
Схема последовательных конформных отображений области комплекса Жуковского $\theta = {{\theta }_{1}} + i{{\theta }_{2}}$ на комплексную связующую полуплоскость $\varsigma = \xi + i\eta $.
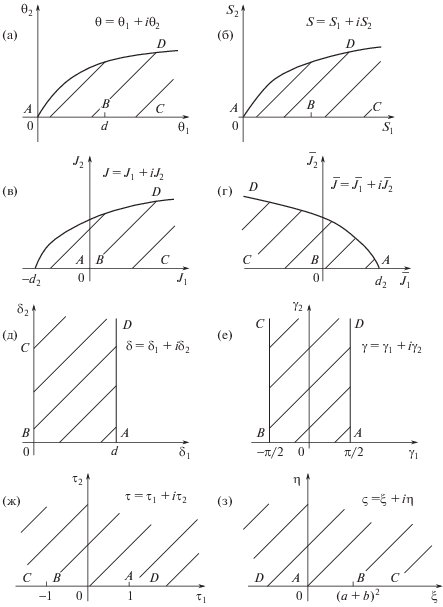
В области комплексного потенциала W = = $\psi + i\varphi $ (рис. 2а) кривая $AB$ соответствует участку высачивания склона, а в области комплекса Жуковского $\theta = {{\theta }_{1}} + i{{\theta }_{2}}$ (рис. 3а) область фильтрации заключена между прямой $AC$ – горизонтальной полуосью $0x$ и кривой $AD$, соответствующей поверхности водоупора.
Значения $W$, $\psi $, $\varphi $, а также удельного фильтрационного расхода $q$ являются “приведенными” величинами к условным линейным размерам:
(2)
$W = \frac{{{{W}_{n}}}}{k},\quad \psi = \frac{{{{\psi }_{n}}}}{k},\quad \varphi = \frac{{{{\varphi }_{n}}}}{k},\quad q = \frac{{{{q}_{n}}}}{k},$Примем следующие граничные условия расчетной схемы области фильтрации $ABCD$ (рис. 1):
1) решение задачи рассматривается в плоскопараллельной постановке;
2) функция тока $\psi $ возрастает от нулевого значения $\psi = 0$ на линии водоупора $AD$ до максимальной величины $\psi = q$ на депрессионной поверхности $BC$, в том числе и по высоте участка высачивания $AB$;
3) напорная функция $\varphi $ на участке высачивания $AB$ и поверхности депрессии $BC$ возрастает линейно $\varphi = y$;
4) значения напорной функции $\varphi $ по линиям депрессионной поверхности $BC$ и водоупора $AD$ при $x \to \infty $ также $\varphi \to \infty $;
5) высота $h$ участка высачивания $AB$ принята равной $h = 1$ (в усл. ед.);
6) поверхность водоупора $AD$ непроницаема и является линией тока $\frac{{\partial \varphi }}{{\partial n}} = 0$.
В рассматриваемой задаче очертания линий водоупора $AD$, участка высачивания $AB$ и депрессионной поверхности $BC$ определяются заданными значениями фильтрационного расхода $q$, заложения $L$ участка высачивания $AB$, а также формами областей комплексного потенциала $W = \psi + i\varphi $ (рис. 2а) и комплекса Жуковского θ = ${{\theta }_{1}} + i{{\theta }_{2}}$ (рис. 3а). Изложенное предопределяет использование полуобратного метода с получением точного решения для большого числа (семейства) задач.
Аналитическую взаимосвязь между комплексными областями $W = \psi + i\varphi $ и $\theta = {{\theta }_{1}} + i{{\theta }_{2}}$ устанавливаем путем последовательных конформных отображений их на связующую полуплоскость $\varsigma = \xi + i\eta $ (рис. 2е, рис. 3з) посредством промежуточных комплексных областей ${{W}_{1}} = {{\psi }_{1}}$ + iφ1, N = ${{N}_{1}} + i{{N}_{2}}$, $t = {{t}_{1}} + i{{t}_{2}}$, $\varepsilon = {{\varepsilon }_{1}} + i{{\varepsilon }_{2}}$ (рис. 2б–д) и S = ${{S}_{1}} + i{{S}_{2}}$, $J = {{J}_{1}} + i{{J}_{2}}$, $\bar {J} = {{\bar {J}}_{1}}$ + $i{{\bar {J}}_{2}}$, $\delta = {{\delta }_{1}} + i{{\delta }_{2}}$, γ = ${{\gamma }_{1}} + i{{\gamma }_{2}}$, $\tau = {{\tau }_{1}} + i{{\tau }_{2}}$, $\bar {\tau } = - {{\tau }_{1}} + i{{\tau }_{2}}$ (рис. 3б–3ж).
При этом используем следующие отображающие функции [7, 9, 10]:
(4)
$\begin{gathered} S = {{\theta }^{2}},\quad J = S - {{d}^{2}},\quad \bar {J} = - {{J}_{1}} + i{{J}_{2}},\quad \delta = \sqrt {\bar {J}} , \\ \gamma = \pi \left( {\frac{\delta }{d} - \frac{1}{2}} \right),\quad \tau = \sin \gamma , \\ \bar {\tau } = - {{\tau }_{1}} + i{{\tau }_{2}},\quad \varsigma = \left( {\bar {\tau } + 1} \right)\frac{{{{{\left( {a + b} \right)}}^{2}}}}{2}, \\ \end{gathered} $Следует отметить, что в процессе указанных отображений кривая $AB$ области комплексного потенциала $W = \psi + i\varphi $ (рис. 2а) получает в промежуточной области $t = {{t}_{1}} + i{{t}_{2}}$ очертание четверти эллипса (рис. 2г), а кривая $AD$ области комплекса Жуковского $\theta = {{\theta }_{1}} + i{{\theta }_{2}}$ (рис. 3а) в промежуточной области $\bar {J} = {{\bar {J}}_{1}} + i{{\bar {J}}_{2}}$ соответствует уравнению ${{\bar {J}}_{2}} = 2d\sqrt {{{d}^{2}} - {{{\bar {J}}}_{1}}} $ [10] (рис. 3г).
После изложенных конформных отображений и последующих преобразований, разделяя действительную и мнимую части итоговых аналитических выражений, окончательно получим значения функции тока $\psi $ и напорной функции $\varphi $ в виде
(6)
$\psi = \frac{{2q}}{\pi }\arcsin \frac{{2{{N}_{1}}}}{M},\quad \varphi = \frac{{2q}}{\pi }Arch\frac{M}{2},$в которых
(7)
${{\varepsilon }_{1}} = \sqrt {\frac{{\sqrt {{{\xi }^{2}} + {{\eta }^{2}}} + \xi }}{2}} ,\quad {{\varepsilon }_{2}} = \sqrt {\frac{{\sqrt {{{\xi }^{2}} + {{\eta }^{2}}} - \xi }}{2}} ,$Полученные расчетные зависимости позволяют определять очертания линий водоупора $AD$, участка высачивания $AB$ и депрессионной поверхности $BC$ подземных вод, высачивающихся через дренирующий склон $AE$, а также все необходимые параметры фильтрационного потока с построением гидродинамической сетки фильтрации. При этом в зависимости от задаваемых параметров $h$, $L$, $q$ и величины $b$ получаем решения множества (семейства) различных геофизических задач дренирующего склона.
На рис. 1 приведены результаты решения рассматриваемой задачи применительно для частного случая при исходных данных: h = 1, $L = 1.5$, $q = 0.6$, $b = 0.8$ с построением гидродинамической сетки фильтрационного потока, высачивающегося через дренирующий склон, в котором ортогональность пересекающихся линий и квадратичность ячеек (размерами $0.25q$) указанной гидродинамической сетки фильтрации свидетельствует о строгости используемого гидромеханического решения. Полученные результаты имеют важное значения для оценки величины и направления гидродинамического давления фильтрационного потока при расчетах устойчивости дренирующих склонов, а также суффозионной устойчивости грунтов. В частности, в рассматриваемом случае наблюдается наибольшая концентрация гидродинамического давления фильтрационного потока в нижней части дренирующего склона $AE$ с направлением потока, близким к горизонтальному (с некоторым отрицательным уклоном), а наибольшее “сдвигающее” усилие (с направлением, приближающимся к уклону склона) фильтрационный поток получает в верхней части участка высачивания $AB$, где и следует ожидать первоначального развития эрозионных процессов с оползневым отрывом грунтового массива склона.
Таким образом, в работе получено точное полуобратное гидромеханическое решение для семейства геофизических задач дренирующего склона на основе теории функции комплексного переменного с использованием метода последовательных конформных отображений. При этом установлена аналитическая взаимосвязь между областями комплексного потенциала и комплекса Жуковского, позволяющая определять необходимые параметры области фильтрации. Приводится пример расчета с построением ортогональной и квадратичной гидродинамической сетки фильтрационного потока.
Список литературы
Ведерников В.В. Теория фильтрации и ее применение в области ирригации и дренажа. М.; Л.: Госстройиздат, 1939. 248 с.
Павловский Н.Н. Собр. соч. Т. 2. Движение грунтовых вод. М.; Л.: Изд-во АН СССР, 1956. 771 с.
Полубаринова-Кочина П.Я. Теория движения грунтовых вод. М.: Наука, 1977. 664 с.
Анахаев К.Н. Гидромеханический расчет свободной фильтрации из водотоков криволинейного профиля со смещенным тальвегом // ДАН. 2004. Т. 395. № 6. С. 761–766.
Анахаев К.Н. Свободная фильтрация из водотоков // Известия РАН. МЖГ. 2004. № 5. С. 94–99.
Анахаев К.Н. Строгое решение задачи свободной фильтрации из водотоков полуобратным методом // Прикладна гiдромеханiка. Киев. 2008. Т. 10 (82). № 1. С. 80–85.
Анахаев К.Н. Развитие методов решения задач механики со специальными функциями. Нальчик, 2016. 252 с.
Базанов М.И. Исследование фильтрации для случая притока воды к осушительным каналам // Прикладная математика и механика. ОТН АН СССР. 1938. Т. 2. В. 2. С. 223–241.
Лаврик В.И., Фильчакова В.П., Яшин А.А. Конформные отображения физико-топологических моделей. Киев.: Наукова думка, 1990. 374 с.
Лаврик В.И., Савенков В.Н. Справочник по конформным отображениям. Киев: Наукова думка, 1970. 252 с.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Физика, технические науки


