Доклады Российской академии наук. Физика, технические науки, 2020, T. 490, № 1, стр. 66-69

1. Ниже $r,\;\varphi ,\;z$ обозначают цилиндрические координаты в ${{{\text{R}}}^{3}}$, t – время, u = $({{u}^{r}},{{u}^{\varphi }},{{u}^{z}})$ – вектор скорости, p – давление, $\nu $ – коэффициент кинематической вязкости, $\rho = {\text{const}}$ – плотность жидкости. Предполагается, что внешние массовые силы отсутствуют. Рассматривается осесимметричное решение уравнений Навье–Стокса

в слое Ω_T = $\{ r,z,t{\kern 1pt} :\;r > 0,0 < z < s(t),0 < t < T\} .$ Это означает, что ${{u}^{\varphi }} = 0$ и функции ${{u}^{r}},{{u}^{z}},p$ не зависят от φ. Известно [1, 2], что система (1) обладает семейством решений вида

Обозначим через $l = s(0)$ начальную толщину слоя и введем безразмерные переменные, выбирая в качестве масштабов длины, времени, скорости и давления величины l, ${{l}^{2}}{{\nu }^{{ - 1}}},$ $\nu {{l}^{{ - 1}}},$ $\rho {{\nu }^{2}}{{l}^{{ - 2}}}$ соответственно, сохранив за новыми переменными их прежние обозначения. Вследствие (1), (2) функция ${v}$ удовлетворяет уравнению

в полосе ${{\omega }_{T}} = \{ z,t{\kern 1pt} :\;0 < z < s(t),\;0 < t < T\} $.

Далее предполагается, что плоскость $z = s(t)$ является свободной поверхностью. Это требует выполнения условий

Первое условие (4) означает, что скорость перемещения свободной поверхности в направлении внешней нормали совпадает с нормальной скоростью жидкости, а второе условие обеспечивает отсутствие касательных напряжений на свободной поверхности.

Условие отсутствия нормальных напряжений, в силу представления (2), сводится к равенству $h(s,t)$ = 0. Ему можно удовлетворить апостериори, поскольку давление в решении системы (1) определяется с точностью до аддитивной функции времени.

Перейдем к формулировке краевого условия на плоскости z = 0. Полагая

мы приходим к равенству ${\mathbf{u}} = 0$ при z = 0. Это означает, что на плоскости z = 0 удовлетворяется условие прилипания, и эта плоскость может быть принята за твердую поверхность. Дополнив соотношения (3)–(5) начальными условиями мы получаем формулировку задачи: найти функции $v(z,t)$ и $s(t)$, чтобы выполнялись соотношения (3)–(6). Решение задачи интерпретируется как движение вязкой жидкости в слое, который ограничен твердой плоскостью и параллельной ей плоской свободной поверхностью.

2. Задача с неизвестной границей (3)–(6) ранее не рассматривалась. Плоский аналог задачи изучался в работах [3, 4]. В статье [3] найдено автомодельное решение этой задачи. В работе [4] численно был обнаружен эффект разрушения решения. Он проявляется в том, что свободная граница уходит на бесконечность за конечное время. Подобные решения уравнений идеальной жидкости были построены Л.В. Овсянниковым [5] и М.С. Лонге-Хиггинсом [6]. Оказалось, что невязкая асимптотика дает главный член особенности в поведении функции s(t) при приближении к моменту катастрофы [4]. В книге [2] и статьях [3, 7] исследована задача о движении вязкой полосы, ограниченной двумя свободными границами.

Целью настоящей работы является получение достаточных условий существования решения задачи (3)–(6) в целом по времени и условий разрушения решения за конечное время. Качественное поведение ее решения иллюстрируется вычислениями.

3. Далее предполагается, что начальная функция ${{v}_{0}}$ удовлетворяет условиям гладкости и согласования,

Предложение 1. Пусть выполнены условия (7). Тогда задача (3)–(6) имеет единственное решение $v(z,t) \in {{C}^{{2 + \beta ,\,1 + \beta /2}}}({{\bar {\omega }}_{T}})$, $s(t) \in {{C}^{{2 + \beta /2}}}[0,T]$, если T достаточно мало.

Доказательство предложения 1 проводится по методике, изложенной в монографии [8]. Его утверждение носит локальный характер. Нелокальные результаты достигаются с помощью дополнительных условий, накладываемых на начальную функцию ${{v}_{0}}$.

Сначала рассмотрим случай, когда начальная функция ${{v}_{0}}$ отрицательна, ${{v}_{0}} = - {{u}_{0}}$ и $0 < {{u}_{0}} \leqslant a$, $z \in [0,1]$. Перейдем в задаче (3)–(6) к новой искомой функции $u = - v$:

Ввиду положительности функции u₀, этим же свойством обладает решение задачи (8), (9). Этот факт вытекает из принципа максимума [9], примененного к уравнению (8). Более того, имеют место оценки $0 \leqslant u \leqslant a$, $(z,t) \in {{\omega }_{T}}$. Данное решение описывает сжатие слоя, которое продолжается неограниченное время. Мы предполагаем, что функция ${{u}_{0}}$ удовлетворяет условиям гладкости и согласования, индуцированным соотношениями (7).

Предложение 2. В этих условиях задача (8), (9) имеет, и притом единственное, решение u(z, $t)\, \in \,{{C}^{{2 + \beta ,\,1 + \beta /2}}}({{\bar {\omega }}_{T}})$, $s(t) \in {{C}^{{2 + \beta /2}}}[0,T]$ при любом $T > 0$. Справедлива оценка

Двусторонняя оценка функции $u$ позволяет воспользоваться для доказательства разрешимости задачи методикой, изложенной в монографии [8]. Оценка снизу толщины слоя следует из неравенства $u \leqslant f$ ≡ $a{\text{exp}}\left( { - \frac{{{{\pi }^{2}}t}}{4}} \right)\sin \left( {\frac{{\pi z}}{{2s}}} \right)$. В свою очередь, это неравенство основано на теореме сравнения [9] функции f и решения задачи (8), (9). Полученная оценка имеет принципиальное значение. Из нее следует, что вследствие действия вязкости предельная толщина слоя при $t \to \infty $ положительна. В этом состоит отличие изучаемой задачи от задачи деформации невязкого слоя, где с ростом $t$ его толщина асимптотически стремится к нулю.

4. Предположим теперь, что начальная функ-ция ${{v}_{0}}$ положительна. В зависимости от ее свойств, здесь возможны три ситуации: разрушение решения за конечное время, стабилизация движения к состоянию покоя при $t \to \infty $ и автомодельный режим, в котором слой неограниченно расширяется за бесконечное время.

Ниже формулируются достаточные условия для реализации первого из указанных режимов и дается оценка времени жизни решения. Наши построения основаны на наличии в задаче (3)–(6) функционала Ляпунова

(здесь нижний индекс t отмечает зависимость значений функционала ${{L}_{t}}$ от времени).

Предложение 3. Предположим, что существует классическое решение $(v,s)$ задачи в области ${{\omega }_{T}}$. Пусть выполнены условия

Тогда функционал ${{L}_{t}}$ является неубывающей функцией $t$ на отрезке $[0,\;T]$.

Для доказательства вычислим производную $\frac{{d{{L}_{t}}}}{{dt}}$ и учтем, что в силу принципа максимума и первого условия (11) всюду в области ${{\omega }_{T}}$ выполнено неравенство $v \geqslant 0.$ Имеем:

причем равенство достигается лишь в случае ${v}$ = 0.

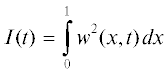Введем обозначения $x = \frac{z}{{s(t)}}$, $w(x,t) = v(z,t)$, , ${{I}_{0}} = I(0).$

Предложение 4. Предположим, что выполнены условия (11). Тогда время жизни ${{t}_{*}}$ решения задачи (3)–(6) оценивается сверху величиной ${{t}_{*}} = 3I_{0}^{{ - 1/2}}$.

Доказательство предложения 4 базируется на вытекающем из соотношений (10)–(12) неравенстве ${{L}_{t}}[v] > 0$ при $0 < t < T$ и тождестве, которому удовлетворяет решение задачи (3)–(6):

Эти соотношения обеспечивают оценку

Отсюда и из определения функции I(t) мы выводим дифференциальное неравенство $\frac{{dI}}{{dt}} > \frac{{2{{I}^{{3/2}}}}}{3}$, интегрируя которое, мы приходим к желаемой оценке величины ${{t}_{ * }}$.

5. Ниже приводятся результаты численного решения задачи (3)–(6). Введем новую пространственную переменную ζ (лагранжеву координату) и новую искомую функцию V(ζ, t) = ${v}$[z(ζ, t)] с помощью соотношений

В результате область ${{\omega }_{T}}$ переходит в прямоугольник Π_T = $\{ \zeta ,t{\kern 1pt} :\,0 < \zeta < 1,0 < t < T\} $, а исходная задача преобразуется к виду

Дополнительная искомая функция $\lambda $ имеет смысл деформации: $\lambda = {{x}_{\zeta }}$. Толщина слоя s выражается формулой $s(t) = \int\limits_0^1 {\lambda (\zeta ,t)d\zeta } $. Задача (14)–(16) решалась методом конечных разностей. Расчеты проводились с начальной функцией ${{{v}}_{0}} = c\sin \left( {\frac{{\pi \zeta }}{2}} \right),$ $c = {\text{const}}$. На рис. 1 приведены графики зависимости $s(t)$ для значений c = 0.6 (линия 1) и c = 0.75 (линия 3). Мы видим, что в первом случае со временем движение стабилизируется к покою, несмотря на то, что начальная функция ${{v}_{0}}$ положительна. Второй случай демонстрирует коллапс решения. Разделяющая эти два графика кривая 2 соответствует автомодельному решению задачи, найденному в работе [10]. В этом решении s = ${{b}^{{ - 1/2}}}{{(t + b)}^{{1/2}}},$ $b = {\text{const}}$. Исходная задача (3)–(6) решалась также методом Галёркина. Приближенное решение искалось в виде

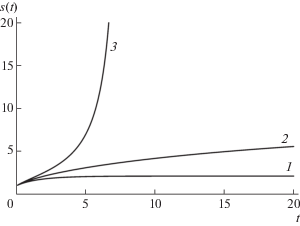
Функции s и ${{a}_{k}}\;(k = 1,2,...,N)$ удовлетворяют системе обыкновенных уравнений, которая здесь не выписывается. Оказалось, что для получения приемлемой точности достаточно взять решение (17) с N = 4. Численные решения, полученные методом Галёркина и конечно-разностным методом, хорошо согласуются друг с другом.

Суммируя сказанное, мы можем заключить, что эффект разрушения решения за конечное время имеет пороговый характер. Условие отрицательности начальной функции не является необходимым для существования решения при любом t > 0. Помимо режима, в котором толщина слоя стремится к положительной постоянной, имеется близкий к автомодельному режим с асимптотикой толщины слоя $s = {{\left( {\frac{t}{b}} \right)}^{{1/2}}} + O({{t}^{{ - 1/2}}})$ при $t \to \infty $. Вычисления показали, что этот режим обладает малым запасом устойчивости.