Доклады Российской академии наук. Физика, технические науки, 2020, T. 491, № 1, стр. 71-74
ПРОЕКТИРОВАНИЕ ТЕПЛОВЫХ КОНЦЕНТРАТОРОВ НАИВЫСШЕЙ ЭФФЕКТИВНОСТИ НА ОСНОВЕ ОПТИМИЗАЦИОННОГО МЕТОДА
Г. В. Алексеев 1, *, академик РАН В. А. Левин 2, 3, Д. А. Терешко 1
1 Институт прикладной математики
Дальневосточного отделения Российской академии наук
Владивосток, Россия
2 Московский государственный университет
им. М.В. Ломоносова
Москва, Россия
3 Институт автоматики и процессов управления Дальневосточного отделения Российской академии наук
Владивосток, Россия
* E-mail: alekseev@iam.dvo.ru
Поступила в редакцию 20.12.2019
После доработки 20.12.2019
Принята к публикации 05.02.2020
Аннотация
Рассматриваются обратные задачи для двухмерной модели теплопереноса, возникающие при разработке технологий проектирования тепловых концентраторов. С помощью оптимизационного метода указанные задачи сводятся к конечномерным экстремальным задачам, для решения которых применяется метод роя частиц. Показано, что спроектированные с помощью оптимизационного метода концентраторы просты в реализации и обладают наивысшей эффективностью в рассматриваемом классе устройств.
Большое внимание в последние годы уделяется исследованию задач проектирования функциональных устройств, служащих для управления тепловыми полями в сплошных средах. В первых работах по решению указанных задач применялся метод оптических преобразований (ТО-метод) [1], перенесенный в теплообмен из электромагнетизма. Но нужно отметить, что полученные с помощью ТО-метода решения задач проектирования обладают существенным недостатком. Они описывают параметры сред, которые невозможно реализовать на практике [2, 3]. Поэтому для решения указанных задач проектирования исследователи стали разрабатывать другие подходы. Особую роль среди них играют оптимизационные методы, поскольку они позволяют получать максимально эффективные устройства, учитывающие практические ограничения (см. подробнее об этом в [4–8]).
Оптимизационный анализ применяется и в настоящем сообщении, посвященном разработке и анализу эффективного численного алгоритма решения задач проектирования тепловых концентраторов. Мы рассмотрим два сценария, математически описываемые задачей чистого концентрирования и задачей концентрирования-маскировки соответственно. На основе анализа вычислительных экспериментов мы продемонстрируем, что применение разработанного алгоритма, основанного на методе роя частиц (PSO) [9], позволяет проектировать концентраторы, обладающие наивысшей эффективностью в рассматриваемом классе устройств и простотой технической реализации.
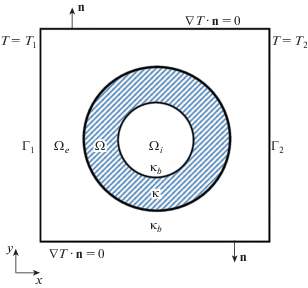
Начнем с постановки прямой задачи теплопереноса, рассматриваемой в прямоугольнике D = = {(x, y): $ - {{x}_{0}} < x < {{x}_{0}}, - {{y}_{0}} < y < {{y}_{0}}\} $ (см. рис. 1). Будем предполагать, что фоновое поле T b создается двумя нагретыми до разных температур ${{T}_{1}}$ и ${{T}_{2}}$ пластинами $x = \mp {{x}_{0}}$, тогда как нижняя и верхняя граница теплоизолированы. Предположим также, что внутри D находится оболочка ($\Omega $, $k$), где $\Omega $ – кольцо $\left\{ {a < \left| {\mathbf{x}} \right| < b} \right\}$ с границами ${{\Gamma }_{i}}$ и ${{\Gamma }_{e}}$, а k – коэффициент теплопроводности неоднородной среды, заполняющей $\Omega $. Будем считать, что внутренность ${{\Omega }_{i}}{\text{:}}\;\left| {\mathbf{x}} \right| < a$ и внешность ${{\Omega }_{e}}{\text{:}}\;\left| {\mathbf{x}} \right| > b$ области $\Omega $ заполнены однородной средой с коэффициентом теплопроводности kb.
В таком случае прямая задача теплопереноса состоит в нахождении тройки функций ${{T}_{i}}$ в ${{\Omega }_{i}}$, T в $\Omega $ и ${{T}_{e}}$ в ${{\Omega }_{e}}$, удовлетворяющих уравнениям
(1)
$\begin{gathered} {{k}_{b}}\Delta {{T}_{i}} = 0\,\,\,{\text{в}}\,\,\,{{\Omega }_{i}},\quad {\text{div}} (k{\text{grad}} T) = 0\,\,\,{\text{в}}\,\,\,\Omega , \\ {{k}_{b}}\Delta {{T}_{e}} = 0\,\,\,{\text{в}}\,\,\,{{\Omega }_{e}}, \\ \end{gathered} $(2)
${{\left. T \right|}_{{x = - {{x}_{0}}}}} = {{T}_{1}},\quad {{\left. T \right|}_{{x = {{x}_{0}}}}} = {{T}_{2}},\quad {{\left. {\frac{{\partial T}}{{\partial y}}} \right|}_{{y = \pm {{y}_{0}}}}} = 0$(3)
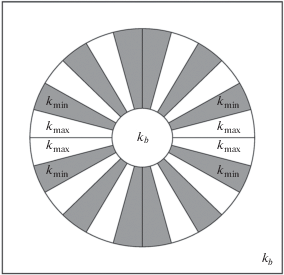
$\begin{gathered} {{T}_{i}} = T,\quad {{k}_{b}}\frac{{\partial {{T}_{i}}}}{{\partial n}} = k\frac{{\partial T}}{{\partial n}}\quad {\text{на}}\quad {{\Gamma }_{i}}, \\ {{T}_{e}} = T,\quad {{k}_{b}}\frac{{\partial {{T}_{e}}}}{{\partial n}} = k\frac{{\partial T}}{{\partial n}}\quad {\text{на}}\quad {{\Gamma }_{e}}. \\ \end{gathered} $Будем предполагать, что оболочка $\Omega $ симметрична относительно координатных осей и состоит из $4M$ секторов ${{\Omega }_{j}}$, заполненных однородными изотропными материалами, где $M$ – число секторов в первой четверти $\Omega {\text{*}}$. Тогда $k\left( {\mathbf{x}} \right)$ представима в виде
(4)
$k\left( {\mathbf{x}} \right) = \sum\limits_1^M {{{k}_{j}}{{\chi }_{j}}\left( {\mathbf{x}} \right)} ,\quad {\mathbf{x}} \in \Omega {\text{*}}.$Здесь ${{\chi }_{j}}\left( {\mathbf{x}} \right)$ – характеристическая функция сектора ${{\Omega }_{j}}$ в $\Omega {\text{*}}$, а kj – коэффициент теплопроводности среды, заполняющей ${{\Omega }_{j}}$, $j = 1,\;2,\; \ldots \;M$.
Напомним, что задача чистого концентрирования (в рамках первого сценария) заключается в нахождении параметров среды, заполняющей $\Omega $, из условия максимального концентрирования потока тепла в ${{\Omega }_{i}}$. Во втором сценарии также требуется, чтобы концентратор как можно меньше искажал поле ${{T}^{b}}$ в ${{\Omega }_{e}}$ [6]. Указанные задачи сводятся к нахождению чисел kj путем решения экстремальных задач.
Чтобы их сформулировать, введем M-мерный вектор ${\mathbf{k}} = \left( {{{k}_{1}},{{k}_{2}},\; \ldots ,\;{{k}_{M}}} \right)$ и определим множество $K$ формулой
(5)
$\begin{gathered} K = \{ {\text{ }}{\mathbf{k}} = ({{k}_{1}},{{k}_{2}}, \ldots ,{{k}_{M}}){\text{: }}{{k}_{{\min }}} \leqslant {{k}_{j}} \leqslant {{k}_{{\max }}}, \\ {\text{ }}j = 1,2, \ldots M\} . \\ \end{gathered} $Здесь ${{k}_{{\min }}}$ и ${{k}_{{\max }}}$ – положительные константы.
Пусть $T[{\mathbf{k}}]$ – решение задачи (1)–(3), отвечающее функции (4). Введем функционалы
(6)
$\begin{gathered} {{J}_{e}}\left( {\mathbf{k}} \right) = \frac{{{{{\left\| {T\left[ {\mathbf{k}} \right] - {{T}^{b}}} \right\|}}_{{{{L}^{2}}\left( {{{\Omega }_{e}}} \right)}}}}}{{{{{\left\| {{{T}^{b}}} \right\|}}_{{{{L}^{2}}\left( {{{\Omega }_{e}}} \right)}}}}}, \hfill \\ {{J}_{i}}\left( {\mathbf{k}} \right) = \frac{{a{\text{ }}{{{\left\| {\nabla T\left[ {\mathbf{k}} \right]} \right\|}}_{{{{L}^{2}}\left( {{{\Omega }_{i}}} \right)}}}}}{{b{\text{ }}{{{\left\| {\nabla {{T}^{b}}} \right\|}}_{{{{L}^{2}}\left( {{{\Omega }_{i}}} \right)}}}}}. \hfill \\ \end{gathered} $Mаксимум функционала ${{J}_{i}}\left( {\mathbf{k}} \right)$ на множестве K не превосходит 1. Поэтому ${{J}_{i}}\left( {\mathbf{k}} \right)$ имеет смысл нормализованной меры концентрационной эффективности оболочки $\left( {\Omega ,{\mathbf{k}}} \right)$, которая тем выше, чем ближе ${{J}_{i}}\left( {\mathbf{k}} \right)$ к единице. Точно также ${{J}_{e}}$ является мерой возмущения фонового поля T b в ${{\Omega }_{e}}$. Чем меньше ${{J}_{e}}\left( {\mathbf{k}} \right)$, тем выше внешний маскировочный эффект, создаваемый оболочкой $\left( {\Omega ,{\mathbf{k}}} \right)$ (см. [6]).
Задача концентрирования потока тепла в ${{\Omega }_{i}}$ сводится к задаче максимизации функционала ${{J}_{i}}\left( {\mathbf{k}} \right)$, эквивалентной задаче
Задача (7) направлена на проектирование устройства, обладающего наивысшей концентрационной эффективностью. Но ее решение ${{{\mathbf{k}}}^{{opt}}}$ не обязано обладать маскировочным эффектом. Поэтому мы также будем рассматривать более общую задачу
(8)
$\begin{gathered} {{J}_{\alpha }}({\mathbf{k}}) = \alpha {{J}_{e}}({\mathbf{k}}) - {{J}_{i}}({\mathbf{k}}) \to \min , \\ {\mathbf{k}} = \left( {{{k}_{1}},{{k}_{2}}, \ldots {{k}_{M}}} \right) \in K,\quad \alpha = {\text{cont}} \geqslant 0. \\ \end{gathered} $Для решения задач (7) и (8) будем использовать метод роя частиц [9] по схеме, предложенной в [6–8].
Как и в [4], мы выбрали значения ${{x}_{0}} = 4.5$ см, ${{y}_{0}} = 9$ см, a = 1 см, $b = 3.25$ см, ${{T}_{1}} = 321.25$ K, T2 = = $283.15$ K и параметры
(9)
$\begin{gathered} {{k}_{b}} = 0.57{{k}_{0}},\quad {{k}_{{\min }}} = 0.22{{k}_{0}}, \\ {{k}_{{\max }}} = 403{{k}_{0}},\quad \frac{{{{k}_{{\max }}}}}{{{{k}_{{\min }}}}} = 1832, \\ \end{gathered} $Применение PSO для решения задачи (8) показало, что для всех значений M управления $k_{j}^{{opt}}$ принимают одно из значений ${{k}_{{\min }}}$ или ${{k}_{{\max }}}$, причем
(10)
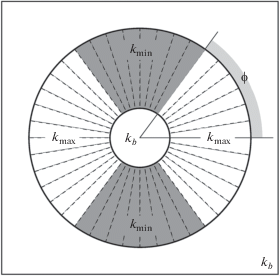
$\begin{gathered} k_{1}^{{opt}} = k_{2}^{{opt}} = \ldots = k_{p}^{{opt}} = {{k}_{{\max }}}, \\ k_{{p + 1}}^{{opt}} = \ldots = k_{M}^{{opt}} = {{k}_{{\min }}}. \\ \end{gathered} $Здесь $p \in \left[ {1,M} \right]$ – некоторый номер, зависящий от M. Из (10) следует, что спроектированная оболочка ($\Omega $, ${{{\mathbf{k}}}^{{opt}}}$) состоит из четырех глобальных секторов, изображенных при $M = 10$ и $p = 6$ на рис. 2. Вычисленные значения $p$, ${{J}_{i}}({{{\mathbf{k}}}^{{opt}}})$ и ${{J}_{e}}({{{\mathbf{k}}}^{{opt}}})$ приведены в табл. 1.
Таблица 1.
Результаты для α = 0, ${{k}_{b}} = 0.57{{k}_{0}}$, kmin = = $0.22{{k}_{0}}$, ${{k}_{{\max }}} = 403{{k}_{0}}$
| M | p | ${{J}_{i}}({{{\mathbf{k}}}^{{opt}}})$ | ${{J}_{e}}({{{\mathbf{k}}}^{{opt}}})$ | CE |
|---|---|---|---|---|
| 4 | 2 | 0.835 | 1.69 × 10–3 | 0.997 |
| 8 | 4 | 0.835 | 1.69 × 10–3 | 0.997 |
| 12 | 6 | 0.835 | 1.69 × 10–3 | 0.997 |
| 16 | 9 | 0.836 | 3.97 × 10–3 | 0.997 |
| 20 | 11 | 0.837 | 2.23 × 10–3 | 0.997 |
Кроме того, в табл. 1 приведены значения величины
Спроектированные нами оптимальные концентраторы обладают высокими значениями CE. Действительно, ${\text{CE}} = 0.997$ для всех значений M, что существенно превышает значения CE, полученные в [5, 10, 11].
Второй тест соответствует параметрам
(11)
$\begin{gathered} {{k}_{b}} = 16{{k}_{0}},\quad {{k}_{{\min }}} = 0.03{{k}_{0}}, \\ {{k}_{{\max }}} = 403{{k}_{0}},\quad \frac{{{{k}_{{\max }}}}}{{{{k}_{{\min }}}}} = 13\,433, \\ \end{gathered} $Таблица 2.
Результаты для α = 0, ${{k}_{b}} = 16{{k}_{0}}$, kmin = = $0.03{{k}_{0}}$, ${{k}_{{\max }}} = 403{{k}_{0}}$
| M | p | ${{J}_{i}}({{{\mathbf{k}}}^{{opt}}})$ | ${{J}_{e}}({{{\mathbf{k}}}^{{opt}}})$ | CE |
|---|---|---|---|---|
| 4 | 3 | 0.951 | 2.21 × 10–3 | 0.936 |
| 8 | 5 | 0.954 | 1.81 × 10–3 | 0.943 |
| 12 | 8 | 0.955 | 1.86 × 10–3 | 0.942 |
| 16 | 11 | 0.955 | 1.98 × 10–3 | 0.941 |
| 20 | 13 | 0.955 | 1.86 × 10–3 | 0.942 |
Сравнение табл. 1 и 2 показывает, что увеличение контраста $\frac{{{{k}_{{\max }}}}}{{{{k}_{{\min }}}}}$ (с 1832 до 13 433) и ${{k}_{b}}$ существенно увеличивает эффективность проектируемых концентраторов. Однако их маскировочная эффективность, описываемая значением ${{J}_{e}}({{{\mathbf{k}}}^{{opt}}}) \approx 10{}^{{ - 3}}$, не высока.
Обратимся теперь к общей задаче (8) и обсудим результаты, полученные при ее численном решении для значения $\alpha = {{10}^{3}}$ при условии, что ${{k}_{{\min }}}{{k}_{{\max }}} \leqslant k_{b}^{2}$. В этом случае, в отличие от (10), для решения задачи (8) выполняются соотношения
Таблица 3.
Результаты для α = 103, ${{k}_{b}} = 16{{k}_{0}}$, kmin = = $0.03{{k}_{0}}$, ${{k}_{{\max }}} = 403{{k}_{0}}$
| M | ${{J}_{i}}({{{\mathbf{k}}}^{{opt}}})$ | ${{J}_{e}}({{{\mathbf{k}}}^{{opt}}})$ | CE |
|---|---|---|---|
| 4 | 0.898 | 7.91 × 10–4 | 0.938 |
| 8 | 0.909 | 3.68 × 10–4 | 0.934 |
| 14 | 0.918 | 2.74 × 10–4 | 0.932 |
| 16 | 0.922 | 2.46 × 10–4 | 0.931 |
| 20 | 0.924 | 2.33 × 10–4 | 0.931 |
Проведенный анализ позволяет заключить, что для построения высокоэффективных концентраторов достаточно использовать лишь два материала с высококонтрастными проводимостями kmin или kmax. Полученные результаты могут найти широкое применение при создании легко реализуемых концентраторов потоков тепла нового типа, осуществляющих накопление тепловой энергии с высокой эффективностью.
Список литературы
Pendry J.B., Schurig D., Smith D.R. // Science. 2006. V. 312. P. 1780–1782.
Guenneau S., Amra C., Veynante D. // Opt. Express. 2012. V. 20. 8207.
Han T., Qiu C.-W. // Opt. 2016. V. 18. 044003.
Fachinotti V.D., Ciarbonetti A.A., Peralta I., et al. // Int. J. Therm. Sci. 2018. V. 128. P. 38–48.
Peralta I., Fachinotti V.D., Ciarbonetti A.A. // Sci. Rep. 2017. V. 7. 40591.
Алексеев Г.В., Левин В.А., Терешко Д.А. // ДАН. 2017. Т. 472. № 4. С. 398–402.
Алексеев Г.В., Левин В.А., Терешко Д.А. // Прикл. мех. техн. физ. 2019. Т. 60. № 2. С. 158–168.
Alekseev G.V., Tereshko D.A. // Int. J. Heat Mass Transf. 2019. V. 135. P. 1269–1277.
Poli R., Kennedy J., Blackwell T. // Swarm Intel. 2007. V. 1. P. 33–57.
Chen F., Lei D.Y. // Sci. Rep. 2015. V. 5. 11552.
Xu G., Zhou X., Zhang J. // Int. J. Heat Mass Transf. 2019. V. 142. 118434.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Физика, технические науки