Доклады Российской академии наук. Физика, технические науки, 2020, T. 494, № 1, стр. 57-63

ДИНАМИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ ПРОДОЛЬНЫХ И ИЗГИБНЫХ КОЛЕБАНИЙ СТЕРЖНЯ ПРИ ЛАЗЕРНОМ ВОЗДЕЙСТВИИ

Академик РАН Н. Ф. Морозов^1, 2, *, член-корреспондент РАН Д. А. Индейцев^2, 3, А. В. Лукин^2, 3, **, И. А. Попов³, О. В. Привалова³, Л. В. Штукин^2, 3

¹ Санкт-Петербургский государственный университет
Санкт-Петербург, Россия

² Институт проблем машиноведения Российской академии наук
Санкт-Петербург, Россия

³ Санкт-Петербургский политехнический университет
Санкт-Петербург, Россия

^* E-mail: n.morozov@spbu.ru
^** E-mail: lukin_av@spbstu.ru

Поступила в редакцию 07.07.2020
После доработки 07.07.2020
Принята к публикации 10.07.2020

DOI: 10.31857/S2686740020050120

Полный текст (PDF)

Аннотация

Рассматривается задача о взаимодействии продольных и поперечных колебаний стержня при тепловых воздействиях с помощью лазерного излучения. Одновременный учет нелинейных слагаемых в уравнениях для изгибных и для продольных деформаций позволяет объяснить взаимодействие изгибных и продольных колебаний. Указаны области значений параметров стержня, в которых при импульсном тепловом воздействии возможно возбуждение более низкочастотных изгибных колебаний за счет высокочастотных продольных и, наоборот, возбуждение более высокочастотных продольных за счет низкочастотных изгибных колебаний.

Ключевые слова: упругая устойчивость, балка Бернулли–Эйлера, лазерное воздействие, изгибные колебания, продольные колебания, комбинационные резонансы

В настоящее время растущую актуальность приобретают задачи возбуждения и управления колебаниями подвижных элементов нано- и микроэлектромеханических систем (НЭМС, МЭМС) с помощью лазерных термооптических воздействий [1–3]. При рассмотрении динамики упругих элементов резонаторов, входящих в состав МЭМС и НЭМС, часто применяются модели балки Бернулли–Эйлера. На эту тему есть обширная литература. Здесь упомянем две работы [4, 5], в которых решены задачи, наиболее близкие по постановке к представленной далее.

Существуют различные конструкции упругих элементов МЭМС и НЭМС. Довольно распространенным типом таких элементов является балка-полоса. Она представляет собой пластину прямоугольного сечения, у которой ширина значительно больше толщины, а длина – значительно больше ширины. Концы элемента могут быть закреплены как в поперечном, так и в продольном направлении. Закрепление может быть как жестким, так и податливым. При нагреве элемента в нем могут возникать значительные продольные сжимающие усилия. Возникающие прогибы, как правило, имеют порядок толщины элемента, либо превосходят ее.

В выполненных ранее работах [6–8] исследуется возможность потери устойчивости положения равновесия упругого элемента МЭМС и НЭМС при кратковременных воздействиях. В этих работах рассмотрен этап формирования волны изгиба на достаточно малых временах. Представляется теперь полезным исследовать, что будет происходить на более длительных временах, в том числе при закритической продольной сжимающей нагрузке.

В настоящей работе внимание уделено взаимодействию разных форм колебаний, как поперечных, так и продольных, в случае, когда прогиб стержня имеет порядок его толщины, либо превосходит ее. При этом начинают играть роль нелинейные слагаемые как в уравнениях изгибных колебаний, так и в продольных. Именно эти нелинейные слагаемые создают подобное взаимодействие.

1. УРАВНЕНИЯ ПРОДОЛЬНЫХ И ПОПЕРЕЧНЫХ КОЛЕБАНИЙ

Продольные и изгибные деформации являются независимыми, пока не учтены некоторые нелинейные слагаемые. Нелинейные слагаемые не требуется учитывать в ситуации, пока прогибы малы по сравнению с толщиной стержня (например, при изучении изгиба ротора турбогенератора). Для упругих элементов микрорезонаторов подобные допущения не всегда справедливы.

Возбуждение колебаний может быть проведено различными способами. В настоящей работе будет рассмотрен резкий нагрев элемента по всей поверхности.

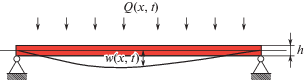
На рис. 1 показана схема упругого элемента.

Рис. 1.

Схема упругого элемента.

Лазерный импульс воздействует на всю поверхность стержня одновременно. В работах [3, 4] показано, что прогрев стержня по толщине происходит достаточно быстро, время прогрева по толщине сравнимо с периодом низшей изгибной собственной частоты. Условия охлаждения таковы, что после окончания действия лазерного источника стержень остается нагретым в течение достаточно длительного времени. Используя результаты работы [3], полагаем, что распределение температуры равномерно по всей длине стержня:

(1)

${\Theta }(x,t) = {{{\Theta }}_{0}}(1 - {{e}^{{ - t/T}}}),$

где Θ₀ – установившееся значение температуры, T – характерное время переходного процесса.

Предполагается, что стержень имеет достаточно вытянутое прямоугольное сечение и изгиб возможен только в направлении наименьшей изгибной жесткости. Запишем уравнения продольных и изгибных деформаций с учетом нелинейной связи. Введем продольное смещение u(x, t), продольную силу N(x, t), прогиб w(x, t), изгибающий момент M(x, t). Тогда система уравнений, описывающая напряженно-деформированное состояние стержня, имеет вид

(2)

$\begin{gathered} - ~\frac{{\partial N}}{{\partial x}} + \rho S\frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}} = 0, \\ \frac{{\partial u}}{{\partial x}} = \frac{1}{{ES}}N - \frac{1}{2}{{\left( {\frac{{\partial w}}{{\partial x}}} \right)}^{2}} + \propto \Theta (x,t), \\ \end{gathered} $

(3)

$ - \frac{{{{\partial }^{2}}M}}{{\partial {{x}^{2}}}} - \frac{\partial }{{\partial x}}\left( {N\frac{{\partial w}}{{\partial x}}} \right) + \rho S\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} = 0,\quad - \frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}}\, = \,\frac{1}{{EI}}M,$

где Θ(x, t) – заданное в соответствии с (1) распределение температуры в материале стержня.

Для изгибных деформаций примем в качестве граничных условий шарнирное опирание на обоих концах:

$\begin{gathered} w(0,t) = 0,\quad w(l,t) = 0, \\ M(0,t) = 0,\quad M(l,t) = 0. \\ \end{gathered} $

Шарнирное опирание принято по той причине, что это упрощает вычисление собственных частот и форм линейной системы. Для реальных конструкций более подходит вариант с жесткими заделками на обоих концах. Однако принципиальных отличий для полученных результатов нет.

Граничные условия по продольным перемещениям – заделка на обоих концах

(4)

$u(0,t) = 0,\quad u(l,t) = 0.$

Важно отметить, что рассматриваемые граничные условия по продольным деформациям ограничивают продольное смещение концов стержня, что будет способствовать возникновению продольных усилий.

Начальные условия пока не конкретизируем. Отметим только, что при нулевых начальных условиях по изгибу и отсутствии поперечной нагрузки решением поставленной задачи может быть только нулевой прогиб. В реальной ситуации ненулевые начальные условия могут быть вызваны какими-то начальными неправильностями, например, некоторой несоосностью опор, наличием прогиба под действием электростатического поля и т.д.

Уравнения записаны в форме, удобной для применения метода двух аппроксимаций, поскольку в уравнении для продольных колебаний задана тепловая деформация, а в соответствующих граничных условиях могут быть заданы усилия.

2. МЕТОД ГАЛЕРКИНА

Решение поставленной задачи разыскивается методом Галеркина в виде отрезков рядов по собственным формам линейной задачи при однородных граничных условиях с добавлением слагаемого, позволяющего удовлетворить неоднородным условиям на продольные усилия:

(5)

$\begin{gathered} u(x,t) = \mathop \sum \limits_{m = 1}^{m = {{K}_{1}}} {{b}_{m}}(t){{u}_{m}}(x), \\ N(x,t) = {{a}_{0}}(t){{N}_{0}} + \mathop \sum \limits_{m = 1}^{m = {{K}_{1}}} {{a}_{m}}(t){{N}_{m}}(x), \\ \end{gathered} $

(6)

$\begin{gathered} w(x,t) = \mathop \sum \limits_{n = 1}^{n = {{K}_{2}}} {{\beta }_{n}}(t){{w}_{n}}(x), \\ M(x,t) = \sum\limits_{n = 1}^{n = {{K}_{2}}} {{{\alpha }_{n}}(t){{M}_{n}}(x).} \\ \end{gathered} $

Собственные формы удовлетворяют уравнениям

(7)

$\begin{gathered} - N_{m}^{'} - \bar {\lambda }_{m}^{2}\rho S{{u}_{m}} = 0,\quad u_{m}^{'} - \frac{1}{{ES}}{{N}_{m}} = 0, \\ m = 1,2,...,{{K}_{1}},\quad {{N}_{0}} = 1, \\ - M_{n}^{{''}} - \lambda _{n}^{2}\rho S{{w}_{n}} = 0,\quad - {\kern 1pt} w_{n}^{{''}} - \frac{1}{{EI}}{{M}_{n}} = 0, \\ n = 1,2,...,{{K}_{2}}, \\ \end{gathered} $

и граничным условиям

(8)

$\begin{gathered} {{u}_{m}}(0) = 0,\quad {{u}_{m}}(l) = 0,\quad m = 1,2,...,{{K}_{1}}; \\ {{w}_{n}}(0) = 0,\quad {{w}_{n}}(l) = 0,\quad {{M}_{n}}(0) = 0, \\ {{M}_{n}}(l) = 0,\quad m = 1,2,...,{{K}_{1}}. \\ \end{gathered} $

Условия метода Галеркина для искомых коэффициентов разложения:

$\begin{gathered} \mathop \smallint \limits_0^l \left( { - ~\frac{{\partial N}}{{\partial x}} + \rho S\frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}}} \right){{u}_{m}}dx = 0, \\ m = 1,~2,~ \ldots ~{{K}_{1}}, \\ \end{gathered} $

$\begin{gathered} \mathop \smallint \limits_0^l \left( {\frac{{\partial u}}{{\partial x}} - \frac{1}{{ES}}N + \frac{1}{2}{{{\left( {\frac{{\partial w}}{{\partial x}}} \right)}}^{2}} - ~\, \propto {\kern 1pt} {\Theta }(x,t)} \right){{N}_{m}}dx = 0, \\ m = 0,1,2, \ldots ,{{K}_{1}}, \\ \end{gathered} $

$\begin{gathered} \mathop \smallint \limits_0^l \left( { - \frac{{{{\partial }^{2}}M}}{{\partial {{x}^{2}}}} - \frac{\partial }{{\partial x}}\left( {N\frac{{\partial w}}{{\partial x}}} \right) + \rho \frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} - F\left( {x,t} \right)} \right){{w}_{n}}dx = 0, \\ n = 1,2, \ldots ,{{K}_{2}}, \\ \end{gathered} $

(9)

$\begin{gathered} \mathop \smallint \limits_0^l \left( { - \frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} - \frac{1}{{EI}}M} \right){{M}_{m}}dx = 0, \\ n = 1,2, \ldots ,{{K}_{2}}. \\ \end{gathered} $

Если не учитывать нелинейные слагаемые, то взаимное влияние продольных и изгибных колебаний отсутствует, поскольку слагаемое $\frac{\partial }{{\partial x}}\left( {N\frac{{\partial w}}{{\partial x}}} \right)$ в уравнении изгибных колебаний, вообще говоря, нелинейное. Но тогда мы принципиально не можем учесть влияние продольной силы на изгиб.

Число слагаемых K₁ для продольных деформаций и число слагаемых K₂ для изгибных деформаций, сохраняемых в разложениях (5), (6), должны быть различными при условии, что все учитываемые собственные частоты должны лежать в одном диапазоне. Этот частотный диапазон должен быть выбран, во-первых, в соответствии с характерными временами во внешнем воздействии, во-вторых, число изгибных собственных форм должно быть таково, чтобы для самой высшей из них можно было бы оставаться в рамках модели балки Бернулли–Эйлера. Низшая собственная частота продольных колебаний по отношению к низшей собственной частоте изгибных колебаний при отсутствии продольных усилий зависит только от геометрии стержня. Для стержня прямоугольного сечения это отношение

(10)

$\frac{{\overline {{{\lambda }_{1}}} }}{{{{\lambda }_{1}}}} = \frac{{\sqrt {12} }}{\pi }\frac{l}{{{{h}_{0}}}},$

где h₀ – толщина стержня.

Следует также учесть, что изгибные собственные частоты пропорциональны квадрату их номера (для случая шарнирных опор). Если выбрать отношение длины к толщине $\frac{l}{{{{h}_{0}}}}$ порядка 25, то окажется, что пятая изгибная частота близка к первой продольной собственной частоте. При этом для пятой изгибной формы отношение толщины стержня к длине полуволны изгибной формы будет всего порядка 5. Это уже почти сомнительно для применения модели балки Бернулли–Эйлера. При большем числе изгибных форм модель балки будет неприменима. Но тогда для продольных колебаний можно ограничиться только одной формой.

Для более толстых стержней имеет смысл учета еще меньшего числа изгибных форм, тем более не придется учитывать и следующие продольные формы. Для более тонких стержней можно подобрать случай, когда есть смысл учитывать и вторую продольную форму.

3. УРАВНЕНИЯ ДЛЯ КОЭФФИЦИЕНТОВ РАЗЛОЖЕНИЯ

Для анализа уравнений для коэффициентов разложения полезно перейти к безразмерному виду. Введем безразмерное время $\tau = \frac{t}{{{{\lambda }_{1}}}}$ и некоторый масштаб для прогиба r₀. Это может быть, например, зазор r₀ между упругим элементом резонатора и неподвижным электродом. В связи с этим появляется малый параметр r = $\frac{{{{r}_{0}}}}{l}$ – отношение зазора к длине упругого элемента. Введем также безразмерный параметр, характеризующий соотношение между площадью поперечного сечения S и моментом инерции I. Для прямоугольного сечения таким безразмерным параметром можно принять h = $\frac{{{{h}_{0}}}}{l}$, где h₀ – толщина упругого элемента.

После этого вводим безразмерные коэффициенты разложения

${{B}_{1}} = \frac{{{{b}_{1}}}}{{{{r}_{0}}}},\quad {{A}_{1}} = \frac{{{{a}_{1}}}}{{{{r}_{0}}}},\quad {{A}_{0}} = \frac{{{{a}_{0}}~}}{{ES}},\quad {{z}_{k}} = \frac{{{{\beta }_{k}}}}{{{{r}_{0}}}}.$

Условия Галеркина (8) приводят к уравнениям для безразмерных коэффициентов разложения

${{A}_{0}} = - \alpha {{{\Theta }}_{0}}(1 - {{e}^{{ - t/T}}}){\text{\;}} + \frac{1}{4}{{\pi }^{2}}{{r}^{2}}\mathop \sum \limits_{k = 1}^{{{K}_{2}}} {{k}^{2}}z_{k}^{2},$

${{A}_{1}} = {{B}_{1}} + \frac{\pi }{2}\mathop \sum \limits_{k = 1}^{{{K}_{2}}} k\left( {k + 1} \right){{z}_{k}}{{z}_{{k + 1}}},$

(11)

${{\ddot {B}}_{1}} + \frac{{12}}{{{{\pi }^{2}}}}{{\left( {\frac{1}{h}} \right)}^{2}}{{B}_{1}} + \frac{6}{\pi }{{\left( {\frac{1}{h}} \right)}^{2}}r\mathop \sum \limits_{k = 1}^{{{K}_{2}}} k\left( {k + 1} \right){{z}_{k}}{{z}_{{k + 1}}} = 0,$

$\begin{gathered} {{{\ddot {z}}}_{k}} + {{k}^{4}}\left( {1 + \frac{{12}}{{{{k}^{2}}{{\pi }^{2}}}}{{{\left( {\frac{1}{h}} \right)}}^{2}}{{A}_{0}}} \right){{z}_{k}} + \\ + \frac{6}{\pi }\frac{1}{h}r\left( {k\left( {k - 1} \right){{z}_{{k - 1}}} + k\left( {k + 1} \right){{z}_{{k + 1}}}} \right){{A}_{1}} = 0, \\ k = 1,2, \ldots ,{{K}_{2}}. \\ \end{gathered} $

Все уравнения, за исключением первого уравнения для средней составляющей продольной силы A₀, являются однородными. При нулевых начальных условиях возникнет только равномерно распределенная по длине стержня продольная сила, продольных и изгибных колебаний не возникнет. Более того, даже при ненулевых начальных условиях по продольным перемещениям не возникнет изгиб.

В приведенных уравнениях можно выделить две группы нелинейных слагаемых.

Первая группа слагаемых связывает среднее значение продольной силы A₀ и коэффициенты разложения по изгибным формам z_k. В уравнение для продольной силы входит слагаемое $\mathop \sum \limits_{k = 1}^{{{K}_{2}}} {{k}^{2}}z_{k}^{2}$ – сумма квадратов коэффициентов разложения по изгибным формам. Это слагаемое – дополнительная растягивающая сила, возникающая при наличии изгиба. С другой стороны, изгибная жесткость ${{k}^{4}}\left( {1 + \frac{{12}}{{{{k}^{2}}{{\pi }^{2}}}}{{{\left( {\frac{1}{h}} \right)}}^{2}}{{A}_{0}}} \right)$ зависит от величины средней составляющей продольной силы A₀. Это приводит к зависимости изгибных собственных частот от средней составляющей продольной силы A₀. При достаточно большой сжимающей силе изгибная жесткость может стать отрицательной, что приводит к потере устойчивости нулевого положения равновесия. При этом нелинейная связь между A₀ и z_k обусловливает появление ненулевых устойчивых положений равновесия и возможность взаимодействия различных изгибных форм между собой.

Вторая группа слагаемых связывает переменную составляющую продольной силы A₁ и коэффициенты разложения по изгибным формам z_k. В уравнение для A₁ входит слагаемое $\mathop \sum \limits_{k = 1}^{{{K}_{2}}} k(k + 1){{z}_{k}}{{z}_{{k + 1}}}$ – сумма произведений коэффициентов разложения по изгибным формам с соседними номерами. В уравнения для коэффициентов разложения по изгибным формам входит слагаемое $(k(k - 1){{z}_{{k - 1}}} + k(k + 1){{z}_{{k + 1}}}){{A}_{1}}$ – произведение переменной составляющей продольной силы A₁ на коэффициенты разложения по изгибным формам с соседними номерами. При возбуждении колебаний с собственными частотами это приводит к появлению колебаний с комбинационными частотами – суммы или разности соседних изгибных собственных частот, либо суммы и разности собственной частоты продольных колебаний и одной из изгибных собственных частот. Как указано в [2], совпадение комбинационной частоты – суммы или разности соседних изгибных собственных частот – с одной из собственных частот продольных колебаний может привести к резонансным явлениям.

В последующих разделах роль каждой из двух групп нелинейных слагаемых будет исследована на конкретных примерах.

4. УЧЕТ ТОЛЬКО СРЕДНЕЙ СОСТАВЛЯЮЩЕЙ ПРОДОЛЬНОЙ СИЛЫ

Рассмотрим ситуацию, когда внешнее воздействие имеет характерные времена намного больше, чем период низшей собственной частоты продольных колебаний. Тогда в уравнениях продольных деформаций (2) можно пренебречь инерционным слагаемым и в разложении (6) следует оставить только одно слагаемое для продольной силы:

(12)

$N\left( {x,t} \right) = {{a}_{0}}\left( t \right){{N}_{0}}.$

Из уравнений (10) остается только одно для средней по длине продольной силы:

(13)

${{A}_{0}} = - \alpha {{{\Theta }}_{0}}(1 - {{e}^{{ - t/T}}}) + \frac{1}{4}{{\pi }^{2}}{{r}^{2}}\mathop \sum \limits_{k = 1}^{{{K}_{2}}} {{k}^{2}}z_{k}^{2}.$

Подставляя это выражение в оставшиеся уравнения (11), получим систему уравнений для изгибных коэффициентов разложения (6)

(14)

$\begin{gathered} {{{\ddot {z}}}_{k}} + {{k}^{4}}\left( {1 - \frac{1}{{{{k}^{2}}}}p\left( t \right)} \right){{z}_{k}} + \mathop \sum \limits_{n = 1}^{{{K}_{2}}} {{\gamma }_{{kn}}}{{z}_{k}}z_{n}^{2} = 0, \\ k = 1,2,...,{{K}_{2}}, \\ \end{gathered} $

где обозначено $p\left( t \right) = \frac{{12}}{{{{k}^{2}}{{\pi }^{2}}}}{{\left( {\frac{1}{h}} \right)}^{2}}\alpha {{{\Theta }}_{0}}(1 - {{e}^{{ - t/T}}}){\text{\;}}$ – безразмерная сжимающая сила, вызванная нагревом.

Уравнения (14) решаются независимо, после чего может быть найдена продольная сила в соответствии с (13).

Нелинейные слагаемые в уравнениях (14) отвечают за взаимодействие изгибных форм между собой. При этом нетрудно убедиться, что нулевые начальные условия по какой-либо из изгибных форм не позволяют получить ее возбуждение другой изгибной формой.

При ненулевых начальных условиях в соответствии с (14) возникнут колебания с изгибными собственными частотами. Важно отметить, что эти частоты зависят от возникшей средней составляющей продольной силы. В свою очередь, средняя составляющая продольной силы будет иметь колебательный характер. Поскольку в выражение (13) входят квадраты изгибных коэффициентов разложения, то частоты этих колебаний будут двойными по отношению к изгибным частотам.

Для иллюстрации сказанного и проведения численного эксперимента ограничимся двумя собственными изгибными формами.

Приведем результаты численного решения системы уравнений (11) при внезапном приложении температурного импульса ${\Theta }(x,t) = {{{\Theta }}_{0}}(1 - {{e}^{{ - t/T}}})$. При этом полагаем, что есть ненулевые начальные условия по каждой из изгибных форм, причем по второй форме начальные условия малы по отношению к таковым по первой форме.

На рис. 2 показаны осциллограммы изгибных колебаний при равномерном нагреве стержня.

Рис. 2.

Осциллограммы изгибных колебаний при равномерном нагреве стержня. 1 – сжимающая сила без учета влияния изгиба, 2 – сжимающая сила с учетом влияния изгиба, 3 – первая форма z₁(t), 4 – вторая форма z₂(t).

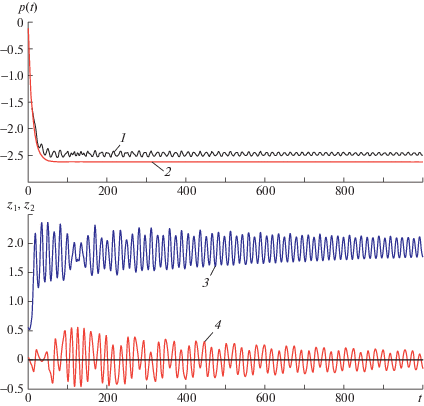
Среднее значение продольной сжимающей силы (кривая 2) с учетом влияния на него изгиба оказывается несколько меньше, чем без учета этого влияния (кривая 1). При нарастании температуры и переходе продольной сжимающей силы через силу Эйлера прогиб по первой форме нарастает (кривая 3), но его рост ограничен наличием ненулевого устойчивого положения равновесия. Начальные условия по второй форме (кривая 4) выбраны в 10 раз меньше, чем по первой форме. Однако с ростом прогиба по первой форме происходит нарастание прогиба и по второй форме, причем этот процесс имеет вид биений. Нарастание амплитуды колебаний по второй форме сопровождается уменьшением амплитуды колебаний по первой форме и наоборот. Получается, что симметричным нагружением можно получить кососимметричный ответ.

5. ВНУТРЕННИЕ РЕЗОНАНСЫ НА КОМБИНАЦИОННЫХ ЧАСТОТАХ

В работе [2] обращено внимание на то, что возможно возбуждение колебаний с достаточно заметными амплитудами при выполнении условия, что комбинационные частоты (суммы или разности) собственных частот изгибных колебаний совпадают с одной из собственных частот продольных колебаний. В этой работе такое возбуждение названо параметрическим.

Для первой собственной частоты продольных колебаний упомянутое условие имеет вид

(15)

${{\lambda }_{k}} + {{\lambda }_{{k + 1}}} = \overline {{{\lambda }_{1}}} ,$

где k – некоторый номер изгибной собственной частоты из диапазона k = 1, 2, … K₂ . Это приводит к выполнению условия на относительную толщину стержня h:

(16)

${{h}_{*}} = \frac{{\sqrt {12} }}{\pi }\frac{1}{{{{k}^{2}} + {{{\left( {k + 1} \right)}}^{2}}}}.$

Наименьшее значение, при котором можно полагать правильной модель балки для высших форм, может быть принято k = 3. При этом получается, что относительная толщина балки должна быть

(17)

${{h}_{*}} = \frac{{\sqrt {12} }}{\pi }\frac{1}{{25}}.$

При значении относительной толщины h = ${{h}_{*}}$ длина полуволны для 4-й формы оказывается еще приемлемой для возможности применения модели балки Бернулли–Эйлера.

Следует обратить внимание на то, что условие (15) записано без учета влияния медленной составляющей продольной силы на величину собственной частоты, что, вообще говоря, нетрудно учесть.

Проведены численные эксперименты по исследованию влияния относительной толщины балки при ее варьировании вблизи значения из (17). Введена относительная расстройка относительной толщины ${\Delta }h = \frac{{h - {{h}_{*}}}}{{{{h}_{*}}}}$.

На рис. 3 показаны результаты численного решения задачи о равномерном нагреве поверхности стержня при различных расстройках от условия (15) на комбинационные частоты.

Рис. 3.

Осциллограммы при нагреве стержня по всей поверхности: 1 – третья изгибная форма, 2 – четвертая изгибная форма, 3 – переменная составляющая продольной силы, а – расстройка 0.02, б – расстройка 0.0365, в – расстройка 0.04.

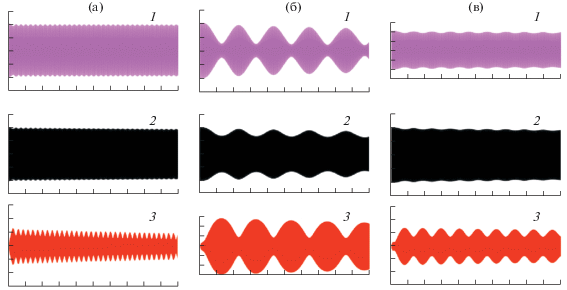
По изгибным формам приняты ненулевые начальные условия, а по продольным – нулевые. На приведенных осциллограммах видно, что за счет нелинейных слагаемых происходит возбуждение продольных колебаний изгибными, причем процесс имеет характер биений, поскольку нет точного выполнения условия (15). При этом огибающая для изгибных форм меняется в противофазе с огибающей продольных колебаний, происходит перекачка энергии от изгиба к продольным деформациям и наоборот.

ВЫВОДЫ

Частота продольных колебаний зависит только от физических и геометрических свойств стержня и не зависит от нелинейных слагаемых.

Частоты изгибных колебаний зависят от величины средней по длине стержня продольной силы. При внезапном нагреве стержня эти частоты будут уменьшаться.

В случае достижения средней по величине продольной силы критического значения (квадрат собственной частоты становится отрицательным) нулевое положение равновесия становится неустойчивым. Учет нелинейных слагаемых показывает, что в этом случае появляются новые ненулевые устойчивые положения равновесия. Таких положений равновесия всего два, они пропорциональны первой изгибной собственной форме.

При наличии ненулевых начальных условий по изгибу возникают изгибные колебания с частотами, близкими к собственным изгибным частотам с учетом влияния средней составляющей продольной силы.

В процессе этих колебаний возможен обмен энергией между различными изгибными формами, процесс приобретает вид биений.

В средней составляющей продольной силы при этом появляется дополнительная растягивающая сила, зависящая от квадратов амплитуд изгибных колебаний, а также колебательная составляющая с удвоенными изгибными частотами.

В случае, когда комбинационная частота – сумма двух соседних изгибных частот – близка к собственной частоте продольных колебаний, даже при нулевых начальных условиях по продольным перемещениям возможно появление продольных колебаний с комбинационной частотой, причем этот процесс также имеет вид биений.

Список литературы

Dolleman R.J. Opto-thermally Excited Multimode Parametric Resonance in Graphene Membranes // Nature Scientific Reports. 2018. № 8.
Yang T., Bellouard Y. Laser-Induced Transition between Nonlinear and Linear Resonant Behaviors of a Micromechanical Oscillator // Physical Review Applied. 2017. № 7.
Zehnder A.T. et al. Locking of electrostatically coupled thermo-optically driven MEMS limit cycle oscillators // Intern. J. Non-Linear Mechanics. 2018. № 102. P. 92–100.
Морозов Н.Ф., Товстик П.Е. О динамической потере устойчивости стержня при продольной нагрузке, меньшей эйлеровой // ДАН. 2013. Т. 453. № 3. С. 282–285.
Беляев А.К., Морозов Н.Ф., Товстик П.Е., Товстик Т.П. Параметрические резонансы в задаче о продольном ударе по тонкому стержню // Вестник СПб ун-та. Сер. 1. 2016.
Морозов Н.Ф., Индейцев Д.А., Лукин А.В., Попов И.А., Привалова О.В., Штукин Л.В. Динамика и устойчивость электростатического преобразователя под действием теплового импульса // Известия вузов. Северо-Кавказский регион. Технические науки. 2018. Т. 197. № 2.
Morozov N.F., Indeitsev D.A., Lukin A.V., Popov I.A., Privalova O.V., Shtukin L.V. Stability of the Bernoulli–Euler Beam in Coupled Electric and Thermal Fields // Doklady Physics. 2018. V. 63. № 8. P. 342–347.
Морозов Н.Ф., Индейцев Д.А., Лукин А.В., Попов И.А., Привалова О.В., Штукин Л.В. Устойчивость балки Бернулли–Эйлера под действием движущегося теплового источника // Доклады РАН. Физика, технические науки. 2020. Т. 490. С. 73–78.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал