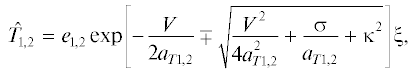Доклады Российской академии наук. Физика, технические науки, 2020, T. 494, № 1, стр. 64-68

СРАВНИТЕЛЬНЫЙ АНАЛИЗ ВОЗНИКНОВЕНИЯ ПЕРЕГРЕВА ВОДЫ И НЕУСТОЙЧИВОСТИ ФРОНТА КИПЕНИЯ В ПОРИСТОЙ СРЕДЕ

Г. Г. Цыпкин^1, *, А. Т. Ильичев^2, **

¹ Институт проблем механики им. А.Ю. Ишлинского Российской академии наук
Москва, Россия

² Математический институт им. В.А. Стеклова Российской академии наук
Москва, Россия

^* E-mail: tsypkin@ipmnet.ru
^** E-mail: ilichev@mi.ras.ru

Поступила в редакцию 10.06.2020
После доработки 17.06.2020
Принята к публикации 19.06.2020

DOI: 10.31857/S2686740020050156

Полный текст (PDF)

Аннотация

Методом нормальных мод проведено исследование устойчивости фронта кипения, распространяющегося с постоянной скоростью в геотермальном резервуаре. На плоскости параметров определены области, соответствующие неустойчивости и перегреву воды в области перед фронтом. Найдено, что неустойчивости фронта фазового перехода всегда предшествует переход воды перед фронтом в метастабильное состояние.

Ключевые слова: пористая среда, испарение, поверхность разрыва, перегрев воды, неустойчивость

1. Известно, что неустойчивость поверхностей раздела при фильтрации жидкостей и газов может быть различной природы и инициироваться, например, силой тяжести или различием вязкостей жидкостей, расположенных по разные стороны от поверхности раздела [1]. Существует также механизм дестабилизации, связанный с переходом фазы перед фронтом фазового перехода в метастабильное состояние, которое может быть состоянием переохлаждения или перегрева. Впервые на возможность переохлаждения жидкой фазы перед фронтом кристаллизации бинарного расплава было указано в работе [2]. В [3] аналитически показано, что неустойчивость фронта кристаллизации, называемая морфологической, может наступать без переохлаждения расплава, а переохлаждение расплава может достигаться при сохранении устойчивости фронта.

Неустойчивость фронта при кипении в пористой среде была обнаружена экспериментально [4]. Эта неустойчивость инициирует образование пальцев, также как неустойчивость бинарного расплава приводит к формированию дендритов. При математическом моделировании распространения фронта фазового перехода вода–пар в геотермальных системах, были найдены режимы фильтрации как с перегревом воды, так и с переохлаждением пара [5, 6]. В работе [7] исследовалась устойчивость фронта кипения, движущегося с постоянной скоростью. Были сделаны выводы, качественно согласующиеся с выводами работы [3], что переход к неустойчивости может происходить как при наличии перегрева воды перед фронтом, так и без перегрева.

В настоящей работе, следуя [7], изучается устойчивость в более общем случае, когда учитывается влияние малых возмущений температуры в области пара за фронтом. Найдено, что переход воды в области перед фронтом в метастабильное перегретое состояние всегда предшествует переходу к неустойчивому режиму, что является качественным отличием от выводов, сделанных в работах [3, 7]. Делаются предположения о структуре течений при значениях параметрах, соответствующих режимам перегрева воды и неустойчивости фронта.

2. Рассмотрим водонасыщенный одномерный полубесконечный геотермальный пласт с начальной температурой ${{T}_{0}}$ и давлением ${{P}_{0}}$. При падении давления в точке $x = 0$ ниже давления кипения формируется область пара. Такой процесс может быть вызван как природными процессами, так и эксплуатацией геотермальных резервуаров. Было показано, что в низкопроницаемых породах образуется резкий фронт фазового перехода [6], разделяющий области воды и пара.

Системы уравнений в обеих областях следуют из законов сохранения и уравнений состояния при условии термодинамического равновесия [6]:

(1)

$\phi \frac{{\partial {{\rho }_{j}}}}{{\partial t}} + {\text{div}}{{\rho }_{j}}{{{\mathbf{v}}}_{j}} = 0,\quad {{{\mathbf{v}}}_{j}} = - \frac{k}{{{{\mu }_{j}}}}{\text{grad}}\;P,$

$\frac{{\partial T}}{{\partial t}} + \frac{{{{\rho }_{j}}{{C}_{j}}}}{{{{{(\rho C)}}_{{1,2}}}}}{{{\mathbf{v}}}_{j}} \cdot {\text{grad}}\;T = {{a}_{{T1,2}}}\Delta T,\quad {{a}_{{T1,2}}} = \frac{{{{\lambda }_{{1,2}}}}}{{{{{(\rho C)}}_{{1,2}}}}},$

$\begin{gathered} {{\lambda }_{{1,2}}} = m{{\lambda }_{j}} + (1 - m){{\lambda }_{s}}, \\ {{(\rho C)}_{{1,2}}} = m{{\rho }_{j}}{{C}_{j}} + (1 - m){{\rho }_{s}}{{C}_{s}}, \\ \end{gathered} $

${{\rho }_{w}} = {{\rho }_{{w0}}}[1 + {{\alpha }_{w}}(P - {{P}_{0}})],\quad P = {{\rho }_{{v}}}RT,\quad j = {v},w.$

Здесь $\phi $ – пористость, k – проницаемость, $\mu $ – вязкость, ${{\alpha }_{w}}$ – сжимаемость воды, $\rho $ – плотность, ${\mathbf{v}}$ – вектор скорости фильтрации, $R$ – газовая постоянная, C – удельная теплоемкость, $\lambda $ – теплопроводность. Индексы: $w$, ${v}$, $s$ – вода, пар и скелет пористой среды, 1 и 2 – области воды и пара.

Условия на поверхности фазового перехода представляют собой условия баланса массы, энергии, импульса и уравнение Клаузиуса–Клапейрона термодинамического равновесия воды и пара на фронте кипения:

(2)

$\begin{gathered} \phi \left( {1 - \frac{{{{P}_{ * }}}}{{{{\rho }_{w}}R{{T}_{ * }}}}} \right){{V}_{n}} = \\ = \frac{{k{{P}_{ * }}}}{{{{\mu }_{{v}}}{{\rho }_{w}}R{{T}_{ * }}}}{{({\text{grad}}\;P)}_{{n - }}} - \frac{k}{{{{\mu }_{w}}}}{{({\text{grad}}\;P)}_{{n + }}}, \\ \end{gathered} $

(3)

$\phi q{{\rho }_{w}}{{V}_{n}} = {{\lambda }_{1}}{{({\text{grad}}\;T)}_{{n + }}} - \frac{{kq{{\rho }_{w}}}}{{{{\mu }_{w}}}}{{({\text{grad}}\;P)}_{{n + }}},$

(4)

${{T}_{ + }} = {{T}_{ - }} = {{T}_{ * }},\quad {{P}_{ + }} = {{P}_{ - }} = {{P}_{ * }},$

(5)

${{P}_{ * }} = f({{T}_{ * }}) \equiv {{P}_{a}}exp\left( {A + \frac{B}{{{{T}_{ * }}}}} \right),$

$A = 12.512,\quad B = - 4611.73,\quad {{P}_{a}} = {{10}^{5}}\;{\text{Па}}{\text{.}}$

Здесь $V$ – скорость фронта, $q$ – теплота фазового превращения. Индексы: $n$ – нормаль, $ * $ – величины на фронте, плюс и минус – значения на фронте справа и слева, соответственно.

Было показано [8], что при малых проницаемостях конвективным переносом тепла можно пренебречь. Если изменения давления в области пара меньше характерного давления $P$, а в области воды $P{{\alpha }_{w}} \ll 1$, то система (1) в обеих областях упрощается:

(6)

$\begin{gathered} \frac{{\partial P}}{{\partial t}} = {{a}_{{P1,2}}}\Delta P,\quad \frac{{\partial T}}{{\partial t}} = {{a}_{{T1,2}}}\Delta T, \\ {{a}_{{P1}}} = \frac{k}{{\phi {{\alpha }_{w}}{{\mu }_{w}}}},\quad {{a}_{{P2}}} = \frac{{k{{P}_{0}}}}{{\phi {{\mu }_{{v}}}}}. \\ \end{gathered} $

В области пара для невозмущенного состояния справедливо уравнение Лапласа для давления, поскольку выполняется условие квазистационарности [6]. Это условие соответствует медленному движению фронта по сравнению со скоростью перераспределения давления.

Оценки показывают, что в области за фронтом можно пренебречь охлаждением пара вследствие его расширения [6]. Тогда температура пара постоянна и на выходе в точке x = 0 равна температуре на фронте ${{T}_{ * }}$. Если поддерживать постоянным градиент давления за фронтом, понижая давление в точке x = 0, то фронт будет двигаться с постоянной скоростью и распределение давления в области пара определяется соотношением

(7)

${{P}_{{2st}}} = {{P}_{ * }} + \nabla {{P}_{ - }}\xi ,\quad \xi = x - Vt.$

В области перед фронтом решения имеют вид [7]

(8)

$\begin{gathered} {{P}_{{1st}}} = ({{P}_{ * }} - {{P}_{0}})exp\left( { - \frac{V}{{{{a}_{{P1}}}}}} \right)\xi + {{P}_{0}}, \\ {{T}_{{1st}}} = ({{T}_{ * }} - {{T}_{0}})exp\left( { - \frac{V}{{{{a}_{{T1}}}}}} \right)\xi + {{T}_{0}}. \\ \end{gathered} $

Подставляя решения (8) в уравнение баланса энергии на поверхности раздела (3), получаем

(9)

$1\, - \,\frac{{{{a}_{{P0}}}}}{{{{a}_{{P1}}}}}\left( {\frac{{{{P}_{ * }}}}{{{{P}_{0}}}}\, - \,1} \right)\, + \,\frac{{{{T}_{0}}{{{(\rho C)}}_{1}}}}{{\phi q{{\rho }_{w}}}}\left( {\frac{{{{T}_{ * }}}}{{{{T}_{0}}}}\, - \,1} \right) = 0,\quad {{a}_{{P0}}}\, = \,\frac{{k{{P}_{0}}}}{{\phi {{\mu }_{w}}}}.$

Из (5) и (9) определяем ${{P}_{ * }}$ и ${{T}_{ * }}$. Скорость V находится при подстановке (7) и (8) в соотношение баланса массы (3) и заданном градиенте давления $\nabla {{P}_{ - }}$:

$\begin{gathered} \tfrac{{{{a}_{{P2}}}\nabla {{P}_{ - }}}}{{{{P}_{0}}V}} = \tfrac{{{{\rho }_{w}}R{{T}_{0}}}}{{{{P}_{0}}}}\tfrac{{{{T}_{ * }}{\text{/}}{{T}_{0}}}}{{{{P}_{ * }}{\text{/}}{{P}_{0}}}} - \\ - \;\tfrac{{{{a}_{{P0}}}}}{{{{a}_{{P1}}}}}\tfrac{{{{\rho }_{w}}R{{T}_{0}}}}{{{{P}_{0}}}}\tfrac{{{{T}_{ * }}{\text{/}}{{T}_{0}}}}{{{{P}_{ * }}{\text{/}}{{P}_{0}}}}\left( {\tfrac{{{{P}_{ * }}}}{{{{P}_{0}}}} - 1} \right) - 1. \\ \end{gathered} $

Вода перед фронтом перегрета, если ее температура выше температуры кипения, найденной по распределению давления перед фронтом (8) из соотношения (5). Условие перегрева имеет вид

$0 > 1 - \tfrac{{{{T}_{0}}}}{{{{T}_{ * }}}} + \tfrac{{{{T}_{ * }}}}{B}\tfrac{{{{a}_{{T1}}}}}{{{{a}_{{P1}}}}}\left( {1 - \tfrac{{{{P}_{0}}}}{{{{P}_{ * }}}}} \right).$

3. Устойчивость решения в виде бегущей волны исследуем методом нормальных мод. Пусть ${{P}_{i}}\, = \,{{P}_{i}}(\xi ,z,t)\, = \,{{P}_{{ist}}}\, + \,\delta {{P}_{i}}$, i = 1, 2, T_i= ${{T}_{i}}(\xi ,z,t) = {{T}_{{ist}}}$ + + δT_i, $\eta = \eta (z,t)$ – возмущение плоского фронта ξ = 0. Будем искать возмущения в виде:

$\begin{gathered} \delta {{P}_{{1,2}}} = \hat {P}_{{_{{1,2}}}}^{{}}(\xi )exp({\text{i}}\kappa z + \sigma t),\,\,\, \hfill \\ \delta {{T}_{{1,2}}} = {{{\hat {T}}}_{{1,2}}}(\xi )exp({\text{i}}\kappa z + \sigma t), \hfill \\ \end{gathered} $

$\eta = \hat {\eta }exp({\text{i}}z + \sigma t),\quad \hat {\eta } = {\text{const}}{\text{.}}$

Представленное выше решение в виде бегущей волны справедливо на больших временах и для исследования поведения малых возмущений за фронтом область 2 можно считать полубесконечной $ - \infty < \xi \leqslant 0$. Для возмущений не выполняется условие квазистационарности и в обеих областях используем нестационарные уравнения (6). Учитывая убывание возмущений на $ + \infty $ и $ - \infty $, имеем

${{\hat {P}}_{{1,2}}} = {{d}_{{1,2}}}exp\left[ { - \frac{V}{{2{{a}_{{P1,2}}}}} \mp \sqrt {\frac{{{{V}^{2}}}}{{4a_{{P1,2}}^{2}}} + \frac{\sigma }{{{{a}_{{P1,2}}}}} + {{\kappa }^{2}}} } \right]\xi ,$

(10)

где ${{d}_{{1,2}}}$, ${{e}_{{1,2}}}$ – постоянные.

Подставляем решения (10) в систему (2)–(5) и оставляя члены первого порядка малости, получаем однородную систему для определения амплитуд ${{d}_{{1,2}}}$, ${{e}_{{1,2}}}$, $\hat {\eta }$. Из условия нетривиальности решения однородной системы следует дисперсионное соотношение

$D(\Sigma ,K) \equiv {{\alpha }_{1}}{{\alpha }_{2}} + {{\alpha }_{3}}{{\alpha }_{4}} = 0,$

${{\alpha }_{1}} = \tfrac{{df{\text{/}}{{P}_{0}}}}{{dT{\text{/}}{{T}_{0}}}}\tfrac{{\phi {{\rho }_{w}}q}}{{{{\lambda }_{1}}{{T}_{0}}}}{{a}_{{T1}}}{{\Gamma }_{1}} - \tfrac{{{{a}_{{T1}}}}}{{{{a}_{{P0}}}}}{{\Gamma }_{0}},$

$\begin{gathered} {{\alpha }_{2}} = \Sigma + \tfrac{{{{a}_{{P0}}}{{a}_{{T1}}}}}{{a_{{P1}}^{2}}}\left( {\tfrac{{{{P}_{ * }}}}{{{{P}_{0}}}} - 1} \right) + \\ + \;\tfrac{{{{a}_{{P2}}}}}{{{{a}_{{T1}}}}}\tfrac{{{{\rho }_{v}}}}{{{{\rho }_{w}}}}\left[ {\tfrac{{{{a}_{{T1}}}}}{{{{a}_{{P1}}}}}\left( {\tfrac{{{{P}_{ * }}}}{{{{P}_{0}}}} - 1} \right) + \tfrac{{{{a}_{{T1}}}}}{V}\tfrac{{\nabla {{P}_{ - }}}}{{{{P}_{0}}}}} \right]{{\Gamma }_{2}}, \\ {{\alpha }_{3}} = {{\Gamma }_{1}} + \tfrac{{{{\mu }_{w}}}}{{{{\mu }_{{v}}}}}\tfrac{{{{\rho }_{{v}}}}}{{{{\rho }_{w}}}}{{\Gamma }_{2}}, \\ \end{gathered} $

$\begin{gathered} {{\alpha }_{4}} = \tfrac{{df{\text{/}}{{P}_{0}}}}{{dT{\text{/}}{{T}_{0}}}}\left[ {\tfrac{{{{T}_{ * }}}}{{{{T}_{0}}}}} \right. - 1 - \tfrac{{\phi {{\rho }_{w}}q}}{{{{\lambda }_{1}}{{T}_{0}}}}{{a}_{{T1}}}\Sigma - \\ - \;\tfrac{{\phi {{\rho }_{w}}q}}{{{{\lambda }_{1}}{{T}_{0}}}}\tfrac{{{{a}_{{P0}}}a_{{T1}}^{2}}}{{a_{{P1}}^{2}}}\left. {\left( {\tfrac{{{{P}_{ * }}}}{{{{P}_{0}}}} - 1} \right)} \right] + \\ \end{gathered} $

$ + \;\left[ {\tfrac{{df{\text{/}}{{P}_{0}}}}{{dT{\text{/}}{{T}_{0}}}}\left( {1 - \tfrac{{{{T}_{ * }}}}{{{{T}_{0}}}}} \right) + \tfrac{{{{a}_{{T1}}}}}{{{{a}_{{P1}}}}}\left( {\tfrac{{{{P}_{ * }}}}{{{{P}_{0}}}} - 1} \right)} \right]{{\Gamma }_{0}},$

$\Sigma = \frac{{{{a}_{{T1}}}}}{{{{V}^{2}}}}\sigma ,\quad K = \frac{{{{a}_{{T1}}}}}{V}\kappa ,\quad {{\Gamma }_{0}} = \frac{1}{2} + \sqrt {\frac{1}{4} + \Sigma + {{K}^{2}}} ,$

$\begin{gathered} {{\Gamma }_{1}} = \frac{{{{a}_{{T1}}}}}{{2{{a}_{{P1}}}}} + \sqrt {\frac{{a_{{T1}}^{2}}}{{4a_{{P1}}^{2}}} + \frac{{{{a}_{{T1}}}}}{{{{a}_{{P1}}}}}\Sigma + {{K}^{2}}} , \\ {{\Gamma }_{2}} = - \frac{{{{a}_{{T1}}}}}{{2{{a}_{{P2}}}}} + \sqrt {\frac{{a_{{T1}}^{2}}}{{4a_{{P2}}^{2}}} + \frac{{{{a}_{{T1}}}}}{{{{a}_{{P2}}}}}\Sigma + {{K}^{2}}} . \\ \end{gathered} $

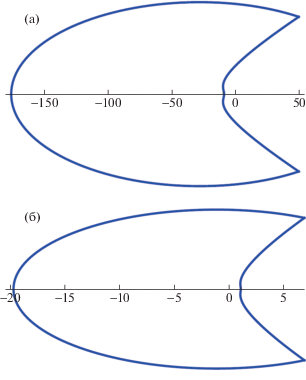
4. Следуя [8], применим принцип аргумента для исследования корней дисперсионного уравнения $D(\Sigma ,K) = 0$. На комплексной плоскости $\Sigma $ при фиксированном K определялись условия наличия корней уравнения в правой полуплоскости, соответствующие неустойчивости физической системы. На комплексной плоскости $D$ представлены образы замкнутого контура на комплексной плоскости $\Sigma $ (рис. 1), соответствующие случаям устойчивости и неустойчивости.

Рис. 1.

Образ замкнутого контура на комплексной плоскости (${\text{Re}}D(\Sigma ,{{K}_{0}}),{\text{Im}}D(\Sigma ,{{K}_{0}})$). $\phi = 0.05$, P₀ = = $3 \times {{10}^{7}}$ Па, ${{T}_{0}} = 500$ K, ${{K}_{0}} = 2$, (а) $k = {{10}^{{ - 18}}}$ м². Отсутствие корней $\Sigma $ в правой полуплоскости соответствует устойчивому режиму. (б) $k = {{10}^{{ - 17}}}$ м$^{2}$. Наличие корня $\Sigma $ в правой полуплоскости в случае неустойчивости фронта.

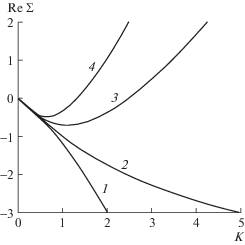
Расчеты дисперсионных кривых показывают (рис. 2), что переход к неустойчивости происходит при бесконечно большом волновом числе, соответствующем бесконечно малому линейному масштабу длины. Закон Дарси применим для сред, когда характерный масштаб задачи больше размера частиц (~10^–3 м) матрицы пористой среды. Следовательно, применение закона Дарси корректно для $K \leqslant {{10}^{2}}$. Возможное модифицированное уравнение фильтрации, учитывающее развитие возмущений на малых масштабах, требуется только для уточнения критического значения проницаемости ${{k}_{{{\text{cr}}}}}$ в узком диапазоне $0.4 \times {{10}^{{ - 17}}} < {{k}_{{{\text{cr}}}}} < 0.41 \times {{10}^{{ - 17}}}$.

Рис. 2.

Дисперсионные кривые. $\phi = 0.05$, ${{P}_{0}} = 3 \times $ $ \times {{10}^{7}}$ Па, ${{T}_{0}} = 500$ K. Кривые 1–4: $k = 3,\;4,\;5,\;6 \times $ $ \times {{10}^{{ - 18}}}$ м².

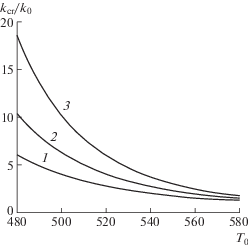
Численные эксперименты показали, что устойчивость фронта и возникновение перегрева воды определяется, главным образом, проницаемостью, пористостью, начальными температурой и давлением. На плоскости (T₀, $k{\text{/}}{{k}_{0}}$) (рис. 3) представлена критическая диаграмма, на которой область устойчивости расположена под кривыми. При увеличении пористости растет количество поглощаемого тепла при кипении и температура на фронте уменьшается. Соответственно, увеличивается градиент температуры, который оказывает стабилизирующее воздействие.

Рис. 3.

Кривые нейтральной устойчивости. Область устойчивости расположена под кривыми. ${{P}_{0}} = 3 \times $ $ \times {{10}^{7}}$ Па, ${{k}_{0}} = {{10}^{{ - 18}}}$ м². Кривые 1–3: $\phi = 0.05,\;0.1,\;0.15$.

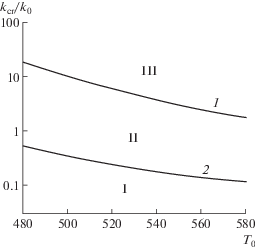
На рис. 4 представлены критические кривые устойчивости (кривая 1) и перегрева воды (кривая 2). В области I реализуется фронтовой режим кипения, который адекватно описывается представленной математической моделью. При увеличении температуры или проницаемости вода переходит в перегретое состояние, а фронт остается устойчивым (область II). Естественно предположить, что этот режим соответствует кипению воды в объеме перед фронтом с образованием пузырей пара. Объемная доля, занимаемая пузырями, мала, они являются изолированными друг от друга и двигаются вместе с жидкой фазой. Для описания этого режима модель должна быть усложнена и включать описание трех областей с различным фазовым составом.

Рис. 4.

Критические кривые. ${{k}_{0}} = {{10}^{{ - 18}}}$ м², $\phi = 0.15$, ${{P}_{0}} = 3 \times {{10}^{7}}$ Па. В области I перегрев воды отсутствует, поверхность фазового перехода устойчива. В области II – устойчивость при наличии перегрева воды перед фронтом. В области III – неустойчивость с перегревом воды.

При параметрах, соответствующих неустойчивости фронта и перегреву (область III), можно предполагать реализацию сценария, когда вместо фронта образуется область кипения смеси пар–вода. В этой области часть поровых каналов заполнена водой, часть – паром и допускается переток как воды, так и пара. Перед этой областью возможно также существование области с пузырями пара. Здесь уже для адекватного описания потребуется вводить четыре области различного состояния H₂O.

Учет распространения малых возмущений в области пара привел к качественному изменению в результатах по исследованию устойчивости и перегреву воды перед фронтом. Критерии, полученные в [3] для задачи кристаллизации бинарного расплава и в [7] для фронта кипения воды, в пористой среде допускают существование области неустойчивости фронта без возникновения метастабильного состояния фазы перед фронтом, а критические кривые пересекаются. В настоящей работе получено, что критические кривые перегрева воды и кривые нейтральной устойчивости не пересекаются, а переходу к неустойчивости всегда предшествует возникновение метастабильного состояния фазы перед фронтом.

Список литературы

Drazin P.G. Introduction to Hydrodynamic stability. Cambridge: Cambridge University Press, 2002.
Иванцов Г.П. // ДАН СССР. 1951. Т. 81. № 2. С. 179–181.
Mullins W.W., Sekerka R.F. // J. Appl. Phys. 1964. V. 35. № 2. P. 444–451.
Fitzgerald S.D., Woods A.W. // Nature. 1994. V. 367. P. 450–453.
Бармин А.А., Цыпкин Г.Г. // ДАН. 1996. Т. 350. № 2. 195–197.
Tsypkin G.G., Woods A.W. // J. Fluid Mech. 2004. V. 506. P. 315–330.
Ильичев А.Т., Цыпкин Г.Г. // Изв. РАН. МЖГ. 2016. № 6. С. 64–70.
Tsypkin G.G. Il’ichev A.T. // Transport in porous media. 2004. V. 55. P. 183–199.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал