1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Физика, технические науки
  4. T. 494, № 1, 2020

Доклады Российской академии наук. Физика, технические науки, 2020, T. 494, № 1, стр. 51-56

МОДЕЛЬ МИКРОМЕХАНИЧЕСКОГО АКСЕЛЕРОМЕТРА, ОСНОВАННОГО НА ЯВЛЕНИИ МОДАЛЬНОЙ ЛОКАЛИЗАЦИИ

Академик РАН Н. Ф. Морозов 1, 2, *, член-корреспондент РАН Д. А. Индейцев 2, 3, В. С. Игумнова 3, Я. В. Беляев 4, А. В. Лукин 3, **, И. А. Попов 3, Л. В. Штукин 2, 3

1 Санкт-Петербургский государственный университет
Санкт-Петербург, Россия

2 Институт проблем машиноведения Российской академии наук
Санкт-Петербург, Россия

3 Санкт-Петербургский политехнический университет
Санкт-Петербург, Россия

4 АО “Концерн “ЦНИИ “Электроприбор”
Санкт-Петербург, Россия

* E-mail: n.morozov@spbu.ru
** E-mail: lukin_av@spbstu.ru

Поступила в редакцию 13.07.2020
После доработки 13.07.2020
Принята к публикации 14.07.2020

Полный текст (PDF)

Аннотация

Предложена модель микроэлектромеханического акселерометра с двумя подвижными балочными элементами, расположенными между двумя неподвижными электродами. Действие переносных сил инерции в продольном направлении приводит к изменению спектральных свойств системы, что является полезным выходным сигналом датчика. Динамика системы при наличии слабой электростатической связи между чувствительными элементами характеризуется явлением модальной локализации – значительным изменением амплитудных соотношений для форм синфазных и противофазных колебаний при малых изменениях измеряемой компоненты вектора ускорения объекта. Показано, что чувствительность датчика, основанного на модальной локализации, может на порядки превосходить чувствительность известных систем, основанных на измерении сдвига собственных частот.

Ключевые слова: МЭМС, акселерометр, слабосвязанные системы, модальная локализация

ВВЕДЕНИЕ

Классическая схема микромеханического акселерометра представляет собой инерционную массу, характеризуемую одной степенью свободы, на упругом подвесе [1]. При наличии переносного ускорения инерционная масса квазистатически смещается, что приводит к изменению емкости гребенчатой или плоскопараллельной электродной структуры и появлению полезного сигнала в электрической цепи. Хорошо известны схемы работы микромеханических акселерометров в режиме открытого контура [2] и в компенсационном режиме [3, 4].

Современным направлением развития в области микромеханических акселерометров является создание резонансных датчиков [5]. В отличие от квазистатических схем, в резонансном акселерометре чувствительный элемент совершает гармонические колебания на одной из собственных частот. Переносные силы инерции приводят к изменению спектральных свойств упругой системы (смещению резонансных частот), что и является выходным сигналом датчика. Применение дифференциальных схем с частотным выходом позволяет достигать высокой температурной стабильности и вибрационной устойчивости системы [6, 7].

В последние годы интенсивное развитие получило новое поколение микромеханических резонаторов. Новый класс приборов основан на использовании явления модальной локализации в слабосвязанных системах [8–10]. Способность систем со многими степенями свободы локализовывать энергию колебаний в отдельных своих элементах хорошо известна в механике [11, 12] и физике [13]. Полезным сигналом в датчиках такого типа является изменение в отношении компонент собственного вектора, соответствующего рабочей форме колебаний, при действии внешнего возмущения [14, 15].

1. ПОСТАНОВКА ЗАДАЧИ

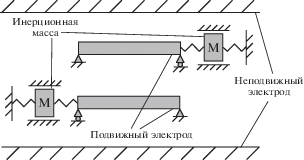
В настоящей работе предлагается новая модель акселерометра, состоящего из двух проводящих балочных упругих элементов, расположенных между двумя неподвижными электродами (рис. 1). К каждой из балок на податливой пружине присоединена инерционная масса.

Рис. 1.

Схема акселерометра.

При возникновении продольного ускорения в системе инерционные массы приходят в движение, что, в свою очередь, создает продольную сжимающую силу для одного резонатора и растягивающую силу для другого резонатора. Действие переносных сил инерции в продольном направлении приводит к изменению спектральных свойств системы. Как показано далее, при наличии слабой электростатической связи между чувствительными элементами динамика системы характеризуется явлением модальной локализации – значительным изменением амплитудных соотношений для форм синфазных и противофазных колебаний при малых изменениях измеряемой компоненты вектора ускорения объекта.

Уравнения движения первой и второй инерционных масс (ИМ) имеют вид:

$ - M{{\ddot {y}}_{1}} - c{{y}_{1}} - c\left( {{{y}_{1}} - {{u}_{1}}\left( l \right)} \right) - MW = 0,$
$M{{\ddot {y}}_{2}} + c{{y}_{2}} + c\left( {{{y}_{2}} - {{u}_{2}}\left( l \right)} \right) - MW = 0,$
где y1, y2 – продольное перемещение первой и второй ИМ соответственно, M – масса, c – жесткость пружины, W – ускорение корпуса, u1(l), u2(l) – смещение конца первого и второго балочного элемента.

Пренебрегая относительным ускорением, получим закон движения первой и второй ИМ соответственно:

${{y}_{1}} = \frac{1}{{2c}}\left( {c{{u}_{1}}\left( l \right) - MW} \right),\quad {{y}_{2}} = \frac{1}{{2c}}\left( {c{{u}_{2}}\left( l \right) + MW} \right).$

Уравнение продольных смещений и граничные условия имеют вид

$ES\left( {u{\kern 1pt} ''\, + \left( {\frac{1}{2}w{\kern 1pt} {{'}^{2}}} \right)} \right) = 0,$
$u\left( 0 \right) = 0,\quad N\left( l \right) = c\left[ {u\left( l \right) - y} \right],$
где u – продольное перемещение сечения балки, $w$ – поперечное перемещение, E – модуль Юнга, S – площадь поперечного сечения. Слагаемое $\frac{1}{2}w{\kern 1pt} {{'}^{2}}$ связано с упругой восстанавливающей силой, N(l) – продольная сила в концевом сечении. Собственные силы инерции балки в осевом направлении не учитываем, поэтому продольная сила постоянна по всей длине балки.

Выражения для продольных сил N1 и N2 будут иметь вид

$\begin{gathered} {{N}_{1}} = \frac{1}{2}\left[ {MW - \frac{1}{2}c\mathop \smallint \limits_0^l w_{1}^{{'2}}dx} \right], \\ {{N}_{2}} = \frac{1}{2}\left[ { - MW - \frac{1}{2}c\mathop \smallint \limits_0^l w_{2}^{{'2}}dx} \right]. \\ \end{gathered} $

Подставляя выражения для N1 и N2 в уравнение изгибных колебаний с учетом электростатических сил в межэлектродных зазорах, получим

$\begin{gathered} EIw_{1}^{{''''}} + {{c}_{d}}{{{\dot {w}}}_{1}} + \left[ {\frac{1}{2}MW - \frac{1}{4}c\int\limits_0^l {w_{1}^{{'2}}dx} } \right]w_{1}^{{''}} + \\ \, + \rho S{{{\ddot {w}}}_{1}} - \frac{1}{2}\frac{{{{\varepsilon }_{0}}b{{V}^{2}}}}{{{{{(d - {{w}_{1}})}}^{2}}}} + \frac{1}{2}\frac{{{{\varepsilon }_{0}}b\Delta {{V}^{2}}}}{{{{{(d + {{w}_{1}} - {{w}_{2}})}}^{2}}}} = 0, \\ \end{gathered} $
$\begin{gathered} EIw_{2}^{{''''}} + {{c}_{d}}{{{\dot {w}}}_{2}} + \left[ { - \frac{1}{2}MW - \frac{1}{4}c\int\limits_0^l {w_{1}^{{'2}}dx} } \right]w_{2}^{{''}} + \\ \, + \rho S{{{\ddot {w}}}_{2}} + \frac{1}{2}\frac{{{{\varepsilon }_{0}}b{{V}^{2}}}}{{{{{(d + {{w}_{1}})}}^{2}}}} - \frac{1}{2}\frac{{{{\varepsilon }_{0}}b\Delta {{V}^{2}}}}{{{{{(d + {{w}_{1}} - {{w}_{2}})}}^{2}}}} = 0, \\ \end{gathered} $
где ε0 – диэлектрическая постоянная, b – ширина балки, V – напряжение между неподвижным электродом и балкой, ΔV – напряжение между двумя балочными элементами, S – площадь поперечного сечения.

Вводим безразмерные параметры:

$\begin{gathered} {{C}_{{non}}} = \frac{{12{{c}_{d}}{{l}^{4}}}}{{ETb{{h}^{3}}}},\quad {{C}_{{sp}}} = \frac{{3c{{d}^{2}}l}}{{Eb{{h}^{3}}}}, \\ {{P}_{{non}}} = \frac{{6MW{{l}^{2}}}}{{Eb{{h}^{3}}}},\quad \alpha = \frac{{6{{\varepsilon }_{0}}{{l}^{4}}}}{{E{{h}^{3}}{{d}^{3}}}}, \\ \end{gathered} $
$\begin{gathered} {{w}_{1}} = {{{\tilde {w}}}_{1}}d,\quad {{w}_{2}} = {{{\tilde {w}}}_{2}}d,\quad x = \tilde {x}l, \\ t = \tilde {t}T,\quad T = \sqrt {\frac{{\rho S{{l}^{4}}}}{{EI}}} . \\ \end{gathered} $

Опуская знак ∼, получим систему уравнений в безразмерном виде:

(1)
$\begin{array}{*{20}{c}} \begin{gathered} w_{1}^{{''''}} + {{C}_{{non}}}{{{\dot {w}}}_{1}} + {{{\ddot {w}}}_{1}} + \left[ {{{P}_{{non}}} - {{C}_{{sp}}}\mathop \smallint \limits_0^1 w_{1}^{{'2}}dx} \right]w_{1}^{{''}} - \\ - \,\frac{{\alpha {{V}^{2}}}}{{{{{(1 - {{w}_{1}})}}^{2}}}} + \frac{{\alpha \Delta {{V}^{2}}}}{{{{{(1 + {{w}_{1}} - {{w}_{2}})}}^{2}}}} = 0,{\text{\;}} \\ \end{gathered} \\ \begin{gathered} w_{2}^{{''''}} + {{C}_{{non}}}{{{\dot {w}}}_{2}} + {{{\ddot {w}}}_{2}} + \left[ { - {{P}_{{non}}} - {{C}_{{sp}}}\mathop \smallint \limits_0^1 w_{2}^{{'2}}dx} \right]w_{2}^{{''}} + \\ + \frac{{\alpha {{V}^{2}}}}{{{{{(1 + {{w}_{2}})}}^{2}}}} - \frac{{\alpha \Delta {{V}^{2}}}}{{{{{(1 + {{w}_{1}} - {{w}_{2}})}}^{2}}}} = 0.{\text{\;}} \\ \end{gathered} \end{array}$

2. НАХОЖДЕНИЕ СТАТИЧЕСКИХ ПРОГИБОВ

Исследуем зависимость положений равновесия системы от силы электрического поля. Первое уравнение (1) умножим на знаменатель (1 – w1)2${{(1 + {{w}_{1}} - {{w}_{2}})}^{2}}$, второе уравнение – на (1 + w2)2${{(1 + {{w}_{1}} - {{w}_{2}})}^{2}}$ и применим метод Галеркина в разложении по собственным формам шарнирно опертой балки:

${{w}_{1}}(x,t) = \mathop \sum \limits_{i = 1}^n {{С}_{i}}(t){{\phi }_{i}}(x),\quad {{w}_{2}}(x,t) = \mathop \sum \limits_{i = 1}^n {{D}_{i}}(t){{\phi }_{i}}(x).$

Нелинейные уравнения статики будут иметь вид

$\begin{gathered} \int\limits_0^1 {{{\phi }_{j}}\sum\limits_{i = 1}^n {{{C}_{i}}\phi _{i}^{{''''}}dx + {{P}_{{non}}}\int\limits_0^1 {{{\phi }_{j}}\sum\limits_{i = 1}^n {{{C}_{i}}} } } } \phi _{i}^{{''}}dx - \\ \, - {{C}_{{sp}}}\int\limits_0^1 {\sum\limits_{i = 1}^n {{{C}_{i}}\phi _{i}^{{'2}}dx\int\limits_0^1 {{{\phi }_{j}}\sum\limits_{i = 1}^n {{{C}_{i}}} } } } \phi _{i}^{{''}}dx - \\ \end{gathered} $
(2)
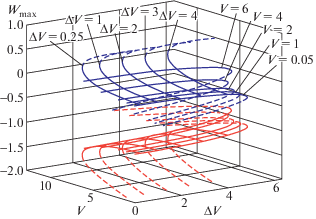
$\begin{gathered} \, - \,\int\limits_0^1 {{{\phi }_{j}}\frac{{\alpha {{V}^{2}}}}{{{{{\left( {1\, - \,\sum\limits_{i = 1}^n {{{C}_{i}}{{\phi }_{i}}} } \right)}}^{2}}}}\, + \,\int\limits_0^1 {{{\phi }_{j}}\frac{{\alpha \Delta {{V}^{2}}}}{{{{{\left( {1\, + \,\sum\limits_{i = 1}^n {{{C}_{i}}{{\phi }_{i}}\, - \,\sum\limits_{i = 1}^n {{{D}_{i}}{{\phi }_{i}}} } } \right)}}^{2}}}}\, = \,0,} } \\ \int\limits_0^1 {{{\phi }_{j}}\sum\limits_{i = 1}^n {{{D}_{i}}\phi _{i}^{{''''}}dx - {{P}_{{non}}}\int\limits_0^1 {{{\phi }_{j}}\sum\limits_{i = 1}^n {{{D}_{i}}} } } } \phi _{i}^{{''}}dx - \\ \end{gathered} $
$\begin{gathered} \, - {{C}_{{sp}}}\int\limits_0^1 {\sum\limits_{i = 1}^n {{{D}_{i}}\phi _{i}^{{'2}}dx\int\limits_0^1 {{{\phi }_{j}}\sum\limits_{i = 1}^n {{{D}_{i}}} } } } \phi _{i}^{{''}}dx + \\ \, + \,\int\limits_0^1 {{{\phi }_{j}}\frac{{\alpha {{V}^{2}}}}{{{{{\left( {1\, - \,\sum\limits_{i = 1}^n {{{D}_{i}}{{\phi }_{i}}} } \right)}}^{2}}}}\, - \,\int\limits_0^1 {{{\phi }_{j}}\frac{{\alpha \Delta {{V}^{2}}}}{{{{{\left( {1\, + \,\sum\limits_{i = 1}^n {{{C}_{i}}{{\phi }_{i}}\, - \,\sum\limits_{i = 1}^n {{{D}_{i}}{{\phi }_{i}}} } } \right)}}^{2}}}}\, = \,0.} } \\ \end{gathered} $

На рис. 2 показаны диаграммы положений равновесия (ПР) в зависимости от разностей потенциалов V и ΔV. Сплошной линией указаны устойчивые ПР, пунктирной линией – неустойчивые.

Рис. 2.

Диаграмма положений равновесия для различных значений V и ΔV. Вверху показан прогиб для верхней балки, внизу – прогиб нижней балки.

3. АНАЛИЗ СПЕКТРАЛЬНЫХ СВОЙСТВ СИСТЕМЫ

Вернемся к системе уравнений (1). Разложим прогибы балочных элементов на статическую и динамическую часть:

$\begin{gathered} {{w}_{1}}(x,t) = {{w}_{{1s}}}(x) + {{w}_{{1d}}}(x,t),~ \\ {{w}_{2}}(x,t) = {{w}_{{2s}}}(x) + {{w}_{{2d}}}(x,t), \\ \end{gathered} $
где w1s(x) и w2s(x) являются результатом решения статической задачи. Получаем уравнения относительно динамической составляющей:

$\begin{gathered} w_{{1d}}^{{''''}} + {{C}_{{non}}}{{{\dot {w}}}_{{1d}}} + {{{\ddot {w}}}_{{1d}}} + \left[ {{{P}_{{non}}} - {{C}_{{sp}}}\int\limits_0^1 {w_{{1d}}^{{'2}}dx} } \right]w_{{1d}}^{{''}} + \\ + \frac{{2\alpha {{V}^{2}}}}{{{{{(1 - {{w}_{{1s}}})}}^{3}}}}{{w}_{{1d}}} + \frac{{2\alpha \Delta {{V}^{2}}}}{{{{{(1 + {{w}_{{1s}}} - {{w}_{{2s}}})}}^{2}}}}({{w}_{{2d}}} - {{w}_{{1d}}}) = 0, \\ \end{gathered} $
$\begin{gathered} w_{{2d}}^{{''''}} + {{C}_{{non}}}{{{\dot {w}}}_{{2d}}} + {{{\ddot {w}}}_{{2d}}} + \left[ { - {{P}_{{non}}} - {{C}_{{sp}}}\int\limits_0^1 {w_{{2d}}^{{'2}}dx} } \right]w_{{2d}}^{{''}} - \\ - \frac{{2\alpha {{V}^{2}}}}{{{{{(1 + {{w}_{{2s}}})}}^{3}}}}{{w}_{{2d}}} - \frac{{2\alpha \Delta {{V}^{2}}}}{{{{{(1 + {{w}_{{1s}}} - {{w}_{{2s}}})}}^{3}}}}({{w}_{{2d}}} - {{w}_{{1d}}}) = 0. \\ \end{gathered} $

Для анализа свободных колебаний также применим метод Галеркина, учитывая лишь нижние формы колебаний двух балок:

${{w}_{{1d}}}(x,t) = {{u}_{1}}(t){{\phi }_{1}}(x),~\quad {{w}_{{2d}}}(x,t) = {{{v}}_{1}}(t){{\phi }_{1}}(x).$

Уравнения движения в матричном виде могут записаны как

(4)
$M\ddot {U} + C\dot {U} + KU = 0,$
где $M = \left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right]$ – матрица масс, $C = \left[ {\begin{array}{*{20}{c}} {{{C}_{{non}}}}&0 \\ 0&{{{C}_{{non}}}} \end{array}} \right]$ – матрица диссипации (в дальнейшем считаем C = 0), $U = \left[ {\begin{array}{*{20}{c}} {{{u}_{1}}} \\ {{{{v}}_{1}}} \end{array}} \right]$ – вектор перемещений,

$K = \left[ {\begin{array}{*{20}{c}} { - {{K}_{2}}{{C}_{{sp}}} + {{K}_{3}}{{V}^{2}} - {{K}_{4}}{\Delta }{{V}^{2}} + {{K}_{1}}{{P}_{{non}}}}&{{{K}_{4}}{\Delta }{{V}^{2}}} \\ {{{K}_{4}}{\Delta }{{V}^{2}}}&{ - {{K}_{5}}{{C}_{{sp}}} - {{K}_{6}}{{V}^{2}} - {{K}_{4}}{\Delta }{{V}^{2}} - {{K}_{1}}{{P}_{{non}}}} \end{array}} \right]$ – матрица жесткостей, коэффициенты матрицы жесткости имеют вид

$\begin{gathered} {{K}_{1}} = \int\limits_0^1 {{{\phi }_{1}}\phi _{1}^{{''}}dx,} \\ {{K}_{2}} = \int\limits_0^1 {w_{{1s}}^{{'2}}dx\int\limits_0^1 {{{\phi }_{1}}\phi _{1}^{{''}}dx} } + 2\int\limits_0^1 {w_{{1s}}^{'}\phi _{1}^{'}dx\int\limits_0^1 {{{\phi }_{1}}w_{{1s}}^{{''}}dx,} } \\ \end{gathered} $
$\begin{gathered} {{K}_{3}} = \int\limits_0^1 {\frac{{2\alpha }}{{{{{({{w}_{{1s}}} - 1)}}^{3}}}}{{\phi }_{1}}{{\phi }_{1}}dx,} \\ {{K}_{4}} = \int\limits_0^1 {\frac{{2\alpha }}{{{{{(1 + {{w}_{{1s}}} - {{w}_{{2s}}})}}^{2}}}}{{\phi }_{1}}{{\phi }_{1}}dx,} \\ \end{gathered} $
${{K}_{5}} = \int\limits_0^1 {w_{{2s}}^{{'{\kern 1pt} 2}}dx\int\limits_0^1 {{{\phi }_{1}}\phi _{1}^{{''}}dx + 2\int\limits_0^1 {w_{{2s}}^{'}\phi _{1}^{'}dx\int\limits_0^1 {{{\phi }_{1}}w_{{2s}}^{{''}}dx,} } } } $
${{K}_{6}} = \int\limits_0^1 {\frac{{2\alpha }}{{{{{({{w}_{{2s}}} + 1)}}^{3}}}}{{\phi }_{1}}{{\phi }_{1}}dx.} $

Собственные частоты ω1,2 и собственные векторы U1,2 системы уравнений (4) зависят от безразмерной переносной силы инерции Pnon. Анализ характера этих зависимостей позволяет оценить чувствительность предлагаемой модели датчика.

Проведем сравнение двух методов измерения: с частотным выходом и с амплитудным выходом. На рис. 3 показана зависимость частоты колебаний и отношения компонент собственных векторов свободных колебаний от внешнего возмущения.

Рис. 3.

Зависимость частоты и отношения амплитуд колебаний от внешнего возмущения Pnon. Цифрой “1” обозначается синфазный режим, а цифрой “2” – антифазный режим. При параметре V = 0.05 В.

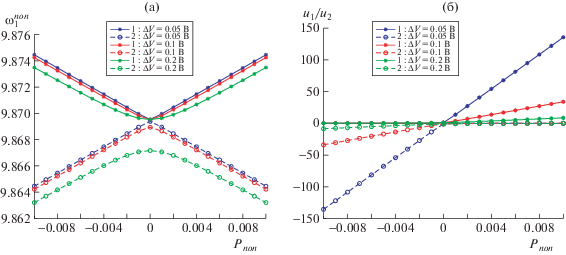
На рис. 3 показана зависимость частоты и отношения компонент собственных векторов свободных колебаний от внешнего возмущения при различных значениях ΔV. Как видно из рисунков, с уменьшением величины слабой связи ΔV зависимость как частотных, так и амплитудных показателей от внешнего ускорения становится более сильной.

Чувствительность датчиков с частотным съемом и с амплитудным съемом можно рассчитать по формулам

${{S}_{\omega }} = \left| {\frac{{{{\omega }_{i}} - \omega _{i}^{0}}}{{\omega _{i}^{0}}}} \right|,\quad {{S}_{a}} = \left| {\frac{{{{u}_{i}} - u_{i}^{0}}}{{u_{i}^{0}}}} \right|,$

где $\omega _{i}^{0}$ и $u_{i}^{0}$ – собственная частота и амплитудное отношение компонент собственного вектора при отсутствии слабой связи, т.е. ΔV = 0, где i = 1, 2 обозначает первый режим (синфазный) и второй режим (антифазный) соответственно. На рис. 4 показаны зависимости параметров Sω и Sa от безразмерной осевой компоненты ускорения Pnon.

Рис. 4.

Чувствительность датчиков, основанных на частотном съеме и на модальной локализации$.$ Цифрой “1” обозначается синфазный режим, цифрой “2” – антифазный режим. При V = 1 В.

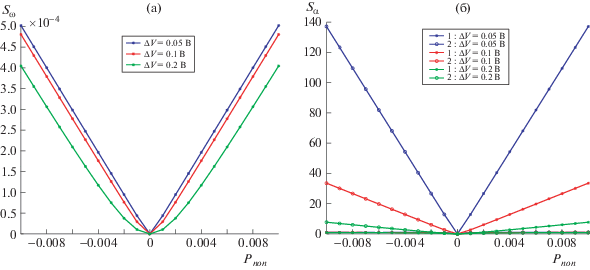
Как видно из рисунков, степень чувствительности акселерометра, использующего принцип локализации колебаний, на несколько порядков выше, чем в датчике с частотным выходом.

ЗАКЛЮЧЕНИЕ

В представленной работе предложена модель микроэлектромеханического акселерометра с двумя подвижными балочными элементами, расположенными между двумя неподвижными электродами. Показано, что чувствительность датчика, основанного на явлении локализации колебаний в слабосвязанных системах, может на порядки превосходить чувствительность системы в режиме измерения сдвига собственных частот. Симметричность предложенной архитектуры датчика обеспечивает также его высокую устойчивость к изменениям окружающей среды (температурным возмущениям, изменениям давления).

Список литературы

  1. Распопов В.Я. Микромеханические приборы. М.: Машиностроение, 2007. 400 с.

  2. Hasani Y. Design and optimization of fully differential capacitive MEMS accelerometer based on surface micromachining // Microsystem Technologies. 2019. V. 25. P. 1369–1377.

  3. Kraft M., et al. A Single-Side Fabricated Triaxis (111)-Silicon Microaccelerometer With Electromechanical Sigma–Delta Modulation // IEEE Sensors J. 2018. V. 18. № 5. March 1, 2018.

  4. Belyaev Y.V., et al. Design of a micromechanical accelerometer. 2018. 25th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), St. Petersburg, 2018. P. 1–7.

  5. Zotov S., et al. High Quality Factor Resonant MEMS Accelerometer with Continuous Thermal Compensation // IEEE Sensors J. 2015. V. 15. № 9, September 2015.

  6. Wang S., et al. A MEMS resonant accelerometer for low-frequency vibration detection. Sensors and Actuators A 283 (2018) P. 151–158.

  7. Shi F., et al. Modeling and Analysis of a Novel Ultrasensitive Differential Resonant Graphene Micro-Accelerometer with Wide Measurement Range. Sensors. 2018. V. 18. P. 2266.

  8. Pierre C. Localization of Vibrations by Structural Irregularity // J. Sound and Vibration. 1987. V. 144. № 3. P. 549–564.

  9. Kraft M. A review on coupled MEMS resonators for sensing applications utilizing mode localization // Sensors and Actuators A. 2016. V. 249. P. 93–111.

  10. Ilyas S., Younis M.I. Theoretical and Experimental Investigation of Mode Localization in Electrostatically and Mechanically Coupled Microbeam Resonators // Intern. J. Non-Linear Mechanics. 2020. https://doi.org/10.1016/j.ijnonlinmec.2020.103516.

  11. Мандельштам Л.И. Лекции по теории колебаний. М.: Наука, 1972.

  12. Банах Л.Я. Методы декомпозиции при исследовании колебаний механических систем. М.: R&C Dynamics, 2016.

  13. Anderson P.W. Absence of diffusion in certain random lattices // Physical Review. 1958. V. 109. P. 1492–1505.

  14. Pandit M., et al. A High Resolution Differential Mode-Localized MEMS Accelerometer // J. Microelectromechanical Systems. 2019. V. 28. № 5. October 2019.

  15. Peng B., et al. A Sensitivity Tunable Accelerometer Based on Series-Parallel Electromechanically Coupled Resonators Using Mode Localization // J. Microelectromechanical Systems. 2020.V. 29. № 1. February 2020.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал